High-Dimensional Modeling of Huanglongbing Dynamics with Time-Varying Impulsive Control

Abstract

This study develops a high-dimensional impulsive differential equation model to analyze Huanglongbing (HLB) transmission dynamics, incorporating seasonal fluctuations in vector psyllid populations and multi-pronged control measures: (1) periodic removal of infected/dead citrus trees to eliminate pathogen reservoirs and (2) non-uniform pesticide applications timed to disrupt psyllid life cycles. The model analytically derives the basic reproduction number ($R_0$) and proves the existence of a unique disease-free periodic solution. Theoretical analysis reveals a threshold-dependent stability: when $R_0<1$, the disease-free solution is globally asymptotically stable, ensuring pathogen extinction; when $R_0>1$, the system becomes uniformly persistent, indicating endemic HLB. Numerical simulations validate these findings and demonstrate that integrated interventions, combining psyllid population control and removal of infected plants, can significantly suppress HLB spread. The results provide a mathematical framework for optimizing intervention timing and intensity, offering actionable strategies for citrus growers.

1. Introduction

Citrus Huanglongbing (HLB), caused by phloem-limited bacteria of the Candidatus Liberibacter genus, represents the most severe economic threat to global citrus production. First documented in China’s Chaoshan region in 1919, the disease manifests through systemic symptoms such as growth stunting, leaf chlorosis, blotchy mottling, and reduced fruit yield, ultimately leading to tree decline within 2–5 years post-infection [1,2,3]. Over the past century, HLB has spread to nearly 50 citrus-producing countries across Asia, Africa, the Americas, and Europe, with epidemiological models suggesting that over 80% of global citrus cultivation areas are now at risk [4,5,6].

The absence of commercially available resistant Citrus cultivars, combined with the pathogen’s irreversible damage to host physiology, renders HLB incurable under current phytosanitary frameworks [7]. Infected orchards typically require eradication to mitigate further spread, exacerbating economic losses [8]. These factors collectively sustain HLB’s status as a critical biosecurity challenge, demanding urgent interdisciplinary solutions to safeguard citrus industries worldwide.

The Asian citrus psyllid (Diaphorina citri), the sole known vector of Huanglongbing (HLB), undergoes incomplete metamorphosis (hemimetabolism), progressing through three distinct life stages: egg, nymph, and adult. Each stage is evolutionarily adapted to specific ecological niches and host-plant interactions, underpinning its efficiency as the primary vector of HLB. Both nymphs and adults acquire Candidatus Liberibacter pathogens during phloem feeding on infected trees, with salivary secretions playing a critical role in pathogen uptake and systemic infection. Notably, individual adult psyllids can achieve transmission efficiencies of up to 80% [9]. Once infected, these psyllids transmit the bacteria to healthy citrus trees during subsequent feeding events, establishing new HLB infections and perpetuating disease spread.

Current HLB management relies on two key strategies: (1) rapid removal of infected trees through PCR-based detection and destruction to eliminate bacterial reservoirs, and (2) coordinated insecticide applications (neonicotinoids, pyrethroids, organophosphates) targeting Diaphorina citri psyllids at critical life stages, achieving 90–95% population reduction when properly timed. Winter and spring are crucial periods for removing infected trees [10,11]. During winter, symptomatic trees are more easily identified due to disease expression, while citrus psyllid activity is relatively low, making it an ideal time to eliminate pathogen reservoirs. In spring, removing infected trees prevents bacterial transmission during the vulnerable new shoot growth phase. Additionally, for year-round psyllid control, targeted pesticide applications should align with key biological and phenological stages: (i) winter orchard cleanup (post-harvest sanitation), (ii) pre-spring budbreak, (iii) summer shoot growth period, (iv) autumn shoot phase, and (v) late-season shoots (winter or late autumn shoots in affected orchards). Therefore, by integrating seasonal tree removal with systematic psyllid management, growers can effectively suppress HLB spread.

Recent research has significantly advanced the understanding of HLB transmission dynamics through epidemiological modeling, particularly using Susceptible-Infected-Removed ($SIR$) frameworks adapted for plant-pathogen systems. Their work has provided substantial theoretical underpinnings for HLB prevention and control efforts. Raphael et al. [12] developed a kind of HLB dynamic model incorporating human intervention, based on compartmental modeling principles. Considering that nymphs aged 1–3 and eggs cannot transmit the HLB pathogen, Jacobsen et al. [3] divided the Asian citrus psyllid into three categories: non-disease-spreading nymphs, infected psyllids, and susceptible psyllids, and established a stage-structured vector-borne epidemic model to thoroughly investigate the potential impact of continuous removal of infected plants on the spread of HLB. The relevant literature [13,14] has also established a compartmental model with stage structure to accurately describe the transmission dynamics of HLB between citrus trees and the Asian citrus psyllid. The research results clearly show that the integrated control strategy of combining pesticide spraying with the removal of HLB-symptomatic trees is the most cost-effective measure.

However, the aforementioned models are all autonomous systems, which assume that control actions are continuous. In practice, HLB control strategies, such as removing infected trees and spraying pesticides to suppress the population of Diaphorina citri, are not implemented continuously [10,11]. In fact, these interventions are usually carried out periodically based on seasonal fluctuations. Therefore, pulse control strategies are more practical and targeted than continuous methods. Wang et al. [15] integrated the discrete nature of agricultural interventions (fixed-time impulses) with vector-borne transmission dynamics, establishing a periodic impulsive control model for HLB. Their work systematically investigated the threshold dynamics of the system, providing critical insights into disease eradication criteria.

Despite these advancements, a critical research gap persists in HLB epidemiological modeling. Current literature lacks comprehensive frameworks that simultaneously incorporate (1) multiple non-uniform pulse removals of infected trees and (2) synchronized psyllid elimination strategies within a single epidemiological cycle. To address this gap, the present study develops an innovative pulsed differential equation model that integrates two key intervention components: (i) time-variable removal of infected citrus trees and (ii) coordinated pesticide applications targeting Diaphorina citri populations. This modeling approach uniquely captures the dynamic interplay between seasonally adaptive tree culling protocols and vector suppression strategies across an entire disease transmission cycle.

2. Model Formulation

In this section, we analyze the impact of the interaction between citrus trees and citrus psyllids on the spread of HLB. The life cycle of citrus psyllids comprises seven non-overlapping phases, which we consolidate into three developmental stages: egg, nymph, and adult. Both nymphs and adults act as vectors for the HLB pathogen, directly threatening citrus plants. To model this dynamic, we classify the psyllid population into three groups: susceptible adult psyllids ($S_v\left(t\right)$, adults infected during the adult stage ($(I_v^a\left(t\right)$), and adults infected during the nymph stage ($(I_v^n\left(t\right)$). Thus, the total psyllid population is given by $N_v\left(t\right)=S_v\left(t\right)+I_v^a\left(t\right)+I_v^n\left(t\right)$. Similarly, citrus trees are categorized as follows: susceptible trees ($S_h\left(t\right)$), infected asymptomatic trees ($I_{h1}\left(t\right)$), and diseased symptomatic trees ($I_{h2}\left(t\right)$), with the total tree population defined as $N_h\left(t\right)=S_h\left(t\right)+I_{h1}\left(t\right)+I_{h2}\left(t\right)$. Building on prior epidemiological frameworks (see [3,12,16,17,18]), we develop a continuous model, incorporating a standard incidence rate and logistic growth for the psyllid population.

$$\left\{\begin{array}{c}{\displaystyle \frac{d{S}_h\left(t\right)}{dt}}=\alpha (K_1-S_h\left(t\right)-I_{h1}\left(t\right)-I_{h2}\left(t\right))-{\displaystyle \frac{b{S}_h\left(t\right)(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))}{N_h\left(t\right)}}-{\mu }_1{S}_h\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_{h1}\left(t\right)}{dt}}={\displaystyle \frac{b{S}_h\left(t\right)(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))}{N_h\left(t\right)}}-\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h1}\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_{h2}\left(t\right)}{dt}}=\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h2}\left(t\right)-{\mu }_2{I}_{h2}\left(t\right),\hfill \\ {\displaystyle \frac{d{S}_v\left(t\right)}{dt}}=r{N}_v\left(t\right)\left(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}\right){\displaystyle \frac{S_h\left(t\right)}{N_h\left(t\right)}}-b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{N_h\left(t\right)}}{S}_v\left(t\right)-\mu S_v\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^a\left(t\right)}{dt}}=b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{N_h\left(t\right)}}{S}_v\left(t\right)-\mu I_v^a\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^n\left(t\right)}{dt}}=r{N}_v\left(t\right)\left(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}\right){\displaystyle \frac{I_{h1}\left(t\right)+I_{h2}\left(t\right)}{N_h\left(t\right)}}-\mu I_v^n\left(t\right),\hfill \end{array}\right.$$

(1)

where $K_1$ and $K_2$ represent the maximum carrying capacities for citrus trees and citrus psyllids in the orchard, respectively. The parameter $\alpha >0$ is the replanting rate. The natural mortality rate and disease-related mortality rate of citrus trees are represented by ${\mu }_1$ and ${\mu }_2$, respectively. The conversion rate from $I_{h1}$ to $I_{h2}$ is denoted by $\sigma$, with ${\displaystyle \frac{1}{\sigma }}$ representing the symptomatic period. The feeding rate of psyllids on citrus trees is given by b. The transmission abilities of pathogens by $I_v^n$ and $I_v^a$ are represented by $P_h^n$ and $P_h^a$, respectively. The successful pathogen acquisition rate of $I_v^a$ when feeding on citrus trees is denoted by $p_v$, while $\theta$ ($\theta \ge 1$) is the proportionality coefficient of the pathogen acquisition rate of $I_{h2}$ relative to $I_{h1}$. The intrinsic growth rate of psyllids is represented by r, and their natural mortality rate is denoted by $\mu$.

Field observations reveal distinct psyllid population peaks (from late June to late July, from mid-August to mid-September, and from early October to early November) corresponding to citrus flush cycles [19]. This indicates that we need to adopt time-dependent control strategies. Pre-spring budburst (dormancy period), spring shoot maturation (April–May), and peak suppression phases (June, August, September, October) are the critical intervention windows for controlling the citrus psyllids. In addition, it is worth noting that before each removal of diseased trees, pesticide spraying must be carried out on the citrus trees [11]. In addition, it is worth noting that citrus psyllids must be killed before cutting down citrus trees [11]. Based on the above discussion and taking into account the time-varying impulsive control, we have optimized and improved system (1) as follows:

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{S}_h\left(t\right)}{dt}}=\alpha (K_1-S_h\left(t\right)-I_{h1}\left(t\right)-I_{h2}\left(t\right))-{\displaystyle \frac{b{S}_h\left(t\right)(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))}{N_h\left(t\right)}}\hfill \\ -{\mu }_1{S}_h\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_{h1}\left(t\right)}{dt}}={\displaystyle \frac{b{S}_h\left(t\right)(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))}{N_h\left(t\right)}}-\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h1}\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_{h2}\left(t\right)}{dt}}=\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h2}\left(t\right)-{\mu }_2{I}_{h2}\left(t\right),\hfill \\ {\displaystyle \frac{d{S}_v\left(t\right)}{dt}}=r{N}_v\left(t\right)\left(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}\right){\displaystyle \frac{S_h\left(t\right)}{N_h\left(t\right)}}-b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{N_h\left(t\right)}}{S}_v\left(t\right)-\mu S_v\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^a\left(t\right)}{dt}}=b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{N_h\left(t\right)}}{S}_v\left(t\right)-\mu I_v^a\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^n\left(t\right)}{dt}}=r{N}_v\left(t\right)\left(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}\right){\displaystyle \frac{I_{h1}\left(t\right)+I_{h2}\left(t\right)}{N_h\left(t\right)}}-\mu I_v^n\left(t\right),\hfill \end{array}\right\}t\ne t_k,\hfill \\ \left.\begin{array}{c}{S}_h\left(t^{+}\right)=S_h\left(t\right),\hfill \\ I_{h1}\left(t^{+}\right)=(1-d_{1k})I_{h1}\left(t\right),\hfill \\ I_{h2}\left(t^{+}\right)=(1-d_{2k})I_{h2}\left(t\right),\hfill \\ S_v\left(t^{+}\right)=(1-{\theta }_k)S_v\left(t\right),\hfill \\ I_v^a\left(t^{+}\right)=(1-{\theta }_k)I_v^a\left(t\right),\hfill \\ I_v^n\left(t^{+}\right)=(1-{\theta }_k)I_v^n\left(t\right),\hfill \end{array}\right\}t=t_k,(k\in \mathbb{N}),\hfill \end{array}\right.$$

(2)

where $\omega$ denotes the system period, q is the number of impulses within each period. The impulse control moments are denoted by $t_k(k\in \mathbb{N})$. The parameters $d_{1k}$ and $d_{2k}(0\le d_{ik}<1,i=1,2)$ represent the removal rates of infected plants $I_{h1}$ and $I_{h2}$ at impulsive time $t_k$, respectively. ${\theta }_k$ represents the killing rates of psyllids due to pesticide spraying at impulsive time $t_k$. These parameters satisfy the following conditions:

$$t_{k+q}=t_k+\omega ,{\theta }_k={\theta }_{k+q},d_{ik}=d_{i(k+q)}.$$

The description and value of parameters of model (2) are provided in Table 1.

Table 1. Parameter descriptions and values in model (2).

Parameters	Description	Value	Unit	References
$K_1$	Carrying capacity of citrus trees	2	−	Assumed
$K_2$	Carrying capacity of psyllids	20	−	Assumed
$\alpha$	Replanting rate of citrus trees	$0.6$	${\mathrm{year}}^{-1}$	[20]
$\sigma$	The transition rate from $I_{h1}$ to $I_{h2}$	$12.97$	${\mathrm{year}}^{-1}$	[16]
$\omega$	System period	1	year	[19]
q	Number of pulses per system period	4	${\mathrm{year}}^{-1}$	[19]
b	Feeding rate of psyllids on citrus trees	0.1–10	${\mathrm{year}}^{-1}$	Assumed
$P_h^n$	Probability of disease transmission from infected psyllids $I_v^n$ to citrus trees	$0.67$	${\mathrm{year}}^{-1}$	[17]
$P_h^a$	Probability of disease transmission from infected psyllids $I_v^a$ to citrus tree	0.037–0.07	${\mathrm{year}}^{-1}$	[17]
$p_v$	The pathogen acquisition rate when feeding on infected trees $I_{h1}$	$0.13$	${\mathrm{year}}^{-1}$	[21]
$\theta$	The proportionality coefficient of the pathogen acquisition rate of $I_{h2}$ relative to $I_{h1}$	$3.3077$	${\mathrm{year}}^{-1}$	[17,21]
${\mu }_1$	Natural mortality rate of citrus trees	0.00275–0.004167	${\mathrm{year}}^{-1}$	[22]
${\mu }_2$	Disease-induced mortality rate of citrus trees	0.016667–0.027775	${\mathrm{year}}^{-1}$	[23]
r	Psyllid birth rate	3.78327–33.526137	${\mathrm{year}}^{-1}$	[22,24]
$\mu$	Natural mortality rate of psyllids	0.1169825–0.95052	${\mathrm{year}}^{-1}$	[25]
$d_{1k}$	The removal rates of infected plants $I_{h1}$ at impulsive time $t_k$	$0-1$	−	Assumed
$d_{2k}$	The removal rates of infected plants $I_{h2}$ at impulsive time $t_k$	$0-1$	−	Assumed
${\theta }_k$	The killing rates of psyllids at impulsive time $t_k$	$0-1$	−	Assumed

The initial values for impulsive system (2) are

$$S_h\left(0\right)>0,I_{h1}\left(0\right)\ge 0,I_{h2}\left(0\right)\ge 0,S_v\left(0\right)>0,I_v^a\left(0\right)\ge 0,I_v^n\left(0\right)\ge 0.$$

(3)

The non-negativity of the solution to system (2) can be readily established under the initial conditions (3).

Lemma 1.

Suppose $Z\left(t\right)=(S_h\left(t\right),I_{h1}\left(t\right),I_{h2}\left(t\right),S_v\left(t\right),I_v^a\left(t\right),I_v^n\left(t\right))$ is the solution of system (2) with initial values (3), then $Z\left(t\right)\geqq 0$ for all $t\ge 0$.

To establish our main results, we introduce the following lemma, which will play a crucial role in our subsequent proofs.

Lemma 2.

Consider the following impulsive differential equation:

$$\left\{\begin{array}{c}{\displaystyle \frac{dx\left(t\right)}{dt}}=-a{x}^2\left(t\right)+bx\left(t\right),t\ne t_k,\hfill \\ x\left(t^{+}\right)=(1-{\zeta }_k)x\left(t\right),t=t_k,(k\in \mathbb{N}),\hfill \end{array}\right.$$

(4)

where a and b are positive constants, $t_0=0$, $0\le {\zeta }_k<1$, and there exist positive integer q and positive number ω such that ${\zeta }_{k+q}={\zeta }_k$, $t_{k+q}=t_k+\omega$, $k\in \mathbb{N}$. Then, system (4) has a unique ω-periodic solution $\tilde{x}\left(t\right)$, which is globally asymptotically stable, where

$$\tilde{x}\left(t\right)={\displaystyle \frac{{\displaystyle \prod _{i=1}^{k-1}\left((1-{\zeta }_{i-1})e^{b{t}_i}\right)e^{b(t-n\omega )}}}{{\displaystyle {\displaystyle \frac{1}{x_0^{\ast }}}-\sum _{i=1}^{k-1}\left({\displaystyle \frac{a}{b}(1-e^{b{t}_i})\prod _{j=1}^{i-1}(1-{\zeta }_j)e^{b{t}_j}}\right)-\frac{a}{b}\prod _{j=1}^{k-1}(1-{\zeta }_j)e^{b{t}_j}(1-e^{b(t-n\omega )})}}},$$

$$t\in (t_{k-1}+n\omega ,t_k+n\omega ],k=1,2,...,q,$$

and

$$x_0^{\ast }={\displaystyle \frac{{\displaystyle 1-\prod _{i=1}^q(1-{\zeta }_{i-1})e^{b{t}_i}}}{{\displaystyle \sum _{i=1}^q\left({\displaystyle \frac{a}{b}(1-e^{b{t}_i})\prod _{j=1}^{i-1}(1-{\zeta }_j)e^{b{t}_j}}\right)}}}.$$

Proof. 

From the first equation of system (4), we have

$$x\left(t\right)={\displaystyle \frac{e^{b(t-n\omega )}}{{\displaystyle \frac{1}{x(n\omega +t_i^{+})}}-{\displaystyle \frac{a}{b}}(1-e^{b(t-n\omega )})}},for{t}_i+n\omega \le t\le t_{i+1}+n\omega ,$$

(5)

where $x(n\omega +t_i^{+})=(1-{\zeta }_k)x(n\omega +t_i)$ and $i=0,1,\cdots ,q-1$, $n\in \mathbb{N}$. It follows from (5) that

$$x(n\omega +t_1^{+})={\displaystyle \frac{(1-{\zeta }_1)e^{b{t}_1}}{{\displaystyle \frac{1}{x\left(n{\omega }^{+}\right)}}-{\displaystyle \frac{a}{b}}(1-e^{b{t}_1})}},$$

$$x(n\omega +t_2^{+})={\displaystyle \frac{(1-{\zeta }_2)(1-{\zeta }_1)e^{b(t_1+t_2)}}{{\displaystyle \frac{1}{x\left(n{\omega }^{+}\right)}}-{\displaystyle \frac{a}{b}}(1-e^{b{t}_1})-{\displaystyle \frac{a}{b}}(1-{\zeta }_1)e^{b(t_1+t_2)}}}.$$

By analogy, we can conclude that

$$x(n\omega +t_q^{+})={\displaystyle \frac{{\displaystyle \prod _{i=1}^q(1-{\zeta }_{i-1})e^{b{t}_i}}}{{\displaystyle {\displaystyle \frac{1}{x\left(n{\omega }^{+}\right)}}-\sum _{i=1}^q\left({\displaystyle \frac{a}{b}(1-e^{b{t}_i})\prod _{j=1}^{i-1}(1-{\zeta }_j)e^{b{t}_j}}\right)}}}.$$

Let $U_n=x\left(n{\omega }^{+}\right)$. Since $\omega =t_q$, we obtain the following stroboscopic map:

$$U_{n+1}={\displaystyle \frac{{\displaystyle \prod _{i=1}^q(1-{\zeta }_{i-1})e^{b{t}_i}}}{{\displaystyle {\displaystyle \frac{1}{U_n}}-\sum _{i=1}^q\left({\displaystyle \frac{a}{b}(1-e^{b{t}_i})\prod _{j=1}^{i-1}(1-{\zeta }_j)e^{b{t}_j}}\right)}}}\triangleq f\left(U_n\right),$$

(6)

It is easy to know that (6) has a unique fixed point

$$U_0^{\ast }={\displaystyle \frac{{\displaystyle 1-\prod _{i=1}^q(1-{\zeta }_{i-1})e^{b{t}_i}}}{{\displaystyle \sum _{i=1}^q\left({\displaystyle \frac{a}{b}(1-e^{b{t}_i})\prod _{j=1}^{i-1}(1-{\zeta }_j)e^{b{t}_j}}\right)}}}.$$

Since $|f^{\prime }\left(U_0^{\ast }\right)|<1$, this fixed point $U_0^{\ast }$ is globally asymptotically stable. Consequently, the corresponding periodic solution $\tilde{x}\left(t\right)$ of system (4) is also globally asymptotically stable. □

3. Basic Reproduction Number for a General Impulsive Epidemic System

To derive the basic reproduction number $R_0$ of a general impulsive system, we first establish foundational results for linear impulsive systems. Consider the following linear impulsive differential system:

$$\begin{array}{c}\left\{\begin{array}{c}\dot{x}\left(t\right)=Ax\left(t\right),t\ne t_k,\hfill \\ x\left(t_k^{+}\right)=P_{k}x\left(t_k\right),t=t_k,(k\in \mathbb{N}),\hfill \\ x\left(t_0^{+}\right)=x_0,t_0\ge 0,\hfill \end{array}\right.\end{array}$$

(7)

where the system satisfies the following assumptions:

$\left(C_1\right)$$P_k\in {\mathbb{R}}^{n\times n},det(E+P_k)\ne 0,P_0=I$, where I is the $n\times n$ identity matrix;

$\left(C_2\right)$ There exists a positive integer q such that $P_{k+q}=P_k,t_{k+q}=t_k+\omega (k\in \mathbb{N})$.

Denote

$${\mathrm{\Phi }}_{A{P}_k}\left(\omega \right):=\prod _{k=1}^q\left(P_{q-k+1}exp\left(A{T}_{q-k+1}\right)\right),$$

where $T_k=t_k-t_{k-1}$, $r\left({\mathrm{\Phi }}_{A{P}_k}\left(\omega \right)\right)$ is the spectral radius of the matrix ${\mathrm{\Phi }}_{A{P}_k}\left(\omega \right)$, and ${\nu }^{\ast }$ is the eigenvector corresponding to the principal eigenvalue $r\left({\mathrm{\Phi }}_{A{P}_k}\left(\omega \right)\right)$. According to Theorem 2.1 in [26], we can obtain the following result.

Lemma 3.

Let $\eta ={\displaystyle \frac{1}{\omega }}lnr\left({\mathrm{\Phi }}_{A{P}_k}\left(\omega \right)\right)$; then, there exists a positive ω-periodic function $v\left(t\right)$ such that $e^{\eta t}v\left(t\right)$ is a solution of the system (7).

Building on this framework, we now rigorously derive the basic reproduction number $R_0$ for the following nonlinear impulsive differential system, incorporating both continuous dynamics and discrete impulsive effects:

$$\begin{array}{c}\left\{\begin{array}{c}\dot{\mathbf{x}}\left(t\right)=f\left(\mathbf{x}\right),t\ne t_k,\hfill \\ \mathbf{x}\left(t_k^{+}\right)=\mathbf{x}\left(t_k\right)+{\psi }^k\left(\mathbf{x}\left(t_k\right)\right),t=t_k,(k\in \mathbb{N}),\hfill \\ \mathbf{x}\left(t_0^{+}\right)={\mathbf{x}}_0,t_0\ge 0.\hfill \end{array}\right.\end{array}$$

(8)

where $x={(x_1,x_2,\cdots ,x_n)}^T$. For a compartmental epidemic model, we can split the compartments by two types with the first m compartments ${(x_1,x_2,\cdots ,x_m)}^T\doteq X$ the infected individuals, and ${(x_{m+1},x_{m+2},\cdots ,x_n)}^T\doteq Y$ the uninfected individuals. Following the notation in [26], we rewrite system (8) as follows:

$$\left\{\begin{array}{c}\dot{\mathbf{x}}\left(t\right)=\mathcal{F}\left(\mathbf{x}\right)-\mathcal{V}\left(\mathbf{x}\right),t\ne t_k,\hfill \\ \left.\begin{array}{c}X\left(t_k^{+}\right)=h^k\left(\mathbf{x}\left(t_k\right)\right),\hfill \\ Y\left(t_k^{+}\right)=g^k\left(\mathbf{x}\left(t_k\right)\right),\hfill \end{array}\right\}t=t_k,(k\in \mathbb{N}),\hfill \\ \mathbf{x}\left(t_0^{+}\right)={\mathbf{x}}_0,t_0\ge 0.\hfill \end{array}\right.$$

(9)

where $\mathcal{F}$ represents the newly infected rate, $\mathcal{V}$ is the net transfer rate out of compartments, ${\psi }^k={(h^k,g^k)}^T$, $h^k=({\psi }_1^k,\cdots ,{\psi }_m^k)$, $g^k=({\psi }_{m+1}^k,\cdots ,{\psi }_n^k)$. Assume that the system (9) has a disease-free periodic solution, denoted as

$${\mathbf{x}}^{\ast }\left(t\right)=(0,\cdots ,0,x_{m+1}^{\ast }\left(t\right),\cdots ,x_n^{\ast }\left(t\right)).$$

Similar to [26], we present the following eight hypotheses.

Hypothesis 1.

If $x_i\ge 0$, then ${\mathcal{F}}_i\left(\mathbf{x}\right)\ge 0$, ${\mathcal{V}}_i^{+}\left(\mathbf{x}\right)\ge 0$, ${\mathcal{V}}_i^{-}\left(\mathbf{x}\right)\ge 0$, $i=1,2,\cdots ,n$.

Hypothesis 2.

If $x_i=0$, then ${\mathcal{V}}_i^{-}\left(\mathbf{x}\right)=0$. In particular, if $\mathbf{x}\in X_s$, then ${\mathcal{V}}_i^{-}\left(\mathbf{x}\right)=0,i=1,\cdots ,m$.

Hypothesis 3.

For $i>m$, ${\mathcal{F}}_i\left(\mathbf{x}\right)=0$.

Hypothesis 4.

If $\mathbf{x}\in X_s$, then ${\mathcal{F}}_i\left(\mathbf{x}\right)={\mathcal{V}}_i^{+}\left(\mathbf{x}\right)=0$, $i=1,\cdots ,m$.

Hypothesis 5.

The impulses of individuals in the infected compartments are independent of the non-infected compartments; that is, $h^k\left(x\left(t_k\right)\right)=h^k\left(X\left(t_k\right)\right)$.

Hypothesis 6.

$h^k\left(0\right)=0$ holds.

Hypothesis 7.

$r\left({\mathrm{\Phi }}_{N{Q}_k}\left(\omega \right)\right)<1$, where ${\mathrm{\Phi }}_{NQ}\left(\omega \right):={\prod }_{k=1}^q\left(Q_{q-k+1}exp\left(N{T}_{q-k+1}\right)\right)$, and ${\mathrm{\Phi }}_{N{Q}_k}\left(t\right)$ is the fundamental solution matrix of the following impulsive system.

$$\begin{array}{c}\hfill \begin{array}{c}\left\{\begin{array}{c}\dot{Z}=NZ\left(t\right),t\ne t_k,\hfill \\ Z\left(t_k^{+}\right)=Q_{k}Z\left(t_k\right),t=t_k,(k\in \mathbb{N}),\hfill \end{array}\right.\end{array}\end{array}$$

$$N={\left({\displaystyle \frac{\partial f_i\left(x^{\ast }\left(t\right)\right)}{\partial x_j}}\right)}_{m+1\le i,j\le n},Q_k={\left({\displaystyle \frac{\partial {\psi }_i^k\left(x^{\ast }\left(t\right)\right)}{\partial x_j}}\right)}_{m+1\le i,j\le n}.$$

(10)

Hypothesis 8.

$r\left({\mathrm{\Phi }}_{-V{P}_k}\left(\omega \right)\right)<1$, where ${\mathrm{\Phi }}_{-V{P}_k}\left(t\right)$ is the fundamental solution matrix of the following system:

$$\begin{array}{c}\hfill \begin{array}{c}\left\{\begin{array}{c}\dot{y}=-Vy\left(t\right),t\ne t_k,\hfill \\ y\left(t_k^{+}\right)=P_{k}y\left(t_k\right),t=t_k,(k\in \mathbb{N}),\hfill \\ x\left(t_0^{+}\right)=x_0,\hfill \end{array}\right.\end{array}\end{array}$$

where

$$V={\left({\displaystyle \frac{\partial {\mathcal{V}}_i\left(x^{\ast }\left(t\right)\right)}{\partial x_j}}\right)}_{1\le i,j\le m},P_k={\left({\displaystyle \frac{\partial {\psi }_i^k\left(x^{\ast }\left(t\right)\right)}{\partial x_j}}\right)}_{1\le i,j\le m}.$$

(11)

Next, we consider the following impulsive system:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{d\psi \left(t\right)}{dt}}=-V\psi \left(t\right),t\ne t_k,\hfill \\ \psi \left(t_k^{+}\right)=P_k\psi \left(t_k\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.\hfill \end{array}$$

(12)

Obviously, for any $t>0$, there exist two positive integers l and m$(0\le m\le q)$ such that $l\omega +t_m<t\le l\omega +t_{m+1}$. Solving Equation (12), we have for $t\in (l\omega +t_m,l\omega +t_{m+1}]$,

$${\displaystyle \psi \left(t\right)=exp(-V(t-l\omega -t_m))\prod _{i=1}^m\left(P_{m-i+1}exp[-V{T}_{m-i+1}]\right)\times {\left({\mathrm{\Phi }}_{-V{P}_k}\left(w\right)\right)}^l\psi \left(0\right),}$$

(13)

where $T_i=t_i-t_{i-1}$ and $T_0=0$. Integrating both sides of the first equation in (12) from 0 to $\omega$, we obtain

$$\begin{array}{cc}\hfill {\displaystyle {\int }_0^{\omega }\psi \left(t\right)dt}& ={\int }_0^{t_1}\psi \left(t\right)dt+{\int }_{t_1}^{t_2}\psi \left(t\right)dt+\cdots +{\int }_{t_{q-1}}^{t_q}\psi \left(t\right)dt\hfill \\ \hfill & =V^{-1}\left(E-exp(-V{T}_1)\right)P_0\psi \left(0\right)+V^{-1}\left(E-exp(-V{T}_2)\right)P_1\psi \left(t_1\right)\hfill \\ \hfill & +\cdots +V^{-1}\left(E-exp(-V{T}_q)\right)P_{q-1}\psi \left(t_{q-1}\right).\hfill \end{array}$$

According to (13), we can derive

$$\begin{array}{cc}\hfill {\displaystyle {\int }_0^{\omega }\psi \left(t\right)dt}& {\displaystyle =V^{-1}\left((E-exp(-V{T}_1)\right)P_0\psi \left(0\right)+\left(E-exp(-V{T}_2)\right)P_{1}exp(-V{T}_1)\psi \left(0\right)}\hfill \\ \hfill & +\cdots +\left(E-exp(-V{T}_q)\right)P_{q-1}exp(-V{T}_{q-1})\cdots P_{1}exp(-V{T}_1)P_0\psi \left(0\right))\hfill \\ \hfill & {\displaystyle =V^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right)\psi \left(0\right).}\hfill \end{array}$$

Denote

$$Q=\prod _{k=0}^{q-1}{P}_{k}exp(-V{T}_k).$$

(14)

Hence, $\psi \left({\omega }^{+}\right)=Q\psi \left(0\right)$. Obviously, $\Vert Q\Vert <1$. Thus,

$$\begin{array}{cc}\hfill {\displaystyle {\int }_{\omega }^{2\omega }\psi \left(t\right)dt}& {\displaystyle =V^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right)\psi \left({\omega }^{+}\right)}\hfill \\ \hfill & {\displaystyle =V^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right]\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right)Q\psi \left(0\right),}\hfill \end{array}$$

Similarly, we can obtain

$${\displaystyle {\int }_{n\omega }^{(n+1)\omega }\psi \left(t\right)dt=V^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right)Q^n\psi \left(0\right).}$$

In conclusion, we have

$$\begin{array}{cc}\hfill {\displaystyle {\int }_0^{\infty }\psi \left(t\right)dt}& =\sum _{n=0}^{\infty }{\int }_{n\omega }^{(n+1)\omega }\psi \left(t\right)dt\hfill \\ \hfill & =\sum _{n=0}^{\infty }\left({\displaystyle V^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right)Q^n\psi \left(0\right)}\right)\hfill \\ \hfill & {\displaystyle =V^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right)\sum _{n=0}^{\infty }{Q}^n\psi \left(0\right)}\hfill \\ \hfill & {\displaystyle =V^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right){(E-Q)}^{-1}\psi \left(0\right).}\hfill \end{array}$$

Following the idea of [27], we define the basic reproduction number $R_0$ of system (8) as follows:

$$R_0=r\left({\displaystyle F{V}^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right){(E-Q)}^{-1}}\right),$$

(15)

where

$$F={\left({\displaystyle \frac{\partial {\mathcal{F}}_i\left(x^{\ast }\left(t\right)\right)}{\partial x_j}}\right)}_{1\le i,j\le m}.$$

(16)

Theorem 1.

If $\left(H_1\right)-\left(H_8\right)$ hold, then the following conclusions are valid:

(i) 

   $R_0=1$ if and only if $r\left({\mathrm{\Phi }}_{(F-V)P_k}\left(\omega \right)\right)=1$;

(ii) 

  $R_0<1$ if and only if $r\left({\mathrm{\Phi }}_{(F-V)P_k}\left(\omega \right)\right)<1$;

(iii) 

 $R_0>1$ if and only if $r\left({\mathrm{\Phi }}_{(F-V)P_k}\left(\omega \right)\right)>1$.

Therefore, the disease-free periodic solution $x^{\ast }\left(t\right)$ is locally stable when $R_0<1$; otherwise, it is unstable.

The proof of this Theorem 1 is similar to that in reference [28] and is therefore omitted here.

4. Main Results for System (2)

In order to analyze the stability of system (2), we first need to obtain the basic reproduction number, $R_0$, which is a key parameter that determines the dynamic behavior of the model.

4.1. Basic Reproduction Number

In this subsection, we initiate our analysis of system (2) by first demonstrating the existence of a disease-free periodic solution. In this solution, infected individuals are entirely absent from the population at all times, i.e., $I_{h1}\left(t\right)=0,I_{h2}\left(t\right)=0,I_v^a\left(t\right)=0$, and $I_v^n\left(t\right)=0$ for all $t\ge 0$. Under this condition, the growth of susceptible tresses and psyllids must satisfy the following:

$${\displaystyle \frac{d{S}_h\left(t\right)}{dt}}=\alpha (K_1-S_h\left(t\right))-{\mu }_1{S}_h\left(t\right),$$

(17)

and

$$\left\{\begin{array}{c}{\displaystyle \frac{d{S}_v\left(t\right)}{dt}}=r{S}_v\left(t\right)\left(1-{\displaystyle \frac{S_v\left(t\right)}{K_2}}\right)-\mu S_v\left(t\right),t\ne t_k,\hfill \\ S_v\left(t^{+}\right)=(1-{\theta }_k)S_v\left(t\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.$$

(18)

From (17), it is easy to obtain that ${lim}_{t\to +\infty }{S}_h\left(t\right)={\displaystyle \frac{\alpha K_1}{\alpha +{\mu }_1}}\doteq S_h^{\ast }\left(t\right)$. According to Lemma 2, we know that system (18) has a unique periodic solution $S_v^{\ast }\left(t\right)$, which is globally asymptotically stable, where

$$S_v^{\ast }\left(t\right)={\displaystyle \frac{{\displaystyle \prod _{i=1}^{k-1}(1-{\theta }_{i-1})e^{(r-\mu )t_i}{e}^{(r-\mu )(t-n\omega )}}}{{\displaystyle \frac{1}{S_{v0}^{\ast }}}+J_1+W_1}},\mathrm{for}t\in (t_{k-1}+n\omega ,t_k+n\omega ],$$

here

$${\displaystyle J_1=\sum _{i=1}^{k-1}\left({\displaystyle {\displaystyle \frac{r(1-e^{(r-\mu )t_i})}{(\mu -r)K_2}}\prod _{j=1}^{i-1}(1-{\theta }_j)e^{(r-\mu )t_j}}\right),}$$

$${\displaystyle W_1={\displaystyle \frac{r}{(r-\mu )K_2}}\prod _{j=1}^{k-1}(1-{\theta }_j)e^{(r-\mu )t_j}(1-e^{(r-\mu )(t-n\omega )}),}$$

$$S_{v0}^{\ast }={\displaystyle \frac{{\displaystyle 1-\prod _{i=1}^q(1-{\theta }_{i-1})e^{(r-\mu )t_i}}}{{\displaystyle \sum _{i=1}^q\left({\displaystyle {\displaystyle \frac{r(1-e^{(r-\mu )t_i})}{(r-\mu )K_2}}\prod _{j=1}^{i-1}(1-{\theta }_j)e^{(r-\mu )t_j}}\right)}}}.$$

Therefore, system (2) has a unique disease-free periodic solution $(S_h^{\ast }\left(t\right),0,0,S_v^{\ast }\left(t\right),0,0)$.

According to the discussion in Section 3, we can calculate the basic reproduction number $R_0$. Let $\mathbf{x}={(x_1,x_2,x_3,x_4,x_5,x_6)}^T={(I_{h1},I_{h2},I_v^a,I_v^n,S_h,S_v)}^T$. It is easy to know that the system (2) has a unique disease-free periodic solution $x^{\ast }\left(t\right)=(0,0,0,0,S_h^{\ast }\left(t\right),S_v^{\ast }\left(t\right))$. For system (2), the newly infected rate $\mathcal{F}$ and the net transfer rate out of compartments $\mathcal{V}$ are given by the following:

$$\mathcal{F}\left(x\right)=\left(\begin{array}{c}b{\displaystyle \frac{S_h\left(t\right)}{N_h\left(t\right)}}(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))\\ 0\\ b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{N_h\left(t\right)}}{S}_v\left(t\right)\\ r{N}_v\left(t\right)(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}){\displaystyle \frac{I_{h1}\left(t\right)+I_{h2}\left(t\right)}{N_h\left(t\right)}}\\ 0\\ 0\end{array}\right),$$

$$\mathcal{V}\left(x\right)=\left(\begin{array}{c}\sigma I_{h1}\left(t\right)+{\mu }_1{I}_{h1}\left(t\right)\\ -\sigma I_{h1}\left(t\right)+{\mu }_1{I}_{h2}\left(t\right)+{\mu }_2{I}_{h2}\left(t\right)\\ \mu I_v^a\left(t\right)\\ \mu I_v^n\left(t\right)\\ -\alpha (K_1-S_h\left(t\right)-I_{h1}\left(t\right)-I_{h2}\left(t\right))+{\displaystyle \frac{b{S}_h\left(t\right)(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))}{N_h\left(t\right)}}+{\mu }_{1}S\left(t\right)\\ -r{N}_v\left(t\right)(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}){\displaystyle \frac{S_h\left(t\right)}{N_h\left(t\right)}}+b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{N_h\left(t\right)}}{S}_v\left(t\right)+\mu S_v\left(t\right)\end{array}\right).$$

It is easy to verify that system (2) satisfies the assumptions $\left(H_1\right)-\left(H_6\right)$. Next, we verify the conditions $\left(H_7\right)$ and $\left(H_8\right)$.

From (10), we have

$$N\left(t\right)=\left(\begin{array}{cc}-\alpha -{\mu }_1& 0\\ 0& r(1-{\displaystyle \frac{2S_v^{\ast }}{K_2}})-\mu \end{array}\right),Q_k=\left(\begin{array}{cc}1& 0\\ 0& 1-{\theta }_k\end{array}\right),$$

By calculation, we can obtain

$${\displaystyle {\mathrm{\Phi }}_{N{Q}_k}\left(\omega \right):=\left(\begin{array}{cc}exp\left[(-\alpha -{\mu }_1)\omega \right]& 0\\ 0& {\displaystyle \prod _{k=1}^q(1-{\theta }_k)exp\left[r\left(1-{\displaystyle \frac{2S_v^{\ast }}{K_2}}\right)\omega -\mu \omega \right]}\end{array}\right).}$$

Obviously, $r\left({\mathrm{\Phi }}_{N{Q}_k}\left(\omega \right)\right)<1$; thus, $\left(H_7\right)$ holds.

From (11), we have

$$P_k=\left(\begin{array}{cccc}1-d_{1k}& 0& 0& 0\\ 0& 1-d_{2k}& 0& 0\\ 0& 0& 1-{\theta }_k& 0\\ 0& 0& 0& 1-{\theta }_k\end{array}\right),V\left(t\right)=\left(\begin{array}{cccc}\sigma +{\mu }_1& 0& 0& 0\\ -\sigma & {\mu }_1+{\mu }_2& 0& 0\\ 0& 0& \mu & 0\\ 0& 0& 0& \mu \end{array}\right),$$

Consequently,

$${\mathrm{\Phi }}_{-V{P}_k}\left(\omega \right):=\left(\begin{array}{cccc}\prod _{k=1}^q(1-d_{1k})e^{(-\sigma -{\gamma }_1-{\mu }_2)\omega }& 0& 0& 0\\ \ast & \prod _{k=1}^q(1-d_{1k})e^{(-{\gamma }_2-{\mu }_3)\omega }& 0& 0\\ 0& 0& J_2& 0\\ 0& 0& 0& J_2\end{array}\right),$$

where $J_2={\prod }_{k=1}^q(1-{\theta }_k)e^{-\mu \omega }.$ It is easy to know that $r\left({\mathrm{\Phi }}_{-V{P}_k}\left(\omega \right)\right)<1$. Hence, $\left(H_8\right)$ holds.

It follows from (14) and (16) that

$$\begin{array}{c}{\displaystyle Q=\prod _{k=0}^{q-1}{P}_{k}exp(-V{T}_k),}\hfill \\ F=\left(\begin{array}{cccc}0& 0& b{\displaystyle \frac{S_h^{\ast }\left(t\right)}{S_h^{\ast }\left(t\right)}}{P}_h^a& b{\displaystyle \frac{S_h^{\ast }\left(t\right)}{S_h^{\ast }\left(t\right)}}{P}_h^n\\ 0& 0& 0& 0\\ b{P}_v{\displaystyle \frac{S_v^{\ast }}{S_h^{\ast }}}& \theta b{P}_v{\displaystyle \frac{S_v^{\ast }}{S_h^{\ast }}}& 0& 0\\ {\displaystyle \frac{r{S}_v^{\ast }}{S_h^{\ast }}}(1-{\displaystyle \frac{S_v^{\ast }}{K_2}})& {\displaystyle \frac{r{S}_v^{\ast }}{S_h^{\ast }}}(1-{\displaystyle \frac{S_v^{\ast }}{K_2}})& 0& 0\end{array}\right).\hfill \end{array}$$

(19)

It follows from (15) that the basic reproduction number of system (2) is

$$R_0=r\left({\displaystyle F{V}^{-1}\sum _{k=1}^q\left(\left(E-exp(-V{T}_k)\right)\prod _{i=0}^{k-1}{P}_{i}exp(-V{T}_i)\right){(E-Q)}^{-1}}\right),$$

where $V,P_i,F,Q$ are defined in (11) and (19).

According to the result of Theorem 1, we have the following conclusion.

Theorem 2.

The disease-free periodic solution $x^{\ast }\left(t\right)$ of system (2) is locally stable if $R_0<1$, and unstable if $R_0>1$.

4.2. Global Asymptotic Stability of the Disease-Free Periodic Solution

In this subsection, we will discuss the global stability of the disease-free periodic solution. First, we give the following lemma.

Lemma 4.

For system (2), the following conclusions are valid:

$$\underset{t\to +\infty }{lim}(N_h\left(t\right)-S_h^{\ast }\left(t\right))=0,and\underset{t\to +\infty }{lim}(N_v\left(t\right)-S_v^{\ast }\left(t\right))=0,$$

where $S_h^{\ast }\left(t\right)$ and $S_v^{\ast }\left(t\right))$ are the positive periodic solutions of the systems (17) and (18), respectively.

Proof. 

It follows from system (2) that

$$\left\{\begin{array}{cc}\hfill {\displaystyle \frac{d{N}_h\left(t\right)}{dt}}& =\alpha (K_1-S_h\left(t\right)-I_{h1}\left(t\right)-I_{h2}\left(t\right))-{\mu }_1(S_h\left(t\right)+I_{h1}\left(t\right)+I_{h2}\left(t\right))-{\mu }_2{I}_{h2}\left(t\right)\hfill \\ \hfill & \le \alpha (K_1-N_h\left(t\right))-{\mu }_1{N}_h\left(t\right),\hfill \\ \hfill N_h\left(t^{+}\right)& =(1-d_{1k})I_{h1}\left(t\right)+(1-d_{2k})I_{h2}\left(t\right)+S_h\left(t\right),\hfill \end{array}\right.$$

(20)

Set $H\left(t\right)=N_h\left(t\right)-S_h^{\ast }\left(t\right)$. In view of (20), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{dH\left(t\right)}{dt}}& \le -{\mu }_{1}H\left(t\right),\hfill \\ \hfill H\left(t^{+}\right)& =(1-d_{1k})I_{h1}\left(t\right)+(1-d_{2k})I_{h2}\left(t\right)+S_h\left(t\right)-S_h^{\ast }\left(t\right)\hfill \\ & =(1-d_{1k})(N_h\left(t\right)-I_{h2}\left(t\right)-S_h\left(t\right))+(1-d_{2k})I_{h2}\left(t\right)+S_h\left(t\right)-S_h^{\ast }\left(t\right)\hfill \\ & =(1-d_{1k})N_h\left(t\right)-(1-d_{1k})I_{h2}\left(t\right)+d_{1k}{S}_h\left(t\right)+(1-d_{2k})I_{h2}\left(t\right)-S_h^{\ast }\left(t\right)\hfill \\ & \le (1-d_{1k})H\left(t\right),\hfill \end{array}\end{array}$$

Therefore, $\underset{t\to +\infty }{lim}H\left(t\right)=\underset{t\to +\infty }{lim}(N_h\left(t\right)-S_h^{\ast }\left(t\right))=0.$

Similarly, from system (2), we can derive

$$\left\{\begin{array}{cc}\hfill {\displaystyle \frac{d{N}_v\left(t\right)}{dt}}& =r{N}_v\left(t\right)(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}){\displaystyle \frac{S_h\left(t\right)}{N_h\left(t\right)}}+r{N}_v\left(t\right)(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}}){\displaystyle \frac{I_{h1}\left(t\right)+I_{h2}\left(t\right)}{N_h\left(t\right)}}-\mu N_v\left(t\right)\hfill \\ \hfill & =r{N}_v\left(t\right)(1-{\displaystyle \frac{N_v\left(t\right)}{K_2}})-\mu N_v\left(t\right),\hfill \\ \hfill N_v\left(t^{+}\right)& =(1-{\theta }_k)N_v\left(t\right).\hfill \end{array}\right.$$

(21)

It follows from (21) and (18) that $\underset{t\to +\infty }{lim}(N_v\left(t\right)-S_v^{\ast }\left(t\right))=0$. □

Theorem 3.

If $R_0<1$, the disease-free periodic solution $x^{\ast }\left(t\right)=(s_h^{\ast }\left(t\right),0,0,s_v^{\ast }\left(t\right),0,0)$ is globally asymptotically stable.

Proof. 

By Theorem 1, we know that $R_0<1$ if and only if $r\left({\mathrm{\Phi }}_{(F-V)P_k}\left(\omega \right)\right)<1$, and then there exists $\epsilon >0$, which is sufficiently small such that

$$r\left({\mathrm{\Phi }}_{(F_{\epsilon }-V)P_k}\left(\omega \right)\right)<1,$$

(22)

where

$$F_{\epsilon }=\left(\begin{array}{cccc}0& 0& b{\displaystyle \frac{S_h^{\ast }\left(t\right)+\epsilon }{S_h^{\ast }\left(t\right)-\epsilon }}{P}_h^a& b{\displaystyle \frac{S_h^{\ast }\left(t\right)+\epsilon }{S_h^{\ast }\left(t\right)-\epsilon }}{P}_h^n\\ 0& 0& 0& 0\\ b{P}_v{\displaystyle \frac{S_v^{\ast }+\epsilon }{S_h^{\ast }-\epsilon }}& \theta b{P}_v{\displaystyle \frac{S_v^{\ast }+\epsilon }{S_h^{\ast }-\epsilon }}& 0& 0\\ {\displaystyle \frac{r(S_v^{\ast }+\epsilon )}{S_h^{\ast }-\epsilon }}(1-{\displaystyle \frac{S_v^{\ast }-\epsilon }{K_2}})& {\displaystyle \frac{r(S_v^{\ast }+\epsilon )}{S_h^{\ast }-\epsilon }}(1-{\displaystyle \frac{S_v^{\ast }-\epsilon }{K_2}})& 0& 0\end{array}\right).$$

According to Theorem 2, $x^{\ast }\left(t\right)$ is locally asymptotically stable. We only need to prove that $x^{\ast }\left(t\right)$ is globally attractive.

Let $x\left(t\right)=(S_h\left(t\right),I_{h1}\left(t\right),I_{h2}\left(t\right),S_v\left(t\right),I_v^a\left(t\right),I_v^n\left(t\right))$ be any solution of system (2). From the system (2) and the non-negativity of the solution, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{d{S}_h\left(t\right)}{dt}}\le \alpha (K_1-S_h\left(t\right))-{\mu }_1{S}_h\left(t\right),\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{S}_v\left(t\right)}{dt}}\le r{S}_v\left(t\right)(1-{\displaystyle \frac{S_v\left(t\right)}{K_2}})-\mu S_v\left(t\right),t\ne t_k,\hfill \\ S_v\left(t^{+}\right)=(1-{\theta }_k)S_v\left(t\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.\end{array}$$

Consider the following comparison system:

$$\begin{array}{c}\hfill {\displaystyle \frac{d{\widehat{S}}_h\left(t\right)}{dt}}=\alpha (K_1-\widehat{S}{S}_h\left(t\right))-{\mu }_1{\widehat{S}}_h\left(t\right),\end{array}$$

(23)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{\widehat{S}}_v\left(t\right)}{dt}}=r{\widehat{S}}_v\left(t\right)(1-{\displaystyle \frac{{\widehat{S}}_v\left(t\right)}{K_2}})-\mu {\widehat{S}}_v\left(t\right),t\ne t_k,\hfill \\ {\widehat{S}}_v\left(t^{+}\right)=(1-{\theta }_k){\widehat{S}}_v\left(t\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.\end{array}$$

(24)

It is easy to obtain that the comparison system (23) has a unique equilibrium point ${\widehat{S}}_h^{\ast }\left(t\right)$, which is globally asymptotically stable. Thus, ${lim}_{t\to +\infty }{\widehat{S}}_h\left(t\right)=S_h^{\ast }\left(t\right)$. In view of the comparison theorem in for differential equations, we have $S_h\left(t\right)\le {\widehat{S}}_h\left(t\right)$. Similarly, there exists a unique periodic solution ${\widehat{S}}_h^{\ast }\left(t\right)$ of system (24), which is globally asymptotically stable. Hence, ${lim}_{t\to +\infty }{\widehat{S}}_v\left(t\right)=S_v^{\ast }\left(t\right)$. According to the comparison theorem for impulsive differential equations, we have $S_h\left(t\right)\le {\widehat{S}}_h\left(t\right)$. Consequently, for the above-mentioned $\epsilon >0$, there exists $t^0>0$, such that for $t\ge t^0$,

$$S_h\left(t\right)\le S_h^{\ast }\left(t\right)+\epsilon ,\mathrm{and}{S}_v\left(t\right)\le S_v^{\ast }\left(t\right)+\epsilon .$$

(25)

According to Lemma 4 and (25), we obtain for $t\ge t_0$

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{I}_{h1}\left(t\right)}{dt}}\le {\displaystyle \frac{b(S_h^{\ast }\left(t\right)+\epsilon )(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))}{S_h^{\ast }\left(t\right)-\epsilon }}-\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h1}\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_{h2}\left(t\right)}{dt}}=\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h2}\left(t\right)-{\mu }_2{I}_{h2}\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^a\left(t\right)}{dt}}\le b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{S_h^{\ast }\left(t\right)-\epsilon }}(S_v^{\ast }\left(t\right)+\epsilon )-\mu I_v^a\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^n\left(t\right)}{dt}}\le r(S_v^{\ast }\left(t\right)+\epsilon )(1-{\displaystyle \frac{S_v^{\ast }\left(t\right)-\epsilon }{K_2}}){\displaystyle \frac{I_{h1}\left(t\right)+I_{h2}\left(t\right)}{S_h^{\ast }\left(t\right)-\epsilon }}-\mu I_v^n\left(t\right),\hfill \end{array}\right\}t\ne t_k,\hfill \\ \left.\begin{array}{c}{I}_{h1}\left(t^{+}\right)=(1-d_{1k})I_{h1}\left(t\right),\hfill \\ I_{h2}\left(t^{+}\right)=(1-d_{2k})I_{h2}\left(t\right),\hfill \\ I_v^a\left(t^{+}\right)=(1-{\theta }_k)I_v^a\left(t\right),\hfill \\ I_v^n\left(t^{+}\right)=(1-{\theta }_k)I_v^n\left(t\right),\hfill \end{array}\right\}t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.$$

(26)

Denote ${(I_{h1}\left(t\right),I_{h2}\left(t\right),I_v^a\left(t\right),I_v^n\left(t\right))}^T=G\left(t\right)$. Consider the following comparison system of (26):

$$\left\{\begin{array}{c}{G}^{\prime }\left(t\right)=(F_{\epsilon }-V)G\left(t\right),t\ne t_k,\hfill \\ G\left(t_k^{+}\right)=P_{k}G\left(t_k\right),t=t_k,(k\in \mathbb{N}),\hfill \end{array}\right.$$

(27)

According to Lemma 3, there exists a positive $\omega$-periodic function $\nu \left(t\right)$, such that $e^{{\eta }_{1}t}\nu \left(t\right)$ is a solution of the system (27), where ${\eta }_1={\displaystyle \frac{1}{\omega }}lnr\left({\mathrm{\Phi }}_{(F_{\epsilon }-V)P_k}\left(\omega \right)\right)$. Equation (22) implies that ${\eta }_1<0$. So $e^{{\eta }_{1}t}\nu \left(t\right)\to \mathbf{0}$ as $t\to +\infty$. According to the comparison theorem for impulsive differential equations, we have

$$\underset{t\to +\infty }{lim}(I_{h1}\left(t\right),I_{h2}\left(t\right),I_v^a\left(t\right),I_v^n\left(t\right))=(0,0,0,0).$$

By the theory of asymptotically autonomous semiflows, we can obtain that if $R_0<1$, then ${lim}_{t\to +\infty }(S_h\left(t\right),I_{h1}\left(t\right),I_{h2}\left(t\right),S_v\left(t\right),I_v^a\left(t\right),I_v^n\left(t\right))=x^{\ast }\left(t\right)$; that is, the disease-free periodic solution $x^{\ast }\left(t\right)$ of system (2) is globally attractive. This completes the proof. □

4.3. Uniform Persistence

In this subsection, we delve into the persistence of the system (2). To lay the groundwork, we first present the following lemma.

Lemma 5

([29]). Consider the following differential system:

$$\left\{\begin{array}{c}\dot{u}\left(t\right)=a-bu\left(t\right),t\ne t_k,\hfill \\ u\left(t^{+}\right)=(1-{\xi }_k)u\left(t\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.$$

(28)

where a and b are constants, $0\le {\xi }_k<1$, ${\xi }_{k+q}={\zeta }_k$, $k\in \mathbb{N}$, $t_q=\omega$. Then, the system (28) has a unique positive ω-periodic solution $\tilde{u}\left(t\right)$, which is globally asymptotically stable, where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \tilde{u}\left(t\right)=& {\displaystyle \frac{a}{b}}(1-e^{-b(t-n\omega -t_{k-1})})\hfill \\ & +{\displaystyle \frac{a}{b}}\sum _{j=1}^{k-1}\left(\prod _{i=j}^{k-1}(1-{\xi }_i)e^{-b(t-n\omega -t_j)}(1-e^{-b(t_j-t_{j-1})})\right)\prod _{i=1}^{k-1}(1-{\xi }_i)e^{-b(t-n\omega )}{u}_0^{\ast },\hfill \end{array}\end{array}$$

and

$$u_0^{\ast }={\displaystyle \frac{{\displaystyle \frac{a}{b}}{\displaystyle \sum _{j=1}^q}\left({\displaystyle \prod _{i=j}^q}(1-{\xi }_i)e^{-b(t_q-t_j)}(1-e^{-b(t_j-t_{j-1})})\right)}{1-{\displaystyle \prod _{i=1}^q}(1-{\xi }_i)e^{-b{t}_q}}},t\in (t_{k-1}+n\omega ,t_k+n\omega ],k\in \mathbb{N}.$$

Theorem 4.

If $R_0>1$, then there exists a positive constant ρ such that for all positive solutions $(S_h\left(t\right),I_{h1}\left(t\right),I_{h2}\left(t\right),S_v\left(t\right),I_v^a\left(t\right),I_v^n\left(t\right))$ of system (2) satisfies

$$\underset{t\to +\infty }{lim\; inf}{I}_{h1}\left(t\right)\ge \rho ,\underset{t\to +\infty }{lim\; inf}{I}_{h2}\left(t\right)\ge \rho ,\underset{t\to +\infty }{lim\; inf}{I}_v^a\left(t\right)\ge \rho ,\underset{t\to +\infty }{lim\; inf}{I}_v^n\left(t\right)\ge \rho .$$

Proof. 

Let $x=(S_h,I_{h1},I_{h2},S_v,I_v^a,I_v^n)$. Define $M=\{x\mid x\in {\mathbb{R}}_{+}^6\}$, $M_0=\{x\in M\mid I_{h1}\left(t\right)>0,I_{h2}\left(t\right)>0,I_v^a\left(t\right)>0,I_v^n\left(t\right)>0\}$, and $\partial M_0=M\setminus M_0$.

Obviously, both M and $M_0$ are positively invariant and $\partial M_0$ is relatively closed in M and (2) is point dissipative.

Let $u(t,x_0)$ be the solution of the system (2) passing through the initial value $x_0=(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\in M_0$.

Construct the Poincaré map $P:M\to M$,

$$P\left(x_0\right)=u({\omega }^{+},x_0),\forall x_0\in M.$$

Define

$$M_{\partial }=\{(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\in \partial M_0\mid P^m(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\in \partial M_0,\forall m\in \mathbb{N}\}.$$

Then, we have $M_{\partial }=\{(S_h\left(t\right),0,0,S_v\left(t\right),0,0)\in X\mid S_h\left(t\right)\ge 0,S_v\left(t\right)\ge 0,fort\in {\mathbb{R}}_{+}\}$. It is evident that $M_{\partial }\supseteq \{(S_h\left(t\right),0,0,S_v\left(t\right),0,0)\mid S_h\left(t\right)\ge 0,S_v\left(t\right)\ge 0\forall t\ge 0\}$. Next, we aim to show that

$$M_{\partial }\setminus \{(S_h\left(t\right),0,0,S_v\left(t\right),0,0)\in X\mid S_h\left(t\right)\ge 0,S_v\left(t\right)\ge 0,fort\in {\mathbb{R}}_{+}\}=\varnothing .$$

Suppose, for the sake of contradiction, that this is not the case. Then, there exists a point $(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\in M_{\partial }\setminus \{(S_h\left(t\right),0,0,S_v\left(t\right),0,0)\in X\mid S_h\left(t\right)\ge 0,S_v\left(t\right)\ge 0,\mathrm{for}t\in {\mathbb{R}}_{+}\}$. In other words, at least one of $I_{h1}^0,I_{h2}^0,I_v^{a0},I_v^{n0}$ is greater than zero. Without loss of generality, assume $I_{h1}^0>0$, $I_{h2}^0=0,I_v^{a0}=0,I_v^{n0}=0$. From the second equation of system (2), we have for all $t>0$,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{I}_{h1}\left(t\right)}{dt}}\ge -(\sigma +{\mu }_1)I_{h1},t\ne t_k,\hfill \\ I_{h1}\left(t^{+}\right)=(1-d_{1k})I_{h1}\left(t\right),t=t_k,\hfill \\ I_{h1}\left(0^{+}\right)=I_{h1}^0>0.\hfill \end{array}\right.\end{array}$$

Thus, $I_{h1}\left(t\right)>0$ for all $t>0$.

From the third equation of system (2), we have

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{d{I}_{h2}\left(t\right)}{dt}}{|}_{t=0}=\sigma I_{h1}^0>0.\hfill \end{array}\end{array}$$

Thus, we have $I_{h2}>0$ for all $t>0$.

Similarly, we can proof $I_v^a\left(t\right)>0,I_v^n\left(t\right)>0$ for all $t>0$.

Consequently, there exists a positive integer $m_1$ such that $P^{m_1}(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\notin \partial M_0$, that is, $(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\notin M_{\partial }$, which contradicts the assumption. Therefore,

$$M_{\partial }=\{(S_h\left(t\right),0,0,S_v\left(t\right),0,0)\mid S_h\left(t\right)\ge 0,S_v\left(t\right)\ge 0,\forall t\ge 0\}.$$

Denote $P_0=(S_h^{\ast }\left(0\right),0,0,S_v^{\ast }\left(0\right),0,0)$. Next, we prove that $W^s\left(P_0\right)\cap M_0=\varnothing$.

Let $x^0=(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\in M_0$. By the continuous dependence of solutions on initial values, for any $\epsilon >0$, there exists ${\delta }_0>0$ such that if $\Vert x^0-P_0\Vert \le {\delta }_0$, then

$$\Vert u(t,x^0)-u(t,P_0)\Vert \le \epsilon ,t\in [0,\omega ].$$

Next, we first prove that the system is uniformly weakly persistent, that is, there exists a positive constant $\delta$ such that

$$\underset{m\to +\infty }{lim\; sup}d(P^m(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0}),P_0)\ge \delta .$$

Suppose, for the sake of contradiction, that there exists a point $(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})\in M_0$ such that

$$\underset{m\to +\infty }{lim\; sup}d(P^m(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0}),P_0)<\delta .$$

Without loss of generality, we assume that

$$d(P^m(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0}),P_0)<\delta ,\forall m\in N_{+}.$$

Due to the continuity of solutions with respect to initial values, there exists a sufficiently small ${\epsilon }_1>0$ such that

$$\Vert u(t,P^m(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0}))-u(t,P_0)\Vert \le {\epsilon }_1,\forall t\in [0,\omega ],\forall m\in N_{+}.$$

(29)

For any $t^{\prime }\ge 0$, there exists $m\in N_{+}$, such that $t^{\prime }=m\omega +t_1$, where $t_1\in [0,\omega ]$. According to (29), we have

$$\begin{array}{c}\hfill \begin{array}{cc}& \Vert u(t^{\prime },(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0})-u(t^{\prime },P_0)\Vert \hfill \\ & =\Vert u(t_1,P^m(S_h^0,I_{h1}^0,I_{h2}^0,S_v^0,I_v^{a0},I_v^{n0}))-u(t_1,P_0)\Vert \hfill \\ & \le {\epsilon }_1,\hfill \end{array}\end{array}$$

That is, for any $t\ge 0$,

$$0<I_{h_1}\left(t\right)\le {\epsilon }_1,0<I_{h_2}\left(t\right)\le {\epsilon }_1,0<I_v^a\left(t\right)\le {\epsilon }_1,0<I_v^n\left(t\right)\le {\epsilon }_1.$$

(30)

It follows from system (2) and inequalities (30) that

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{S}_h\left(t\right)}{dt}}\ge \alpha (K_1-S_h\left(t\right)-2{\epsilon }_1)-b(P_h^a{\epsilon }_1+P_h^n{\epsilon }_1)-{\mu }_1{S}_h\left(t\right),\hfill \\ {\displaystyle \frac{d{S}_v\left(t\right)}{dt}}\ge r{S}_v\left(t\right)\left(1-{\displaystyle \frac{S_v\left(t\right)+2{\epsilon }_1}{K_2}}\right){\displaystyle \frac{S_h\left(t\right)}{S_h\left(t\right)+2{\epsilon }_1}}-b{p}_v{\displaystyle \frac{{\epsilon }_1+\theta {\epsilon }_1}{S_h\left(t\right)}}{S}_v\left(t\right)\hfill \\ -\mu S_v\left(t\right),\hfill \end{array}\right\}t\ne t_k,\hfill \\ S_v\left(t^{+}\right)=(1-{\theta }_k)S_v\left(t\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.$$

Consider the following impulsive comparison system:

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{\tilde{S}}_h\left(t\right)}{dt}}=\alpha (K_1-{\tilde{S}}_h\left(t\right)-2{\epsilon }_1)-b(P_h^a{\epsilon }_1+P_h^n{\epsilon }_1)-{\mu }_1{\tilde{S}}_h\left(t\right),\hfill \\ {\displaystyle \frac{d{\tilde{S}}_v\left(t\right)}{dt}}=r{\tilde{S}}_v\left(t\right)\left(1-{\displaystyle \frac{{\tilde{S}}_v\left(t\right)+2{\epsilon }_1}{K_2}}\right){\displaystyle \frac{{\tilde{S}}_h\left(t\right)}{{\tilde{S}}_h\left(t\right)+2{\epsilon }_1}}-b{p}_v{\displaystyle \frac{{\epsilon }_1+\theta {\epsilon }_1}{{\tilde{S}}_h\left(t\right)}}{\tilde{S}}_v\left(t\right)\hfill \\ -\mu {\tilde{S}}_v\left(t\right),\hfill \end{array}\right\}t\ne t_k,\hfill \\ {\tilde{S}}_v\left(t^{+}\right)=(1-{\theta }_k){\tilde{S}}_v\left(t\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.$$

(31)

According to Lemma 2 and Lemma 5, we can conclude that system (31) has a positive periodic solution $({\tilde{S}}_h^{\ast }\left(t\right),{\tilde{S}}_v^{\ast }\left(t\right))$, which is globally asymptotically stable. Moreover, $\underset{{\epsilon }_1\to 0}{lim}{\tilde{S}}_h^{\ast }\left(t\right)=S_h^{\ast }\left(t\right)$ and $\underset{{\epsilon }_1\to 0}{lim}{\tilde{S}}_v^{\ast }\left(t\right)=S_v^{\ast }\left(t\right)$. Then, there exists ${\epsilon }_2$ ($0<{\epsilon }_2<\epsilon$) such that

$${\tilde{S}}_h^{\ast }\left(t\right)\ge S_h^{\ast }\left(t\right)-{\epsilon }_2\mathrm{and}{\tilde{S}}_v^{\ast }\left(t\right)\ge S_v^{\ast }\left(t\right)-{\epsilon }_2.$$

In view of the comparison theorem for impulsive differential equations, there exist $t_2\ge t_1$, such that for $t>t_2$,

$$S_h\left(t\right)\ge S_h^{\ast }\left(t\right)-{\epsilon }_{2}and{S}_v\left(t\right)\ge S_v^{\ast }\left(t\right)-{\epsilon }_2.$$

(32)

In addition, by Lemma 4, we know that $\underset{t\to +\infty }{lim}{N}_h\left(t\right)=S_h^{\ast }\left(t\right)$ and $\underset{t\to +\infty }{lim}{N}_v\left(t\right)=S_v^{\ast }\left(t\right)$. Therefore, for the above ${\epsilon }_2$, there exists $t_3>t_2$, such that for $t>t_3$,

$$N_h\left(t\right)\le S_h^{\ast }\left(t\right)+{\epsilon }_2,N_v\left(t\right)\le S_v^{\ast }\left(t\right)+{\epsilon }_2.$$

(33)

From (2), (32), and (33), we have that, for $t>t_3$,

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{I}_{h1}\left(t\right)}{dt}}\ge {\displaystyle \frac{b(S_h^{\ast }\left(t\right)-{\epsilon }_2)(P_h^a{I}_v^a\left(t\right)+P_h^n{I}_v^n\left(t\right))}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}-\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h1}\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_{h2}\left(t\right)}{dt}}=\sigma I_{h1}\left(t\right)-{\mu }_1{I}_{h2}\left(t\right)-{\mu }_2{I}_{h2}\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^a\left(t\right)}{dt}}\ge b{p}_v{\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}(S_v^{\ast }\left(t\right)-{\epsilon }_2)-\mu I_v^a\left(t\right),\hfill \\ {\displaystyle \frac{d{I}_v^n\left(t\right)}{dt}}\ge r(S_v^{\ast }\left(t\right)-{\epsilon }_2)\left(1-{\displaystyle \frac{S_v^{\ast }\left(t\right)+{\epsilon }_2}{K_2}}\right){\displaystyle \frac{I_{h1}\left(t\right)+\theta I_{h2}\left(t\right)}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}-\mu I_v^n\left(t\right),\hfill \end{array}\right\}t\ne t_k,\hfill \\ \left.\begin{array}{c}{I}_{h1}\left(t^{+}\right)=(1-{\theta }_k)I_v^a\left(t\right),\hfill \\ I_{h2}\left(t^{+}\right)=(1-{\theta }_k)I_v^a\left(t\right),\hfill \\ I_v^a\left(t^{+}\right)=(1-{\theta }_k)I_v^a\left(t\right),\hfill \\ I_v^n\left(t^{+}\right)=(1-{\theta }_k)I_v^n\left(t\right),\hfill \end{array}\right\}t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.$$

Similar to the proof method in the previous section, denote

$$U\left(t\right)={({\overline{I}}_{h1}\left(t\right),{\overline{I}}_{h2}\left(t\right),{\overline{I}}_v^a\left(t\right),{\overline{I}}_v^n\left(t\right))}^T$$

and consider the following comparison system:

$$\left\{\begin{array}{c}{U}^{\prime }\left(t\right)={(F-V)}_{{\epsilon }_2}U\left(t\right),t\ne t_k,\hfill \\ U\left(t_k^{+}\right)=P_{k}U\left(t_k\right),t=t_k,(k\in \mathbb{N}).\hfill \end{array}\right.$$

(34)

where

$${(F-V)}_{{\epsilon }_2}=\left(\begin{array}{cccc}-(\sigma +{\mu }_1)& 0& b{\displaystyle \frac{S_h^{\ast }\left(t\right)-{\epsilon }_2}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}{P}_h^a& b{\displaystyle \frac{S_h^{\ast }\left(t\right)-{\epsilon }_2}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}{P}_h^n\\ \sigma & -({\mu }_1+{\mu }_2)& 0& 0\\ b{P}_v{\displaystyle \frac{S_v^{\ast }\left(t\right)-{\epsilon }_2}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}& \theta b{P}_v{\displaystyle \frac{S_v^{\ast }\left(t\right)+{\epsilon }_2}{S_h^{\ast }\left(t\right)-{\epsilon }_2}}& -\mu & 0\\ W_2& W_3& 0& -\mu \end{array}\right)$$

and $W_2={\displaystyle \frac{r(S_v^{\ast }\left(t\right)-{\epsilon }_2)}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}\left(1-{\displaystyle \frac{S_v^{\ast }\left(t\right)+{\epsilon }_2}{K_2}}\right)$, $W_3={\displaystyle \frac{r(S_v^{\ast }\left(t\right)-{\epsilon }_2)}{S_h^{\ast }\left(t\right)+{\epsilon }_2}}\left(1-{\displaystyle \frac{S_v^{\ast }\left(t\right)+{\epsilon }_2}{K_2}}\right)$.

By Theorem 1, we know that $R_0>1$ is equivalent to $r\left({\mathrm{\Phi }}_{(F-V)P_k}\left(\omega \right)\right)>1$. Therefore, for above sufficiently small ${\epsilon }_2$, we have

$$r\left({\mathrm{\Phi }}_{{(F-V)}_{{\epsilon }_2}{P}_k}\left(\omega \right)\right)>1.$$

(35)

According to Lemma 3, there exists a positive periodic function $\varrho \left(t\right)=({\overline{I}}_{h1}\left(t\right),{\overline{I}}_{h2}\left(t\right),{\overline{I}}_v^a\left(t\right),$${\overline{I}}_v^n\left(t\right))$ such that $e^{{\eta }_{2}t}\varrho \left(t\right)$ is a solution of (34), where ${\eta }_2={\displaystyle \frac{1}{\omega }}lnr\left({\mathrm{\Phi }}_{{(F-V)}_{{\epsilon }_2}{P}_k}\left(\omega \right)\right)$. From (35), we know that ${\eta }_2>0$. Therefore, as $t\to +\infty$, $e^{{\eta }_{2}t}\varrho \left(t\right)\to +\infty$. By the comparison theorem, it follows that as $t\to +\infty$, $I_{h1}\left(t\right)\to +\infty$, $I_{h2}\left(t\right)\to +\infty$, $I_v^n\left(t\right)\to +\infty$, $I_v^a\left(t\right)\to +\infty$. This contradicts the assumption. Thus, $W^s\left(P_0\right)\cap M_0=\varnothing$.

In conclusion, when $R_0>1$, the disease will be uniformly persistent. □

5. Numerical Simulation

This section presents numerical simulations to validate the threshold conditions for disease extinction ($R_0<1$) versus persistence ($R_0>1$) in HLB. The model tracks susceptible ($S_h$) and infected ($I_{h1},I_{h2}$) citrus trees, alongside susceptible ($S_v$) and infected ($I_v^a,I_v^n$) psyllids. The initial values are taken as: $S_h\left(0\right)=1.8$, $I_{h1}\left(0\right)=0.18$, $I_{h2}\left(0\right)=0.02$,$S_v\left(0\right)=18$, $I_v^a\left(0\right)=1.8$, $I_v^n\left(0\right)=0.2$.

At the impulsive time $t_k,k=1,2,3,4$, we set the specific parameters as follows: ${\theta }_1=0.5$, ${\theta }_2=0.3$, ${\theta }_3=0.3$, ${\theta }_4=0.3$, $d_{11}=0.3,$ $d_{12}=0.2,$ $d_{13}=0.25,$ $d_{14}=0.1,$ $d_{21}=0.7,$ $d_{22}=0.3,$ $d_{23}=0.35,$ $d_{24}=0.1.$ Additionally, the feeding rate of psyllids on citrus trees is set to $b=0.4$, and other parameters are listed in Table 1, the basic reproduction number $R_0=0.7294<1$, indicating the disease will be eventually extinct (see Figure 1). For $b=2$, the basic reproduction number $R_0=1.6447>1$, indicating the disease will be endemic (see Figure 2). Therefore, when $R_0<1$, interventions (e.g., agricultural control, biological control, and physical control) that reduce the feeding rate b below critical thresholds can eradicate HLB.

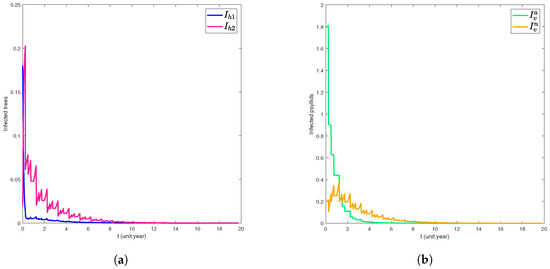
Figure 1. Time series graph of citrus trees and ACP dynamics. For the parameter $b=0.4$, the basic reproduction number $R_0=0.7294<1$, indicating disease suppression under this condition. (a) infected citrus trees $I_{h1}$ and $I_{h2}$. (b) infected ACP $I_v^a$ and $I_v^n$.

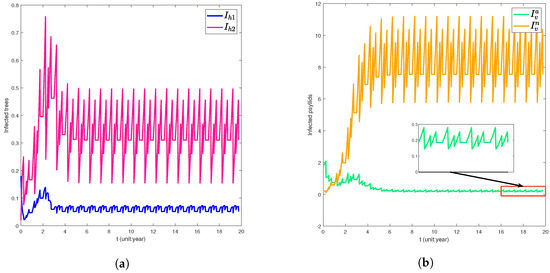
Figure 2. Time series graph of citrus trees and ACP dynamics. For the parameter $b=2$, the basic reproduction number $R_0=1.6447>1$, indicating sustained disease transmission. (a) infected citrus trees $I_{h1}$ and $I_{h2}$. (b) infected ACP $I_v^a$ and $I_v^n$.

We examine the influence of several model parameters on the basic reproduction number $R_0$ as illustrated in Figure 3. Specifically, we set the removal rates of infected plants ($I_{h1}$ and $I_{h2}$), as well as the killing rates of psyllids due to pesticide spraying, to be equal at impulsive time $t_k$. That is, $d_{1k}=d_{2k},k=1,2,3,4$, and ${\theta }_k={\theta }_0,k=1,2,3,4$. Figure 3a shows how $R_0$ varies with the feeding rate b. We observe that $R_0$ increases as b increases. Figure 3b shows how $R_0$ varies with the killing rate of psyllids ${\theta }_0$. We observe that $R_0$ decreases as ${\theta }_0$ increases. When ${\theta }_0\ge 0.6061$, $R_0$ is close to zero and becomes insensitive to changes in ${\theta }_0$. And Figure 3c shows how $R_0$ varies with the removal rate of infected tree d. We observe that $R_0$ decreases as d increases.

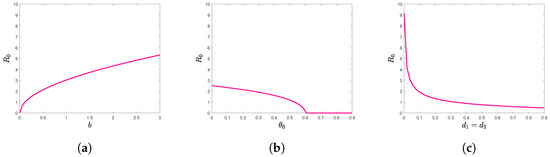
Figure 3. The relationship graphs between $R_0$ and some parameters, (a) b versus $R_0$, (b) ${\theta }_0$ versus $R_0$, (c) d versus $R_0$.

6. Conclusions and Discussion

This study develops an innovative impulsive differential equation model to address HLB transmission dynamics by integrating seasonal psyllid population fluctuations with multi-pronged control strategies: (1) periodic removal of infected/dead citrus trees to eliminate pathogen reservoirs, and (2) non-uniformly timed pesticide applications optimized for psyllid life cycles. The model analytically derives the basic reproduction number ($R_0$) and rigorously establishes the existence of a unique disease-free periodic solution. Theoretical breakthroughs demonstrate threshold-dependent stability: when $R_0<1$, the disease-free periodic solution is globally asymptotically stable, ensuring disease extinction; when $R_0>1$, the system transitions to uniform persistence, indicating endemic HLB. These results quantitatively link intervention timing/intensity to $R_0$ suppression, offering a mathematical foundation for strategic pest management.

The results presented in Figure 3 of the numerical simulations clearly illustrate the relationships between the parameters b (feeding rate of psyllids), ${\theta }_0$ (removal rate of infected trees), d (killing rate of psyllids), and the basic reproduction number $R_0$, respectively. As a result, a combination of integrated interventions, such as vector control focusing on psyllid management, timely removal of infected plants, and reduction in psyllid feeding rates, can substantially impede the spread of citrus HLB. This model provides citrus growers with the following scientifically supported control strategies:

(i) 

Multi-pronged psyllid population control

• Chemical control: rational use of high-efficiency, low-toxicity pesticides to target adult psyllids, with careful attention to resistance management.
• Cultural management: practices such as pruning water sprouts and synchronizing flush cycles can reduce psyllid oviposition sites and disrupt their reproductive cycle.
• Biological and physical control: combining yellow sticky traps (exploiting adult phototaxis) with natural enemies (e.g., Tamarixia radiata) for eco-friendly pest suppression.

(ii) 

Application of botanical repellents

Given psyllids’ sensitivity to plant-derived volatiles (e.g., neem oil, azadirachtin), spraying such formulations during new flush stages can reduce feeding activity, lowering pathogen transmission risk while avoiding chemical pesticide residues.

Although the numerical simulations in this study offer critical insights into HLB transmission dynamics under impulsive control, the lack of empirical field data for direct validation remains a limitation. To enhance the model’s robustness and real-world relevance, future research should focus on acquiring field measurements under representative conditions. These empirical datasets would facilitate rigorous benchmarking against simulated outputs, enabling refinement of model accuracy and identification of systemic discrepancies.