Reconstruction of Random Structures Based on Generative Adversarial Networks: Statistical Variability of Mechanical and Morphological Properties
Abstract
1. Introduction
2. Models and Methods
2.1. Synthesis of Random Open-Cell Bicontinuous Geometry
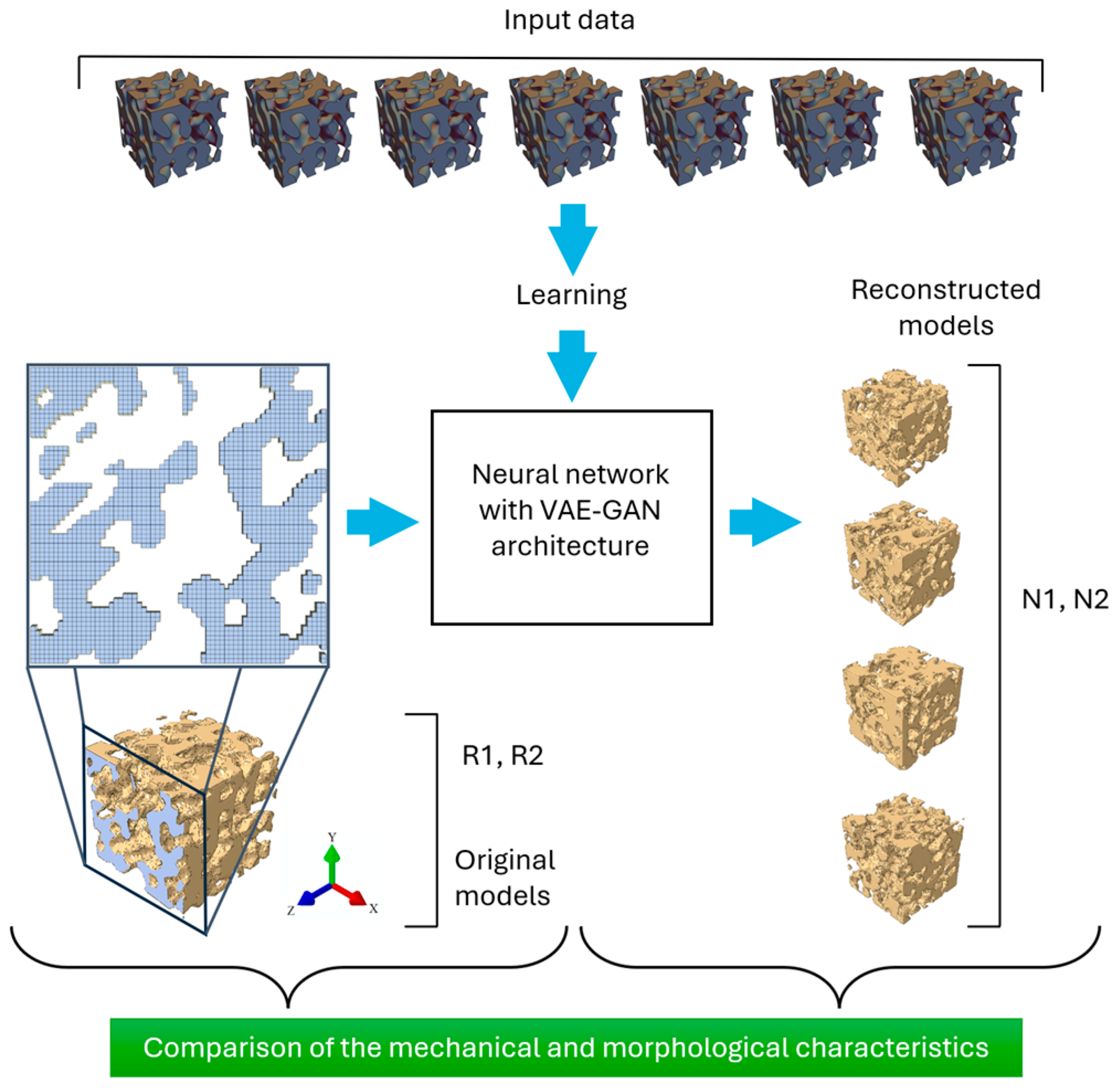
2.2. NN for 3D Reconstruction
2.3. Mechanical Characterization
2.4. Morphological Characterization
3. Results
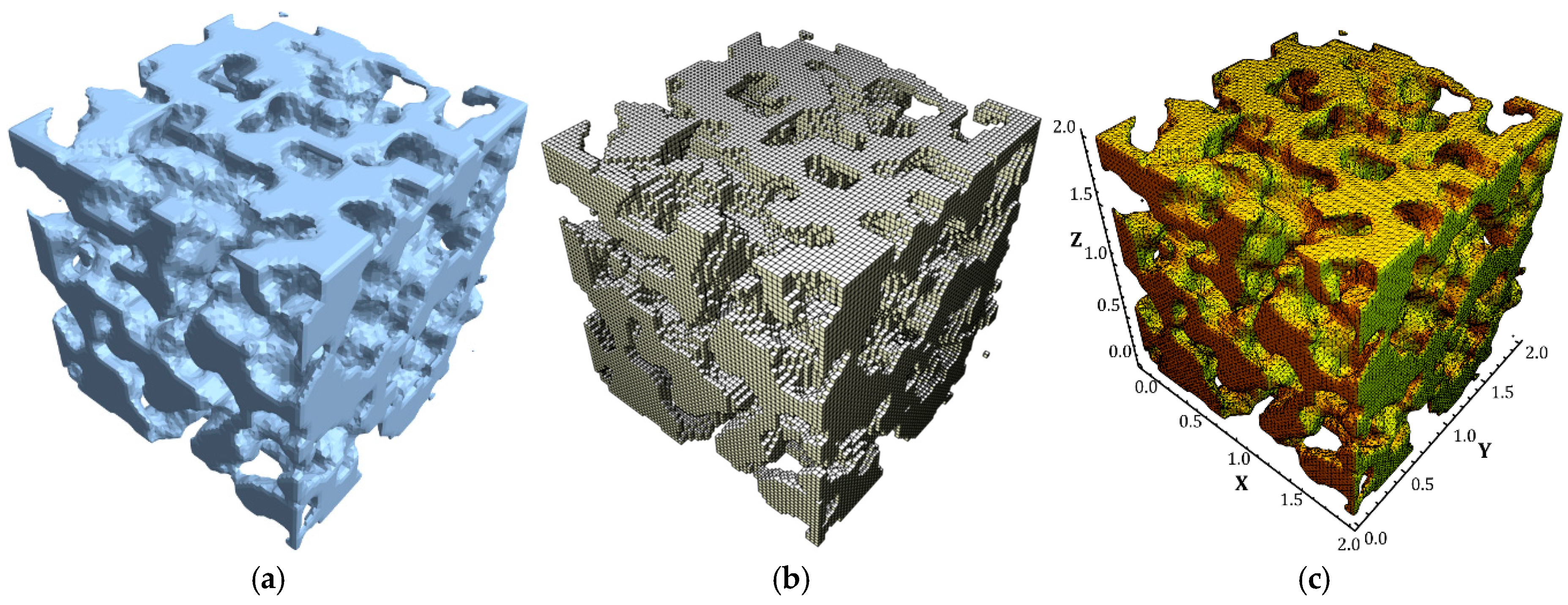
3.1. 3D Model Reconstruction
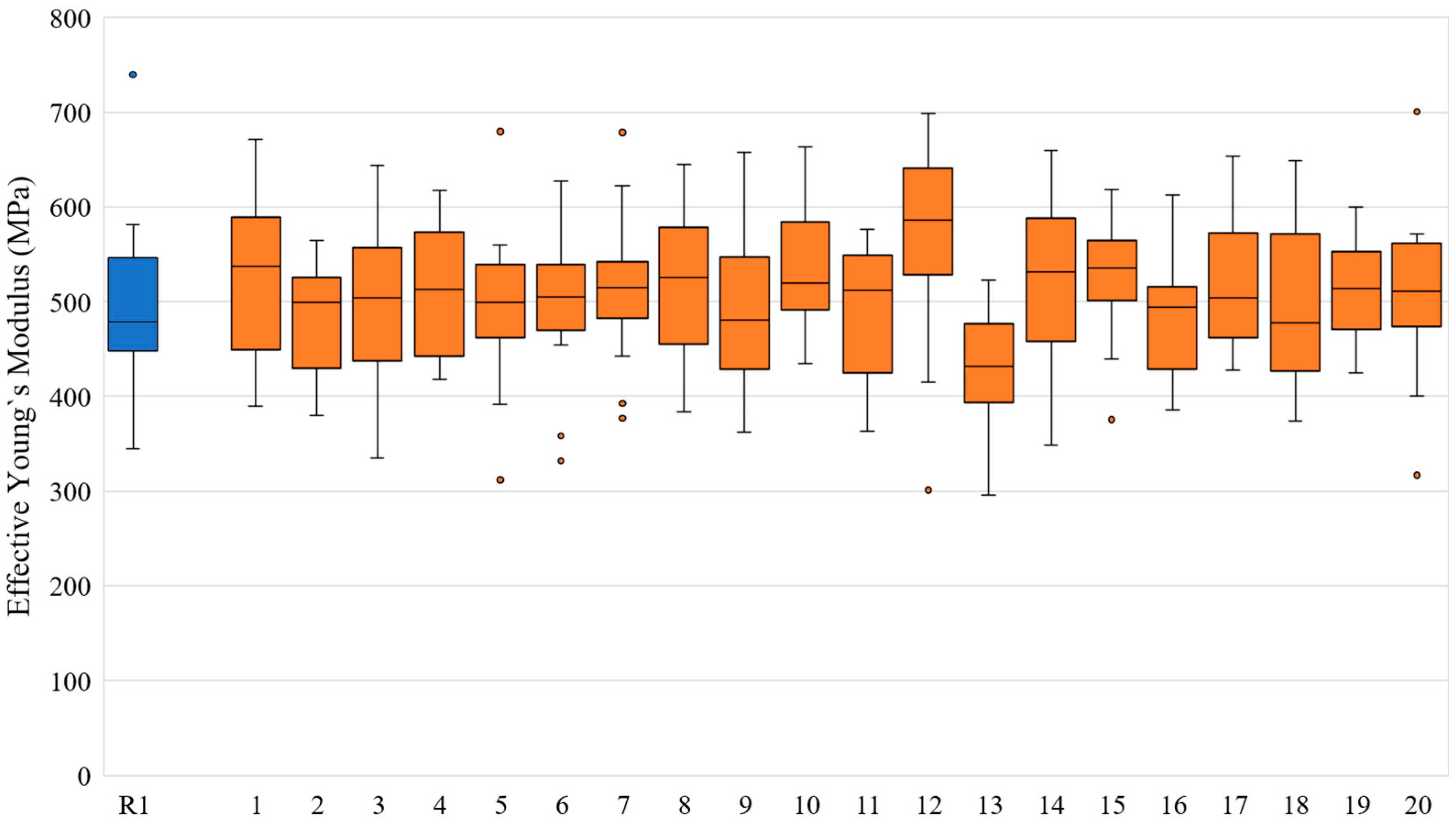
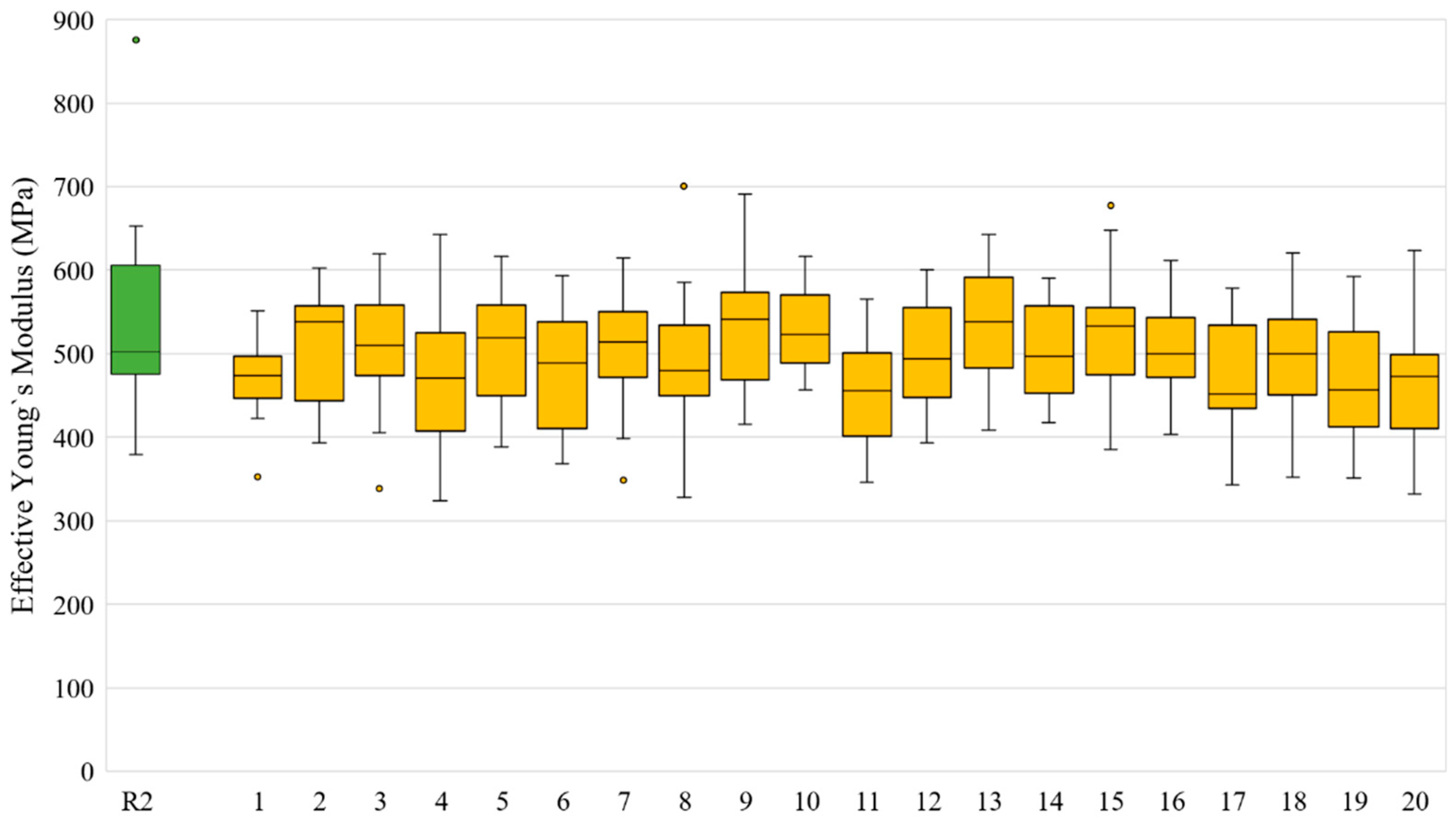
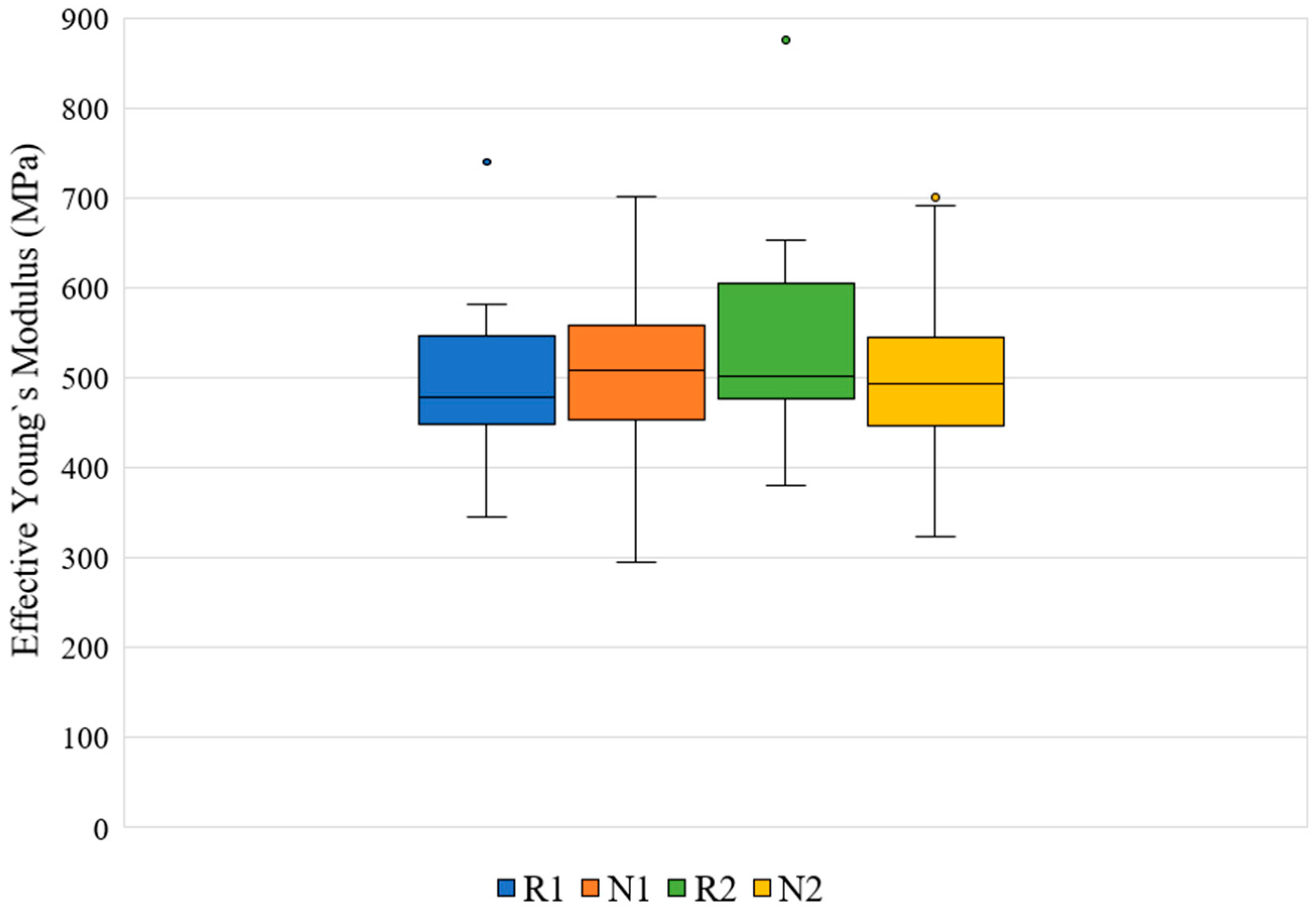
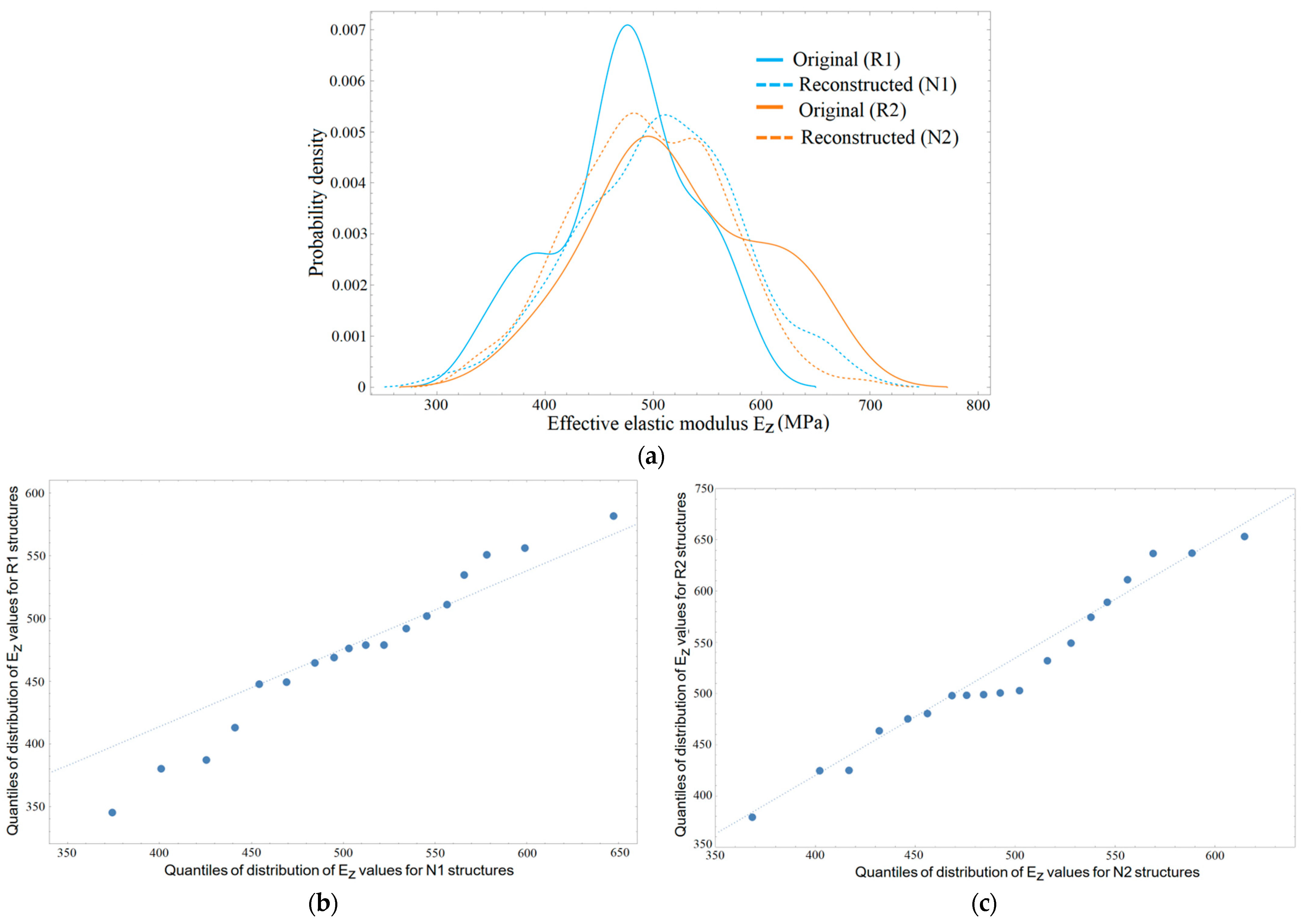
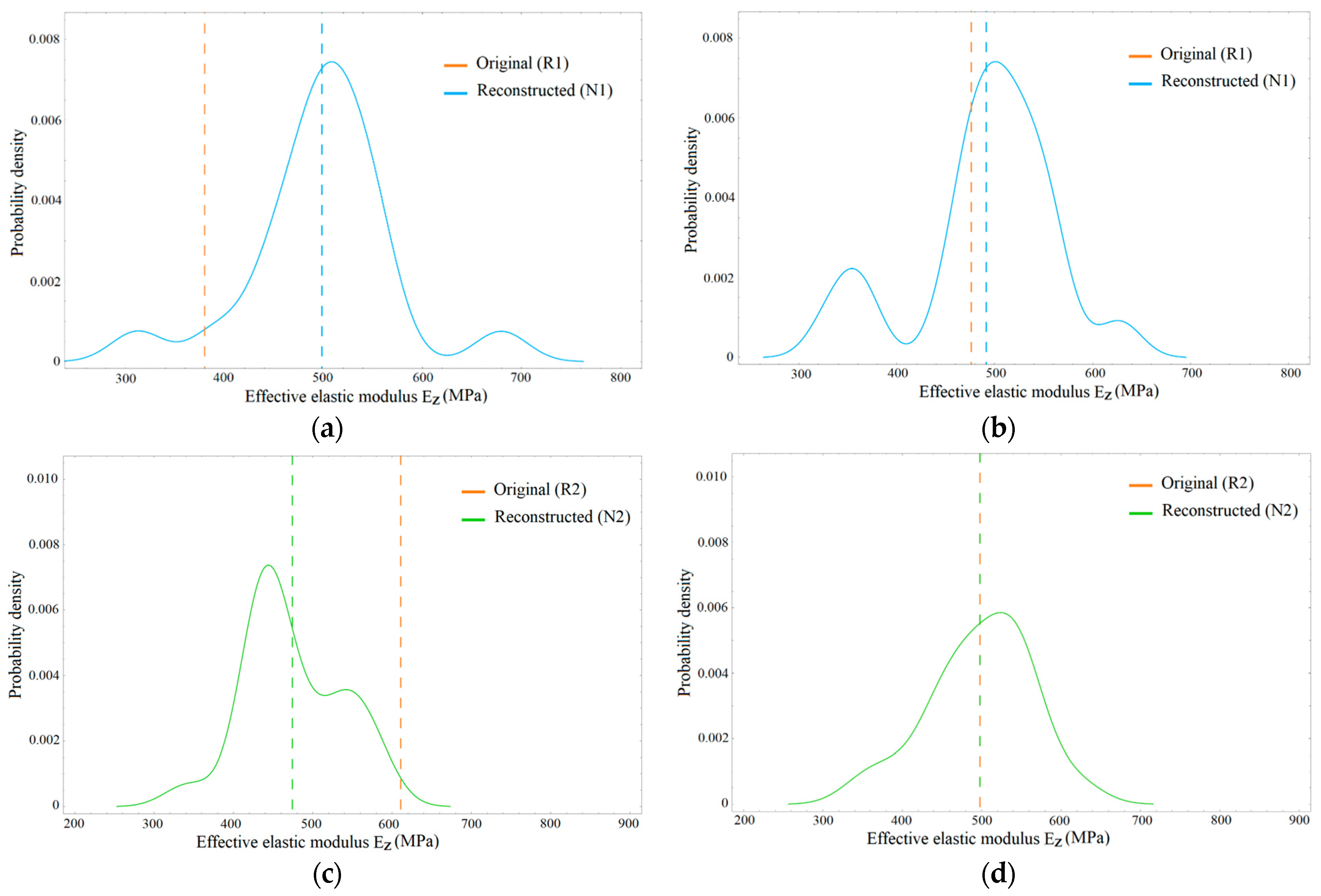
3.2. Distribution of Elastic Properties
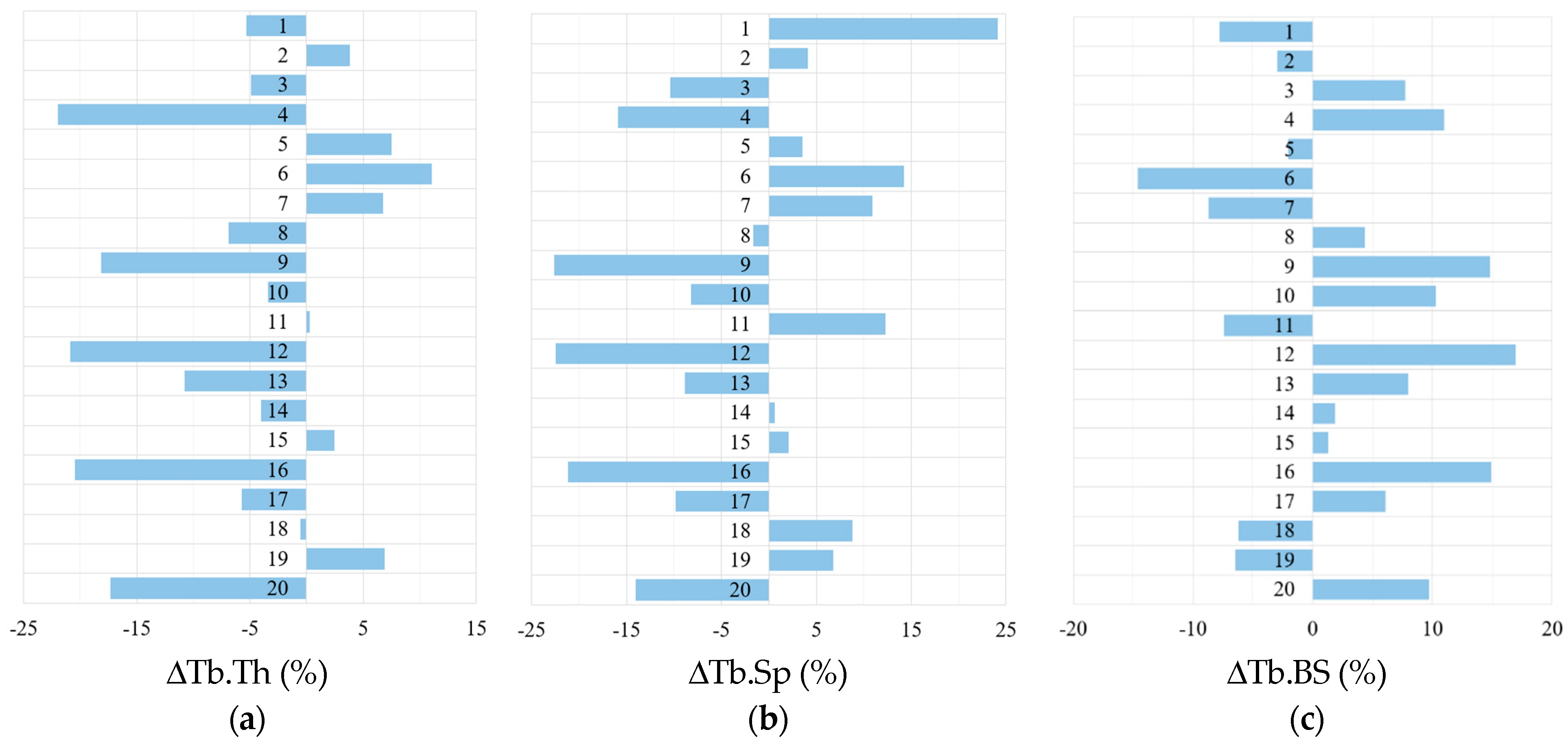
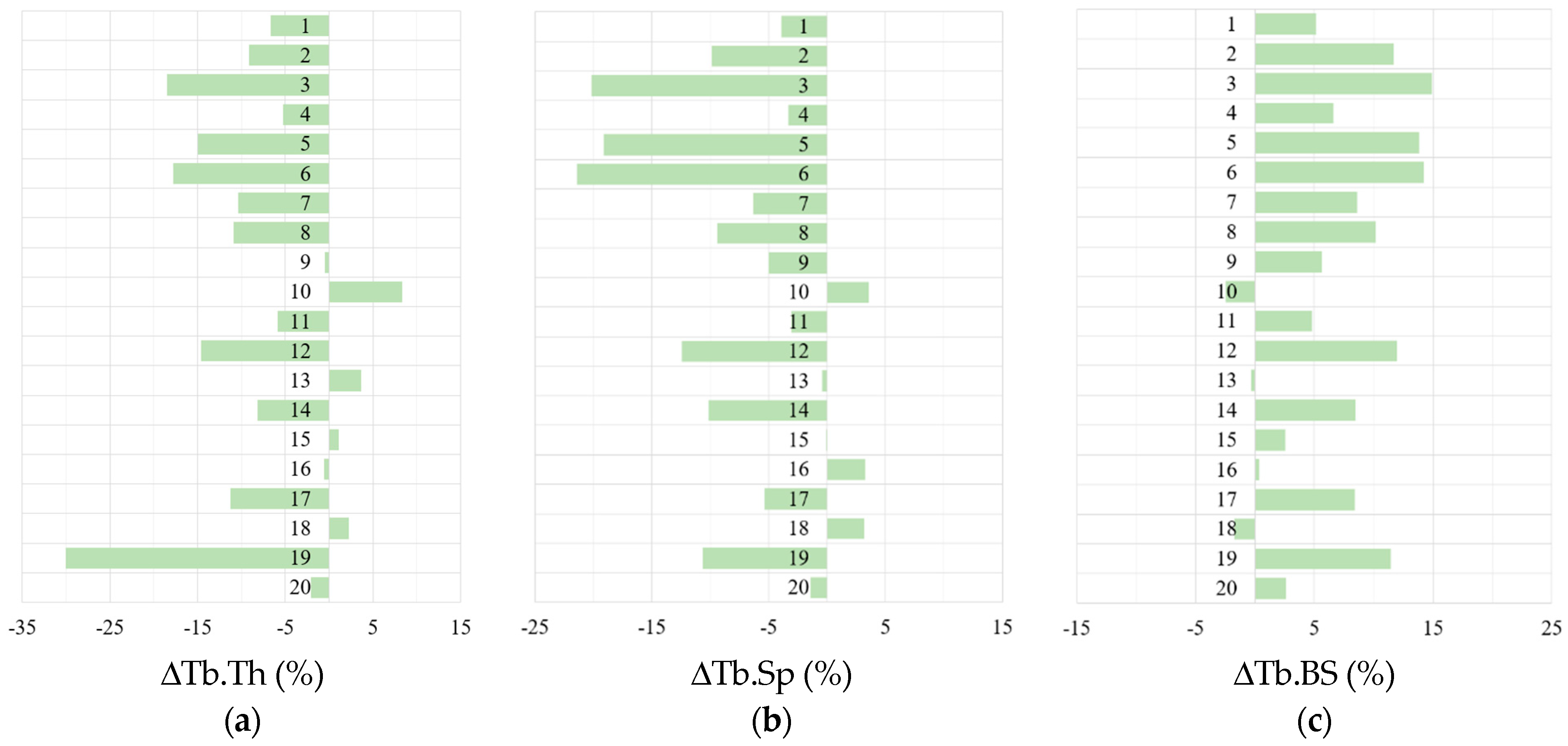
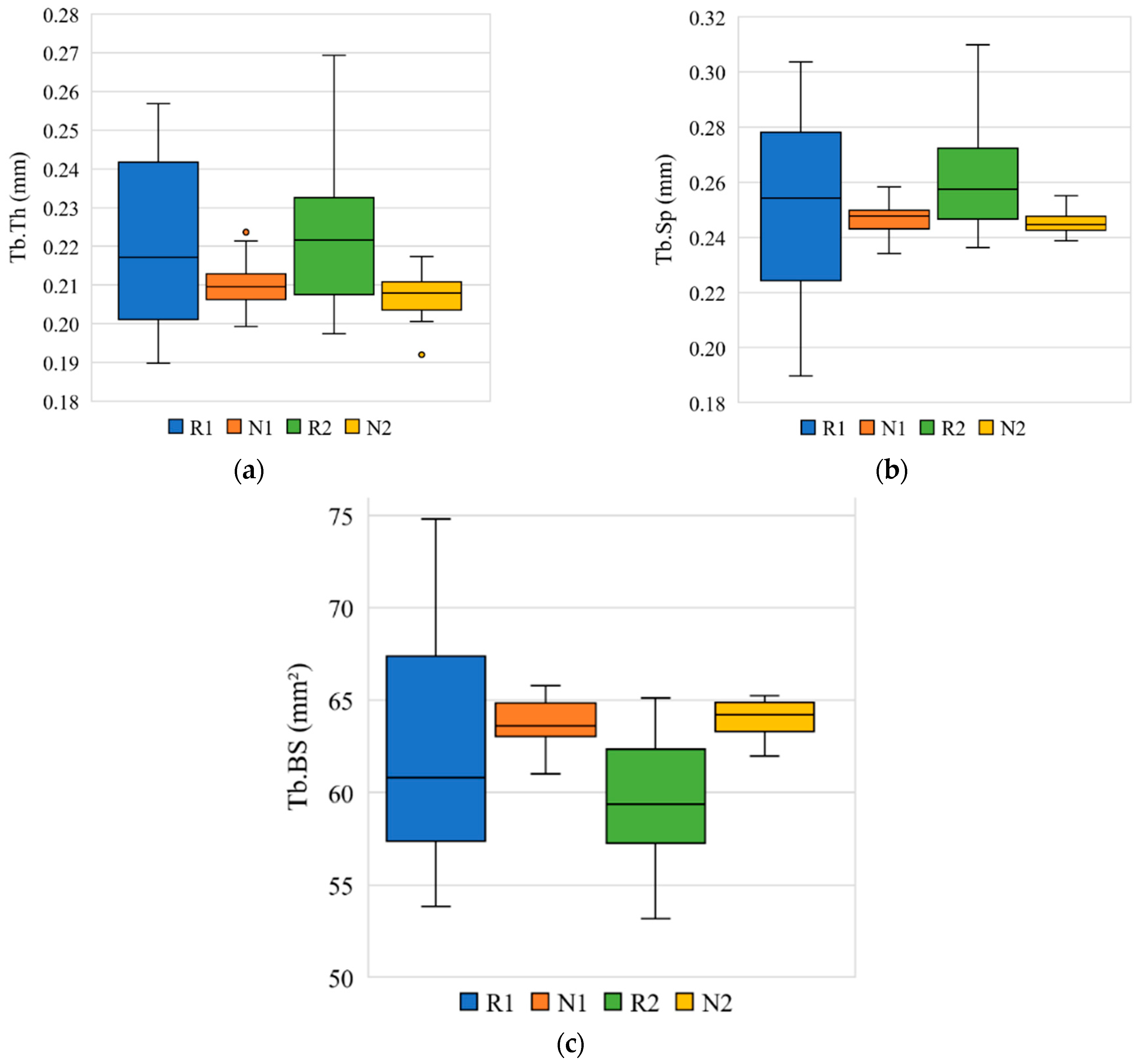
3.3. Morphometric Analysis
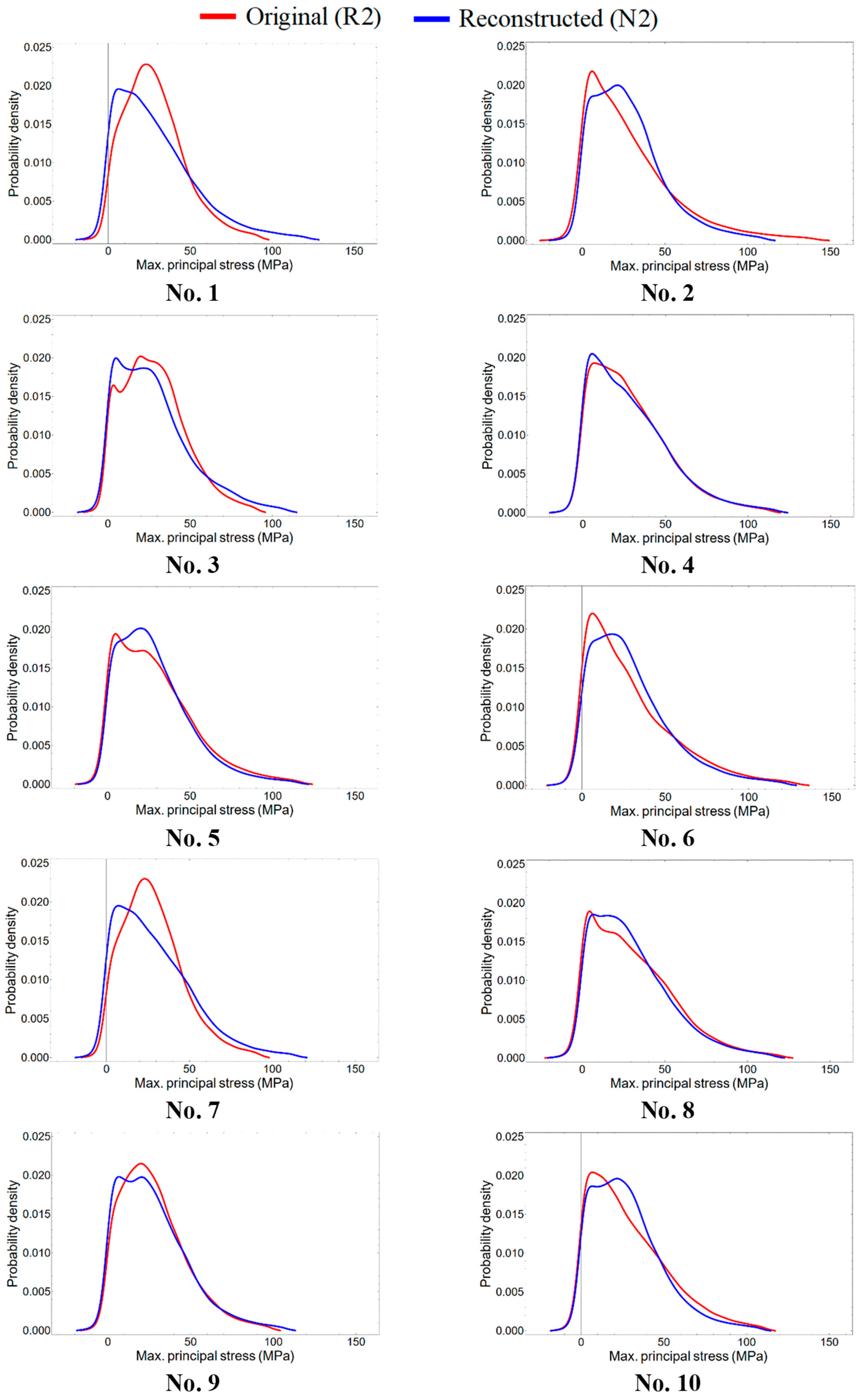
3.4. Stress Distributions
4. Discussion
4.1. Effective Elastic Modulus
4.2. Correspondence of Internal Stress State
4.3. Morphometric Characteristics and Statistical Metrics
4.4. Achievements, Limitations and Possible Extensions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, X.; Zhu, W.; Yang, Z.; He, N.; Chen, F.; Han, X.; Zhou, K. Recent Advances in 3D Printing of Smart Scaffolds for Bone Tissue Engineering and Regeneration. Adv. Mater. 2024, 36, e2403641. [Google Scholar] [CrossRef] [PubMed]
- Brown, N.K.; Garland, A.P.; Fadel, G.M.; Li, G. Deep reinforcement learning for the rapid on-demand design of mechanical metamaterials with targeted nonlinear deformation responses. Eng. Appl. Artif. Intell. 2023, 126, 106998. [Google Scholar] [CrossRef]
- Hsu, Y.C.; Yang, Z.; Buehler, M.J. Generative design, manufacturing, and molecular modeling of 3D architected materials based on natural language input. APL Mater. 2022, 10, 041107. [Google Scholar] [CrossRef]
- Generale, A.P.; Robertson, A.E.; Kelly, C.; Kalidindi, S.R. Inverse stochastic microstructure design. Acta Mater. 2024, 271, 119877. [Google Scholar] [CrossRef]
- Ng, W.L.; Goh, G.L.; Goh, G.D.; Sheuan, J.; Ten, J.; Yeong, W.Y. Progress and Opportunities for Machine Learning in Materials and Processes of Additive Manufacturing. Adv. Mater. 2024, 36, e2310006. [Google Scholar] [CrossRef]
- Mao, Y.; He, Q.; Zhao, X. Designing complex architectured materials with generative adversarial networks. Sci. Adv. 2020, 6, eaaz4169. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Z.; Song, Z. A generative machine learning model for the 3D reconstruction of material microstructure and performance evaluation. Comput. Methods Appl. Mech. Eng. 2024, 430, 117224. [Google Scholar] [CrossRef]
- Lyu, X.; Ren, X. Microstructure reconstruction of 2D/3D random materials via diffusion-based deep generative models. Sci. Rep. 2024, 14, 5041. [Google Scholar] [CrossRef]
- He, J.; Kushwaha, S.; Abueidda, D.; Jasiuk, I. Exploring the structure-property relations of thin-walled, 2D extruded lattices using neural networks. Comput. Struct. 2023, 277, 106940. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhao, Z.; Lei, H.; Wang, P. A deep learning approach for inverse design of gradient mechanical metamaterials. Int. J. Mech. Sci. 2023, 240, 107920. [Google Scholar] [CrossRef]
- Challapalli, A.; Patel, D.; Li, G. Inverse machine learning framework for optimizing lightweight metamaterials. Mater. Des. 2021, 208, 109937. [Google Scholar] [CrossRef]
- Jiao, P.; Alavi, A.H. Artificial intelligence-enabled smart mechanical metamaterials: Advent and future trends. Int. Mater. Rev. 2021, 66, 365–393. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Zahedi, S.A.; Ismail, S.O.; Olawade, D.B. Recent advances in biopolymeric composite materials: Future sustainability of bone-implant. Renew. Sustain. Energy Rev. 2021, 150, 111505. [Google Scholar] [CrossRef]
- Fujita, A.; Goto, K.; Ueda, A.; Kuroda, Y.; Kawai, T.; Okuzu, Y.; Okuno, Y.; Matsuda, S. Measurement of the Acetabular Cup Orientation After Total Hip Arthroplasty Based on 3-Dimensional Reconstruction From a Single X-Ray Image Using Generative Adversarial Networks. J. Arthroplast. 2024, 40, 136–143. [Google Scholar] [CrossRef]
- Wu, C.; Wan, B.; Entezari, A.; Fang, J.; Xu, Y.; Li, Q. Machine learning-based design for additive manufacturing in biomedical engineering. Int. J. Mech. Sci. 2024, 266, 108828. [Google Scholar] [CrossRef]
- Yang, Z.; Yabansu, Y.C.; Al-Bahrani, R.; Liao, W.K.; Choudhary, A.N.; Kalidindi, S.R.; Agrawal, A. Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Comput. Mater. Sci. 2018, 151, 278–287. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Brinson, L.C.; Choudhary, A.N.; Chen, W.; Agrawal, A. Microstructural materials design via deep adversarial learning methodology. J. Mech. Des. Trans. ASME 2018, 140, 111416. [Google Scholar] [CrossRef]
- Yang, Z.; Yabansu, Y.C.; Jha, D.; Liao, W.K.; Choudhary, A.N.; Kalidindi, S.R.; Agrawal, A. Establishing structure-property localization linkages for elastic deformation of three-dimensional high contrast composites using deep learning approaches. Acta Mater. 2019, 166, 335–345. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, L.; Li, C.; Wu, B.; Wang, W. ScaffoldGAN: Synthesis of Scaffold Materials based on Generative Adversarial Networks. CAD Comput. Aided Des. 2021, 138, 103041. [Google Scholar] [CrossRef]
- Shams, R.; Masihi, M.; Boozarjomehry, R.B.; Blunt, M.J. A hybrid of statistical and conditional generative adversarial neural network approaches for reconstruction of 3D porous media (ST-CGAN). Adv. Water Resour. 2021, 158, 104064. [Google Scholar] [CrossRef]
- Zhang, F.; Teng, Q.; Chen, H.; He, X.; Dong, X. Slice-to-voxel stochastic reconstructions on porous media with hybrid deep generative model. Comput. Mater. Sci. 2021, 186, 110018. [Google Scholar] [CrossRef]
- Chiang, Y.H.; Tseng, B.Y.; Wang, J.P.; Chen, Y.W.; Tung, C.C.; Yu, C.H.; Chen, P.Y.; Chen, C.S. Generating three-dimensional bioinspired microstructures using transformer-based generative adversarial network. J. Mater. Res. Technol. 2023, 27, 6117–6134. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, H.; Dong, Q. Machine learning-based inverse design of auxetic metamaterial with zero Poisson’s ratio. Mater. Today Commun. 2022, 30, 103186. [Google Scholar] [CrossRef]
- Bhuwal, A.S.; Pang, Y.; Ashcroft, I.; Sun, W.; Liu, T. Discovery of quasi-disordered truss metamaterials inspired by natural cellular materials. J. Mech. Phys. Solids 2023, 175, 105294. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, X.; Chen, T.T.; Watanabe, I. Deep Learning in Mechanical Metamaterials: From Prediction and Generation to Inverse Design. Adv. Mater. 2023, 35, 2302530. [Google Scholar] [CrossRef]
- Qian, C.; Tan, R.K.; Ye, W. Design of architectured composite materials with an efficient, adaptive artificial neural network-based generative design method. Acta Mater. 2022, 225, 117548. [Google Scholar] [CrossRef]
- Fullwood, D.T.; Niezgoda, S.R.; Adams, B.L.; Kalidindi, S.R. Microstructure sensitive design for performance optimization. Prog. Mater. Sci. 2010, 55, 477–562. [Google Scholar] [CrossRef]
- Pirogova, Y.; Tashkinov, M.; Vindokurov, I.; Silberschmidt, V.V. Elastic properties and compressive mechanical behaviour of closed-cell porous materials: Effect of microstructural morphology. Int. J. Solids Struct. 2024, 295, 112791. [Google Scholar] [CrossRef]
- Zhu, R.; Galoogahi, H.K.; Wang, C.; Lucey, S. Rethinking Reprojection: Closing the Loop for Pose-Aware Shape Reconstruction from a Single Image. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 57–65. [Google Scholar]
- Mosser, L.; Dubrule, O.; Blunt, M.J. Reconstruction of three-dimensional porous media using generative adversarial neural networks. Phys. Rev. E 2017, 96, 043309. [Google Scholar] [CrossRef]
- Kononov, E.; Tashkinov, M.; Silberschmidt, V.V. Reconstruction of 3D Random Media from 2D Images: Generative Adversarial Learning Approach. CAD Comput. Aided Des. 2023, 158, 103498. [Google Scholar] [CrossRef]
- Shalimov, A.; Tashkinov, M. Numerical investigation of damage accumulation and failure processes in random porous bicontinuous media. Procedia Struct. Integr. 2020, 25, 386–393. [Google Scholar] [CrossRef]
- Larsen, A.B.L.; Sønderby, S.K.; Larochelle, H.; Winther, O. Autoencoding beyond pixels using a learned similarity metric. 33rd Int. Conf. Mach. Learn. ICML 2015, 4, 2341–2349. [Google Scholar] [CrossRef]
- Torquato, S. Statistical description of microstructures. Annu. Rev. Mater. Sci. 2002, 32, 77–111. [Google Scholar] [CrossRef]
- Tashkinov, M. Micro-scale modeling of phase-level elastic fields of SiC reinforced metal matrix multiphase composites using statistical approach. Comput. Mater. Sci. 2016, 116, 113–121. [Google Scholar] [CrossRef]
- Tashkinov, M.; Wildemann, V.; Mikhailova, N. Method of successive approximations in stochastic elastic boundary value problem for structurally heterogenous materials. Comput. Mater. Sci. 2012, 52, 101–106. [Google Scholar] [CrossRef]
- Nielson, G.M. Dual Marching Cubes. In Proceedings of the IEEE Visualization 2004, Austin, TX, USA, 10–15 October 2004; pp. 489–496. [Google Scholar] [CrossRef]
- Du, J.; Brooke-Wavell, K.; Paggiosi, M.A.; Hartley, C.; Walsh, J.S.; Silberschmidt, V.V.; Li, S. Characterising variability and regional correlations of microstructure and mechanical competence of human tibial trabecular bone: An in-vivo HR-pQCT study. Bone 2019, 121, 139–148. [Google Scholar] [CrossRef]
- Vafaeefar, M.; Moerman, K.M.; Kavousi, M.; Vaughan, T.J. A morphological, topological and mechanical investigation of gyroid, spinodoid and dual-lattice algorithms as structural models of trabecular bone. J. Mech. Behav. Biomed. Mater. 2023, 138, 105584. [Google Scholar] [CrossRef] [PubMed]
- Steiner, L.; Synek, A.; Pahr, D.H. Comparison of different microCT-based morphology assessment tools using human trabecular bone. Bone Rep. 2020, 12, 100261. [Google Scholar] [CrossRef] [PubMed]
- Hildebrand, T.; Rüegsegger, P. A new method for the model-independent assessment of thickness in three-dimensional images. J. Microsc. 1997, 185, 67–75. [Google Scholar] [CrossRef]
- Ajayi, E.A.; Lim, K.M.; Chong, S.-C.; Lee, C.P. 3D Shape Generation via Variational Autoencoder with Signed Distance Function Relativistic Average Generative Adversarial Network. Appl. Sci. 2023, 13, 5925. [Google Scholar] [CrossRef]
- Yu, M.-S.; Jung, T.-W.; Yun, D.-Y.; Hwang, C.-G.; Park, S.-Y.; Kwon, S.-C.; Jung, K.-D. A Variational Autoencoder Cascade Generative Adversarial Network for Scalable 3D Object Generation and Reconstruction. Sensors 2024, 24, 751. [Google Scholar] [CrossRef] [PubMed]
- Sami, M.; Mobin, I. A Comparative Study on Variational Autoencoders and Generative Adversarial Networks. In Proceedings of the 2019 International Conference on Artificial Intelligence and Information Technology (ICAIIT), Wuhan, China, 12–13 July 2019; pp. 1–5. [Google Scholar]
- Molnár, S.; Tamás, L. Variational autoencoders for 3D data processing. Artif. Intell. Rev. 2024, 57, 42. [Google Scholar] [CrossRef]
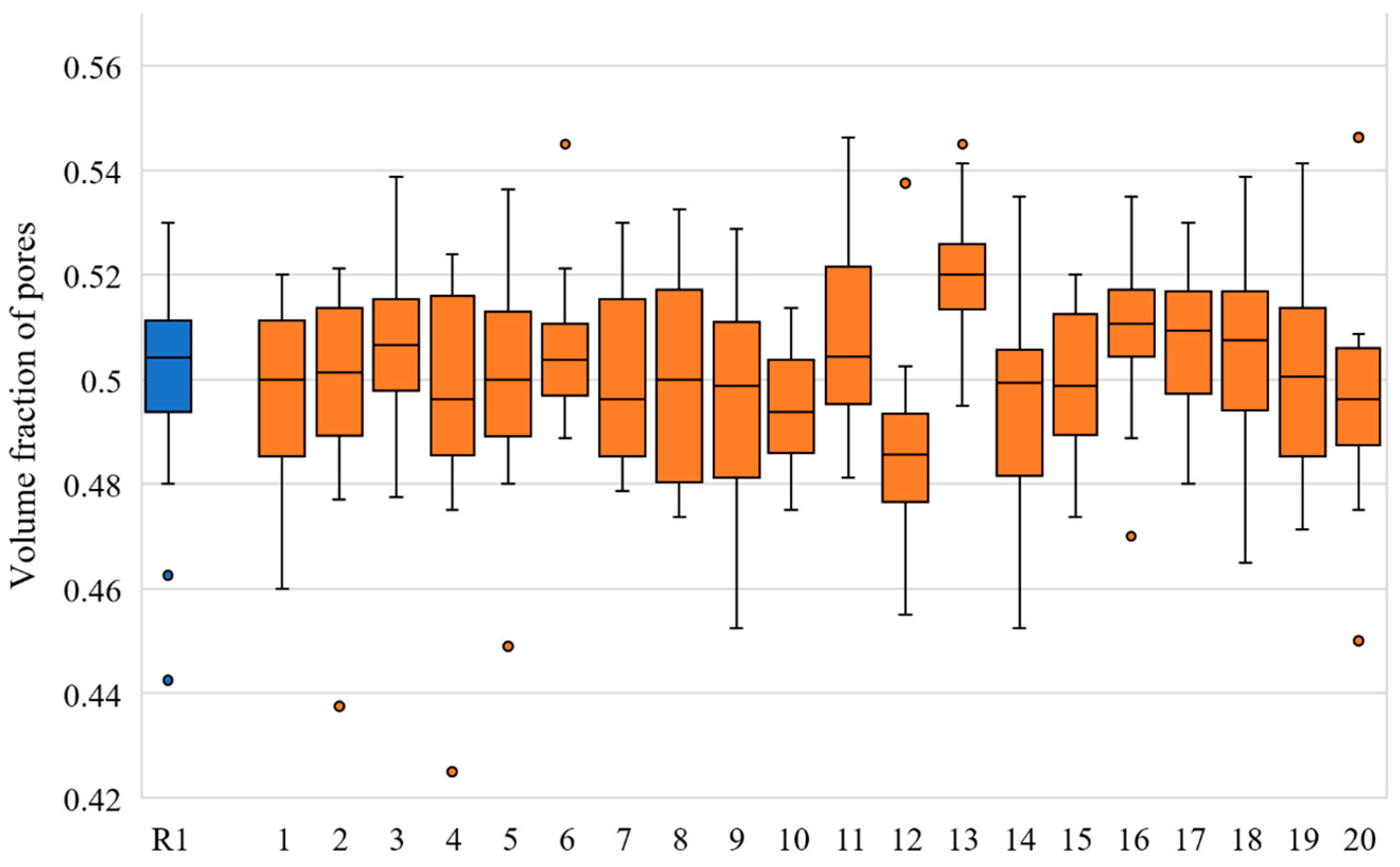
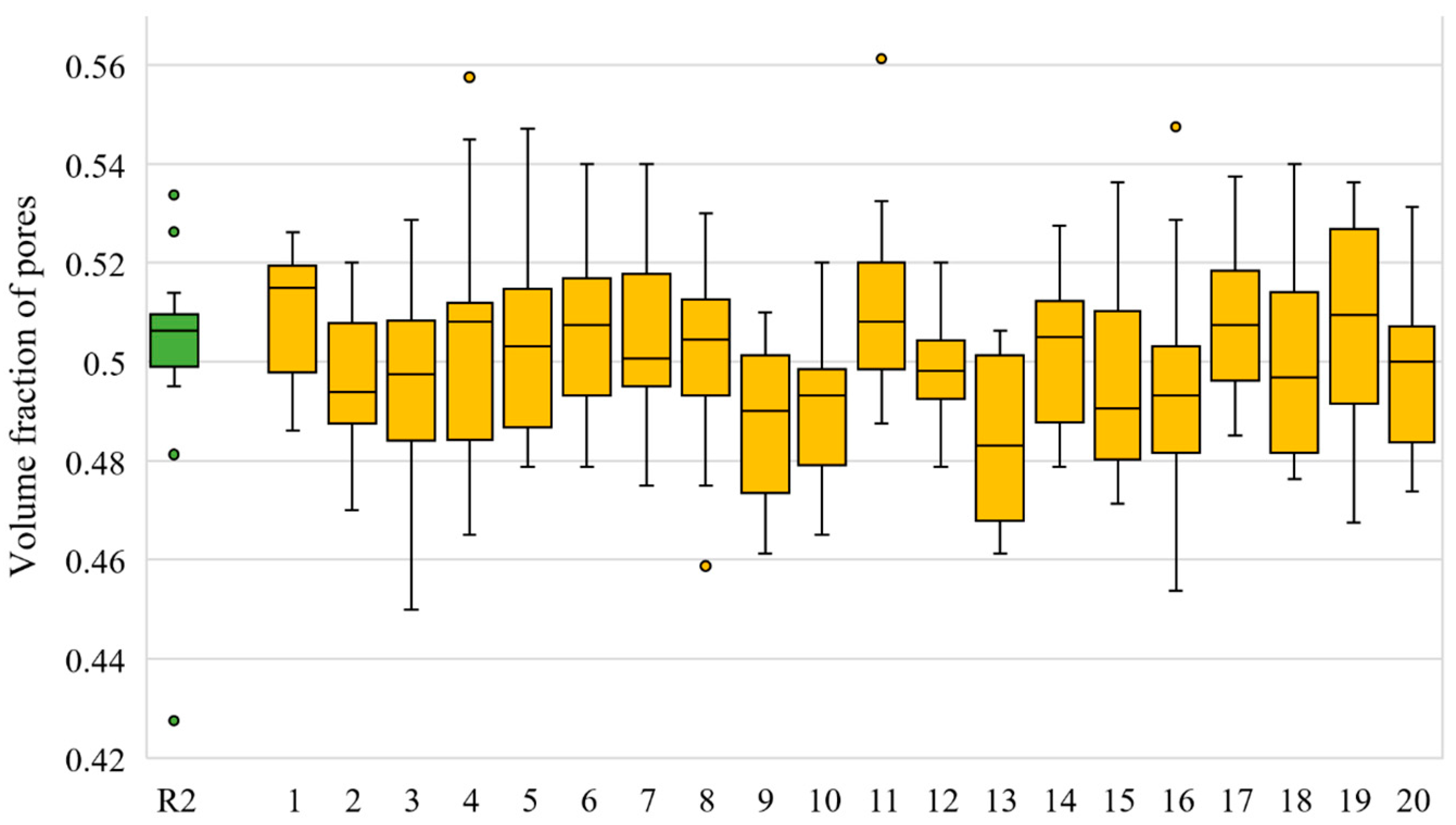


| Slice No. | VF of R1 Model | VF Range in Twenty N1 Models | Slice No. | VF of R1 Model | VF Range in Twenty N1 Models |
|---|---|---|---|---|---|
| 1 | 0.494 | 0.46–0.52 | 11 | 0.443 | 0.481–0.546 |
| 2 | 0.506 | 0.438–0.522 | 12 | 0.498 | 0.455–0.538 |
| 3 | 0.509 | 0.478–0.539 | 13 | 0.499 | 0.495–0.545 |
| 4 | 0.514 | 0.425–0.524 | 14 | 0.495 | 0.453–0.535 |
| 5 | 0.511 | 0.449–0.536 | 15 | 0.503 | 0.474–0.52 |
| 6 | 0.463 | 0.489–0.545 | 16 | 0.511 | 0.47–0.535 |
| 7 | 0.494 | 0.479–0.53 | 17 | 0.511 | 0.48–0.53 |
| 8 | 0.53 | 0.474–0.532 | 18 | 0.443 | 0.465–0.539 |
| 9 | 0.506 | 0.453–0.529 | 19 | 0.525 | 0.471–0.541 |
| 10 | 0.525 | 0.475–0.514 | 20 | 0.48 | 0.45–0.546 |
| Slice No. | VF of R2 Model | VF Range in Twenty N2 Models | Slice No. | VF of R2 Model | VF Range in Twenty N2 Models |
|---|---|---|---|---|---|
| 1 | 0.5 | 0.486–0.526 | 11 | 0.509 | 0.487–0.561 |
| 2 | 0.514 | 0.47–0.52 | 12 | 0.496 | 0.479–0.52 |
| 3 | 0.51 | 0.45–0.529 | 13 | 0.509 | 0.461–0.506 |
| 4 | 0.495 | 0.465–0.558 | 14 | 0.499 | 0.479–0.527 |
| 5 | 0.502 | 0.479–0.547 | 15 | 0.504 | 0.471–0.536 |
| 6 | 0.526 | 0.479–0.54 | 16 | 0.505 | 0.453–0.547 |
| 7 | 0.5 | 0.475–0.54 | 17 | 0.51 | 0.485–0.538 |
| 8 | 0.534 | 0.459–0.53 | 18 | 0.508 | 0.476–0.54 |
| 9 | 0.481 | 0.461–0.51 | 19 | 0.428 | 0.467–0.536 |
| 10 | 0.508 | 0.465–0.52 | 20 | 0.508 | 0.474–0.531 |
| Slice No. | for R1 Models (MPa) | for 20 Corresponding N1 Models (MPa) | for 20 Corresponding N1 Models (MPa) | for 20 Corresponding N1 Models (MPa) | Standard Deviation for 20 Corresponding N1 Models (MPa) |
|---|---|---|---|---|---|
| 1 | 478.50 | 537.43 | 527.90 | 528.42 | 77.63 |
| 2 | 344.93 | 499.39 | 483.14 | 482.27 | 54.66 |
| 3 | 468.57 | 503.89 | 502.52 | 503.22 | 77.28 |
| 4 | 534.22 | 512.83 | 509.74 | 510.49 | 69.81 |
| 5 | 379.80 | 498.89 | 498.40 | 496.11 | 72.38 |
| 6 | 476.04 | 504.72 | 492.58 | 489.46 | 72.22 |
| 7 | 478.50 | 514.56 | 511.56 | 511.14 | 69.78 |
| 8 | 555.98 | 525.79 | 522.43 | 521.66 | 77.19 |
| 9 | 491.85 | 480.24 | 484.56 | 485.88 | 78.18 |
| 10 | 501.85 | 519.70 | 531.97 | 533.13 | 66.36 |
| 11 | 739.72 | 511.62 | 494.01 | 491.40 | 70.19 |
| 12 | 449.01 | 585.96 | 578.18 | 574.29 | 92.85 |
| 13 | 550.57 | 432.03 | 429.85 | 427.87 | 58.31 |
| 14 | 386.92 | 531.04 | 526.41 | 525.60 | 85.91 |
| 15 | 510.97 | 535.63 | 527.47 | 526.24 | 55.94 |
| 16 | 412.73 | 494.08 | 480.32 | 479.58 | 60.51 |
| 17 | 447.53 | 504.20 | 513.87 | 516.50 | 66.60 |
| 18 | 739.71 | 477.58 | 488.47 | 488.64 | 79.37 |
| 19 | 464.28 | 514.03 | 513.03 | 512.71 | 52.74 |
| 20 | 581.40 | 510.79 | 514.02 | 511.21 | 76.60 |
| Average | 532.81 | 535.43 | 527.81 | 524.24 | 117.86 |
| Slice No. | for R2 Models (MPa) | for 20 Corresponding N2 Models (MPa) | for 20 Corresponding N2 Models (MPa) | for 20 Corresponding N2 Models (MPa) | Standard Deviation for 20 Corresponding N2 Models (MPa) |
|---|---|---|---|---|---|
| 1 | 636.42 | 473.70 | 472.02 | 472.60 | 44.31 |
| 2 | 379.01 | 537.96 | 510.56 | 509.71 | 67.67 |
| 3 | 652.94 | 509.55 | 512.63 | 512.26 | 70.51 |
| 4 | 500.36 | 470.38 | 472.57 | 473.63 | 78.17 |
| 5 | 474.85 | 518.48 | 504.32 | 504.48 | 66.95 |
| 6 | 424.79 | 488.62 | 476.54 | 476.88 | 73.71 |
| 7 | 636.73 | 513.74 | 506.85 | 505.62 | 66.83 |
| 8 | 463.30 | 480.01 | 482.89 | 482.93 | 79.75 |
| 9 | 589.12 | 540.67 | 527.99 | 529.48 | 73.18 |
| 10 | 497.85 | 523.00 | 524.97 | 524.85 | 49.46 |
| 11 | 424.18 | 455.25 | 449.39 | 448.56 | 61.16 |
| 12 | 549.15 | 493.57 | 498.13 | 498.15 | 60.58 |
| 13 | 502.68 | 538.19 | 533.11 | 532.47 | 68.05 |
| 14 | 531.89 | 496.76 | 500.67 | 499.99 | 55.01 |
| 15 | 498.59 | 533.04 | 522.16 | 522.11 | 78.55 |
| 16 | 480.08 | 500.03 | 504.31 | 503.31 | 52.58 |
| 17 | 610.82 | 451.57 | 475.69 | 478.28 | 60.39 |
| 18 | 497.93 | 500.07 | 499.19 | 496.79 | 64.78 |
| 19 | 875.21 | 456.66 | 460.50 | 459.69 | 65.88 |
| 20 | 574.36 | 472.18 | 459.28 | 458.75 | 73.65 |
| Average | 562.67 | 513.71 | 518.14 | 526.33 | 111.33 |
| Type 1 | Type 2 | ||
|---|---|---|---|
| Slice No. | Slice No. | ||
| 1 | 0.01 | 1 | 0.26 |
| 2 | 0 | 2 | 0.3 |
| 3 | 0.01 | 3 | 0.09 |
| 4 | 0.2 | 4 | 0 |
| 5 | 0.02 | 5 | 0.29 |
| 6 | 0.05 | 6 | 0.05 |
| 7 | 0 | 7 | 0.15 |
| 8 | 0.02 | 8 | 0.1 |
| 9 | 0 | 9 | 0.06 |
| 10 | 0.25 | 10 | 0.3 |
| Average | 0.056 | Average | 0.16 |
| Tool | Description | Function |
|---|---|---|
| Fréchet Inception Distance (FID) [44] | Measures the distance between the feature distributions of real and generated images | Quality and diversity of generated samples |
| Chamfer Distance (CD) [45] | Quantifies the similarity between sets by calculating the average distance from each point in one set to its nearest neighbor in the other set | 3D shapes and their variability |
| Root Mean Square Error (RMSE) [45] | A standard metric for measuring the differences between predicted and actual values | Reconstruction accuracy and variability in generated 3D models |
| Latent Space Visualization Techniques [46] | Allow visualization of high-dimensional latent space representations in a lower dimensional form | How variations in latent variables affect generated outputs |
| Statistical analysis of geometrical quantities [47] | Analyses variance, standard deviation, and entropy of geometrical features of generated samples | Provides quantitative assessment of geometrical |
| Statistical analysis of mechanical and morphological properties (the present work) | Analyzes morphological characteristics, elastic properties, and stress distributions | Provides quantitative assessment of geometrical features as well as of mechanical response |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tashkinov, M.; Pirogova, Y.; Kononov, E.; Shalimov, A.; Silberschmidt, V.V. Reconstruction of Random Structures Based on Generative Adversarial Networks: Statistical Variability of Mechanical and Morphological Properties. Mathematics 2025, 13, 7. https://doi.org/10.3390/math13010007
Tashkinov M, Pirogova Y, Kononov E, Shalimov A, Silberschmidt VV. Reconstruction of Random Structures Based on Generative Adversarial Networks: Statistical Variability of Mechanical and Morphological Properties. Mathematics. 2025; 13(1):7. https://doi.org/10.3390/math13010007
Chicago/Turabian StyleTashkinov, Mikhail, Yulia Pirogova, Evgeniy Kononov, Aleksandr Shalimov, and Vadim V. Silberschmidt. 2025. "Reconstruction of Random Structures Based on Generative Adversarial Networks: Statistical Variability of Mechanical and Morphological Properties" Mathematics 13, no. 1: 7. https://doi.org/10.3390/math13010007
APA StyleTashkinov, M., Pirogova, Y., Kononov, E., Shalimov, A., & Silberschmidt, V. V. (2025). Reconstruction of Random Structures Based on Generative Adversarial Networks: Statistical Variability of Mechanical and Morphological Properties. Mathematics, 13(1), 7. https://doi.org/10.3390/math13010007






