Determination of Sequential Well Placements Using a Multi-Modal Convolutional Neural Network Integrated with Evolutionary Optimization
Abstract
1. Introduction
- Development of a Hybrid Optimization Framework:Introduced a novel hybrid framework integrating the M-CNN with PSO and iterative learning to optimize sequential well placement in reservoir management.
- Implementation of Iterative Learning for Enhanced Accuracy:Incorporated iterative learning to refine the training dataset, focusing on high-productivity scenarios to address extrapolation challenges and improve model generalization.
- Utilization of PSO for Efficient Data Generation:Leveraged PSO to generate learning data for the M-CNN, substantially reducing computational costs typically associated with full-physics reservoir simulations.
- Validation in Dynamic Reservoir Simulation Scenarios:Validated the proposed hybrid framework on the UNISIM-I-D benchmark model, demonstrating high predictive accuracy with reduced computational requirements.
- Pioneer Application of Integrated M-CNN Framework:To our knowledge, this study presents the first application of a hybrid M-CNN framework combined with PSO and iterative learning for dataset generation in sequential well placement optimization.
2. Methodology
2.1. Well Placement Problem
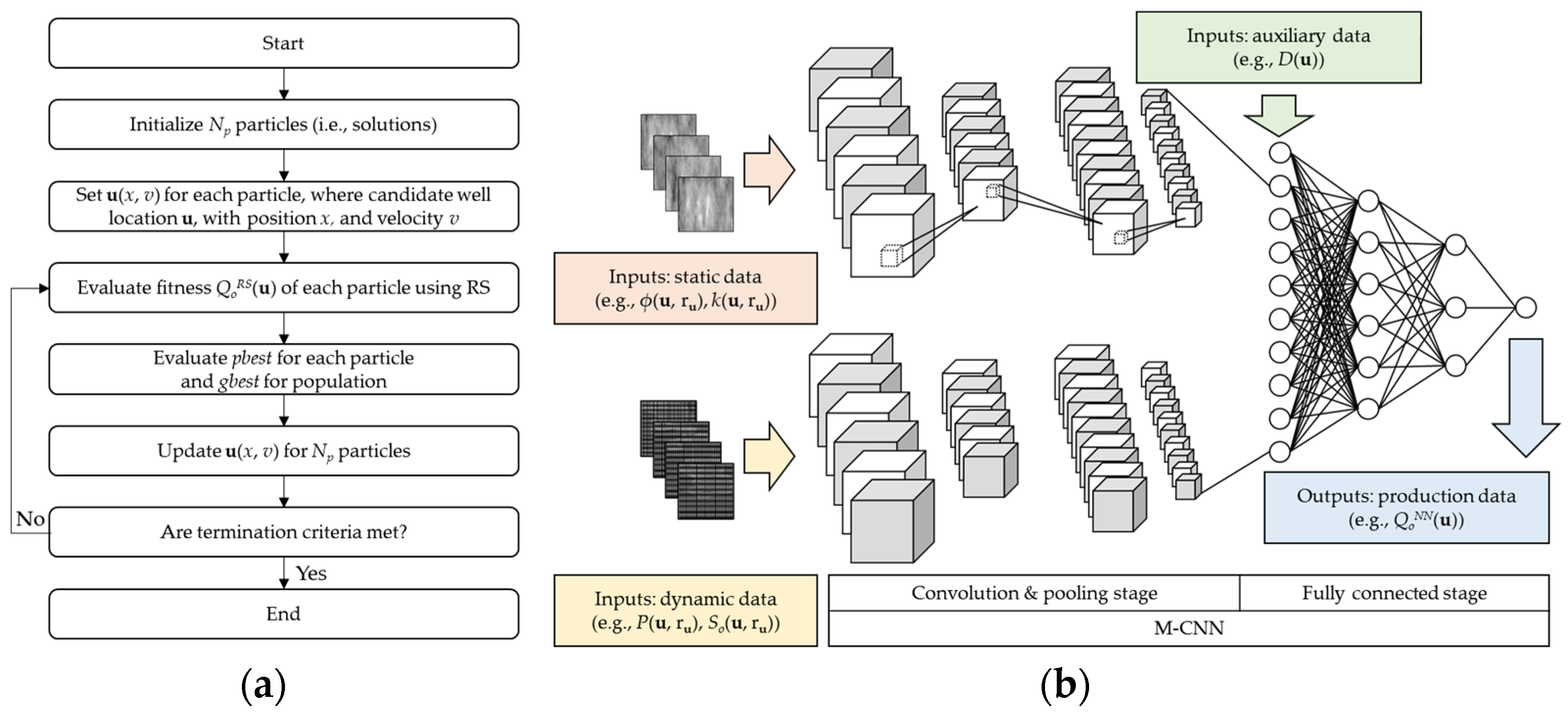
2.2. Particle Swarm Optimization
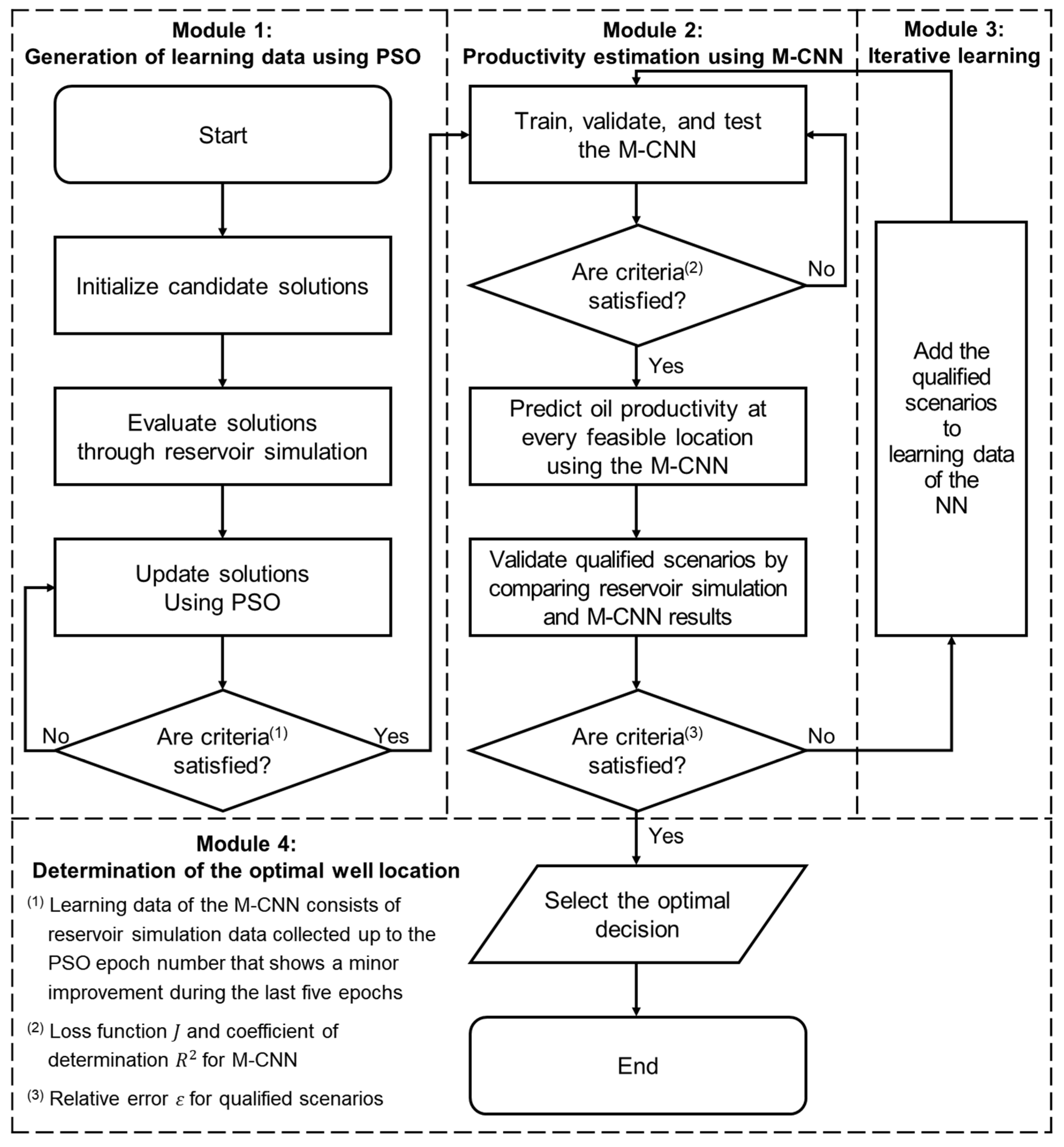
2.3. Multi-Modal Convolutional Neural Network with Iterative Learning
3. Results and Discussion
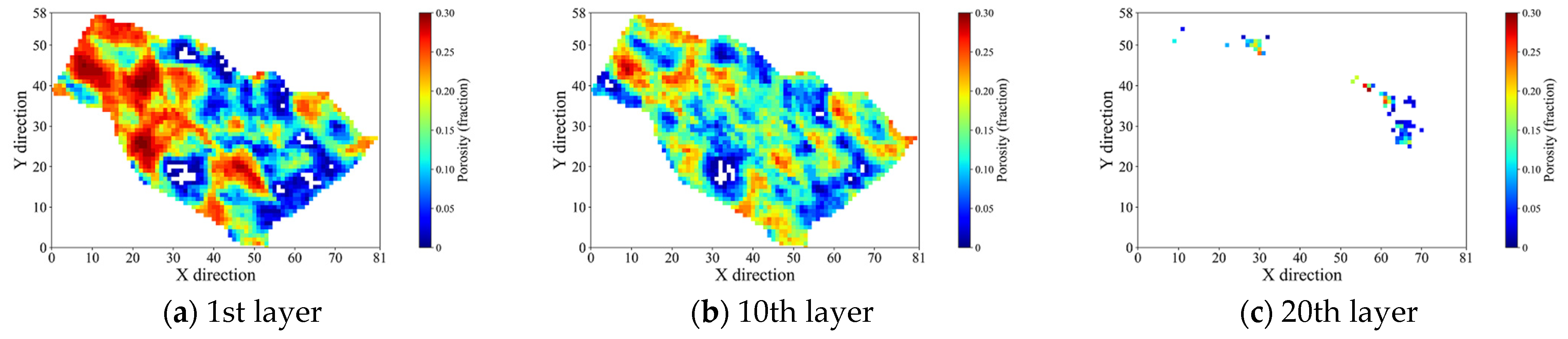
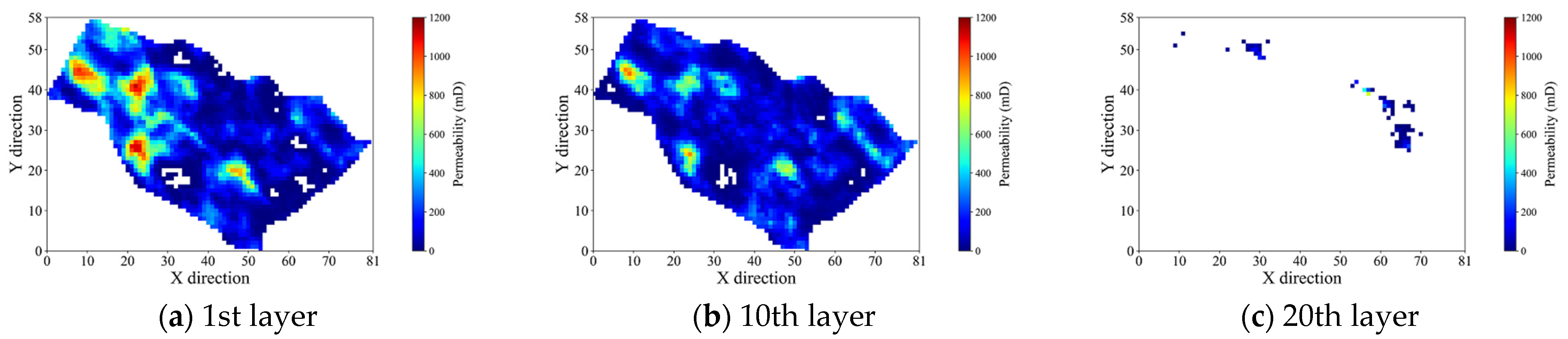
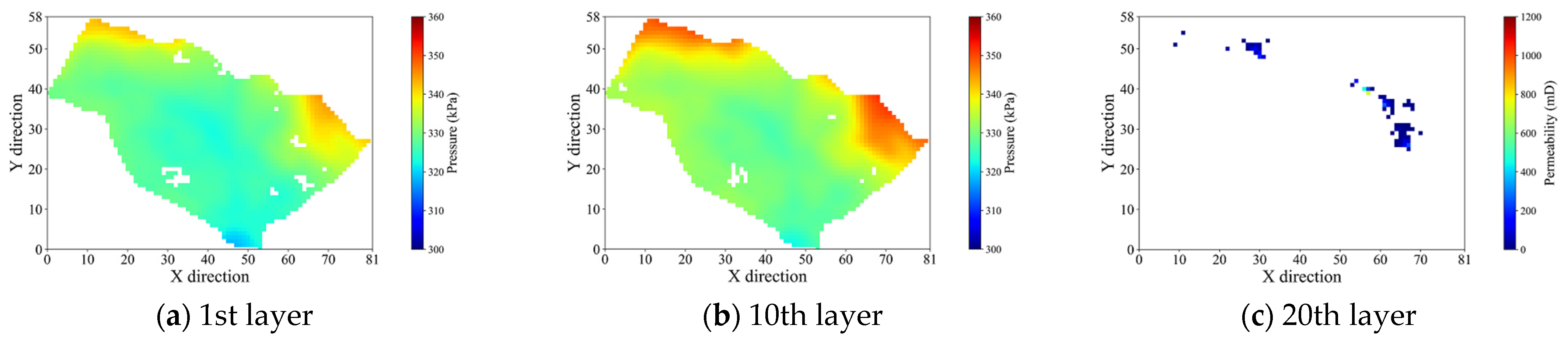
3.1. Field Description
3.2. Generation of Learning Data Using Particle Swarm Optimization
3.3. Design of Multi-Modal Convolutional Neural Network
3.4. Determination of the Well Locations and Performan ce Evaluation
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zandvliet, M.J.; Handels, M.; van Essen, G.M.; Brouwer, D.R.; Jansen, J.D. Adjoint-based well placement optimization under production constraints. SPE J. 2008, 13, 392–399. [Google Scholar] [CrossRef]
- Pouladi, B.; Karkevandi-Talkhooncheh, A.; Sharifi, M.; Gerami, S.; Nourmohammad, A.; VahidiLi, A. Enhancement of SPSA algorithm performance using reservoir quality maps: Application to coupled well placement and control optimization problems. J. Petrol. Sci. Eng. 2020, 189, 106984. [Google Scholar] [CrossRef]
- Boah, A.E.; Kondo, O.K.S.; Borsah, A.A.; Brantson, E.T. Critical evaluation of infill well placement and optimization of well spacing using the particle swarm algorithm. J. Pet. Explor. Prod. Technol. 2019, 9, 3113–3133. [Google Scholar] [CrossRef]
- Ding, S.; Lu, R.; Xi, Y.; Liu, G.; Ma, J. Efficient well placement optimization coupling hybrid objective function with particle swarm optimization algorithm. Appl. Soft Comput. 2020, 95, 106511. [Google Scholar] [CrossRef]
- Wang, X.; Haynes, R.D.; Feng, Q. Well control optimization using derivative-free algorithms and a multiscale approach. Comput. Chem. Eng. 2019, 123, 12–33. [Google Scholar] [CrossRef]
- Bertini, J.R., Jr.; Funcia, M.A.; Santos, A.A.; Schiozer, D.J. A comparison of machine learning algorithms as surrogate model for net present value prediction from wells arrangement data. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 14–19 July 2019. [Google Scholar]
- Lu, R.; Reynolds, A.C. Joint optimization of well locations, types, drilling order and controls given a set of potential drilling paths. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 10–11 April 2019. [Google Scholar]
- Wang, N.; Chang, H.; Zhang, D.; Xue, L.; Chen, Y. Efficient well placement optimization based on theory-guided convolutional neural network. J. Petrol. Sci. Eng. 2022, 208, 109545. [Google Scholar] [CrossRef]
- Fonseca, R.R.-M.; Chen, B.; Jansen, J.D.; Reynolds, A. A stochastic simplex approximate gradient for optimization under uncertainty. Int. J. Numer. Meth. Eng. 2017, 109, 1756–1776. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A new optimizer using particle swarm theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Lee, K.Y.; Park, J.B. Application of particle swarm optimization to economic dispatch problem: Advantages and disadvantages. In Proceedings of the 2006 IEEE PES Pewer Systems Conference and Esposition, Atlanta, GA, USA, 7 February 2006. [Google Scholar]
- Lee, S.; Min, B.; Wheeler, M.F. Optimal design of hydraulic fracturing in porous media using the phase field fracture model coupled with genetic algorithm. Comput. Geosci. 2018, 22, 833–849. [Google Scholar] [CrossRef]
- Schlumberger. MEPO User Guide (Version 2020.01); Schlumberger: Houston, TX, USA, 2020. [Google Scholar]
- CMG. CMOST-AI User Guide (Version 2021.10); Computer Modeling Group LTD: Calgary, AB, Canada, 2021. [Google Scholar]
- Salehian, M.; Haghighat, M.; Muradov, K. Multi-solution well placement optimization using ensemble learning of surrogate models. J. Petrol. Sci. Eng. 2022, 210, 110076. [Google Scholar] [CrossRef]
- Min, B.; Sun, A.Y.; Wheeler, M.F.; Jeong, H. Utilization of multiobjective optimization for pulse testing dataset from a CO2-EOR/sequestration field. J. Petrol. Sci. Eng. 2018, 170, 244–266. [Google Scholar] [CrossRef]
- Guo, Z.; Reynolds, A.C.; Zhao, H. Waterflooding optimization with the INISIM-FT data-driven model. Comput. Geosci. 2018, 22, 745–761. [Google Scholar] [CrossRef]
- de Brito, D.U.; Durlofsky, L.J. Well control optimization using a two-step surrogate treatment. J. Petrol. Sci. Eng. 2020, 187, 106565. [Google Scholar] [CrossRef]
- Kuang, L.; Liu, H.; Ren, Y.; Luo, K.; Shi, M.; Su, J.; Li, X. Application and development trend of artificial intelligence in petroleum exploration and development. Petrol. Explor. Dev. 2021, 48, 1–14. [Google Scholar] [CrossRef]
- Ali Ahmadi, M.; Bahadori, A. A LSSVM approach for determining well placement and conning phenomena in horizontal wells. Fuel 2015, 153, 276–283. [Google Scholar] [CrossRef]
- Panja, P.; Velasco, R.; Pathak, M.; Deo, M. Application of artificial intelligence to forecast hydrocarbon production from shales. Petroleum 2018, 4, 75–89. [Google Scholar] [CrossRef]
- Nwachukwu, A.; Jeong, H.; Pyrcz, M.; Lake, L.W. Fast evaluation of well placements in heterogeneous reservoir models using machine learning. J. Petrol. Sci. Eng. 2018, 163, 463–475. [Google Scholar] [CrossRef]
- Wang, M.; Hui, G.; Pang, Y.; Wang, S.; Chen, S. Optimization of machine learning approaches for shale gas production forecast. Geoenergy Sci. Eng. 2023, 226, 211719. [Google Scholar] [CrossRef]
- Zhu, Q.; Lin, B.; Yang, G.; Wang, L.; Chen, M. Intelligent production optimization method for a low pressure and low productivity shale gas well. Petrol. Explor. Dev. 2022, 49, 886–894. [Google Scholar] [CrossRef]
- Centilmen, A.; Ertekin, T.; Grader, A.S. Applications of neural networks in multiwell field development. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Min, B.; Park, C.; Kang, J.M.; Park, H.J.; Jang, I.S. Optimal well placement based on artificial neural network incorporating the productivity potential. Energy Sources 2011, 33, 1726–1738. [Google Scholar] [CrossRef]
- Jang, I.S.; Oh, S.E.; Kim, Y.; Park, C.; Kang, H. Well-placement optimisation using sequential artificial neural networks. Energy Explor. Exploit. 2018, 36, 433–449. [Google Scholar] [CrossRef]
- Kwon, S.; Park, G.; Jang, Y.; Cho, J.; Chu, M.; Min, B. Determination of oil well placement using convolutional neural network coupled with robust optimization under geological uncertainty. J. Petrol. Sci. Eng. 2021, 201, 108118. [Google Scholar] [CrossRef]
- Chu M -g Min, B.; Kwon, S.; Park, G.; Kim, S.; Huy, N.X. Determination of an infill well placement using a data-driven multi-modal convolutional neural network. J. Petrol. Sci. Eng. 2020, 195, 106805. [Google Scholar]
- Kim, J.; Lee, K.; Choe, J. Efficient and robust optimization for well patterns using a PSO algorithm with a CNN-based proxy model. J. Petrol. Sci. Eng. 2021, 207, 109088. [Google Scholar] [CrossRef]
- Atrey, P.; Hossain, A.; El Saddik, A.; Kankanhalli, M. Multi-modal fusion for multimedia analysis: A survey. Multimed. Syst. 2010, 16, 345–379. [Google Scholar] [CrossRef]
- Dodge, S.; Karam, L. Understanding how image quality affects deep neural networks. In Proceedings of the 8th International Conference on Quality of Multimedia Experience, Lisbon, Portugal, 6–8 June 2016. [Google Scholar]
- Busemeyer, J.R.; Byun, E.; Delosh, E.L.; McDaniel, M.A. Learning Functional Relations Based on Experience with Input-Output Pairs by Humans and Artificial Neural Networks; The MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Delosh, E.L.; Busemeyer, J.R.; McDaniel, M.A. Extrapolation: The sine qua non for abstraction in function learning. J. Exp. Psychol. Learn. Mem. Cogn. 1997, 23, 968–986. [Google Scholar] [CrossRef] [PubMed]
- McDaniel, M.A.; Busemeyer, J.R. The conceptual basis of function learning and extrapolation: Comparison of rule-based and associative-based models. Psychon. Bull. Rev. 2005, 12, 24–42. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- da Cruz, P.S.; Horne, R.N.; Deutsch, C.V. The quality map: A tool for reservoir uncertainty quantification and decision making. SPE Reserv. Eval. Eng. 1999, 7, 6–14. [Google Scholar] [CrossRef]
- Gaspar, A.T.F.S.; Avansi, G.D.; Santos, A.D.S.; Hohendorff Filho, J.C.V.; Schiozer, D.J. UNISIM-I-D: Benchmark studies for oil field development and production strategy selection. Int. J. Model. Simul. Pet. Ind. 2015, 9, 47–55. [Google Scholar]
- Almeida, F.; Davolio, A.; Schiozer, D.J. Reducing uncertainties of reservoir properties in an automatized process coupled with geological modeling considering scalar and spatial uncertain attributes. J. Petrol. Sci. Eng. 2020, 189, 106993. [Google Scholar] [CrossRef]
- Gaspar, A.T.F.S.; Santos, S.M.G.; Ferreira, C.J.; Davolio, A.; Schiozer, D.J. Estimation of the chance of success of a four-dimensional seismic project for a developed oil field. Comput. Geosci. 2022, 26, 463–475. [Google Scholar] [CrossRef]
- Negash, B.M.; Tufa, L.D.; Ramasamy, M.; Awang, M.B. System identification-based proxy model of a reservoir under water injection. Model. Simul. Eng. 2017, 2017, 7645470. [Google Scholar] [CrossRef]
- Avansi, G.D.; Schiozer, D.J. UNISIM-I: Synthetic model for reservoir development and management applications. J. Model. Simul. Petrol. Ind. 2015, 9, 21–30. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011. [Google Scholar]
- Gómez, D.; Rojas, A. An empirical overview of the no free lunch theorem and its effect on real-world machine learning classification. Neural Comput. 2016, 28, 216–228. [Google Scholar] [CrossRef] [PubMed]
- Balestriero, R.; Pesenti, J.; LeCun, Y. Learning in high dimension always amount to extrapolation. arXiv 2021, arXiv:2100.09485. [Google Scholar]
- Jo, S.; Jeong, H.; Min, B.; Park, C.; Kim, Y.; Kwon, S.; Sun, A. Efficient deep-learning-based history matching for fluvial channel reservoirs. J. Petrol. Sci. Eng. 2022, 208 Pt E, 109247. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J.; Vo, T.H.; Wood, D.A.; Min, B. Stochastic lithofacies and petrophysical property modeling for fast history matching in heterogeneous clastic reservoir applications. Sci. Rep. 2024, 14, 22. [Google Scholar] [CrossRef] [PubMed]
- Shaik, N.B.; Jongkittinarukorn, K.; Benjapolakul, W.; Bingi, K. A novel neural network-based framework to estimate oil and gas pipelines life with missing input parameters. Sci. Rep. 2024, 14, 4511. [Google Scholar] [CrossRef]
- Shaik, N.B.; Benjapolakul, W.; Pedapati, S.R.; Bingi, K.; Le, N.T.; Asdornwised, W.; Chaitusaney, S. Recurrent neural network-based model for estimating the life condition of a dry gas pipeline. Process Saf. Environ. 2022, 164, 639–650. [Google Scholar] [CrossRef]
- Choi, S.; Kim, T.-W.; Choi, B.; Min, B. Design of integrated CO2 transportation-injection-storage system based on multi-objective optimization. J. Korean Inst. Min. Energy Resour. Eng. 2024, 61, 347–362. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]





| Property | Value |
|---|---|
| Number of total grid blocks (X × Y × Z) | 93,960 = 81 × 58 × 20 |
| Number of active grid blocks | 36,403 |
| Grid block size (X × Y × Z), m × m × m | 100 × 100 × 8 |
| Depth of top layer, m | 3000 |
| Initial reservoir pressure, kg/cm2 | 327.0 |
| Porosity (µ ± σ), fraction | 0.13 ± 0.08 |
| Permeability (µ ± σ), mD | 132.53 ± 184.95 |
| Oil saturation (µ ± σ), fraction | 0.56 ± 0.38 |
| Parameter | Value |
|---|---|
| 20 | |
| 20 | |
| 0.730 | |
| 1.496 | |
| 1.496 |
| Parameter | Value |
|---|---|
| Number of input types | 4 |
| Type of inputs | |
| Number of convolutional layers | 2 |
| Order of convolutional stage | Conv3D, BatchNormalization, AveragePooling3D |
| Number of hidden layers | 3 |
| Number of outputs | 1 |
| Type of outputs | |
| Optimizer | Adam |
| Activation function | ReLU |
| Ratio of learning data splitting | Training 60%, validation 20%, test 20% |
| Well | Number of Iterative Learning | Number of Feasible Well Locations | Number of Learning Data | R2 | (%) for Ten Qualified Scenarios | |
|---|---|---|---|---|---|---|
| Training Data | Test Data | |||||
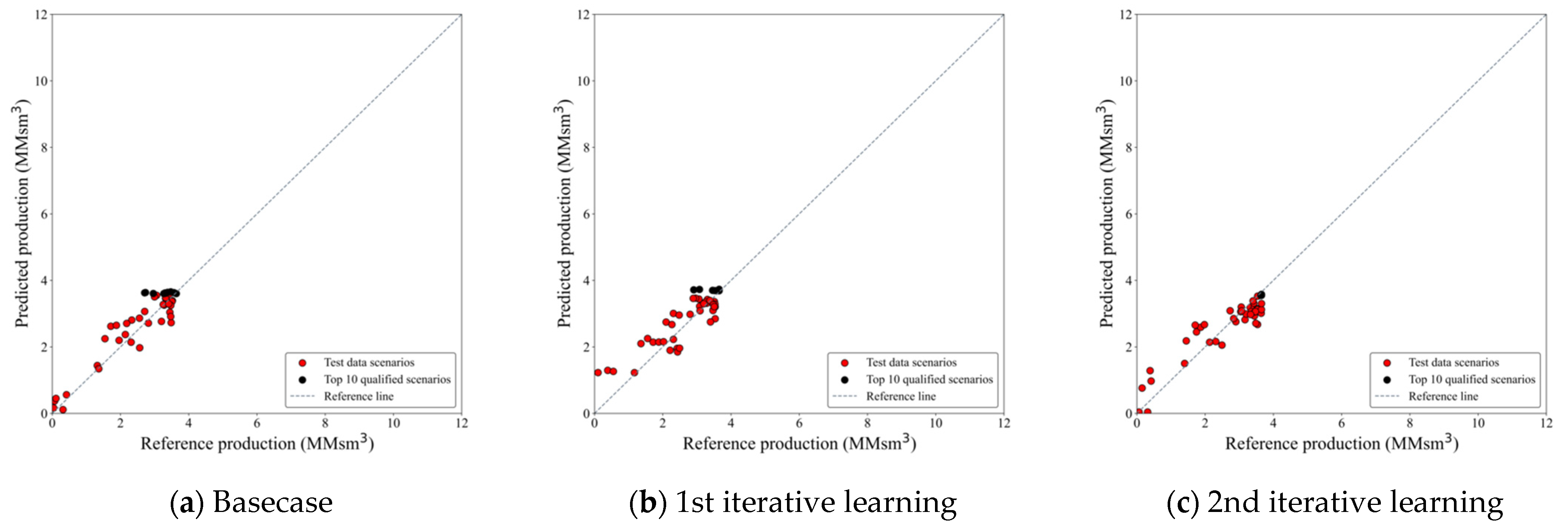
| 1st well | Basecase | 2282 | 176 | 0.93 | 0.87 | 13.34 |
| 1st | 186 | 0.85 | 0.77 | 7.13 | ||
| 2nd (final) | 196 | 0.89 | 0.84 | 2.64 | ||
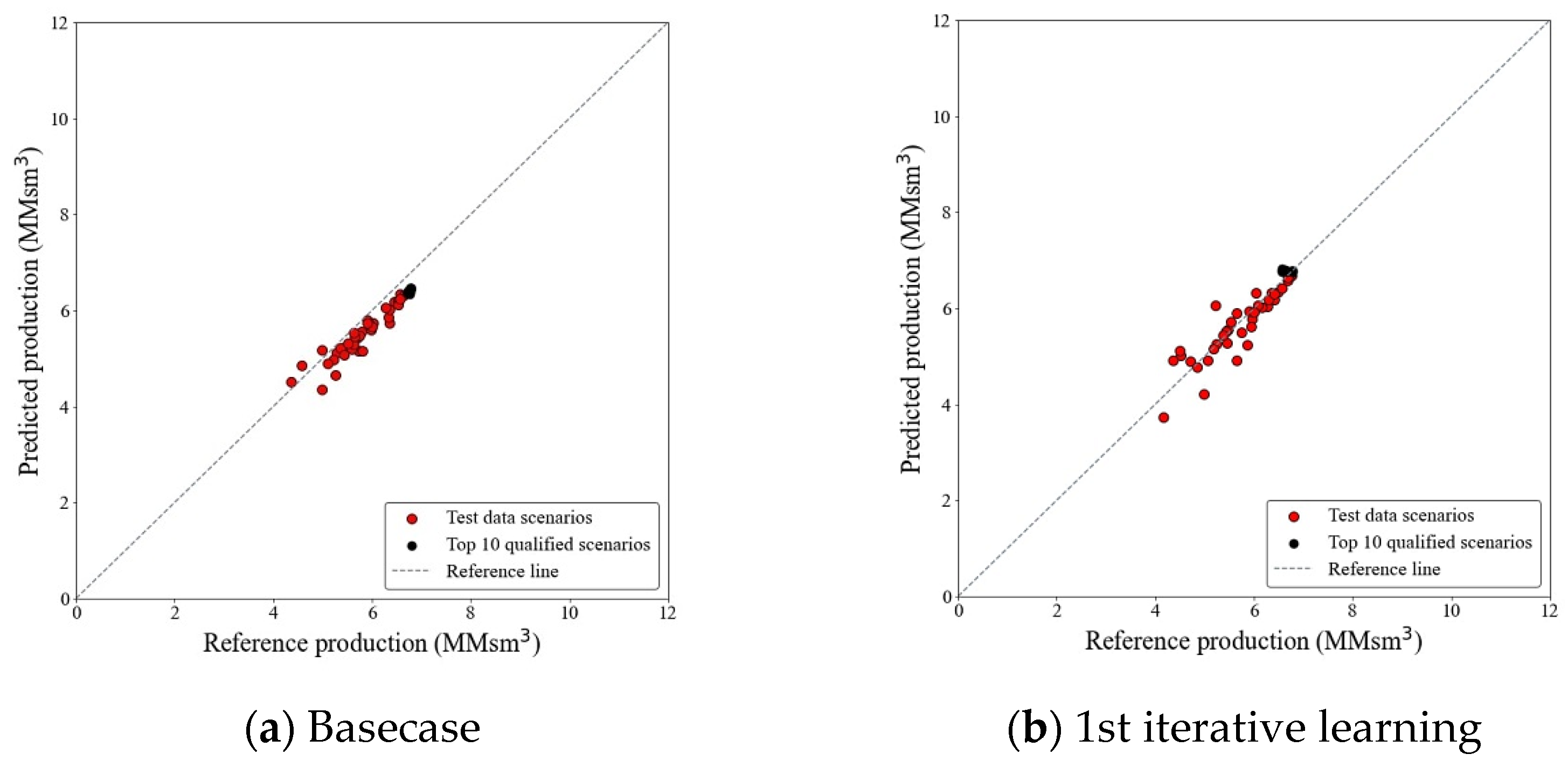
| 2nd well | Basecase | 2281 | 209 | 0.95 | 0.93 | 5.31 |
| 1st (final) | 219 | 0.94 | 0.90 | 1.66 | ||
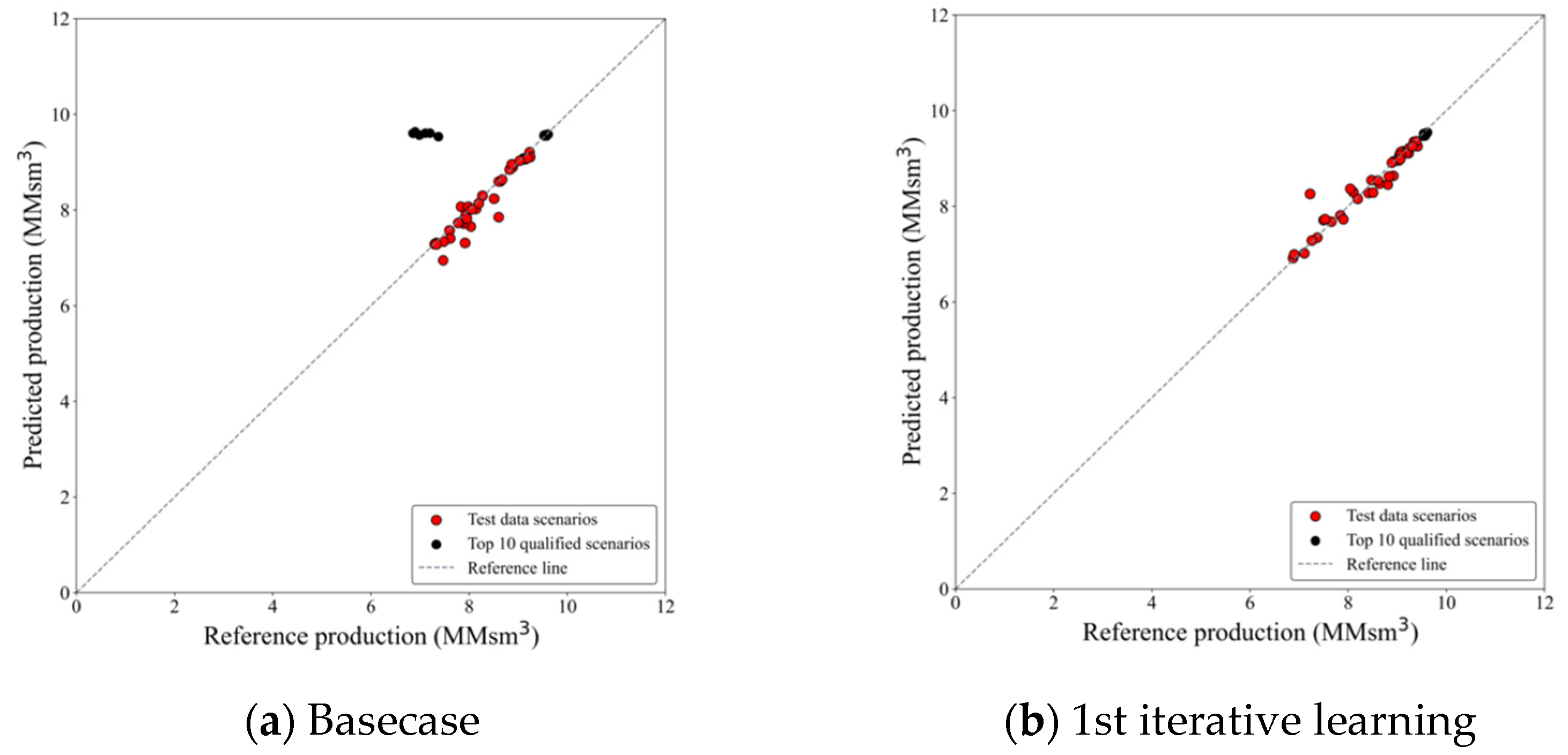
| 3rd well | Basecase | 2280 | 180 | 0.91 | 0.87 | 21.53 |
| 1st (final) | 190 | 0.96 | 0.94 | 0.68 | ||
| 4th well | Basecase (final) | 2279 | 80 | 0.94 | 0.86 | 2.23 |
| Method | Final Well Location (X, Y) | Field Cumulative Oil Production (MMsm3) | ||||
|---|---|---|---|---|---|---|
| 1st Well | 2nd Well | 3rd Well | 4th Well | |||
| Original well placement [38] | (38, 36) | (21, 36) | (44, 43) | (31, 27) | 7.742 | |
| Sequential well placement | PSO w/ES | (25, 24) | (24, 41) | (64, 22) | (46, 10) | 11.320 |
| M-CNN | (24, 36) | (42, 11) | (64, 22) | (37, 41) | 11.412 | |
| Simultaneous well placement | PSO w/o ES | (43, 13) | (63, 23) | (34, 34) | (14, 43) | 11.379 |
| Method | Number of RS Runs | |||||
|---|---|---|---|---|---|---|
| 1st Well (A) | 2nd Well (B) | 3rd Well (C) | 4th Well (D) | Total (E = A + B + C + D) | ||
| RS for all feasible scenarios | Full search | 2282 | 2281 | 2280 | 2279 | 9122 |
| Sequential placement | PSO w/ES | 280 | 300 | 280 | 120 | 980 |
| M-CNN | 300 | 310 | 290 | 120 | 1020 | |
| Simultaneous placement | PSO w/o ES | 1600 | 1600 | |||
| Method | Computational Cost for RS Runs (s) | Computational Cost for M-CNN (s) | Total Computational Cost (s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st Well | 2nd Well | 3rd Well | 4th Well | 1st Well | 2nd Well | 3rd Well | 4th Well | |||
| RS for all feasible scenarios | Full search | 75,739.6 | 75,706.4 | 75,673.2 | 75,640.0 | - | - | - | - | 302,759.2 |
| Sequential placement | PSO w/ES | 9293.2 | 9957.0 | 9293.2 | 3982.8 | - | - | - | - | 32,526.2 |
| M-CNN | 9957.0 | 10,288.9 | 9625.1 | 3982.8 | 271.0 | 129.2 | 101.8 | 39.5 | 34,395.3 | |
| Simultaneous placement | PSO w/o ES | 65,097.0 | - | - | - | - | 65,097.0 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, S.; Ji, M.; Kim, M.; Leung, J.Y.; Min, B. Determination of Sequential Well Placements Using a Multi-Modal Convolutional Neural Network Integrated with Evolutionary Optimization. Mathematics 2025, 13, 36. https://doi.org/10.3390/math13010036
Kwon S, Ji M, Kim M, Leung JY, Min B. Determination of Sequential Well Placements Using a Multi-Modal Convolutional Neural Network Integrated with Evolutionary Optimization. Mathematics. 2025; 13(1):36. https://doi.org/10.3390/math13010036
Chicago/Turabian StyleKwon, Seoyoon, Minsoo Ji, Min Kim, Juliana Y. Leung, and Baehyun Min. 2025. "Determination of Sequential Well Placements Using a Multi-Modal Convolutional Neural Network Integrated with Evolutionary Optimization" Mathematics 13, no. 1: 36. https://doi.org/10.3390/math13010036
APA StyleKwon, S., Ji, M., Kim, M., Leung, J. Y., & Min, B. (2025). Determination of Sequential Well Placements Using a Multi-Modal Convolutional Neural Network Integrated with Evolutionary Optimization. Mathematics, 13(1), 36. https://doi.org/10.3390/math13010036







