Abstract
In this paper, we propose a hybrid genetic algorithm (HGA) that embeds the tabu search mechanism into the genetic algorithm (GA) for multiple-input multiple-output (MIMO) detection. We modified the selection and crossover operation to maintain the diverse and wide exploration areas, which is an advantage of the GA, and the mutation operation to perform a local search for a specific region. In the mutation process, the ’tabu’ concept is also employed to prevent the repeated search of the same area. In addition, a layered detection process is applied simultaneously with the proposed algorithm, which not only improves the bit error rate performance but also reduces the computational complexity. We apply the layered HGA (LHGA) to the MIMO system with very high modulation order such as 64-quadrature amplitude modulation (QAM), 256-QAM, and 1024-QAM. Simulation results show that the LHGA outperforms conventional detection approaches. Especially, in the 1024-QAM MIMO system, the LHGA has less than 10% of computational complexity but a 6 dB signal-to-noise ratio (SNR) gain compared to the conventional GA-based MIMO detection scheme.
MSC:
94A13
1. Introduction
Multiple-input multiple-output (MIMO) technology has been extensively studied and applied in various commercial mobile telecommunication systems as it can significantly improve system throughput and network coverage [1,2,3,4,5,6]. In MIMO systems, multiple symbols can be transmitted simultaneously by multiplexing them in the spatial domain. At the receiver, these symbols are expected to be detected subject to contamination by random noise or interference. Typically, the symbol detection is performed jointly, i.e., the interdependence between desired symbols and other interfering symbols is considered to detect the desired symbols [7,8,9].
The optimal MIMO detection method based on the maximum-likelihood (ML) criterion is basically a non-deterministic polynomial-time hard (NP-hard) problem [10,11], and its computational complexity increases exponentially with the number of decision variables [7]. To reduce the complexity, various suboptimal MIMO detection techniques have been developed, such as the linear zero-forcing (ZF) detector, which minimizes interference by inverting the channel matrix, the linear minimum mean-square error (MMSE) detector, and interference cancellation-based detectors [12,13,14,15]. Although these suboptimal methods are much simpler than ML detection, their performance is noticeably inferior.
In this paper, we introduce a novel approach based on meta-heuristic algorithms for MIMO detection, utilizing a Genetic algorithm (GA) [16]. GA can efficiently handle the optimization problem based on its three core operations: selection, crossover, and mutation. Thanks to the global explorative power of GA, it can find the optimal or near-optimal solution for solving large search space problems [17]. Since the MIMO detection problem can be considered the closest point problem [18], the GA is an effective approach to solving the MIMO detection problem.
In [19,20], the authors applied the basic GA to MIMO detection by controlling the probability that a mutation operation is selected. However, the basic GA approach in [19] and [20] suffers from premature convergence when the population of the GA reaches such a suboptimal state. This premature convergence reduces the diversity of the population and causes redundant exploration of the already searched space. Moreover, due to the random nature of the GA, the exploration direction of the GA is hard to control. Since an intensive search for space with high fitness is not guaranteed in the GA process, the use of GA does not guarantee the finding of the optimal solution to the problem [21,22]. Consequently, although the GA-based MIMO techniques in [19,20] improve bit error rate (BER) performance, defined as a metric of the total number of errors in transmitted bits, over the conventional MIMO detection techniques, this is still far from the optimal ML performance.
An important challenge in search-based MIMO detection is a balance between the global search capability for a broad search area and the local search capability for an intensive search to areas where an optimal solution is likely to exist. To achieve this goal, we propose a hybrid GA (HGA) technique that integrates a tabu search (TS) mechanism into the basic GA for MIMO detection. The proposed HGA improves search efficiency by avoiding redundant searches and enhances the GA’s capability by providing a solution near the optimal by balancing the global search and the local search, while HGA approaches have been applied in various fields and problems as in [23,24,25,26], this study is the first to adopt such a hybrid strategy for MIMO detection.
In the proposed HGA, we modify the mutation operation of the GA to perform TS operations. Unlike the conventional GA, which performs mutation using the population of the previous generation, the mutation of the proposed HGA performs a neighborhood search by selecting multiple individuals from the crossover results of the current generation. To prevent redundant searches, these individuals are memorized in a mutation list , ensuring that previously explored spaces are excluded from future searches. Integrating the local search operation to the GA retains the original advantage of GA, which that is its global explorative power, and simultaneously achieves an enhanced search performance thanks to the intensive local search ability.
On top of the proposed HGA, we further apply a layered detection method to enhance BER performance and reduce computational complexity. The layered structure is inspired by a previously proposed approach based on successive cancellation systems [14]. The convergence of layered structure and search algorithm-based MIMO detection has been studied in [20,27]. In [20], the authors sequentially connected QR decomposition-based detection and basic GA-based detection, but the improvement in BER performance was marginal. The authors of [27] tried to combine a layered structure with TS-based MIMO detection and achieved better BER performance and reduced computational complexity by updating the solution vector based on local search per the specific layer. Therefore, we consider the layered structure of the method to update the solution by layer as in [27] with the proposed HGA.
The main contributions can be summarized as follows:
- First, an HGA scheme embedding tabu search is proposed for high-order quadrature amplitude modulation (QAM) in MIMO detection. The hybrid techniques of GA and TS enable efficient MIMO detection by balancing global and local searches.
- A layered detection technique is applied to the proposed HGA scheme, which not only dramatically improves BER performance but also reduces computational complexity.
- The advantages of the proposed HGA scheme over the conventional scheme are verified through various simulations considering up to 1024-QAM. Notably, the proposed HGA scheme shows enhanced performance compared to conventional detection schemes.
- A complexity comparison between the proposed HGA and conventional detection schemes was performed. The HGA scheme leads to a substantial reduction in the complexity of MIMO detection for high-order QAM.
The remainder of this paper is organized as follows. In Section 2, the MIMO system model is presented, and the basic GA and the GA-based MIMO detection scheme are briefly reviewed. In Section 3, the proposed HGA scheme using a layered process for MIMO detection is introduced. The performance of the proposed HGA scheme is evaluated in Section 4. Finally, Section 5 summarizes the results of this study.
2. System Model
2.1. MIMO Channel Model
We consider a flat fading MIMO system with transmit antennas at the transmitter and receive antennas at the receiver as shown in Figure 1. For the flat fading channels, the fading coefficients are assumed to be constant during a frame modeled as independent zero-mean complex Gaussian random variables with a variance of 1/2 per dimension. The perfect channel knowledge is assumed to be known at the receiver.
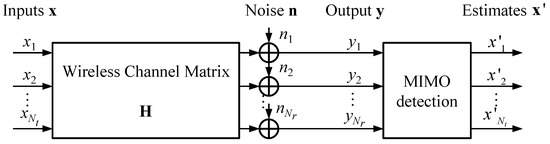
Figure 1.
MIMO system.
The received signal vector can be expressed as
where is the Rayleigh fading channel matrix. Channel element, , denotes the complex gain between jth transmit antenna and ith receive antenna and is an independent zero mean circularly symmetric complex Gaussian random variable with unit variance. represents the additive white Gaussian noise (AWGN) vector in which the entries are the independent and identically distributed (i.i.d) complex Gaussian random variables with zero mean and a variance . The transmitted signal vector is , where the element of is drawn from a finite constellation alphabet, , of cardinality M. The constellation alphabets that we consider in this paper are 64-QAM, 256-QAM, and 1024-QAM.
For computational reasons, we shall replace the complex-valued model (1) by its real-valued equivalent (2) in the usual way, where and denote the real and imaginary parts of , respectively.
The basic task of MIMO detection is to estimate the input vector relying on the knowledge of the received signal and the channel matrix . In other words, the objective function of MIMO detection is to find the closest lattice point to the received signal in a lattice as follows
where the input vector belong to an -dimensional lattice of size and is an Euclidean distance metric defined by [28]
In order to estimate the optimal , all , , and -dimensional lattice included in should be searched for 64-QAM, 256-QAM, and 1024-QAM, respectively, according to , which can consider one to thousands. The number of the lattice that should be considered for optimal MIMO detection increases exponentially with and M. However, it is practically impossible to implement an ML method that finds the optimal by considering the lattice in all cases because it requires too much computational complexity. Therefore, meta-heuristic algorithms [20,27] conduct broad and intensive searches with hundreds to thousands of lattices for , where an optimal solution is likely to exist for estimating suboptimal , which enable low-complexity MIMO detectoion while providing ML-like performance.
2.2. Genetic Algorithm
The GA is iterative optimization procedure that repeatedly applies the genetic operations (such as selection, crossover, and mutation) to a group of solutions until a certain criterion is met. In the GA, a search point (solution), which is the setting of a search space with m dimensions (m variables), is coded into a string similar to the chromosome (or individual). The individual is composed of m characters, , which are analogous to the m genes. A fitness value is used to represent the degree of goodness of the individual. The set of individuals is called the population, , and each iteration step to obtain a new population is called a generation. In each generation, GA generates a new population from the previous population using a given set of genetic operations (such as selection, crossover, and mutation). It then replaces inferior individuals with a superior newly generated individual to obtain a better population [16]. A typical selection operation reproduces an individual. A typical crossover operation randomly splits the two individuals at a randomly selected point and exchanges parts between them. A typical mutation operation alters an individual at a random point. The mechanism of each genetic operation and the process of generating the new population through genetic operations are shown in Figure 2. The basic GA procedures include the following steps.
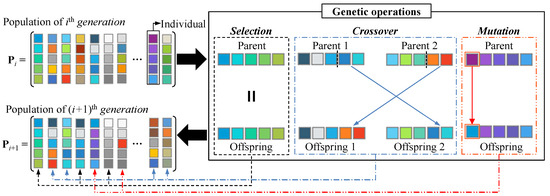
Figure 2.
Generation process of a new population through the genetic operations.
- (a)
- Define a fitness function, and set the GA operations (such as population size P, maximum number of generations G, parent selection method, selection probability, crossover probability, and mutation probability).
- (b)
- Generate the initial population.
- (c)
- Evaluate the fitness of each individual in the initial population.
- (d)
- Generate an offspring(s) by using one of the genetic operations. The genetic operation to generate the offspring(s) is selected according to each rate, and the parent(s) for the genetic operation is determined according to the parent selection method. Insert the offspring(s) into the next population.
- (e)
- Evaluate the fitness of each individual in the new population.
- (f)
- If a stopping criterion is satisfied, then the procedure is halted. Otherwise, go to Step (d).
After completing the GA procedure, the optimal solution is obtained by selecting the fittest individual from the final generated population. The flowchart of the base GA is shown in Figure 3.
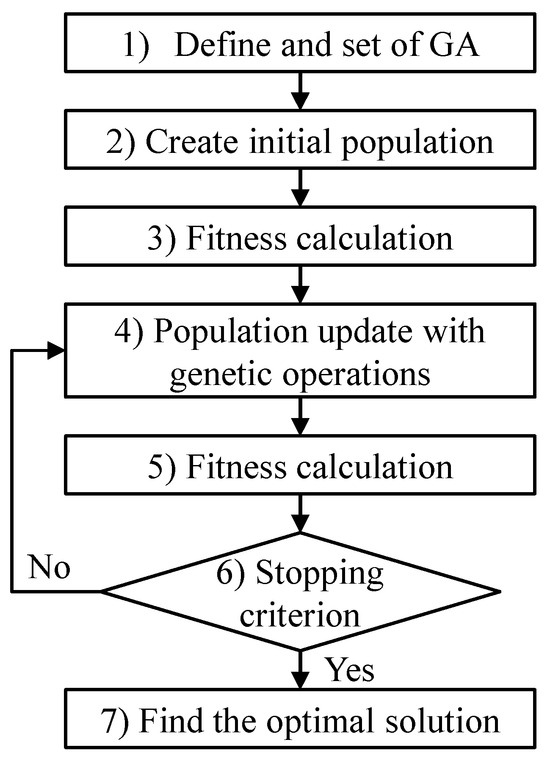
Figure 3.
Flowchart of the basic GA process.
2.3. GA-Based MIMO Detection
For MIMO detection based on the GA, several terms between the GA algorithm and MIMO system need to be matched. An individual represent the candidate transmitted signal vectors and the gene means the element of the constellation alphabet . Since we consider a real-valued MIMO system, the dimension of an individual is and the population forms a matrix, where P denote a population size. Choosing a suitable initial population is an important factor in GA convergence [29]. Some initialization procedures (e.g., using ZF or MMSE solutions) can accelerate GA convergence [29,30]. Therefore, we use a randomly generated set of individuals, including the MMSE solution, as an initial population for MIMO detection.
The fitness function should evaluate each individual and provide each individual’s assessment information. In MIMO detection, the measure of goodness for each individual can be determined by the distance from the transmitted signal vector. Thus, the reciprocal of Euclidean distance (4) is appropriate as a fitness function, as follows
A higher value of fitness function indicates a fitter candidate solution.
In order to gradually improve the candidate solutions in the population, the parents for the next generation should be selected based on their fitness value. Here, we use the roulette wheel selection method in which the probability of selection for genetic operations is determined by the fitness of the parent individual. Unfortunately, there are no rules for determining GA parameters such as population size, maximum number of generations, selection probability, crossover probability, and mutation probability. Therefore, it is necessary to select an appropriate value according to the number of transmission antennas and the modulation order M to be used. Based on the conversion of GA to MIMO detection, GA can be used as a detection method for MIMO systems through the procedure described in Figure 3.
In order to find the optimal solution using search-based techniques, it is important to perform efficient searches that explore as much as possible in areas where the fitness is expected to be good. However, in the basic GA, premature convergence reduces the diversity of the population and leads to the problem of the repeated exploration of already searched space. Moreover, the genetic operations of the basic GA are randomly selected according to each operation’s rate, and the operation of each genetic operation is also performed using the randomness. Because of these high randomnesses, we can not control the searching direction of GA, which means that it is hard to perform an intensive search in a high fitness area. These repeated search and randomness weakens the search ability of the GA, which degrades its BER performance and increases the computational complexity of GA-based MIMO detection.
3. Hybrid GA with Layered Process for MIMO Detection
In this section, we first discuss the modification strategy of the basic GA with embedded TS mechanism for MIMO detection. We then discuss the proposed layered HGA for better BER performance and lower computational complexity for MIMO detection.
3.1. Proposed Hybrid Genetic Algorithm
We propose a hybrid GA (HGA) technique for MIMO detection to improve the search ability to explore as much as possible in areas where the fit is expected to be good. The core idea of the proposed HGA is to keep the GA in order to have a large search space while also incorporating a local neighborhood search mechanism in the form of the TS algorithm to intensify the search around the selected regions. In addition, to improve the search efficiency, the memory feature of the TS algorithm is used to keep track of search history of areas that should be avoided for the second visit. For these purposes, we separate the role of the different genetic operations and modify them by embedding the TS algorithm.
3.1.1. Selection
The selection operation of the proposed HGA is responsible for convergence that preserves the best solution during the population generation process. Unlike the basic GA’s selection, which transfers several of the current population to the next generation, the proposed HGA’s selection operation transfers only one individual with the highest fit, a mechanism known as elitism. By doing so, it is possible to avoid repeated searches while preserving the best individual during the population generation process.
3.1.2. Crossover
The crossover operation of the proposed HGA plays the role of maintaining the diverse and wide exploration area that is a key feature of the basic GA. The crossover mechanism of the proposed HGA is similar to that of the basic GA; however, it is performed until a fixed number (crossover size of different offspring are generated. By generating different offspring to those selected for intensive searches performed in the mutation operation, the proposed HGA maintains a diverse and wide exploration area.
3.1.3. Mutation
The mutation operation of the HGA is modified to act as an intensive search for the areas where the fitness is expected to be good by adopting the concept of neighborhood search of the TS. Because the neighbors of individual with good fitness are also likely to have good fitness, a neighborhood search for an individual with good fitness can find a solution that is closer to the optimal. The concept of neighborhood search is introduced in [31].
Let denote the cardinality of . Define a set , as a fixed subset of , which we refer to as the symbol neighborhood of . We choose the cardinality of this set to be the same for all ; i.e., we take . Note that the maximum and minimum values of N are and 1, respectively. We choose the symbol neighborhood based on the Euclidean distance, i.e., for a given symbol, those N symbols which are the nearest will form its neighborhood; the nearest symbol will be the first neighbor, the next nearest symbol will be the second neighbor, and so on. For, e.g., for 4-PAM, and choosing N to be 2, , , , and are possible symbol neighborhoods. Let denote the th element in : i.e., we say is the th symbol neighbor of .
Let denote the data vector belonging to the solution space, where . We refer to the vector
as th vector-neighbor (or simply the th neighbor) of , , if () differs from in the th coordinate only, and () the th element of is the th symbol-neighbor of . That is,
So we will have vectors that differ from a given vector in the solution space in only one coordinate. These vectors form the neighborhood of the given vector. The neighborhood search repeats the process of moving to the best vector among the neighbor vectors.
The mutation of proposed HGA performs a neighborhood search in the generation process. That is, a fixed number (mutation size of different individuals among the current crossover results is selected and used as a center of a neighborhood. After that, the mutation creates a vector-neighbor of selected individuals and inserts them into the population of the next generation. The individuals selected for the neighborhood searches are determined by the roulette wheel selection approach, so an intensive search around the individuals with good fitness can be performed. Furthermore, if the offspring selected using the current selection operation differs from the result of previous selection operation, this means that a new best solution has been searched. Since there is a high probability that the more fit solution exists around the new best solution, we perform the intensive search by performing the proposed mutation on the current selection result.
To prevent repeated searches of already searched space, the proposed mutation memorize the center of the performed neighborhood search in what is called the ‘mutation list ’, which adopts the memory feature of the TS algorithm. During all generations, the accumulates the individuals selected as the center of the neighborhood search in the mutation operation and the newly updated individuals in the selection operation. By using the , the algorithm attempts to avoid repeated searches by marking the already searched space, which ensures efficient search of the solution space.
Through the above process, the proposed HGA avoids repeated searches of the same areas and enables the intensive search of areas where fitness is likely to be good.
3.1.4. Procedure of the Proposed HGA
The procedure of the proposed HGA is almost identical to that of the basic GA, except for a mechanism to update the population using genetic operations. Figure 4 shows the population update mechanism of the proposed HGA. As described in Section 3.1, the selection operation of the proposed HGA is performed only once, and only the fittest individual is selected and copied to the next population. Unlike the crossover of the basic GA, the crossover of the proposed HGA generates only one offspring in a single crossover operation such that all offspring generated by the crossover can be different. The mutation operation of the proposed HGA performs a completely different operation to that of the mutation operation of the basic GA. The mutation operation of proposed HGA performs a neighborhood search that generates the vector-neighbor of a parent and insert them into the next population, where m is the dimension of the individual and N denotes the number of nearby neighbors, respectively. Moreover, the parent for the mutation operation of the proposed HGA is selected from the crossover, not the current population. Therefore, the genetic operations of the proposed HGA are performed in the order of selection, crossover, and mutation.
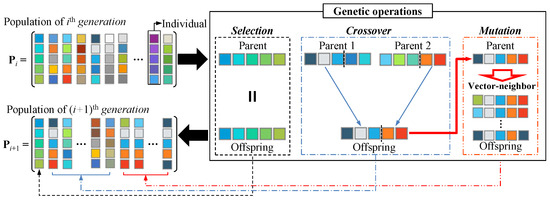
Figure 4.
New population generation process of the proposed HGA.
Through the proposed HGA, we can find better solutions by efficiently searching using approaches such as avoiding repeated searches and performing intensive searches of a wide range of areas. The overall procedure of the proposed HGA can be summarized as follows.
- (a)
- Define an fitness function, and set the GA operations.
- (b)
- Initialize the algorithm.
- (1)
- Generate the initial population .
- (2)
- Evaluate the fitness of the initial population .
- (3)
- Generate the mutation list as a empty set.
- (c)
- Update the population by using the genetic operations.
- (1)
- Initialize the current population and the checker for selection .
- (2)
- Selection: select the fittest individual of and copy to . If is not an element of , set to one.
- (3)
- Crossover
- i
- Generate the crossover result set as a empty set and , which is the number of times crossover has been performed is zero.
- ii
- Select the two different parents from the using the roulette wheel selection method, and randomly select the crossover length .
- iii
- Perform a single-point crossover using two parents and the to generate crossover offspring .
- iv
- If the is not an element of , insert the into and increase by one.
- v
- If is less than the crossover size , go back to step (ii).
- vi
- Insert the to .
- (4)
- Mutation
- i
- Generate the mutation result set as a empty set and , which is the number of times mutation has been performed is zero.
- ii
- Select a single parent from the using the roulette wheel selection.
- iii
- Remove the individual selected as the parent from . If the parent is not an element of , insert the parent and vector-neighbor of the parent into the . Furthermore, insert the parent into the and increase by one.
- iv
- If is less than the mutation size , go back to step (ii).
- v
- If is one, insert the and vector-neighbor of into the and insert the into the .
- vi
- Insert the to .
- (d)
- Evaluate the fitness of the current population .
- (e)
- If the stop criterion is met, the procedure is stopped. Otherwise, go to Step (d).
The above summary is represented in Algorithm 1 where ⌀ denotes the empty set and is a roulette wheel selection method that select the individual in population based on the fitness value B. is a set difference defined by .
| Algorithm 1 The proposed hybrid genetic algorithm |
| Require: , , |
| Generate and evaluate . base on |
| Generate |
| for do |
| Generate , |
| Fittest individual in is copy and insert to |
| if then |
| end if |
| Generate , |
| while do |
| Randomly choose the crossover length |
| if then |
| Insert into |
| . |
| end if |
| end while |
| Insert into |
| Generate , |
| while do |
| if then |
| Insert and the vector-neighbor of |
| into |
| Insert into |
| . |
| end if |
| end while |
| if then |
| Insert and the vector-neighbor of into |
| into |
| end if |
| Insert into |
| Calculate base on |
| end for |
3.2. Hybrid GA-Based MIMO Detection with Layered Process
The proposed HGA-based MIMO detection demonstrates improved BER performance over conventional detectors through intensive search for large signal spaces. However, HGA requires more computational complexity to find better solutions. In other words, the computational complexity for applying the proposed HGA to real systems is still very high. For better BER performance and reduced computational complexity, we adopt a strategy of detecting symbols in a layered manner.
The layered structure is inspired by the approaches suggested in [14,20,27]. In particular, the detection with a layered structure [27] that update the solution vector under consideration within the specific layer is adopted with the proposed HGA. The layered HGA (LHGA) basically performs MMSE successive interference cancellation detection based on QR decomposition, and the proposed HGA in each layer is applied.
Let denote the upper triangular matrix obtained from the QR decomposition of and denote the element in the ith row and jth column of the matrix. Then, the objective equivalent to (3) will be to find the transmitted vector that minimizes , where
is the MMSE detection result and denotes the ith element of the vector . The proposed layered HGA processes one layer at a time with the ordering based on the post-detection SNR of the symbols. The optimum order , which is a permutation of , can be obtained as follows. Perform the following steps for with :
- (i)
- Find the where is obtained by zeroing columns of .
- (ii)
- Find , the index that corresponds to the row with the lowest norm among all rows of .
Detection is conducted in the following order: and so on. That is, the layer with highest post-detection SNR should be detected first. In the th layer, , the algorithm detects the -sized subvector . We detect the symbols of this subvector jointly because they interfere with each other. The joint detection method employed in each layer is the proposed HGA described in Section 3.1. If a cancellation of interference due to the already detected symbols in the previous layer results in a good quality output, the LHGA skips the joint detection search in a layer. The resulting LHGA is represented in Figure 5 and stated below.
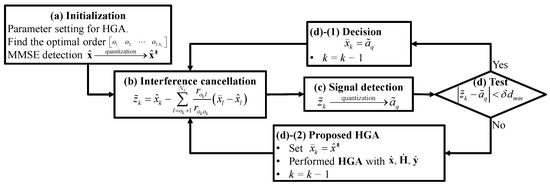
Figure 5.
LHGA flowchart.
Let be the MMSE solution and be the quantized version of , i.e., each element in is rounded-off to its nearest symbol in the alphabet to obtain , so that . Let be the minimum Euclidean distance between any two symbols in the alphabet . The steps performed in the th layer, , are as follows:
- (a)
- Initialization.Define the Euclidean distance in (4) as an fitness function, and set the HGA operations such as G, and .
- (b)
- Interference cancellation.Calculatewhich is a cancellation operation that removes the interference due to the symbols detected in the previous layer (i.e., ’s).
- (c)
- Signal detection.Find the symbol in the alphabet which is closest to in Euclidean distance.
- (d)
- Test: ,
- (1)
- Decision.
- If , then . Make and return to (b)
- (2)
- Proposed HGA.
- If , then set . Perform the proposed HGA by replacing the initial individual with , with , with , where , , and for the kth layer are taken asThe output vector form is made as the update subvector. Make and return to (b)
After processing all the layers, the output of the last layer vector is declared as the final detected vector.
The solution space to explore in the HGA process is very large. For example, in a MIMO system with 1024-QAM, the total number of possible symbol vectors is . The HGA without layering is carried out once on the full system model, which means we have to perform a single HGA to find the final solution. Although the HGA has improved search ability compared to the basic GA, it is very difficult to find an optimal solution in a very wide solution space with a single HGA implementation, and/or the computational complexity to pay for finding a good solution is very high. Whereas, in the LHGA, the HGA is performed multiple times with the IC, at most once on each layer. The size of the symbol space that the HGA has to explore for by each layer is smaller than or equal to the total symbol space, and the searching process is performed after the inter-layer interference is removed, so the probability of finding a better solution increases. Furthermore, since the HGA is selectively performed according to the IC result, the computational complexity is lower than that of the HGA without layering.
By embedding the local search mechanism into the GA, the proposed HGA can balance diversification and intensification of the exploration. In addition, by introducing the tabu concept in the search process, it has improved search efficiency compared to the basic GA. Furthermore, the proposed HGA-based MIMO detection scheme can reduce the computational complexity and better improve BER performance through use of a layered process.
4. Simulation Results
4.1. Parameter Setting
The performance of the proposed HGA-based approach was evaluated by simulations in an MIMO system with transmit antennas, receive antennas and 64-QAM, 256-QAM, and 1024-QAM modulation. The channel entries are assumed to be i.i.d. complex Gaussian random variables and we assume perfect channel knowledge at the receiver.
An important issue for GA-based detection is the choice of various parameters for the genetic operations. The parameters to be determined for the basic GA are the maximum number of generations , the population size P, and the probability that each genetic operation is selected; and the parameters to be determined for the proposed HGA are the maximum number of generations , the number of nearest neighbors N, , and . Unlike the basic GA, the population size of the proposed HGA is changed according to the result of the selection operation for each generation, and is determined as follows
where is the individual selected by the selection operation in the generation. If the population size is too small, there is insufficient evolution, and there is a risk of the whole population becoming extinct. This will eventually drive the system into a local optimum (not the global optimum). Conversely, if the population size is too large, more evaluations of fitness function are needed, which will require extensive computing time. Therefore, we should determine the appropriate GA parameters to increase BER performance and reduce computational complexity.
Unfortunately, there is no known method for determining GA parameters, so we need to make a heuristic decision. Figure 6 shows BER performance and the number of vectors to be searched in the HGA process for various parameters in a MIMO with 64-QAM at a signal-to-noise ratio (SNR) of 30 dB. In this paper, we use the number of vectors that should be searched by the HGA as a measure of complexity. From Figure 6a, BER performance is improved as the and increase, but can not significantly affect the BER performance. However, in Figure 6b, the complexity of the HGA process increases sharply as increases, whereas the change in and slowly increase the complexity of the HGA. From these simulation results, we can select the HGA parameters with lower complexity and better BER performance. The selected parameters according to the modulation order for a MIMO system are summarized in Table 1. In addition, for fair performance comparisons, the parameters for the basic GA have been chosen to have a similar population structure to that of the HGA, and are listed in Table 2.
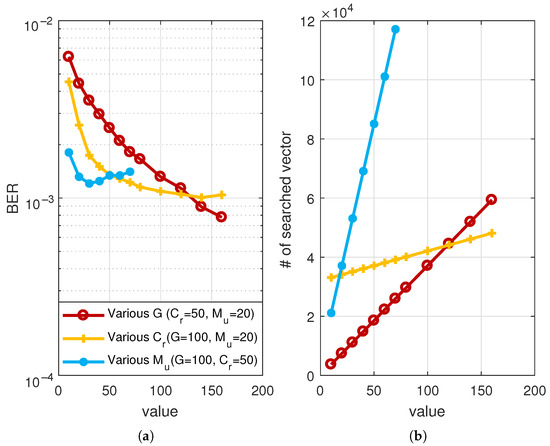
Figure 6.
For a MIMO with 64-QAM at SNR = 30 dB, (a) BER performance and (b) the number of vectors to be searched in the HGA process with various parameters.

Table 1.
Parameters of the proposed HGA.

Table 2.
Parameters of the basic GA.
4.2. BER and Complexity Analysis
Figure 7a shows a BER performances comparison between the proposed HGA without and with layering and the basic GA (BGA) without layering in a MIMO system with 64-QAM, 256-QAM, and 1024-QAM. It can be seen that compared to the basic GA without layering, the proposed layered HGA approach significantly improves BER performance. For example, the basic GA without layering needs an SNR of 39 dB to achieve a BER for 64-QAM, whereas the proposed HGA without layering achieves the same BER at 31 dB, which amounts to an SNR gain of 8 dB. Moreover, the LHGA further improves BER performance. For 256-QAM and 1024-QAM, this SNR gain is equal or even higher.
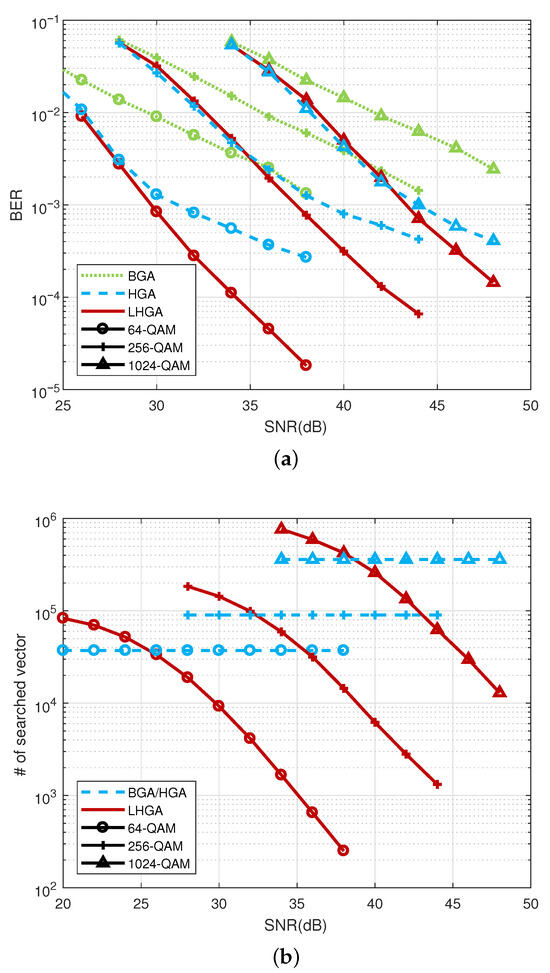
Figure 7.
Performance comparison between the proposed HGA without and with layering, and the typical GA without layering for a MIMO system with 64-QAM, 256-QAM, and 1024-QAM. (a) BER performance. (b) Computational complexity.
Figure 7b shows a computational complexity comparison between the algorithms, where we have plotted the average number of searched vectors in each algorithm. Since the number of searched vectors greatly affects the computational complexity, we compare and analyze the computational complexity through the number of searched vectors. In other words, as the number of search vectors decreases, the amount of computation required to select one of the searched vectors decreases. For example, it is much simpler to detect 1 out of 100 searched vectors than to detect 1 out of 10,000 searched vectors. The BGA and HGA have fixed numbers of searched vectors according to the modulation order regardless of SNR, while the number of searched vectors in the LHGA depends on SNR. In the low SNR region, the LHGA has higher computational complexity than the BGA and the HGA without considering the layered process. However, the computational complexity of the LHGA decreases as the SNR increases. Especially, in the high SNR region, the LHGA has much less complexity than the algorithms without a layered process. As the SNR increases, the accuracy of SIC detection also improves, which reduces the probability of entering the HGA phase in the layered process. Considering the target BER as , the LHGA has significantly lower computational complexity than the BGA and HGA.
4.3. BER Comparison with Other Detectors
The numerical results of the following existing detectors are also given for comparison: (1) minimum mean squared error (MMSE) detection [13], (2) sorted QR decomposition (SQRD) detection [15], (3) basic GA (BGA) based detection [19], (4) basic GA (BGA) with SQRD detection [20], and (5) layered tabu search (LTS) algorithm [27]. The ML detection results were only performed in 64-QAM, and are not given for 256-QAM and 1024-QAM because of the prohibitively high complexity of carrying out a simulation in such large dimensions. All parameters for the proposed HGA and the basic GA are summarized in Table 1 and Table 2, respectively.
Figure 8 shows the BER performance of the various detectors. As mentioned before, it can be seen that the linear receiver, SQRD, BGA and the simple combination of the SQRD and BGA have poor BER performance in the higher order QAM systems. The proposed layered-HGA-based MIMO detection approach shows the best BER performance. The BGA-based MIMO detectors show poor BER performance due to their characteristics of searching large areas and difficulty in carrying out intensive searches of specific areas. The LTS shows significantly improved BER performance compared to GA-based detectors through its application of intensive searches in specific regions; however, it can be confirmed that the BER performance improvement gradually decreases with increasing SNR. In the high SNR region, the LTS focuses on a more intensive search of a specific region, making it difficult to consider the search of different regions. The LHGA shows improved BER performance compared to LTS by effectively utilizing the characteristics of the broad search in the GA and the local search in the TS. In particular, it can be seen that the performance improvement of LHGA increases compared to LTS as the modulation order increases.
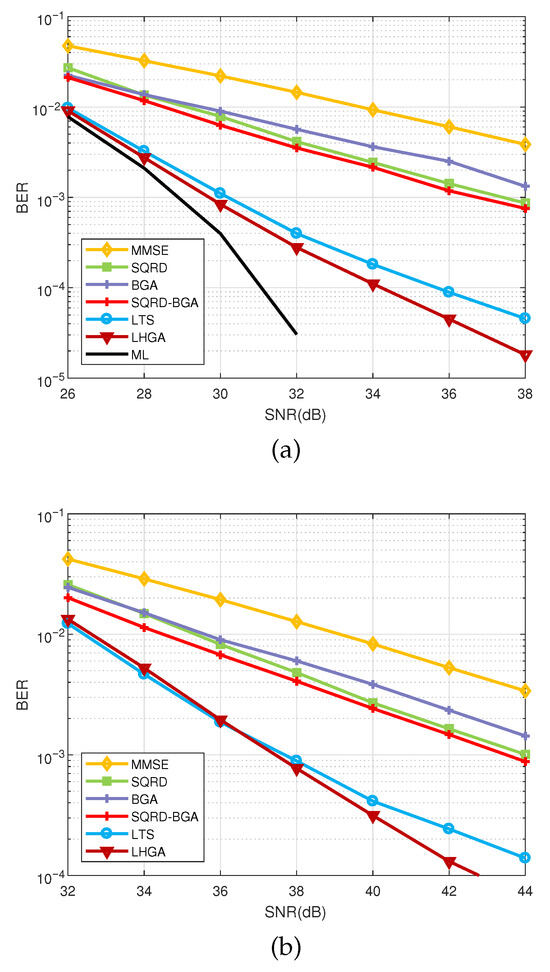
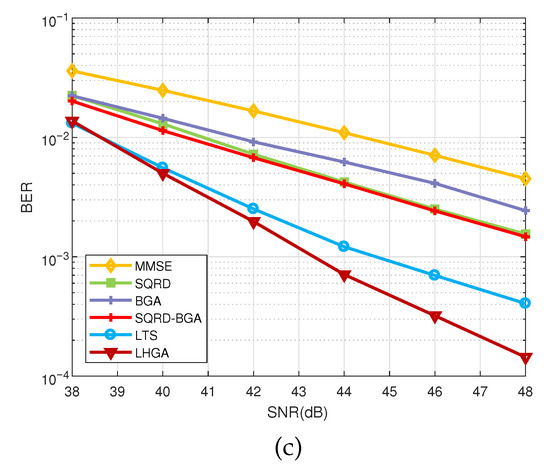
Figure 8.
BER performance versus SNR of the proposed method and conventional detectors using (a) 64-QAM (b) 256-QAM, and (c) 1024-QAM with a MIMO system.
5. Conclusions
In this paper, we presented a hybrid GA incorporating a tabu-based local neighborhood search within the GA framework to simultaneously meet the need for both diversification and intensification of the search. In addition, a layered process was applied to improve BER performance as well as reduce computational complexity. We applied the tabu search (i) once at the center for intensive search, to avoid repeated searches, thereby allowing the exploration of large areas and (ii) later as a neighborhood search in the mutation operation, to perform intensive searches of high fitness areas. We experimentally showed that the LHGA outperforms conventional detectors. The quality of the solutions found in the LHGA algorithm depends on the choice of parameters, and the values obtained empirically by the parameters of LHGA were considered. The development of optimal LHGA parameters is left to future research.
Author Contributions
Conceptualization, T.K.; methodology, T.K. and G.K.; software, T.K. and G.K.; validation, T.K. and G.K.; formal analysis, G.K.; investigation, T.K. and G.K.; resources, T.K. and G.K.; data curation, T.K. and G.K.; writing—original draft preparation, T.K. and G.K.; writing—review and editing, T.K. and G.K.; visualization, T.K.; supervision, T.K.; project administration, T.K. and G.K.; funding acquisition, T.K. and G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a National Research Foundation of Korea (NRF) Grant through the Korea Government [Ministry of Science and Information and Communication Technology (MSIT)] under Grant NRF-2022R1F1A1064106 for Taehyoung Kim. Furthermore, this research was financially supported by Hansung University for Gyuyeol Kong.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Foschini, G.J.; Gans, M.J. On limits of wireless communications in a fading Environment when using multiple antennas. Wirel. Pers. Commun. 1998, 6, 315–335. [Google Scholar] [CrossRef]
- Telatar, E. Capacity of multi-antenna Gaussian channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, Z.; Li, H.; Zheng, L.; Liu, L. RC-Struct: A structure-based neural network approach for MIMO-OFDM detection. IEEE Trans. Wirel. Commun. 2022, 21, 7181–7193. [Google Scholar] [CrossRef]
- Ali, M.S.; Ehossai, N.; Kim, D. Non-Orthogonal Multiple Access (NOMA) for Downlink Multiuser MIMO Systems: User Clustering, Beamforming, and Power Allocation. IEEE Access 2017, 5, 565–577. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Yeo, T.-S.; Cheng, Y.; Zhang, Y. Sparse reconstruction-Based joint signal processing for MIMO-OFDM-IM integrated radar and communication systems. Remote Sens. 2024, 16, 1773. [Google Scholar] [CrossRef]
- Naeem, M.; Bashir, S.; Ullah, Z.; Syed, A.A. A Near Optimal Scheduling Algorithm for Efficient Radio Resource Management in Multi-user MIMO Systems. Wirel. Pers. Commun. 2019, 106, 1411–1427. [Google Scholar] [CrossRef]
- Yang, S.; Hanzo, L. Fifty years of MIMO detection: The road to large-scale MIMOs. IEEE Commun. Surv. Tutor. 2015, 17, 1941–1988. [Google Scholar] [CrossRef]
- Zhai, K.; Zheng, M.A.; Lei, X. Accurate Performance Analysis of Coded Large-Scale Multiuser MIMO Systems with MMSE Receivers. Sensors 2019, 19, 2884. [Google Scholar] [CrossRef]
- Wong, K.; Cheng, R.; Letaeif, K.B.; Murch, R.D. Adaptive antennas at the mobile and base stations in an OFDM/TDMA system. IEEE Trans. Commun. 2001, 49, 195–206. [Google Scholar] [CrossRef]
- Verdú, S. Computational complexity of optimum multiuser detection. Algorithmica 1989, 4, 303–312. [Google Scholar] [CrossRef]
- Micciancio, D. The hardness of the closest vector problem with preprocessing. IEEE Trans. Inf. Theory 2001, 47, 1212–1215. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Kay, S.M. Statistical Signal Processing: Estimation Theory; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Foschini, G.J. Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Labs Tech. J. 1996, 1, 41–59. [Google Scholar] [CrossRef]
- Wubben, D.; Bohnke, R.; Rinas, J.; Kuhn, V.; Kammeyer, K.D. Efficient algorithm for decoding layered space-time codes. Electron. Lett. 2001, 37, 1348–1350. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Agrell, E.; Eriksson, T.; Vardy, A.; Zeger, K. Closest point search in lattices. IEEE Trans. Inf. Theory 2002, 48, 2201–2214. [Google Scholar] [CrossRef]
- Hong, Y.; Dong, Z. Genetic algorithms with applications in wireless communications. Int. J. Syst. Sci. 2004, 35, 751–762. [Google Scholar] [CrossRef]
- Pan, C.-H. An efficient MIMO detection algorithm employed in imperfect noise estimation. WSEAS Trans. Commun. 2009, 8, 941–958. [Google Scholar]
- Fogel, D.B. An Introduction to simulated evolutionary optimization. IEEE Trans. Neural Netw. 1994, 5, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Grefenstette, J.J. Incorporating problem specific knowledge into genetic algorithms. Genet. Algorithms Simulated Annealing 1987, 42–60. [Google Scholar]
- Alhamad, K.; Alkhezi, Y. Hybrid genetic algorithm and tabu search for solving preventive maintenance scheduling problem for cogeneration plants. Mathematics 2021, 9, 1705. [Google Scholar] [CrossRef]
- Ju, C.; Yuan, G.; Shareduwan, K.; Chengfeng, Z.; Atiqah, R.; Asyraf, M.; Ezlin, Z.; Chuanbiao, W. MTS-PRO2SAT: Hybrid mutation tabu search algorithm in optimizing probabilistic 2 satisfiability in discrete hopfield neural network. Mathematics 2024, 12, 721. [Google Scholar] [CrossRef]
- Xu, L.; Yu, C.; Wu, B.; Gao, M. A hybrid genetic algorithm for ground station scheduling problems. Appl. Sci. 2024, 14, 5045. [Google Scholar] [CrossRef]
- Maroof, A.; Ayvaz, B.; Naeem, K. Logistics optimization using hybrid genetic algorithm (HGA): A solution to the vehicle routing problem with time windows (VRPTW). IEEE Access 2024, 12, 369074. [Google Scholar] [CrossRef]
- Srinidhi, N.; Datta, T.; Chockalingam, A.; Rajan, B.S. Layered Tabu search algorithm for large-MIMO detection and a lower bound on ML performance. IEEE Trans. Commun. 2010, 59, 2955–2963. [Google Scholar] [CrossRef]
- Mansour, M.M.; Alex, S.P.; Jalloul, L.M.A. Reduced complexity soft-output MIMO sphere detectors-Part I: Algorithmic optimizations. IEEE Trans. Signal Process. 2014, 62, 5505–5520. [Google Scholar] [CrossRef]
- Jiang, M.; Hanzo, L. Multiuser MIMO-OFDM for next-generation wireless systems. Proc. IEEE 2007, 95, 1430–1469. [Google Scholar] [CrossRef]
- Colman, G.; Willink, T. Overloaded array processing using genetic algorithms with soft-biased initialization. IEEE Trans. Veh. Technol. 2008, 57, 2123–2131. [Google Scholar] [CrossRef]
- Chockalingam, A.; Rajan, B.S. Large MIMO Systems; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).