Abstract
Multi-robot collaborative autonomous exploration in communication-constrained scenarios is essential in areas such as search and rescue. During the exploration process, the robot teams must minimize the occurrence of redundant scanning of the environment. To this end, we propose to view the robot team as an agent and obtain a policy network that can be centrally executed by training with an improved SAC deep reinforcement learning algorithm. In addition, we transform the obtained policy network into distributed networks that can be adapted to communication-constrained scenarios using knowledge distillation. Our proposed method offers an innovative solution to the decision-making problem for multiple robots. We conducted experiments on our proposed method within simulated environments. The experimental results show the adaptability of our proposed method to various sizes of environments and its superior performance compared to the current mainstream methods.
MSC:
68T40
1. Introduction
The problem of multi-robot autonomous exploration involves the collaborative efforts of multiple robots to explore and create a map of an unknown environment autonomously [1]. This technology possesses a wide range of potential applications, including but not limited to floor-sweeping robots [2], search and rescue operations [3], and the construction of warehouse maps [4].
Multi-robot collaborative autonomous exploration methods can be classified as centralized [5] and decentralized [6]. Centralized execution approaches must prioritize maintaining reliable communication between individual robots throughout exploration. Consequently, this technique is unsuitable for scenarios with communication constraints.
Traditional distributed multi-robot collaborative autonomous exploration approaches often rely on heuristics to direct robots in choosing target points for exploration. These heuristics may consider factors such as the distance between the robot and the frontier (the boundary between free and unknown spaces) [7] or the amount of new information that can be obtained at a target point [8]. Conventional approaches are constrained by reliance on heuristics and exhibit poor performance in complex environments, particularly when communication is constrained.
The advancement of deep reinforcement learning (DRL) technology [9] has led to its progressive integration into robotics, demonstrating more excellent performance than primitive methods in various domains. Niroui et al. presented a novel DRL-based method to enable a single robot to explore unknown environments autonomously [10]. This methodology demonstrated superior performance compared to conventional methods. Additionally, specific multi-agent deep reinforcement learning (MADRL) techniques, such as VDN [11], MADDPG [12], and QMIX [13], are designed to address multi-agent decision-making problems. He et al. introduced a multi-robot autonomous exploration technique utilizing MADDPG [14]. The method involves selecting the closest frontier position as the exploration target point in a specific direction. However, due to the limited action space, not all frontier positions can be included, resulting in a significant constraint on the selection range of the target point. Meanwhile, utilizing multi-agent deep reinforcement learning methods directly with the centralized training with decentralized execution (CTDE) [15] structure requires complete retraining when modifying the network size, which consumes significant time interacting with the environment.
According to the limitations of the existing traditional and DRL-based methods, we are prompted to propose a new way of thinking to solve the problem of autonomous exploration of multiple robots in unknown environments. We have enhanced the SAC deep reinforcement learning technique [16] to accommodate multi-robot systems. We consider the multi-robot team as a whole and employ the improved SAC deep reinforcement learning method to acquire centrally executable autonomous exploration strategies for the team. Subsequently, we employ the knowledge distillation technique [17] to convert multi-robot autonomous exploration strategies that necessitate centralized execution into a network of various strategies that may be executed in a distributed manner on individual robots.
In general, the contributions of this paper include the following:
- We provide an enhanced deep reinforcement learning approach that builds upon the SAC deep reinforcement learning algorithm, enabling it to address decision-making challenges in multi-robot systems.
- We view the multi-agent system as a whole and obtain a policy network that allocates decisions to individual agents via centralized training. This network is converted into several distributed policy networks that can be implemented on individual agents with knowledge distillation techniques. Our proposed strategy offers an innovative approach to address the multi-agent collaboration task.
2. Related Work
2.1. Multi-Robot Exploration
Both traditional multi-robot autonomous exploration approaches and DRL-based multi-robot autonomous exploration approaches commonly employ the notion of frontier. A frontier is a boundary line where the free space of the environment meets the unknown space while a robot is exploring an unknown environment.
The Nearest Frontier method proposed by Yamauchi et al. is a straightforward method for multi-robot autonomous exploration [7]. The approach involves iteratively choosing the nearest frontiers to the robots for exploration. Stachniss et al. proposed utilizing AdaBoost [18] to train a classifier that can recognize the type of environment the robot is in to assist with exploration [19,20]. Haumann et al. introduced the Voronoi partitioning concept [21] and developed an exploration approach that optimizes an objective function. This function includes costs related to distance and direction and estimated information gain [22]. Colares et al. proposed using a utility function that considers information gain and distance cost to guide robots in exploring based on the frontier-based method [8]. Bautin et al. introduced a computationally efficient technique for assigning frontiers that considers the spatial distribution of the robots in the environment and reduces redundant scanning of the environment by the robot [23]. Similar utility-based approaches can be found in [24,25]. Aside from utility-based exploration approaches, some strategies introduce market-based multi-robot co-ordination approaches [26] to guide robots in distributed collaborative exploration [27,28,29].
In addition to conventional approaches, learning-based methodologies are utilized for multi-robot autonomous exploration. He et al. introduced a multi-robot autonomous exploration technique utilizing MADDPG [14]. The method involves selecting the closest frontier position as the exploration target point in a specific direction. He et al. suggested employing multi-agent deep reinforcement learning methods to develop a strategy for guiding a robot’s exploration [14]. This strategy involves analyzing the robot’s current state, selecting a direction, and identifying the nearest frontier position in that direction as the target. Zhang et al. introduced a coarse-to-fine exploration approach [30]. They combined graph neural networks (GNNs) with MADRL to help robots implicitly learn co-operative strategies. By applying the notion of macro actions [31], Tan et al. created a decentralized exploration planner based on macro actions that enabled the robot to consider the intentions of its teammates while conducting exploration [32].
2.2. Deep Reinforcement Learning
Developing artificial intelligence (AI) systems that can learn and respond effectively has been a persistent and challenging problem. Reinforcement learning (RL) is a mathematical framework that enables autonomous agents to acquire knowledge independently [33]. RL-based methods have achieved success in solving specific uncomplicated decision problems. Kohl et al. employed RL to direct the movement of a quadrupedal robot [34]. Ng et al. developed a controller for inverted helicopter flight using RL [35]. While RL-based methods have shown benefits in specific straightforward decision-making problems, they have become impractical for solving complex decision-making problems due to the issue of the curse of dimensionality.
With the development of deep neural network-based techniques, learning-based methods are gradually being used to solve decision-making tasks. A representative event was the building of the top Go program by Silver et al. using DRL methods [36]. Recently, DRL algorithms have been progressively used in robotic systems, including path planning [37], robotic manipulation [38], and autonomous driving [39]. SAC [16] is presently a widely utilized and highly effective DRL technique. This approach introduces the idea of maximizing the entropy of the action distribution. This enables the agent to explore actions more effectively, avoid falling into local optima, and maintain stable learning. Deep reinforcement learning algorithms for multi-agents commonly employ a CTDE scheme, such as MADDPG [12] and QMIX [13].
3. Methodology
This section defines the multi-robot autonomous exploration problem and presents our approach.
3.1. Problem Formulation
A multi-robot autonomous exploration mission refers to the systematic procedure wherein a group of robots, comprising many units traverse an unknown environment and progressively create a global map, M, of that environment by collecting data through their onboard sensors. The global map, M, is stitched together from local maps built by individual robots. In this study, each robot senses its surroundings using a LiDAR carried by itself with a detection range of 25 m. During exploration, the robots build a map of the unknown environment by scanning obstacles around themselves with LiDARs. Grid maps are commonly employed to represent environmental maps. These grids can be classified into three distinct types: unknown space, free space, and obstacle space. The term “unknown space” denotes an uncharted region yet to be explored, “free space” pertains to an unobstructed area that has been thoroughly investigated, while “obstacle space” designates a region characterized by the presence of obstacles. While a team of robots is exploring an unknown environment, they can interact with each other by exchanging local maps, robot positions, and goal positions. This communication is possible as long as the distance between the robots is smaller than , which is 30 m in this article. The objective of multi-robot autonomous exploration is to minimize the time spent while completing the exploration of the unknown environment:
where T denotes the total number of time steps, and denotes the duration of the i-th time step.
3.2. Technical Framework
In this study, we present an innovative deep reinforcement learning framework for distributed multi-agent systems, which leverages the concept of knowledge distillation. This framework divides training into two phases: centralized reinforcement learning and knowledge distillation, as shown in Figure 1. During the phase of centralized reinforcement learning, the collective of robots is perceived as a unified agent, and the SAC approach is employed for reinforcement learning. Notably, the SAC approach employed in this paper is an enhanced version designed explicitly for multi-robot decision-making. During the knowledge distillation phase, the actor network acquired through the first phase of SAC is converted into the policy network for each robot using the knowledge distillation technique, which enables the multi-robot autonomous exploration policy to be distributed. In knowledge distillation, the observation data in the replay buffer is directly used for knowledge distillation, which avoids interaction with the environment and can save training time. There are two notable advantages to this approach. Firstly, it can leverage the efficiency of the SAC deep reinforcement learning method. Secondly, there is no necessity to re-interact with the environment while resizing the final network, resulting in significant time savings for training.
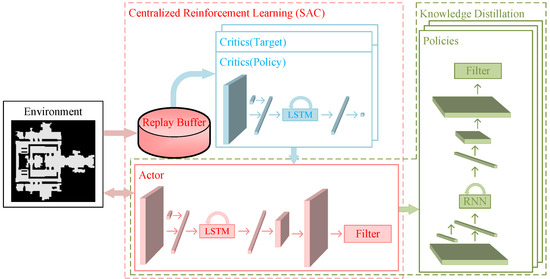
Figure 1.
This figure illustrates the technical framework of our proposed method. The methodology consists of two steps: SAC-based Centralized Reinforcement Learning and Knowledge Distillation. During the first phase, all robots are considered single agents and learn autonomous exploration strategies using the SAC DRL method. During the second phase, the exploration strategies acquired in the first stage are converted into distributed exploration strategies that individual robots may implement. This transformation is achieved through the process of knowledge distillation.
3.3. Centralized Reinforcement Learning
Centralized reinforcement learning is the first part of our proposed methodological framework. This part is based on the SAC deep reinforcement learning method to obtain a multi-robot autonomous exploration strategy that can be executed centrally. We improve the entropy calculation in the original SAC to be used for multi-robot decision-making problems. During the training process, the proposed method considers all robots as a whole, and the actor network directly outputs the actions of all robots.
3.3.1. Modeling
A Markov Decision Process (MDP) is defined by a tuple , where S is a set of states, A is a set of action vectors, R is a reward function , T is a transfer function , and is a discount factor. In this paper, the value of is empirically taken as 0.99. When the robots take actions, , at state s, the environment reaches a new state, , according to the probability distribution and returns a reward . The goal is to find a centralized strategy, , that allows a team of robots to capture the maximum cumulative reward when completing exploration tasks:
where T is the total number of time steps, and is the initial state.
3.3.2. Multi-Robot SAC
In this section, we present the Multi-Robot SAC (MR-SAC). The actor network in the primitive SAC method [16] outputs a single action probability distribution. In contrast, the actor network in this study’s modified SAC method optimized for the multi-robot decision-making problem outputs a set of action probability distributions, , to be assigned to individual robots in the robot team. In the method proposed in this paper, the entropy of the action probability distribution is calculated separately for each robot, while the corresponding temperature parameters are optimized individually. Thus, the soft Bellman residual used to train the parameters of the soft Q-function is given by the following equation:
where
and (sampled from the replay buffer) denote the state at the t-th time step and the action taken by the actor network, respectively, and and are the action probability distribution and temperature parameter of the i-th robot respectively, and finally, and are the parameters of the policy networks and target networks, respectively. The temperature parameter determines the relative importance of the entropy term to the reward, thus controlling the stochastic nature of the optimal policy [16]. Although we view the entire team of robots as a single agent, we perform independent entropy calculations and assign independent temperature parameters to each robot for the sake of the stochastic nature of each robot’s strategy in the team, which is very different from the traditional SAC approach.
Similarly, the loss function of the actor network is given by the following equation:
where represents the parameters of the actor network.
Optimizing the temperature parameter of each robot separately can make the entropy of each robot’s action probability distribution converge to the target entropy. The loss function for the temperature parameter is
where is a hyper-parameter denoting the desired entropy of the probability distribution of each robot’s action.
The complete process of Soft Actor-Critic for Multi-Robot Decision Making is shown in Algorithm 1.
| Algorithm 1 Soft Actor-Critic for Multi-Robot Decision Making | |
| Input: | ▹ Initial parameters. |
| ▹ Initialize target network. |
| ▹ Initialize replay buffer. |
| |
| |
| ▹ Sample actions from the policy. |
| ▹ Sample a transition from the environment. |
| |
| |
| |
| ▹ Update policy critic network weights. |
| ▹ Update actor network weights. |
| ▹ Adjust temperature. |
| |
| |
| |
| Output: | ▹ Optimized parameters |
3.3.3. Learning
During exploration, the arrival of one of the robots at a goal point triggers a decision to assign a new goal point to each robot. We designed each robot’s action space as a set of all frontier center locations. To ensure that each robot is assigned a different goal point, it adds its position to the action space when the number of frontiers is less than the total number of robots, allowing it to stay stationary at this time step.
The reward function consists of five components: area explored, area of scanning overlap, distance traveled by the robot, cost of time, and number of decisions:
where denotes the area of each grid, denotes the unknown space, denotes the free space region scanned by the i-th robot in this step of exploration, n is the total number of robots, denotes the length of the distance traveled by the i-th robot in the step of exploration, and denotes the time spent in this step of exploration. The item area explored is the area of new free space discovered by the robot team at each exploration step. We designed the scanning overlap penalty term to drive the robots to spread out during exploration, defined as the area of the overlapping region scanned by two robots, where 0.3 is the weighting factor. After each exploration step, we drive the trained strategy to spend as little distance and time as possible by giving penalties based on the distance traveled and time spent by the robot, respectively. After each decision step, a fixed penalty prevents the robot from always choosing its own position as the goal point.
We use spatial information and a scale to represent a state. The spatial information is a two-dimensional tensor of layers corresponding to the unknown space, the free space, the obstacle space, the frontier centers, and the positions of the n robots. The scale used to represent the state is the edge length corresponding to each element in the tensor. Before generating the tensor and the corresponding scalar, the information needs to be preprocessed so that its data dimensions match the network input. The preprocessing process is shown in Figure 2 and can be divided into cropping, scaling, and padding:

Figure 2.
Preprocessing of map information. The gray area in the figure is unknown space, the black area is the obstacle boundary, and the white area is free space. The figure’s red points are the frontiers’ center points, and the orange, green, and purple points are the robot positions. The preprocessing is divided into cropping, scaling, and padding.
- The smallest rectangular region containing valid information is boxed out, and irrelevant unknown regions are excluded;
- The boxed rectangular region is scaled so that the number of pixels on its long side matches the input dimension of the network (100 pixels in this study);
- The scaled rectangular region is padded into a square with unknown space, making it the same dimension as the input to the network (100 pixels × 100 pixels in this study).
Each layer in the tensor is a binary map with positive regions of 1 and negative regions of 0.
The structure of the actor network is shown in Figure 3 and consists of a map feature extractor and n policy heads, where n is the number of robots. The inputs to the actor network are categorized into spatial information and scale. The spatial information contains the map information, robots’ positions, and candidate target positions, and the scale is the side length of each pixel of the map after preprocessing (in meters). The map feature extractor obtains the feature vector corresponding to the current state from the input data. The strategy head obtains the corresponding action probability distribution of each robot through the spatial information and the feature vector corresponding to the current state. The filter in the policy head assigns the tensor of the non-frontier position to negative infinity so that the probability of the action corresponding to the non-frontier position is 0 after the softmax operation.
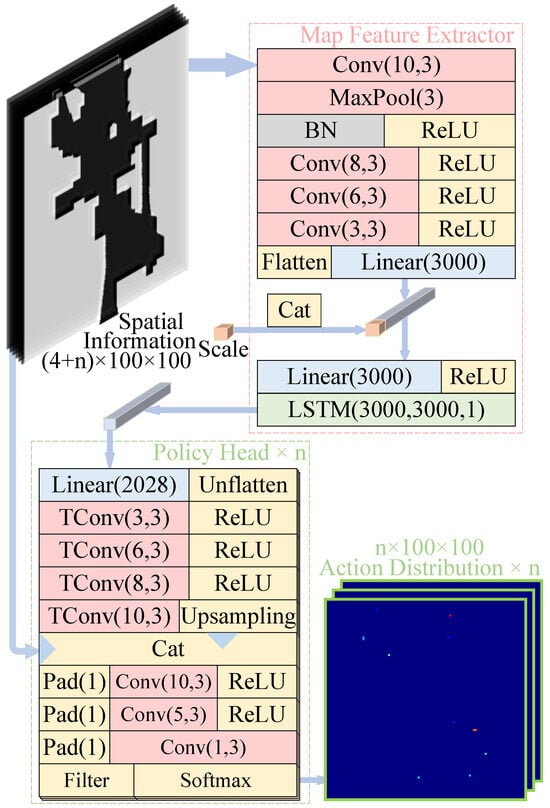
Figure 3.
The structure of the actor network. MaxPool is the maximum pooling layer, BN is the batch normalization layer, ReLU is the rectified linear unit, Cat is the concatenate operation, TConv stands for transposed convolution, LSTM stands for long short-term memory, Pad stands for zero padding, and n is the number of robots. The numbers in the brackets of the convolutional and transposed convolutional layers denote the number of output layers and the kernel size, respectively. The numbers in the brackets of the LSTM layer denote the output dimension, the hidden layer dimension, and the number of layers of the LSTM, respectively. The number in the brackets for the maximum pooling layer represents the number of input layers, the number in the brackets for the linear layer represents the output dimension, and the number in the zero-padding brackets represents the thickness of the surrounding padding pixels.
The structure of the critic network is shown in Figure 4. The input data of the critic network contains the input data of the actor network as well as the action probability distributions of the individual robots’ output by the actor network. The expected Q value of the action probability distribution is output by the critic network to evaluate the goodness of the action probability distribution.

Figure 4.
The structure of the critic network. MaxPool is the maximum pooling layer, BN is the batch normalization layer, ReLU is the rectified linear unit, Cat is the concatenate operation, LSTM stands for long short-term memory, and n is the number of robots. The numbers in the brackets of the convolutional layers denote the number of output layers and the kernel size, respectively. The numbers in the brackets of the LSTM layer denote the output dimension, the hidden layer dimension, and the number of layers of the LSTM, respectively. The number in the brackets for the maximum pooling layer represents the number of input layers, and the number in the brackets for the linear layer represents the output dimension.
3.4. Knowledge Distillation
Knowledge distillation is the second part of our proposed method, consisting of one teacher and n student networks, where n is the number of robots. We use the actor network obtained by training in MR-SAC to train the decentralized policy networks using offline knowledge distillation. In this case, the teacher network is the actor network trained in MR-SAC, and the student networks are the distributed policy networks that can be used on individual robots. In this section, we propose a novel approach to allow student networks to learn communication-invariant features by feeding global and local observations to the teacher network and student networks, respectively.
3.4.1. Training Dataset Generation
Primitive offline knowledge distillation is performed by feeding the same data to the teacher network and the student network and training the student network with the output of the teacher network as the labels. However, the direct use of the same input data does not allow the policy network obtained using knowledge distillation to be adapted to communication-constrained scenarios. We feed the teacher network the complete observations of all robots and feed the student networks the local observations available to individual robots in communication-constrained scenarios to force the student networks to be able to output big-picture strategies even when only local observations are available. During the centralized reinforcement learning process, we record the positions of individual robots at different time steps and the scanned environment information to generate the training dataset needed for the knowledge distillation session. On the one hand, we use these records to generate global observations as input to the teacher network. On the other hand, local observations of different robots are generated as inputs to the student network by introducing communication range and communication success rate in these records. When the distance between two robots is less than the communication range, they exchange information about their local maps. We also randomly simulate robots with communication failures when generating training data, and when a robot has a communication failure, it does not exchange information with other robots for 5 s.
3.4.2. Training Method
We use the actor network trained in MR-SAC as the teacher network and train the student network with the generated training dataset.
The training method is shown in Figure 5. The student networks are the policy networks used by each robot for independent decision-making. A student network is similar in structure to the teacher network, but smaller than the teacher network. The input to the teacher network is a global observation not constrained by communication; in contrast, the input to a student network is a local observation constrained by communication. The teacher network outputs action probability distributions for all robots, while a student network outputs an action probability distribution for only the corresponding robot. The action with the highest probability in the action probability distribution of each robot output by the teacher’s network is denoted as . The center of each frontier is extracted through local observation as the action space of the corresponding robot, and the closest position in the action space to is chosen to be noted as as the label to train the corresponding student network, where n is the number of robots. In most cases, and overlap in the environment.
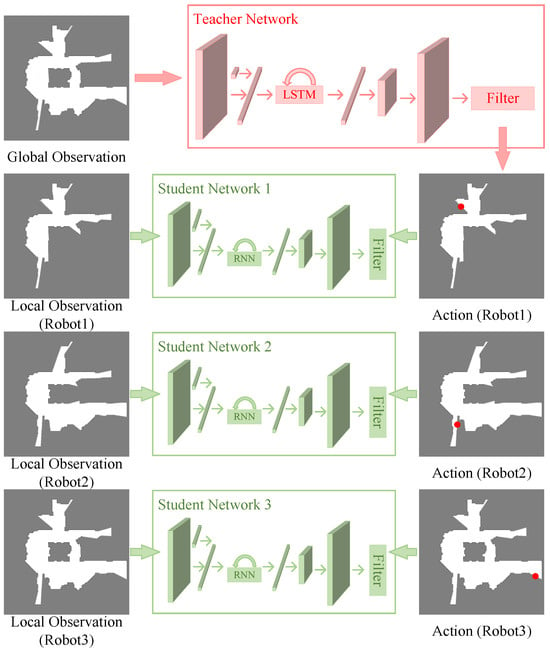
Figure 5.
Training process based on knowledge distillation. In the case of a team of three robots, the teacher’s network outputs the actions of the individual robots through global observation. The local observation of each robot is used as input data for each student network, and the action of each robot given by the teacher network is used as the label to train the student network.
This training method can force the robots to make decisions with a big-picture perspective even when only receiving information from local observations. At the same time, the knowledge distillation process does not require the robot to re-interact with the environment, and the size of the student network can be easily adjusted.
4. Training
The training process is divided into two parts: MR-SAC and knowledge distillation. The robot team is viewed as an agent that interacts with the environment. The MR-SAC approach is then utilized to train and develop a policy network. The knowledge distillation process converts the policy network obtained from MR-SAC, which requires centralized execution, into several policy networks that can be executed distributively. We use the first three environments shown in Figure 6 for training, with different obstacle distributions, sizes, and aspect ratios. The training involved scenarios of robot teams consisting of three, four, and five robots, utilizing two Intel Xeon Silver 4210 CPUs (Intel, California, USA) and one NVIDIA RTX 2080 Ti GPU (NVIDIA, California, USA).

Figure 6.
Environments for training and experiments. These environments were sourced from benchmark sets released by Moving AI Lab [40]. The white regions represent free space, and the black areas represent obstacle space.
In the MR-SAC part, it took an average of 300 h to complete training for one size of robot team. We cycled through the first three environments shown in Figure 6 for training and recorded the total reward received by the robot team each time it completed the exploration of Environment 1. The cumulative reward and elapsed exploration time during training are shown in Figure 7. The network can be trained to converge in around 80,000 episodes for every robot team size. Following the convergence of training, the team of five robots achieved the lowest cumulative reward but completed the exploration in the shortest time. This was due to a relatively high penalty term from overlapping scanning regions ().

Figure 7.
Rewards and time-consuming changes. The curves in the left and right subfigures represent the change in average reward and time consumption over the training process as the robot team completes its exploration of the environment, respectively. The different colors of the lines in the subfigures represent various sizes of robot teams, and the shaded areas indicate the standard deviations.
Within the knowledge distillation part, we designed student networks of varying sizes. The student networks share the same fundamental design, resembling the actor network in MR-SAC (depicted in Figure 3) but with only one policy head. The student networks sequentially pass through a map feature extractor, which is composed of multiple convolutional layers, two fully connected layers, one recurrent neural network (RNN), and a policy head that includes one fully connected layer, multiple transposed convolutional layers, and multiple convolutional layers. The batch size for the training procedure was set at 64, and an Adam optimizer was employed with an initial learning rate of 1 × . After completing a single epoch of training, the policy network that had undergone training was employed to explore Environment 1 (shown in Figure 6). Once the average value of the elapsed time of the last 100 completed explorations reaches a point of stagnation, the training process is considered to have reached convergence, leading to the termination of training.
Various policy networks of various sizes were established for training in the knowledge distillation part. Regardless of their respective sizes, all policy networks could achieve convergence within 1 h. According to Table 1, there are 12 distinct sizes of student networks. In this table, C1 represents the number of layers in the convolutional layer of the map feature extractor. RNN represents the selected type of RNN, TC represents the number of layers in the transposed convolutional layer of the policy head, and C2 represents the number of layers in the convolutional layer of the policy head. The elapsed time in the table is the average elapsed time of a robot team consisting of three, four, and five robots completing exploration 100 times in Environment 1 (shown in Figure 6), respectively. At the start of each exploration, the robot team is assigned a random location on the map, and the timer starts. The timer ends when the robot team finishes exploring. All training was conducted with a communication success rate of 80%. According to the data presented in Table 1, the network’s performance improves as its size increases. However, the kind of RNN has little impact on performance.

Table 1.
Different student network depths.
5. Experiment
We conducted a comparative analysis of our proposed method (the networks are indexed as 6 in Table 1) and other multi-robot autonomous exploration methods in a simulated environment. The exploration of the 4th to 8th environments in Figure 6 was accomplished using these methods to compare the performance of the different methods. We built the simulation environment used for the experiments in CoppeliaSim. Within the simulation experiment, we set the communication success rate. The robot had a probability of communication failure with each communication attempt. When this failure occurs, the robot cannot communicate with other robots for 5 s. Furthermore, the generalization ability of our suggested approaches may be verified by considering the varying aspect ratios and sizes of these environments. The experiment compares the method suggested in this research, two classic methods, and a DRL-based method.
- Nearest Frontier [7]: The robots consistently choose the nearest positions on the frontiers as target points to explore;
- Information Gain [8]: The methodology involves the selection of goals for individual robots through the calculation of information gain resulting from the exploration of various frontier locations. This gain is then combined with the path length cost. Additionally, a co-ordination factor is employed to encourage the robot formation to disperse, thereby enhancing exploration efficiency;
- DME-DRL [14]: DME-DRL is based on the MADDPG deep reinforcement learning method with the introduction of structural information and time series. The robots employ this technique to choose the closest frontiers in specific directions as goal points for exploration.
We have tested the performance of different methods in different environments, and the results are shown in Figure 8. Our proposed method achieved the best results in most of the environments. This experimental result shows, on the one hand, that our proposed deep reinforcement learning-based exploration strategy outperforms the current mainstream exploration methods in terms of exploration efficiency. On the other hand, the knowledge distillation technique enables the robot team to explore unknown environments stably despite the communication constraints.

Figure 8.
Comparison of the time elapsed to complete the exploration using different methods. The three subgraphs represent robot team sizes of three, four, and five. Within each subgraph, the five sets of data on the left represent the average time taken by each technique to finish exploring different environments with a communication success rate of 80%. Similarly, the five datasets on the right represent the scenario with a communication success rate of 60%. The error bars in the graph indicate the standard deviations.
We used different methods to conduct 100 explorations in Environment 7, which has the largest free space, measuring 3093.1 m2, using a team of four robots and a communication success rate of 80%. As shown in Figure 9, we collected data on the average area explored for each method over time. The figure shows that our proposed strategy demonstrated an early advantage in the exploration job. This is because our proposed method can effectively decentralize the robot’s formation.
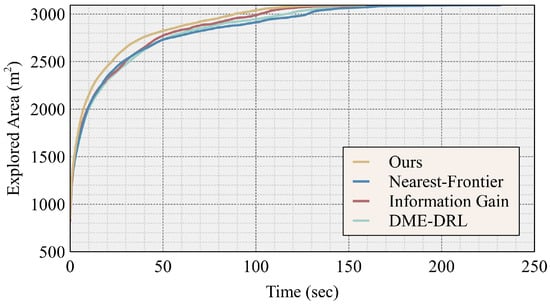
Figure 9.
Curves of the average explored area over time when a team of four robots explored Environment 7 using different methods at a communication success rate of 80%.
6. Conclusions
This study presents a novel technique for treating a multi-agent system as a whole and learning the strategies using a single-agent deep reinforcement learning method. The learned strategies can be executed in a distributed manner using knowledge distillation. We apply this method to a multi-robot autonomous exploration task, and the training process demonstrates that our suggested approach can effortlessly modify the size of the policy network without the need to interface with the environment repeatedly. This capability significantly reduces the time required for environmental interaction. The experimental results indicate that our suggested method can adjust to environments of varying sizes and aspect ratios while outperforming traditional approaches. Nevertheless, our suggested approach still possesses certain constraints. Once the size of the robot team has been modified, our proposed technique needs to undergo retraining to accommodate the new team size. Further investigation is required to determine how the trained policy network may be directly extended to varying-sized robot teams.
Author Contributions
Conceptualization, R.W.; methodology, R.W.; software, J.Z.; validation, R.W., M.L. and J.Z.; formal analysis, J.Z.; investigation, R.W.; resources, R.W.; data curation, R.W.; writing—original draft preparation, R.W.; writing—review and editing, R.W.; visualization, R.W.; supervision, J.Z.; project administration, M.L.; funding acquisition, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Provincial frontier leading technology basic research major project fund under Grant BK20232028.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DRL | Deep reinforcement learning |
| MADRL | Multi-agent deep reinforcement learning |
| CTDE | Centralized training with decentralized execution |
| GNN | Graph neural network |
| AI | Artificial intelligence |
| RL | Reinforcement learning |
| MDP | Markov Decision Process |
| MR-SAC | Multi-Robot SAC |
| RNN | Recurrent neural network |
References
- Burgard, W.; Moors, M.; Stachniss, C.; Schneider, F.E. Coordinated multi-robot exploration. IEEE Trans. Robot. 2005, 21, 376–386. [Google Scholar] [CrossRef]
- Ahmadi, M.; Stone, P. A multi-robot system for continuous area sweeping tasks. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 1724–1729. [Google Scholar] [CrossRef]
- Queralta, J.P.; Taipalmaa, J.; Pullinen, B.C.; Sarker, V.K.; Gia, T.N.; Tenhunen, H.; Gabbouj, M.; Raitoharju, J.; Westerlund, T. Collaborative multi-robot search and rescue: Planning, coordination, perception, and active vision. IEEE Access 2020, 8, 191617–191643. [Google Scholar] [CrossRef]
- Ng, M.K.; Chong, Y.W.; Ko, K.m.; Park, Y.H.; Leau, Y.B. Adaptive path finding algorithm in dynamic environment for warehouse robot. Neural Comput. Appl. 2020, 32, 13155–13171. [Google Scholar] [CrossRef]
- Gul, F.; Mir, A.; Mir, I.; Mir, S.; Islaam, T.U.; Abualigah, L.; Forestiero, A. A Centralized Strategy for Multi-Agent Exploration. IEEE Access 2022, 10, 126871–126884. [Google Scholar] [CrossRef]
- Matignon, L.; Jeanpierre, L.; Mouaddib, A.I. Coordinated multi-robot exploration under communication constraints using decentralized markov decision processes. In Proceedings of the AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012; Volume 26, pp. 2017–2023. [Google Scholar]
- Yamauchi, B. Frontier-based exploration using multiple robots. In Proceedings of the Second International Conference on Autonomous Agents, St. Paul, MN, USA, 9–13 May 1998; pp. 47–53. [Google Scholar]
- Colares, R.G.; Chaimowicz, L. The next frontier: Combining information gain and distance cost for decentralized multi-robot exploration. In Proceedings of the 31st Annual ACM Symposium on Applied Computing, Pisa, Italy, 4–8 April 2016; pp. 268–274. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Niroui, F.; Zhang, K.; Kashino, Z.; Nejat, G. Deep reinforcement learning robot for search and rescue applications: Exploration in unknown cluttered environments. IEEE Robot. Autom. Lett. 2019, 4, 610–617. [Google Scholar] [CrossRef]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-decomposition networks for cooperative multi-agent learning. arXiv 2017, arXiv:1706.05296. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6379–6390. [Google Scholar]
- Rashid, T.; Samvelyan, M.; De Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. Monotonic value function factorisation for deep multi-agent reinforcement learning. J. Mach. Learn. Res. 2020, 21, 1–51. [Google Scholar]
- He, D.; Feng, D.; Jia, H.; Liu, H. Decentralized exploration of a structured environment based on multi-agent deep reinforcement learning. In Proceedings of the 2020 IEEE 26th International Conference on Parallel and Distributed Systems (ICPADS), Hong Kong, China, 2–4 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 172–179. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Cham, Switzerland, 2021; pp. 321–384. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge distillation: A survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Stachniss, C.; Martinez Mozos, O.; Burgard, W. Speeding-up multi-robot exploration by considering semantic place information. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 1692–1697. [Google Scholar] [CrossRef]
- Stachniss, C.; Martínez Mozos, Ó.; Burgard, W. Efficient exploration of unknown indoor environments using a team of mobile robots. Ann. Math. Artif. Intell. 2008, 52, 205–227. [Google Scholar] [CrossRef]
- Aurenhammer, F. Voronoi diagrams—A survey of a fundamental geometric data structure. ACM Comput. Surv. (CSUR) 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Haumann, A.D.; Listmann, K.D.; Willert, V. DisCoverage: A new paradigm for multi-robot exploration. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–8 May 2010; pp. 929–934. [Google Scholar]
- Bautin, A.; Simonin, O.; Charpillet, F. MinPos: A Novel Frontier Allocation Algorithm for Multi-robot Exploration. In Proceedings of the Intelligent Robotics and Applications; Su, C.Y., Rakheja, S., Liu, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 496–508. [Google Scholar]
- Irturk, A.U. Distributed Multi-robot Coordination For Area Exploration and Mapping; University of California Santa Barbara: Santa Barbara, CA, USA, 2006. [Google Scholar]
- Rogers, J.G.; Nieto-Granda, C.; Christensen, H.I. Coordination Strategies for Multi-robot Exploration and Mapping. In Experimental Robotics: The 13th International Symposium on Experimental Robotics; Desai, J.P., Dudek, G., Khatib, O., Kumar, V., Eds.; Springer International Publishing: Heidelberg, Germany, 2013; pp. 231–243. [Google Scholar] [CrossRef]
- Dias, M.; Zlot, R.; Kalra, N.; Stentz, A. Market-Based Multirobot Coordination: A Survey and Analysis. Proc. IEEE 2006, 94, 1257–1270. [Google Scholar] [CrossRef]
- Zlot, R.; Stentz, A.; Dias, M.; Thayer, S. Multi-robot exploration controlled by a market economy. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 3, pp. 3016–3023. [Google Scholar] [CrossRef]
- Yan, Z.; Jouandeau, N.; Cherif, A.A. Multi-robot decentralized exploration using a trade-based approach. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics, Noordwijkerhout, The Netherlands, 28–31 July 2011; SciTePress: Setubal, Portugal, 2011; Volume 2, pp. 99–105. [Google Scholar]
- Otte, M.; Kuhlman, M.J.; Sofge, D. Auctions for multi-robot task allocation in communication limited environments. Auton. Robot. 2020, 44, 547–584. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, J.; Zhang, L.; Li, Y.; Zhang, W. H2GNN: Hierarchical-Hops Graph Neural Networks for Multi-Robot Exploration in Unknown Environments. IEEE Robot. Autom. Lett. 2022, 7, 3435–3442. [Google Scholar] [CrossRef]
- Sutton, R.S.; Precup, D.; Singh, S. Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artif. Intell. 1999, 112, 181–211. [Google Scholar] [CrossRef]
- Tan, A.H.; Bejarano, F.P.; Zhu, Y.; Ren, R.; Nejat, G. Deep Reinforcement Learning for Decentralized Multi-Robot Exploration With Macro Actions. IEEE Robot. Autom. Lett. 2023, 8, 272–279. [Google Scholar] [CrossRef]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 2023, 231, 120495. [Google Scholar] [CrossRef]
- Kohl, N.; Stone, P. Policy gradient reinforcement learning for fast quadrupedal locomotion. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA’04. 2004, New Orleans, LA, USA, 26 April–1 May 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 2619–2624. [Google Scholar]
- Ng, A.Y.; Coates, A.; Diel, M.; Ganapathi, V.; Schulte, J.; Tse, B.; Berger, E.; Liang, E. Autonomous inverted helicopter flight via reinforcement learning. In Experimental Robotics IX: The 9th International Symposium on Experimental Robotics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 363–372. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Wang, S. A review of mobile robot path planning based on deep reinforcement learning algorithm. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 2138, p. 012011. [Google Scholar]
- Liu, R.; Nageotte, F.; Zanne, P.; de Mathelin, M.; Dresp-Langley, B. Deep reinforcement learning for the control of robotic manipulation: A focussed mini-review. Robotics 2021, 10, 22. [Google Scholar] [CrossRef]
- Elallid, B.B.; Benamar, N.; Hafid, A.S.; Rachidi, T.; Mrani, N. A comprehensive survey on the application of deep and reinforcement learning approaches in autonomous driving. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 7366–7390. [Google Scholar] [CrossRef]
- Sturtevant, N. Benchmarks for Grid-Based Pathfinding. Trans. Comput. Intell. AI Games 2012, 4, 144–148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).