Abnormal Monitoring Data Detection Based on Matrix Manipulation and the Cuckoo Search Algorithm
Abstract
1. Introduction
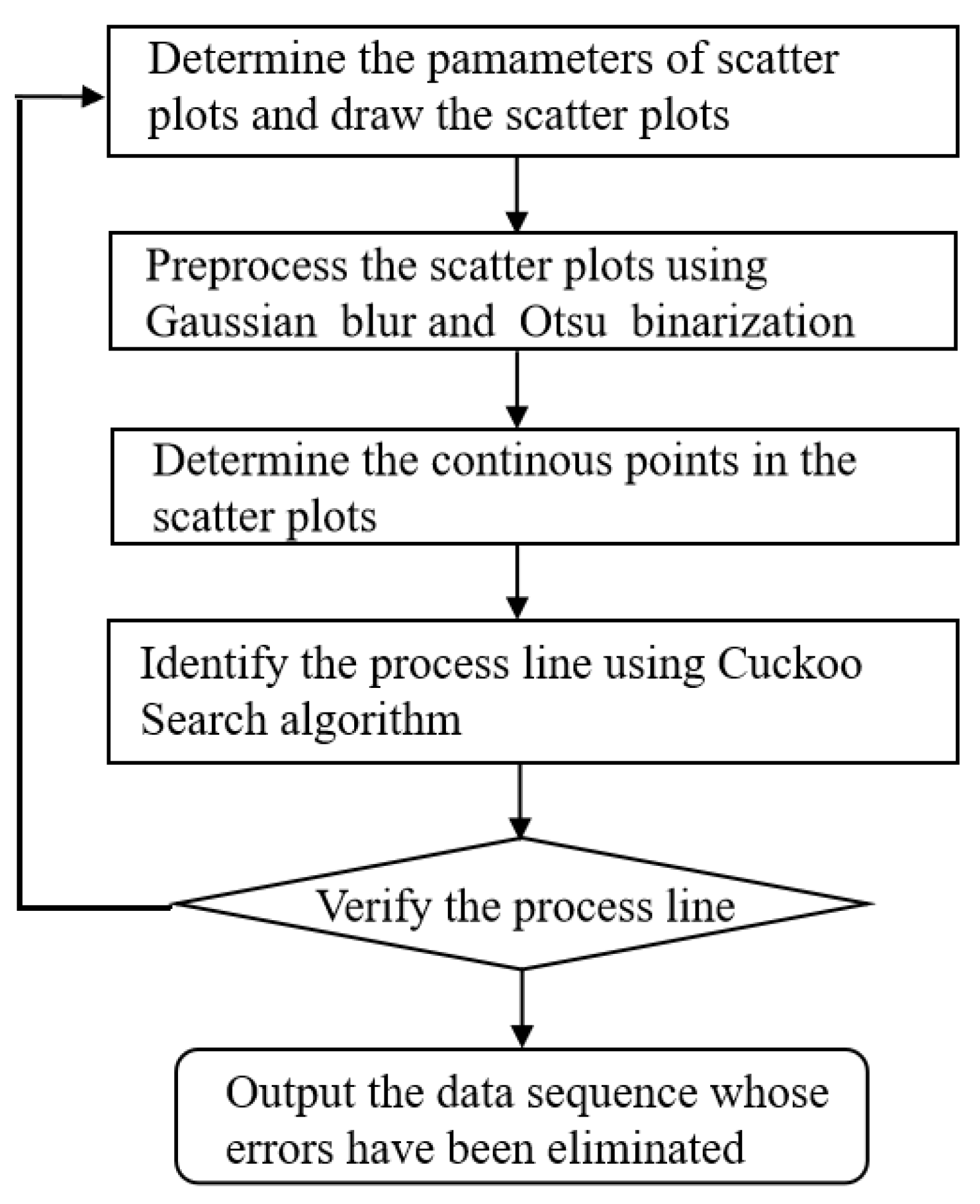
2. Data Processing Method Using Matrix Manipulation and the Cuckoo Search Algorithm
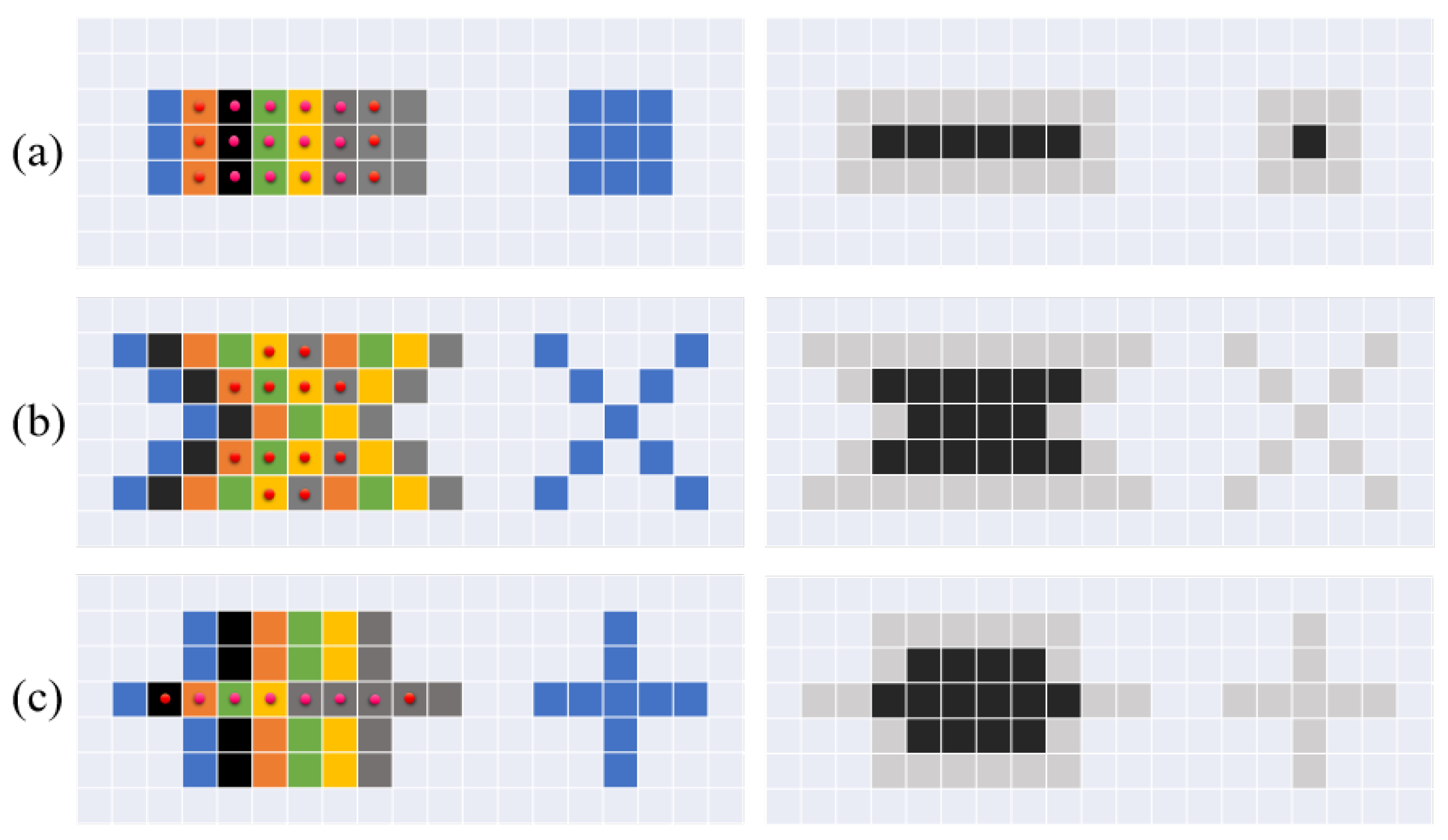
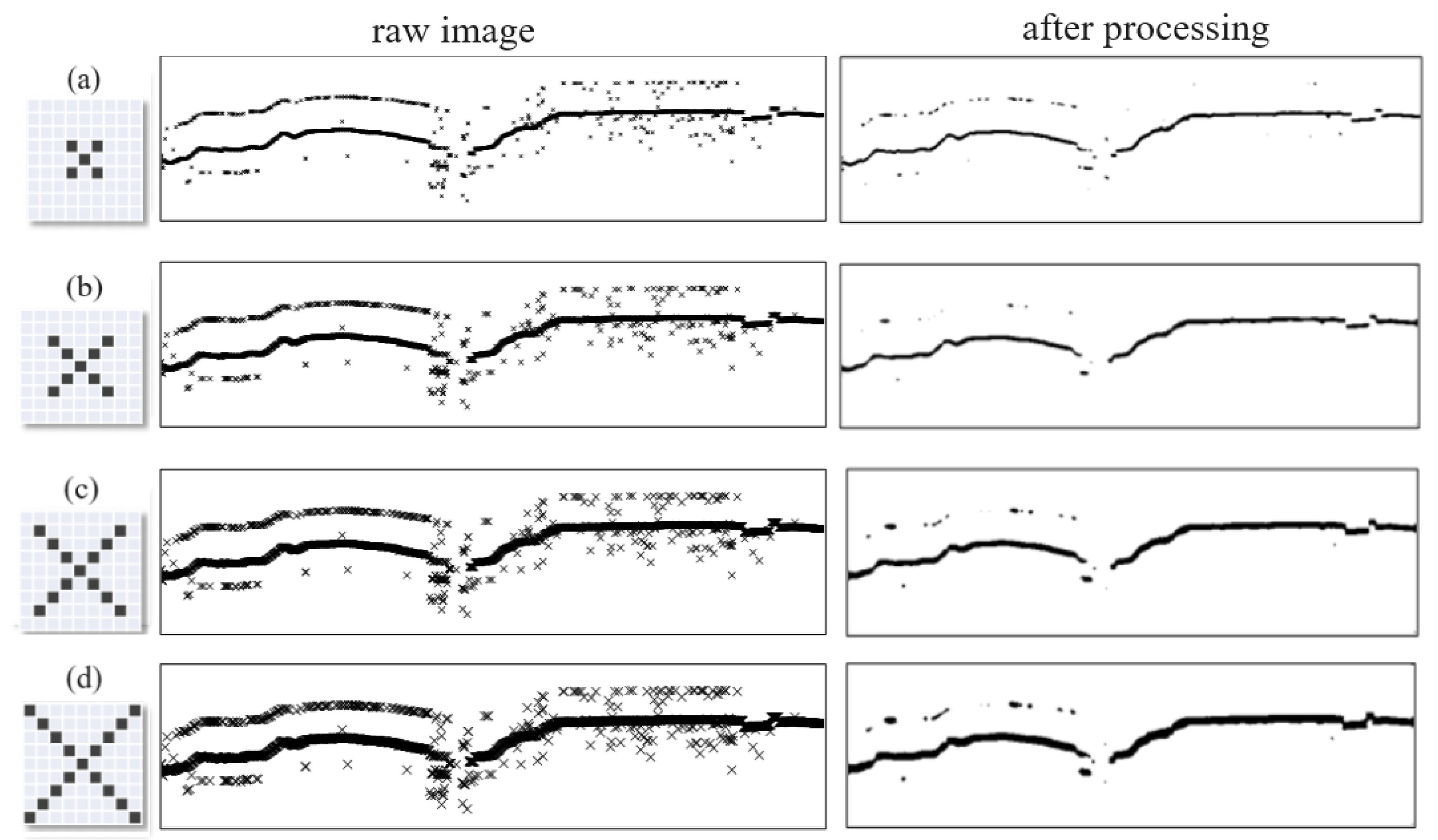
2.1. Data Pre-Processing Using Gaussian Blur and Ostu Binarization
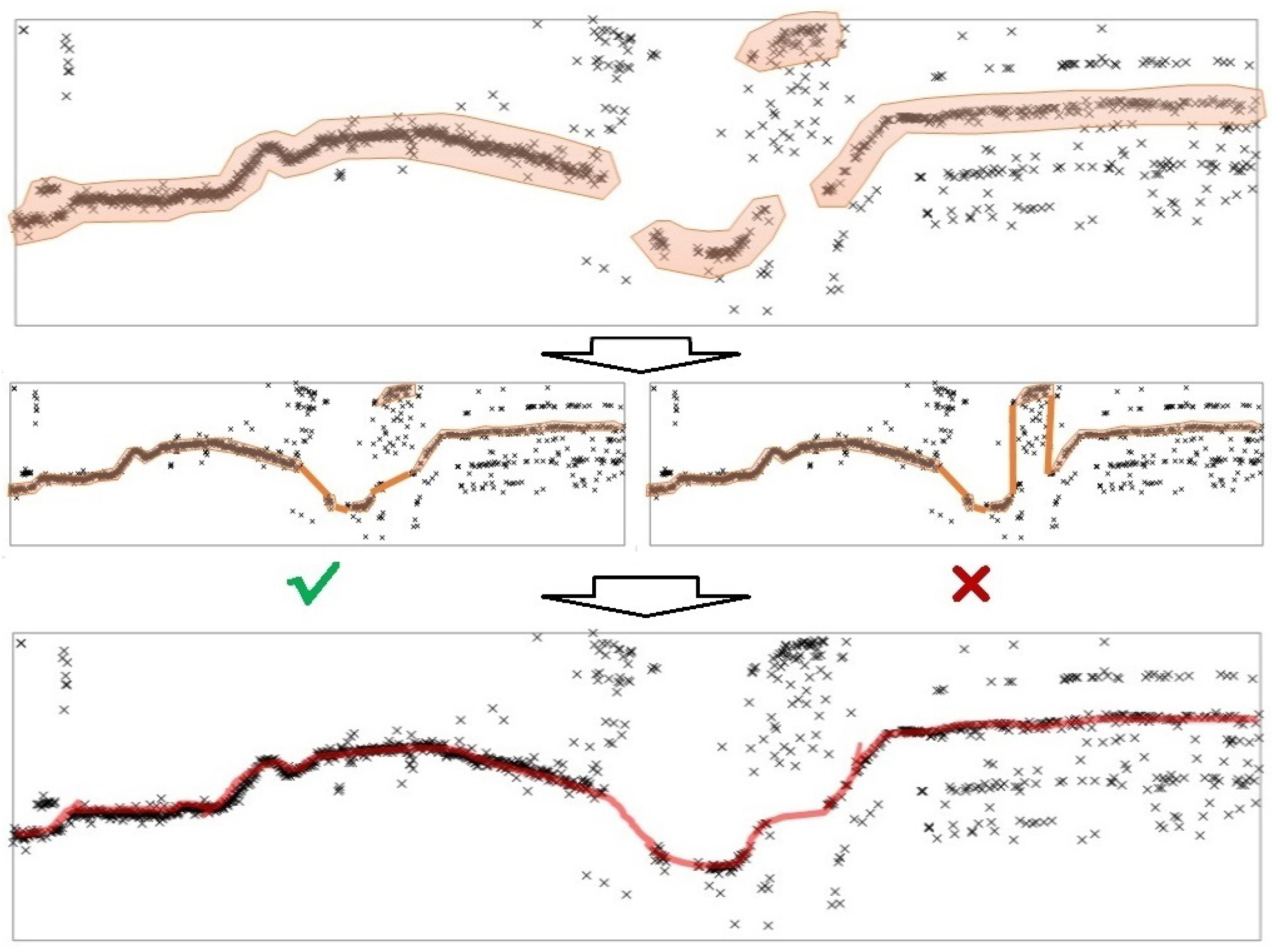
2.2. Process Line Identification Using Cuckoo Search Algorithm
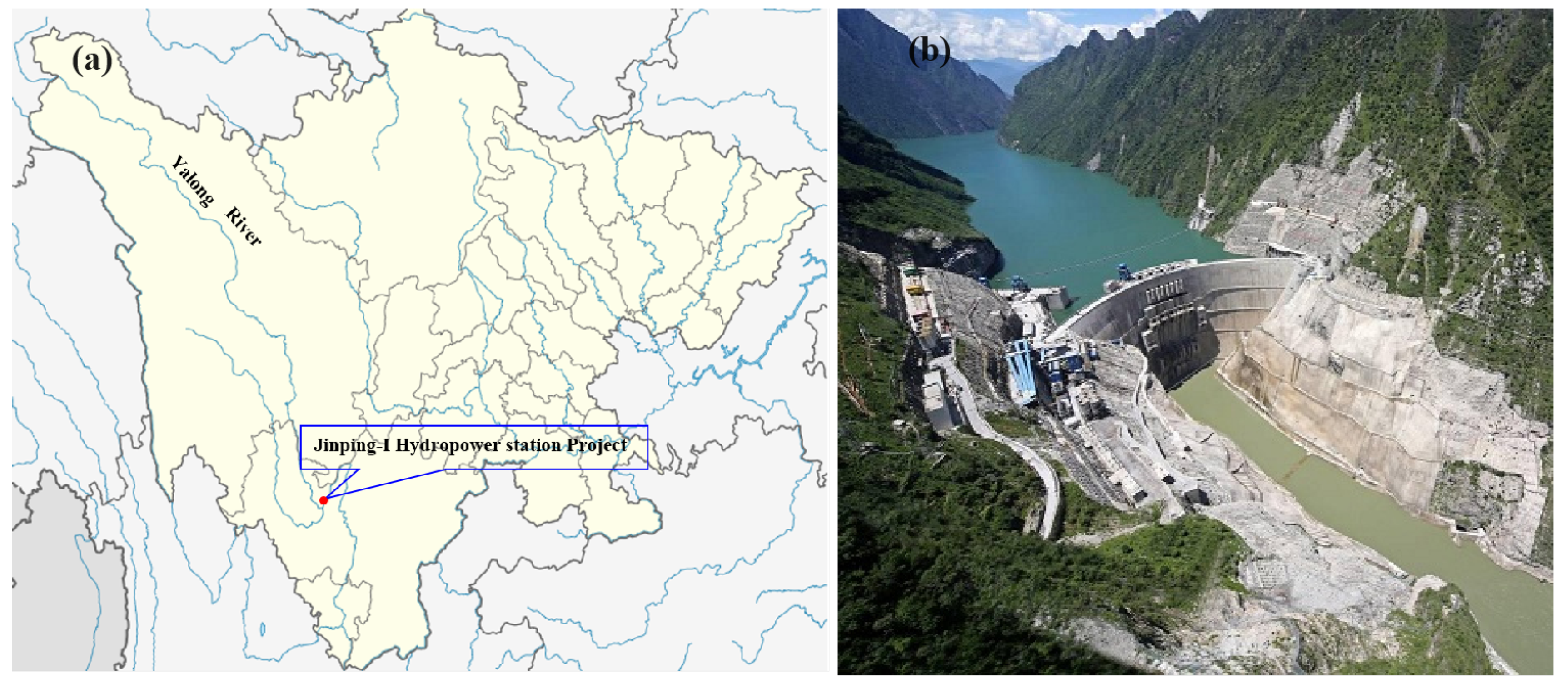
3. Dataset
4. Results
4.1. Optimal Settings of the Scatter Plot of the Original Data
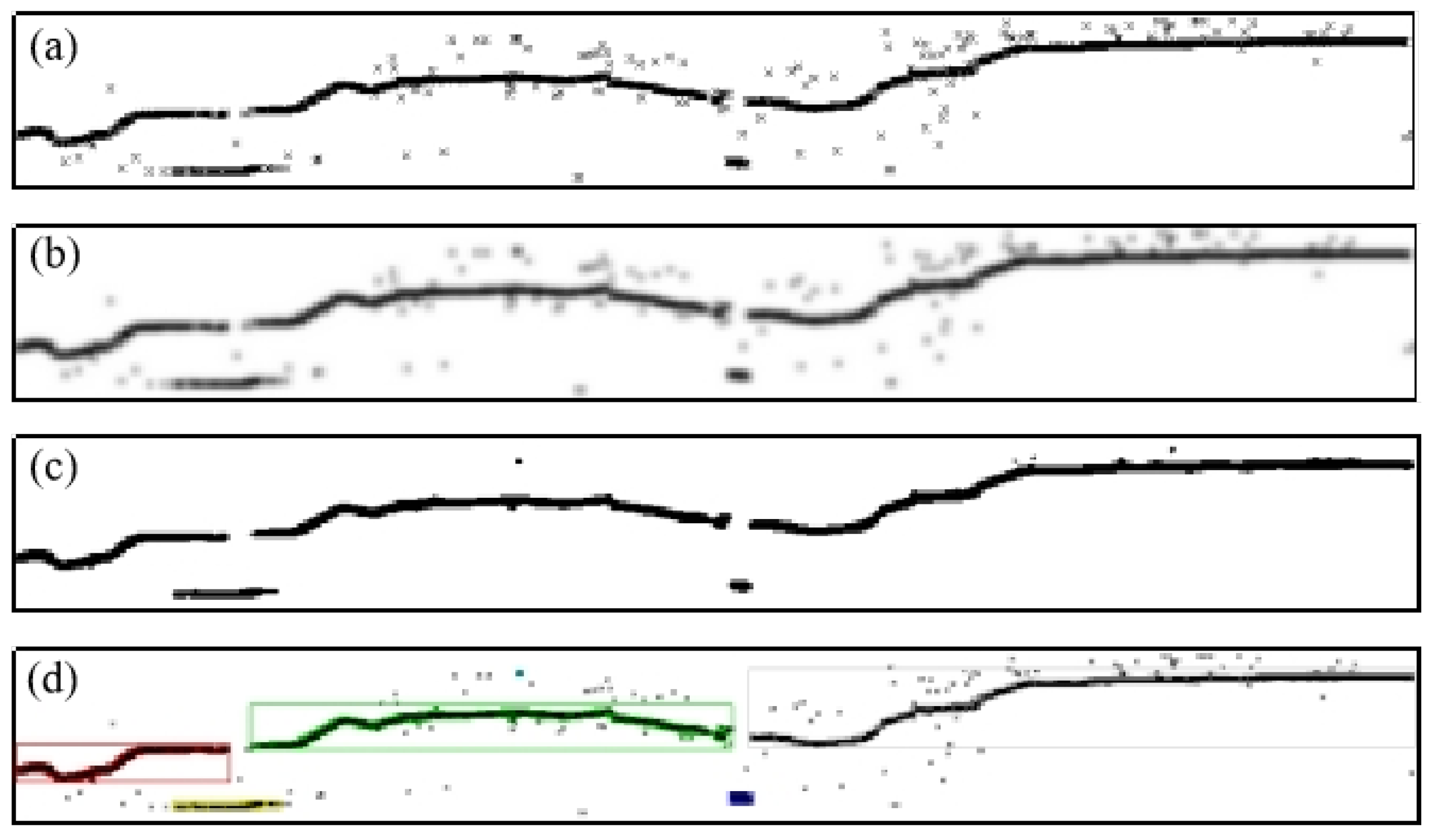
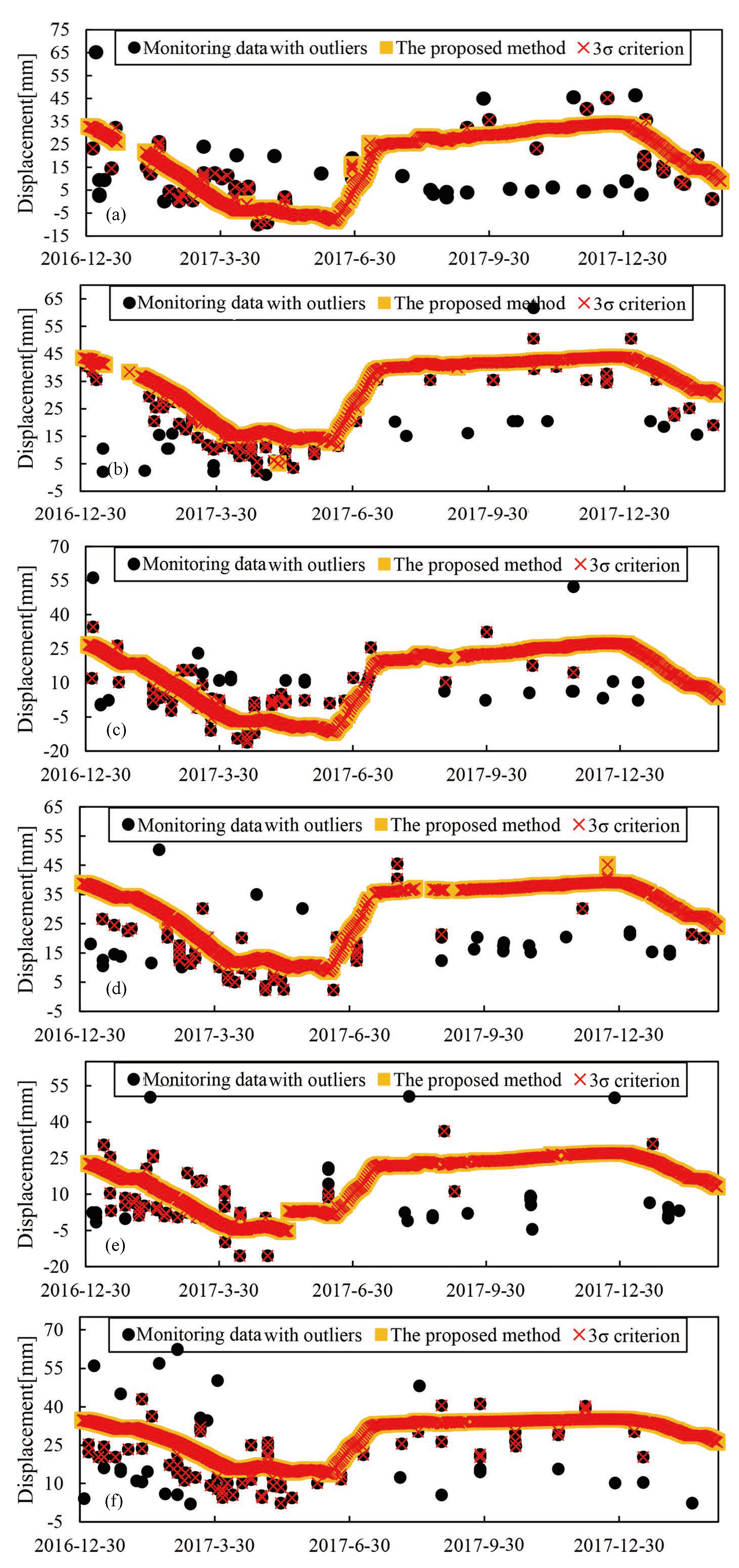
4.2. Results of Abnormal Data Detection Based on the Proposed Method
4.3. Comparison of the Proposed Method with 3- Method
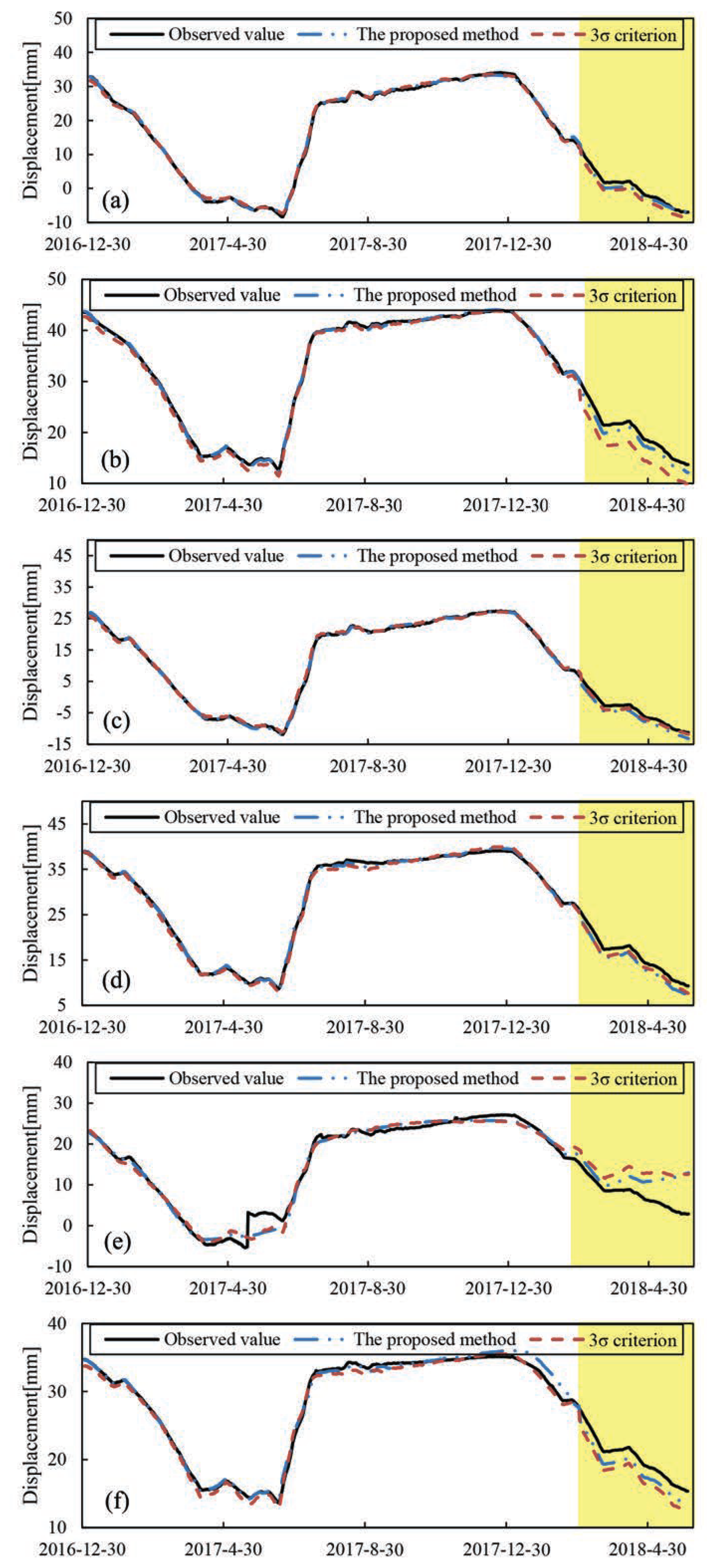
4.4. Regression Model Development Using Processed Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, Y.S.; Kim, B.T. Prediction of relative crest settlement of concrete-faced rockfill dams analyzed using an artificial neural network model. Comput. Geotech. 2008, 35, 313–322. [Google Scholar] [CrossRef]
- De Sortis, A.; Paoliani, P. Statistical analysis and structural identification in concrete dam monitoring. Eng. Struct. 2007, 29, 110–120. [Google Scholar] [CrossRef]
- Kao, C.Y.; Loh, C.H. Monitoring of long-term static deformation data of Fei-Tsui arch dam using artificial neural network-based approaches. Struct. Control Health Monit. 2013, 20, 282–303. [Google Scholar] [CrossRef]
- Dardanelli, G.; La Loggia, G.; Perfetti, N.; Capodici, F.; Puccio, L.; Maltese, A. Monitoring displacements of an earthen dam using GNSS and remote sensing. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XVI, Amsterdam, The Netherlands, 22–25 September 2014; Volume 9239, pp. 574–589. [Google Scholar]
- Wu, Z. Safety Monitoring Theory and Its Application of Hydraulic Structures; Higher Education: Beijing, China, 2003. [Google Scholar]
- Bukenya, P.; Moyo, P.; Beushausen, H.; Oosthuizen, C. Health monitoring of concrete dams: A literature review. J. Civ. Struct. Health Monit. 2014, 4, 235–244. [Google Scholar] [CrossRef]
- Leger, P.; Leclerc, M. Hydrostatic, temperature, time-displacement model for concrete dams. J. Eng. Mech. 2007, 133, 267–277. [Google Scholar] [CrossRef]
- Mata, J. Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models. Eng. Struct. 2011, 33, 903–910. [Google Scholar] [CrossRef]
- Hipni, A.; El-shafie, A.; Najah, A.; Karim, O.A.; Hussain, A.; Mukhlisin, M. Daily forecasting of dam water levels: Comparing a support vector machine (SVM) model with adaptive neuro fuzzy inference system (ANFIS). Water Resour. Manag. 2013, 27, 3803–3823. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Pourkamali-Anaraki, F. Support vector machine based reliability analysis of concrete dams. Soil Dyn. Earthq. Eng. 2018, 104, 276–295. [Google Scholar] [CrossRef]
- Kang, F.; Liu, J.; Li, J.; Li, S. Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct. Control Health Monit. 2017, 24, e1997. [Google Scholar] [CrossRef]
- Avendano-Valencia, L.D.; Fassois, S.D. Gaussian mixture random coefficient model based framework for shm in structures with time–dependent dynamics under uncertainty. Mech. Syst. Signal Process. 2017, 97, 59–83. [Google Scholar] [CrossRef]
- Alimohammadi, H.; Chen, S.N. Performance evaluation of outlier detection techniques in production timeseries: A systematic review and meta-analysis. Expert Syst. Appl. 2022, 191, 116371. [Google Scholar] [CrossRef]
- Samara, M.A.; Bennis, I.; Abouaissa, A.; Lorenz, P. A survey of outlier detection techniques in IoT: Review and classification. J. Sens. Actuator Netw. 2022, 11, 4. [Google Scholar] [CrossRef]
- Chen, L.; Gu, C.; Zheng, S.; Wang, Y. A Method for Identifying Gross Errors in Dam Monitoring Data. Water 2024, 16, 978. [Google Scholar] [CrossRef]
- Bourquin, J.; Schmidli, H.; van Hoogevest, P.; Leuenberger, H. Pitfalls of artificial neural networks (ANN) modelling technique for data sets containing outlier measurements using a study on mixture properties of a direct compressed dosage form. Eur. J. Pharm. Sci. 1998, 7, 17–28. [Google Scholar] [CrossRef]
- Chakravarty, S.; Demirhan, H.; Baser, F. Fuzzy regression functions with a noise cluster and the impact of outliers on mainstream machine learning methods in the regression setting. Appl. Soft Comput. 2020, 96, 106535. [Google Scholar] [CrossRef]
- Zhao, L.; Akoglu, L. On using classification datasets to evaluate graph outlier detection: Peculiar observations and new insights. Big Data 2023, 11, 151–180. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Xu, Y.P.; Teegavarapu, R.S.; Guo, Y.; Nie, H.; Xie, H. Using baseflow ensembles for hydrologic hysteresis characterization in humid basins of Southeastern China. Water Resour. Res. 2024, 60, e2023WR036195. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, Z.; Li, H.; Zhang, Y. Computer vision and deep learning–based data anomaly detection method for structural health monitoring. Struct. Health Monit. 2019, 18, 401–421. [Google Scholar] [CrossRef]
- Domingues, R.; Filippone, M.; Michiardi, P.; Zouaoui, J. A comparative evaluation of outlier detection algorithms: Experiments and analyses. Pattern Recognit. 2018, 74, 406–421. [Google Scholar] [CrossRef]
- Miao, Y.; Su, H.; Xu, O.; Chu, J. Support vector regression approach for simultaneous data reconciliation and gross error or outlier detection. Ind. Eng. Chem. Res. 2009, 48, 10903–10911. [Google Scholar] [CrossRef]
- Malhotra, P.; Ramakrishnan, A.; Anand, G.; Vig, L.; Agarwal, P.; Shroff, G. LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv 2016, arXiv:1607.00148. [Google Scholar]
- Rico, J.; Barateiro, J.; Mata, J.; Antunes, A.; Cardoso, E. Applying advanced data analytics and machine learning to enhance the safety control of dams. In Machine Learning Paradigms: Applications of Learning and Analytics in Intelligent Systems; Springer: Cham, Switzerland, 2019; pp. 315–350. [Google Scholar]
- Mishra, G.; Kumar, R. An individual fairness based outlier detection ensemble. Pattern Recognit. Lett. 2023, 171, 76–83. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, K.; Zhang, H.; Li, Y.; Wu, Z. The method of gross error identification of dam monitoring data based on robust estimation. J. Water Resour. Power 2018, 36, 68–71. [Google Scholar]
- Song, J.; Zhang, S.; Tong, F.; Yang, J.; Zeng, Z.; Yuan, S. Outlier detection based on multivariable panel data and K-means clustering for dam deformation monitoring data. Adv. Civ. Eng. 2021, 2021, 3739551. [Google Scholar] [CrossRef]
- Zhang, P.; Li, T.; Wang, G.; Wang, D.; Lai, P.; Zhang, F. A multi-source information fusion model for outlier detection. Inf. Fusion 2023, 93, 192–208. [Google Scholar] [CrossRef]
- Li, M.; Li, M.; Ren, Q.; Li, H.; Song, L. DRLSTM: A dual-stage deep learning approach driven by raw monitoring data for dam displacement prediction. Adv. Eng. Inform. 2022, 51, 101510. [Google Scholar] [CrossRef]
- Petrou, M.M.; Petrou, C. Image Processing: The Fundamentals; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Flusser, J.; Farokhi, S.; Höschl, C.; Suk, T.; Zitova, B.; Pedone, M. Recognition of images degraded by Gaussian blur. IEEE Trans. Image Process. 2015, 25, 790–806. [Google Scholar] [CrossRef]
- Waltz, F.M.; Miller, J.W. Efficient algorithm for gaussian blur using finite-state machines. In Proceedings of the Machine Vision Systems for Inspection and Metrology VII, Boston, MA, USA, 4–5 November 1998; Volume 3521, pp. 334–341. [Google Scholar]
- Russ, J.C. The Image Processing Handbook; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Mareli, M.; Twala, B. An adaptive Cuckoo search algorithm for optimisation. Appl. Comput. Inform. 2018, 14, 107–115. [Google Scholar] [CrossRef]




| Monitoring Points | PL11-1 | PL11-3 | PL13-1 | PL13-3 | PL16-1 | PL16-3 |
|---|---|---|---|---|---|---|
| 830 | 788 | 872 | 820 | 860 | 860 | |
| 86 | 91 | 75 | 76 | 70 | 89 |
| Monitoring Points | The Proposed Method | 3 Method | ||
|---|---|---|---|---|
| (%) | (%) | |||
| PL11-1 | 75 | 87.20 | 31 | 36.04 |
| PL11-3 | 84 | 92.31 | 24 | 26.37 |
| PL13-1 | 72 | 96.00 | 29 | 38.66 |
| PL13-3 | 72 | 94.73 | 28 | 36.84 |
| PL16-1 | 70 | 100.00 | 36 | 51.42 |
| PL16-3 | 88 | 98.87 | 31 | 34.83 |
| Monitoring Points | RMSE | |||
|---|---|---|---|---|
| The Proposed Method | 3- Method | The Proposed Method | 3- Method | |
| PL11-1 | 0.982 | 0.954 | 0.943 | 2.371 |
| PL11-3 | 0.983 | 0.959 | 0.538 | 2.228 |
| PL13-1 | 0.998 | 0.941 | 0.228 | 2.274 |
| PL13-3 | 0.993 | 0.974 | 0.393 | 2.213 |
| PL16-1 | 0.933 | 0.962 | 1.236 | 2.734 |
| PL16-3 | 0.992 | 0.947 | 0.304 | 2.561 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Z.; Wang, Y.; Zheng, S.; Wang, X.; Liu, D.; Zhang, J.; Shao, Y. Abnormal Monitoring Data Detection Based on Matrix Manipulation and the Cuckoo Search Algorithm. Mathematics 2024, 12, 1345. https://doi.org/10.3390/math12091345
Meng Z, Wang Y, Zheng S, Wang X, Liu D, Zhang J, Shao Y. Abnormal Monitoring Data Detection Based on Matrix Manipulation and the Cuckoo Search Algorithm. Mathematics. 2024; 12(9):1345. https://doi.org/10.3390/math12091345
Chicago/Turabian StyleMeng, Zhenzhu, Yiren Wang, Sen Zheng, Xiao Wang, Dan Liu, Jinxin Zhang, and Yiting Shao. 2024. "Abnormal Monitoring Data Detection Based on Matrix Manipulation and the Cuckoo Search Algorithm" Mathematics 12, no. 9: 1345. https://doi.org/10.3390/math12091345
APA StyleMeng, Z., Wang, Y., Zheng, S., Wang, X., Liu, D., Zhang, J., & Shao, Y. (2024). Abnormal Monitoring Data Detection Based on Matrix Manipulation and the Cuckoo Search Algorithm. Mathematics, 12(9), 1345. https://doi.org/10.3390/math12091345






