Abstract
The stability of abandoned open-pit mine slopes and their ecological environment are threatened owing to their fragile, complicated, and uncertain characteristics. This study establishes a novel evaluation indicator system for enhancing mine design and environmental protection insight. The weights in the system are assigned using a combined method, which consists of the game theory, the interval analytic hierarchy process (IAHP), and the entropy weight method (EWM). The IAHP is optimized by the improved radial movement optimal (IRMO) algorithm and the simulated annealing (SA) algorithm to ensure calculation stability and efficiency. Meanwhile, a two-dimensional cloud model (TDCM) is developed to obtain the slope resilience level and visualize the result. This comprehensive evaluation method is applied to three abandoned mine slopes in the Yellow River Basin, and the results demonstrate that the method can provide crucial insights for rational mine slope stabilization and ecological restoration.
Keywords:
resilience evaluation; combined weight method; IRMO-SA method; TDCM; IAHP; EWM; abandoned open-pit mine slopes MSC:
90-08; 62-08; 03B70; 91A86; 65Z05; 00A06; 65Z04
1. Introduction
Mining is one of the foundational industries for a country’s economic and social development, with open-pit mining being one of its primary methods. Improper mining practices have damaged mines and their ecological surroundings, forming high and steep slopes. This has increased the risk of landslides and incidents, posing significant hazards. The failure of mine slopes can cause substantial economic losses and even endanger the safety of surrounding residents [1,2,3,4]. Meanwhile, as people’s awareness of environmental protection gradually strengthens, mine ecological environment management has become essential to environmental protection construction. The ecological restoration of a mining area is an integral part of the ecological civilization construction process. Therefore, conducting a comprehensive evaluation of mine slopes is a complex interdisciplinary endeavor [5] requiring assessment from various perspectives, such as safety and ecological restoration suitability [6]. This is of paramount significance in mine design and production processes.
In the mining industry, which focuses on safety production, reliable safety evaluation is a prerequisite to ensure the orderly and safe production of mines [7]. The safety evaluation is usually viewed as a multi-criteria decision-making problem containing both qualitative and quantitative characteristics [8]. A single risk evaluation method cannot satisfy the evaluation requirements of complex project targets, so a composite evaluation method combining multiple methods is often used. Researchers usually combine the AHP with other methods for safety evaluation. The authors of [8] utilized extended interval trapezoidal fuzzy soft set and the fuzzy hierarchy analysis method (FAHP) to calculate the risk factor weights of high and steep slopes in open-pit mines. The authors of [9] used the AHP, the topology object element method, and EWM to comprehensively evaluate the safety of high, steep rocky slopes, forming a multi-indicator dynamic safety evaluation method. The authors of [10] assigned causative factors to sub-factors and weightage according to the AHP. A landslide hazard map along the national highway was prepared to evaluate slope safety using the AHP model. However, the AHP involves subjective uncertainty to some extent. To mitigate the impact of subjective judgment and uncertainty, the IAHP constructs interval number judgment matrices [11], which better reflect the subjective preferences of experts and the uncertainty of the evaluation criteria. Meanwhile, the EWM [12] is an objective weighting method that determines the weights of each criterion based on the information content of the evaluation indicators, possessing advantages such as objectivity and adaptability. This paper will employ a combination of the IAHP and EWM for weighting. However, the IAHP’s interval number judgment matrices may lack precision or be computationally complex [13]. Therefore, to enhance the accuracy of subjective weighting and simplify computation, the IRMO algorithm will be used to establish an optimization model for objective search, obtaining optimal subjective weights for each evaluation indicator, thereby complementing both subjective and objective biases.
The current study uses a retrieval strategy to perform a keyword co-occurrence analysis through VOSviewer. The search query “mining/mine slope evaluation/assessment” is employed to query the Web of Science database. As illustrated in Figure 1, the current evaluations of slopes predominantly focus on safety or stability, with less emphasis on the ecological restoration suitability of mining slopes. However, following a series of mining activities, the surrounding ecological environment becomes fragile, and rock structures are fractured. This mining process parallels the seismic hazards experienced by urban buildings, resulting in devastating impacts. An evaluation of the suitability of ecological restoration will help to select appropriate restoration measures to ensure that the surrounding ecological environment can be effectively restored and protected [14]. Therefore, the ecological restoration suitability of slopes should also be included in the evaluation object, as well as safety, to ensure the stability and health of their surrounding ecological environment. This paper combines safety and ecological evaluations of abandoned open-pit mine slopes to comprehensively evaluate slope resilience from two dimensions based on the resilience theory. Resilience was initially used to describe the mechanical properties of metals. It was later applied to systems ecology [15,16,17] to describe the ability of ecosystems to maintain normal functioning or restore balance after being damaged. The resilience evaluation encompasses both risk and recovery assessments. In 2020, China adopted the construction of “resilient cities” as a national sustainable development strategy. The continuous development of the resilience theory has made exploring cities’ or systems’ ability to cope with destruction a hot topic in disaster prevention and mitigation [18], spanning various applications such as deep foundation pit construction [19], buildings [20], critical infrastructure systems [21], urban systems [22,23], bridges [24], etc. Based on this, an evaluation of the slope resilience of abandoned open-pit mines can be based on two dimensions: slope safety and slope ecological restoration suitability. This has significant theoretical and practical significance for safety management and ecological environment restoration.
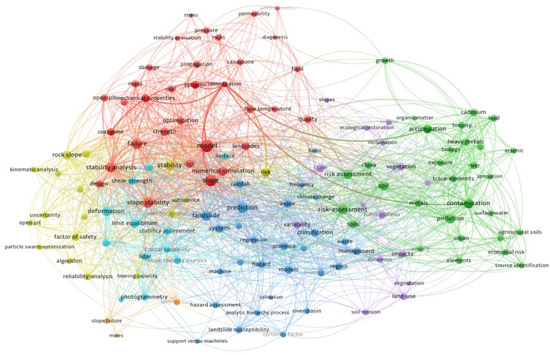
Figure 1.
Keyword co-occurrence network diagram.
In addition, due to the evaluation process not fully considering the impacts of evaluative fuzziness and uncertainty, the assessment results are limited. As a cognitive model based on the normal distribution function and membership function, a cloud model [25] can describe the uncertainty of quantitative information and can be used to describe qualitative concepts, achieving bidirectional transformation between the two [26,27,28]. In recent years, a cloud model has been gradually introduced into the evaluation of engineering projects [29], such as subways [30,31,32], slopes [11,33], railways [34], and urban engineering construction projects [35]. A TDCM is synthesized from two one-dimensional clouds, comprehensively describing the randomness and fuzziness issues under the combined influence of two factors. This paper employs the combination weighting method to derive the weights. It constructs a TDCM based on the cloud theory from both safety and ecological perspectives, comprehensively evaluating the resilience of abandoned open-pit mine slopes.
This paper addresses the inherent uncertainties in current slope evaluations by constructing a comprehensive resilience evaluation model for abandoned open-pit mine slopes. This study leverages the combination weighting method with a TDCM to enhance the accuracy of assessments, mitigating issues such as subjectivity, uncertainties, fuzziness, and randomness that may arise during the evaluation process. In terms of evaluation methods, this study proposes the subjective weight optimization method based on the IAHP-IRMO-SA. This hybrid algorithm is applied to calculate the subjective weights in the interval judgment matrix. The corresponding algorithmic calculation program is developed, leveraging the self-feedback ability of particles in the IRMO algorithm and the SA algorithm to escape from local optimal solutions based on the Metropolis criterion to accurately determine the optimal solution for subjective weights.
This paper is organized as follows: Section 2 introduces the data and methods, including the process of constructing the toughness evaluation indicator system and selecting the grading criteria. The Section 3 shows the establishment of the toughness assessment model for abandoned open-pit mine slopes based on the IAHP-IRMO-SA. The Section 4 presents a case study to verify the validity and practicality of the provided safety assessment model. The results are discussed with the main conclusions and insights in the Section 5 and Section 6.
2. Construction of Resilience Evaluation Indicator System for Abandoned Open-Pit Mine Slopes
2.1. Basis for Indicator Selection
This paper constructs a comprehensive evaluation model from two dimensions of slope safety and ecological restoration suitability. To share a standard system of slope safety and ecological evaluation indicators to ensure objectivity, this paper evaluates the slope ecological restoration suitability side by side through the existing slope safety evaluation method. Hence, the slope safety and ecological evaluation indicators share a standard system. This study uses existing research [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52] as a reference to select a comprehensive evaluation indicator for abandoned open-pit mine slopes, based on which the assessment indicator system in Table 1 is established.

Table 1.
Comprehensive evaluation indicator system of resilience in abandoned open-pit mine slopes.
The resilience of abandoned open-pit mine slopes is described using four aspects: geological features, slope geometric features, slope rock features, and external factors. In the proposed evaluation indicator system, geological features (primary indicator A) include the degree of weathering of the slope rock body, the damaged area of the abandoned mine, and the degree of development of the slope joints and cracks, which can reflect the influence of the geological features of the abandoned open-pit mine slopes on the safety and ecological restoration of the abandoned open-pit mine slopes. The geometric characteristics of the slope (primary indicator B) are divided into slope length and slope height, which characterize the geometric characteristics of the abandoned mine slope. Slope rock mass features (primary indicator C) includes the hardness of the slope rock, the basic quality grade of the rock, the self-stabilizing ability of the vertical slope, the classification of the integrity of the slope rock, and the cohesive force of the rock and soil body, which can reflect the rock stability of the abandoned open-pit mine slopes. The external factors (primary indicator D) include the average annual precipitation, the seismic intensity, the risk of geologic hazards, and the degree of vulnerability of ecological environments, which can reflect the impacts of the external factors of abandoned open-pit mine slopes on the safety of mine slopes and the suitability of ecological restoration. The influence of external factors on the safety and ecological restoration suitability of abandoned open-pit mine slopes can be more comprehensively reflected.
2.2. Indicator Grading Criteria
The system consists of 15 evaluation indicators. Due to the different classification standards of each indicator, it is necessary to hierarchically quantify evaluation indicators and determine a unified, comprehensive evaluation criterion for the resilience of open-pit mine slopes. Using the literature [53,54], the established evaluation indicator system was quantitatively analyzed to obtain the range of values of the secondary indicators in the index layer, as shown in Table 2. There are two types of indicators: “qualitative (QL)” and “quantitative (QN)”.

Table 2.
Grading criteria for abandoned open-pit mine slopes’ comprehensive evaluation indicators.
In this paper, the grading criteria for the evaluation indicator system are unified concerning the principles of risk grading and control [41,55]. The comprehensive evaluation grade for the resilience of abandoned open-pit mine slopes is divided into four levels, Level I, Level II, Level III, and Level IV, as shown in Table 3.

Table 3.
Evaluation level criteria.
3. Comprehensive Evaluation Model of Resilience Based on Combination Weighting and TDCM
The established model solved the indicators’ optimal subjective weights using the IAHP-IRMO-SA method. The EWM was used to calculate the objective weights; the comprehensive weights were obtained based on the game theory. The TDCM was used to generate the cloud droplets and make the two-dimensional standard cloud diagram. After calculating the cloud eigenvalues of each evaluation indicator, the combined weight of these eigenvalues was calculated. Subsequently, the level of safety and ecological restoration suitability of the slopes by the degree of affiliation and proximity and the comprehensive grade were determined. The specific process can be seen in Figure 2.
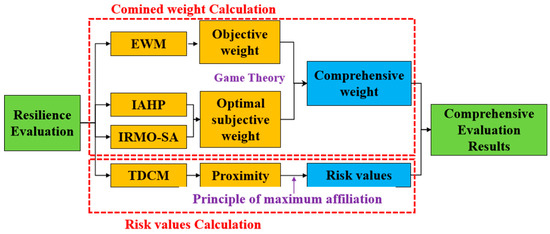
Figure 2.
Flow chart of comprehensive evaluation of abandoned open-pit mine slopes.
3.1. Combination Weighting Method
3.1.1. IAHP-IRMO-SA Method for Solving Optimal Subjective Weights
- IAHP method
The IAHP constructs the interval number judgment matrix to reduce the impacts of subjective judgment and uncertainty. This paper establishes a hierarchical model based on the IAHP, constructs the interval number judgment matrix, and introduces the concept of the degree of divergence to establish the objective optimization model. The model’s objective function is the IRMO algorithm’s fitness function. The IRMO algorithm is used to optimize the search and obtain the optimal subjective weights of the evaluation indicators, and the specific steps are described below.
- (1)
- Construct a judgment matrix of intervals.
The 1–9 scale method compares the importance degree of each evaluation indicator at the same level and assigns values. The interval number judgment matrix , is the relative importance of the two comparisons of indicator i and indicator j. The interval number is used to indicate that should satisfy Equation (1):
- (2)
- Build an objective optimization model.
Set the number of intervals as and :
—The degree of divergence between the sum of interval numbers. When , is the degree of divergence from point b to interval a. The objective optimization model is established by combining the concept of the degree of divergence between interval numbers:
where Equation (3) is the objective function in the objective optimization model; is the optimal subjective weight of each assessment indicator; denotes the judgment range when indicator i and indicator j are compared; and . and are the optimal subjective weights of indicator i and indicator j, respectively, and is the degree of divergence of intervals and . When the optimal subjective weight is taken for both indicator i and indicator j, denotes the degree of divergence of the point to interval .
- b.
- IRMO algorithm
The IRMO is a global optimization algorithm used to quickly solve the optimal value of multi-dimensional objective functions and aims at the problems of unstable search results and the insufficient search accuracy of the Radial Movement Algorithm (RMO). The data structure of the IRMO is further optimized and adjusted to enhance the self-feedback ability between particles. The search stability and accuracy are improved. Figure 3 shows the basic principle diagram of the IRMO [56].
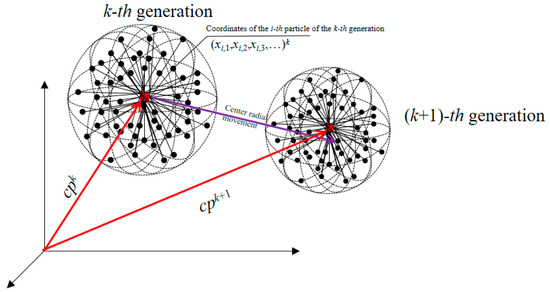
Figure 3.
Basic principle diagram of IRMO.
In this paper, when applying the IRMO algorithm to optimize the search, the objective function denoted as Equation (3) in the optimization model is used as the fitness function of the IRMO algorithm. The fitness function computes the fitness function value corresponding to each generation of particles, and the calculated fitness function values are compared to select the contemporary optimal solution. The solution space is reduced to one point when the algorithm calculates the last generation. The fitness function value corresponding to this point is the global optimal solution, and the parameter corresponding to it is the optimal subjective weight of the evaluation indicator . To accurately search and calculate the optimal subjective weight of the evaluation indicator , it is necessary to constrain the range of values of each variable. According to the constructed objective optimization model, each variable must satisfy the constraints of Equation (4) in the objective optimization model.
- c.
- IRMO-SA
The IRMO is an excellent heuristic algorithm with good global search ability, more stable search results, and rapid convergence, and it is not easily premature. It can quickly search out the global optimal solution, but it may fall into the local optimal situation during the search process [56]. SA is based on the Metropolis criterion and can jump out of the local optimal solution while searching for a global optimal solution of the objective function [57,58]. In this paper, by combining the two algorithms to improve the overall performance, a hybrid IRMO-SA algorithm is designed to solve the optimal weight solution based on the IAHP. The specific steps are described below.
- (1)
- Construct the objective function of the IRMO-SA algorithm.
In this paper, Equation (3) is used as the objective function of the IRMO-SA algorithm as follows:
- (2)
- Obtain the optimal weight solution of the interval number judgment matrix based on IAHP-IRMO-SA.
In the IRMO-SA algorithm, N particles are generated in each generation, and the position of each particle in the space represents a solution vector . These solution vectors are composed of the variables with the dimension of the interval number judgment matrix constructed using the IAHP method with the dimension of M. The information of all of the particles’ positions is shown in Equation (7). When the IRMO-SA algorithm is applied to optimize the search, the objective function Equation (6) is used as the fitness function of the IRMO-SA algorithm. The fitness value of the objective function corresponding to the k-th generation of particles is calculated using the fitness function. The computed fitness values of the objective function are compared. The contemporary optimal solution is selected by using the Metropolis criterion. The solution space is reduced to one point when the algorithm calculates the last generation. The objective function fitness value corresponding to this point is the global optimal solution, and its corresponding parameter is the optimal value of the interval number judgment matrix weights . The variable superscripts in the matrix [X] denote the variables of the i-th indicator, and the subscripts denote the positions of the variables in the matrix.
In this paper, we set the initial parameters, the initial temperature T0, the annealing rate α, the termination temperature Tf, and the maximum number of iterations G so that the number of iterations (, Tk = T, f(Rbest)) is the contemporary optimal fitness value in the algorithm and f(Gbest) is the global optimal fitness value. The flowchart of the IRMO-SA algorithm is shown in Figure 4.
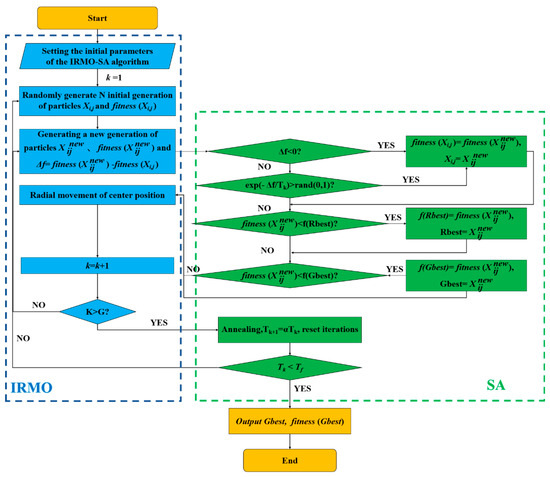
Figure 4.
The flowchart of the IRMO-SA algorithm.
3.1.2. The Entropy Weighting Method Used to Solve the Objective Weights
Due to the subjectivity of IAHP, it is necessary to introduce an objective weighting method to assign weights to each indicator objectively. Entropy is a measure of uncertainty [59]. The information entropy value can determine the degree of dispersion of an indicator. The steps are described below.
- (1)
- Standardize the data.
To eliminate the influence of the data outline and unit of each assessment indicator, it is necessary to standardize the original data in the original sample matrix . According to the meaning of the indicator, it can be divided into a positive indicator (the larger, the better) and a negative indicator (the smaller, the better).
represents the j-th indicator of the i-th evaluation object; is the value of the j-th indicator of the i-th evaluation object after standardization; is the minimum value of all evaluation objects in the column of the j-th indicator; and is the maximum value of the sample data of the j-th indicator evaluation object.
- (2)
- Normalize the data to obtain the normalization matrix .
- (3)
- Calculate the information entropy value for the j-th indicator.
- (4)
- Calculate the objective weight for the j-th indicator.
3.1.3. Combination Weighting Method Based on Game Theory
This paper uses the AHP and EWM to conduct subjective and objective weighting assignments. The previously obtained subjective and objective weight values are combined through game theory to obtain the final weights of each indicator, which can largely minimize the bias between subjective and objective. The combination steps are as follows:
- (1)
- Construct the set of basis weight vectors .
- (2)
- Construct a linear combination of weight vectors .
is the linear combination weight coefficient.
- (3)
- Optimally solve the linear combination of weight coefficients .
Based on the game theory, the linear combination of weight coefficients is optimized to minimize the divergence between the linear combination of weight vectors w and the underlying set of weight vectors :
According to the matrix differentiation property, a system of linear equations with optimized first-order derivative conditions can be obtained:
By solving Equation (16), the optimized linear combination weight coefficients βk = [β1, β2, …, βM] are obtained.
- (4)
- Normalize to obtain the optimal linear combination weight coefficients .
- (5)
- Calculate the combined weight .
The optimal subjective weights obtained using the IAHP-IRMO method are combined and assigned with the objective weights determined using the EWM to obtain the comprehensive weights w of the assessment indicators:
3.2. TDCM
3.2.1. Basic Concepts
The cloud model not only realizes the two-way conversion of qualitative concepts and quantitative data [60] but also considers uncertainty problems, such as the ambiguity and randomness of the assessment system [61]. The two-dimensional cloud model is obtained by synthesizing two one-dimensional clouds, comprehensively describing the stochasticity and ambiguity problems under the joint action of two factors. F is a two-dimensional random function obeying normal distribution, and the cloud model composed of cloud drops is a two-dimensional normal cloud model, which is calculated as follows:
are the cloud droplet coordinates, are the expectant values, are the standard deviation values, are the conditional cloud droplet coordinates, are the hyper entropy values, and is the degree of certainty. The smaller the expectant, the lower the evaluation level of the indicator; the smaller the standard deviation, the higher the acceptance of the result, and the higher the reliability of the assessment result; and the smaller the value of the hyper entropy, the smaller the dispersion of the cloud droplet, and the higher the accuracy of the evaluation result.
3.2.2. Two-Dimensional Cloud Modeling
- (1)
- Standard cloud
The evaluation indicator toughness level is equalized into four subintervals according to the interval [0, 10], where the j-th subinterval is denoted as . The numerical features of the standard cloud are calculated to obtain the value intervals and numerical features of Levels I~IV:
is the expectation of the standard cloud, is the standard deviation of the standard cloud, is the upper limit value of the j-th interval, is the lower limit value of the j-th interval, and is the hyper entropy of the standard cloud. The numerical characteristics of the evaluated standard cloud are shown in Table 4. The standard cloud diagram is shown in Figure 5.

Table 4.
Risk evaluation criteria cloud digital characterization.
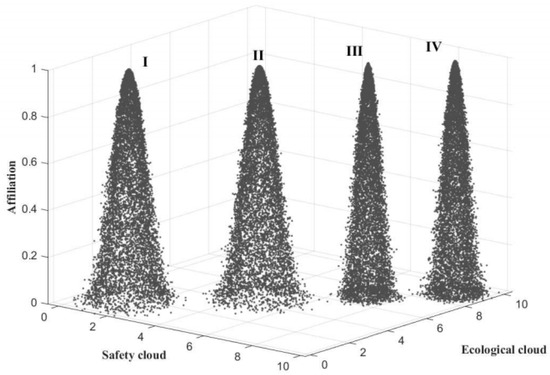
Figure 5.
Standard cloud diagram(I: High resilience, II: Relatively high resilience, III: Relatively low resilience, IV: Low resilience).
- (2)
- Comprehensive evaluation cloud
This paper conducts a comprehensive evaluation of mine slopes regarding the two dimensions of safety and ecological restoration suitability. The two-dimensional eigenvalues of the evaluation indicators are selected as the two sets of basic variables of the two-dimensional cloud model. The safety dimension and the ecological restoration suitability dimension of each evaluation indicator form a cloud droplet, which constitutes the safety evaluation cloud and the indicator’s ecological restoration suitability evaluation cloud, known as the second-level cloud. Subsequently, the synthetic operation is performed, and the formula is shown below, where are higher-level digital features:
- (3)
- Proximity
Since the two-dimensional cloud map is displayed as a three-dimensional view, the spatial graphics will cause visual errors, so a more precise method is needed to determine the comprehensive evaluation grade of each mine. The proximity degree is introduced to make judgments as a means of obtaining accurate evaluation ratings, calculated using the following formula:
where N is the proximity of the composite level; is the expectant of the safety standard cloud and is the expectant of the actual safety cloud; and is the expectant of the ecological standard cloud and is the expectant of the actual ecological cloud.
3.3. Comparative Analysis
3.3.1. Accuracy Analysis of IRMO-SA
To prove that the optimal subjective weights obtained using the IRMO-SA algorithm optimizing the search interval weight solution are more reliable and reasonable, this paper applies the IAHP-IRMO-SA method with the interval number eigenvalue method (IEM) to solve the third-, fourth-, and fifth-order judgment matrices of the literature [62,63,64]. The authors of [62] used a hierarchical analysis and interval fuzzy hierarchical analysis to calculate the judgment matrix in the decision-making process for a flood risk assessment of a subway system; the authors of [63] calculated the interval number judgment matrix based on nonlinear fuzzy mathematics and a hierarchical analysis to evaluate the risk of sudden water on the coal mine floor; and the authors of [64] optimized the acquired research data for quantitative analyzation based on a hierarchical analysis, interval hierarchical analysis, and the interval number theory. As can be seen in Table 5, Table 6 and Table 7, the results in this paper are consistent with those in the literature.

Table 5.
Results for third-order subjective weights.

Table 6.
Results for fourth-order subjective weights.

Table 7.
Results for fifth-order subjective weights.
3.3.2. Stability and Efficiency Verification of IRMO-SA Method
To verify the stability and efficiency of the proposed method, this paper selects the interval number judgment matrix in the literature [65] and adopts the three global optimization algorithms of RMO, IRMO, and IRMO-SA to consecutively search the interval number break matrix of the algorithm 20 times, and then it compares the results, as shown in Table 8 and Figure 6.

Table 8.
Objective function fitness values for three algorithms.
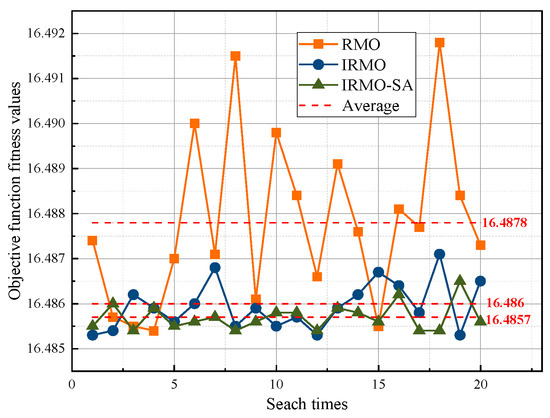
Figure 6.
Results of 20 searches of objective function fitness value by different algorithms.
As seen in Table 8, the maximum of the objective function fitness obtained using the IRMO-SA algorithm is 16.4865, the minimum is 16.4854, and the average is 16.4857. The standard deviation is only 0.00028, which is optimal among the three global optimization algorithms. Meanwhile, the volatility of Figure 6 indicates that the change in the results of the 20 consecutive searches of the IRMO-SA algorithm is the smallest, which means it is more stable, followed by the IRMO algorithm, and the RMO algorithm has the worst stability. Meanwhile, as seen in the volatility of Figure 6, the IRMO-SA algorithm has the smallest amplitude, which is more stable, followed by the IRMO algorithm, and the RMO algorithm is the worst. It shows that the IRMO-SA algorithm has good stability and is more advantageous when used to solve the weights of interval number judgment matrices under the IAHP.
As seen in Figure 7, the IRMO-SA algorithm initially stabilized at about 75 generations of iterations at the same number of iterations for three consecutive searches. In contrast, the RMO algorithm started to be initially stabilized at 98 generations of searches. This shows that the IRMO-SA algorithm has the fastest convergence speed, the IRMO algorithm is the second fastest, and the RMO algorithm is the slowest. The above comparison shows that the IRMO-SA algorithm has more outstanding efficiency in solving the weights of the interval number judgment matrix under the IAHP, and its convergence efficiency is more ideal.
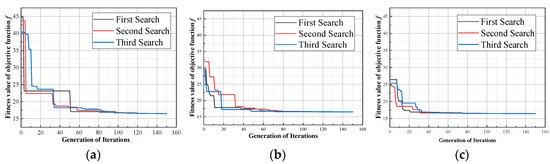
Figure 7.
Convergence efficiency analysis for three consecutive searches: (a) RMO; (b) IRMO; and (c) IRMO-SA.
4. Case Study
4.1. Overview
This paper selects high and steep slopes in three areas of the Yellow River Basin Ecological Restoration Demonstration Project area, namely the Yanhua Quarry, Torch Quarry, and Zhubei Quarry #1, for a comprehensive resilience evaluation. The primary mining method in this area is “gourd-type” blasting at the bottom, forming high and steep traumatic surfaces with large topographic ups and downs. High and steep slopes remain from the previous mining project, with an overall slope inclination of approximately 140°; the land is excavated and occupied, and the vegetation is seriously destroyed. The current situation of the slopes of abandoned mines in the Yellow River Basin is shown in Figure 8 and Figure 9. The characteristic period of the seismic reflection spectrum is 0.40 s. The peak acceleration value of ground vibration is 0.15 g, corresponding to the seismic intensity of VII levels. The magnitude is seven levels, and the comprehensive horizontal seismic coefficient is 0.035.

Figure 8.
Aerial photograph of abandoned open-pit mine slopes in Yellow River Basin: (a) Yanhua Quarry; (b) Torch Quarry; (c) Zhubei Quarry #1. (The quarry area is shown within the red curve on the figures.)

Figure 9.
Status of abandoned open-pit mine slopes in Yellow River Basin: (a) Yanhua Quarry; (b) Torch Quarry; (c) Zhubei Quarry #1.
- (1)
- Basic situation
Table 9 lists the three quarries’ basic high and steep slope conditions. Table 10 is a grading table of each quarry’s ecological and environmental problems. The “Degree of Joint and Fissure Development” column describes joint and fissure development for the upper and lower sections of each quarry’s rock body. The “Slope Rock Body Type” column lists the types of rock bodies found on the slope. All three quarries belong to the low mountainous and hilly area, and the compressive strength of slightly weathered and strongly weathered rocks is within the range of 50–60 MPa.

Table 9.
Basic conditions of quarries.

Table 10.
Grading table of ecological and environmental problems in quarries.
- (2)
- Meteorological and Hydrological Conditions
Hancheng City has a warm, temperate, continental, semi-arid climate, with less annual precipitation than evaporation. The winter is dry and cold with little snow, the spring is dry with little rain and wind, the summer is hot and dry with many rainstorms, and the fall cools down rapidly with cloudy and rainy days. In 2021, Hancheng City had an overall high rainfall, with more than 1100 mm of precipitation.
4.2. Determination of Indicator Weights
4.2.1. Determination of Optimal Subjective Weights using SA-RMO-IAHP
This example scoring uses the 1–9 scale method to assess safety and ecological restoration suitability. The scoring results are shown in Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6, Table A7, Table A8, Table A9, Table A10, respectively. After constructing the judgment matrix and applying the IAHP-IRMO-SA algorithm to determine the optimal subjective weights, the optimal values of the subjective weights of safety w and ecology w’ for each indicator are obtained, as shown in Figure 10.
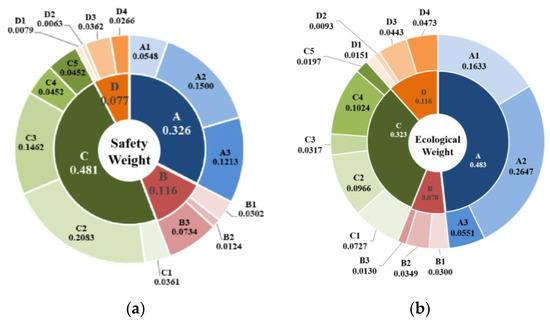
Figure 10.
Optimal values of subjective weights of comprehensive evaluation indicators. (a) Safety subjective weights; (b) ecological subjective weights.
4.2.2. Determination of Objective Weights Using EWM
The initial matrix is constructed, the entropy value of the safety evaluation indicator information is determined, and the EWM is applied to obtain the objective weights of the evaluation indicators. The quantitative values of the evaluation indicators of abandoned open-pit mine slopes and the corresponding objective weights are shown in Table 11.

Table 11.
Quantitative data and corresponding objective weights of indicators.
4.2.3. Determination of Comprehensive Weights
This model adopts the IAHP-IRMO-SA and EWM to determine the subjective and objective weights of the evaluation indicators, which can be obtained as the combined weight coefficients of the subjective and objective weights of the evaluation indicators of the guideline layer of the slope resilience of abandoned mines, which are, respectively, β1 = 0.2389 and β2 = 0.7456, and the normalization process is used to obtain the β1* and β2* values of 0.2427 and 0.7573, respectively. The combined weight coefficients of the subjective and objective weights of the evaluation indicators for the suitability of ecological restoration for abandoned mines can be obtained as β′1 = 0.01 and β′2 = 0.9903. After normalization, the values for β1*′ and β2*′ are 0.01 and 0.99, respectively. The results are shown in Figure 11.
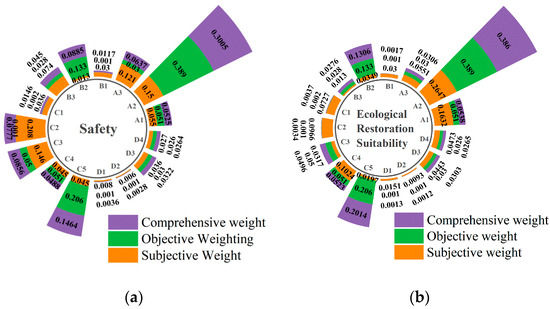
Figure 11.
Weights of indicators in index layer: (a) safety weights; (b) ecological restoration suitability weights.
The comparison of the security weights of the evaluation indicators at the indicator level is shown in Figure 12.
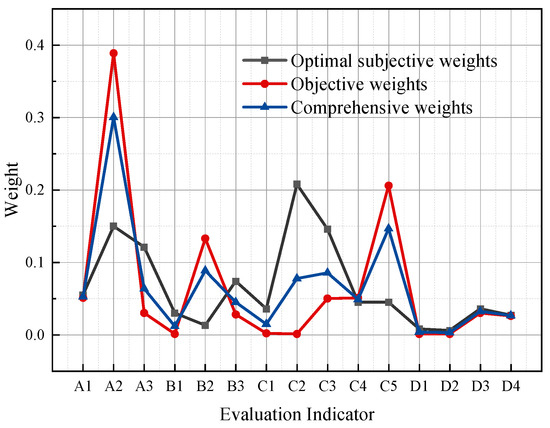
Figure 12.
Comparison of weights of indicators to assess security of indicators.
As shown in Figure 12, the optimal subjective weights, comprehensive weights, and objective weights have the same trend of change with the different evaluation indicators, but the magnitude of change of the objective weights is larger compared to that of the subjective weights. This is because the objective weighting method only evaluates the indicators from the mathematical aspect, which is too absolute. In contrast, the subjective weighting method often relies on the experience of experts. The evaluation process between the indicators can affect the indicators when the weight calculation is performed, which can show the influence degree of each indicator more objectively. Compared with the single subjective or objective assignment method, the comprehensive weight of the game theory combination assignment method is between the optimal subjective weight and objective weight, and the combination assignment process considers the influence of subjective human factors and combines the actual objective data, which makes the evaluation results more reasonable and reliable.
4.3. Comprehensive Evaluation and Verification
This paper comprehensively evaluates the resilience of abandoned open-pit mine slopes in terms of both safety and ecology. The stability of a slope mainly determines its safety. Ecological restoration suitability refers to the difficulty of ecologically restoring a slope. The expert scoring method was used to score the underlying indicators within each level’s thresholds and calculate the evaluation cloud numerical characteristics for each underlying event concerning the natural language descriptions of each level in Table 4. This evaluation model was applied to evaluate high and steep slopes in three areas to calculate the second-level sub-safety cloud and ecological cloud, the first-level sub-safety cloud and ecological cloud digital features, and the integrated safety cloud and ecological cloud digital features. Table 12 presents the Digital characteristic parameters of cloud model for comprehensive evaluation of abandoned open-pit mine slopes.

Table 12.
Digital characteristic parameters of cloud model for comprehensive evaluation of abandoned open-pit mine slopes.
This study employed the traditional TOPSIS method [66] to validate and calculate the engineering case. Table 13 presents the results of the safety assessment and ecological suitability assessment obtained through the TOPSIS method. The ranking outcomes align with the results in this study, indicating the accuracy of the novel comprehensive evaluation method proposed for abandoned open-pit mine slope resilience in this paper.

Table 13.
Evaluation calculation results.
A comprehensive cloud of resilience for these slopes was generated using the MATLAB R2021b software based on the digital features of the two-dimensional evaluation cloud model from Table 12 and the standard cloud digital features from Table 4. Figure 13 illustrates the two-dimensional cloud map for the resilience assessment of the steep slopes in Zhubei Quarry #1. A preliminary analysis suggests that Zhubei Quarry #1’s resilience level falls between Levels II and III.
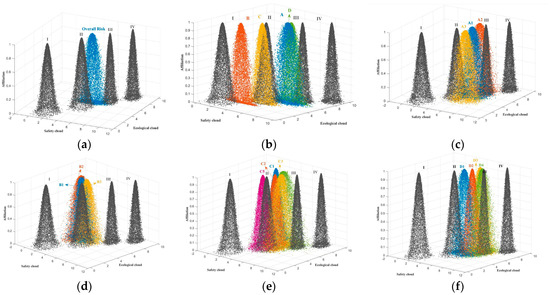
Figure 13.
Graph showing evaluation results of TDCM: (a) overall evaluation; (b) criterion layer evaluation; (c) index layer A evaluation; (d) index layer B evaluation; (e) index layer C evaluation; (f) index layer D evaluation.
When displayed as a three-dimensional view, using the two-dimensional cloud map to conduct a resilience assessment of abandoned open-pit mine slopes may lead to visual errors and result in overly coarse evaluation outcomes. Therefore, it is necessary to calculate proximity to more accurately characterize the resilience levels of individual indicators. Proximity is computed based on the digital features of the two-dimensional cloud model. The resilience assessment levels for steep slopes in abandoned mines can be determined accordingly, as shown in Table 14.

Table 14.
Calculation of proximity of slopes.
By applying the maximum membership principle, the overall resilience assessment levels for steep slopes in the Yanhua Quarry, Torch Quarry, and Zhubei Quarry #1 are determined as follows: the Yanhua Quarry is classified as Level II, indicating that it has “relatively high resilience”; the Torch Quarry is also rated as Level II, denoting “relatively high resilience”; and Zhubei Quarry #1 is categorized as Level III, representing “moderate resilience”. The resilience ranking is as follows: Zhubei Quarry #1 > Yanhua Quarry > Torch Quarry.
5. Discussion
This paper proposes a new method based on the TDCM with combination weighting to comprehensively evaluate slope resilience in abandoned open-pit mines. Four primary indicators (i.e., geological structural features, slope geometric characteristics, slope rock mass features, and external factors) are selected to establish the evaluation system. Fifteen secondary indicators (i.e., rock weathering degree, mine damage area, and degree of development of slope joints and fractures) are considered. The method is applied to three areas of the Yellow River Basin Ecological Restoration Demonstration Project area and compared with other methods. The results indicate that it exhibits superior stability, efficiency, and accuracy. A comparison with the actual engineering data further validates the effectiveness of the method. This section aims to further discuss the data in this paper.
- (1)
- As indicated in Table 12, the safety ranking is as follows: Zhubei Quarry #1 > Yanhua Quarry > Torch Quarry. The ecological restoration suitability ranking is as follows: Zhubei Quarry #1 > Yanhua Quarry > Torch Quarry. By comparing the actual conditions of the mines and the data in Table 10, the safety evaluation results are generally consistent with the actual situation. The total investment in ecological restoration in Table 9 is ranked as follows: Zhubei Quarry #1 > Yanhua Quarry > Torch Quarry. This sequence indirectly reflects the ecological restoration suitability of the respective quarry slopes, aligning with the ecological assessment results obtained using the evaluation methodology employed in this study.
- (2)
- During the management process in mining areas, researchers often integrate concepts such as the comprehensive utilization of waste rock resources, the elimination of geological safety hazards, slope stability, and ecological restoration. This is achieved through practices such as slope reduction, the lowering of step slope ratios, height control, platform installation, and the creation of tiered slopes to ensure overall slope stability. The reduction in slope load and slope ratio through slope cutting can eliminate geological safety hazards and maintain slope stability. The determination of the amount of rock cutting considers the ecological restoration suitability and slope safety of the mining area, reflecting the resilience level of abandoned open-pit mine steep slopes. Based on the data in Table 9, the quantity of cutting stone ranking is as follows: Zhubei Quarry #1 > Yanhua Quarry > Torch Quarry. The evaluation results align closely with the on-site situation, validating the applicability and feasibility of the method proposed in this paper.
- (3)
- Zhubei Quarry #1 is categorized as Level III and requires intensified ecological restoration and safety management efforts. Zhubei Quarry #1 has a large area of exposed rock walls, with a significant presence of residual hills, posing challenges for ecological restoration, as illustrated in Figure 14. It is situated in a high-risk geological disaster area with severe vegetation damage. Mining activities have profoundly impacted its topography and landscape, resulting in significant soil erosion. It needs to undergo slope-cutting construction, and vegetation needs to be planted for slope surface recovery.
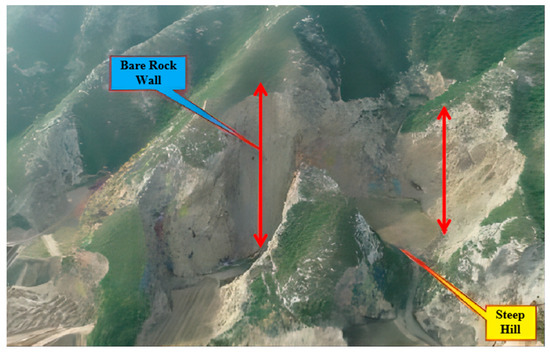 Figure 14. Distribution of exposed rock walls and residual hills in Zhubei Quarry #1.
Figure 14. Distribution of exposed rock walls and residual hills in Zhubei Quarry #1.
6. Conclusions
This paper proposed a new method for comprehensively evaluating slope resilience in abandoned open-pit mines. A comprehensive evaluation indicator system was established by considering the two dimensions of safety and ecological restoration suitability. Then, the IRMO-SA algorithm was employed to optimize the IAHP to enhance the calculation stability and efficiency when solving subjective weights. The TDCM was used to obtain the resilience levels. The details are as follows:
- (1)
- By integrating the resilience theory, this paper analyzed the safety and ecological restoration suitability of abandoned open-pit mine slopes. A comprehensive evaluation model was proposed to evaluate the safety and suitability for ecological restoration of abandoned open-pit mine slopes.
- (2)
- By integrating the IAHP, EWM, and the enhanced IRMO-SA algorithm, a combined weighting method was established. The results indicate that the proposed method can improve the objectivity and rationality of the evaluation and increase the calculation stability compared to traditional evaluation approaches.
- (3)
- The resilience of mine slopes was categorized into risk and ecological dimensions, and the TDCM was introduced. The cloud model was utilized to quantify fuzziness and uncertainty, obtain the resilience level of the mine slopes, and visualize the evaluation results.
- (4)
- The developed resilience assessment model was applied to evaluate steep slopes in three areas: the Yanhua Quarry, Torch Quarry, and Zhubei Quarry #1. The results are consistent with the actual engineering situations, demonstrating the model’s applicability and feasibility.
- (5)
- This paper proposed a novel method for assessing slope resilience in abandoned open-pit mines. This method offers theoretical support for the safety management and ecological restoration of mine slopes. It assists construction personnel in taking targeted actions based on evaluation results to ensure the structural safety of abandoned mine slopes and protect their ecological environment. It also provides valuable guidance for reinforcement and ecological management projects on such slopes.
Author Contributions
Conceptualization, L.J.; methodology, L.J.; software, P.L.; validation, P.L.; formal analysis, P.L.; investigation, P.L.; resources, P.L.; data curation, P.L.; writing—original draft preparation, P.L.; writing—review and editing, P.L. and W.Y.; visualization, P.L. and W.Y.; supervision, J.W.; project administration, P.L. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data related to all of the laboratory tests performed during the study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Judgment matrix of number of safe subjective weight intervals for target layer U.
Table A1.
Judgment matrix of number of safe subjective weight intervals for target layer U.
| U | A | B | C | D |
|---|---|---|---|---|
| A | [1, 1] | [3, 4] | [1/4, 1/3] | [4, 5] |
| B | [1/4, 1/3] | [1, 1] | [1/5, 1/4] | [3, 4] |
| C | [3, 4] | [4, 5] | [1, 1] | [5, 6] |
| D | [1/5, 1/4] | [1/4, 1/3] | [1/6, 1/5] | [1, 1] |

Table A2.
Judgment matrix for number of safe subjective weight intervals for criterion layer A.
Table A2.
Judgment matrix for number of safe subjective weight intervals for criterion layer A.
| A | A1 | A2 | A3 |
|---|---|---|---|
| A1 | [1, 1] | [1/3, 1/2] | [1/3, 1/2] |
| A2 | [2, 3] | [1, 1] | [1, 2] |
| A3 | [2, 3] | [1/3, 1/2] | [1, 1] |

Table A3.
Judgment matrix for number of safe subjective weight intervals for criterion layer B.
Table A3.
Judgment matrix for number of safe subjective weight intervals for criterion layer B.
| B | B1 | B2 | B3 |
|---|---|---|---|
| B1 | [1, 1] | [3, 4] | [1/4, 1/3] |
| B2 | [1/4, 1/3] | [1, 1] | [1/6, 1/5] |
| B3 | [3, 4] | [5, 6] | [1, 1] |

Table A4.
Judgment matrix for number of safe subjective weight intervals for criterion layer C.
Table A4.
Judgment matrix for number of safe subjective weight intervals for criterion layer C.
| C | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| C1 | [1, 1] | [1/6, 1/5] | [1/5, 1/4] | [1, 1] | [1/2, 1] |
| C2 | [5, 6] | [1, 1] | [3, 4] | [4, 5] | [4, 5] |
| C3 | [4, 5] | [1/4, 1/3] | [1, 1] | [3, 4] | [3, 4] |
| C4 | [1, 1] | [1/5, 1/4] | [1/4, 1/3] | [1, 1] | [1, 1] |
| C5 | [1, 2] | [1/5, 1/4] | [1/4, 1/3] | [1, 1] | [1, 1] |

Table A5.
Judgment matrix for number of safe subjective weight intervals for criterion layer D.
Table A5.
Judgment matrix for number of safe subjective weight intervals for criterion layer D.
| D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|
| D1 | [1, 1] | [1, 2] | [1/5, 1/4] | [1/4, 1/3] |
| D2 | [1/2, 1] | [1, 1] | [1/6, 1/5] | [1/5, 1/4] |
| D3 | [4, 5] | [5, 6] | [1, 1] | [2, 3] |
| D4 | [3, 4] | [4, 5] | [1/3, 1/2] | [1, 1] |

Table A6.
Judgment matrix for number of ecological subjective weight intervals in target layer U.
Table A6.
Judgment matrix for number of ecological subjective weight intervals in target layer U.
| U | A | B | C | D |
|---|---|---|---|---|
| A | [1, 1] | [5, 6] | [3, 4] | [4, 5] |
| B | [1/6, 1/5] | [1, 1] | [1/5, 1/4] | [1/4, 1/3] |
| C | [1/4, 1/3] | [4, 5] | [1, 1] | [3, 4] |
| D | [1/5, 1/4] | [3, 4] | [1/4, 1/3] | [1, 1] |

Table A7.
Judgment matrix for number of ecological subjective weight intervals for criterion layer A.
Table A7.
Judgment matrix for number of ecological subjective weight intervals for criterion layer A.
| A | A1 | A2 | A3 |
|---|---|---|---|
| A1 | [1, 1] | [1/3, 1/2] | [3, 4] |
| A2 | [2, 3] | [1, 1] | [4, 5] |
| A3 | [1/4, 1/3] | [1/5, 1/4] | [1, 1] |

Table A8.
Judgment matrix for number of ecological subjective weight intervals for criterion layer B.
Table A8.
Judgment matrix for number of ecological subjective weight intervals for criterion layer B.
| B | B1 | B2 | B3 |
|---|---|---|---|
| B1 | [1, 1] | [1/2, 1] | [2, 3] |
| B2 | [1, 2] | [1, 1] | [2, 3] |
| B3 | [1/3, 1/2] | [1/3, 1/2] | [1, 1] |

Table A9.
Judgment matrix for number of ecological subjective weight intervals for criterion layer C.
Table A9.
Judgment matrix for number of ecological subjective weight intervals for criterion layer C.
| C | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| C1 | [1, 1] | [1/3, 1/2] | [2, 3] | [1/3, 1/2] | [4, 5] |
| C2 | [2, 3] | [1, 1] | [3, 4] | [1/2, 1] | [4, 5] |
| C3 | [1/3, 1/2] | [1/4, 1/3] | [1, 1] | [1/4, 1/3] | [3, 4] |
| C4 | [2, 3] | [1, 2] | [3, 4] | [1, 1] | [4, 5] |
| C5 | [1/5, 1/4] | [1/5, 1/4] | [1/4, 1/3] | [1/5, 1/4] | [1, 1] |

Table A10.
Judgment matrix for number of ecological subjective weight intervals for criterion layer D.
Table A10.
Judgment matrix for number of ecological subjective weight intervals for criterion layer D.
| D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|
| D1 | [1, 1] | [1, 2] | [1/3, 1/2] | [1/4, 1/3] |
| D2 | [1/2, 1] | [1, 1] | [1/6, 1/5] | [1/5, 1/4] |
| D3 | [2, 3] | [5, 6] | [1, 1] | [1/3, 1/2] |
| D4 | [3, 4] | [4, 5] | [2, 3] | [1, 1] |
References
- Whittall, J.R.; McDougall, S.; Eberhardt, E. A risk-based methodology for establishing landslide exclusion zones in operating open pit mines. Int. J. Rock Mech. Min. Sci. 2017, 100, 100–107. [Google Scholar] [CrossRef]
- Zhang, J.X.; Li, B.; Liu, Y.W.; Li, P.; Fu, J.W.; Chen, L.; Ding, P.C. Dynamic multifield coupling model of gas drainage and a new remedy method for borehole leakage. Acta Geotech. 2022, 17, 4699–4715. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.X.; Liu, Y.W.; Qu, L.A.; Liu, Q.; Sun, Y.X.; Xu, G. Interfacial porosity model and modification mechanism of broken coal grouting: A theoretical and experimental study. Surf. Interfaces 2022, 33, 11. [Google Scholar] [CrossRef]
- Hamza, O.; De Vargas, T.; Boff, F.E.; Hussain, Y.; Sian Davies-Vollum, K. Geohazard Assessment of Landslides in South Brazil: Case Study. Geotech. Geol. Eng. 2019, 38, 971–984. [Google Scholar] [CrossRef]
- Igwe, O.; Ayogu, C.N.; Maduka, R.I.; Ayogu, N.O.; Ugwoke, T.A.S. Slope failures and safety index assessment of waste rock dumps in Nigeria’s major mines. Nat. Hazards 2023, 115, 1331–1370. [Google Scholar] [CrossRef]
- Du, S.G.; Saroglou, C.; Chen, Y.F.; Lin, H.; Yong, R. A new approach for evaluation of slope stability in large open-pit mines: A case study at the Dexing Copper Mine, China. Environ. Earth Sci. 2022, 81, 21. [Google Scholar] [CrossRef]
- Xu, Q.W.; Xu, K.L. Mine safety assessment using gray relational analysis and bow tie model. PLoS ONE 2018, 13, 14. [Google Scholar] [CrossRef]
- Wang, Z.L.; Hu, M.X.; Zhang, P.; Li, X.M.; Yin, S. Dynamic Risk Assessment of High Slope in Open-Pit Coalmines Based on Interval Trapezoidal Fuzzy Soft Set Method: A Case Study. Processes 2022, 10, 2168. [Google Scholar] [CrossRef]
- Su, H.Z.; Yang, M.; Wen, Z.P. An approach using multi-factor combination to evaluate high rocky slope safety. Nat. Hazards Earth Syst. Sci. 2016, 16, 1449–1463. [Google Scholar] [CrossRef]
- Panchal, S.; Shrivastava, A.K. Landslide hazard assessment using analytic hierarchy process (AHP): A case study of National Highway 5 in India. Ain Shams Eng. J. 2022, 13, 101626. [Google Scholar] [CrossRef]
- Chen, H.K.; Guo, Q.B.; Wang, L.; Meng, X.R. Evaluation of Slope Stability within the Influence of Mining Based on Combined Weighting and Finite Cloud Model. Energy Explor. Exploit. 2023, 41, 636–655. [Google Scholar] [CrossRef]
- Li, Z.; Sun, L.; Liu, L.; Guan, C. Research on safety evaluation method of high-fill slope considering heterogeneity and anisotropy. Bull. Eng. Geol. Environ. 2022, 81, 275. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, Q.S.; Geng, J.H. New approach to multiple attribute decision making with interval numbers. J. Syst. Eng. Electron. 2008, 19, 304–310. [Google Scholar]
- Qin, F.Y.; Liu, T.X.; Yang, F.L.; Ge, Q.Y. Stability of side slopes in mining area and the evaluation of eco-environment health. J. Environ. Prot. Ecol. 2022, 23, 1407–1416. [Google Scholar]
- Jiao, L.D.; Wang, L.; Lu, H.; Fan, Y.W.; Zhang, Y.; Wu, Y. An assessment model for urban resilience based on the pressure-state-response framework and BP-GA neural network. Urban Climb 2023, 49, 20. [Google Scholar] [CrossRef]
- Wang, Y.; Hulse, D.; Von Meding, J.; Brown, M.; Dedenbach, L. Conceiving resilience: Lexical shifts and proximal meanings in the human-centered natural and built environment literature from 1990 to 2018. Dev. Built Environ. 2020, 1, 19. [Google Scholar] [CrossRef]
- Li, Y.; Du, Q.; Zhang, J.S.; Jiang, Y.; Zhou, J.J.; Ye, Z.N. Visualizing the intellectual landscape and evolution of transportation system resilience: A bibliometric analysis in CiteSpace. Dev. Built Environ. 2023, 14, 12. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Shen, L.; Xue, Z.J.; Tang, L.Y.; Ge, H.Y. Research on Resilience Evaluation and Enhancement of Deep Foundation Pit Construction Safety System. Buildings 2022, 12, 1922. [Google Scholar] [CrossRef]
- Roostaie, S.; Nawari, N. The DEMATEL approach for integrating resilience indicators into building sustainability assessment frameworks. Build. Environ. 2022, 207, 108113. [Google Scholar] [CrossRef]
- Mottahedi, A.; Sereshki, F.; Ataei, M.; Qarahasanlou, A.N.; Barabadi, A. Resilience estimation of critical infrastructure systems: Application of expert judgment. Reliab. Eng. Syst. Saf. 2021, 215, 16. [Google Scholar] [CrossRef]
- Pei, J.J.; Liu, W.; Han, L. Research on Evaluation Index System of Chinese City Safety Resilience Based on Delphi Method and Cloud Model. Int. J. Environ. Res. Public Health 2019, 16, 3802. [Google Scholar] [CrossRef]
- Zhang, J. Study on Seismic Resilience Evaluation of Urban System Based on Two-Dimensional Cloud Model. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2023. [Google Scholar]
- Liu, Y.; Xiang, C. A Comprehensive Framework for Evaluating Bridge Resilience: Safety, Social, Environmental, and Economic Perspectives. Sustainability 2024, 16, 1135. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, C.; Liu, L. Study on the Universality of the Normal Cloud Model. Eng. Sci. 2005, 3, 18–24. [Google Scholar] [CrossRef]
- Bai, M.H.; Liu, Q. Evaluating Urban Fire Risk Based on Entropy-Cloud Model Method Considering Urban Safety Resilience. Fire 2023, 6, 62. [Google Scholar] [CrossRef]
- Liu, H.C.; Wang, L.E.; Li, Z.W.; Hu, Y.P. Improving Risk Evaluation in FMEA With Cloud Model and Hierarchical TOPSIS Method. IEEE Trans. Fuzzy Syst. 2019, 27, 84–95. [Google Scholar] [CrossRef]
- Sang, L.S.; Wang, J.C.; Sui, J.Y.; Dziedzic, M. A New Approach for Dam Safety Assessment Using the Extended Cloud Model. Water Resour. Manag. 2022, 36, 5785–5798. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Z.F. Risk assessment of seepage failure in deep excavations based on fuzzy analytic hierarchy process and cloud model. Acta Geotech. 2023, 18, 5635–5658. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, G.D.; Fathollahi-Fard, A.M.; Wang, W.J.; Wu, P.; Li, Z.W. Interval-Valued Intuitionistic Uncertain Linguistic Cloud Petri Net and Its Application to Risk Assessment for Subway Fire Accident. IEEE Trans. Autom. Sci. Eng. 2022, 19, 163–177. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, W.; Sun, H.Y.; Pan, Q.J.; Zhang, J.B.; Li, Y.F. Risk uncertainty analysis in shield tunnel projects. Tunn. Undergr. Space Technol. 2023, 132, 25. [Google Scholar] [CrossRef]
- Meng, G.W.; Ye, Y.C.; Wu, B.; Luo, G.J.; Zhang, X.; Zhou, Z.Q.; Sun, W.T. Risk Assessment of Shield Tunnel Construction in Karst Strata Based on Fuzzy Analytic Hierarchy Process and Cloud Model. Shock Vib. 2021, 2021, 16. [Google Scholar] [CrossRef]
- Guangyue, W.; Jiong, L.; Feifan, Y.; Guorui, S. Fuzzy comprehensive assessment stability of vegetated slope with 3D geomat protection using cloud model. Open Civ. Eng. J. 2017, 11, 70–81. [Google Scholar] [CrossRef][Green Version]
- Qiu, D.; Liu, Y.; Xue, Y.; Su, M.; Zhao, Y.; Cui, J.; Li, Z. Prediction of the surrounding rock deformation grade for a high-speed railway tunnel based on rough set theory and a cloud model. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 303–314. [Google Scholar] [CrossRef]
- Gao, Y.H.; Han, B.; Miao, J.J.; Jin, S.; Liu, H.W. Research on Suitability Evaluation of Urban Engineering Construction Based on Entropy Weight Hierarchy-Cloud Model: A Case Study in Xiongan New Area, China. Appl. Sci. 2023, 13, 10655. [Google Scholar] [CrossRef]
- Huang, J.L.; Zeng, X.Y.; Fu, J.; Han, Y.; Chen, H.H. Safety Risk Assessment Using a BP Neural Network of High Cutting Slope Construction in High-Speed Railway. Buildings 2022, 12, 598. [Google Scholar] [CrossRef]
- Xu, W.X.; Wang, J.M.; Zhang, M.; Li, S.J. Construction of landscape ecological network based on landscape ecological risk assessment in a large-scale opencast coal mine area. J. Clean. Prod. 2021, 286, 11. [Google Scholar] [CrossRef]
- Tu, M.; Ke, B.; Lu, S.; Zhou, H.; Zhang, D.; Pan, R. Study on Division and Ecological Restoration Suitability of Rock Slope inTongshankou Copper Mine. Min. Res. Dev. 2021, 41, 5. [Google Scholar] [CrossRef]
- Feng, S.; Deng, W.; Sun, S. Analysis of Waste Dump Slope Resilience Evaluation Method Based on Fuzzy Analytic Hierarchy Process. J. Beijing Polytech. Coll. 2022, 21, 6. [Google Scholar]
- Xu, X.; Wang, X.; Ye, L.; Zhao, M.; Lei, G. Study on Slope Stability of the Open-pit Mine Based on GA-AHP and Cloud Matter-element Model. Met. Mine 2021, 10, 168–172. [Google Scholar] [CrossRef]
- Du, Y.; Bai, Y.; Zhang, X.; Xie, M.; Ma, G. Risk Assessment of Coal Gangue Slope Considering Multiple Risk Factors. Eng. Mech. 2022, 39, 8. [Google Scholar] [CrossRef]
- Xia, P.; Hu, X.L.; Wu, S.S.; Ying, C.Y.; Liu, C. Slope Stability Analysis Based on Group Decision Theory and Fuzzy Comprehensive Evaluation. J. Earth Sci. 2020, 31, 1121–1132. [Google Scholar] [CrossRef]
- Association, C.C.C. Code for Investigation of Geotechnicalengineering in the Coal Mine Goaf; China Planning Press: Beijing, China, 2014. [Google Scholar]
- Ministry of Commerce, People’s Republic of China. Technical Code for Building Slope Engineering; China Architecture & Building Press: Beijing, China, 2014. [Google Scholar]
- Zedek, L.; Šembera, J.; Kurka, J. Inclusion of Nature-Based Solution in the Evaluation of Slope Stability in Large Areas. Land 2024, 13, 372. [Google Scholar] [CrossRef]
- Li, Z.; Xu, T.; Liu, Y.; Zhao, L.; Xu, Y.; Yang, T.; Zheng, X. Open-pit mine slopes stability analysis based on analytic hierarchy process-fuzzy comprehensive evaluation model. Chin. J. Geol. Hazard Control 2024, 35, 116–123. [Google Scholar] [CrossRef]
- Li, J.L.; Deng, C.C.C.; Xu, J.Y.; Ma, Z.J.; Shuai, P.; Zhang, L.B. Safety Risk Assessment and Management of Panzhihua Open Pit (OP)-Underground (UG) Iron Mine Based on AHP-FCE, Sichuan Province, China. Sustainability 2023, 15, 4497. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Liu, S. Application of an Improved Cloud Model and Distance Discrimination to Evaluate Slope Stability. Math. Probl. Eng. 2019, 2019, 8315894. [Google Scholar] [CrossRef]
- Wei, G.; Liu, J.; Zhao, T.; Yang, J.; Li, R.; Kui, G.; Ai, X.; Xiao, F. Evaluate the Reclamation Suitability of Dumps of Open-pit Coal Mines based on Niche Fitness in the Eastern Arid Desert Area in Northwest China. J. Resour. Ecol. 2023, 14, 805–815. [Google Scholar] [CrossRef]
- Li, Y.H. Suitability evaluation of land reclamation as arable land in coal mining area based on catastrophe theory. SN Appl. Sci. 2023, 5, 146. [Google Scholar] [CrossRef]
- Jiang, J.; Sun, J.; Wang, D.; Wang, L.; Cao, L.; Cai, M. An evaluation method of open-pit slope stability based on Poset theory. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 11. [Google Scholar] [CrossRef]
- XU, R.; Zhang, W.; Sui, G.; Wang, G.; Li, X.; Yang, W. Mine geological environment evaluation based on IFS-TOPSIS. J. Saf. Environ. 2023, 23, 230–239. [Google Scholar] [CrossRef]
- China, Ministry of Transport of the People’s Republic of China. Guidelines for Safety Risk Assessment of Highway Graben High Slope Construction Works; China Communications Press: Beijing, China, 2015. [Google Scholar]
- Xie, Z. Lutian Kuangshan Bianpo he Paituchangzaihai Yujing Ji Kongzhi Jishu; Metallurgical Industry Press: Beijing, China, 2015. [Google Scholar]
- McQuillan, A.; Canbulat, I.; Payne, D.; Oh, J. New risk assessment methodology for coal mine excavated slopes. Int. J. Min. Sci. Technol. 2018, 28, 583–592. [Google Scholar] [CrossRef]
- Jin, L.X.; Qin, T.; Liu, P.T. Upper Bound Solution Analysis of the Ultimate Bearing Capacity of Two-Layered Strip Foundation Based on Improved Radial Movement Optimization. Appl. Sci. 2023, 13, 7299. [Google Scholar] [CrossRef]
- He, F.; Ye, Q. A Bearing Fault Diagnosis Method Based on Wavelet Packet Transform and Convolutional Neural Network Optimized by Simulated Annealing Algorithm. Sensors 2022, 22, 1410. [Google Scholar] [CrossRef]
- Zhou, J.; Lin, H.F.; Li, S.G.; Jin, H.W.; Zhao, B.; Liu, S.H. Leakage diagnosis and localization of the gas extraction pipeline based on SA-PSO BP neural network. Reliab. Eng. Syst. Saf. 2023, 232, 11. [Google Scholar] [CrossRef]
- Wang, S.X.; Ge, L.J.; Cai, S.X.; Wu, L. Hybrid interval AHP-entropy method for electricity user evaluation in smart electricity utilization. J. Mod. Power Syst. Clean Energy 2018, 6, 701–711. [Google Scholar] [CrossRef]
- Ma, Z.Z.; Zhang, S.T. Risk-Based Multi-Attribute Decision-Making for Normal Cloud Model Considering Pre-Evaluation Information. IEEE Access 2020, 8, 153891–153904. [Google Scholar] [CrossRef]
- Guo, M.; Zhao, J.W.; Pan, D.; Sun, M.X.; Zhou, Y.Q.; Yan, B.N. Normal cloud model theory-based comprehensive fuzzy assessment of wooden pagoda safety. J. Cult. Herit. 2022, 55, 1–10. [Google Scholar] [CrossRef]
- Lyu, H.M.; Shen, S.L.; Zhou, A.N.; Zhou, W.H. Data in flood risk assessment of metro systems in a subsiding environment using the interval FAHP-FCA approach. Data Brief 2019, 26, 7. [Google Scholar] [CrossRef]
- Wang, X.T.; Li, S.C.; Xu, Z.H.; Lin, P.; Hu, J.; Wang, W.Y. Analysis of Factors Influencing Floor Water Inrush in Coal Mines: A Nonlinear Fuzzy Interval Assessment Method. Mine Water Environ. 2019, 38, 81–92. [Google Scholar] [CrossRef]
- Wang, Y. Analysis of the Factors Influencing the Career Development of University Librarians Based on Interval AnalyticHierarchy Process(1-AHP)-Taking Seven Universities in Kunming as Examples. Master’s Thesis, Yunnan University, Kunming, China, 2023. [Google Scholar]
- Xu, G.; Xie, X. Identifying and Improving Method for Consistency of Interval Reciprocal Judgment Matrices. J. Guilin Univ. Technol. 2013, 33, 6. [Google Scholar] [CrossRef]
- Ali, S.I.; Lalji, S.M.; Hashmi, S.; Awan, Z.; Iqbal, A.; Al-Ammar, E.A.; Gull, A. Risk quantification and ranking of oil fields and wells facing asphaltene deposition problem using fuzzy TOPSIS coupled with AHP. Ain Shams Eng. J. 2024, 15, 102289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).