A Novel Data-Envelopment Analysis Interval-Valued Fuzzy-Rough-Number Multi-Criteria Decision-Making (DEA-IFRN MCDM) Model for Determining the Efficiency of Road Sections Based on Headway Analysis
Abstract
1. Introduction
- In accordance with the previously defined importance of headways for the entire area of road transport, a total of 14 sections of road infrastructure were considered and a new model to determine their efficiency was created. In addition to five headway classifications, AADT (annual average daily traffic) and road gradient were taken as influential parameters.
- A new multiphase efficiency model, which includes the DEA model, SWARA, and WASPAS methods in the form of interval fuzzy rough numbers, was created. IFRNs were used due to their ability to treat uncertainty in the decision-making process adequately. The greatest contribution of the paper can be seen from the aspect of a new algorithm of the IFRN WASPAS method, which, according to the authors’ knowledge, is presented for the first time in the literature. So far, certain comparative analyses have been presented, but without the algorithm of this method.
- Another aspect of the contribution is reflected through the sustainable management of road infrastructure based on the results obtained and future recommendations. From a practical aspect, the study provides valuable insights for infrastructure managers and traffic experts, helping them make informed decisions to optimize road section efficiency.
2. Literature Review
3. Methods
3.1. Preliminaries
3.2. Interval Fuzzy-Rough-Number SWARA Method
3.3. A Novel Interval Fuzzy-Rough-Number WASPAS Method
4. Efficiency of Road Sections Based on Headway Analysis
4.1. Collection and Processing of Data
4.2. Application of DEA Model
4.3. Determining the Importance of Parameters Using the IFRN SWARA Method
4.4. Determining Overall Efficiency Using the IFRN WASPAS Method
5. Verification Tests
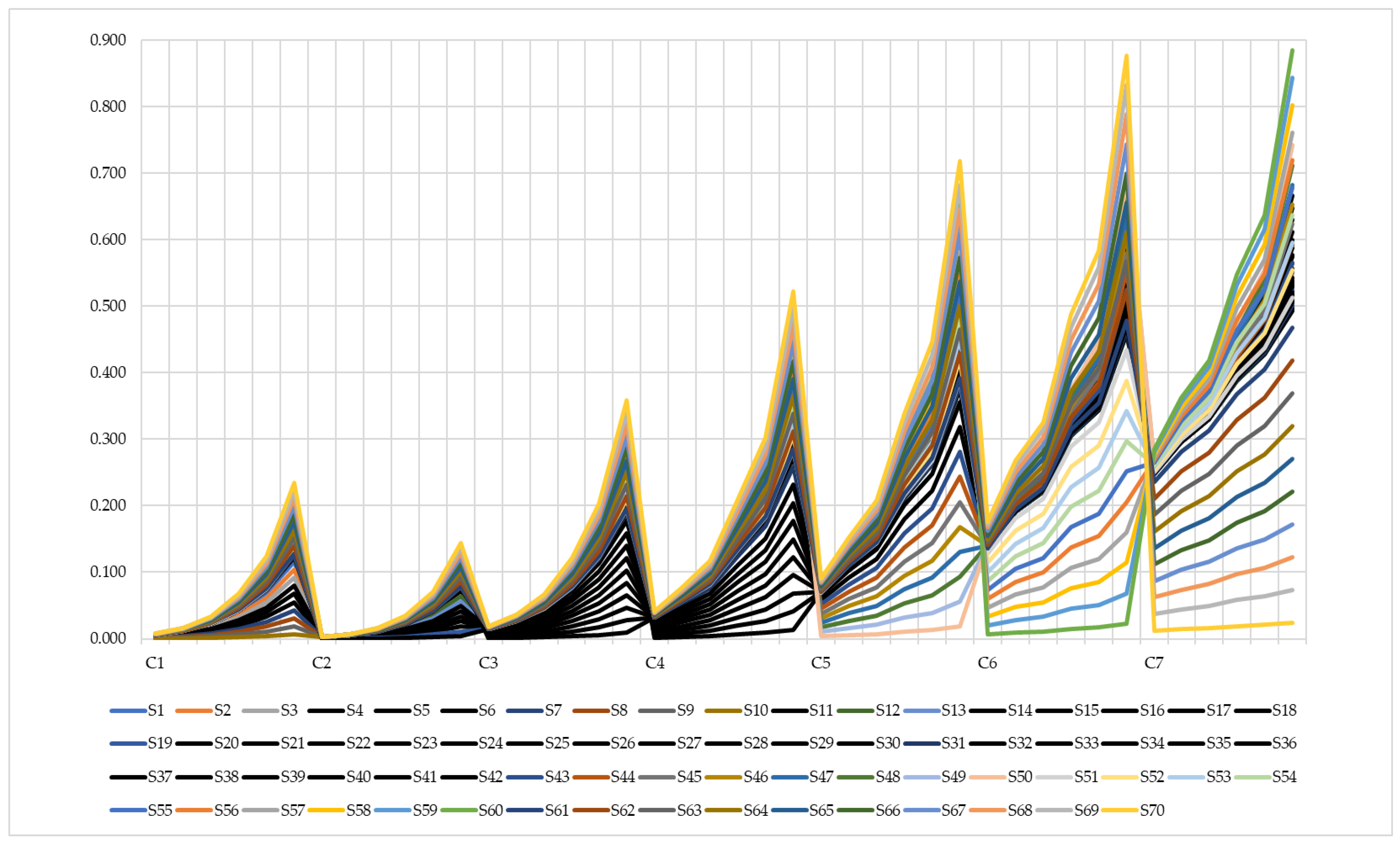
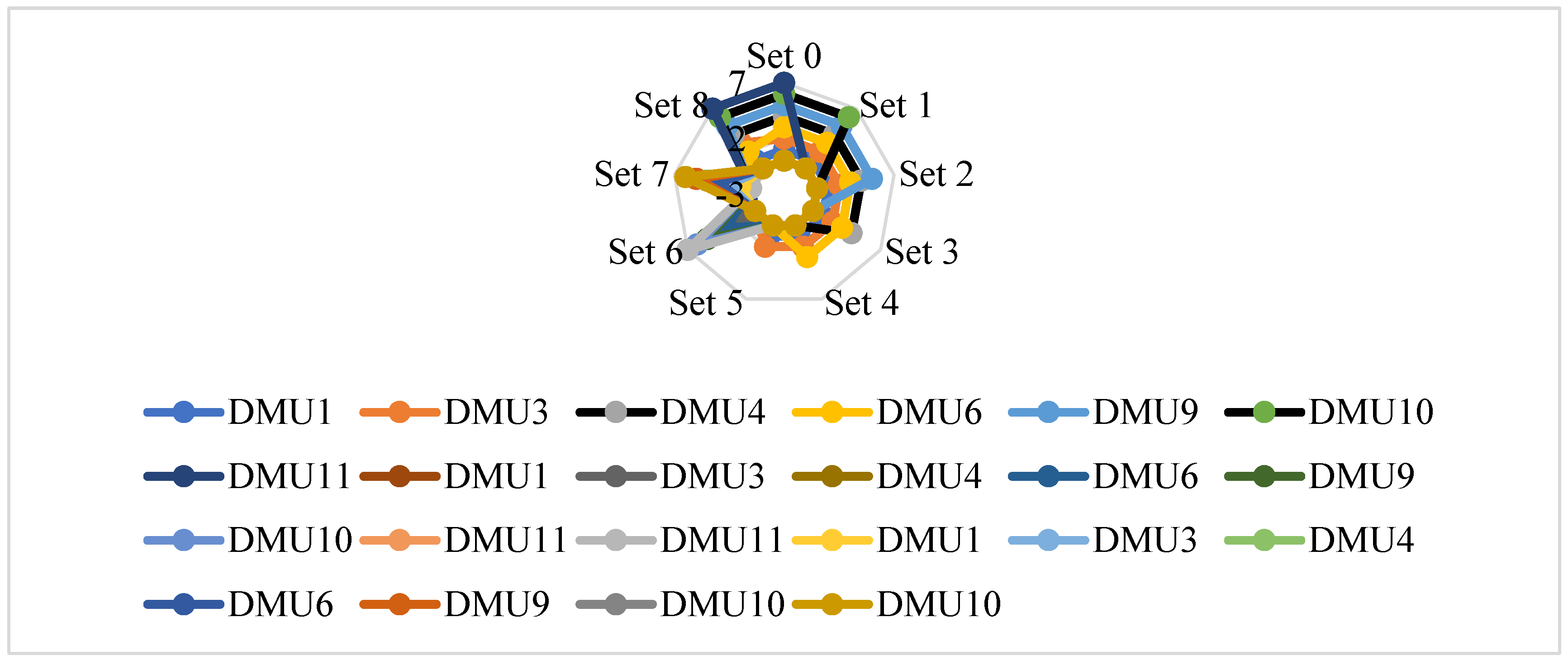
5.1. Sensitivity Analysis (SA)
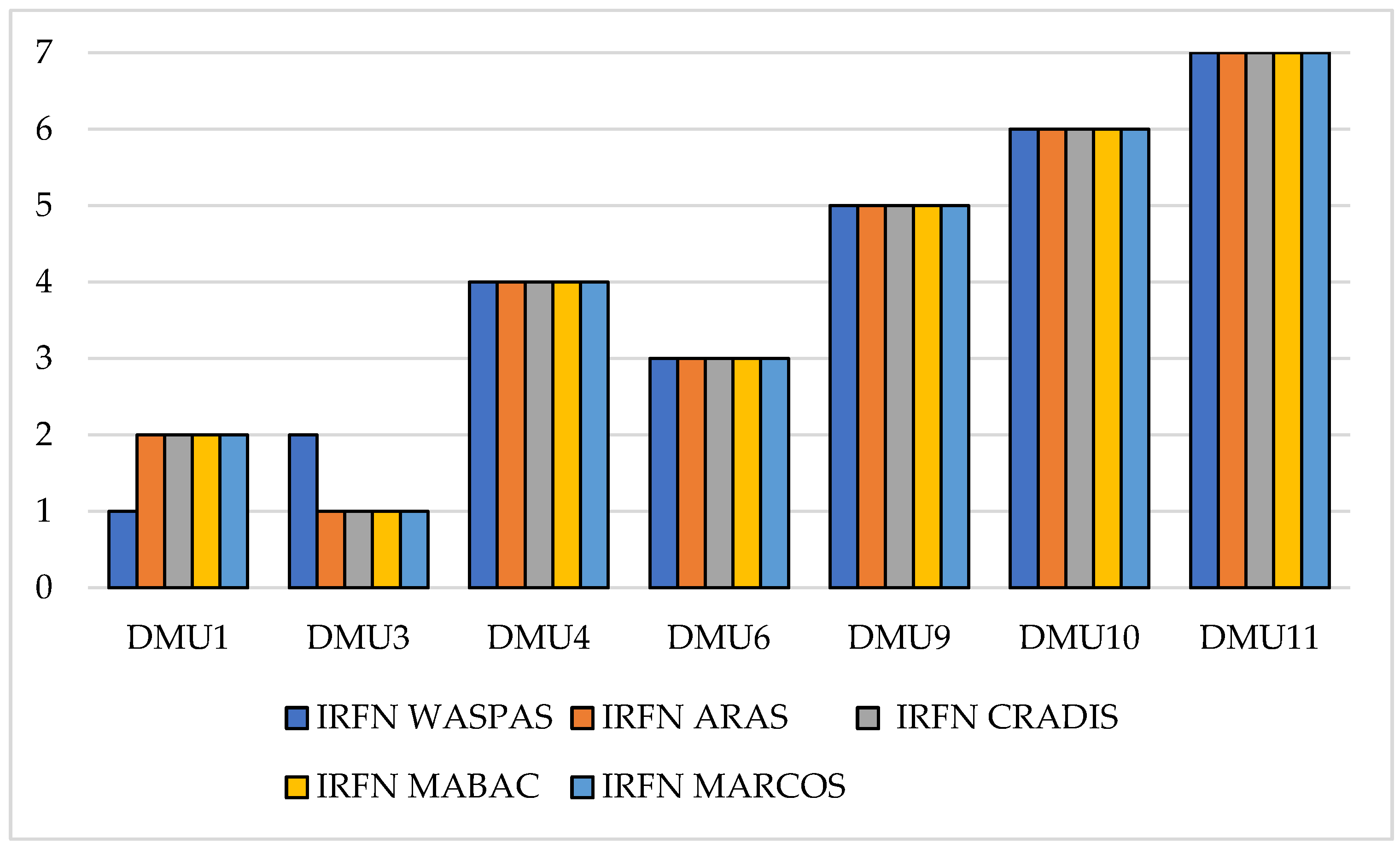
5.2. Comparative Analysis (CA)
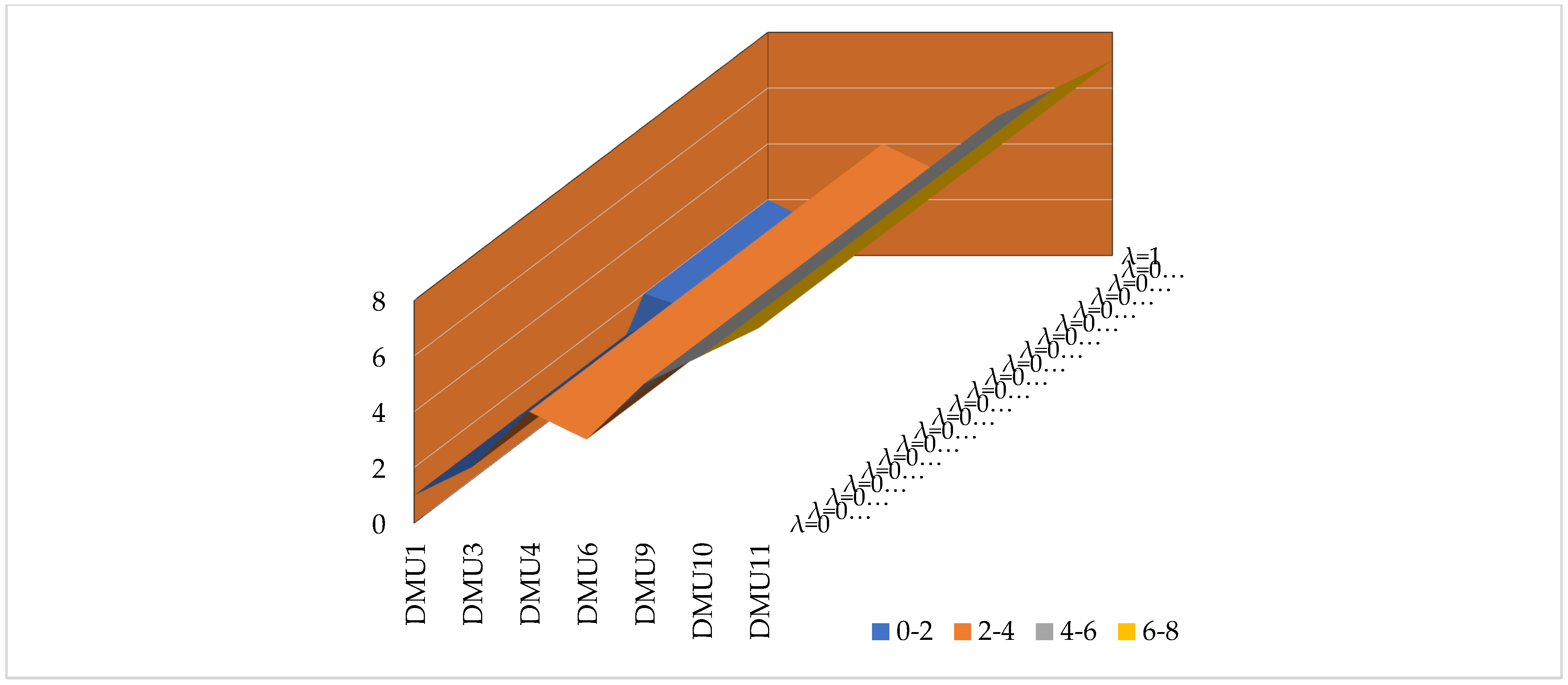
5.3. Changing the λ Parameter
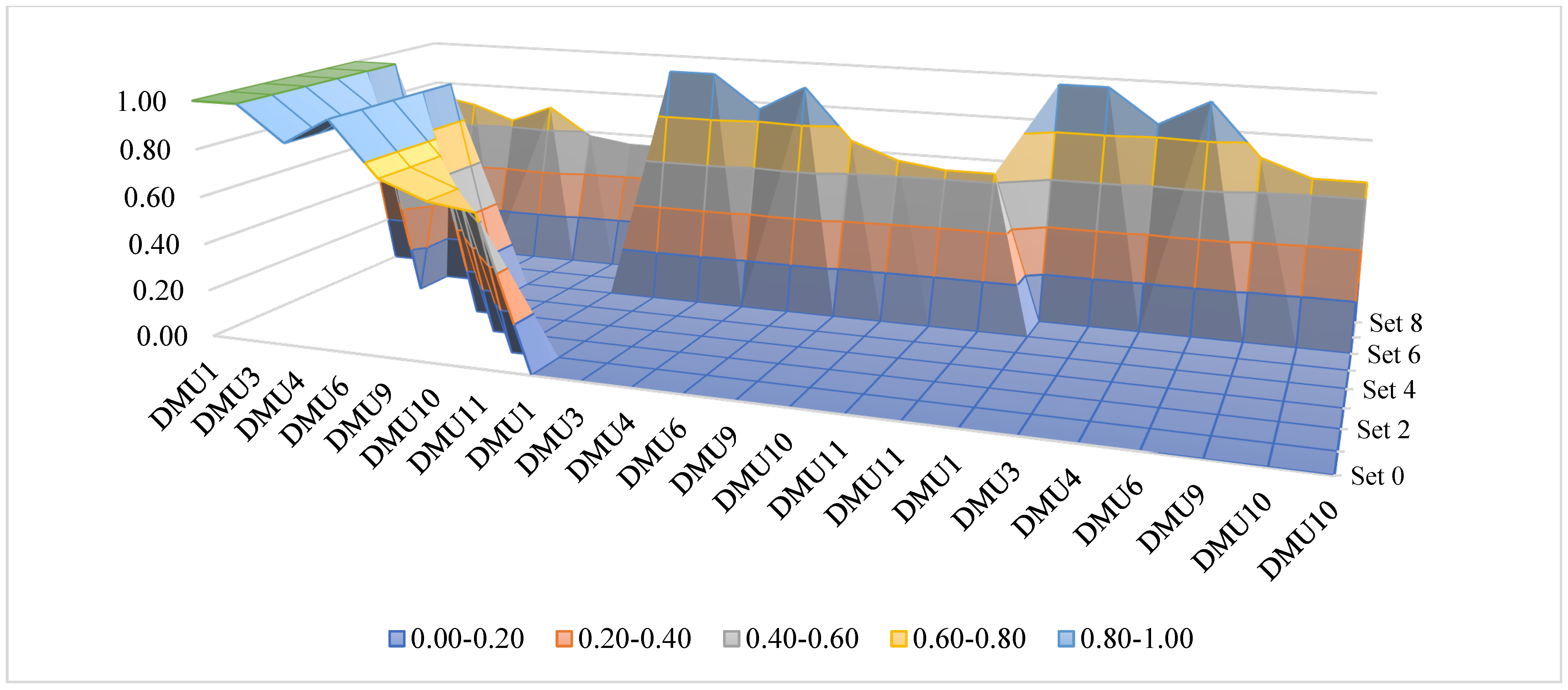
5.4. Reverse Rank (RR) Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, A.B.F.; Ivan, P. Integrating Machine Learning and Deep Learning in Smart Cities for Enhanced Traffic Congestion Management: An Empirical Review. J. Urban Dev. Manag. 2023, 2, 211–221. [Google Scholar] [CrossRef]
- Biswas, R.K.; Friswell, R.; Olivier, J.; Williamson, A.; Senserrick, T. A systematic review of definitions of motor vehicle headways in driver behaviour and performance studies. Transp. Res. Part F Traffic Psychol. Behav. 2021, 77, 38–54. [Google Scholar] [CrossRef]
- Khan, J.A.; Shah, A.U. Comparison of Headway Measurement Methods for Heterogeneous Traffic Conditions. Int. J. Res. Appl. Sci. Eng. Technol. 2023, 11, 1362–1367. [Google Scholar] [CrossRef]
- Cantisani, G.; Del Serrone, G.; Mauro, R.; Peluso, P.; Pompigna, A. Traffic Stream Analysis by Radar Sensors on Two-Lane Roads for Free-Moving and Constrained Vehicles Identification. Sensors 2023, 23, 6922. [Google Scholar] [CrossRef] [PubMed]
- Abtahi, S.M.; Tamannaei, M.; Haghshenash, H. Analysis and modeling time headway distributions under heavy traffic flow conditions in the urban highways: Case of Isfahan. Transport 2011, 26, 375–382. [Google Scholar] [CrossRef]
- Boora, A.; Ghosh, I.; Chandra, S.; Rani, K. Measurement of free-flow conditions on multilane intercity highways under heterogeneous traffic conditions. J. South Afr. Inst. Civ. Eng. 2018, 60, 2–9. [Google Scholar] [CrossRef]
- Oghoyafedo, K.N.; Enunwa, B.T.; Nwankwo, E. Capacity Evaluation Along Benin-Lagos Expressway by Traffic Flow and Time Headway Approach. NIPES J. Sci. Technol. Res. 2022, 4, 322–328. [Google Scholar] [CrossRef]
- Samadi, H.; Aghayan, I.; Nasiri, A.S.A.; Rahmani, O.; Hasanvand, M. Platoon-Based Assessment of Two-Way Two-Lane Roads Performance Measure: A Classification Method. J. Adv. Transp. 2023, 2023, 5054427. [Google Scholar] [CrossRef]
- Roy, R.; Saha, P. Headway distribution models of two-lane roads under mixed traffic conditions: A case study from India. Eur. Transp. Res. Rev. 2017, 10, 3. [Google Scholar] [CrossRef]
- Weng, J.; Meng, Q.; Fwa, T.F. Vehicle headway distribution in work zones. Transp. A Transp. Sci. 2013, 10, 285–303. [Google Scholar] [CrossRef]
- Yu, R.; Zhang, Y.; Wang, L.; Du, X. Time headway distribution analysis of naturalistic road users based on aerial datasets. J. Intell. Connect. Veh. 2022, 5, 149–156. [Google Scholar] [CrossRef]
- Abdul Mawjoud, A.A. Headway Modeling in Northern Iraqi Two-Lane Highways. Acad. J. Nawroz Univ. 2018, 7, 1–8. [Google Scholar] [CrossRef]
- Shoaeb, A.; El-Badawy, S.; Shawly, S.; Shahdah, U.E. Time headway distributions for two-lane two-way roads: Case study from Dakahliya Governorate, Egypt. Innov. Infrastruct. Solut. 2021, 6, 165. [Google Scholar] [CrossRef]
- Khansari, E.R.; Tabibi, M.; Nejad, F.M. A study on following behavior based on the time headway. J. Kejuruter. 2020, 32, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Masud, S.S.B. Traffic Time Headway Prediction and Analysis: A Deep Learning Approach. Ph.D. Thesis, The University of Texas Rio Grande Valley, Edinburg, TX, USA.
- Li, L.; Chen, X. Vehicle headway modeling and its inferences in macroscopic/microscopic traffic flow theory: A survey. Transp. Res. Part C Emerg. Technol. 2017, 76, 170–188. [Google Scholar] [CrossRef]
- Roy, R.; Saha, P. Analysis of vehicle-type-specific headways on two-lane roads with mixed traffic. Transport 2020, 35, 588–604. [Google Scholar] [CrossRef]
- Samadi, H.; Aghayan, I.; Shaaban, K.; Hadadi, F. Development of Performance Measurement Models for Two-Lane Roads under Vehicular Platooning Using Conjugate Bayesian Analysis. Sustainability 2023, 15, 4037. [Google Scholar] [CrossRef]
- HCM. Highway Capacity Manual. In Transportation Research Board; National Research Council: Washington, DC, USA, 2016. [Google Scholar]
- Luttinen, R.T. Percent time-spent-following as performance measure for two-lane highways. Transp. Res. Rec. 2001, 1776, 52–59. [Google Scholar] [CrossRef]
- HCM. Highway Capacity Manual, 3rd ed.; Transportation Research Board, National Research Council: Washington, DC, USA, 1985. [Google Scholar]
- HCM. Highway Capacity Manual, 5th ed.; Transportation Research Board, National Research Council: Washington, DC, USA, 2010. [Google Scholar]
- Stepanović, N.; Tubić, V.; Zdravković, S. Determining Free-Flow Speed on Different Classes of Rural Two-Lane Highways. Promet–Traffic Transp. 2023, 35, 315–330. [Google Scholar] [CrossRef]
- Loulizi, A.; Bichiou, Y.; Rakha, H. Steady-State Car-Following Time Gaps: An Empirical Study Using Naturalistic Driving Data. J. Adv. Transp. 2019, 2019, 7659496. [Google Scholar] [CrossRef]
- Pamučar, D.; Petrović, I.; Ćirović, G. Modification of the Best–Worst and MABAC methods: A novel approach based on interval-valued fuzzy-rough numbers. Expert Syst. Appl. 2018, 91, 89–106. [Google Scholar] [CrossRef]
- Wang, N.; Xu, Y.; Puška, A.; Stević, A.; Alrasheedi, A.F. Multi-Criteria Selection of Electric Delivery Vehicles Using Fuzzy–Rough Methods. Sustainability 2023, 15, 15541. [Google Scholar] [CrossRef]
- Korucuk, S.; Aytekin, A. Evaluating logistics flexibility in Istanbul-based companies using Interval-Valued Fermatean Fuzzy SWARA. J. Intell Manag. Decis. 2023, 2, 192–201. [Google Scholar] [CrossRef]
- Badi, I.; Bouraima, M.B. Development of MCDM-Based Frameworks for proactively managing the most critical risk factors for transport accidents: A case study in Libya. Spectr. Eng. Manag. Sci. 2023, 1, 38–47. [Google Scholar] [CrossRef]
- Qiu, Y.; Bouraima, M.B.; Kiptum, C.K.; Ayyildiz, E.; Stević, E.; Badi, I.; Ndiema, K.M. Strategies for Enhancing Industry 4.0 Adoption in East Africa: An Integrated Spherical Fuzzy SWARA-WASPAS Approach. J. Ind. Intell. 2023, 1, 87–100. [Google Scholar] [CrossRef]
- Seikh, M.R.; Chatterjee, P. Determination of best renewable energy sources in India using SWARA-ARAS in confidence level based interval-valued Fermatean fuzzy environment. Appl. Soft Comput. 2024, 155, 111495. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, B.; Štilić, A.; Stević, E.; Puška, A. A Fuzzy–Rough MCDM Approach for Selecting Green Suppliers in the Furniture Manufacturing Industry: A Case Study of Eco-Friendly Material Production. Sustainability 2023, 15, 10745. [Google Scholar] [CrossRef]
- Khan, A.A.; Mashat, D.S.; Dong, K. Evaluating Sustainable Urban Development Strategies through Spherical CRITIC-WASPAS Analysis. J. Urban Dev. Manag. 2024, 3, 1–17. [Google Scholar] [CrossRef]
- Pamučar, D.; Sremac, S.; Stević, Ž.; Ćirović, G.; Tomić, D. New multi-criteria LNN WASPAS model for evaluating the work of advisors in the transport of hazardous goods. Neural Comput. Appl. 2019, 31, 5045–5068. [Google Scholar] [CrossRef]
- Damjanović, M.; Stević, M.; Stanimirović, D.; Tanackov, I.; Marinković, D. Impact of the number of vehicles on traffic safety: Multiphase modeling. Facta Univ. Series Mech. Eng. 2022, 20, 177–197. [Google Scholar] [CrossRef]
- Božanić, D.; Epler, I.; Puška, A.; Biswas, S.; Marinković, D.; Koprivica, S. Application of the DIBR II–rough MABAC decision-making model for ranking methods and techniques of lean organization systems management in the process of technical maintenance. Facta Univ. Ser. Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. How do the criteria affect sustainable supplier evaluation?—A case study using multi-criteria decision analysis methods in a fuzzy environment. J. Eng. Manag. Syst. Eng. 2023, 2, 37–52. [Google Scholar] [CrossRef]
- Tešić, D.; Božanić, D.; Radovanović, M.; Petrovski, A. Optimising assault boat selection for military operations: An application of the DIBR II-BM-CoCoSo MCDM model. J. Intell. Manag. Decis. 2023, 2, 160–171. [Google Scholar] [CrossRef]
- Albahri, O.; Alamoodi, A.; Deveci, M.; Albahri, A.; Mahmoud, M.A.; Al-Quraishi, T.; Moslem, S.; Sharaf, I.M. Evaluation of organizational culture in companies for fostering a digital innovation using q-rung picture fuzzy based decision-making model. Adv. Eng. Inform. 2023, 58, 102191. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MAR-COS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chatterjee, P.; Das, P.P. Compromise Ranking of Alternatives from Distance to Ideal Solution (CRADIS) Method. In Multi-Criteria Decision-Making Methods in Manufacturing Environments; Apple Academic Press: New York, NY, USA, 2024; pp. 343–347. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Bazrafshan, R.; Ecer, F.; Karamaşa, F. The suitability-feasibility-acceptability strategy integrated with Bayesian BWM-MARCOS methods to determine the optimal lithium battery plant located in South America. Mathematics 2022, 10, 2401. [Google Scholar] [CrossRef]
- Seikh, M.R.; Mandal, U. Multiple attribute decision-making based on 3, 4-quasirung fuzzy sets. Granul. Comput. 2022, 7, 965–978. [Google Scholar] [CrossRef]
- Beg, I.; Abbas, M.; Asghar, M.W. Polytopic fuzzy sets and their applications to multiple-attribute decision-making problems. Int. J. Fuzzy Syst. 2022, 24, 2969–2981. [Google Scholar] [CrossRef]
- Das, K.; Kumar, R. A Comprehensive Review of Categorization and Perspectives on State-of-Charge Estimation Using Deep Learning Methods for Electric Transportation. Wirel. Pers. Commun. 2023, 133, 1599–1618. [Google Scholar] [CrossRef]
- Das, K.; Kumar, R. Electric vehicle battery capacity degradation and health estimation using machine-learning techniques: A review. Clean Energy 2023, 7, 1268–1281. [Google Scholar] [CrossRef]
- Das, K.; Kumar, R. Assessment of Electric Two-Wheeler Ecosystem Using Novel Pareto Optimality and TOPSIS Methods for an Ideal Design Solution. World Electr. Veh. J. 2023, 14, 215. [Google Scholar] [CrossRef]

| Technical and Operational Characteristics of the Sections | Measurement Sample Size (No. of Measurements) | AM of Headways by Measuring Segments of Sections | ||||||||
| Section Symbol | Measuring-Segment Length | Road Gradient | Section Length (km) | Th [s] (PC-PC) | Th [s] (LDV-PC) | Th [s] (HDV-PC) | Th [s] (BUS-PC) | Th [s] (AT-PC) | ||
| DMU1 | M-I-108 | min 1000 m | −5.50% | 14.967 | 1000 | 5.349 | 7.714 | 7.577 | 8.633 | 10.136 |
| DMU2 | M-I-103 | min 1000 m | −5.00% | 14.073 | 1000 | 19.269 | 25.272 | 40.269 | 29.491 | 44.767 |
| DMU3 | M-I-108 | min 1000 m | −3.00% | 14.967 | 1000 | 5.331 | 9.406 | 9.107 | 4.979 | 7.934 |
| DMU4 | M-I-108 | min 1000 m | 1.50% | 14.967 | 1000 | 12.553 | 21.713 | 19.393 | 23.681 | 12.926 |
| DMU5 | M-I-103 | min 1000 m | −1.00% | 14.073 | 1010 | 18.174 | 21.102 | 36.395 | 26.04 | 33.222 |
| DMU6 | M-I-105 | min 1000 m | 0% | 7.405 | 1011 | 3.6 | 8.609 | 11.969 | 10.162 | 16.488 |
| DMU7 | M-I-106 | min 1000 m | 1.00% | 38.553 | 912 | 9.794 | 25.096 | 18.537 | 26.949 | 16.669 |
| DMU8 | M-I-108 | min 1000 m | 2.00% | 16.734 | 775 | 24.22 | 65.23 | 66.46 | 64.88 | 97.99 |
| DMU9 | M-I-106 | min 1000 m | 3.00% | 38.553 | 908 | 12.43 | 31.124 | 24.458 | 21.191 | 64.944 |
| DMU10 | M-I-106 | min 1000 m | 4.00% | 38.553 | 1007 | 8.48 | 31.271 | 31.253 | 34.794 | 63.897 |
| DMU11 | M-I-103 | min 1000 m | 5.00% | 14.073 | 918 | 4.79 | 32.367 | 36.991 | 36.362 | 82.858 |
| DMU12 | M-I-108 | min 1000 m | 6.00% | 20.134 | 736 | 12.907 | 82.888 | 126.711 | 118.67 | 189.593 |
| DMU13 | M-I-108 | min 1000 m | 7.00% | 20.134 | 713 | 14.739 | 90.027 | 132.791 | 135.949 | 236.574 |
| DMU14 | M-I-108 | min 1000 m | 7.50% | 20.134 | 811 | 16.559 | 97.84 | 141.196 | 146.706 | 264.434 |
| Criterion | DM1 | DM2 | DM3 | |
| C1 | AADT | (3,4,5) | (4,5,6) | (4,5,6) |
| C2 | Road gradient | (4,5,6) | (4,5,6) | (5,6,7) |
| C3 | Th [s] (PC-PC) | (3,4,5) | (3,4,5) | (3,4,5) |
| C4 | Th [s] (LDV-PC) | (2,3,4) | (3,4,5) | (3,4,5) |
| C5 | Th [s] (HDV-PC) | (2,3,4) | (2,3,4) | (1,2,3) |
| C6 | Th [s] (BUS-PC) | (1,2,3) | (2,3,4) | (0,1,2) |
| C7 | Th [s] (AT-PC) | (0,1,2) | (1,2,3) | (1,2,3) |
| Xj | |
| C7 | [(0.447,0.890),(1.447,1.890),(2.447,2.890)] |
| C6 | [(0.500,1.500),(1.500,2.500),(2.500,3.500)] |
| C5 | [(1.447,1.890),(2.447,2.890),(3.447,3.890)] |
| C4 | [(2.447,2.890),(3.447,3.890),(4.447,4.890)] |
| C3 | [(3.000,3.000),(4.000,4.000),(5.000,5.000)] |
| C1 | [(3.447,3.890),(4.447,4.890),(5.447,5.890)] |
| C2 | [(4.110,4.553),(5.110,5.553),(6.110,6.553)] |
| wj | wj | ||
| C7 | [(0.248,0.296),(0.330,0.387),(0.426,0.492)] | C1 | [(0.006,0.012),(0.023,0.042),(0.073,0.122)] |
| C6 | [(0.134,0.191),(0.221,0.305),(0.342,0.457)] | C2 | [(0.002,0.005),(0.011,0.022),(0.042,0.075)] |
| C5 | [(0.069,0.109),(0.141,0.212),(0.261,0.374)] | C3 | [(0.014,0.026),(0.045,0.076),(0.119,0.187)] |
| C4 | [(0.031,0.055),(0.080,0.131),(0.178,0.272)] | C4 | [(0.031,0.055),(0.080,0.131),(0.178,0.272)] |
| C3 | [(0.014,0.026),(0.045,0.076),(0.119,0.187)] | C5 | [(0.069,0.109),(0.141,0.212),(0.261,0.374)] |
| C1 | [(0.006,0.012),(0.023,0.042),(0.073,0.122)] | C6 | [(0.134,0.191),(0.221,0.305),(0.342,0.457)] |
| C2 | [(0.002,0.005),(0.011,0.022),(0.042,0.075)] | C7 | [(0.248,0.296),(0.330,0.387),(0.426,0.492)] |
| DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | |
| l | m | u | |||||||
| C1 | 5 | 5 | 5 | 7 | 7 | 7 | 9 | 9 | 9 |
| C2 | 7 | 7 | 5 | 7 | 9 | 7 | 9 | 9 | 9 |
| C3 | 5 | 7 | 5 | 7 | 9 | 7 | 9 | 9 | 9 |
| C4 | 7 | 7 | 7 | 9 | 9 | 9 | 9 | 9 | 9 |
| C5 | 7 | 9 | 7 | 9 | 9 | 9 | 9 | 9 | 9 |
| C6 | 7 | 7 | 7 | 7 | 7 | 7 | 9 | 7 | 7 |
| C7 | 7 | 7 | 7 | 7 | 9 | 7 | 9 | 9 | 9 |
| C1 | C2 | … | C7 | |
| DMU1 | [(5.00,5.00),(7.00,7.00),(9.00,9.00)] | [(5.89,6.78),(7.22,8.11),(9.00,9.00)] | … | [(7.00,7.00),(7.22,8.11),(9.00,9.00)] |
| DMU3 | [(5.00,5.00),(7.00,7.00),(9.00,9.00)] | [(5.00,5.00),(7.00,7.00),(7.22,8.11)] | … | [(7.00,7.00),(9.00,9.00),(9.00,9.00)] |
| DMU4 | [(5.00,5.00),(7.00,7.00),(9.00,9.00)] | [(5.00,5.00),(7.00,7.00),(7.00,7.00)] | … | [(7.00,7.00),(7.00,7.00),(7.22,8.11)] |
| DMU6 | [(7.22,8.11),(9.00,9.00),(9.00,9.00)] | [(3.00,3.00),(3.89,4.78),(7.00,7.00)] | … | [(5.00,5.00),(7.00,7.00),(7.00,7.00)] |
| DMU9 | [(3.00,3.00),(3.89,4.78),(5.89,6.78)] | [(5.22,6.11),(7.00,7.00),(9.00,9.00)] | … | [(3.00,3.00),(5.00,5.00),(5.00,5.00)] |
| DMU10 | [(3.00,3.00),(5.00,5.00),(7.00,7.00)] | [(7.00,7.00),(7.00,7.00),(9.00,9.00)] | … | [(3.00,3.00),(3.00,3.00),(5.00,5.00)] |
| DMU11 | [(5.00,5.00),(7.00,7.00),(9.00,9.00)] | [(5.89,6.78),(7.22,8.11),(9.00,9.00)] | … | [(7.00,7.00),(7.22,8.11),(9.00,9.00)] |
| Max | [(7.22,8.11),(9.00,9.00),(9.00,9.00)] | [(7.00,7.00),(7.22,8.11),(9.00,9.00)] | … | [(7.00,7.00),(9.00,9.00),(9.00,9.00)] |
| C1 | C2 | … | C7 | |
| DMU1 | [(0.56,0.56),(0.78,0.78),(1.11,1.25)] | [(0.65,0.75),(0.89,1.12),(1.29,1.29)] | … | [(0.78,0.78),(0.80,0.90),(1.29,1.29)] |
| DMU3 | [(0.56,0.56),(0.78,0.78),(1.11,1.25)] | [(0.56,0.56),(0.86,0.97),(1.03,1.16)] | … | [(0.78,0.78),(1.00,1.00),(1.29,1.29)] |
| DMU4 | [(0.56,0.56),(0.78,0.78),(1.11,1.25)] | [(0.56,0.56),(0.86,0.97),(1.00,1.00)] | … | [(0.78,0.78),(0.78,0.78),(1.03,1.16)] |
| DMU6 | [(0.80,0.90),(1.00,1.00),(1.11,1.25)] | [(0.33,0.33),(0.48,0.66),(1.00,1.00)] | … | [(0.56,0.56),(0.78,0.78),(1.00,1.00)] |
| DMU9 | [(0.33,0.33),(0.43,0.53),(0.73,0.94)] | [(0.58,0.68),(0.86,0.97),(1.29,1.29)] | … | [(0.33,0.33),(0.56,0.56),(0.71,0.71)] |
| DMU10 | [(0.33,0.33),(0.56,0.56),(0.86,0.97)] | [(0.78,0.78),(0.86,0.97),(1.29,1.29)] | … | [(0.33,0.33),(0.33,0.33),(0.71,0.71)] |
| DMU11 | [(0.56,0.56),(0.78,0.78),(1.11,1.25)] | [(0.65,0.75),(0.89,1.12),(1.29,1.29)] | … | [(0.78,0.78),(0.80,0.90),(1.29,1.29)] |
| Rank | ||||
| DMU1 | [(0.39,0.548),(0.728,1.097),(1.707,2.468)] | [(0.743,0.864),(0.962,0.994),(1.013,1.057)] | 1.05 | 1 |
| DMU3 | [(0.384,0.529),(0.768,1.14),(1.733,2.438)] | [(0.706,0.822),(0.951,0.985),(1.01,1.069)] | 1.04 | 2 |
| DMU4 | [(0.297,0.401),(0.52,0.794),(1.295,1.893)] | [(0.538,0.717),(0.874,0.949),(0.992,0.976)] | 0.85 | 4 |
| DMU6 | [(0.292,0.406),(0.682,1.004),(1.563,2.233)] | [(0.664,0.791),(0.935,0.981),(1.009,1.006)] | 0.96 | 3 |
| DMU9 | [(0.163,0.228),(0.462,0.677),(1.093,1.58)] | [(0.395,0.607),(0.843,0.928),(0.984,0.918)] | 0.74 | 5 |
| DMU10 | [(0.122,0.174),(0.279,0.443),(1.014,1.501)] | [(0.333,0.542),(0.789,0.894),(0.979,0.917)] | 0.67 | 6 |
| DMU11 | [(0.07,0.124),(0.324,0.517),(0.902,1.309)] | [(0.314,0.529),(0.819,0.912),(0.976,0.86)] | 0.64 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andjelković, D.; Stojić, G.; Nikolić, N.; Das, D.K.; Subotić, M.; Stević, Ž. A Novel Data-Envelopment Analysis Interval-Valued Fuzzy-Rough-Number Multi-Criteria Decision-Making (DEA-IFRN MCDM) Model for Determining the Efficiency of Road Sections Based on Headway Analysis. Mathematics 2024, 12, 976. https://doi.org/10.3390/math12070976
Andjelković D, Stojić G, Nikolić N, Das DK, Subotić M, Stević Ž. A Novel Data-Envelopment Analysis Interval-Valued Fuzzy-Rough-Number Multi-Criteria Decision-Making (DEA-IFRN MCDM) Model for Determining the Efficiency of Road Sections Based on Headway Analysis. Mathematics. 2024; 12(7):976. https://doi.org/10.3390/math12070976
Chicago/Turabian StyleAndjelković, Dejan, Gordan Stojić, Nikola Nikolić, Dillip Kumar Das, Marko Subotić, and Željko Stević. 2024. "A Novel Data-Envelopment Analysis Interval-Valued Fuzzy-Rough-Number Multi-Criteria Decision-Making (DEA-IFRN MCDM) Model for Determining the Efficiency of Road Sections Based on Headway Analysis" Mathematics 12, no. 7: 976. https://doi.org/10.3390/math12070976
APA StyleAndjelković, D., Stojić, G., Nikolić, N., Das, D. K., Subotić, M., & Stević, Ž. (2024). A Novel Data-Envelopment Analysis Interval-Valued Fuzzy-Rough-Number Multi-Criteria Decision-Making (DEA-IFRN MCDM) Model for Determining the Efficiency of Road Sections Based on Headway Analysis. Mathematics, 12(7), 976. https://doi.org/10.3390/math12070976








