Integrated the Artificial Potential Field with the Leader–Follower Approach for Unmanned Aerial Vehicles Cooperative Obstacle Avoidance
Abstract
1. Introduction
- (1)
- The combination of graph theory and APF methods demonstrates robust adaptability to environmental challenges.
- (2)
- Innovatively applying the Leader–Follower method overcomes the limitation of unreachable targets in the APF.
- (3)
- By employing rotational force, the issue of APFs easily falling into local minima is addressed.
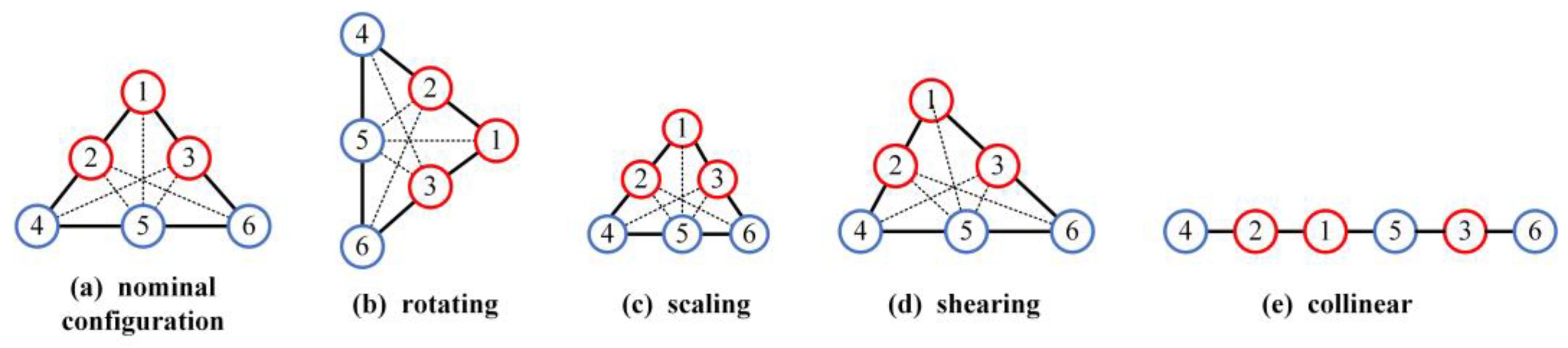
2. Graph Theory-Based Cooperative Formation Control
3. Design Improvement of the APF Method
3.1. Designing an Improved APF Method
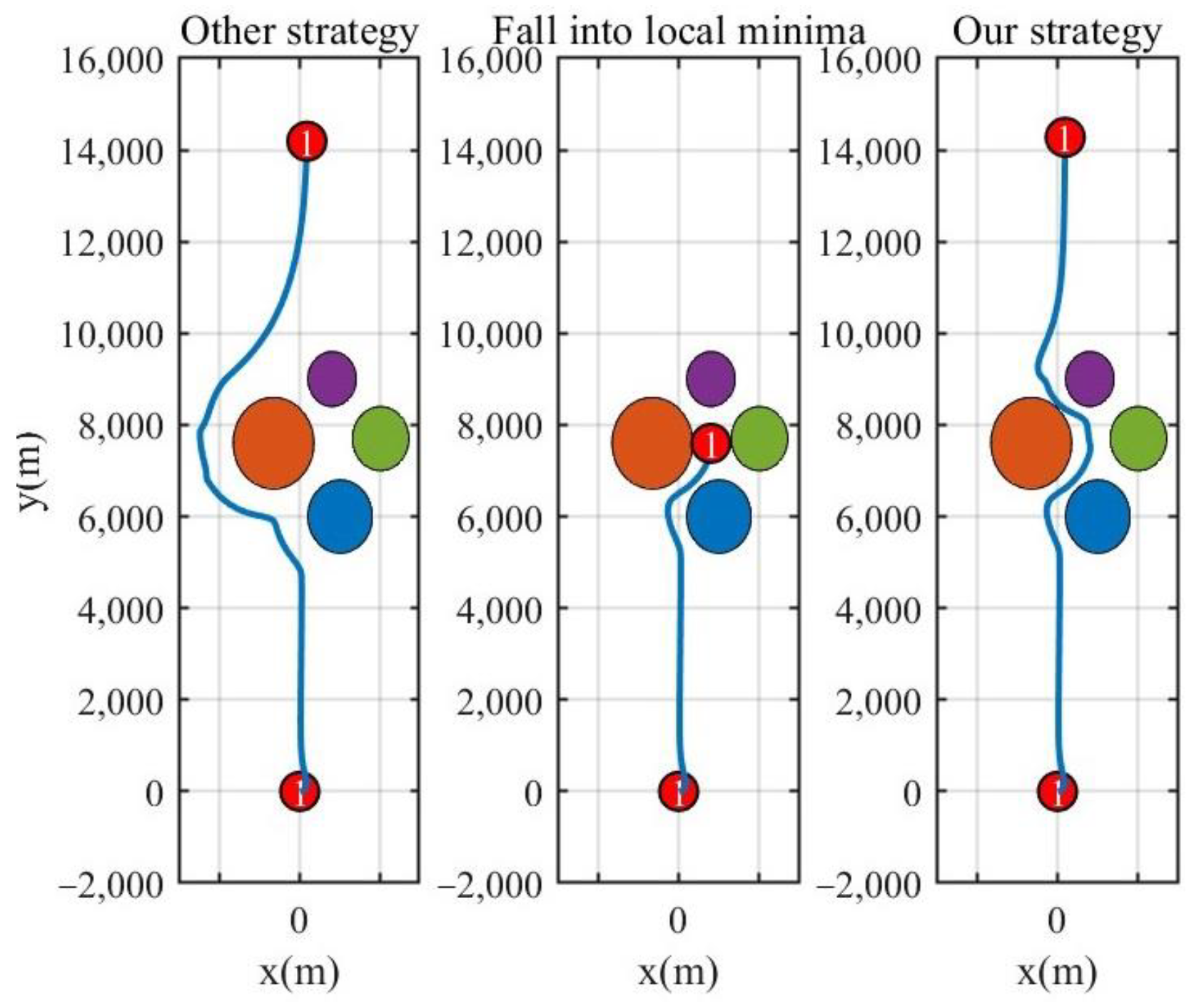
3.2. Addressing the Issue of Local Extrema in the APF Method
4. Control of UAV Swarm Formation Based on the Improved APF Method
- Initialization Phase: Initialization of the number and spacing of UAVs in the formation, positions of obstacles, and the range of repulsive forces; computation of the adjacency matrix and stress matrix for configuration topology; initialization of the parameters for the enhanced APF and consistency algorithm.
- Generate Interaction Force: Calculate the control forces needed to maintain the formation configuration among UAVs based on the formation structure, stress matrix, and the positions and velocities of neighboring UAVs.
- Computation and Detection: Compute the distances between each UAV and various obstacles and determine whether obstacle avoidance is necessary. Calculate the repulsive forces acting on each UAV based on the designed potential field.
- Force Summation: Following steps 2 and 3, obtain the resultant force acting on the UAV and assess whether the UAV is trapped in a local extremum. If so, introduce rotational force and update the net external force.
- Update States: Update the time, and according to the swarm model, calculate the positions, velocities, and accelerations of each UAV for the next time step.
- Evaluation Outcomes: Check whether the UAVs have reached the target point. If they have, the formation task concludes. If not, return to step 2.
5. Stability Verification of the UAV Swarm System
6. Simulation Analysis of Drone Swarm on Multiple Platforms
6.1. MATLAB Simulation
6.1.1. Formation Control Simulation Analysis
6.1.2. Local Extremum Issues in APF
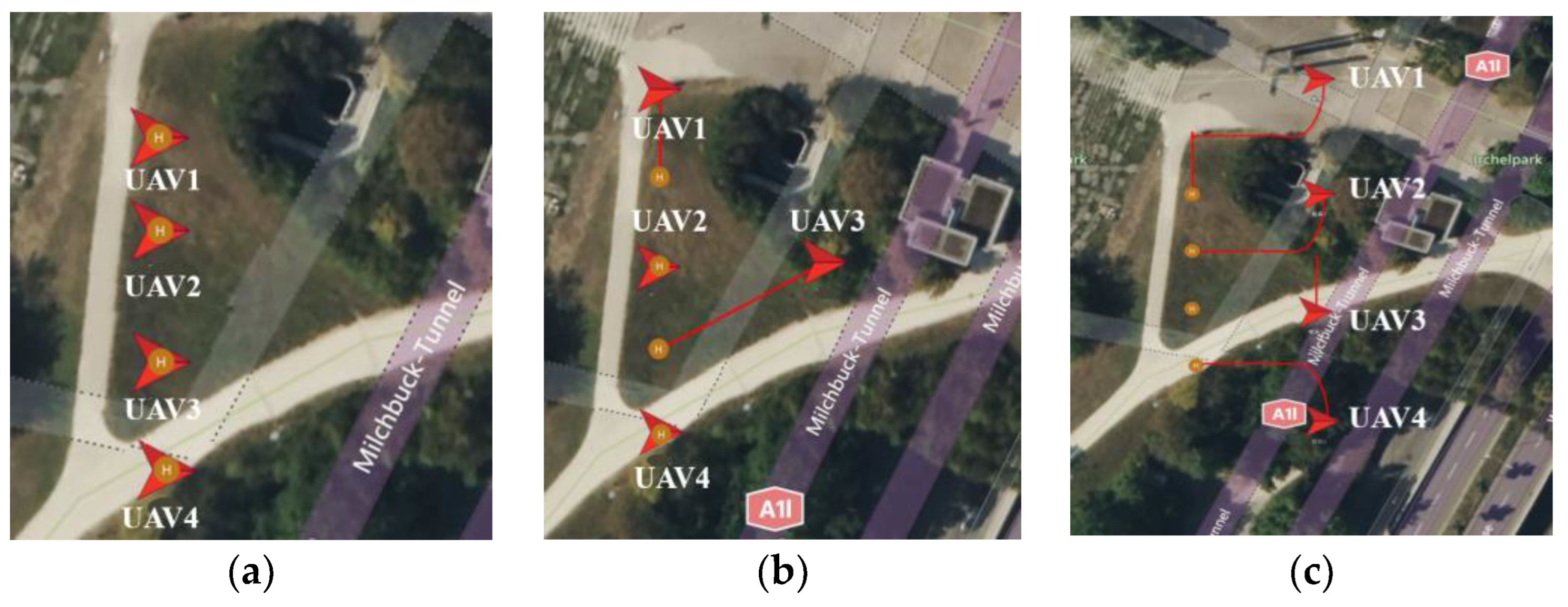
6.2. The Simulation on the ROS
Formation and Reconstruction of UAV Swarm
6.3. Formation Transformation of Quadcopter UAV Swarm
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, J.; Sun, X.; He, L. Time-Varying Formation Tracking for Multiple UAVs with Nonholonomic Constraints and Input Quantization via Adaptive Backstepping Control. Int. J. Aeronaut. Space Sci. 2019, 20, 710–721. [Google Scholar] [CrossRef]
- Wang, J.; Leone, R.D.; Fu, S.; Xia, J.; Qiao, L. Event-Triggered Control Design for Networked Evolutionary Games with Time-Invariant Delay in Strategies. Int. J. Syst. Sci. 2021, 52, 493–504. [Google Scholar] [CrossRef]
- Chen, J.; Tan, C.; Mo, R.; Zhang, H.; Cai, G.; Li, H. Research on path planning of three-neighbor search A* algorithm combined with artificial potential field. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211026449. [Google Scholar] [CrossRef]
- Wang, J.; Gu, W.; Dou, L. Leader-Follower Formation Control for Multiple UAVs with Trajectory Tracking Design. Acta Aeronaut. Astronaut. Sin. 2020, 41, 88–98. [Google Scholar]
- Lee, G.; Chwa, D. Decentralized Behavior-based Formation Control of Multiple Robots Considering Obstacle Avoidance. Intell. Serv. Robot. 2018, 11, 127–138. [Google Scholar] [CrossRef]
- Zhen, Q.; Wan, L.; Li, Y. Formation Control of a Multi-AUVs System Based on Virtual Structure and Artificial Potential Field on SE(3). Ocean Eng. 2022, 253, 111148.1–111148.12. [Google Scholar] [CrossRef]
- Pan, W.; Jiang, D.; Pang, Y.; Li, Y. A Multi-AUV Formation Algorithm Combining Artificial Potential Field and Virtual Structure. Acta Armamentarii 2017, 38, 326–334. [Google Scholar]
- Li, J.; Ji, L.; Li, H. Optimal Consensus Control for Unknown Second-Order Multi-Agent Systems: Using Model-Free Rein-forcement Learning Method. Appl. Math. Comput. 2021, 410, 126451. [Google Scholar] [CrossRef]
- Wang, C.; Liu, C.L.; Liu, S. Robust Fixed-Time Connectivity-Preserving Consensus for Second-Order Multi-Agent Systems with External Disturbances. IET Control Theory Appl. 2020, 14, 2674–2681. [Google Scholar] [CrossRef]
- Li, W.; Sun, J.; Chen, W. Real-Time Obstacle Avoidance Algorithm for Robots Based on BP Neural Network. Chin. J. Sci. Instrum. 2019, 40, 204–211. [Google Scholar]
- Surname, G.N.; Huang, J.; Wu, S.; Fan, R. Obstacle Avoidance Algorithm of Simulation Robotic Fish Based on Ant Colony Algorithm. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3461–3464. [Google Scholar]
- Ning, W.; Dai, J.; Jin, Y.; Li, Y.; Lu, L. Multi-UAV Trajectory Planning Simulation Based on Adaptive Extended Potential Field. J. Syst. Simul. 2021, 33, 2147–2156. [Google Scholar]
- Zhao, R.; Lee, H.K. Fuzzy-Based Path Planning for Multiple Mobile Robots in Unknown Dynamic Environment. J. Electr. Eng. Technol. 2017, 12, 918–925. [Google Scholar] [CrossRef]
- Xia, Q.S.; Tang, Q.H.; Zhang, L.P. Cooperative Path Planning and Operation Collision Avoidance for Multiple Storage Robots. Inf. Control 2019, 48, 22–28+34. [Google Scholar]
- Wang, Z.; Li, M.; Dou, L.; Li, Y.; Zhao, Q.; Li, J. A Novel Multi-objective Artificial Bee Colony Algorithm for Multi-robot Path Planning. In Proceedings of the IEEE International Conference on Information & Automation, Lijiang, China, 8–10 August 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Matoui, F.; Boussaid, B.; Metoui, B.; Abdelkrim, M.N. Contribution to the Path Planning of a Multi-Robot System: Centralized Architecture. Intell. Serv. Robot. 2020, 13, 147–158. [Google Scholar] [CrossRef]
- Trujillo, J.-C.; Munguia, R.; Guerra, E.; Grau, A. Cooperative Monocular-Based SLAM for Multi-UAV Systems in GPS-Denied Environments. Sensors 2018, 18, 1351. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Mou, J.; Chen, P.; Li, M. Path Planning for Autonomous Ships: A Hybrid Approach Based on Improved APF and Modified VO Methods. J. Mar. Sci. Eng. 2021, 9, 761. [Google Scholar] [CrossRef]
- Wang, J.; Ding, X.; Wang, C.; Liang, L.; Hu, H. Affine Formation Control for Multi-Agent Systems with Prescribed Convergence Time. J. Frankl. Inst. 2021, 358, 7055–7072. [Google Scholar] [CrossRef]
- Cao, Y.; Sun, Y. Necessary and Sufficient Conditions for Consensus of Third-Order Discrete-Time Multi-Agent Systems in Directed Networks. J. Appl. Math. Comput. 2018, 57, 199–210. [Google Scholar] [CrossRef]
- Ma, X.; Mei, H. Mobile Robot Global Path Planning Based on Improved Ant Colony System Algorithm with Potential Field. J. Mech. Eng. 2021, 57, 19–27. [Google Scholar]
- Zhang, J.; Yan, J.; Zhang, P. Fixed-Wing UAV Formation Control Design with Collision Avoidance Based on an Improved Artificial Potential Field. IEEE Access 2018, 6, 78342–78351. [Google Scholar] [CrossRef]
- Qi, B. Research on UAV Formation Control Technology. Master’s Thesis, Changchun University of Science and Technology, Changchun, China, 2022. [Google Scholar]
- Zhang, Q.; Chen, B.; Liu, X.; Liu, X.; Yang, H. Ant Colony Optimization with Improved Potential Field Heuristic for Robot Path Planning. Trans. Chin. Soc. Agric. Mach. 2019, 50, 23–32. [Google Scholar]
- Chen, X.; Liu, K.W.; Mao, H.L. Trajectory Planning of Unmanned Aerial Vehicles Based on APF-RRT Algorithm. Electron. Opt. Control 2022, 5, 17–22. [Google Scholar]
- Han, L.; Dong, X.; Li, Q.; Ren, Z. Formation-containment Control for Second-order Multi-agent Systems with Time-varying Delays. Neurocomputing 2016, 218, 439–447. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, D.; You, Y.; Duan, H. Affine Transformation Based Formation Maneuvering for Discrete-Time Directed Networked Systems. Sci. China Technol. Sci. 2020, 63, 73–85. [Google Scholar] [CrossRef]
- Zhao, S. Affine Formation Maneuver Control of Multiagent Systems. IEEE Trans. Autom. Control 2018, 63, 4140–4155. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, M.; Chen, J.; Chen, C.; Yu, H.; Zhang, Y.; Deng, X. Time-Varying Topology Formation Reconfiguration Control of the Multi-Agent System Based on the Improved Hungarian Algorithm. Appl. Sci. 2023, 13, 11581. [Google Scholar] [CrossRef]
- Tan, W.; Huang, N.; Huang, C.; Yu, C.; Zhong, C. Fixed-Time Rigidity-Based 3-D Formation Maneuvering Control with Distributed Finite-Time Velocity Estimators. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3237–3242. [Google Scholar]
- Yang, Q.; Sun, Z.; Cao, M.; Fang, H.; Chen, J. Construction of Universally Rigid Tensegrity Frameworks and Their Applications in Formation Scaling Control. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 8177–8182. [Google Scholar]
- Gortler, S.J.; Thurston, D.P. Characterizing the Universal Rigidity of Generic Frameworks. Discret. Comput. Geom. 2014, 51, 1017–1036. [Google Scholar] [CrossRef]
- Wu, G.; Hammers, J. Leader-Following Consensus of Nonlinear Discrete-Time Multi-Agent Systems with Limited Bandwidth and Switching Topologies. Am. J. Clin. Pathol. 2019, 152, S76. [Google Scholar] [CrossRef]
- Yang, Q.; Cao, M.; Fang, H.; Chen, J. Constructing Universally Rigid Tensegrity Frameworks with Application in Multiagent Formation Control. IEEE Trans. Autom. Control 2019, 64, 381–388. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, M.; Chen, J.; Chen, C.; Yu, H. Time-Varying Target Formation Control for Multi-agent Systems Based on Stress-Matrix. In Advances in Mechanism, Machine Science and Engineering in China; Lecture Notes in Mechanical Engineering; Liu, X., Ed.; Springer: Singapore, 2023. [Google Scholar]
- Lyu, H.; Yin, Y. COLREGS-Constrained Real-Time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2019, 72, 588–608. [Google Scholar] [CrossRef]
- Xiong, J.Q. Research on Consensus of Multi-UAV Route Planning Based on Artificial Potential Field. Ph.D. Thesis, Nanchang Hangkong University, Nanchang, China, 2017. [Google Scholar]
- Zhao, H.B. Research on Key Problems of Multi-Agent Motion Formation Control. Master’s Thesis, Inner Mongolia University of Science and Technology, Mongolia, China, 2019. [Google Scholar]
- Jia, T.X. Research on Agent Path Planning and Formation Control. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2021. [Google Scholar]
- Zhang, L.T. On Cooperative Control Algorithm of Heterogeneous Multi-Vehicle System. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2022. [Google Scholar]
- Sun, Y.; Zhou, J.; Wei, Y.; Fan, Z. Dynamic Flight Trajectory Planning of Distribution UAV Cluster Based on Artificial Potential Field. J. Mil. Transp. Univ. 2022, 6, 80–85. [Google Scholar]
- Zhang, Y.C.; Jiang, Y.; Dai, J.Y. Dynamic Obstacle Avoidance Control of Three-order Multi-robot Cooperative Formation. J. Syst. Simul. 2022, 34, 1762–1774. [Google Scholar]
- Yamakou, M.E. Chaotic Synchronization of Memristive Neurons: Lyapunov Function Versus Hamilton Function. Nonlinear Dyn. 2020, 101, 487–500. [Google Scholar] [CrossRef]
- Han, Z.; Wang, L.; Lin, Z.; Zheng, R. Formation Control with Size Scaling Via a Complex Laplacian-Based Approach. IEEE Trans. Cybern. 2016, 46, 2348–2359. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P. Design of UAV Formation and Obstacle Avoidance Control System Based on Virtual Leader. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2021. [Google Scholar]














| j\i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | −0.3992 | 0.3922 | 0.3922 | 0 | −0.3922 | 0 |
| 2 | 0.3922 | −0.7845 | 0 | 0.1961 | 0.3922 | −0.1961 |
| 3 | 0.3922 | 0 | −0.7845 | −0.1961 | 0.3922 | 0.1961 |
| 4 | 0 | 0.1961 | −0.1961 | −0.1961 | 0.1961 | 0 |
| 5 | −0.3922 | 0.3922 | 0.3922 | 0.1961 | −0.7845 | 0.1961 |
| 6 | 0 | −0.1961 | 0.1961 | 0 | 0.1961 | −0.1961 |
| Drone Number | Drone Role | Initial Position |
|---|---|---|
| 1 | Leader | (200, 0) |
| 2 | Leader | (−900, −200) |
| 3 | Leader | (200, −500) |
| 4 | Follower | (−100, −1500) |
| 5 | Follower | (800, −1250) |
| 6 | Follower | (1000, −750) |
| Obstacle Number | Position Coordinate | |
|---|---|---|
| 1 | (700, 2000) | 300 m |
| 2 | (−250, 3600) | 250 m |
| 3 | (650, 5200) | 250 m |
| Parameter | Value |
|---|---|
| 0.5 | |
| 2 | |
| (Speed of a leader) | |
| (Minimum speed of the follower) | |
| (The maximum speed of the follower) | |
| 30 | |
| 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chen, J.; Chen, M.; Chen, C.; Zhang, Z.; Deng, X. Integrated the Artificial Potential Field with the Leader–Follower Approach for Unmanned Aerial Vehicles Cooperative Obstacle Avoidance. Mathematics 2024, 12, 954. https://doi.org/10.3390/math12070954
Zhang Y, Chen J, Chen M, Chen C, Zhang Z, Deng X. Integrated the Artificial Potential Field with the Leader–Follower Approach for Unmanned Aerial Vehicles Cooperative Obstacle Avoidance. Mathematics. 2024; 12(7):954. https://doi.org/10.3390/math12070954
Chicago/Turabian StyleZhang, Yingxue, Jinbao Chen, Meng Chen, Chuanzhi Chen, Zeyu Zhang, and Xiaokang Deng. 2024. "Integrated the Artificial Potential Field with the Leader–Follower Approach for Unmanned Aerial Vehicles Cooperative Obstacle Avoidance" Mathematics 12, no. 7: 954. https://doi.org/10.3390/math12070954
APA StyleZhang, Y., Chen, J., Chen, M., Chen, C., Zhang, Z., & Deng, X. (2024). Integrated the Artificial Potential Field with the Leader–Follower Approach for Unmanned Aerial Vehicles Cooperative Obstacle Avoidance. Mathematics, 12(7), 954. https://doi.org/10.3390/math12070954





