Robust Control for Underactuated Fixed-Wing Unmanned Aerial Vehicles

Abstract

Dynamic surface control (DSC) is a recognized nonlinear control approach for high-order systems. However, as the complexity of the system increases and the first-order filter (FOF) is introduced, there exists a singularity problem, i.e., the control input will reach infinity. This limits the application of the DSC algorithm to a class of real-world systems with complex dynamics. To address the problem of singularity, we present a novel DSC approach called nonsingular dynamic surface control (NDSC), which completely avoids the singularity problem and significantly improves the overall control performance. NDSC includes a nonsingular hypersurface, which is constructed by the error between system states and virtual control inputs. Then the nonsingular hypersurface will be applied to derive the corresponding control law with the aid of the DSC approach to ensure the output of the system can track arbitrary desired trajectories. NDSC has the following novel features: (1) finite time asymptotic stabilization can be guaranteed; (2) the performance of NDSC is insensitive to the FOF’s parameter variation once the maximum tracking error of FOF is bounded, which significantly reduces reliance on the control sampling frequency. We thoroughly evaluate the proposed NDSC algorithm in an unmanned aerial vehicle (UAV) system with an underactuated nature. Finally, the simulation results illustrate and highlight the effectiveness and superiority of the proposed control algorithm.

1. Introduction

To date, backstepping control (BSC) is a well-known powerful tool for high-order systems with essential nonlinearity [1,2]. The key idea behind BSC is decomposing the complex high-order system into subsystems whose order is lower than that of the origin system. And then for each subsystem, a virtual control law is defined based on the Lyapunov method. However, performing the above approach under a nonlinear unmanned aerial vehicle (UAV) system with under-actuated characteristics commonly poses the following challenge problems: (1) the ”explosion of complexity” phenomenon arising due to the repeated derivations of virtual control law; (2) the smoothness requirement of UAV dynamic functions and the reference signal. To deal with the problems above, dynamic surface control (DSC) is developed by introducing a first-order filter (FOF) in each subsystem to track virtual control law and automatically obtain their derivatives, so that the derivation of virtual control law will be unnecessary [3,4].

DSC avoids the “explosion of complexity” phenomenon and relaxes the smoothness requirement on dynamic functions and reference signals. The effectiveness of DSC has been increasingly demonstrated in various challenging applications, such as spacecraft control [5], aircraft landing control [6], aircraft overspeed maneuver control [7], quadrotor attitude control [8,9,10], morphing aircraft control [11], and containment control of multiple quadrotors [12,13,14]. However, the DSC controller has a singular issue, that is because, due to the presence of an FOF tracking error, DSC loses its asymptotic stabilization property, i.e., the state error can only converge to a bounded interval near the origin, thus resulting in low robustness and high sensitivity to the system parameter variations. Swaroop has proved that the state error can only be made infinitesimal by employing a high gain and a sufficiently small time constant of the filter [3]. Furthermore, Pan Yongping proved that a sufficiently small time constant (without the need for a high gain) ensures semi-global exponential stabilization of the system using the singular ingress theory [4]. In practical application, the time constant of FOF cannot be infinitely small, it is limited by the sampling time of the system [15]. Additionally, manual tuning is hard and the standards are obscure. To improve the performance of DSC, in addition to adjusting the time constant, Bu Xiangwei et al. replaced FOF with the tracking differentiator (TD) [16]. Equivalently, Shao Xingling et al. used a sigmoid TD to estimate the virtual control law and its derivatives [17]. However, despite its empirical success, there is no theoretical understanding of its convergence and no theoretical guideline for key parameter tunning, especially the time constant τ.

In this paper, we present a novel nonsingular dynamic surface control (NDSC) algorithm, which has the following three properties:

(1)

Firstly, the proposed NDSC overcomes the singularity problem by employing a nonsingular hypersurface to replace the original linear error term. Then, finite time convergence theory is adopted to derive the control law, ensuring the system state converges to the origin in finite time.

(2)

When the FOF tracking error is limited, we prove the global stability of the proposed NDSC method. Based on such analysis, we find NDSC is insensitive to the variation in the time constant τ. This enables a great deal of flexibility in choosing parameters.

(3)

We thoroughly evaluate the proposed NDSC method in an underactuated UAV control task. In particular, the NDSC has been shown to be superior to the standard DSC approach in terms of convergence rate, robustness, and trajectory tracking accuracy.

2. Problem Statement

2.1. UAV Dynamics

We aim to improve the robustness and trajectory tracking accuracy of the UAV through the NDSC method. The UAV is modeled as a 6-degree-of-freedom (DOF) rigid body in two frames: the inertial frame I and the body frame B, which are denoted by superscripts n and b, respectively. The dynamic of the UAV is given by [18]:

$$\begin{array}{l}{\dot{p}}^n=R_b^n{v}^b\\ {\dot{v}}^b=\frac{1}{m}{F}^b-{\rm Y}\left(w^b\right)v^b+\frac{1}{m}{u}_1\\ J{\dot{w}}^b=M^b-{\rm Y}\left(w^b\right)J{w}^b+A{u}_2\\ {\dot{q}}_{nb}=\Gamma \left(q_{nb}\right)\left[\begin{array}{c}0\\ w^b\end{array}\right],\end{array}$$

(1)

where $p^n\in {ℝ}^3$ is the position of UAV in I, $v^b\in {ℝ}^3$ is the velocity in B, $R_b^n\in {ℝ}^{3\times 3}$ is the rotation matrix from B to I, $w^b\in {ℝ}^3$ is the angular velocity in B, and $q_{nb}$ is the quaternion denoting the attitude of B with respect to I. $m\in {ℝ}^{+}$ and $J\in {ℝ}^{3\times 3}$ are the mass and the inertia matrix of the UAV, respectively. $F^b$ and $M^b$ are the joint force and joint moment of gravity and aerodynamic forces depicted in B. Symbolic ${\rm Y}(\cdot )$ denotes the skew-symmetric operator and $\Gamma (\cdot )$ the quadratic multiplication operator. Usually, thrust only contains the component of the x-axis: $u_1:={[T,0,0]}^T$. $u_2:={[{\tau }_1,{\tau }_2,{\tau }_3]}^T$ represents the torques produced by the rudder deflection. The applied thrust $T$ and torques ${\tau }_1,{\tau }_2,{\tau }_3$ will be designed to drive the UAV to realize the trajectory tracking task. However, the underactuated nature of the UAV system (i.e., the number of actuators is less than the degrees of freedom of the UAV system) generally complicates the dynamic of the controlled UAV and exacerbates the difficulty of controller design [19].

2.2. Control Objective

Given a reachable trajectory $p_d={[p_{d,x},p_{d,y},p_{d,z}]}^T$ and its derivation ${\dot{p}}_d={[{\dot{p}}_{d,x},{\dot{p}}_{d,y},{\dot{p}}_{d,z}]}^T$, to realize the trajectory tracking control of an underactuated UAV system, a common practice is to consider the hierarchical strategy [20,21]. Specifically, a nominal command $u_n$ is first derived to track $p_d$ and ${\dot{p}}_d$. In particular, we have:

$$\underset{t\to \infty }{\lim }\left(p^n\left(t\right)-p_d\left(t\right)\right)=0,\underset{t\to \infty }{\lim }\left(v^n\left(t\right)-{\dot{p}}_d\left(t\right)\right)=0$$

(2)

.

The desired thrust T and torque $u_2$ are then extracted from $u_n$ to stabilize the translation and rotation loop of the UAV, respectively. Next, based on the state-of-the-art NDSC approach, we develop an algorithm for calculating online control commands to track the desired trajectory with a fast dynamic response.

3. Nonsingular Dynamic Surface

Considering the general N-th-order time invariant system

$$\left\{\begin{array}{l}{\dot{x}}_i=f_i\left({\xi }_i\right)+x_{i+1}\left(i=1,2,\dots ,N-1\right)\hfill \\ {\dot{x}}_N=f_N\left({\xi }_N\right)+u\hfill \end{array}\right.$$

(3)

where ${\xi }_i:={[x_1,\dots ,x_2]}^T\in {ℝ}^i$ is defined as the state sequence, $f_i({\xi }_i):\in {ℝ}^i\mapsto ℝ$ (i = 1, 2, …, N) can be a generally nonlinear function, and u and $x_1$ are the control input and system output, respectively. The task of NDSC is to design a control input u so that $x_1$ tracks the desired output $x_d$ in finite time.

Review the design of the BSC, where $x_i$ of each subsystem in (3) is considered as a virtue control input ${\Phi }_i(i=1,2,\dots ,N-1)$, which is utilized to ensure a state of $x_i(i=1,2,\dots ,N-1)$ asymptotic stability. Since the solution of the state cannot fully satisfy $x_i={\Phi }_i(i=1,2,\dots ,N-1)$ all the time. Therefore, variable $z_i:=x_i-{\Phi }_i$ is defined to formulate the tracking error for i = 1, 2, …, N − 1. The error system is given by:

$$\left\{\begin{array}{l}{z}_1=x_1-x_d\hfill \\ z_2=x_2-{\Phi }_1\left(x_1\right)\hfill \\ \hspace{1em}\hspace{1em} ⋮\hfill \\ z_N=x_N-{\Phi }_{N-1}\left({\xi }_{N-1}\right)\hfill \end{array}\right.$$

(4)

where ${\Phi }_i(i=1,2,\dots ,N-1)$ can be designed according to:

$$\left\{\begin{array}{l}{\Phi }_1=-k_1{z}_1+{\dot{x}}_d-f_1\left({\xi }_1\right)\\ {\Phi }_i=-k_i{z}_i+{\dot{\widehat{\Phi }}}_{i-1}-f_i\left({\xi }_i\right)-z_{i-1}\hspace{1em}\left(i=2,3,\dots ,N-1\right)\\ u=-k_N{z}_N+{\dot{\widehat{\Phi }}}_{N-1}-f_N\left({\xi }_N\right)-z_{N-1}\end{array}\right.$$

(5)

where $k_i(i=1,2,\dots ,N)$ are control parameters.

Theorem 1. 

For system (3), if u is given by (5), then the closed-loop tracking error dynamics (4) is globally exponentially stable.

In (5), we can observe the repeated derivation of ${\Phi }_i$ for i = 1, …, N can increase the complexity as the system order N increases, which is the well-known “explosion of complexity” phenomenon. This can be overcome by simply introducing a first-order filter (FOF): $\tau {\dot{\widehat{\Phi }}}_i(t)=-{\widehat{\Phi }}_i(t)+{\Phi }_i(t),(i=1,\dots ,N)$, where τ is the time constant, and ${\widehat{\Phi }}_i(0)={\Phi }_i(0)$. Combining, and following the design ideas of DSC, (5) can be redefined as:

$$\left\{\begin{array}{l}{\Phi }_1=-k_1{z}_1+{\dot{x}}_d-f_1\left({\xi }_1\right)\\ {\Phi }_i=-k_i{z}_i+{\dot{\widehat{\Phi }}}_{i-1}-f_i\left({\xi }_i\right)-z_{i-1}\hspace{1em}\left(i=2,3,\dots ,N-1\right)\\ u=-k_N{z}_N+{\dot{\widehat{\Phi }}}_{N-1}-f_N\left({\xi }_N\right)-z_{N-1}\end{array}\right.$$

(6)

Theorem 2. 

For system (3), if u is designed as (6), (4) can be proved to be semi-global uniformly ultimately bounded stability when parameters $k_i\in {ℝ}^{+}$, (i = 1, …, N) are suitably large and $\tau \in {ℝ}^{+}$ is sufficiently small.

As shown in (6), the original differential term of the virtual control in (5) is replaced with the output of the filter. However, the closed-loop stability and tracking performance heavily rely on the selection of $k_i$ (i = 1, …, N) and τ, which usually require significant efforts and expert knowledge to tune. In addition, these conservative stability results of DSC cannot fully meet the requirements of a highly dynamic system. Motivated by these facts, we develop the NDSC method, which can guarantee the error system (4) converges in finite time and eliminates the singular phenomenon that appears in DSC. The following assumption is needed for NDSC synthesis:

Assumption 1. 

The tracking error ${\epsilon }_i:={\Phi }_i-{\widehat{\Phi }}_i$ is bounded for i = 1, …, N, and satisfied:

$$‖{\dot{\epsilon }}_i(t)‖\le \eta (i=1,2,\dots ,N-1)$$

where η > 0 is the bound of tracking error of FOF. For error system (4), a nonsingular hypersurface is first presented as:

$$s=z_N+\gamma {\left({\displaystyle {\int }_0^t{z}_{N}dt}\right)}^{p/q}$$

(7)

where$\gamma \in {ℝ}^{+}$ is a design parameter, and p and q are positive odd numbers and satisfied: 1 < p/q < 2. Let$l_i:=-\gamma {\left({\displaystyle {\int }_0^t{z}_{i}dt}\right)}^{p/q}$. Then the NDSC method is given by:

$$\left\{\begin{array}{l}{\Phi }_1\left({\xi }_1\right)=i_i-f_1\left({\xi }_1\right)+{\dot{x}}_d\\ {\Phi }_i\left({\xi }_i\right)=i_i-f_i\left({\xi }_i\right)+{\dot{\widehat{\Phi }}}_{i-1}\hspace{1em}\left(i=2,3,\dots ,N-1\right)\\ u=i_N-f_N\left({\xi }_N\right)+{\dot{\widehat{\Phi }}}_{N-1}-\left(K+\eta \right)sgn\left(s\right)\end{array}\right.$$

(8)

where $K\in {ℝ}^{+}$ is a design parameter.

Theorem 3. 

For system (3), if the hypersurface is designed as (7), and u is designed as (8), then the output $x_1(t)$ of (3) can track the desired output $x_d(t)$ in finite time.

Proof. 

Define a Lyapunov function candidate:

$$V=\frac{1}{2}{s}^2$$

(9)

Substituting (7) and (8) into the time derivative of (9), one has

$$\begin{array}{cc}\hfill \dot{V}& =s\dot{s}\hfill \\ & =s\left[f_N\left({\xi }_N\right)+u-{\dot{\Phi }}_{N-1}+\frac{p}{q}\gamma {\left({\displaystyle {\int }_0^t{z}_{n}dt}\right)}^{p/q-1}{z}_N\right]\hfill \\ & =s\left[{\widehat{\dot{\Phi }}}_{N-1}-{\dot{\Phi }}_{n-1}-\left(K+\eta \right)\mathrm{sgn}\left(s\right)\right]\hfill \\ & =s\left[{\dot{\epsilon }}_{N-1}-\left(K+\eta \right)\mathrm{sgn}\left(s\right)\right]\hfill \\ & \le \left|s\right|\left[\left|{\dot{\epsilon }}_{N-1}\right|-\left(K+\eta \right)\right]=-K\left|s\right|,\hfill \end{array}$$

(10)

which can be made negative definite for a choice of $K\in {ℝ}^{+}$. Thus s will converge to 0 in finite time, which indicates $z_N$ and ${\displaystyle {\int }_0^t{z}_N}dt$ reach zero in finite time. □

Remark 1. 

As shown in (10), $K\in {ℝ}^{+}$ is chosen to make (10) a negative definite. Since the upper bound $\eta$ on the error of the FOF is known, NDSC does not depend on a sufficiently large value of $K$, and this is where we have an advantage over traditional DSCs.

In addition, the selection of constants $p,q$ has been discussed extensively in reference [22].

Now, we differentiate $z_1$:

$$\begin{array}{cc}\hfill {\dot{z}}_1& ={\dot{x}}_1-{\dot{x}}_d\hfill \\ & =x_2+f_1\left({\xi }_1\right)-{\dot{x}}_d\hfill \\ & =z_2+{\Phi }_1\left({\xi }_1\right)+f_1\left({\xi }_1\right)-{\dot{x}}_d\hfill \\ & =z_2+i_1\hfill \end{array}$$

(11)

Let us integrate both sides of (11); one has

$${\displaystyle {\int }_0^t{z}_{2}dt=z_1-l_1}$$

(12)

Reviewing the definition of $l_1:=-\gamma {\left({\displaystyle {\int }_0^t{z}_{1}dt}\right)}^{p/q}$, one immediately obtains that $l_1$, $z_1\to 0$ in finite time as ${\displaystyle {\int }_0^t{z}_2}dt\to 0$ in finite time.

Furthermore, differentiating $z_2$, one has

$$\begin{array}{cc}\hfill {\dot{z}}_2& ={\dot{x}}_2-{\dot{\Phi }}_1\left({\xi }_1\right)\hfill \\ & =x_3+f_2\left({\xi }_2\right)-{\dot{\Phi }}_1\left({\xi }_1\right)\hfill \\ & =z_3+{\Phi }_2\left({\xi }_2\right)+f_2\left({\xi }_2\right)-{\dot{\Phi }}_1\left({\xi }_1\right)\hfill \end{array}$$

(13)

Defining ${\Phi }_2({\xi }_2)$ as (8) and applying to (13) yields:

$${\dot{z}}_2=z_3+i_2$$

(14)

Integrating both sides of (14), one has

$${\displaystyle {\int }_0^t{z}_{3}dt=z_2-l_2}$$

(15)

which indicates if ${\displaystyle {\int }_0^t{z}_{3}dt\to 0}$ in finite time, then $z_2$ and ${\displaystyle {\int }_0^t{z}_{2}dt}$ converge to zero in finite time.

Repeating this process for the derivation of $z_i$ with (2 < i ≤ N − 2), until the derivation of $z_{N-1}$:

$$\begin{array}{cc}\hfill {\dot{z}}_{N-1}& ={\dot{x}}_{N-1}-{\dot{\Phi }}_{N-2}\left({\xi }_{N-2}\right)\hfill \\ & =x_N+f_{N-1}\left({\xi }_{N-1}\right)-{\dot{\Phi }}_{N-2}\left({\xi }_{N-2}\right)\hfill \\ & =z_N+{\Phi }_{N-1}\left({\xi }_{N-1}\right)+f_{N-1}\left({\xi }_{N-1}\right)-{\dot{\Phi }}_{N-2}\left({\xi }_{N-2}\right)\hfill \end{array}$$

(16)

Constructing ${\Phi }_{N-1}({\xi }_{N-1})$ as (8) and applying to (16):

$$z_{N-1}=z_N+i_{N-1}$$

(17)

Integrating both sides of (17) yields:

$${\displaystyle {\int }_0^t{z}_{N}dt=z_{N-1}-l_{N-1}}$$

(18)

It is known from (10) that ${\displaystyle {\int }_0^t{z}_{N}dt\to 0}$ in finite time; thus, ${\displaystyle {\int }_0^t{z}_{N-1}dt}$ and $z_{N-1}$ can reach zero in finite time. Consequently, it can be inductively shown that $z_i$ with i = 1, …, N − 1 reach zero in finite time. Therefore, the output $x_1$ of (3) can track the desired output $x_d$ in finite time. This completes the proof for Theorem 3.

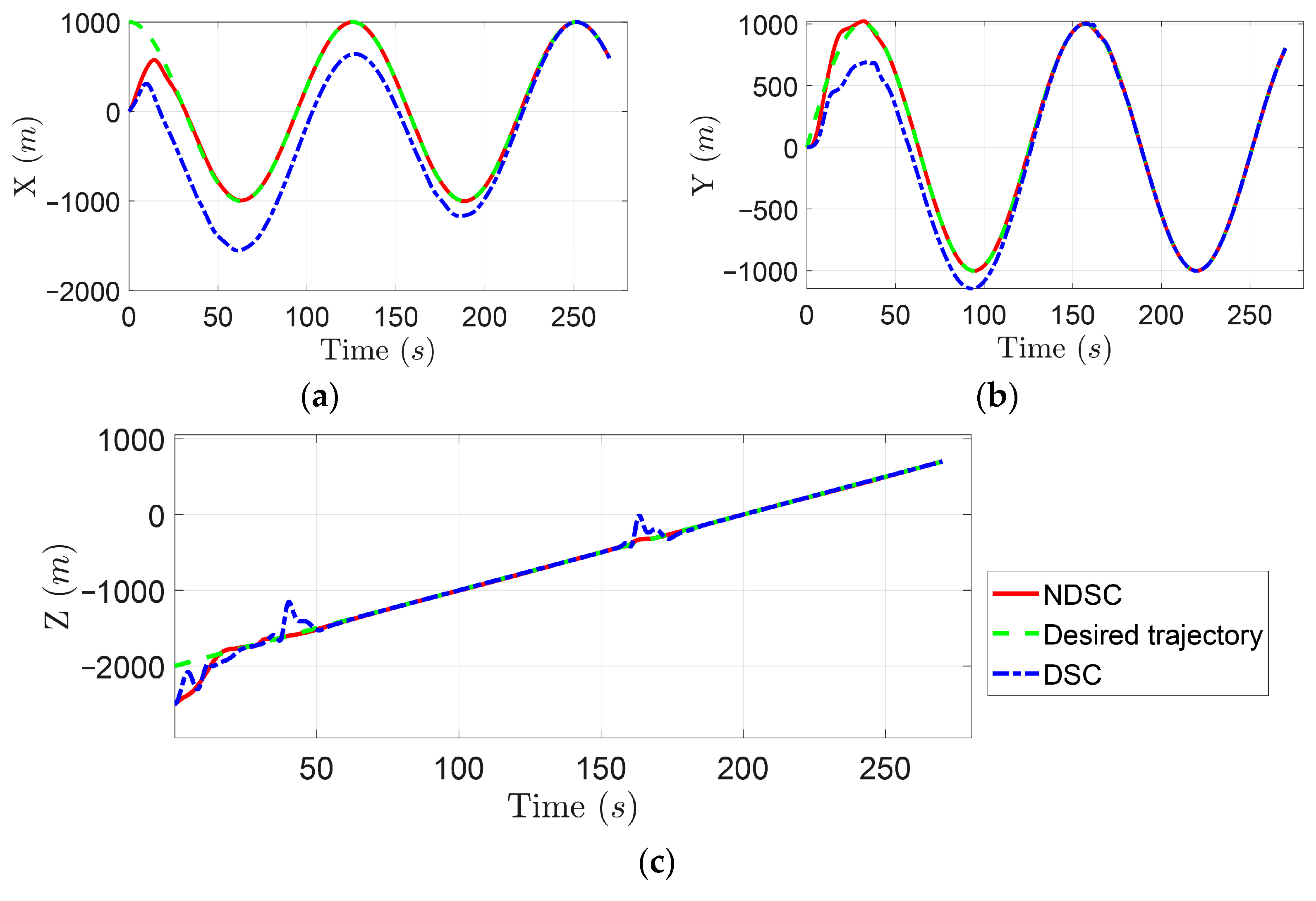
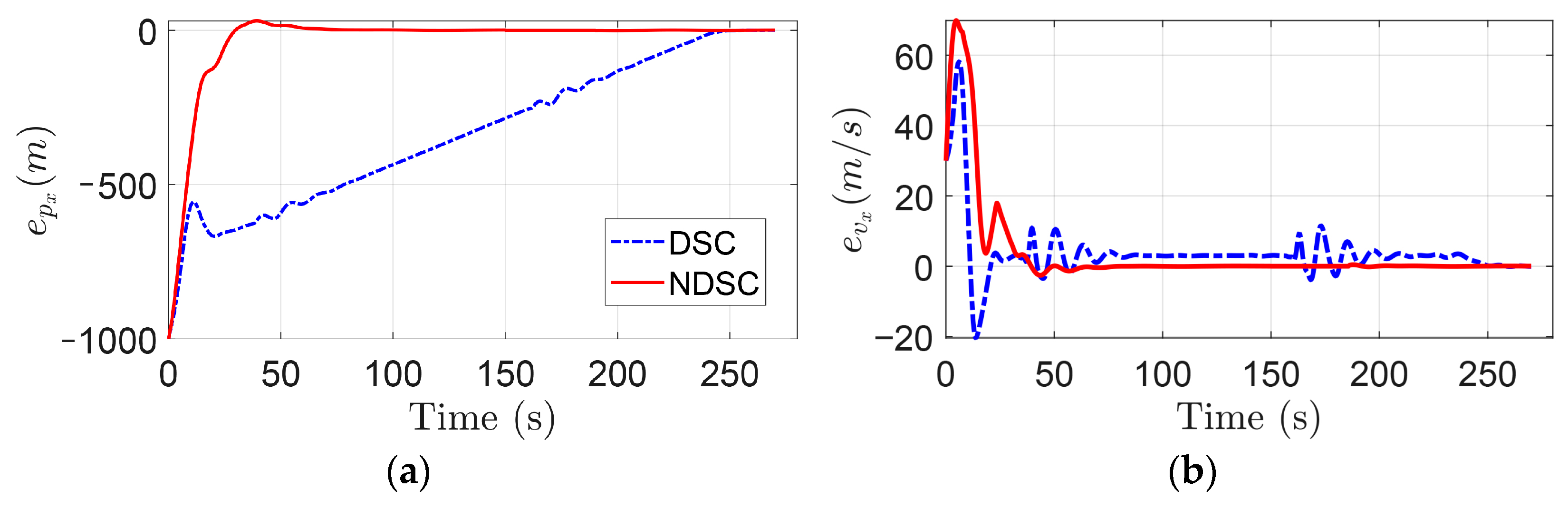
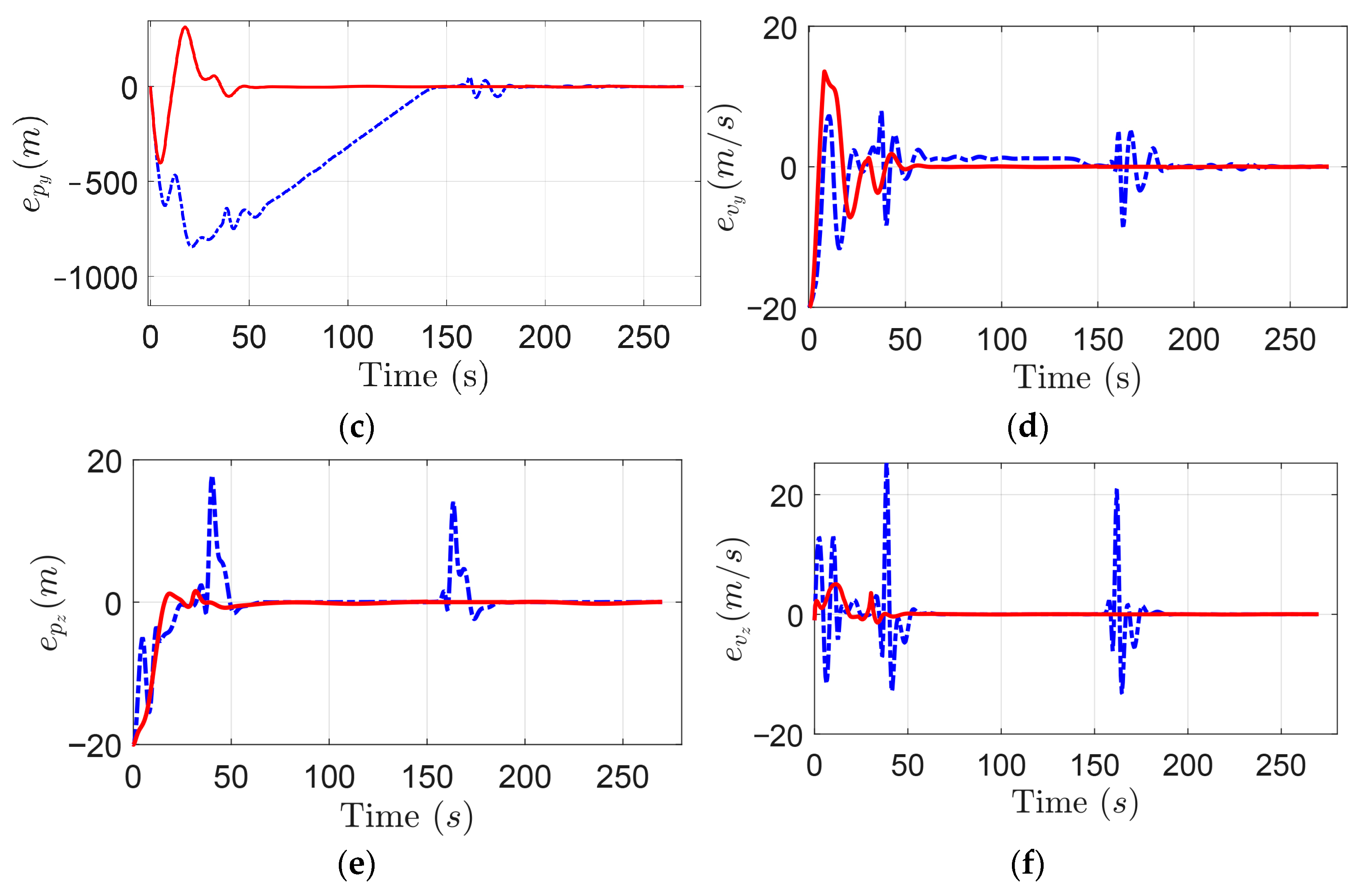
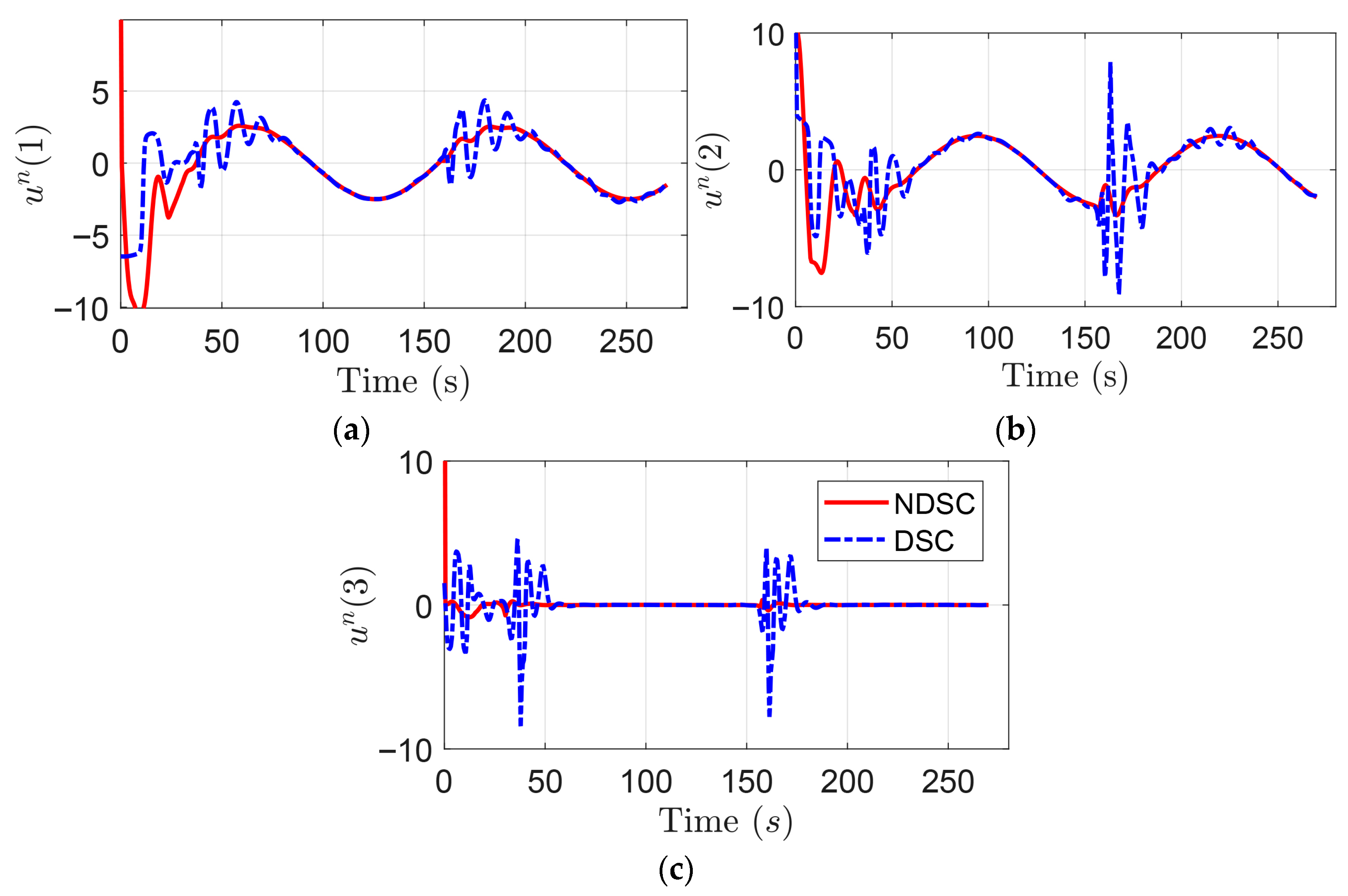
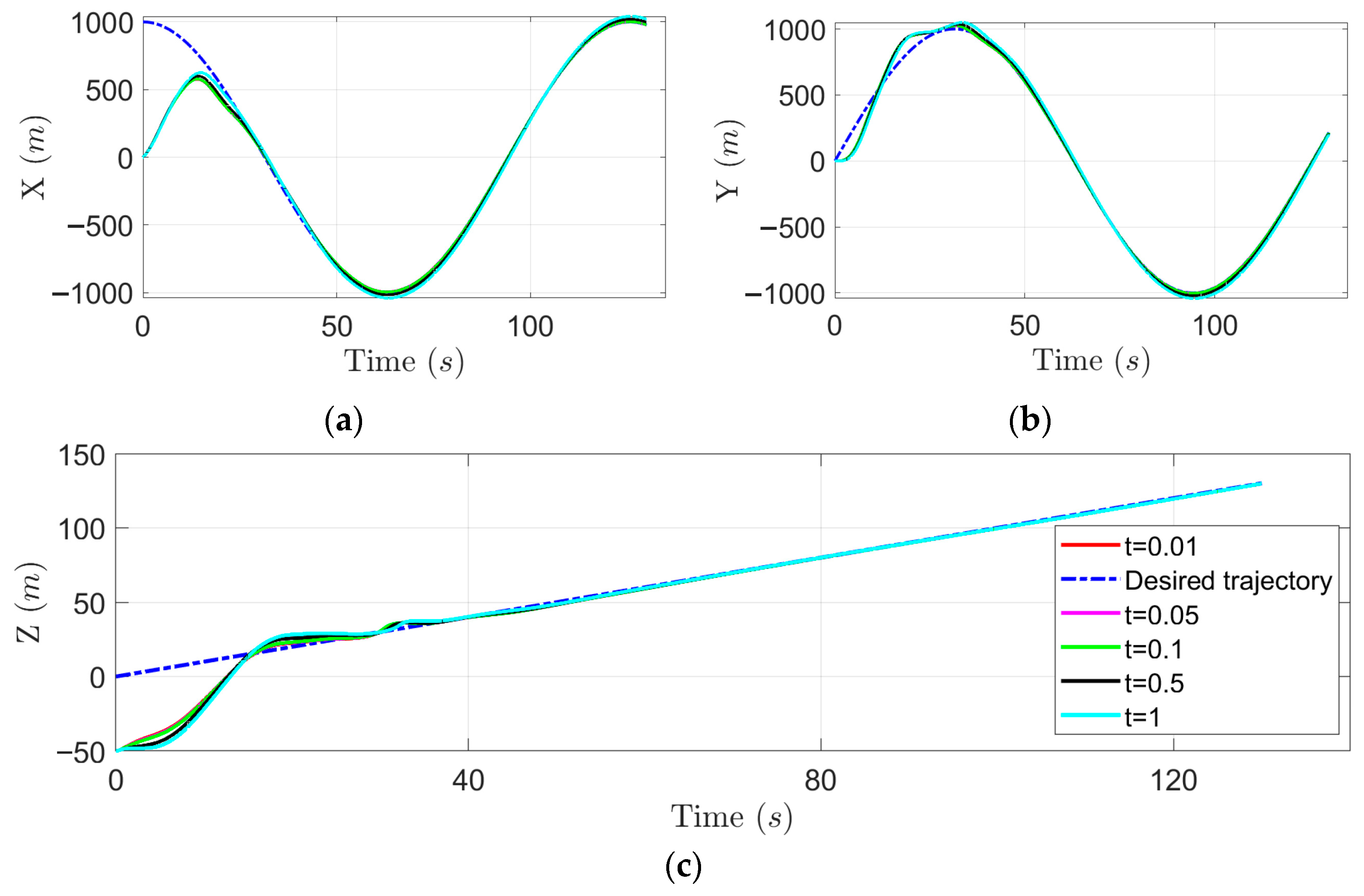
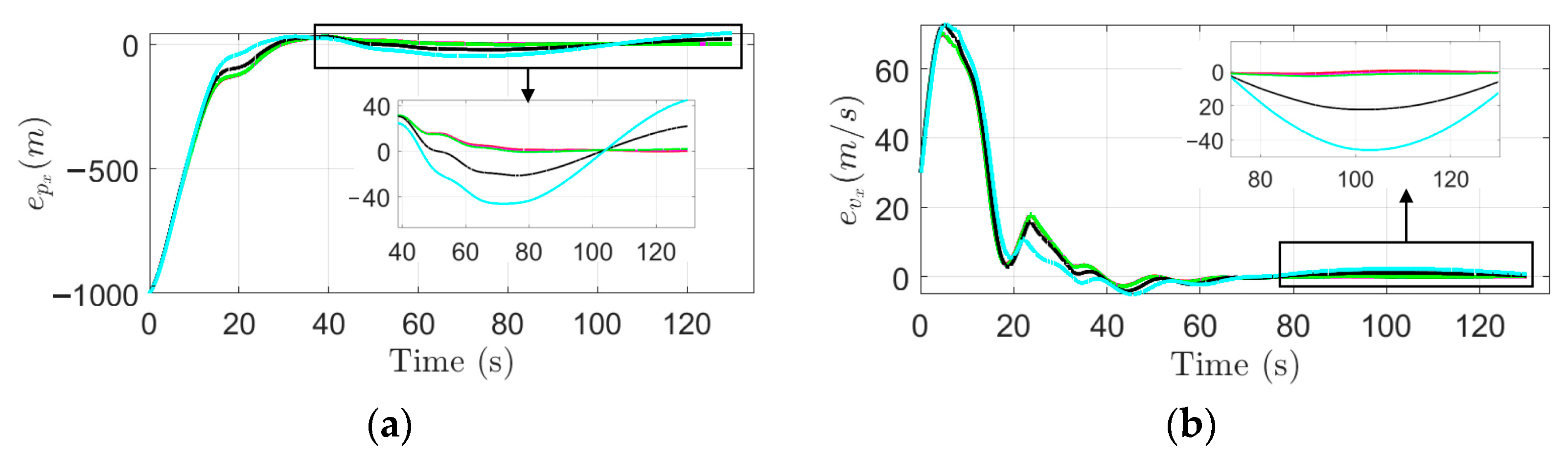
4. An Illustrative Example

We evaluate NDSC in the UAV system (1). To demonstrate the efficiency of NDSC, we compare it with the standard DSC method. To further understand the insensitivity of NDSC to the parameter τ, we test the tracking performance with different τ.

As stated in Section 2.2, the control objective is to synthesize the nominal command $u_n$ to track the desired trajectory $p_d$; to this end, a simple nominal system is given by:

$${\dot{p}}^n=v^n,{\dot{v}}^n=u^n$$

(19)

where $p^n$ is the output of (19), and the reachable trajectory is defined as: $p_d=1000{\left[cos\left(0.05t\right),sin\left(0.05t\right),0.001t\right]}^T$. The details of designing a DSC and an NDSC controller $u_n$ for the nominal system are omitted here for simplicity.

To address the control problem of an underactuated system, one important step is mapping the nominal control command $u_n$ into a desired velocity, angular velocity, and attitude. To track these desired states, thrust and torque control laws (i.e., T, $u_2$) belonging to the transaction loop and rotation loop are then derived.

Desired states are defined in the desired frame, which is denoted by the superscript d and defined by formulating the relation between two different reference frames. For instance, the relation between I frame and the desired frame can be given by:

$$v^d:={\left[‖v^n‖,0,0\right]}^T=R_n^d{v}^n$$

(20)

where we project the velocity in I frame onto the desired $x^d$ axis. Then the rotation angle and rotation axis can be computed as follows:

$${\theta }_{nd}={\cos }^{-1}\left(\frac{v^d\cdot v^n}{{‖v^n‖}^2}\right),\hspace{1em}{k}_{nd}=\frac{v^d\times v^n}{‖v^d\times v^n‖}$$

(21)

Based on (21), quaternion $q_{nd}$ between I frame and the desired frame can be constructed in the following method:

$$\begin{array}{cc}\hfill q_{nd}& ={\left[{\eta }_{nd}\hspace{1em}{\epsilon }_{nd}^{{\rm T}}\right]}^{{\rm T}}\hfill \\ & ={\left[\cos \left(\frac{{\theta }_{nd}}{2}\right)\hspace{1em}{k_{nd}}^{{\rm T}}\sin \left(\frac{{\theta }_{nd}}{2}\right)\right]}^{{\rm T}}\hfill \end{array}$$

(22)

where $q_{nd}$ is computed to construct $R_n^d=I+2{\eta }_{nd}{\rm Y}({\epsilon }_{nd})+2{{\rm Y}}^2({\epsilon }_{nd})$. To obtain the desired angular velocity, we take the derivation of (20), resulting in:

$$\begin{array}{c}{\dot{v}}^d=-{\rm Y}\left(w^d\right)R_n^d{v}^n+R_n^d{u}^n\\ =-{\rm Y}\left(w^d\right)v^d+R_n^d{u}^n\end{array}$$

(23)

which can be solved for the angular velocity as:

$$w^d=-{{\rm Y}}^{†}\left(v^d\right)R_n^d{u}^n$$

(24)

$w^d$ is derived based on the fact that ${{\rm Y}}^{†}\left(v^d\right){\dot{v}}^d=0$. In practice, a thrust controller T will be designed to make $‖v^n‖\to ‖v^d‖$, and an attitude controller $u_2$ will be constructed to make $w^b\to w^d$, $\Gamma (q_{dn})q_{nb}\to {[1,0,0,0]}^T$. Several control approaches can be applied, such as tracking trajectories under DSC and NDSC approaches represented in Figure 1. It is clearly shown that both controllers can make the UAV track its desired trajectory, and the tracking trajectory by NDSC is smoother.

Figure 2 illustrates the position response of both DSC and the proposed NDSC. Figure 2a,b show that NDSC reduces the convergence time significantly, which can be viewed as a consequence of employing the finite time convergence theory to derive the nominal control laws.

Figure 3 compares the control performance of both DSC and NDSC. As shown in Figure 3a,c, NDSC’s convergence speed is significantly faster than that of DSC. Figure 3b,d–f, show DSC has serious singularities, thus diminishing the tracking performance. In contrast, NDSC shows excellent asymptotic performance and completely avoids singularity.

Figure 4 shows the corresponding nominal control command of DSC and NDSC, where we can observe that the NDSC controller possesses bounded and smooth properties, while singularity can be detected for the DSC approach, which is not conducive to implementing stable control.

Overall, NDSC exhibits higher control performance and eliminates singularity better than the traditional DSC.

To illustrate the influence of the time constant parameter τ on the performance of the overall system, a set of time constants chosen for simulation is $\{{\tau }_1=0.01,{\tau }_2=0.05,{\tau }_3=0.1,{\tau }_4=0.5,{\tau }_5=1\}$.

Figure 5 shows the position response of NDSC under different time constants. It can be seen that the trajectory for all parameters ${\tau }_i$, (i = 1, 2, 3, 4, 5) are very similar.

Furthermore, position and velocity tracking errors are depicted in Figure 6. It is clearly shown that when τ = 0.5, 1 the tracking error $e_{p_x}$, $e_{p_y}$, $e_{v_x}$ and $e_{v_y}$ oscillates around zero. This is because when the time constant is set to be too large (e.g., τ > 0.5), FOF’s tracking error is beyond a predetermined range (e.g., η); thus, tracking convergence will not occur. In contrast, it can be seen that when τ < 0.5, the tracking error of both position and velocity converge to zero, and the amplitude of the tracking errors under τ_i, (i = 1, 2, 3) are similar. observations from the simulations indicate the proposed NDSC is insensitive to the time constant parameter τ when FOF’s tracking error is limited within a predetermined range.

5. Conclusions

In this paper, we present a nonsingular dynamic surface control method based on dynamic surface control. Our approach involves utilizing a nonsingular hypersurface, which is designed to construct the corresponding control law. We have shown that NDSC can guarantee asymptotic stability by the assumption that the filter tracking error is bounded and the systematic error can converge to the origin in a finite time. In contrast, DSC can only guarantee that the tracking error is bounded. In addition, it is shown that NDSC eliminates the singularity observed in high-complexity systems and systematizes the selection of the time constant for filters. The tracking error of the filter can be used to guide the selection of the time constant, where a larger time constant can be selected within the assumed filter tracking error. Our simulations indicate that compared to DSC, NDSC significantly improves the control performance in terms of eliminating the singularity and accelerating convergence speed [23].