Abstract
For regional or even global geophysical problems, the curvature of the geophysical model cannot be approximated as a plane, and its curvature must be considered. Tesseroids can fit the curvature, but their shapes vary from almost rectangular at the equator to almost triangular at the poles, i.e., degradation phenomena. Unlike other spherical discrete grids (e.g., square, triangular, and rhombic grids) that can fit the curvature, the Discrete Global Grid System (DGGS) grid can not only fit the curvature but also effectively avoid degradation phenomena at the poles. In addition, since it has only edge-adjacent grids, DGGS grids have consistent adjacency and excellent angular resolution. Hence, DGGS grids are the best choice for discretizing the sphere into cells with an approximate shape and continuous scale. Compared with the tesseroid, which has no analytical solution but has a well-defined integral limit, the DGGS cell (prisms obtained from DGGS grids) has neither an analytical solution nor a fixed integral limit. Therefore, based on the isoparametric transformation, the non-regular DGGS cell in the system coordinate system is transformed into the regular hexagonal prism in the local coordinate system, and the DGGS-based forwarding algorithm of the gravitational field is realized in the spherical coordinate system. Different coordinate systems have differences in the integral kernels of gravity fields. In the current literature, the forward modeling research of polyhedrons (the DGGS cell, which is a polyhedral cell) is mostly concentrated in the Cartesian coordinate system. Therefore, the reliability of the DGGS-based forwarding algorithm is verified using the tetrahedron-based forwarding algorithm and the tesseroid-based forwarding algorithm with tiny tesseroids. From the numerical results, it can be concluded that if the distance from observations to sources is too small, the corresponding gravity field forwarding results may also have ambiguous values. Therefore, the minimum distance is not recommended for practical applications.
Keywords:
gravity forward modelling; spherical hexagonal prisms; isoparametric transformation; discrete global grid system MSC:
86-08
1. Introduction
The curvature of the geophysical model in small/local areas can be represented as a plane. However, its curvature must be considered for regional or even global-scale issues. Because of the ellipsoidal shape of the Earth, the radius of curvature varies at different positions, resulting in changes in both the acceleration of gravity and the intensity and direction of the magnetic field with respect to longitude and latitude [1]. This change is particularly significant on a large-scale area and has important implications for studies such as the calculation of satellite orbits, crustal equilibrium, the inference of the internal structure of the Earth, the origin and evolution of the geomagnetic field, and geomagnetic navigation [2,3]. Therefore, when studying and solving these large-scale geophysical problems, the influence of earth curvature must be fully considered to obtain more accurate and reliable conclusions.
Generally, the mesh (also entitled as physical property unit or cell) of the geophysical model needs to be expressed and processed using spherical coordinates [4,5,6,7]. In the spherical coordinate system, the gravitational potential calculation can be roughly used in two methods: the spherical harmonic function method in the frequency domain and the direct integration method in the spatial domain. For the former, the spherical harmonic function method is more computationally efficient than the latter at low and middle orders (N < 360); however, it is affected by numerical instability at (super) high orders (N > 2700) [8]. Moreover, the spherical harmonic function method cannot properly consider the vertical extension of a given mass distribution [9]. The calculation results are marginally larger in amplitude, which is slightly inconsistent with the actual problem and unsuitable for accurately modeling the global/local gravity field [10].
How to obtain the analytical or numerical solution of gravitational fields has been one of the central problems in the selection of physical property units when performing the forward modeling of gravitational fields based on the direct integration method in the spherical coordinate system [11].
In practical applications, similar to physical property inversion in the Cartesian coordinate system, the spherical shell of the geophysical model is typically split into a set of discrete cells by using radius, latitude, and longitude as parameters. As far as the spherical discrete meshes are concerned, which mainly includes latitude-longitude and polyhedral meshes based on regular polyhedral subdivisions [12], such as point elements [13], line elements [14], surface elements [15], prism cells [16], tesseroids [17], combined cells of prism and tesseroid [18], or polyhedral cells [19].
In terms of fitting the spherical curvature of the geophysical model, the prism cell has a rigorous analytical solution for gravitational fields. However, when dealing with large-scale or global-scale problems, the model’s curvature needs to be corrected by reducing the distance between adjacent prism cells and changing their direction [20]. When the cells are excessively rough, resulting in the geophysical model is discontinuous and a reduction in the gravitational forward modeling calculation accuracy. Therefore, the prism cell cannot fit the model’s spherical curvature well [21]. Compared to other cells, tesseroids can efficiently fit the model’s spherical curvature. However, tesseroids do not have gravitational analytical solutions and must rely on numerical integration methods to obtain corresponding anomaly responses [5,6,22,23]. As latitude increases from the equator to the poles, tesseroids will produce a degradation phenomenon that tesseroids near the poles will degenerate into triangular prisms, generating a large amount of data redundancy, and their calculation error will accumulate toward high latitudes [23,24,25].
As far as polyhedral cells are concerned, Ren et al. [26] used Newton’s integral method to transform the volume integrals of gravity anomalies caused by homogeneous/non-homogeneous polyhedrons into surface integrals over polygonal faces [27]. Furthermore, singularity-free closed solutions are obtained for these surface integrals. The experimental results show that this method has high calculation accuracy. When polyhedral cells are used as an alternative cell/unit in large-scale or global-scale problems [28], significant polyhedral cells/units are required to fit the spherical curvature [21]. Furthermore, at present, gravity and magnetic forward modeling methods based on polyhedral cells generally use the Gauss/divergence theorem [29] to transform the volume integral of a polyhedral into an area/line integral of polygonal surfaces/lines of the polyhedral through various methods [28,30,31], and subsequently obtain the corresponding analytical solution/numerical solution [32]. How to effectively avoid the numerical ambiguity inherent in the divergence theorem [31] while exploiting the efficient computational properties of area/line integrals [33] is a core issue in the gravitational field forward modeling based on the divergence theorem.
In order to avoid the singularities at the poles and non-uniformity of latitude–longitude grids (e.g., as a particular case, tesseroids are latitude–longitude grids), many studies on spherical discrete grids based on regular polyhedrons have been carried out in recent years [12]. Based on the spherical discrete grid method of regular polyhedrons, the Discrete Global Grid System (DGGS) is a spherical fitting method different from the latitude–longitude grids [34]. The DGGS [34,35] are composed of a series of discrete global grids, which are considered to be a kind of earth-fitting grid. DGGS can divide the sphere into multi-level grids with approximate or equal area and shape and a continuous scale. At any resolution, considering the fitting curvature, it can seamlessly cover the global, and the grids with different resolutions form a highly consistent hierarchical structure [36]. Therefore, DGGS grids are the best choice for discretizing the sphere into cells with an approximate shape and continuous scale. To meet different needs, there are many ways to use DGGS to deal with large-scale geospatial data, including Hierarchical Equal Area isoLatitude Pixelisation of a 2-sphere (HEALPix) [37], Open Equal Area Global GRid (OpenEAGGR) [38], Hierarchical Hexagonal Hierarchical Spatial Indexing System (H3) [39], Science Collaboration Environment for New Zealand Grid (SCENZ-Grid) [40], regularized Hierarchical Equal Area isoLatitude Pixelisation of a 2-sphere (rHEALPix) [41], Geographic Grid System (geogrid), and International Society for the Advancement of Spatial Data Handling (ISEA) [42]. When dealing with large-scale heterogeneous geospatial data, DGGS has the characteristics of convenient management, fast storage, and assembly. Currently, it has become an effective tool for efficient exploration and visualization [43].
Unlike triangles and rhombuses, both of which have edge adjacencies and are therefore inconsistent, the pentagonal/hexagonal cell, which is a kind of DGGS cell (prisms obtained from DGGS grids, which contain spherical pentagons and hexagons) and derived from the ISEA3H grid [44], has only edge neighbors [31,45]. And it is easier to achieve than triangles and rhombuses in the adjacent search of pentagonal/hexagonal grids [12,46]. Compared with square grids (as a particular case, tesseroid are also a kind of square grids), hexagonal grids have excellent angular resolution and also show unified and clear adjacency [34], and their discrete distance measures are closer to Cartesian distances [47].
Essentially, the gravitational forward modeling of DGGS cells in the space domain involves integral calculations. Although tesseroids do not have gravitational analytical solutions, their integration limits are well-defined, so using numerical integration methods can obtain corresponding gravity anomaly responses. However, DGGS cells neither have gravitational analytical solutions nor fixed integration limits.
To solve optimization problems (including integrals) for dealing with complex structures, the finite element method (FEM), as a cornerstone of computational mechanics, has become an indispensable tool of computational in scientific and engineering calculations and numerical simulations [48,49,50,51,52], which plays a crucial role in geophysical research exploring the large-scale atmosphere, oceans, and crust [50]. The target object analyzed by FEM usually has a complex structure [49,53]. Therefore, selecting an appropriate cell is vital to improve the discretization of the target object. Isoparametric elements are widely used in finite element analysis of complex structures because of its excellent adaptability and coordination [54,55].
Presently, to strengthen the use of isoparametric elements in finite element analysis and apply them to solve various practical engineering problems, many scholars have put forward their relevant research insights and achieved specific research results. For example, Jeng and Wexler [56] proposed a new isoparametric finite element numerical algorithm that resolved the variational solution of the boundary integral equations of a general 3D field, which is based on the variational principle and not only approximates the unknown source distributions by the calculation of polynomials but also models surfaces at higher-order, to reduce the errors caused by geometric modeling [56,57].
Lehrenfeld [58] proposed a new geometry-based isoparametric non-fitting FEM for solving problems on non-fitting interfaces, or marginals, and partial differential equations on surfaces. The method is simple to use and relatively new and practical, capable of performing higher-order numerical integration calculations using level set functions over domains as prescribed, with good robustness and high accuracy in dealing with complex geometries [58,59]. Belarbi et al. [60] proposed a new hierarchical isoparametric finite element modeling technique to obtain 2D quadrilateral isoparametric elements that satisfy the “face-core” condition at the interface through a hierarchical method for analyzing the bending problem in sandwich panels. The method can satisfy the continuity of stresses and displacements at the interface, and the model comparison tests show that the algorithm has good accuracy and convergence speed [60,61].
Therefore, drawing a lesson from the unit of analysis process in the FEM [48,62,63], an isoparametric transformation [64,65] is used to transform a non-regular DGGS cell in the system/spherical coordinate system to a regular hexagonal prism in the local/Cartesian coordinate system to determine their integration limits. Then, the gravitational field forward modeling calculation of the DGGS cell is realized under the spherical coordinate system using an isoparametric transformation with the shape functions, integration points, and their integration weights.
2. The Principle of Forward Modeling Tensors and Gravity Gradients
For all observation points, the gravitational effect of each physical property unit can be calculated one by one according to the superposition principle and the corresponding anomalous response can be obtained by cumulative summation. Therefore, the gravitational field forward modeling can be written in matrix form:
where is observation data vector, which can be specifically , , , , , or , etc., with a length of ; parameter vector is the densities value of the units; is the corresponding forward operator (consistent with the inversion kernel matrix) with size of ; and are the units’ number and observation points, respectively.
The forward integral kernel of gravitational fields differs in the Cartesian coordinate system and the spherical coordinate system [66]. Taking the tesseroid as an example, as shown in Figure 1, it is assumed that a homogeneous geological body Q with a density exists in the spherical coordinate system. The gravity vector and the gravity gradient tensor at the source external space of the Q can be expressed as [66], respectively:
where , = is the gravitational constant, = , = , = , = , ℓ = , = .
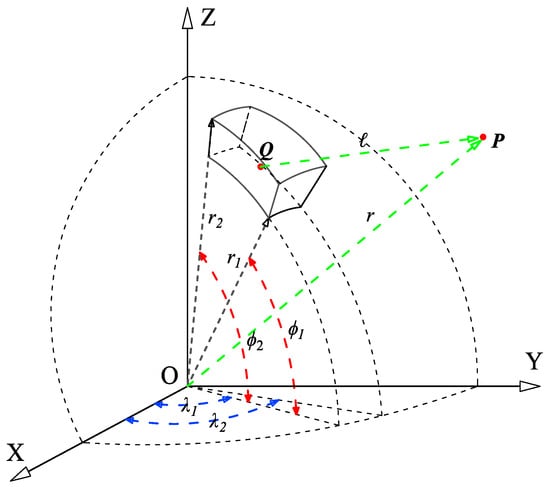
Figure 1.
View of a tesseroid in the geocentric coordinate system. In the spherical coordinate system, integral point Q and computational point P with a local coordinate system. and (blue dashed line) represent the lower and upper limits of the spherical azimuth; and (red dashed line) are the lower and upper limits of the spherical center angle; and (black dashed line) are the lower and upper bounds of the radius of the cell body; r and l (green dashed line) represent the distances from the center point O and the integral point Q to the computational point P, respectively.
Since the tesseroid has no analytical solution, it needs to be processed by numerical integration methods such as the Taylor-series expansion method [23] and the 3D Gauss–Legendre quadrature (GLQ) integration [67,68,69]. Therefore, the GLQ method is used to calculate the gravity vector and the gravity gradient tensor . In order to facilitate the calculation, the integral kernel f [6] is introduced and expressed as a general form of triple integrals [70]:
Using the triple-Gauss quadrature approximation calculation Equation (3) is generally necessary [5]. However, the corresponding integration coefficients must be determined in different integral intervals for various order integrals. It is assumed that the integral interval of Equation (3) along longitude, latitude, and radial direction is , and the integration point is , and the following form is constructed to obtain the corresponding approximate calculation results:
where n is the number of integration points, is the integration weight
where is the first derivative of the n-order Legendre function . After scaling the integral interval of Equation (4) to the interval , the corresponding zero point of is the Gauss point. The root of the higher-order Legendre function can be obtained using the recursive relation of its first derivative .
Using Equation (4), Equation (3) can be re-expressed as a form of the triple numerical integration [70]
where are the number of integration points in longitude, latitude, and radial direction, respectively, and are the corresponding integration weights. In practical applications, the number of integration points can control the calculation’s accuracy. The higher the number of integration points, the better the accuracy of the GLQ, but the corresponding computational efficiency will be lower [68,71]. In this article, is equal to 2, .
3. Forward Modeling of Gravitational Fields Based on DGGS Cells
The tesseroids and triangular or rhombus prisms derived from a discrete spherical shell lack consistency or contain the presence of the degradation phenomenon that spherical discrete grids obtained by subdividing the spherical shell with a regular geometry unit differ in spatial morphology [10,12]. As shown in Figure 2, based on the definition of the DGGS, the first-level grid is constructed on the spherical surface (e.g., other precision grids can also be further constructed on the sphere), including 12 pentagonal and 30 hexagonal DGGS grids. Furthermore, using these grids, the spherical shells within the research area are discretized layer by layer along the radial direction; that is, each layer of the spherical shell is discretized into 12 spherical pentagonal prisms and 30 spherical hexagonal prisms, which are referred to as DGGS cells here. Namely, DGGS cells contain prisms composed of spherical pentagons and spherical hexagons.
Figure 2.
Schematic representation of spherical shell based on the Discrete Global Grid System subdivision.
Compared with the tesseroid, the DGGS cell has neither a corresponding analytical solution nor a fixed integral limit. Therefore, drawing a lesson from the unit analysis process in the FEM, an isoparametric transformation is used to transform a non-regular DGGS cell from the system coordinate system to a regular hexagonal prism in the local coordinate system.
3.1. The Isoparametric Transformation of DGGS Cells
In finite element analysis, the solution region is frequently partitioned into a finite number of small cells, such as triangles, quadrilaterals, tetrahedrons, rectangles, and so on. Those small cells can be connected to each other through their nodes. In order to obtain the corresponding field values by the FEM, it is necessary to calculate the area/volume integral of each unit in order to establish the system of equations for the corresponding field functions f [72]. Since the forward modeling of gravitational fields in this paper only considers the volume effect, only the volume integral of each small unit is considered. Usually, the volume integral of the field function f can be expressed as
In Figure 1, the field function f cannot obtain the corresponding integral limit for a non-regular hexagonal prism in the system coordinate system. Therefore, it is frequently necessary to introduce a specific geometric transformation to transform the DGGS cell into a regular hexagonal prism to gain a distinct integral limit. If and only if both the field function interpolation and coordinate transformation use the same number of node parameters and the same interpolation function, it is called the isoparametric transformation [65,73]. Isoparametric elements use a mathematical mapping to convert coordinates from one system to another, where the original system is called the system/global coordinate system and the second system is called the natural/local coordinate system.
As shown in Figure 3, for both the system coordinate system and the local coordinate system, the relationship between derivatives and volume elements can be established through isoparametric transformation based on interpolation functions or shape functions N [53,65,74]. The shape function is an essential mathematical tool in finite element analysis and can represent displacements, temperatures, or wave velocities in units [53]. They serve as a bridge to transform continuous problems into equivalent discrete problems. For a typical finite element with node, let the displacements at any point within the element be approximated as:
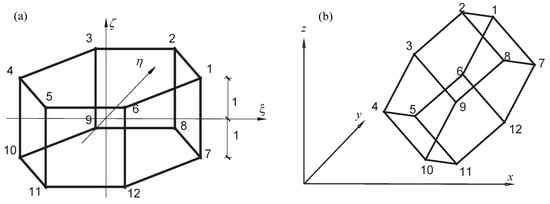
Figure 3.
Isoparametric transformation of Discrete Global Grid System (DGGS) cells. (a) Local coordinate system. (b) System coordinate system. The numbers 1 to 12 represent the serial number of the integration point i.
According to the chain rule in calculus, the partial derivative concerning is obtained for the shape function of the i node of the DGGS cell. Then,
For the other two coordinates , a similar expression can also be written. Now, the partial derivatives of to , and are written in the matrix form
where J is a matrix. In finite element analysis, the physical meaning of is the volume of the corresponding small unit. Thus, according to Equation (10), there are
Here, is the number of unit nodes. Then Equation (10) can be rewritten as
where the inverse matrix , , and are the determinant and adjoint matrices of J, respectively.
After the geometric transformation from the system coordinate system to the local coordinate system, the integral of the field function f in the integral domain in the original system coordinate system can have a definite integral limit in the local coordinate system. Assuming that the corresponding integral limit is , then the integral of the field function f in the local coordinate system can be expressed as
where,
Using the triple-Gauss quadrature [67,75] in conjuction with Equation (7), Equation (13) can be rewritten as:
where and are the number of integration points and the integration weights of the Cartesian coordinate system along the axis direction, respectively.
Referring to the article [53,76] and according to the definition of FEM, ensure that the shape function satisfies the following three conditions [77]: (a) only at node i can have a unit value while all other nodes have zero value; (b) disappears on any boundary of element that does not include node i; (c) the determinant of the Jacobian matrix of the resulting shape function concerning the node coordinates is equal to the volume of the regular hexagon prism. Then, the following set of shape functions is given
3.2. Integral Weights of DGGS Cells
In finite element analysis, integration points are typically placed at specific locations, such as their equipartition points for line/surface elements (see Table 1 and Table 2) and their line/surface equipartition points and barycenter (see Figure 4) for volume elements [78].

Table 1.
1D Gauss quadrature scheme for line elements.

Table 2.
2D Gauss quadrature scheme for rectangular elements.
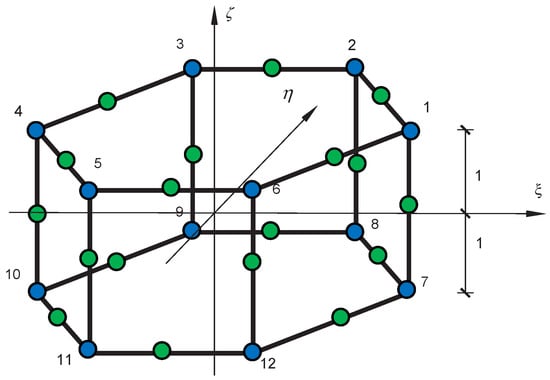
Figure 4.
Schematic representation of traditional integration points for a regular hexagonal prism.
There is some challenge in determining the location of the integration points and the integration weights for a regular hexagon or hexagonal prism. As shown in Figure 5a, a cross-section of a regular hexagonal prism is taken as the object of study, and integration points are arranged on the horizontal hexagon in Figure 5b; while the 1D Gauss quadrature scheme (see Table 1) is employed along the vertical direction of the regular hexagonal prism in Figure 5, setting the (the quantity of 1D Gauss integration points) layer of integration points and the corresponding weight coefficients for the k-th layer of integration points. By the definition of the triple-Gauss quadrature, Equation (13) is rewritten as
where, the triple-Gauss quadrature integration weights = , subscripts , the number of integration points = , , , , and are the coordinates of the j-th integration point, respectively.
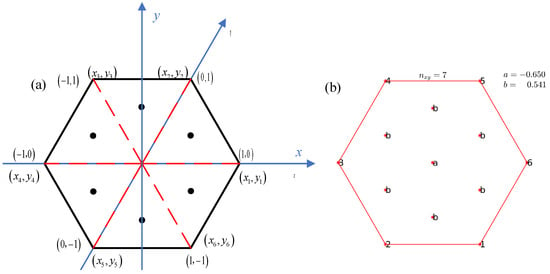
Figure 5.
Integration points on a regular hexagon. (a) Integral point position (), the dash line and colors are represented as auxiliary lines to differentiate six regular triangles. (b) Integral point weight (), the asterisk * of the numbers 1–6 represents the vertex number, where a and b (i.e., red dots in the middle of the regular hexagon) correspond to the positions of the integration points.
4. Forward Modeling of Gravitational Fields Based on Arbitrary Tetrahedral Cells
How to analyze the accuracy of the gravitational field forward modeling calculation is essential in verifying the correctness of the DGGS-based forwarding algorithm of the gravitational field under the spherical coordinate system proposed in this paper. Since the DGGS cell is a particular case of the polyhedral cell, the polyhedral-based forwarding algorithm can be used to verify the correctness of the DGGS-based forwarding algorithm proposed in this paper [26,28]. However, most existing studies on polyhedral-based forwarding algorithms focus on the Cartesian coordinate system, whereas this paper is involved in the spherical coordinate system. Therefore, there are several points to consider:
- Describing the two spherical surfaces (curved surfaces) above and below the DGGS cell in the spherical coordinate system using the facets of polyhedrons is somewhat challenging;
- A significant number of units and nodes are required if polyhedrons (e.g., tetrahedrons) are directly used to fit the DGGS cell [21,28];
- The gravity field integration kernels under the two coordinate systems are not the same [23,26,66].
Based on the above three factors, considering that the DGGS cell does not have the gravitational field analytical solution, and the polyhedral cell does not have the analytical solution/closed solution of gravitational fields under the spherical coordinate system. Therefore, referring to Grombein et al. [23], the forward integral kernel in the Cartesian coordinate system of the tesseroid is given, and a tetrahedron-based forwarding algorithm is introduced to verify the effectiveness and reliability of the DGGS-based forwarding algorithm proposed in this paper (Figure 6).
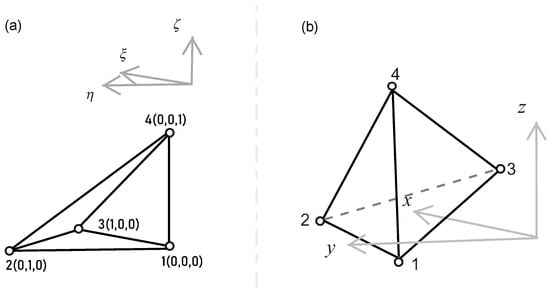
Figure 6.
The coordinate transformation of a tetrahedron. (a) Local coordinate system. (b) System coordinate system.
Referring to Duczek et al. [79], the shape functions of the tetrahedron can be written as follows:
Subsequently, the tetrahedron-based forwarding algorithm of the gravitational field can be calculated using the Gauss integration.
Cao et al. [80] employed the 3D Hammer integration to derive the gravitational field analytical solution for the tetrahedron. The following Equation (2) is utilized to calculate the volume integral of the tetrahedron:
where are volume or natural coordinates, and f and F correspond to the field functions of the system and the natural coordinate system (a kind of local coordinate system), respectively. Parameters , , a, and b are detailed in Table 3.

Table 3.
Integration weights and position of points of the 3D Hammer integration.
Then, Equation (18) is used as the shape function for tetrahedrons. The 3D first-order Haar integration scheme is utilized to obtain the corresponding gravity vector and its gradient tensor value using Equation (19).
When the integration point is situated within the isoparametric element, an isoparametric transformation is utilized to establish the connection between the integration point in the local coordinate system and the system coordinate system. This relationship ensures the avoidance of the numerical ambiguity problem that tends to occur in traditional volume integration during the implementation of the volume integration process [27,28].
In order to validate the effectiveness and reliability of the DGGS-based forwarding algorithm proposed in this paper, the following three phases are required:
Phase 1. Since the forward integral kernel varies in different coordinate systems, and considering the influence of the number of integration points and KU criteria [22] on the calculation accuracy of tesseroids, it is therefore necessary to compare the computational accuracy of the tetrahedron-based forwarding algorithm and the analytical solution of right rectangular prisms [80], under the Cartesian coordinate system, to verify the correctness of the tetrahedron-based forwarding algorithm.
Phase 2. Considering that the DGGS cell has neither an analytical solution nor a clear integration limit in the spherical coordinate system. Therefore, it is necessary to compare the difference in calculation accuracy between tetrahedrons and tesseroids to verify the correctness of the tetrahedron-based forwarding algorithm Equation (2) in the spherical coordinate system [23].
Phase 3. Based on the algorithm verification of the above two phases in the spherical coordinate system, the difference in calculation accuracy between the tetrahedron-based and DGGS-based forwarding algorithms is compared in order to verify the correctness of the DGGS-based forwarding algorithm proposed in this paper based on isoparametric transformation.
5. Algorithm Verification
5.1. Phase 1: To Verify the Tetrahedron-Based Forwarding Algorithm in the Cartesian Coordinate System
In the first step, to verify the correctness of a tetrahedron-based forwarding algorithm [80]. A cube model with a density of 0.3 g/cm3 is specially constructed with a center point at (0 m, 0 m, 650 m) and a side length of 400 m, as shown in Figure 7. The observation grid ranges from x: −1000 m to 1000 m; y: −1000 m to 1000 m. The spacing of the observation points is 50 m × 50 m, and the points are located on the earth’s surface.
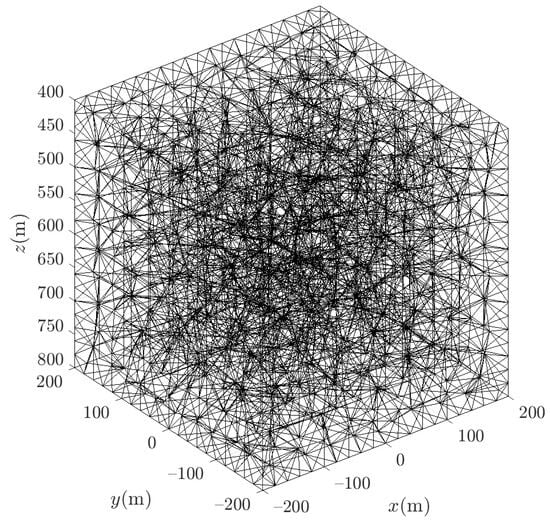
Figure 7.
Schematic of cube discretized by tetrahedrons.
In the second step, the cube is subdivided into tetrahedrons using Delaunay triangulation [81]. It should be noted that if the quality of the tetrahedrons obtained from the Delaunay triangulation discretization is poor, the results of the calculations using Equation (19) may be susceptible to distortion. To ensure calculation accuracy, when using Delaunay triangulation software TetGen (version 1.5) [82], discretizing the cube is necessary to ensure that the odd intensity is less than 1.4.
In the third step, the gravity vector and its gradient tensor values are obtained using the analytical solution of the right rectangular prism [83] and the tetrahedron-based forwarding algorithm [80]. By comparing with Figure 8, it can be seen that under the Cartesian coordinate system, using the forward integral kernel [80], the tetrahedron-based forward modeling using 3D Hammer integration has high computational accuracy. This demonstrates the tetrahedron-based forwarding algorithm as an instrument for the subsequent analysis of the DGGS-based forwarding algorithm.
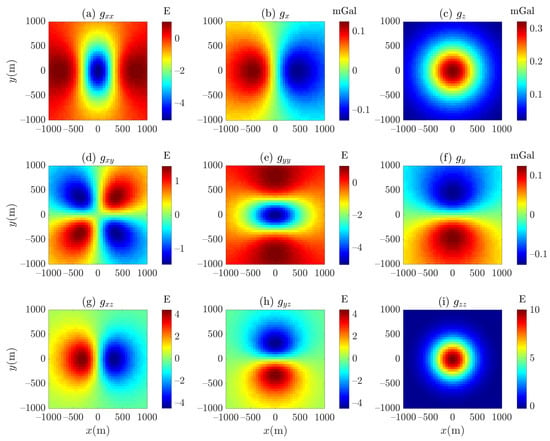
Figure 8.
Results for the cubic model using tetrahedron-based forwarding algorithm (see Figure 7).
Generally, mesh generation is divided into structured and unstructured mesh generation. The so-called structured mesh generation refers to the number of cells adjacent to each internal node after the subdivision is the same, such as in the case of 3D, where the generated cells are generally hexahedrons; unstructured is the opposite of structured, which means that each node can have different adjacent cells. It is easy to make the geometric fitting error [84] larger by using the structured mesh to fit the curved edge/surface, leading to a large error in the numerical solution [80]. Moreover, the nodes of the structured meshes cannot be reasonably distributed in a gradient shape, so the error caused by the geometric discretization of the model cannot be eliminated to the maximum extent. Even if it can be distributed in a certain gradient, it is easy to reduce the shape quality of the structured cells, thus affecting the accuracy of the numerical calculation [85]. Compared with the structured mesh generation method, tetrahedrons have a certain degree of variability and flexibility, i.e., the nodes and units obtained using Tetgen are distributed in a gradient shape in a certain way [86], or some discrete points are inserted (using Tetgen software for multiple time refinement) in the gradient change area [87], which can greatly reduce the geometric fitting error [84].
Cao et al. [80] pointed out that the computational error of the tetrahedron-based forwarding algorithm is proportional to the quality of the tetrahedrons and the geometric fitting error for fitting the model using tetrahedrons [84,88]. Figure 9 shows that the geometric fitting error induced by fitting the cube with tetrahedrons in the Cartesian coordinate system is small, and the residuals between the results of the tetrahedron-based forwarding algorithm Equation (19) and the analytical solutions [83] for the cubic model.
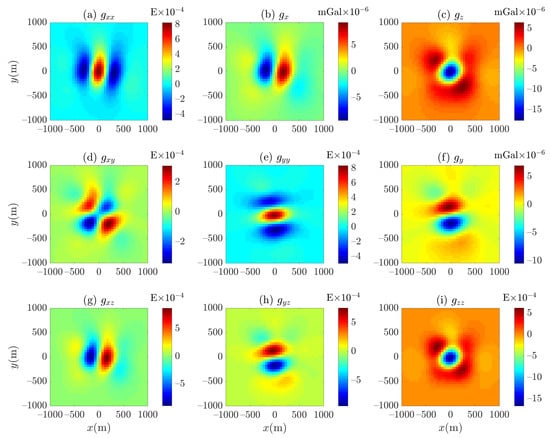
Figure 9.
Residuals between the results of the tetrahedron-based forwarding algorithm Equation (19) and analytical solutions [83] for the cubic model.
5.2. Phase 2: To Verify the Tetrahedron-Based and Tesseroid-Based Forwarding Algorithms in the Spherical Coordinate System
To facilitate comparative analysis, the second stage uses the four model settings given by Uieda et al. [5], whose names are Experiment 1 (pole), Experiment 2 (equator), Experiment 3 (260 km), and Experiment 4 (30° size). Each of them contains a tesseroid with a thickness of 1 km, and its latitude and longitude range are 89∼90° N/0∼1° E, 0∼1° N/0∼1° E, 89∼90° N/0∼1° E, and 60∼90° N/0∼30° E, respectively. All grids corresponding to the above four models are composed of 51 × 51 evenly distributed calculation points, and the fixed altitudes are 2 km, 2 km, 260 km, and 2 km, respectively.
Subsequently, the Delaunay triangulation technique is used in the spherical coordinate system to discretize the tesseroid into a series of subcells. Due to the difference between the latitude and longitude interval of the tesseroid and the proportional coefficient of the thickness, the latitude and longitude interval is 1°, but the thickness is 1 km. Therefore, the interval of tesseroids can be scaled by referring to the small circle radius or arc length of the latitude in which the tesseroid is located. This is to avoid the distortion of the generated tetrahedron in the spherical coordinate system due to the direct use of latitude and longitude information for Delaunay triangulation, i.e., to ensure that the odd intensity is less than 1.4.
To determine whether a tesseroid must be divided, Uieda et al. [5] introduced an inequality as follows
where, the distance d between the observation point and the geometric center of the tesseroid, and , is the dimensions of the tesseroid (the “side lengths” of Li et al. [89]) along longitude, latitude, and radius, respectively. D denotes the “distance-size ratio”, which is a positive scalar [5].
If the inequality is satisfied for all pairs of observation points and tesseroids, then the tesseroid is undivided. Hence, the distance-size ratio dictates the proximity at which the computation point can be located before necessitating the division of the tesseroid. The value of D indirectly influences the accuracy and computation time of the solution. The d is too short, resulting in ambiguity points in the forward modeling results of gravity fields using the tesseroid, especially at the coincidence of the observation point and the source projection, as shown in Figure 10. Uieda et al. [5] noted that the calculation accuracy of the tesseroid-based forwarding algorithm of the gravitational field is influenced by the location of tesseroids, the height of the observation point, and the distance-size ratio.
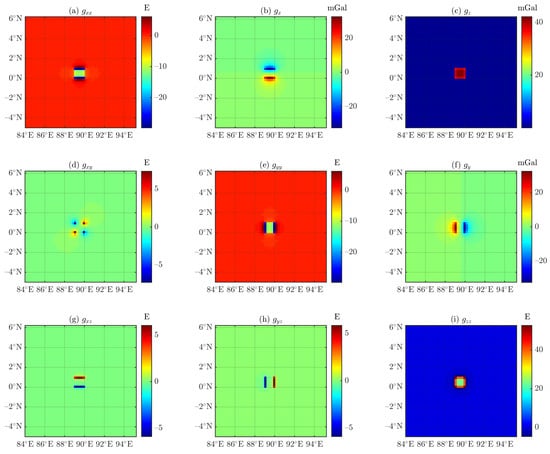
Figure 10.
Results for Experiment 1 with and 28,130,947 subcells using tesseroid-based forwarding algorithm.
To verify the computational accuracy of the tetrahedron-based forwarding algorithm in the spherical coordinate system proposed in this paper, the tesseroid is refined by setting , yielding 28,130,947 subcells, then the results of the tetrahedron-based forwarding algorithm, which is obtained using Equation (2), and the tesseroid-based forwarding algorithm as shown in Figure 10 and Figure 11, for Experiment 1 and Experiment 3, respectively.
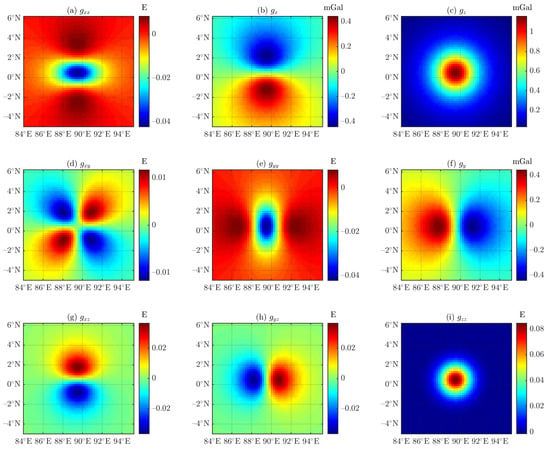
Figure 11.
Results for Experiment 3 with and 4096 subcells using tesseroid-based forwarding algorithm.
With a more detailed subdivision of the model, i.e., the corresponding forward modeling, results are smoother as D increases. However, as D increases, more refined tesseroids are involved in the computation, especially when d is small. Therefore, too small d is not common in practical applications. The Tetgen software uses Delaunay triangulation technology to discretize tesseroids into tetrahedrons in the spherical coordinate system. Considering that it is difficult to describe the curved edges/faces of tesseroids by PLC/PSLG [80,90,91], it is also easy to introduce significant geometric errors. The geometric results were refined several times by Tetgen software (see Figure 12).
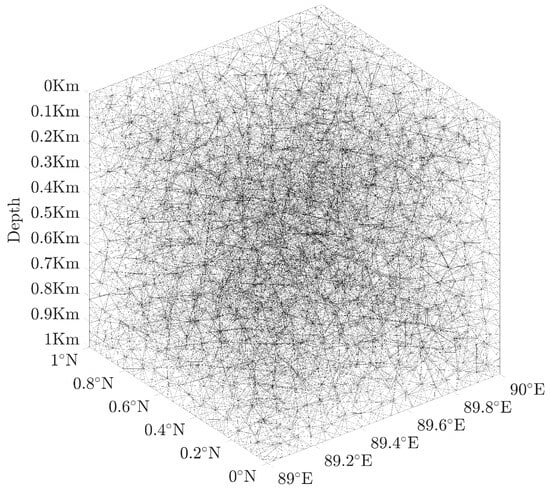
Figure 12.
Schematic diagram of a tesseroid with a size of km discretized by 10,315 tetrahedrons (after 4 refinements).
Figure 13 shows that when the distances d are minimal, even after seven refinements using Tetgen, yielding 423,853 subcells, the residuals between the results of the tetrahedron-based and tesseroid-based forwarding algorithms are still significant. The minimal distances d are also one of the reasons for the large relative error values in Figure 4 and Figure 5 of Uieda et al. [5]. Therefore, small distances d should be avoided for the forwards and inversions of gravitational fields.
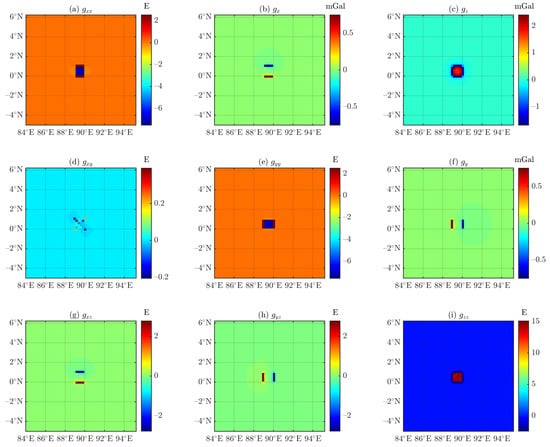
Figure 13.
Residuals between the results of the tetrahedron-based (after 7 refinements) and tesseroid-based forwarding algorithms (see Figure 8) for Experiment 1.
Figure 13, Figure 14, Figure 15 and Figure 16 reveal that as the tetrahedrons obtained by Tetgen are further refined, residuals between the results of the tetrahedron-based and tesseroid-based forwarding algorithms gradually approach 0.
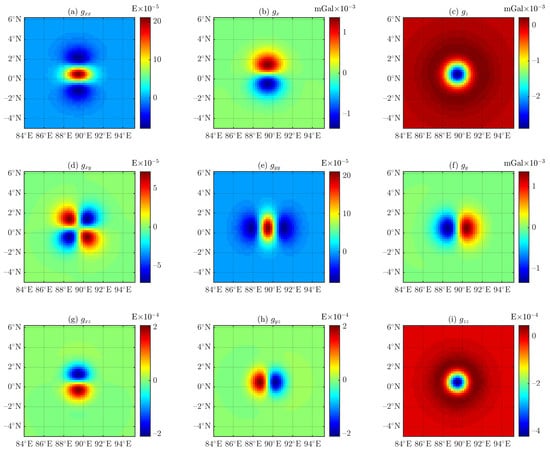
Figure 14.
Residuals between the results of the tetrahedron-based (after 2 refinements with 144 subcells) and tesseroid-based forwarding algorithms (see Figure 11) for Experiment 3.
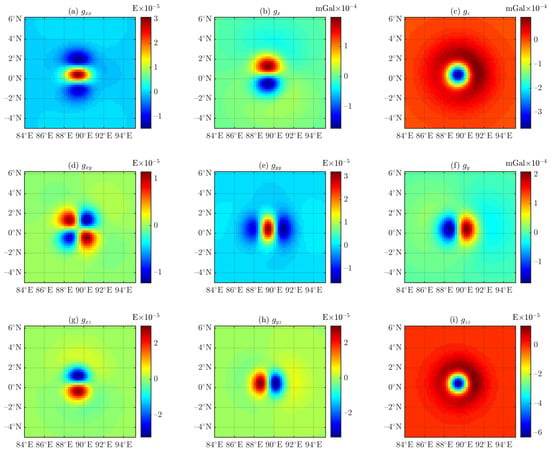
Figure 15.
Residuals between the results of the tetrahedron-based (after 3 refinements with 526 subcells) and tesseroid-based forwarding algorithms (see Figure 11) for Experiment 3.
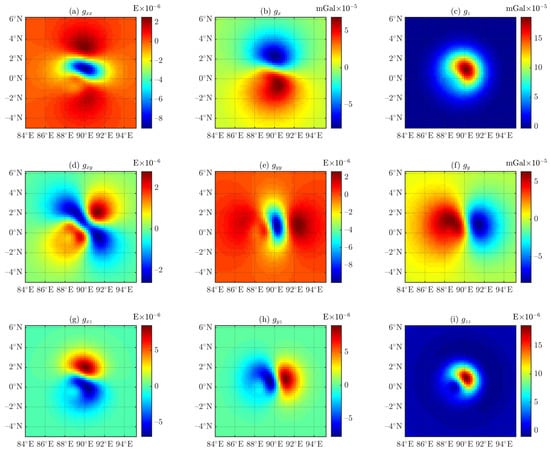
Figure 16.
Residuals between the results of the tetrahedron-based (after 4 refinements with 10,315 subcells) and tesseroid-based forwarding algorithms (see Figure 11) for Experiment 3.
By analyzing Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 simultaneously, when the number of subcells required to refine a cell is small, the tetrahedron-based forwarding results have better accuracy than the tesseroid-based results. These tests indicate that the tetrahedron-based forwarding algorithm proposed in this paper is correct. Therefore, the tetrahedron-based forwarding algorithm can be used as a reference algorithm for analyzing the DGGS-based forwarding algorithm.
5.3. Phase 3: To Verify the DGGS-Based Forwarding Algorithm
Phase 3 is to validate the correctness of the DGGS-based forwarding algorithm proposed in this paper. In the first step, the corresponding DGGS grid is generated using Dggrid version V7.0 [92]. For simplicity, the DGGS grid with a resolution of seven and a serial number of 2136 is selected. The top and bottom plates are set to be 40 km and 60 km, respectively, to obtain the corresponding DGGS cell, as shown in Figure 2, in the spherical coordinate system.
In the second step, the DGGS cell is discretized into tetrahedrons using Tetgen software, as shown in Figure 17. In the third step, taking Equation (2) as the gravitational field forward integral kernel for both tetrahedron-based and DGGS-based forwarding algorithms. Then, the result of the DGGS-based forwarding algorithm was calculated by Equation (17) with Equation (16) as the shape function, (see Figure 5b) and (see Table 1).
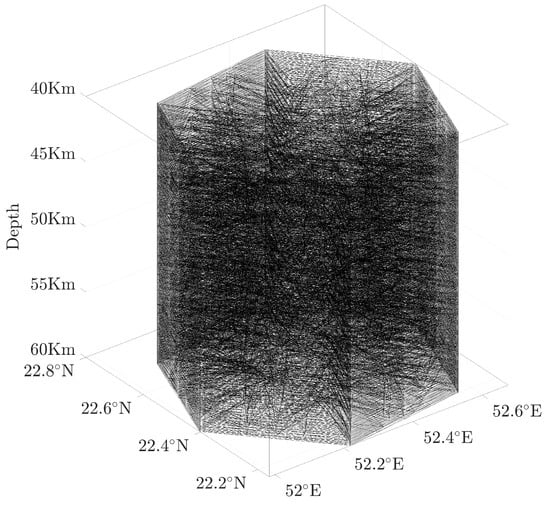
Figure 17.
Schematic diagram of a DGGS cell discretized by tetrahedrons after 3 refinements with 12,762 subcells.
Referring to Figure 4 and Figure 5 in the paper of Uieda et al. [5], when the observation altitude is 10 km, the accuracy of the tesseroid-based forwarding algorithm is more than 10% when . When the observation altitude is 260 km, the accuracy of the tesseroid-based forwarding algorithm is about 0.1% when . For this reason, the two remaining tests to validate the DGGS-based and tetrahedron-based forwarding algorithms assume that the observation point is located at 260 km and 10 km above the surface for Earth and Luna satellites, respectively, referring to the paper by Uieda et al. [5] for the forward parameter settings.
As shown in Figure 18, Figure 19, Figure 20 and Figure 21 by increasing the observed height and indirectly increasing the distance–size ratio, the residuals between the results of the DGGS-based (see Figure 18) and tetrahedron-based forwarding algorithms are significantly reduced, with a difference of about orders of magnitude.
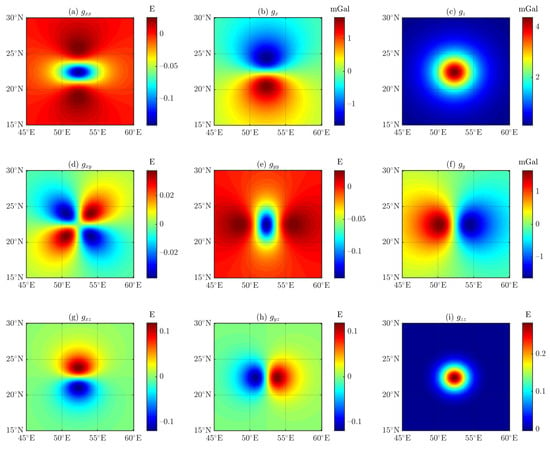
Figure 18.
Results for the DGGS (see Figure 17) using DGGS-based forwarding algorithm, 6378.137 km and the observation height is 260 km.
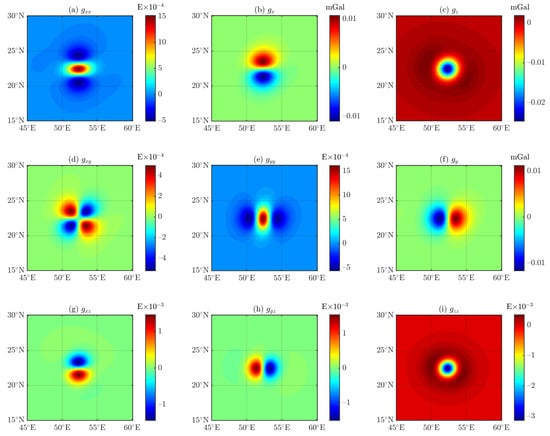
Figure 19.
Residuals between the results of the DGGS-based (see Figure 18) and tetrahedron-based forwarding algorithms (after 6 refinements with 15,491 subcells).
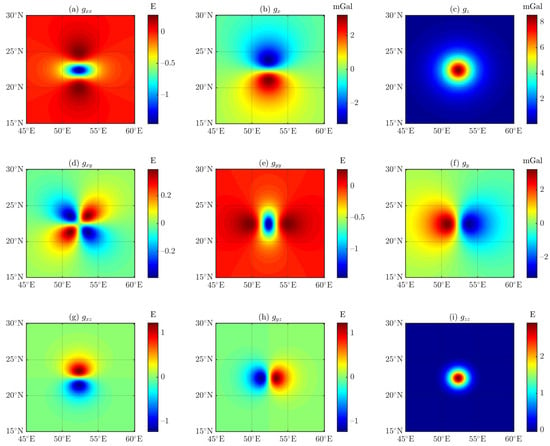
Figure 20.
Results for the DGGS (see Figure 17) using DGGS-based forwarding algorithm, 1738 km and the observation height is 10 km.
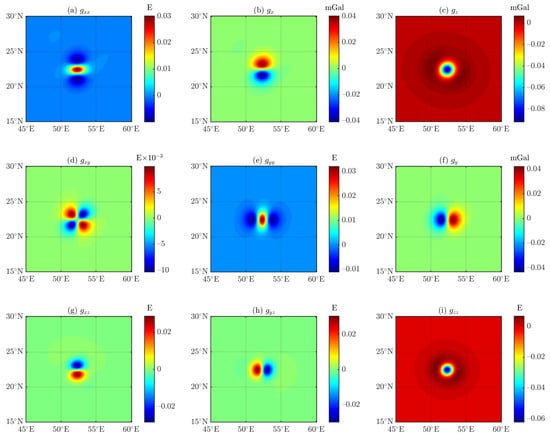
Figure 21.
Residuals between the results of the DGGS-based (see Figure 20) and tetrahedron-based forwarding algorithms (after 6 refinements with 15,491 subcells).
Referring to Figure 4 and Figure 5 in the paper of Uieda et al. [5], the results in Figure 19 and Figure 21 show that under the same parameter conditions, the computational accuracy of the DGGS-based forwarding algorithm via the isoparametric transformation is equivalent to that of the tesseroid-based forwarding algorithm via the GLQ.
5.4. Additional Test: To Verify the DGGS-Based Forwarding Algorithm Via the Tesseroid-Based Forwarding Algorithm with Tiny Tesseroids
To enhance the credibility of the DGGS-based forwarding algorithm proposed in this paper, by referring to the adaptive tesseroid-based forwarding algorithm proposed in Uieda et al. [5], the 3D space enclosed by the maximum and minimum values of the longitude, latitude, and radial directions of the DGGS cell is divided equally into tiny same-sized tesseroids 8000 = × × = 20 × 20 × 20 along the longitude, latitude, and radial directions, respectively. Those tiny tesseroids whose center coordinates are outside the DGGS cell are discarded, while those whose tesseroid center coordinates are inside the DGGS cell are retained. The tesseroid-based forwarding algorithm is used to compute the gravity vector and gravity gradient tensor values of these retained tiny tesseroids. Figure 22 shows the residuals between this experiment and the result of DGGS-based forward modeling (see Figure 18), which are about ∼10−2 and comparable to the accuracy of Figure 19.
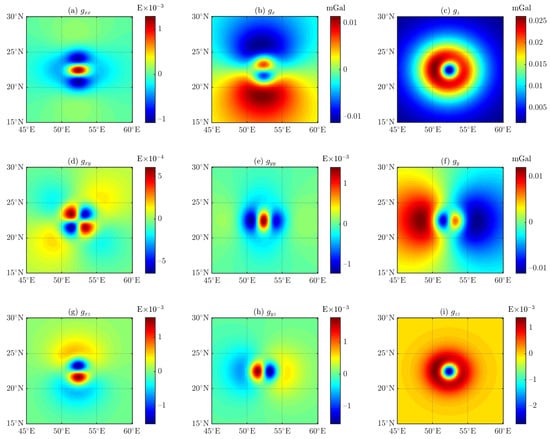
Figure 22.
Residuals between the results of the DGGS-based (see Figure 18) and tesseroid-based forwarding algorithms with 4978 tiny same-sized tesseroids.
When analyzing the lunar DGGS cell, the residual between the results of the DGGS-based and tesseroid-based forwarding algorithms using tiny tesseroids obtained by setting ≡ ≡ ≡ = 25, 50, and 100 (see Figure 22), respectively. Results similar to Figure 23 can be obtained, indicating the correctness of the DGGS-based forwarding algorithm. However, the residuals do not decrease with increasing . Compared with Figure 20, it is inferred that this may be caused by the intrinsic influence of the observation source distances on the tesseroid-based forwarding algorithm. Another indication that the tesseroid-based forwarding algorithm cannot satisfy the computational requirements for too-small observation heights.
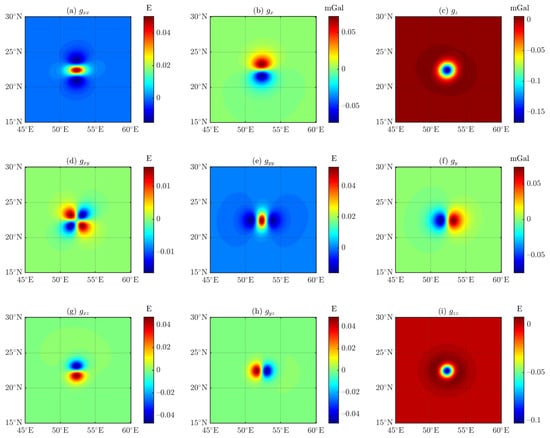
Figure 23.
Residuals between the results of the DGGS-based (see Figure 20) and tesseroid-based forwarding algorithms with 694,287 tiny same-sized tesseroids.
6. Conclusions and Recommendations
The curvature of the geophysical model cannot be approximated as a plane for regional and even global-scale problems. However, if the spherical curvature is taken into account, the prism cell cannot effectively fit the curvature; otherwise, it could reduce the accuracy of the forward computation. The tesseroid can effectively fit the curvature. However, the tesseroid has no gravitational analytical solution, which must be approximated by numerical methods. The greater the number of integration points, the higher the accuracy, but the lower the calculation efficiency.
Although tesseroids do not have gravitational analytical solutions, their integration limits are well-defined; DGGS cells have neither gravitational analytical solutions nor fixed integration limits. The isoparametric transformation converts the non-regular DGGS cell in the system coordinate system to the regular hexagonal prism in the local coordinate system. Thus, the DGGS-based forwarding algorithm is realized in the spherical coordinate system. Similar to the tesseroid-based algorithm, the integral of the proposed algorithm is implemented in the spherical coordinate system using the spherical gravity integral kernel. Therefore, the DGGS-based forwarding algorithm can also accurately fit the curvature.
Due to the difficulty of directly describing the curved surfaces of DGGS cells using facets of polyhedrons, if polyhedrons (i.e., tetrahedrons) are directly used to fit DGGS spherical shell cells, a large number of cells and nodes are required [21,28]. Furthermore, the gravitational field integral kernels are not the same under different coordinate systems [23,66]. Therefore, referring to the paper of Grombein et al. [23] on the forward integral kernel of the tesseroid in the Cartesian coordinate system given, the tetrahedron-based forwarding algorithm under different coordinate systems is used as a “bridge” to compare and analyze the difference in the calculation accuracy of tetrahedrons, rectangular elements, tesseroids, and DGGS cells. The experimental results show that the DGGS-based forwarding algorithm under the spherical coordinate system proposed in this chapter is correct. As shown in Figure 22 and Figure 23, the same accuracy as the tetrahedron-based forwarding algorithm is achieved when fitting the DGGS cell using tiny tesseroids.
With a more detailed subdivision of the model, i.e., the corresponding forward modeling results are smoother as D increases, which results in more refined tesseroids being involved in the computation, especially when d is small. Therefore, too small d or too large D are not common in practical applications.
By increasing the observation height and indirectly increasing the distance-size ratio D, the residuals between the results of the DGGS-based and the tesseroid-based forwarding algorithms are significantly reduced. Under the same parameter conditions, the computational accuracy of the DGGS-based forwarding algorithm is equivalent to that of the tesseroid-based forwarding algorithm.
The DGGS system is based on icosahedron, there are 12 pentagons for the whole globe. For the research area not greater than , existing grid data under the software DGGRID (version 7.0) can be directly used by rotating it to cover the measurement area; otherwise, the parameters must be manually adjusted to obtain the corresponding DGGS grid.
Author Contributions
Conceptualization, S.C.; methodology, S.C.; software, S.C., P.C. and D.Z.; validation, P.C., D.Z. and Y.D.; formal analysis, S.C. and P.C.; investigation, D.Z.; resources, G.L.; data curation, D.Z.; writing—original draft preparation, S.C., P.C. and G.L.; writing—review and editing, S.C., P.C., G.L. and X.C.; visualization, S.C. and Y.D.; supervision, G.L. and X.C.; project administration, S.C., G.L. and X.C.; funding acquisition, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 41704138, Grant 41974148, and in part by the Hunan Provincial Science & Technology Department of China under Grant 2017JJ3069, and in part by the Project of Doctoral Foundation of Hunan University of Science and Technology under Grant E51651, and in part by the Hunan Provincial Key Laboratory of Share Gas Resource Exploitation under Grant E21722.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| DGGS | Discrete Global Grid System |
| FEM | Finite Element Method |
| GLQ | Gauss–Legendre Quadrature |
| PLC | Piecewise Linear Complex |
| PSLG | Planar Straight Line Graph |
References
- Turcotte, D.L.; Schubert, G. Geodynamics; Cambridge University Press: Cambridge, UK, 2002; pp. 34–45. [Google Scholar] [CrossRef]
- Li, X. Curvature of a geometric surface and curvature of gravity and magnetic anomalies. Geophysics 2015, 80, 15–26. [Google Scholar] [CrossRef]
- Karegar, M.A. Theory and Application of Geophysical Geodesy for Studying Earth Surface Deformation. Master’s Thesis, University of South Florida, Tampa, FL, USA, 2018. Available online: https://digitalcommons.usf.edu/etd/7255 (accessed on 5 March 2024).
- Anderson, E.G. The Effect of Topography on Solutions of Stokes’ Problem. Ph.D. Thesis, UNSW Sydney, Kensington, Australia, 1976. [Google Scholar] [CrossRef]
- Uieda, L.; Barbosa, V.C.F.; Braitenberg, C. Tesseroids: Forward-modeling gravitational fields in spherical coordinates. Geophysics 2016, 81, F41–F48. [Google Scholar] [CrossRef]
- Deng, X.L.; Shen, W.B. Evaluation of gravitational curvatures of a tesseroid in spherical integral kernels. J. Geod. 2018, 92, 415–429. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, G.Y.; Zhu, Z.Q.; Cao, S.J. An Improved 3D Magnetization Inversion Based on Smoothness Constraints in Spherical Coordinates. Magnetochemistry 2022, 8, 157. [Google Scholar] [CrossRef]
- Holmes, S.A.; Featherstone, W.E. A unified approach to the Clenshaw summation and the recursive computation of very high degree and order normalised associated Legendre functions. J. Geod. 2002, 76, 279–299. [Google Scholar] [CrossRef]
- Freeden, W.; Michel, V.; Simons, F.J. Spherical harmonics based special function systems and constructive approximation methods. In Handbook of Mathematical Geodesy; Birkhauser: Cham, Switzerland, 2018; pp. 753–819. [Google Scholar] [CrossRef]
- Kuhn, M.; Seitz, K. Comparison of Newton’s Integral in the Space and Frequency Domains. In A Window on the Future of Geodesy; Michael, K., Kurt, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 128, pp. 386–391. [Google Scholar] [CrossRef]
- Du, J.S.; Chen, C.; Liang, Q.; Wang, L.S.; Zhang, Y.; Wang, Q.G. Gravity Anomaly Calculation Based on Volume Integral in Spherical Cap and Comparison with the Tesseroid- Taylor Series Expansion Approach. Acta Geod. Cartogr. Sin. 2012, 41, 339–346. Available online: https://api.semanticscholar.org/CorpusID:124351845 (accessed on 15 January 2024).
- Sahr, K.; White, D.; Kimerling, A.J. Geodesic Discrete Global Grid Systems. Cartogr. Geogr. Inf. Sci. 2003, 30, 121–134. [Google Scholar] [CrossRef]
- Barsoum, R.S. Triangular quarter-point elements as elastic and perfectly-plastic crack tip elements. Int. J. Numer. Methods Eng. 1977, 11, 85–98. [Google Scholar] [CrossRef]
- Carlin, H.J. Distributed circuit design with transmisssion line elements. Proc. IEEE 1971, 59, 1059–1081. [Google Scholar] [CrossRef]
- Pfister, H.; Zwicker, M.; van Baar, J.; Gross, M. Surfels: Surface Elements as Rendering Primitives. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 23–28 July 2000; pp. 335–342. [Google Scholar] [CrossRef]
- Autrey, T.; Foster, N.S.; Klepzig, K.; Amonette, J.E.; Daschbach, J.L. A new angle into time-resolved photoacoustic spectroscopy: A layered prism cell increases experimental flexibility. Rev. Sci. Instrum. 1998, 69, 2246–2258. [Google Scholar] [CrossRef]
- Baykiev, E.; Ebbing, J.; Brönner, M.; Fabian, K. Forward modeling magnetic fields of induced and remanent magnetization in the lithosphere using tesseroids. Comput. Geosci. 2016, 96, 124–135. [Google Scholar] [CrossRef]
- Heck, B.; Seitz, K. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J. Geod. 2007, 81, 121–136. [Google Scholar] [CrossRef]
- Wang, W.; Cao, Y.; Okaze, T. Comparison of hexahedral, tetrahedral and polyhedral cells for reproducing the wind field around an isolated building by LES. Build. Environ. 2021, 195, 107717. [Google Scholar] [CrossRef]
- Sigg, C.; Peikert, R.; Gross, M. Signed Distance Transform Using Graphics Hardware. In Proceedings of the 14th IEEE Visualization 2003, Seattle, WA, USA, 19–24 October 2003; p. 12. [Google Scholar] [CrossRef]
- Zhong, Y.Y.; Ren, Z.Y.; Chen, C.J.; Chen, H.; Yang, Z.; Guo, Z.W. A new method for gravity modeling using tesseroids and 2D Gauss-Legendre quadrature rule. J. Appl. Geophys. 2019, 164, 53–64. [Google Scholar] [CrossRef]
- Ku, C.C. A direct computation of gravity and magnetic anomalies caused by 2- and 3-dimensional bodies of arbitrary shape and arbitrary magnetic polarization by equivalent-point method and a simplified cubic spline. Geophysics 1977, 42, 610–622. [Google Scholar] [CrossRef]
- Grombein, T.; Seitz, K.; Heck, B. Optimized formulas for the gravitational field of a tesseroid. J. Geod. 2013, 87, 645–660. [Google Scholar] [CrossRef]
- Yao, C.; Hao, T.; Guan, Z.; Zhang, Y. High-Speed Computation and Efficient Storage in 3-D Gravity and Magnetic Inversion. Chin. J. Geophys. 2003, 46, 252–258. [Google Scholar] [CrossRef]
- Saraswati, A.T.; Cattin, R.; Mazzotti, S.; Cadio, C. New analytical solution and associated software for computing full-tensor gravitational field due to irregularly shaped bodies. J. Geod. 2019, 93, 2481–2497. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Chen, C.J.; Tang, J.T.; Chen, H.; Hu, S.G.; Zhou, C.; Xiao, X. Closed-form formula of magnetic gradient tensor for a homogeneous polyhedral magnetic target: A tetrahedral grid example. Geophysics 2017, 82, WB21–WB28. [Google Scholar] [CrossRef]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1996; pp. 419–435. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Zhong, Y.Y.; Chen, C.J.; Tang, J.T.; Pan, K.J. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics 2018, 83, G1–G13. [Google Scholar] [CrossRef]
- Wills, A.P.; Kyame, J.J. Vector Analysis with an Introduction to Tensor Analysis. Am. J. Phys. 1959, 27, 433. [Google Scholar] [CrossRef]
- Rathod, H.; Nagaraja, K.; Venkatesudu, B. Numerical integration of some functions over an arbitrary linear tetrahedra in Euclidean three-dimensional space. Appl. Math. Comput. 2007, 191, 397–409. [Google Scholar] [CrossRef]
- Tsoulis, D.; Gavriilidou, G. A computational review of the line integral analytical formulation of the polyhedral gravity signal. Geophys. Prospect. 2021, 69, 1745–1760. [Google Scholar] [CrossRef]
- Conway, J.T. Analytical solution from vector potentials for the gravitational field of a general polyhedron. Celest. Mech. Dyn. Astron. 2015, 121, 17–38. [Google Scholar] [CrossRef]
- Zhou, X.B. General line integrals for gravity anomalies of irregular 2D masses with horizontally and vertically dependent density contrast. Geophysics 2009, 74, I1–I7. [Google Scholar] [CrossRef]
- Zhang, Q.j. Research on the Volumerendering of Global Scalar Databasing on Hexagonal Mesh. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, 2016. Available online: https://cdmd.cnki.com.cn/Article/CDMD-10216-1016764468.htm (accessed on 13 December 2023). (In Chinese).
- Peterson, P.R. Discrete global grid systems. In International Encyclopedia of Geography: People, the Earth, Environment and Technology; Wiley: Hoboken, NJ, USA, 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Lu, N.; Cheng, C.Q.; Ma, H.J.; Yang, Y.B. Global discrete grid systems analysis and comparison. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2771–2774. [Google Scholar] [CrossRef]
- Perraudin, N.; Defferrard, M.; Kacprzak, T.; Sgier, R. DeepSphere: Efficient spherical Convolutional Neural Network with HEALPix sampling for cosmological applications. Astron. Comput. 2018, 27, 130–146. [Google Scholar] [CrossRef]
- Bondaruk, B.; Roberts, S.A.; Robertson, C. Assessing the state of the art in Discrete Global Grid Systems: OGC criteria and present functionality. Geoinformatica 2020, 74, 9–30. [Google Scholar] [CrossRef]
- Status, B. H3: A Hexagonal Hierarchical Geospatial Indexing System. 2015. Available online: https://github.com/xszhaob/h3/blob/master/README.md (accessed on 5 January 2024).
- Cheng, C.Q.; Tong, X.C.; Chen, B.; Zhai, W.X. A Subdivision Method to Unify the Existing Latitude and Longitude Grids. ISPRS Int. J. Geo Inf. 2016, 5, 161. [Google Scholar] [CrossRef]
- Gibb, R.G. The rHEALPix Discrete Global Grid System. IOP Conf. Ser. Earth Environ. Sci. 2016, 34, 012012. [Google Scholar] [CrossRef]
- Ben, J.; Tong, X.C.; Zhang, Y.S.; Zhang, H.Z. Discrete global grid systems: Generating algorithm and software model. In Proceedings of the Geoinformatics 2006: Geospatial Information Technology, Wuhan, China, 28–29 October 2006; Volume 6421, p. 64210J. [Google Scholar] [CrossRef]
- Breunig, M.; Bradley, P.E.; Jahn, M.W.; Kuper, P.V.; Mazroob, N.; Rösch, N.; Al-Doori, M.; Stefanakis, E.; Jadidi, M. Geospatial Data Management Research: Progress and Future Directions. ISPRS Int. J. Geo Inf. 2020, 9, 95. [Google Scholar] [CrossRef]
- Li, M.; McGrath, H.; Stefanakis, E. Integration of heterogeneous terrain data into Discrete Global Grid Systems. Cartogr. Geogr. Inf. Sci. 2021, 48, 546–564. [Google Scholar] [CrossRef]
- Sun, W.B.; Zhao, X.S.; Gao, Y.L.; Wang, H.B. Partition Methods and Character Analysis of Near-Equal Grids on Spherical Facet. Geogr. Geo-Inf. Sci. 2009, 25, 53–56+60. Available online: https://api.semanticscholar.org/CorpusID:123763671 (accessed on 12 November 2023). (In Chinese).
- Peterson, P. Close-Packed, Uniformly Adjacent, Multiresolutional, Overlapping Spatial Data Orderin. 2004. Available online: https://data.epo.org/gpi/EP1654707A1.pdf (accessed on 6 November 2023).
- Apparicio, P.; Gelb, J.; Dubé, A.S.; Kingham, S.; Gauvin, L.; Robitaille, É. The approaches to measuring the potential spatial access to urban health services revisited: Distance types and aggregation-error issues. Int. J. Health Geogr. 2017, 16, 1–24. [Google Scholar] [CrossRef]
- Reddy, J.N. Introduction to the Finite Element Method; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Szabó, B.; Babuška, I. Finite Element Analysis: Method, Verification and Validation; Wiley: Hoboken, NJ, USA, 2021; pp. 1–384. [Google Scholar] [CrossRef]
- Cotter, C.J. Compatible finite element methods for geophysical fluid dynamics. Acta Numer. 2023, 32, 291–393. [Google Scholar] [CrossRef]
- Liu, W.H.; He, Z.T.; Yao, W.; Li, M.H.; Tang, J.G. XFEM simulation of the effects of microstructure on the intergranular fracture in high strength aluminum alloy. Comput. Mater. Sci. 2014, 84, 310–317. [Google Scholar] [CrossRef]
- Jiang, Y.Z.; Hu, Y.F.; Fu, Z.P.; Zhu, S.Q. Defects analysis of the ultra-thick steel pipes using a mixed explicit-implicit FEM. Metall. Res. Technol. 2022, 119, 111. [Google Scholar] [CrossRef]
- Bishop, J.E. A displacement-based finite element formulation for general polyhedra using harmonic shape functions. Int. J. Numer. Methods Eng. 2014, 97, 1–31. [Google Scholar] [CrossRef]
- Qian, X.D.; Ren, Q.W. An Efficient Isoparametric Finite Element Inverse Conversion Method. Eur. J. Comput. Mech. Eur. 1998, 15, 437–441. [Google Scholar]
- Moens, D.; Hanss, M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: Recent advances. Finite Elem. Anal. Des. 2011, 47, 4–16. [Google Scholar] [CrossRef]
- Jeng, G.; Wexler, A. Isoparametric, finite element, variational solution of integral equations for three-dimensional fields. Int. J. Numer. Methods Eng. 1977, 11, 1455–1471. [Google Scholar] [CrossRef]
- Baraldi, D.; Tullini, N. In-plane bending of Timoshenko beams in bilateral frictionless contact with an elastic half-space using a coupled FE-BIE method. Eng. Anal. Bound. Elem. 2018, 97, 114–130. [Google Scholar] [CrossRef]
- Lehrenfeld, C. High order unfitted finite element methods on level set domains using isoparametric mappings. Comput. Methods Appl. Mech. Eng. 2015, 300, 716–733. [Google Scholar] [CrossRef]
- Lehrenfeld, C.; Reusken, A. High Order Unfitted Finite Element Methods for Interface Problems and PDEs on Surfaces. In Transport Processes at Fluidic Interfaces; Birkhauser: Cham, Switzerland, 2017; pp. 33–63. Available online: https://api.semanticscholar.org/CorpusID:46431176 (accessed on 9 January 2024).
- Belarbi, M.O.; Tati, A.; Ounis, H.; Benchabane, A. Development of a 2D isoparametric finite element modelbased on the layerwise approach for the bending analysis of sandwich plates. Struct. Eng. Mech. 2016, 57, 473–506. [Google Scholar] [CrossRef]
- Belkaid, K. Development of a 2D Isoparametric Finite-Element Model Based on Reddy’s Third-Order Theory for the Bending Behavior Analysis of Composite Laminated Plates. Mech. Compos. Mater. 2019, 55, 241–258. [Google Scholar] [CrossRef]
- Liu, W.H.; Qiu, Q.; Chen, Y.Q.; Tang, C.P. Simulation of PFZ on intergranular fracture based on XFEM and CPFEM. J. Cent. South Univ. 2016, 23, 2500–2505. [Google Scholar] [CrossRef]
- Wang, T.H.; Cai, Z.H.; Zhao, Y.F.; Wang, W.; Zheng, G.Q.; Wang, Z.; Wang, Y. The Influence of Cross-Links on Long-Segment Instrumentation Following Spinal Osteotomy: A Finite Element Analysis. World Neurosurg. 2019, 123, e294–e302. [Google Scholar] [CrossRef] [PubMed]
- Celia, M.A.; Gray, W.G. An improved isoparametric transformation for finite element analysis. Int. J. Numer. Methods Eng. 1984, 20, 1443–1459. [Google Scholar] [CrossRef]
- Edelmann, D. Isoparametric finite element analysis of a generalized Robin boundary value problem on curved domains. SMAI J. Comput. Math. 2020, 7, 57–73. [Google Scholar] [CrossRef]
- Deng, X.L.; Shen, W.B. Formulas of Gravitational Curvatures of Tesseroid Both in Spherical and Cartesian Integral Kernels. In Proceedings of the European Geosciences Union General Assembly, Vienna, Austria, 23–28 April 2017; Volume 93, pp. 14–23. [Google Scholar]
- von Frese, R.; Hinze, W.J.; Braile, L.W.; Luca, A.J. Spherical earth gravity and magnetic anomaly modeling by Gauss-Legendre Quadrature integration. J. Geophys. 1981, 49, 234–242. [Google Scholar]
- Asgharzadeh, M.F.; Von Frese, R.R.B.; Kim, H.R.; Leftwich, T.E.; Kim, J.W. Spherical prism gravity effects by Gauss-Legendre quadrature integration. Geophys. J. Int. 2007, 169, 1–11. [Google Scholar] [CrossRef]
- Chen, N.; Zhu, S.Y.; Li, Y.L. The Case Study of Pseudoexcitation Method Combining Self-Adaptive Gauss Integration in Random Vibration Analysis. Shock Vib. 2019, 2019, 9154016. [Google Scholar] [CrossRef]
- Wang, X.C. Fundamentals and Numerical Methods of the Finite Element Method; Tsinghua University Press: Beijing, China, 1997; pp. 33–37. (In Chinese) [Google Scholar]
- Si, D.C.; Wang, J.A.; Wei, G.; Yan, X.J. Method and experimental study of voltage measurement based on electric field integral with Gauss-Legendre algorithm. IEEE Trans. Instrum. Meas. 2019, 69, 2771–2778. [Google Scholar] [CrossRef]
- Cao, S.J. Slope Response in DC Resistivity Model by Using Three-Dimensional Finite Element Method. Master’s Thesis, Central South University, Changsha, China, 2009. (In Chinese). [Google Scholar]
- Wang, X.C. Finite Element Method; Tsinghua University Press: Beijing, China, 2003; pp. 15–40. (In Chinese) [Google Scholar]
- Armattoe, K.M.; Bouby, C.; Haboussi, M.; Zineb, T.B. Modeling of latent heat effects on phase transformation in shape memory alloy thin structures. Int. J. Solids Struct. 2016, 88, 283–295. [Google Scholar] [CrossRef]
- Baye, D.; Eraly, J.D.; Schoofs, P. Structure changes along the lowest rotational band of the antiprotonic helium atom. Phys. Rev. A 2019, 99, 022508. [Google Scholar] [CrossRef]
- Kamiński, M. Hexagonal finite elements in heat conduction. Int. Commun. Heat Mass Transfer 2005, 32, 1143–1151. [Google Scholar] [CrossRef]
- Chari, M.V.; Salon, S.J. Numerical Methods in Electromagnetism; Academic Press: Cambridge, MA, USA, 2000; pp. 494–516. [Google Scholar] [CrossRef]
- Jerome, S.; Axel, R.; Conrad, B. Integrating Finite Element Analysis with Systems Engineering Models. In Proceedings of the NAFEMS World Congress 2017, Stockholm, Sweden, 11–13 June 2017; Available online: https://api.semanticscholar.org/CorpusID:58914576 (accessed on 1 November 2023).
- Duczek, S.; Duvigneau, F.; Gabbert, U. The finite cell method for tetrahedral meshes. Finite Elem. Anal. Des. 2016, 121, 18–32. [Google Scholar] [CrossRef]
- Cao, S.J.; Zhu, Z.J.; Lu, G.Y.; Zeng, S.G.; Guo, W.B. Forward modelling of full gravity gradient tensors based H-Adaptive mesh refinement. Prog. Geophys. 2010, 25, 1015–1023. (In Chinese) [Google Scholar]
- Jiang, S.; Jiang, W.S.; Li, L.L.; Wang, L.Z.; Huang, W. Reliable and Efficient UAV Image Matching via Geometric Constraints Structured by Delaunay Triangulation. Remote Sens. 2020, 12, 3390. [Google Scholar] [CrossRef]
- Hang, S. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Trans. Math. Softw. 2015, 41, 11. [Google Scholar] [CrossRef]
- Li, X.; Chouteau, M. Three dimensional gravity modeling in all space. SEG Tech. Program Expand. Abstr. 1997, 474–477. [Google Scholar] [CrossRef]
- Ren, Z.Y. DC Resistivity Adaptive Finite Element Numerical Simulation Based on Unstructured Grid. Master’s Thesis, Central South University, Changsha, China, 2007. (In Chinese). [Google Scholar]
- Shewchuk, J.R. Delaunay refinement algorithms for triangular mesh generation. Comput. Geom. 2002, 22, 21–74. [Google Scholar] [CrossRef]
- Pain, C.C.; Umpleby, A.P.; de Oliveira, C.; Goddard, A.J.H. Tetrahedral mesh optimisation and adaptivity for steady-state and transient finite element calculations. Comput. Methods Appl. Mech. Eng. 2001, 190, 3771–3796. [Google Scholar] [CrossRef]
- Pierre, A.; David, C.S.; Mariette, Y.; Mathieu, D. Variational tetrahedral meshing. ACM Trans. Graph. 2005, 24, 617–625. [Google Scholar] [CrossRef]
- Liu, J.H.; Li, Q.Y.; Xiong, Z.G.; Zhu, Q.D. L∞- and L2-norms superconvergence of the tetrahedral quadratic finite element. Comput. Math. Appl. 2023, 149, 71–74. [Google Scholar] [CrossRef]
- Li, Z.W.; Hao, T.Y.; Xu, Y.; Xu, Y. An efficient and adaptive approach for modeling gravity effects in spherical coordinates. J. Appl. Geophys. 2011, 73, 221–231. [Google Scholar] [CrossRef]
- Bahl, A.; Teleki, A.; Jakobsen, P.K.; Wright, E.M.; Kolesik, M. Reflectionless Beam Propagation on a Piecewise Linear Complex Domain. J. Light. Technol. 2014, 32, 4272–4278. [Google Scholar] [CrossRef]
- Johnson, M.P.; Sariöz, D. Representing a Planar Straight-Line Graph Using Few Obstacles. In Proceedings of the Canadian Conference on Computational Geometry, Halifax, NS, Canada, 11–13 August 2014; pp. 72–90. Available online: https://api.semanticscholar.org/CorpusID:3901829 (accessed on 18 November 2023).
- Sahr, K. DGGRID Version 7.0: User Documentation for Discrete Global Grid Software; Southern Oregon University: Ashland, OR, USA, 2019; pp. 14–23. Available online: https://webpages.sou.edu/~sahrk/docs/dggridManualV70.pdf (accessed on 2 November 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).