Handling Overlapping Asymmetric Data Sets—A Twice Penalized P-Spline Approach

Abstract

Aims: Overlapping asymmetric data sets are where a large cohort of observations have a small amount of information recorded, and within this group there exists a smaller cohort which have extensive further information available. Missing imputation is unwise if cohort size differs substantially; therefore, we aim to develop a way of modelling the smaller cohort whilst considering the larger. Methods: Through considering traditionally once penalized P-Spline approximations, we create a second penalty term through observing discrepancies in the marginal value of covariates that exist in both cohorts. Our now twice penalized P-Spline is designed to firstly prevent over/under-fitting of the smaller cohort and secondly to consider the larger cohort. Results: Through a series of data simulations, penalty parameter tunings, and model adaptations, our twice penalized model offers up to a 58% and 46% improvement in model fit upon a continuous and binary response, respectively, against existing B-Spline and once penalized P-Spline methods. Applying our model to an individual’s risk of developing steatohepatitis, we report an over 65% improvement over existing methods. Conclusions: We propose a twice penalized P-Spline method which can vastly improve the model fit of overlapping asymmetric data sets upon a common predictive endpoint, without the need for missing data imputation.

1. Introduction

In data science and statistics, it is common to have data sets which mix cheap and easy-to-obtain information for a large sample of cases with more expensive and hard-to-acquire additional information for a small sample of cases. In an epidemiological study, for instance, a cohort may consist of a large number of individuals whose demographic characteristics and phenotypes have been recorded, together with a smaller number who additionally have biomarker data or genetic profiles. The purpose of this paper is to introduce a method which enhances analysis of the smaller group by making best use of data from the larger group.

One approach might be to consider the detailed information as being missing for the larger cohort, and then to adopt one of the many missing-data methodologies now available. Kang (2013) presents several techniques for handling missing data, including case deletion, mean substitution, and multiple imputation [1]. Indeed, one of the most common and popular tools for handling missing data is the missing imputation tool MICE (Multiple Imputation by Chained Equations), which is an available library in a vast number of coding languages [2]. However, when there is a large proportion of missing data, Multiple Imputation (MI) is not considered to be the most effective way of dealing with missing data issues [3]. Many authors have attempted to provide ‘cutoff’ points for an acceptable amount of missing data that MI can handle [4,5]; however, these are found to be largely arbitrary and other factors need to be taken into account such as types of missingness and imputation mechanisms, although vast amounts of missing data are unsuited to MI. This paper explores how we can utilise the larger cohort of individuals to enhance what is learnt from the smaller cohort, without the need for imputation.

Let us assume that there are two data sets: Horizontal Data (denoted $\mathcal{H}$) and Vertical Data (denoted $\mathcal{V})$. For simplicity, $\mathcal{H}$ has a sample size of $N_{\mathcal{H}}$ with two scalar covariates x and z, $\mathcal{V}$ has a sample size of $N_{\mathcal{V}}$ with only one covariate x, and in our case $N_{\mathcal{V}}$≫$N_{\mathcal{H}}$. Both data sets contain a response variable y. In reality, x and z would represent a selection of covariates each as we will show in Section 6. The validity of reducing multiple covariates into single x and z vectors is discussed later. Illustrated in Figure 1 is how each data set may look in practice:

We see that the $\mathcal{V}$ data set is tall and thin, while the $\mathcal{H}$ data set is short and wide; hence the naming, Vertical and Horizontal data sets. Our overarching research question is therefore whether it is possible to utilise what we learn from $\mathcal{V}$ to enhance the predictive performance and modelling upon observations within $\mathcal{H}$, thus improving our knowledge about response variable y.

To tackle this research question, we firstly display the knowledge and motivation for studying non-parametric modelling techniques in Section 2, wherein we specifically focus upon smoothing methods and penalized regression modelling including B-Splines and P-Splines. We show that they display specific qualities that make them attractive for modelling our smaller cohort $\mathcal{H}$ and also show in Section 3 that they can be adapted into a new model that is able to consider the larger cohort $\mathcal{V}$ through including a second penalty term which takes into account discrepancies in the marginal value of x, i.e., covariates that exist in both $\mathcal{H}$ and $\mathcal{V}$. We compare our twice penalized model structure against a linear B-Spline model and single penalty P-Spline estimation upon a series of controlled data simulations in Section 4, before adapting our model further to take into account a binary response y in Section 5. We will finally apply our model upon a real healthcare data set in Section 6, where we utilise a large cohort of individuals who have undergone baseline tests, alongside a smaller cohort who have extensive further testing in order to predict an individual’s risk of developing metabolic dysfunction associated with steatohepatitis (MASH). A discussion surrounding our work is presented in Section 7, before concluding our work in Section 8.

2. Background

2.1. Flexible Smoothing with Splines

Within this work, we focus solely upon non-parametric models specifically to take into account conditional models. Our motivation for going this route is shown in Appendix A. Many non-parametric modelling techniques exist; one popular approach is smoothing, in particular spline methods. Eilers and Marx [6] cite several reasons for their popularity including data sets being too complex to be modelled sufficiently through parametric models, and also an increasing demand for graphical representations and exploratory data analysis.

2.1.1. An Introduction to Smooth Functions

Let us assume that x is a vector. A linear model therefore assumes:

$$E[y|x]={\beta }_0+{\beta }_1{x}_1+\dots$$

(1)

A generalised linear model assumes that:

$$g\left(E[y|x]\right)={\beta }_0+{\beta }_1{x}_1+\dots$$

(2)

where $g(.)$ is some function.

When introducing generalised additive models (GAMs), first proposed by Hastie and Tibshirani (1986) [7], it should first be noted that GAMs build upon familiar likelihood-based regression models in a way that provides more robustness and flexibility, such that more complex distributed data points can be modelled beyond linear or polynomial regression. If there is a single covariate, a GAM assumes a model that is of the form:

$$g\left(E[y|x]\right)={\beta }_0+\gamma \left(x\right)$$

(3)

where $\gamma (.)$ is a smooth function. With regards to how we select x, one way is through a polynomial model that is of the form:

$$g\left(E[y|x]\right)={\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2+{\beta }_3{x}^3+\dots$$

(4)

However, a more flexible alternative is provided by the use of basis functions:

$$g\left(E[y|x]\right)={\beta }_0+{\beta }_1{S}_1\left(x\right)+{\beta }_2{S}_2\left(x\right)+{\beta }_3{S}_3\left(x\right)+\dots$$

(5)

evaluated at $S_1\left(x\right)=x$, $S_2\left(x\right)=x^2$, $S_3\left(x\right)=x^3$ and so on. Here, $S_1(.),S_2(.),S_3(.)$, etc., are smooth basis functions which can be displayed with a basis matrix, with each row being evaluated at different values for x.

2.1.2. An Introduction to Splines

Common basis functions are spline basis functions. Spline models split the x-axis into separate intervals and assume a different model for each, as for example:

$$S_1\left(x\right)=\left\{\begin{array}{c}{S}_1^{*}\left(x\right),0<x\le 1\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(6)

$$S_2\left(x\right)=\left\{\begin{array}{c}{S}_2^{*}\left(x\right),1<x\le 2\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(7)

The joins between each interval are known as ‘knots’. In order for the function to be differentiable everywhere and therefore smooth at the knots, the following conditions must also hold:

$$S_1\left(1\right)=S_2\left(1\right),S_1^{\prime }\left(1\right)=S_2^{\prime }\left(1\right),S_1^{″}\left(1\right)=S_2^{″}\left(1\right),\dots$$

(8)

In practice, it is usually sufficient that the derivatives up to $S^{″}\left(x\right)$ match at the knots; this is because the human eye struggles to detect higher order discontinuities [8]. The number and placement of knots, the choice of smooth polynomial pieces that are fitted between two consecutive knots, and whether or not a penalty term is included, are what defines the type of spline—for now we focus upon non-penalized splines, specifically B-Splines.

2.1.3. B-Splines

First proposed by Schoenberg (1946) [9], B-Splines became an increasingly popular tool for mathematical smoothing in the 1970s following publications by De Boor [10] and Cox [11]. B-Splines are highly attractive in non-parametric modelling and indeed Cox writes that B-Splines are ‘eminently suitable for many numerical calculations’. Eilers and Marx [6] and Perperoglou [8] offer good summaries of the key properties and advantages of modelling with B-Splines, along with a review of the thousands of software packages that exist for spline procedures. A B-Spline of degree q consists of $q+1$ polynomial pieces each of degree q, which join together at q inner knots. At the inner knots, the derivatives up to $q-1$ are continuous and therefore provide a smooth function. The B-Spline is positive upon the support that is spanned over $q+2$ knots and is 0 everywhere else [6]; this provides the advantage of high numerical stability and makes them relatively simple to compute.

Let us temporarily assume a model that is linear in selected spline functions of a single covariate, x. Further, we assume n independent replications, so now for $i=1,2,\dots ,n$

$$y_i=\sum _{j=1}^m{\beta }_j{S}_j\left(x_i\right)+{\epsilon }_i$$

(9)

where ${\epsilon }_i$ is a zero mean error, and exactly one of the spline terms corresponds to an intercept. This is a standard linear model, which can be written in vector form

$$y=D\beta +\epsilon$$

(10)

where y, $\beta$, and $\epsilon$ are vectors of appropriate length, and D is a design matrix with row i corresponding to the spline vector of observation i.

The standard least-squares estimator is

$$\hat{\beta }={\left(D^{T}D\right)}^{-1}{D}^{T}y$$

provided that $D^{T}D$ is invertible.

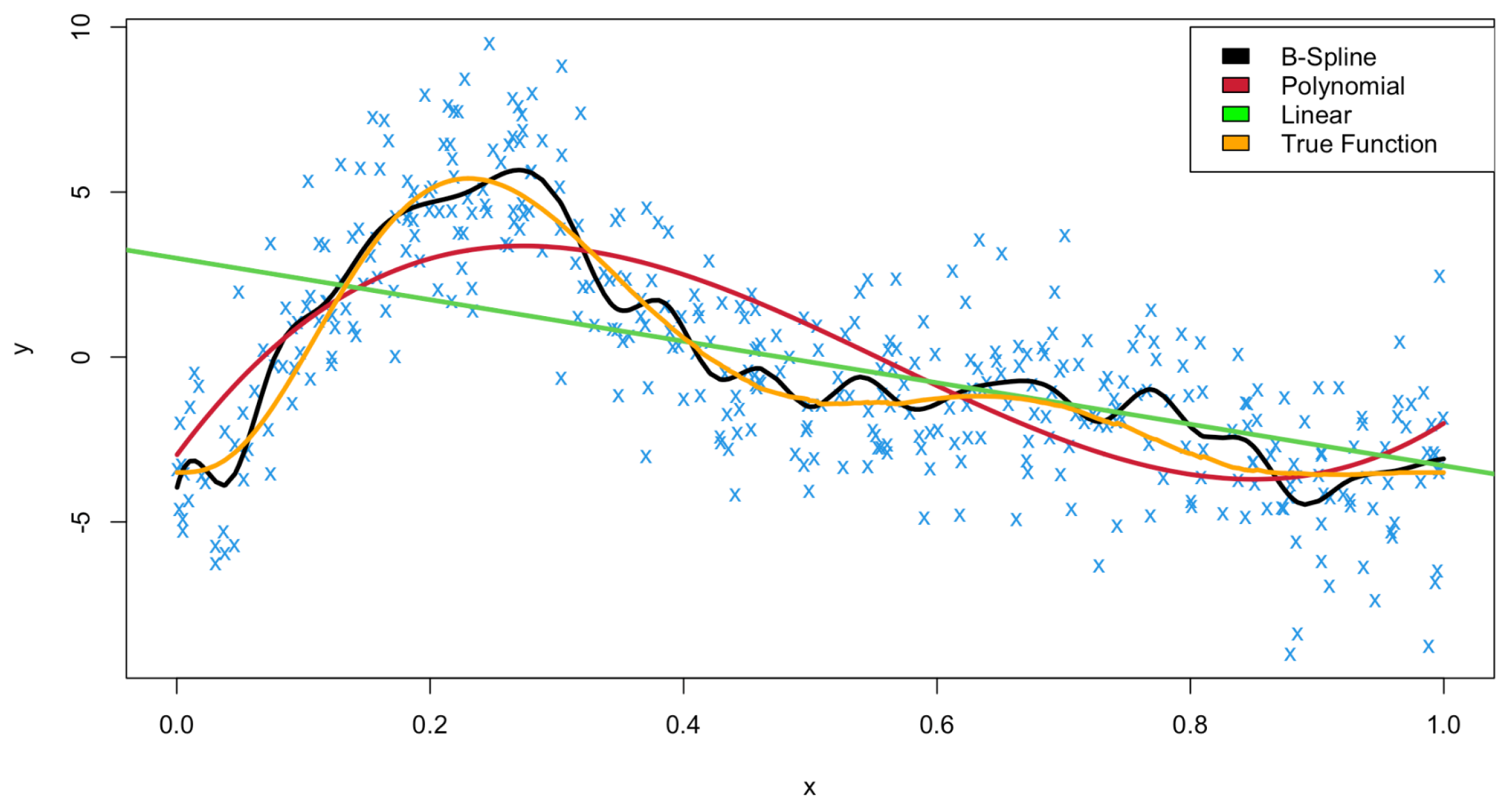
An advantage of expressing coefficient vector ${\beta }_j$ in Equation (9) as linear is that we can interpret the estimation of y as an optimisation problem in $S_j\left(x_i\right)$. This means that traditional estimation methods can be used for splines in generalized multivariable regression models [8]. Through fitting three kinds of model: linear regression (green), polynomial regression (red), and a B-Spline (black) along with the true relationship between x and y (orange) we illustrate in Figure 2 how a B-Spline can flexibly and robustly fit data in which there is no obvious linear or polynomial relationship amongst bivariate data. All graphical outputs within this work were created using R. For details on how this data was generated, see Appendix B.

The B-Spline fit is comprised of polynomials of degree 3; hence, they are cubic polynomials, and the number of knots is set to 50—this splits the domain [0,1] into 51 equidistant parts where a cubic spline is fitted within each subinterval and fused together at each knot by the conditions outlined above. Interestingly, the polynomial fit is fitted also by using a B-Spline basis; however, the number of knots is set to zero, and the result is ultimately a standard cubic polynomial fit. The linear fit is simply a straight-line relationship between x and y. We see from Figure 2 that the B-Spline provides a far more flexible, robust, and accurate modelling interpretation of the data, fitting more closely to the true function in orange than the linear or polynomial fits. Indeed, when comparing the sum of squares for the fitted values, we find that the B-Spline has a value of 139.0, compared to values of 726.4 for the polynomial fit and 2095.3 for the linear fit. Our B-Spline fit in this case provides a 93% improvement over the linear model and an 80% improvement upon the polynomial model.

Selecting the number of knots is important: too high a number of knots can result in overfitting with high variance, whereas if the number of knots is too low, this can result in an underfit with high bias where the relationship is not properly observed [8]. Figure 3 demonstrates four cubic splines with varying numbers of knots. We see from here that when the number of knots is equal to 1, there is an underfit, and there is a gross overfit when the number of knots is equal to 100. The spline fits where the number of knots is equal to 10 and 25, providing a more appropriate fit of the real data.

2.1.4. P-Splines (Penalized B-Splines)

Whilst unpenalized splines (also known as ‘regresssion splines’) have their flexibility controlled by the number of knots, penalized splines also known as ‘smoothing splines’ have theirs controlled by a penalty term, meaning that less emphasis is required on the choice of the number and position of the knots in order to avoid a potential under/over-fit of the data. One example of which is a P-Spline, short for penalized B-Spline. B-Splines are formed sequentially and ordered; therefore, for a smooth function, we expect neighbouring coefficients to be similar. Eilers and Marx in their work “Flexible Smoothing with B-Splines and Penalties” (1996) [6] proposed a penalty term based upon the higher order finite differences of these coefficient terms of adjacent B-Splines. This approach is a generalisation of O’Sullivan’s work in 1986 who created a penalty based upon the second derivative of the fitted curve [12]. The formed objective function, i.e., the sum of squares (SS), is therefore represented as follows:

$$SS=\sum _{i=1}^n{\left\{y_i-\sum _{j=1}^n{\beta }_j{S}_j\left(x_i\right)\right\}}^2+\lambda \sum _{j=3}^m{\left\{{\mathsf{\Delta }}^2{\beta }_j\right\}}^2$$

(11)

in which the first term before the additive is the sum of squares between the observed data and the fitted B-Splines, and the second term after the additive is the penalty term which is controlled by smoothing parameter $\lambda$. The $\lambda$ penalty term determines the level of smoothness that occurs, with smaller values resulting in a more jagged rougher spline, and larger values leading to smoother straighter curves. $\mathsf{\Delta }$ is a difference operator with

$$\mathsf{\Delta }{\beta }_j={\beta }_j-{\beta }_{j-1}$$

(12)

and ${\mathsf{\Delta }}^2$ is the second order difference

$$\begin{array}{cc}\hfill {\mathsf{\Delta }}^2{\beta }_j=\mathsf{\Delta }\left(\mathsf{\Delta }{\beta }_j\right)=\mathsf{\Delta }{\beta }_j-\mathsf{\Delta }{\beta }_{j-1}& =({\beta }_j-{\beta }_{j-1})-({\beta }_{j-1}-{\beta }_{j-2})\hfill \\ \hfill & ={\beta }_j-2{\beta }_{j-1}+{\beta }_{j-2}.\hfill \end{array}$$

(13)

The penalties are therefore squared linear combinations of the coefficients. We can collect the coefficients into a matrix C to give

$$\sum _{j=3}^n{\left\{{\mathsf{\Delta }}^2{\beta }_j\right\}}^2={\beta }^T{C}^{T}C\beta ,$$

(14)

a quadratic in $\beta$, just as for the first term. It therefore follows that the sum of squares (SS) for a B-Spline with the Eilers and Marx higher order difference penalty is

$$\begin{array}{cc}\hfill SS& ={(y-S\beta )}^T(y-S\beta )+\lambda \sum _j{\left({\mathsf{\Delta }}^2{\beta }_j\right)}^2\hfill \\ \hfill & =y^{T}y-2y^{T}S\beta +{\beta }^T{S}^{T}S\beta +\lambda \left({\beta }^T{C}^{T}C\beta \right).\hfill \end{array}$$

(15)

The estimated coefficients $\hat{\beta }$ can be found through minimising the SS. We therefore are able to find an equation for a fitted curve using a B-Spline with a high order difference penalty:

$$\begin{array}{cc}\hfill \frac{\partial \mathrm{SS}}{\partial \beta }& =-2y^{T}S+2S^{T}S\beta +2\lambda C^{T}C\beta =0.\hfill \end{array}$$

(16)

From this

$$\begin{array}{c}\hfill \hat{\beta }={(S^{T}S+\lambda C^{T}C)}^{-1}{y}^{T}S\end{array}$$

(17)

and so

$$\hat{y}=S\hat{\beta }.$$

(18)

Using the same data created within Figure 2 and Figure 3, we fit four P-Splines with varying magnitudes of penalty terms in Figure 4. Note that the number of knots is set at 50 for each fit.

As we can see from Figure 4, where $\lambda =0$ and therefore no difference penalty term is applied, the resulting spline overfits the data and is particularly rough. As the penalty parameter $\lambda$ increases, the splines become smoother and move closer to the true function. Selection of an optimal penalty parameter is something discussed in later sections of this work.

As their creators, Eilers and Marx provide several properties of P-Splines that make them particularly advantageous to use over the standard B-Spline. The key advantage is naturally the reduced need to focus on the number and position of knots that are necessary to create an appropriate fit to data; the implementation of P-Splines is encouraged through selecting a large number of knots and then simply using $\lambda$ to control the level of smoothness within the fitted curve [13]. P-Splines also display no boundary effects, i.e., an erratic behaviour of the spline when modelled beyond the data’s support; this is because the penalty term implements linearity constraints at the outer knots [8]. They are also able to conserve moments of the data, meaning that the estimated density’s mean and variance will be equal to that of the data itself—often other types of smoothing such as a kernel smoother struggle to preserve variance to the data’s level [6]. This property allows for valuable insights into the data’s shape, distribution, and central tendency.

The level of research that has been undertaken with P-Splines is extensive. This research covers a broad range of applications as well as adaptations to the P-Spline method itself, including modifications to the penalty term, as well as the addition of secondary penalty terms to which this work also contributes. P-Splines have been applied within many different domains, including in a medical context such as with Mubarik et al. (2020) [14] applying P-Splines to breast cancer mortality data while managing to outperform existing non-smoothing models, and also within a geospatial environment such as with Rodriguez (2018) [15] using P-Splines to model random spatial variation within plant breeding experiments while taking advantage of properties such as a stable and fast estimate and being able to handle missing data and being able to model a non-normal response. P-Splines have also been adapted to be used within a Bayesian context by Lang and Brezger (2004) [16] and are shown in several works to improve predictive modelling, such as with Brezger and Steiner’s (2012) [17] work of modelling demand for brands of orange juice and also with Bremhorst and Lambert’s (2016) [18] work using survival analysis data.

There have also been several works that have built upon the original P-Spline method to incorporate a second additional penalty parameter; this has been undertaken for a host of reasons. Aldrin (2006) introduces an additive penalty to the original Eilers and Marx P-Spline to improve the sensitivity of the smoothing curve [19], whilst Bollaerts et al. (2006) devise a second penalty to enforce a constraint in which the assumed shape of the relationship between predictors and covariates is taken into account [20]. Simpkin and Newell (2013) also introduce a secondary penalty, suggesting this method helps alleviate fears when derivative estimation is of concern and can also lead to an improvement in the size of errors made during estimation [21]. Perperoglou and Eilers (2009) devise a second penalty term to capture excess variability and to explicitly estimate individual deviance effects; they use a ridge penalty to constrain these effects and the result is a very effective and more suitable model than the single penalty P-Spline [22]. This work aims to contribute within the additionally penalized P-Spline method space; however, the second penalty we use and our reasons for taking this direction are unlike that of other authors.

3. Model and Estimation

Our $\mathcal{H}$ data set consists of $N_{\mathcal{H}}$ observations of response variable y and two covariates $(x,z)$, and data set $\mathcal{V}$ consists of $N_{\mathcal{V}}$ observations of response variable y and single covariate x. We are interested in modelling a relationship between y and the smooth function $\theta (x,z)$ represented using spline basis functions $S(.)$, which we can estimate from $\mathcal{H}$. However, if $N_{\mathcal{H}}$ is small, then there is much uncertainty surrounding this relationship. We therefore look to incorporate $\mathcal{V}$ to enhance our learning surrounding response variable y and the relationship with covariates $(x,z)$. Provided that $\mathcal{V}$ is large, this will provide an accurate marginal estimate which can be incorporated into our analysis. We are planning to develop three models for this relationship, with each one building upon the previous.

3.1. Model Assumptions

We assume in general that

$$g\left(E\right[y|x,z])=\theta (x,z)$$

(19)

where $\theta (x,z)$ is a smooth function. For simulation purposes, we take [0,1] to be the domain of each of x and z, and we will use B-Splines to model $\theta (x,z)$. We do this in two ways:

• No Interaction Between Covariates: The relationship of the response y to covariates $(x,z)$ treats each variable separately such that the model is comprised of two smooth relationships. This is expressed as $\theta (x,z)=S\left(x\right)+S\left(z\right)$.
• Interaction Between Covariates: There is a single smoothing relationship that incorporates an interaction of covariates x and z with response y. This is expressed as $\theta (x,z)=S(x,z)$.

Each relationship results in different ways in which the design matrix of the B-Spline basis function is created which is explained in more detail in Appendix C.

3.2. Linear B-Spline Model

Let us firstly assume a standard linear B-Spline model, which throughout we denote with subscript ‘0’:

$$y=D\beta +\epsilon$$

(20)

where D is the design matrix, $\beta$ are the corresponding coefficients, and $\epsilon$ are $N[0,{\sigma }^2]$ random errors as usual. We find estimated values for coefficients $\hat{\beta }$ by minimising:

$$S{S}_0={(y-D\beta )}^T(y-D\beta ),$$

(21)

ultimately receiving the ordinary least squares estimate:

$${\hat{\beta }}_0={\left(D^{T}D\right)}^{-1}{D}^{T}y.$$

(22)

This value can then be used to receive fitted values for the linear model:

$$\hat{y}=D{\hat{\beta }}_0$$

(23)

3.3. P-Spline Estimation

Building upon the linear model and referring back to the penalty term described by Eilers and Marx in Flexible Smoothing with B-Splines and Penalties (1996) [6], we now apply a penalty to the B-Spline, known as a P-Spline estimation, using a fairly large number of knots to create basis matrices $B_x$ and $B_z$. We denote $P_1$ and $P_2$ to be roughness matrices that are based upon the second-order differences in row and column directions, with $P_1$ referring to covariate x and $P_2$ referring to covariate z. The construction of roughness matrices are discussed in more detail in Appendix D.

The least penalized squares estimate is now found through minimising:

$$\begin{array}{cc}\hfill S{S}_1& ={(y-D\beta )}^T(y-D\beta )+{\lambda }_1({\beta }^T{P}_1^T{P}_1\beta +{\beta }^T{P}_2^T{P}_2\beta )\hfill \\ \hfill & =S{S}_0+{\lambda }_1({\beta }^T{P}_1^T{P}_1\beta +{\beta }^T{P}_2^T{P}_2\beta ).\hfill \end{array}$$

(24)

The least penalized squares estimate is now

$${\hat{\beta }}_1=({D^{T}D+{\lambda }_1(P_1^T{P}_1+P_2^T{P}_2))}^{-1}{D}^{T}y.$$

(25)

A proof of this is provided in Appendix E. This value as previous can then be used to obtain the fitted value for the P-Spline estimation model:

$$\hat{y}=D{\hat{\beta }}_1$$

(26)

In the P-Spline estimation model (denoted with subscript ‘1’), both roughness matrices $P_1$ and $P_2$ are regulated by the same penalty parameter ${\lambda }_1$. This assumes that for our case x and z are symmetrical when simulating the data and for simulation purposes keep the model complexity simple; however, in reality we would need two parameters.

3.4. New Additional Marginalisation Penalty

As of yet, we have not introduced a method of being able to take into account the vertical data set, $\mathcal{V}$; we now introduce an additional second penalty term to aid with this task. Suppose $x_{test}$ is a vector of x values of chosen length to provide a reasonable spread across x domains. Let ${\theta }_{true}\left(x_{test}\right)$ be the true marginal function at $x_{test}$, such that

$${\theta }_{true}\left(x_{test}\right)=g\left(E[y|x_{test}]\right),$$

(27)

which can be estimated from our vertical data $\mathcal{V}$. We are also able to estimate these marginal values from our horizontal data $\mathcal{H}$.

Let

• $\hat{y}=\hat{\theta }(x,z)=D\hat{\beta }$, a vector of size $N_{\mathcal{H}}\times 1$.
• $x_0$ be any element from $x_{test}$ (a scalar).
• $(x_i,z_i)$ be covariates for element i within $\mathcal{H}$.
• $k(.)$ be a kernel function, which we take to be the probability density function of a normal distribution with mean = 0 and standard deviation = 1.
• ${\sigma }_k$ be a smoothing parameter.

A consistent estimator, i.e., converges on the true value when sample size tends to infinity, is therefore:

$${\hat{\theta }}_{\mathcal{H}}\left(x_0\right)=\frac{{\sum }_{i\in \mathcal{H}}k\left(\frac{x_i-x_0}{{\sigma }_k}\right)\hat{\theta }(x_i,z_i)}{{\sum }_{i\in \mathcal{H}}k\left(\frac{x_i-x_0}{{\sigma }_k}\right)}.$$

(28)

In vector arguments, we can write:

$${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)=K\hat{\theta }(x,z)$$

(29)

where K is a matrix comprised of scaled $k(.)$ functions. Recalling $\hat{\theta }(x,z)=D\hat{\beta }$, therefore:

$${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)=K\hat{\theta }(x,z)=KD\hat{\beta }=W\hat{\beta }.$$

(30)

We wish for ${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)$, i.e., our estimated marginal values from $\mathcal{H}$ of x, to be as close as possible to ${\theta }_{true}\left(x_{test}\right)$, i.e., the true marginal values from $\mathcal{V}$ of x. In practice, of course, ${\theta }_{true}\left(x_{test}\right)$ would be unknown; however, we can estimate this from the vertical data using ${\hat{\theta }}_{\mathcal{V}}\left(x_{test}\right)$. Conversely, we have assumed since $N_{\mathcal{V}}\gg N_{\mathcal{H}}$, the error in ${\hat{\theta }}_{\mathcal{V}}\left(x_{test}\right)$ will be relatively small. Hence, for simplicity, we use the true marginal ${\theta }_{true}\left(x_{test}\right)$ rather than the estimator ${\hat{\theta }}_{\mathcal{V}}\left(x_{test}\right)$ for now. Our additional penalty term now added to the least penalized squares estimate takes this into account.

The new least penalized squares estimate is now found through minimising:

$$\begin{array}{cc}\hfill S{S}_2& =S{S}_1+{\lambda }_2{\left(\hat{\theta }\left(x_{test}\right)-{\theta }_{true}\left(x_{test}\right)\right)}^T\left(\hat{\theta }\left(x_{test}\right)-{\theta }_{true}\left(x_{test}\right)\right)\hfill \\ \hfill & =S{S}_1+{\lambda }_2{\left(W\hat{\beta }-{\theta }_{true}\left(x_{test}\right)\right)}^T\left(W\hat{\beta }-{\theta }_{true}\left(x_{test}\right)\right).\hfill \end{array}$$

(31)

This is thus providing the twice least penalized squares estimate:

$$\widehat{{\beta }_2}=(X^{T}X+{\lambda }_1(P_1^T{P}_1+P_2^T{P}_2)+{\lambda }_2{W}^{T}W{)}^{-1}\left(X^{T}y+{\lambda }_2{W}^T{\theta }_{true}\left(x_{test}\right)\right).$$

(32)

The proof for this is shown in Appendix F. This value as previous again can be used to obtain the fitted value for the P-Spline estimation model now fitted with an additional marginalisation penalty to take into account $\mathcal{V}$:

$$\hat{y}=D{\hat{\beta }}_2$$

(33)

In this model, we note that our additional marginalisation penalty is regulated by penalty parameter ${\lambda }_2$, and our P-Spline smoothing penalty is regulated by ${\lambda }_1$ as previously. Within this paper, the model in which we use the additional marginalisation penalty is denoted with a subscript ‘2’.

4. Model Testing

In this section, we test our three models upon a series of data simulations. Simulations allow for the exploration of a controlled space and also the freedom to adapt our models to a range of different parameters, including sample size, data noise, and relationships between covariates. Using data simulations also allows for the use of perfect knowledge of true values for response variable y and true marginal values of x; this provides the advantage that we are accurately able to compare our three models by comparing our fitted values of each model to the ground truth, something that is naturally unknown in real world data. The aim of these simulations is to show that our adapted model featuring the additional marginalisation penalty outperforms both the linear B-Spline method and once penalized P-Spline estimation.

4.1. Data Simulation

4.1.1. Simulating Covariates and Responses

We first of all generate some artificial $\mathcal{H}$ data, generate $N_{\mathcal{H}}=400$ observations, and define x and z within it in order to be distributed upon a regular grid spanning ${(0,1)}^2$. The relationship the covariates have with response variable y depends upon whether we consider x and z to have independent effects (no interaction) from one another or not (interaction); therefore, there are two separate equations, one to represent each model structure. The equations for these bivariate data sets are from Wood’s Thin Plate Regression Splines (2003) [23]. When we assume a model structure of no interaction effect, the true value for y, denoted $y_{true}$, is found through the equation:

$$y_{true}=\frac{0.75}{\pi {\sigma }_x{\sigma }_z}exp\left\{-{(x-0.2)}^2/{\sigma }_x^2-{(x-0.3)}^2/{\sigma }_z^2\right\}+\frac{0.45}{\pi {\sigma }_x{\sigma }_z}exp\left\{-{(z-0.7)}^2/{\sigma }_x^2-{(z-0.8)}^2/{\sigma }_z^2\right\}.$$

(34)

When we assume a model structure with an interaction effect, $y_{true}$ is found through the equation:

$$y_{true}=\frac{0.75}{\pi {\sigma }_x{\sigma }_z}exp\left\{-{(x-0.2)}^2/{\sigma }_x^2-{(z-0.3)}^2/{\sigma }_z^2\right\}+\frac{0.45}{\pi {\sigma }_x{\sigma }_z}exp\left\{-{(x-0.7)}^2/{\sigma }_x^2-{(z-0.8)}^2/{\sigma }_z^2\right\}.$$

(35)

These equations are almost identical, the only difference being that when there is an interaction each exponent contains both x and z, and when there is no interaction one exponent contains just x and the other just z. The constants displayed in these equations are arbitrary and hold no importance to the interaction between covariates x and z and are there to simply create a relationship with response y, so they could feasibly be any value not including 0. Both relationships are each evaluated at ${\sigma }_x=0.3$ and ${\sigma }_z=0.4$. The value for y is provided through adding artificial noise generated by $N_{\mathcal{H}}=400$ independent $N[0,{\sigma }^2]$ random variables to the $y_{true}$ values, which for now we evaluate at $\sigma =0.2$. Figure 5 displays the two relationships between covariates and responses:

4.1.2. Estimating Marginal Effects

We next need to find ${\theta }_{true}\left(x_{test}\right)$ in order to form our second penalty term. In our simulations, take $x_{test}$ to be an equidistant sequence of 100 values between [0,1] to provide a reasonable spread across the x domain whilst remaining low in dimension. We estimate ${\theta }_{true}\left(x_{test}\right)$ by calculating $y_{true}$ using either Equations (34) or (35) as appropriate, at each value of $x_{test}$ using 10,000 values of z equidistant between [0,1] and then averaging. The value of 10,000 was selected to again provide a good spread across the z domain and also to be large enough to provide an accurate true estimate. In this way, we estimate ${\theta }_{true}\left(x_{test}\right)$ under the assumption that z is uniformly distributed. For other distributions, we would need a weighted average. Figure 6 is an illustration of the true marginal values ${\theta }_{true}\left(x_{test}\right)$ for both relationships outlined in Section 4.1.1.

4.1.3. Assessing Model Fit

To assess model fit, we compare the fitted marginal of $\hat{\theta }\left(x\right)$ attained by our models with the true marginal of x found in $\mathcal{H}$, ${\theta }_{true}\left(x\right)$, and we also compare the fitted values $\hat{y}$ of each model with the true values for y, $y_{true}$. The comparison for each case is in the form of sum of squares (SS), i.e., $\sum {\{\hat{y}-y_{true}\}}^2$. The desired value is for this sum to be as close to zero as possible, as this will suggest a better fit. In practice, $y_{true}$ and ${\theta }_{true}\left(x\right)$ would be unknown; however, for model testing/simulation purposes we assume that we have perfect knowledge.

4.2. Model Fit Comparison

We will first of all fit our three models to a single simulated data set with a predetermined number of observations, level of noise, and relationship between covariates x and z using the sum of squares of fitted values and sum of squares of marginal values as a means of comparison. Following this, we will then vary our simulated data’s parameters and increase the number of simulations for each varying parameter combination.

Single Data Set 

The following three model fits are applied to a simulated data set evaluated at $N_{\mathcal{H}}=400$ and $\sigma =0.2$. The data follows a structure where there is an interaction between x and z for now, i.e., the effects are not independent. The number of knots for each covariate is set at the highest even number they can be at $p_x=p_z=18$, noting that the restriction for this is that $p_x{p}_z+1<N_{\mathcal{H}}$ in order to create a valid design matrix. Finally, penalty parameters are given default values of ${\lambda }_1=0.5$ and ${\lambda }_2=2$ for now—we will investigate optimal values later. Recall as shown in Section 3 that the fitted values for each model are defined as follows:

$$\hat{y}=D\hat{\beta }$$

(36)

in which:

$$\begin{array}{cc}\hfill \mathrm{Fit}0:& \hat{\beta }={\hat{\beta }}_0={\left(D^{T}D\right)}^{-1}{D}^{T}y\hfill \\ \hfill \mathrm{Fit}1:& \hat{\beta }={\hat{\beta }}_1=({D^{T}D+{\lambda }_1(P_1^T{P}_1+P_2^T{P}_2))}^{-1}{D}^{T}y\hfill \\ \hfill \mathrm{Fit}2:& \hat{\beta }=\widehat{{\beta }_2}=(D^{T}D+{\lambda }_1(P_1^T{P}_1+P_2^T{P}_2)+{\lambda }_2{W}^{T}W{)}^{-1}\left(D^{T}y+{\lambda }_2{W}^T{\theta }_{true}\left(x_{test}\right)\right).\hfill \end{array}$$

(37)

And the fitted marginal values of x for each model are defined as:

$$\hat{\theta }\left(x\right)=W\hat{\beta }$$

(38)

in which

$$W=KD$$

(39)

with K defined in Section 3.4.

We evaluate each model by finding the sum of squares for the fitted values ($\sum {\{\hat{y}-y_{true}\}}^2$) for all i’s and the sum of squares for the marginal values ($\sum {\{\hat{\theta }\left(x\right)-{\theta }_{true}\left(x\right)\}}^2$) for x in $x_{test}$. The closer both of these sums are to zero, the better the model fit is to the data. In

Table 1. Sum of squares for model fits upon a single data set where $N_{\mathcal{H}}=400,\sigma =0.2$ and the model structure is such that there is an interaction between x and z. Bold indicates best value for each row.

	Fit0	Fit1	Fit2
SS Fitted Values	21.72	8.98	8.79
SS Marginal Values	0.50	0.52	0.27

, we illustrate the sum of squares for each fit:

We see here that the sum of squares for the fitted values and the marginal values are both at their lowest for Fit2, the fit which incorporates the additional penalty term. Fit1 is also a better fit to the data than Fit0 in terms of sum of squares of fitted values; however, Fit0 does display a better fit when comparing the sum of squares of marginal values. We can illustrate the three fits upon the simulated data along with the true function in 3D plots in Figure 7:

We see that the linear model with B-Spline basis functions produces a very jagged fit between response y and covariates $(x,z)$. When the penalty parameter ${\lambda }_1$ is introduced in Fit1, the fit becomes far smoother. It is difficult to spot any real difference between the model fit of Fit2 to Fit1 in the above 3D plots. In Figure 8, we show the estimated marginal functions of x, ${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)$ found from each model fit against the true marginal fit ${\theta }_{true}\left(x_{test}\right)$, recalling that in practice this would not be known.

There is very little difference between the estimated marginal function in Fit0 and Fit1; however, Fit2 does offer an improved fit to the true marginal function of x. This is highlighted in Table 1 where Fit2 has a lower sum of squares of the marginal values than that of Fit0 and Fit1. We have shown that for one particular data set where $N_{\mathcal{H}}=400,\sigma =0.2$, in which there is an interaction between covariates, that Fit2 in which we use our novel additional penalty to take into account the marginal value for x thus outperforms standard linear B-Spline methods and penalized P-Spline estimations in terms of model fit.

4.3. Varying Size, Noise, and Structure

Having observed that Fit2 provides a better model fit to Fit0 and Fit1 upon one simulation of a data set with specific parameters, it is now necessary to investigate across many simulations where parameters now vary. This includes the number of observations within the horizontal data set $N_{\mathcal{H}}$, the level of noise in the data set $\sigma$ (recalling that noise is determined via $N[0,{\sigma }^2]$ independent random variables being added to the $y_{true}$ values), and also the structure of the data set, i.e., whether or not there is an interaction between covariates x and z. We therefore alter $N_{\mathcal{H}}$ to be = 100 or 400, $\sigma =0.2,0.5\mathrm{or}1.0$, and to represent the relationship the two covariates have with one another. We repeat each combination of these three parameters in 100 simulations and report the mean average sum of squares of fitted values and marginal values for each model fit across each parameter set and report our results in

Table 2. Mean average sum of squares of fitted and marginal values for each model fit as model structure, sample size, and noise are varied (100 simulations). Bold indicates best value for each row and SS metric.

Interaction	${\mathit{N}}_{\mathcal{H}}$	$\mathit{\sigma }$	Fit0 SS(Fitted)	Fit1 SS(Fitted)	Fit2 SS(Fitted)	Fit0 SS(Marg)	Fit1 SS(Marg)	Fit2 SS(Marg)
Yes	100	0.2	6.55	4.74	4.71	0.94	0.98	0.73
		0.5	19.95	7.73	7.34	1.71	1.51	0.74
		1.0	70.26	15.41	13.20	4.93	3.53	0.76
Yes	400	0.2	20.64	9.07	8.99	0.32	0.40	0.22
		0.5	88.66	13.18	12.53	0.56	0.67	0.20
		1.0	333.85	23.46	20.32	1.34	1.22	0.16
No	100	0.2	0.68	0.54	0.45	0.81	0.95	0.53
		0.5	4.23	3.04	2.08	1.89	2.13	0.58
		1.0	16.84	10.47	5.88	4.77	4.73	0.48
No	400	0.2	1.56	0.75	0.68	0.75	0.83	0.67
		0.5	8.98	3.43	2.67	0.90	1.10	0.64
		1.0	37.76	11.65	8.19	1.95	2.35	0.62

. It is important to note the number of knots, $p_x=p_z=18$ for when $N_{\mathcal{H}}=400$ and $p_x=p_z=8$ for when $N_{\mathcal{H}}=100$, recalling that $p_x{p}_z+1<N_{\mathcal{H}}$ must hold. Penalty parameters ${\lambda }_1$ and ${\lambda }_2$ are at their optimal values for each sample size, noise, and covariate relationship combination—we will explore in Section 4.4 how these values are evaluated.

The average sum of square values for both the fitted values and the marginal values for x are such that Fit2 is the lowest for every model structure, sample size, and noise combination across 100 simulations. It is also the case that for all mean average sum of squares for fitted values that Fit1 outperforms Fit0; however, when looking at the mean average sum of squares for marginal values, Fit1 does not always perform better than Fit0; this is not particularly surprising as there is nothing within the single penalty P-Spline that pulls the estimated marginal towards the true marginal. It is worth mentioning that comparing model fits between different combinations of parameters and structures is unwise. The key purpose of this exercise was to illustrate that when we take into account the marginal value of x through the use of an additional penalty term, that this offers an improved model fit than that of existing linear and penalized regression methods.

4.4. Approximating Penalty Parameters

In P-Splines, the larger $\lambda$ is, the more penalized the curvature of the fit is; therefore, it is less sensitive to the data providing lower variance and higher bias. As $\lambda \to 0$, bias is low and variance is high. Typically, we would want $N\to \infty$ as $\lambda \to 0$. Our problem is more complex to solve as previous literature offers solutions when there is only a single penalty parameter; in our case with Fit2 and our additional penalty term, we require the selection of two penalty terms, ${\lambda }_1$ and ${\lambda }_2$.

Focusing initially upon one data set which considers an interaction between covariates x and z, and model parameters $N_{\mathcal{H}}=400$ and $\sigma =1.0$, we elect to treat the penalty parameter ${\lambda }_1$ differently within Fit1 and Fit2 such that ${\lambda }_{1a}$ determines Fit1 only and ${\lambda }_{1b}$ determines Fit2 along with ${\lambda }_2$. Within Fit1, we aim to find the value of ${\lambda }_{1a}$ that minimises the value of the sum of squares between the fitted values, $\hat{y}$, and the true values of the response, $y_{true}$. We require $\lambda$ values to be non-negative; therefore, we select an appropriate range of [0, 1, 2, …, 100] for ${\lambda }_{1a}$. Note that in practice this is not possible as $y_{true}$ is unknown (this is discussed later). We find that a value of ${\lambda }_{1a}=13$ provides the lowest value of SS(Fitted) for Fit1 upon this particular data set. Fixing for now ${\lambda }_{1a}={\lambda }_{1b}=13$, we now define ${\lambda }_2$ to be along the range [0, 0.5, 1.0, …, 50.0] and find each SS value corresponding to each ${\lambda }_2$ value. The minimum value for ${\lambda }_2=24$ for this data set. We repeat this process now fixing ${\lambda }_2$ to alter ${\lambda }_{1b}$ of which we find the approximate optimal value for ${\lambda }_{1b}=12$.

Naturally, these penalty parameter values will not hold as data set parameters are altered; similarly, these values may even vary from simulation to simulation. The optimum penalty parameters across 100 simulations of specified parameters are demonstrated within Appendix G.1. We accept that this method is ad hoc; however, within simulations this method of selecting penalty parameters is valid as the sum of squares is a comparison between the fitted and true values of the response. In reality, this is unknown and a new method of optimising $\lambda$ is required which is discussed in Section 6.

5. Logistic Regression for a Binary Response

Several adaptations to our models are required to take into account a binary response variable.

Let us now assume that

$$Pr(Y=1|x,z)=\theta (x,z)$$

(40)

in which $\theta (x,z)$ is a smooth yet unknown function of probabilities. We can calculate the marginal effect of x via

$$Pr(Y=1|x)=\theta \left(x\right)=\int \theta (x,z)f_z(z|x)dz$$

(41)

As previously, we estimate the smooth function $\theta (x,z)$ from our horizontal data $\mathcal{H}$. We modify our estimated smooth function so that the marginal estimate of x from the horizontal data ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$ is close to the more accurate marginal found from the vertical data, ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$. For now, we assume that $N_{\mathcal{V}}$ is so large that the uncertainty which comes from ${\hat{\theta }}_V\left(x\right)$ is so small that we may as well use the true marginal $\theta \left(x\right)$ instead. We reiterate that in reality this would not be possible as we would not know the true marginal; however, for simulation purposes it is useful as we try to achieve a marginal estimate ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$ as close to the truth as possible.

5.1. Data Creation

For data creation in simulations, we allow the true probabilities to be equal to the standard logistic function, also known as the expit:

$$\theta (x,z)=\frac{e^{s(x,z)}}{1+e^{s(x,z)}}$$

(42)

in which $s(x,z)$ is a scaled form of the smooth function we used previously in Section 4 for the linear model simulations. In simulated binary response data, y is created through generating random samples from a uniform distribution. We find the true marginal $\theta \left(x\right)$ in our simulations through the same way as previously.

In the linear model, we will begin with a B-Spline approximation to create design matrix D for the horizontal data $\mathcal{H}$; however, now we will take the logistic model rather than the linear. Therefore, for any case i:

$$\theta (x_i,z_i)=\frac{e^{d_i^T\beta }}{1+e^{d_i^T\beta }}$$

(43)

in which $d_i^T$ is row i in design matrix D.

We can now fit our three models once again, highlighting several differences that occur from the linear approach.

5.2. No Penalty—B-Spline Logistic Regression (Fit0)

The first difference in this approach is that we estimate our coefficient values $\hat{\beta }$ using maximum likelihood estimation rather than through least squares. Allowing ${\theta }_i=\theta (x_i,z_i)$ for $i\in \mathcal{H}$, the likelihood is

$$L\left(\beta \right)=\prod _{i\in \mathcal{H}}{\theta }_i^{y_i}{(1-{\theta }_i)}^{1-y_i}$$

(44)

and the log-likelihood is

$$l\left(\beta \right)=\sum _{i\in \mathcal{H}}\{y_{i}log{\theta }_i+(1-y_i)log(1-{\theta }_i)\}$$

(45)

Unfortunately, there is no simple closed form for $\hat{\beta }$ which maximises $l\left(\beta \right)$, so we therefore require a numerical method. As the first and second derivatives can be easily obtained, the obvious choice is the Newton–Raphson method [24].

Let us assume that design matrix D is $N_{\mathcal{H}}\times p$ in dimension, and so

$$\frac{\partial l}{\partial \beta }\mathrm{and}\frac{{\partial }^{2}l}{\partial {\beta }^2}$$

(46)

are a $p\times 1$ vector of first derivatives and $p\times p$ matrix of second derivatives, respectively. Iteratively, we start with an initial coefficient estimate guess of ${\beta }_0$ and then create a sequence ${\beta }_1,{\beta }_2,\dots$ until the sequence has converged, or is adjudged to have converged, sufficiently.

Allowing the current estimate to be ${\beta }_k$, then the next estimate according to the Newton–Raphson method is defined as follows:

$${\beta }_{k+1}={\beta }_k-{\left(\frac{{\partial }^{2}l}{\partial {\beta }^2}\right)}^{-1}·\frac{\partial l}{\partial \beta }.$$

(47)

If the absolute differences between ${\beta }_k$ and ${\beta }_{k+1}$ are below some predefined tolerance threshold, convergence can be declared and we decide we have obtained the estimated coefficients $\hat{\beta }$. Alternatively, if the algorithm fails to converge, we set a maximum number of iterations to prevent an infinite loop.

We derive the first and second derivatives of the likelihood function with respect to $\beta$ to be

$$\frac{\partial l_i}{\partial {\beta }_j}=\frac{\partial l_i}{\partial {\theta }_i}\frac{\partial {\theta }_i}{\partial {\beta }_j}$$

(48)

and

$$\frac{{\partial }^2{l}_i}{\partial {\beta }_j\partial {\beta }_k}=\frac{\partial l_i}{\partial {\theta }_i}\frac{{\partial }^2{\theta }_i}{\partial {\beta }_j\partial {\beta }_k}+\frac{{\partial }^2{l}_i}{\partial {\theta }_i^2}\frac{\partial {\theta }_i}{\partial {\beta }_j}\frac{\partial {\theta }_i}{\partial {\beta }_k}$$

(49)

A full proof of this is found in Appendix H.1. The Newton–Raphson method for finding $\hat{\beta }$ that maximises the log-likelihood for logistic regression with no additional penalty can therefore be expressed as follows:

$${\beta }_{k+1}={\beta }_k-{\left(\frac{\partial l_i}{\partial {\theta }_i}\frac{{\partial }^2{\theta }_i}{\partial {\beta }_j\partial {\beta }_k}+\frac{{\partial }^2{l}_i}{\partial {\theta }_i^2}\frac{\partial {\theta }_i}{\partial {\beta }_j}\frac{\partial {\theta }_i}{\partial {\beta }_k}\right)}^{-1}\left(\frac{\partial l_i}{\partial {\theta }_i}\frac{\partial {\theta }_i}{\partial {\beta }_j}\right)$$

(50)

Convergence problems can, however, still exist. This occurs when the number of parameters is large compared with the information in the data—as a result two different errors can occur, either the algorithm does not converge or it does converge but some of the estimated $\beta$ coefficients are very high. There are two solutions that we can implement to avoid these errors: replicate the data several times (denoted nrep) or reduce the number of parameters to be estimated by reducing the number of knots, $p_x$ and/or $p_z$. The selection of the number of replications and the numbers of knots is not explored in this work, but as a result of these errors the default simulation setup is $N_{\mathcal{H}}=400$ with two replicates of each observation, using $p_x=p_z=8$ knots when fitting a B-Spline estimate to achieve the design matrix D.

5.3. Single Penalty—P-Spline Estimation (Fit1)

As was the case for the linear model, we penalize using P-Spline estimations, selecting $\beta$ to maximise:

$$l\left(\beta \right)-{\lambda }_1{\beta }^T(P_1^T{P}_1+P_2^T{P}_2)\beta$$

(51)

in which $P_1$ and $P_2$ are the same row/column roughness matrices used previously in the linear model to prevent overfitting. A key difference from the previous single penalty usage, however, is that we are now trying to maximise the objective likelihood function rather than minimise the least squares objective function—therefore, the penalty is now subtracted rather than added.

We find the first and second derivatives of the P-Spline estimation to be used within the Newton–Raphson method (of which a proof is provided in Appendix H.2) such that

$$\frac{\partial l_i}{\partial {\beta }_j}=\frac{\partial l_i}{\partial {\theta }_i}\frac{\partial {\theta }_i}{\partial {\beta }_j}-2{\lambda }_1{\left[(P_1^T{P}_1+P_2^T{P}_2)\beta \right]}_j$$

(52)

and:

$$\frac{{\partial }^2{l}_i}{\partial {\beta }_j\partial {\beta }_k}=\frac{\partial l_i}{\partial {\theta }_i}\frac{{\partial }^2{\theta }_i}{\partial {\beta }_j\partial {\beta }_k}+\frac{{\partial }^2{l}_i}{\partial {\theta }_i^2}\frac{\partial {\theta }_i}{\partial {\beta }_j}\frac{\partial {\theta }_i}{\partial {\beta }_k}-2{\lambda }_1{\left[P_1^T{P}_1+P_2^T{P}_2\right]}_{jk}$$

(53)

We note that the penalty term for the first derivative is a vector and a matrix for the second derivative, and hence the j and $j,k$ subscripts, respectively. We use these values within our Newton–Raphson approximation as outlined previously in Equation (47) to find the estimated $\hat{\beta }$ coefficients.

5.4. Double Penalty—Marginal Penalization (Fit2)

We now wish to add the novel second penalty taking into account the discrepancies between the marginal estimated from the horizontal data $\mathcal{H}$ and vertical data $\mathcal{V}$. To reiterate, for simulation purposes we use the true marginal ${\theta }_{true}\left(x_{test}\right)$ instead of the estimate ${\hat{\theta }}_{\mathcal{V}}\left(x_{test}\right)$.

We use a kernel smoothing method to estimate ${\hat{\theta }}_{\mathcal{H}}\left(x_0\right)$ from the fitted ${\hat{\theta }}_{\mathcal{H}}(x_i,z_i)$ such that

$${\hat{\theta }}_{\mathcal{H}}\left(x_0\right)=\sum _{i\in \mathcal{H}}k\left(\frac{x_i-x_0}{{\sigma }_k}\right){\hat{\theta }}_{\mathcal{H}}(x_i,z_i)/\sum _{i\in \mathcal{H}}k\left(\frac{x_i-x_0}{{\sigma }_k}\right)$$

(54)

with $k(.)$ being a kernel function, ${\sigma }_k$ being a smoothing parameter, $x_0$ being any element from $x_{test}$ (a scalar), and $(x_i,z_i)$ representing covariates for element i within $\mathcal{H}$. We can express this in vector form:

$${\hat{\theta }}_{\mathcal{H}}\left(x_0\right)=K{\theta }_{\mathcal{H}}(x,z)$$

(55)

where K is a $n_0\times N_{\mathcal{H}}$ matrix of weights that have been suitably scaled. These weights do not contain $\beta$ and so therefore K is a fixed constant in the optimisation of the maximum log-likelihood objective function. The objective function now contains two penalties, evaluated at test vector $x_0$. The objective function is as follows:

$$l\left(\beta \right)-{\lambda }_1{\beta }^T(P_1^T{P}_1+P_2^T{P}_2)\beta -{\lambda }_2{\left({\hat{\theta }}_{\mathcal{H}}\left(x_0\right)-\theta \left(x_0\right)\right)}^T\left({\hat{\theta }}_{\mathcal{H}}\left(x_0\right)-\theta \left(x_0\right)\right)$$

(56)

As before and for simplicity, we define the marginal penalty (MP) as follows:

$$MP=-{\lambda }_2{\left(K{\theta }_{\mathcal{H}}(x,z)-\theta \left(x_0\right)\right)}^T\left(K{\theta }_{\mathcal{H}}(x,z)-\theta \left(x_0\right)\right)$$

(57)

and for simplicity:

$$\begin{array}{cc}\hfill MP& =-{\lambda }_2{(K\theta -{\theta }_0)}^T(K\theta -{\theta }_0)\hfill \end{array}$$

(58)

We find the first derivatives of the marginal penalty as follows:

$$\frac{\partial MP}{\partial {\beta }_j}=-2{\lambda }_2({\theta }^T{K}^{T}K-{\theta }_0^{T}K)\frac{\partial \theta }{\partial {\beta }_j}$$

(59)

And the second derivatives as follows:

$$\frac{{\partial }^{2}MP}{\partial {\beta }_j\partial {\beta }_k}=-2{\lambda }_2\left\{{\left(\frac{\partial \theta }{\partial {\beta }_k}\right)}^T{K}^{T}K\frac{\partial \theta }{\partial {\beta }_j}+{\theta }^T{K}^{T}K\frac{{\partial }^2\theta }{\partial {\beta }_j\partial {\beta }_k}-{\theta }_0^{T}K\frac{{\partial }^2\theta }{\partial {\beta }_j\partial {\beta }_k}\right\}$$

(60)

A proof for these derivatives is found in the Appendix H.3. We use these values within our Newton–Raphson approximation as outlined previously in Equation (47) to find the estimated $\hat{\beta }$ coefficients.

5.5. Measure of Fit

As we have undertaken previously, we will measure the fit of these three approaches using the sum of squares, comparing the estimated probabilities ${\hat{\theta }}_{\mathcal{H}}(x,z)$; however, we now take into account heterogeneous variances that may exist within x and z; thus, we use a weighted sum of squares as an alternative:

$$WSS=\sum _{x,z}\frac{{\left({\hat{\theta }}_{\mathcal{H}}(x,z)-\theta (x,z)\right)}^2}{\theta (x,z)\left(1-\theta (x,z)\right)}$$

(61)

Varying sample size $N_{\mathcal{H}}$, number of knots $p_x=p_z$, and the relationship between covariates x and z are recorded. Displayed in

Table 3. Mean average weighted sum of squares of fitted values for each model fit as model structure, sample size, and number of knots are varied (100 simulations). Bold indicates best value for each row and SS metric.

Interaction	${\mathit{N}}_{\mathcal{H}}$	${\mathit{p}}_{\mathit{x}}={\mathit{p}}_{\mathit{z}}$	nrep	Fit0 WSS(Fitted)	Fit1 WSS(Fitted)	Fit2 WSS(Fitted)	Fit0 WSS(Marg)	Fit1 WSS(Marg)	Fit2 WSS(Marg)
No	100	4	4	16.76	11.86	9.22	1.37	1.32	0.99
	100	8	4	16.50	10.34	8.66	1.14	1.21	0.83
	400	8	2	17.75	12.85	9.26	0.85	1.00	0.49
	400	18	2	37.99	12.32	9.13	0.77	0.90	0.47
	900	8	1	17.94	12.62	9.14	0.76	0.88	0.46
Yes	100	8	8	83.63	32.44	30.79	0.85	0.72	0.34
	400	8	2	74.55	22.98	20.71	0.65	0.56	0.24
	900	8	1	73.20	22.48	20.18	0.54	0.45	0.21

are the mean average sums of squares for fitted and marginal values from 100 simulations of each data set with these varying combinations. The penalty parameters ${\lambda }_1$ and ${\lambda }_2$ are at their approximate optimal values and are illustrated in Appendix G.2.

6. Application

6.1. Data Set

We now wish to test whether the double penalty method yields similarly better fitting results upon real data. The data we use within this Application section is the LITMUS (Liver Investigation: Testing Marker Utility in Steatohepatitis) Metacohort, making up a part of the European Non-Alcoholic Fatty Liver Disease (NAFLD) Registry [25]. We utilise 19 covariates that are easily attained through a blood test or a routine GP appointment, whereby this includes information such as age, gender, BMI, and pre-existing health conditions, in order to form our vertical data set $\mathcal{V}$. We focus upon a binary response variable of ‘At-Risk MASH’—a key stage in the MASLD natural progression between benign steatosis and more serious fibrosis and cirrhosis—with ‘1’ representing an individual being positive At-Risk MASH, and ‘0’ representing negative. There are approximately 6000 individuals that have an At-Risk MASH response and have had the 19 covariates that make up the vertical data set $\mathcal{V}$ measured. The horizontal data set $\mathcal{H}$ includes approximately 1500 individuals who have had the 19 core features of $\mathcal{V}$ measured, alongside further genomic sequencing data collected. This includes a further 37 additional covariates within the horizontal data set $\mathcal{H}$.

A summary of the $\mathcal{V}$ and $\mathcal{H}$ data sets is illustrated in

Table 4. Characteristics of $\mathcal{H}$ and $\mathcal{V}$ data sets within the LITMUS Metacohort.

Dataset	N	p	Y = 0	Y = 1
$\mathcal{V}$	6024	19	4014	2010
$\mathcal{H}$	1456	19 + 37	860	596

:

6.2. Adaptations from Simulated Models

6.2.1. Dimensionality Reduction

Data simulations have been limited to where the number of covariates is equal to two. In principle, the methods we have created would work for more than two covariates, but the number of parameters would become very large and the fits therefore unstable. Instead, we will adopt three dimensionality reduction techniques to obtain the best linear combinations of the 19 and 37 covariates: linear predictor following the fit of a GLM; principle component analysis (PCA); and t-distributed stochastic neighbour embedding (tSNE). These will be taken as x and z, respectively. We discuss this issue of dimensionality reduction in Section 7.

The first method of dimensionality reduction applied on the real data set is using the linear predictor fitted on the link scale following the fit of a generalised linear model (GLM) of the covariates to the response [26]. GLMs are formed using three components: a linear predictor—a linear combination of covariates and coefficients; a probability distribution—used to generate the response variable; and a link function—simply a function that ‘links’ together the linear predictors and probability distribution parameter. By fitting a GLM to $\mathcal{H}$ upon the 19 covariates that also exist within $\mathcal{V}$ with the corresponding binary response y for these observations, we take the linear predictor fitted on the link scale and return a single vector that represents x. In the same way, we fit a GLM upon the 37 additional covariates that exist only within $\mathcal{H}$ with the corresponding binary response y for these observations and take the linear predictor fitted on the link scale to return another single vector, this time representing z. This technique is common in prognostic modelling within medical domains where the linear predictor is often used as a prognostic index, i.e., a measure of future risk), for patients [27,28].

The second method used in this section is principal component analysis (PCA). Developed by Karl Pearson [29], PCA is one of the most common methods of dimensionality reduction. In a nutshell, supposing we have p covariates, PCA transforms p variables $e_1,e_2,\dots ,e_p$ called principal components, each of which are linear combinations of the original covariates $x_1,x_2,\dots ,x_p$. We select coefficients for each covariate so that the first principal component $e_1$ explains the most variation within the data, and then the second principal component $e_2$ (uncorrelated with $e_1$) explains the next most variation, and so on. For our purpose, we use the first principal component when performing a PCA on the 19 and then the 37 covariates, thus providing x and z as single vectors we can use within our analysis.

The final method of dimensionality reduction we use is t-distributed stochastic neighbour embedding (tSNE). Based upon the van der Maaten t-distributed variant of stochastic neighbour embedding, developed by Hinton and Roweis [30,31], tSNE, unlike the linear predictor and PCA methods, is a non-linear technique that aims to preserve pairwise similarities between data points in a low-dimensional space. The tSNE method calculates the pairwise similarity of data points within high and low dimensional space and assigns high and low probabilities to data points that are close and far away from a selected data point, respectively. It then maps the higher dimensional data onto a lower dimensional space whilst minimizing the divergence in the probability distributions of data points within the higher and lower dimensional data. This mapping then provides a vector which can be used within our methods to represent both x and z variables. The greatest difference between the PCA and tSNE methods are that PCA aims to preserve the variance of the data whereas tSNE aims to preserve the relationship between the data points.

6.2.2. Estimating ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$

Recall that for a binary response variable y

$$Pr(Y=1|x,z)=\theta (x,z)$$

(62)

where $\theta (x,z)$ is a smooth but unknown function of all fitted probabilities. The associated marginal is given as follows:

$$Pr(Y=1|x)=\theta \left(x\right)={\int }_z\theta (x,z)f_z(z|x)dz$$

(63)

in which $f_z(z|x)$ is the conditional probability density function of z given x.

As we have undertaken previously, we are planning to estimate $\theta (x,z)$ from $\mathcal{H}$ but modify our estimate to make sure that ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$, i.e., the estimated marginal x attained from our horizontal data, is close to the more accurate marginal from our vertical data, ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$. In simulations we used the true marginal $\theta \left(x\right)$; however, it is not possible to calculate in real data, so our first task is therefore to estimate ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$.

6.2.3. Marginal in the Second Penalty

In our simulations to use the second marginalisation penalty, we compare the marginal from our fit using x and z in our horizontal data, and compare this with the true marginal values. Naturally, the true marginal is unknown in our real data, so we therefore use an accurate estimate from $\mathcal{V}$. As mentioned in Section 3, we use a predefined vector $x_{test}$ to calculate the marginal from $\mathcal{H}$. In our real data, we can now simply use $x_{\mathcal{H}}$, including the observed x-values from $\mathcal{H}$, to calculate the marginal. The advantage of this is that we use all values in x from $\mathcal{H}$ rather than just unique values, allowing the second penalty term to have greater weight for more common values of x. Another advantage is the marginal from $\mathcal{H}$, whereby ${\hat{\theta }}_{\mathcal{H}}\left(x_i\right)$ for $i\in \mathcal{H}$ is produced as a part of the fitting procedure.

6.2.4. Means of Comparison

In our real data as mentioned we now do not know the true smooth function $\theta (x,z)$; therefore, a comparison by means of the sum of squares of fitted values as undertaken in simulations is now redundant. By allowing the estimated marginal of x from $\mathcal{V}$ to now replace the true marginal $\theta \left(x\right)$ which is now also unknown, our only means of comparison now is through the sum of squares of the marginal values, with values closer to zero indicating a greater fit. In Section 7, we mention possible future work of evaluating model fits upon data in which we do not have perfect knowledge.

6.2.5. Cross-Validation for Approximating Penalty Parameters

One final adaptation from modelling upon real data to simulations is that it is now feasible to undertake a k-fold cross-validation method in order to determine the smoothing parameter $\lambda$. Recall in simulations how ${\lambda }_1$ was selected through comparing the sum of squares values when fitting the simulated data across a grid of ${\lambda }_1$ values. This sum of squares value was found through comparing model fit values to the truth; however, in our real data application where ground truth is unknown, k-fold cross-validation [32] is now required.

Setting number of folds $k=10$ and allowing for a 90:10 train/test split, each train set data is fitted using a P-Spline approximation whilst iterating through a grid of ${\lambda }_1$ values. The coefficients of each of these fits are then multiplied with the design matrix created from the test set and then put into an expit function to give the estimated fitted probabilities ${\hat{\theta }}_{test}(x,z)$. We use three different metrics to compare ${\hat{\theta }}_{test}(x,z)$ and the values of y within the test set: sum of squares (SS), log-likelihood (LL), and area under curve (AUC). For each ${\lambda }_1$ value, the median value for each metric across the $k=10$ folds is found. The ‘best’ ${\lambda }_1$ value is therefore the median value that is either the smallest SS or the greatest LL or AUC value. We then use all three supposed ‘best’ ${\lambda }_1$ values according to these metrics to find ${\lambda }_2$. This is simply found through using these ${\lambda }_1$ values and scanning through a grid of ${\lambda }_2$ values, until an acceptable improvement in fit from using the additional marginalisation penalty over the single penalty P-Spline approximation is found, whereby in our case this acceptable improvement is a 50% reduction in the sum of squares in marginal values. We can also select ${\lambda }_2$ as simply the value that provides the lowest sum of squares of marginal values when using the additional marginalisation penalty.

We accept that our method of selecting ${\lambda }_2$ is ad hoc and discuss potential future work options to select ${\lambda }_2$ values in Section 7. Increasing ${\lambda }_2$ values will take ${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)$ values ever closer to ${\hat{\theta }}_{\mathcal{V}}\left(x_{test}\right)$ at the expense of a poorer and more biased estimate of $\theta (x,z)$. In practice, we would like ${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)$ to be just close enough to ${\hat{\theta }}_{\mathcal{V}}\left(x_{test}\right)$ to consider a realistic and feasible estimate of the underlying true $\theta \left(x_{test}\right)$. This depends upon the level of noise that exists in ${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)$ and to a lesser extent the noise in ${\hat{\theta }}_{\mathcal{V}}\left(x_{test}\right)$. Selecting ${\lambda }_2$ based upon a 50% reduction in the SS of marginal values is therefore preferable rather than the outright best SS value—this is because we accept that there is a level of noise in ${\hat{\theta }}_{\mathcal{H}}\left(x_{test}\right)$ and that it would not be exactly the same as $\theta \left(x_{test}\right)$ even if we had perfect knowledge on the correct marginal, so we just expect these values to be close. By increasing ${\lambda }_2$, we force these values to be closer together, leading to more bias within ${\hat{\theta }}_{\mathcal{H}}(x,z)$.

6.3. Results

Following the dimensionality reduction of the real data set, x and z are now single vectors. Errors frequently arose at two points during the modelling process for the application data. The first occasion is when fitting the three model types upon the newly scaled data, and the second occasion is when cross-validating upon the data to find optimal values for ${\lambda }_1$. In the second instance, errors occur in particular for values of high ${\lambda }_1$. For both occasions, this is due to the algorithm for fitting a generalised linear model either not converging or producing coefficient $\beta$’s that are ridiculously high. This error happens when the fitted probabilities are extremely close to 0 or 1, occurring when the predictor variable x is able to perfectly separate the response variable. The consequence of this is that maximum likelihood estimates of the coefficients do not exist, and therefore the algorithm fails to converge. These errors can be alleviated by trimming the scaled values for x and z by removing extreme values at either end of the range. Following an extensive search of altering the minimum and maximum values of x and z, the number of data points that are removed without causing either a fitting or cross-validation error was 24 for both the interaction and non-interaction data sets when using PCA as a form of dimensionality reduction. This compares with 46 data points removed in the non-interaction data set and 52 data points removed in the interaction data set when using the Linear Predictor as a means of dimensionality reduction, and no data points removed for both the non-interaction and interaction data sets when using tSNE.

As mentioned within Section 6.2.1, we perform three methods of dimensionality reduction (linear predictor, PCA, and tSNE) and we have throughout two different relationship covariates x and z with one another (interaction or no interaction). Along with having three methods of determining ${\lambda }_1$ as mentioned in Section 6.2.5 (AUC, SS, and Log-likelihood) and two methods of determining ${\lambda }_2$ (outright best SS of marginal values and lowest value that offers a 50% improvement in SS of marginal values compared to Fit1), we simulate all of these combinations of possible changes to our modelling.

Table 5. Complete results for modelling upon the LITMUS Metacohort. Bold indicates best results for each row.

Dim. Reduction	Interaction	${\mathit{\lambda }}_1$ Determination	${\mathit{\lambda }}_2$ Determination	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	Fit 0 SS(Marg)	Fit 1 SS(Marg)	Fit 2 SS(Marg)
Linear Predictor	No	SS	50% Improvement	4	1.2	23.80	22.94	11.32
		SS	Best Fit2	4	2.2	23.80	22.94	7.66
		Log-likelihood	50% Improvement	3	1.2	23.80	22.80	11.12
		Log-likelihood	Best Fit2	3	2.2	23.80	22.80	7.39
		AUC	50% Improvement	6	1.3	23.80	23.16	11.11
		AUC	Best Fit2	6	2.3	23.80	23.16	7.70
Linear Predictor	Yes	SS	50% Improvement	4	NA	-	-	-
		SS	Best Fit2	4	2.4	24.69	25.83	13.42
		Log-likelihood	50% Improvement	3	NA	-	-	-
		Log-likelihood	Best Fit2	3	2.4	24.69	25.66	13.09
		AUC	50% Improvement	6	NA	-	-	-
		AUC	Best Fit2	6	2.4	24.69	26.03	13.76
PCA	No	SS	50% Improvement	2	1.0	42.37	33.85	16.30
		SS	Best Fit2	2	2.0	42.37	33.85	9.81
		Log-likelihood	50% Improvement	2	1.0	42.37	33.85	16.30
		Log-likelihood	Best Fit2	2	2.0	42.37	33.85	9.81
		AUC	50% Improvement	2	1.0	42.37	33.85	16.30
		AUC	Best Fit2	2	2.0	42.37	33.85	9.81
PCA	Yes	SS	50% Improvement	3	1.1	36.20	35.07	17.49
		SS	Best Fit2	3	2.0	36.20	35.07	12.12
		Log-likelihood	50% Improvement	2	1.1	36.20	34.85	17.28
		Log-likelihood	Best Fit2	2	2.0	36.20	34.85	11.87
		AUC	50% Improvement	1	1.1	36.20	34.55	16.91
		AUC	Best Fit2	1	2.0	36.20	34.55	11.48
tSNE	No	SS	50% Improvement	3	1.4	46.66	36.29	17.54
		SS	Best Fit2	3	2.0	46.66	36.29	14.24
		Log-likelihood	50% Improvement	3	1.4	46.66	36.29	17.54
		Log-likelihood	Best Fit2	3	2.0	46.66	36.29	14.24
		AUC	50% Improvement	8	1.5	46.66	34.25	16.74
		AUC	Best Fit2	8	2.0	46.66	34.35	14.26
tSNE	Yes	SS	50% Improvement	5	NA	-	-	-
		SS	Best Fit2	5	2.0	48.59	53.35	30.19
		Log-likelihood	50% Improvement	5	NA	-	-	-
		Log-likelihood	Best Fit2	5	2.0	48.59	53.35	30.19
		AUC	50% Improvement	0	2.1	48.59	48.59	21.00
		AUC	Best Fit2	0	2.1	48.59	48.59	21.00

lists all results of these calculations. We can report that for every combination of dimensionality reduction, choice of ${\lambda }_1$ and ${\lambda }_2$, interaction or no interaction between covariates, Fit2 always provides a notable enhancement in marginal fit of on average 65%; this is because after all setting ${\lambda }_2=0$ would at worst reduce Fit2 to Fit1. Generally for interaction data sets, the additional penalty model offers less of an improvement in comparison to non-interaction data sets—in some cases such as the modelling upon an interaction data set using linear predictor as a dimensionality reduction method and using AUC as the ${\lambda }_1$ determination method, there is no value of ${\lambda }_2$ that offers a greater than 50% improvement in Fit2 over Fit1. This is the case for four other instances, as shown in Table 5. This is arbitrary, however, as it is clear from our results that Fit2 always provides an improvement in fit compared to Fit1 and Fit0. It is also notable that the P-Spline approximation method does not always offer an improvement upon the standard linear model. Generally, log-likelihood and sum of squares methods select the same values for ${\lambda }_1$; however, there is more variation when AUC is the method of determination for ${\lambda }_1$. Values for ${\lambda }_2$ are almost always identical regardless of ${\lambda }_1$ determination method, typically offering ${\lambda }_2$ approximately equal to 2 when selecting Fit2 purely on best fit, and ${\lambda }_2$ approximately equal to 1 when selecting ${\lambda }_2$ based upon a 50% improvement in fit for Fit2 over Fit1.

In Figure 9, we graphically compare the marginal estimates from $\mathcal{H}$, ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$, which we receive from each model fit as outlined in Section 6.2.3 with our estimated marginal of x from $\mathcal{V}$, ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$ (which we receive as outlined in Section 6.2.2), for each model fit and each dimensionality reduction method— note that the relationship between covariates in this case is one of which there is an interaction. The red lines in each plot represent ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$ and blue lines represent ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$. The top row of plots are obtained through using the Linear Predictor as a means of dimensionality reduction; the middle row via PCA; and bottom row through tSNE. Each graph on the left of the plot illustrates the fitted marginal probabilities achieved from Fit0; the middle via Fit1; and the right hand side via Fit2. Better model fit is demonstrated the closer the blue and red lines are to one another, and as we can see for Fit2 ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$ (red) is closest to ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$ (blue) for all dimensionality reduction methods. Fit2 is therefore a better fit for our applications data compared to Fit0 and Fit1.

7. Discussion and Future Work

To our knowledge, this is the first work to propose additional marginal penalties in a flexible regression. There are, however, a number of areas for future development. The first is that we were unable to develop a succinct method of selecting penalty parameter ${\lambda }_2$ relating to the discrepancies between marginal values of x; we relied upon cross-validation to select ${\lambda }_1$; however, this method is not possible in selection for ${\lambda }_2$—we therefore relied upon manual scanning across a range of values to select ${\lambda }_2$. We are prepared to accept a slightly worse fit to the data in $\mathcal{H}$ if a more realistic marginal when compared with that from $\mathcal{V}$ is obtained. This means we are not trying to optimise the fit but we desire as good a fit as possible subject to the marginal estimate ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$ being consistent with ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$. Future work would therefore include the development of a concise method to choose ${\lambda }_2$. We know that as ${\lambda }_2\to \infty$, ${\hat{\theta }}_{\mathcal{H}}\left(x\right)\to {\hat{\theta }}_{\mathcal{V}}\left(x\right)$; therefore, one possibility for future work would be to gradually increase ${\lambda }_2$ until a consistent estimator is reached. Another method would include a computationally intense method of iterating through a grid of ${\lambda }_2$ values, this time fitting our model to a sample of values within $\mathcal{H}$ for each ${\lambda }_2$ value. For each iteration, we can receive the marginal values ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$ from these samples as well as a percentage confidence band for ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$. If ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$ also lies within this band, then we accept this ${\lambda }_2$ value as the ‘optimal’, and if not then we try the next value in our defined ${\lambda }_2$ grid. An alternative solution could be to withhold some of $\mathcal{H}$ to assess fit, through dividing $\mathcal{H}$ into parts similar to a train/test split, using the train set to determine penalty parameter values ${\lambda }_1$ and ${\lambda }_2$ and using the test set to evaluate model performance with these selected values.

Secondly, we are reliant upon the sum of squares of the marginal values to be our sole measurement of fit for modelling within our application to the real data section. As seen in simulations, we also used the sum of squares of fitted values as a means for comparison between different model fits; however, with the true fitted values now unknown, the method we utilised within simulations is now infeasible. Future work would therefore include the development of other methods of evaluating the performance of our model when the ground truth is unknown. One possible method of achieving this objective would be to use two thirds of $\mathcal{H}$ to cross-validate and calculate optimal penalty parameter values ${\lambda }_1$ and ${\lambda }_2$ while using the remaining third of $\mathcal{H}$ to assess fit. However, this is not entirely necessary as our aim for this work was not to model $\mathcal{H}$ as well as possible but rather to integrate the smaller cohort $\mathcal{H}$ and larger cohort $\mathcal{V}$ into a predictive analysis without the requirement of imputation. We would therefore consider accepting a slightly worse model fit for $\mathcal{H}$ to ensure a marginal that is closer to $\mathcal{V}$.

Furthermore, we have developed our method for the case of x and z being scalars in Section 6.2.1. We used dimensionality reduction methods to reduce multivariate covariates to scalar summaries. These techniques naturally come with their own disadvantages. For example, if data is strongly non-linear, then dimensionality techniques such as PCA can struggle to fully capture covariate relationships, potentially resulting in a loss of information. Dimensionality reduction can also result in difficult to interpret transformations of covariates and are not always easy to visualize. Future work therefore includes being able to develop our methods and additional marginalisation penalties to work upon data sets without the need for transforming $\mathcal{H}$ covariates into single x and z vectors. Finally, we have only considered non-parametric models for representing both $\mathcal{V}$ and $\mathcal{H}$. We mentioned in Section 2 and Appendix A our motivation and the suitability for non-parametric modelling, noting that if $f(y|x,z)$ takes a parametric modelling form, then it is unlikely $f(y|x)$ could also be of the same parametric form. However, it is possible for one of $\mathcal{V}$ or $\mathcal{H}$ to be modelled parametrically provided the other is modelled non-parametrically. This is therefore another potential avenue for future work.

8. Conclusions

Referring back to the purpose of this research, it is a common issue within data science of how to maximise the level of information that can be attained from asymmetric overlapping data sets. In a medical context, we have highlighted how particular subjects may have more information available to utilise within predictive analysis than the more common baseline information, such as specialist testing. Common solutions to this problem involve missing data imputation or simply two separate predictive models, one using baseline information only on a large number of individuals and one using baseline plus specialist testing information on a select number of individuals. The issue with missing data imputation is that it is infeasible and bad practice to impute large levels of missing data, particularly if the cohort with larger levels of information available is substantially smaller than that of the larger cohort with less information. Utilising two separate predictive models for each cohort limits analysis and what we can learn from both the response variable and its interaction with covariates.

In this work, we propose a method to integrate the smaller cohort, named horizontal data ($\mathcal{H}$), and the larger cohort, named vertical data ($\mathcal{V}$), without the requirement for data imputation or data deletion. Simplifying the number of covariates down to two, x and z, in which x represents covariates every individual has recorded, and z represents the added covariates only individuals within $\mathcal{H}$ have recorded, we are motivated by non-parametric models for modelling each cohort. We find that utilising flexible smoothing via B-Splines offers opportunities to take into account both cohorts into our analysis. Flexible smoothing models provide more robustness and flexibility to model complexly distributed data points where linear and polynomial regression models are unsatisfactory. Smoothness can be controlled by the introduction of a penalty term to B-Splines, also known as P-Splines—these penalties are desirable to prevent over/under-fitting to data. By looking at discrepancies between the marginal value of x obtained from $\mathcal{H}$, denoted ${\hat{\theta }}_{\mathcal{H}}\left(x\right)$, with the marginal value of x obtained from $\mathcal{V}$, denoted ${\hat{\theta }}_{\mathcal{V}}\left(x\right)$, we introduce a second penalty term to be able to model $\mathcal{H}$ whilst taking into account $\mathcal{V}$.

Through a series of data simulations, penalty parameter tunings, and model adaptations to take into account both a continuous and binary response, we found that the model with the additional marginalisation penalty appended to a P-Spline approximation method outperformed both the linear B-Spline method and the standard P-Spline approximation method utilising the single smoothing penalty. Applying the model to a real life healthcare data set of the LITMUS Metacohort with binary response relating to an individual’s risk of developing MASH (metabolic dysfunction associated steatohepatitis), we let $\mathcal{V}$ represent individuals who had a routine blood test taken, and $\mathcal{H}$ represent individuals who had further specialist genomic sequencing data collected. We found similar results in that this model with the additional marginalisation penalty fitted the marginal values of the data better than both the linear B-Spline model and the single penalty P-Spline approximation.

Areas for future work include the development of a succinct method to select penalty parameter ${\lambda }_2$ and the finding of a measurement to take into account overall model fit when applying models to a real world data set. In this work we omitted this, as our overall aim was to develop a method in which we could integrate asymmetric data sets into a predictive analysis upon a binary target, and therefore we had less of a focus on model fit. Future work will also include adapting our method to not require dimensionality reduction and also to consider parametric modelling for one of the $\mathcal{V}$ and $\mathcal{H}$ data sets. We have shown in this work that the novel additional marginalisation penalty improved the fit of the models as opposed to standard B-Spline and P-Splines approximation methods. These results are encouraging and illustrate a novel technique of how it is possible to integrate asymmetric data sets that share common levels of information without the need for data imputation or separate predictive modelling.