Paraconsistent Labeling Semantics for Abstract Argumentation

Abstract

Dung’s abstract argumentation framework is a popular formalism in formal argumentation. The present work develops paraconsistent labeling semantics for abstract argumentation such that the incomplete and inconsistent information can be expressed, and it introduces a Hilbert-style axiomatic system which is proven to be sound and complete. Additionally, we make a comparison between the logic developed in the present work and some relevant theories of abstract argumentation.

1. Introduction

Formal argumentation is an important research field in artificial intelligence (cf., e.g., [1,2,3,4]). Dung’s theory of abstract argumentation framework is useful for dealing with disputes between agents. This framework is simple but has powerful expressiveness (cf. [5]). An argumentation framework (AF) is a pair $(\mathcal{A},R)$ where $\mathcal{A}$ is a set of arguments and R a binary attack relation on $\mathcal{A}$. For all $a,b\in \mathcal{A}$, $aRb$ means that the argument a attacks b.

There are various kinds of semantics such as grounded, complete, preferred, stable and semi-stable semantics defined for AF in the literature (cf., e.g., [5,6]). For the purpose of representing different kinds of information, AF has been extended to many forms such as AF with uncertain information [4,7,8,9], bipolar AF [10,11,12], AF with preferences [13,14] and AF with constrains [15,16]. In particular, there are two ways to extend AF to represent uncertain information: one is incomplete AF (iAF) where arguments and attacks may be uncertain [7,8], and the other is probabilistic AF (PrAF) where arguments and attacks are associated with probabilities [4,9].

This paper uses AAF to deal with uncertain (incomplete) and paraconsistent information by introducing paraconsistent (four-valued) labeling semantics without utilizing probability. This differs from iAF in the following sense: the attack relation is certain, and the semantics is changed into a bilateral one such that an argument can accept (support) or reject a proposition. Thus, given an argument a and proposition $\phi$, there are four possibilities: (C1) a accepts $\phi$; (C2) a rejects $\phi$; (C3) a both accepts and rejects $\phi$; and (C4) a neither accepts nor rejects $\phi$. Here, (C1) means that $\phi$ is certainly true for a; (C2) means that $\phi$ is certainly not true for a; (C3) means that $\phi$ is a contradictory information for a; and (C4) means that $\phi$ is irrelevant with a.

The paraconsistent approach given in the present paper puts uncertainties on the satisfaction relation but not on the attack relation. Dung said, “an argument is an abstract entity whose role is solely determined by its relations to other arguments. No special attention is paid to the internal structure of the arguments” [5]. In our framework, an argument is an abstract entity whose role is determined both by its relations to other arguments and its relations to properties or propositions (supporting or rejecting). This is due to the fact that two arguments may attack the same arguments, but they are given based on different reasons. Belnap [17,18] and Dunn [19,20] proposed the four-valued semantics for modeling different states of information. In the present paper, the paraconsistent labeling semantics is used to deal with incomplete and paraconsistent information. After we present the bilateral semantics, we will introduce a sound and complete Hilbert-style axiomatic system. Finally, we will compare this kind of semantics with some relevant theories of abstract argumentation.

Some logicians (cf., e.g., [21,22]) have considered paraconsistency both at the level of propositional symbol and at the level of accessibility relation. The present paper has considered paraconsistency only at the level of the propositional symbol, but we generalize four-valued paraconsistent modal logic in a different direction: we generalize a single accessibility relation to bi-directional accessibility relations. Indeed, we use a four-valued paraconsistent tense logic with a global modality. Hence, the logic in the present paper can talk about the relations of both attacking and being attacked.

The structure of this paper is as follows. Section 2 introduces the formal language and paraconsistent labeling semantics. Section 3 gives a Hilbert-style axiomatic system and proves its soundness and completeness. Section 4 gives the comparison between our semantics and other theories. Section 5 gives some concluding remarks and directions of future work.

2. Paraconsistent Labeling Semantics

This section introduces the formal language and the paraconsistent labeling semantics. The modal logic of abstract argumentation under this kind of semantics is introduced.

Definition 1. 

An abstract argumentation framework (AAF) is a pair $\mathcal{F}=(\mathcal{A},R)$ where $\mathcal{A}\ne ⌀$ is a set of arguments, and R is a binary relation on $\mathcal{A}$ which is called the attack relation. The inverse of R is defined as $\breve{R}=\{⟨a,b⟩:bRa\}$. For every argument $a\in \mathcal{A}$, we define

$$R\left(a\right)=\{b\in \mathcal{A}:aRb\}\mathit{and}\breve{R}\left(a\right)=\{b\in \mathcal{A}:bRa\}.$$

Here, $R\left(a\right)$ is the set of all arguments that a attacks, and $\breve{R}\left(a\right)$ is the set of all arguments that attack a. For every set of arguments $X\subseteq \mathcal{A}$, the set of all arguments that arguments in X attack is defined as $R\left[X\right]={\bigcup }_{a\in X}R\left(a\right)$. The set of all arguments that attack arguments in X is defined as $\breve{R}\left[X\right]={\bigcup }_{a\in X}\breve{R}\left(a\right)$. For $n\ge 0$, the set $R^n\left(a\right)$ of all arguments reachable from a in n-steps of attack is defined inductively by $R^0\left(a\right)=\left\{a\right\}$ and $R^{n+1}=R\left[R^n\left(a\right)\right]$. The set ${\breve{R}}^n\left(a\right)$ of all arguments that can reach a in n-steps of attack is defined inductively by ${\breve{R}}^0\left(a\right)=\left\{a\right\}$ and ${\breve{R}}^{n+1}=\breve{R}\left[{\breve{R}}^n\left(a\right)\right]$.

Let $\mathbb{V}=\{p_i:i\in \omega \}$ be a denumerable set of propositional variables. We assume that $\mathbb{V}$ is denumerable, and in practical scenarios, $\mathbb{V}$ can be finite. Let $\mathcal{P}\left(\mathbb{V}\right)$ be the powerset of $\mathbb{V}$. In the standard labeling in an AAF, a set of propositional variables is assigned to each argument. Here, we assign each argument a pair of sets of propositional variables, namely, each argument a takes an element in the product $\mathcal{P}\left(\mathbb{V}\right)\times \mathcal{P}\left(\mathbb{V}\right)$ as its label. For each argument a, the label $l\left(a\right)$ consists of a pair of sets $⟨l^{+}\left(a\right),l^{-}\left(a\right)⟩$ where $l^{+}\left(a\right)$ is the set of all propositional variables that a accepts, and $l^{-}\left(a\right)$ is the set of all propositional variables that a rejects. The two sets of propositional variables have four cases in the following diagram:

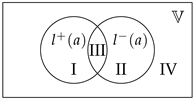
The region (I) consists of propositional variables which a accepts; (II) consists of propositional variables which a rejects; (III) consists of propositional variables which a accepts and rejects; and (IV) consists of propositional variables which a neither accepts nor rejects. Now, we give the formal definition of labeling and model as follows.

Definition 2. 

Let $\mathcal{F}=(\mathcal{A},R)$ be an AAF. A labeling in $\mathcal{F}$ is the function $l:\mathcal{A}\to \mathcal{P}\left(\mathbb{V}\right)\times \mathcal{P}\left(\mathbb{V}\right)$. A model is $\mathcal{M}=(\mathcal{F},l)$ where $\mathcal{F}$ is an AAF, and l is a labeling in $\mathcal{F}$. For every model $\mathcal{M}=(\mathcal{A},R,l)$ and $a\in \mathcal{A}$, the pair $l\left(a\right)=⟨l^{+}\left(a\right),l^{-}\left(a\right)⟩$ is given the label of a. The label $l\left(a\right)$ is consistent if $l^{+}\left(a\right)\cap l^{-}\left(a\right)=⌀$; $l\left(a\right)$ is inconsistent if $l\left(a\right)$ is not consistent; $l\left(a\right)$ is complete if $l^{+}\left(a\right)\cup l^{-}\left(a\right)=\mathbb{V}$; and $l\left(a\right)$ is incomplete if it is not complete.

Example 1. 

Consider the following AAF 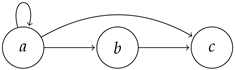$\mathcal{F}=(\mathcal{A},R)$:

Clearly, $R\left(a\right)=\{a,b,c\}$ and $\breve{R}\left(c\right)=\{a,b\}$. Note that $aRa$ means a attacks itself, namely, a is contradictory. Moreover, $\{b,c\}\subseteq R^n\left(a\right)$ for all $n\ge 1$. Let l be the labeling in $\mathcal{F}$ such that $l^{+}\left(a\right)=\left\{q\right\}$ and $l^{-}\left(a\right)=\{q,r\}$. Then, $l\left(a\right)$ is both inconsistent and incomplete.

Properties of arguments are expressed by formulas built from propositional variables using logical operators. In the present paper, we shall consider the following logical operators: ¬ (classical negation), ∼ (paraconsistent negation), ∨ (disjunction), ⋄ (future possibility), ⧫ (past possibility) and $\mathsf{E}$ (existential modality).

Definition 3. 

The set of all formulas $Fm$ is defined inductively as follows:

$$\begin{array}{cc}\hfill Fm\ni \phi & ::=p\mid \neg \phi \mid \sim \phi \mid ({\phi }_1\vee {\phi }_2)\mid ⧫\phi \mid \diamond \phi \mid \mathsf{E}\phi \hfill \end{array}$$

where $p\in \mathbb{V}$. The complexity of a formula φ, denoted by $c\left(\phi \right)$, is defined inductively as follows:

$$\begin{array}{cc}\hfill c\left(p\right)& =0\hfill \\ \hfill c(\circ \phi )& =c\left(\phi \right)+1,where\circ \in \{\neg ,\sim ,⧫,\diamond ,\mathsf{E}\}.\hfill \\ \hfill c(\phi \vee \psi )& =max\left\{c\right(\phi ),c(\psi \left)\right\}+1\hfill \end{array}$$

We use the following abbreviations:

$$\begin{array}{ccc}\hfill \top & :=p\vee \neg p\hfill & \hfill \left(\mathrm{true}\right)\\ \hfill \perp & :=p\wedge \neg p\hfill & \hfill \left(\mathrm{falsum}\right)\\ \hfill \phi \wedge \psi & :=\neg (\neg \phi \vee \neg \psi )\hfill & \hfill \left(\mathrm{conjunction}\right)\\ \hfill \phi \to \psi & :=\neg \phi \vee \psi \hfill & \hfill \left(\mathrm{condition}\right)\\ \hfill \phi \leftrightarrow \psi & :=(\phi \to \psi )\wedge (\psi \to \phi )\hfill & \hfill \left(\mathrm{equivalence}\right)\\ \hfill \square \phi & :=\sim \diamond \sim \phi \hfill & \hfill (\mathrm{future} \mathrm{necessity})\\ \hfill \blacksquare \phi & :=\sim ⧫\sim \phi \hfill & \hfill (\mathrm{past} \mathrm{necessity})\\ \hfill \mathsf{U}\phi & :=\sim \mathsf{E}\sim \phi \hfill & \hfill (\mathrm{universal} \mathrm{modality})\end{array}$$

For $\phi \in Fm$, let $var\left(\phi \right)$ be the set of all propositional variables appearing in φ. For $\odot \in \{\neg ,\sim ,⧫,\diamond ,\blacksquare ,\square ,\mathsf{E},\mathsf{U}\}$ and $n\ge 0$, the formula ${\odot }^n\phi$ is defined inductively by ${\odot }^0\phi =\phi$ and ${\odot }^{n+1}\phi =\odot {\odot }^n\phi$. For $\odot =\diamond$, ⧫ or $\mathsf{E}$, the dual of ⊙ is the operator ${\odot }^{\partial }=\square$, ▪ or $\mathsf{U}$, respectively.

Let a be an argument a in a model and $\phi$ a formula. We give the acceptance relation $a{\vDash }^{+}\phi$ and the rejection relation $a{\vDash }^{-}\phi$ to show the paraconsistent labeling semantics.

Definition 4. 

Let $\mathcal{M}=(\mathcal{A},R,l)$ be a model, $a\in \mathcal{A}$ and $\phi \in Fm$. The acceptance relation $\mathcal{M},a{\vDash }^{+}\phi$ and rejection relation $\mathcal{M},a{\vDash }^{-}\phi$ are defined simultaneously by induction as follows:

• $\mathcal{M},a{\vDash }^{+}p$ if and only if $p\in l^{+}\left(a\right)$.
• $\mathcal{M},a{\vDash }^{-}p$ if and only if $p\in l^{-}\left(a\right)$.
• $\mathcal{M},a{\vDash }^{+}\neg \phi$ if and only if $\mathcal{M},a{⊭}^{+}\phi$.
• $\mathcal{M},a{\vDash }^{-}\neg \phi$ if and only if $\mathcal{M},a{⊭}^{-}\phi$.
• $\mathcal{M},a{\vDash }^{+}\sim \phi$ if and only if $\mathcal{M},a{\vDash }^{-}\phi$.
• $\mathcal{M},a{\vDash }^{-}\sim \phi$ if and only if $\mathcal{M},a{\vDash }^{+}\phi$.
• $\mathcal{M},a{\vDash }^{+}\phi \vee \psi$ if and only if $\mathcal{M},a{\vDash }^{+}\phi$ or $\mathcal{M},a{\vDash }^{+}\psi$.
• $\mathcal{M},a{\vDash }^{-}\phi \vee \psi$ if and only if $\mathcal{M},a{\vDash }^{-}\phi$ and $\mathcal{M},a{\vDash }^{-}\psi$.
• $\mathcal{M},a{\vDash }^{+}\diamond \phi$ if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for some $b\in R\left(a\right)$.
• $\mathcal{M},a{\vDash }^{-}\diamond \phi$ if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for any $b\in R\left(a\right)$.
• $\mathcal{M},a{\vDash }^{+}⧫\phi$ if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for some $b\in \breve{R}\left(a\right)$.
• $\mathcal{M},a{\vDash }^{-}⧫\phi$ if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for any $b\in \breve{R}\left(a\right)$.
• $\mathcal{M},a{\vDash }^{+}\mathsf{E}\phi$ if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for some $b\in \mathcal{A}$.
• $\mathcal{M},a{\vDash }^{-}\mathsf{E}\phi$ if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for any $b\in \mathcal{A}$.

For every $\phi \in Fm$, let $Ar{g}^{+}\left(\phi \right)=\{a\in \mathcal{A}:\mathcal{M},a{\vDash }^{+}\phi \}$ and $Ar{g}^{-}\left(\phi \right)=\{a\in \mathcal{A}:\mathcal{M},a{\vDash }^{-}\phi \}$. Let $Arg\left(\phi \right)=⟨Ar{g}^{+}\left(\phi \right),Ar{g}^{-}\left(\phi \right)⟩$ be the meaning of φ in the model $\mathcal{M}$.

Lemma 1. 

For every model $\mathcal{M}=(\mathcal{A},R,l)$ and $\phi \in Fm$, the following hold:

(1)

$\mathcal{M},a{\vDash }^{+}\top$ and $\mathcal{M},a{⊭}^{-}\top$.

(2)

$\mathcal{M},a{⊭}^{+}\perp$ and $\mathcal{M},a{\vDash }^{-}\perp$.

(3)

$\mathcal{M},a{\vDash }^{+}\phi \wedge \psi$ if and only if $\mathcal{M},a{\vDash }^{+}\phi$ and $\mathcal{M},a{\vDash }^{+}\phi$.

(4)

$\mathcal{M},a{\vDash }^{-}\phi \wedge \psi$ if and only if $\mathcal{M},a{\vDash }^{-}\phi$ or $\mathcal{M},a{\vDash }^{-}\psi$.

(5)

$\mathcal{M},a{\vDash }^{+}\phi \to \psi$ if and only if $\mathcal{M},a{⊭}^{+}\phi$ or $\mathcal{M},a{\vDash }^{+}\phi$.

(6)

$\mathcal{M},a{\vDash }^{-}\phi \to \psi$ if and only if $\mathcal{M},a{⊭}^{-}\phi$ and $\mathcal{M},a{\vDash }^{-}\psi$.

(7)

$\mathcal{M},a{\vDash }^{+}\square \phi$ if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for all $b\in R\left(a\right)$.

(8)

$\mathcal{M},a{\vDash }^{-}\square \phi$ if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for some $b\in R\left(a\right)$.

(9)

$\mathcal{M},a{\vDash }^{+}\blacksquare \phi$ if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for all $b\in \breve{R}\left(a\right)$.

(10)

$\mathcal{M},a{\vDash }^{-}\blacksquare \phi$ if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for some $b\in \breve{R}\left(a\right)$.

(11)

$\mathcal{M},a{\vDash }^{+}\mathsf{U}\phi$ if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for all $b\in \mathcal{A}$.

(12)

$\mathcal{M},a{\vDash }^{-}\mathsf{U}\phi$ if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for some $b\in \mathcal{A}$.

(13)

$\mathcal{M},a{\vDash }^{+}\square \phi$ if and only if $\mathcal{M},b{\vDash }^{+}\neg \diamond \neg \phi$.

(14)

$\mathcal{M},a{\vDash }^{-}\square \phi$ if and only if $\mathcal{M},b{\vDash }^{-}\neg \diamond \neg \phi$.

(15)

$\mathcal{M},a{\vDash }^{+}\blacksquare \phi$ if and only if $\mathcal{M},b{\vDash }^{+}\neg ⧫\neg \phi$.

(16)

$\mathcal{M},a{\vDash }^{-}\blacksquare \phi$ if and only if $\mathcal{M},b{\vDash }^{-}\neg ⧫\neg \phi$.

(17)

$\mathcal{M},a{\vDash }^{+}\mathsf{U}\phi$ if and only if $\mathcal{M},b{\vDash }^{+}\neg \mathsf{E}\neg \phi$.

(18)

$\mathcal{M},a{\vDash }^{-}\mathsf{U}\phi$ if and only if $\mathcal{M},b{\vDash }^{-}\neg \mathsf{E}\neg \phi$.

Proof. 

We only prove the following items, and the proof of others is omitted.

$\left(3\right)$ $\mathcal{M},a{\vDash }^{+}\phi \wedge \psi$ if and only if $\mathcal{M},a{\vDash }^{+}\neg (\neg \phi \vee \neg \psi )$, if and only if $\mathcal{M},a{⊭}^{+}\neg \phi \vee \neg \psi$, if and only if $\mathcal{M},a{⊭}^{+}\neg \phi$ and $\mathcal{M},a{⊭}^{+}\neg \psi$, if and only if $\mathcal{M},a{\vDash }^{+}\phi$ and $\mathcal{M},a{\vDash }^{+}\psi$.

$\left(5\right)$ $\mathcal{M},a{\vDash }^{+}\phi \to \psi$ if and only if $\mathcal{M},a{\vDash }^{+}\neg \phi \vee \psi$, if and only if $\mathcal{M},a{\vDash }^{+}\neg \phi$ or $\mathcal{M},a{\vDash }^{+}\psi$, if and only if $\mathcal{M},a{⊭}^{+}\phi$ or $\mathcal{M},a{\vDash }^{+}\psi$.

$\left(7\right)$ $\mathcal{M},a{\vDash }^{+}\square \phi$ if and only if $\mathcal{M},a{\vDash }^{+}\sim \diamond \sim \phi$, if and only if $\mathcal{M},a{\vDash }^{-}\diamond \sim \phi$, if and only if $\mathcal{M},b{\vDash }^{-}\sim \phi$ for all $b\in R\left(a\right)$, if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for all $b\in R\left(a\right)$.

$\left(12\right)$ $\mathcal{M},a{\vDash }^{-}\mathsf{U}\phi$ if and only if $\mathcal{M},a{\vDash }^{-}\sim \mathsf{E}\sim \phi$, if and only if $\mathcal{M},a{\vDash }^{+}\mathsf{E}\sim \phi$, if and only if $\mathcal{M},b{\vDash }^{+}\sim \phi$ for some $b\in \mathcal{A}$, if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for some $b\in \mathcal{A}$.

$\left(13\right)$ $\mathcal{M},a{\vDash }^{+}\square \phi$ if and only if $\mathcal{M},b{\vDash }^{+}\phi$ for all $b\in R\left(a\right)$ by (7), if and only if $\mathcal{M},b{⊭}^{+}\neg \phi$ for all $b\in R\left(a\right)$, if and only if $\mathcal{M},a{⊭}^{+}\diamond \neg \phi$, if and only if $\mathcal{M},a{\vDash }^{+}\neg \diamond \neg \phi$.

$\left(14\right)$ $\mathcal{M},a{\vDash }^{-}\square \phi$ if and only if $\mathcal{M},b{\vDash }^{-}\phi$ for some $b\in R\left(a\right)$ by (8), if and only if $\mathcal{M},b{⊭}^{-}\neg \phi$ for some $b\in R\left(a\right)$, if and only if $\mathcal{M},a{⊭}^{-}\diamond \neg \phi$, if and only if $\mathcal{M},a{\vDash }^{-}\neg \diamond \neg \phi$. □

Definition 5. 

Let $\mathcal{F}=(\mathcal{A},R)$ be an AAF and $\Gamma \cup \phi \subseteq Fm$. Let $\mathcal{M}=(\mathcal{F},l)$ be a model on $\mathcal{F}$.

• φ is true at a in $\mathcal{M}$ (notation: $\mathcal{M},a\vDash \phi$) if $\mathcal{M},a{\vDash }^{+}\phi$ and $\mathcal{M},a{⊭}^{-}\phi$.
• φ is valid in $\mathcal{F}$ (notation: $\mathcal{F}\vDash \phi$) if $\mathcal{F},l,a\vDash \phi$ for every labeling l in $\mathcal{F}$ and $a\in \mathcal{A}$.
• φ is valid (notation: $\vDash \phi$) if $\mathcal{F}\vDash \phi$ for each AAF $\mathcal{F}$.

The paraconsistent modal logic for abstract argumentation $\mathsf{PML}=\{\phi \in Fm:\vDash \phi \}$. We write $\mathcal{M},a{\vDash }^{+}\Gamma$ if $\mathcal{M},a{\vDash }^{+}\psi$ for all $\psi \in \Gamma$; and $\mathcal{M},a{\vDash }^{-}\Gamma$ if $\mathcal{M},a{\vDash }^{-}\psi$ for some $\psi \in \Gamma$. A formula φ is a semantical consequence of Γ (notation: $\Gamma \vDash \phi$) if for every model $\mathcal{M}=(\mathcal{A},R,l)$ and $a\in \mathcal{A}$, (i) if $\mathcal{M},a{\vDash }^{+}\Gamma$, then $\mathcal{M},a{\vDash }^{+}\phi$; and (ii) if $\mathcal{M},a{\vDash }^{-}\phi$, then $\mathcal{M},a{\vDash }^{-}\Gamma$.

Here, we have defined the paraconsistent modal logic $\mathsf{PML}$ which is the logic of argumentation under the paraconsistent labeling semantics. In the next section, we will give a Hilbert-style axiomatization of $\mathsf{PML}$.

3. Hilbert-Style Axiomatic System

In this section, we shall present a Hilbert-style axiomatic system $\mathsf{S}$ for the logic $\mathsf{PML}$ of abstract argumentation. We shall prove the soundness and completeness of $\mathsf{S}$. Let $\mathsf{CL}$ be the classical propositional logic in the language $\{\neg ,\vee \}$.

Definition 6. 

The axiomatic system $\mathsf{S}$ consists of the following axiom schemata and inference rules:

(1)

Axiom schemata:

$\left(A1\right)$

All instances of $\mathsf{CL}$.

$\left(A2\right)$

$\phi \leftrightarrow \sim \sim \phi$

$\left(A3\right)$

$\neg \sim \phi \leftrightarrow \sim \neg \phi$

$\left(A4\right)$

$\sim \phi \wedge \sim \psi \to \sim (\phi \vee \psi )$

$\left(A5\right)$

$\odot \phi \leftrightarrow \neg {\odot }^{\partial }\neg \phi$ where $\odot \in \{\diamond ,⧫,\mathsf{E}\}$ and ${\odot }^{\partial }$ is the dual of ⊙.

$\left(A6\right)$

$\odot (\phi \to \psi )\to (\odot \phi \to \odot \psi )$ where $\odot \in \{\square ,\blacksquare ,\mathsf{U}\}$.

$\left(A7\right)$

$\phi \to \mathsf{E}\phi$

$\left(A8\right)$

$\mathsf{E}\mathsf{E}\phi \to \mathsf{E}\phi$

$\left(A9\right)$

$\phi \to \mathsf{U}\mathsf{E}\phi$

$\left(A10\right)$

$\mathsf{U}\phi \to \square \phi$

$\left(A11\right)$

$\mathsf{U}\phi \to \blacksquare \phi$

$\left(A12\right)$

$\phi \to \square ⧫\phi$

$\left(A13\right)$

$\phi \to \blacksquare \diamond \phi$

(2)

Inference rules:

$$\frac{\phi \to \psi \phi }{\psi }\left(\mathrm{MP}\right)\frac{\phi \to \psi }{\sim \psi \to \sim \phi }\left(\mathrm{CP}\right)\frac{\phi }{\odot \phi }\left({\mathrm{Gen}}_{\odot }\right),where\odot \in \{\square ,\blacksquare ,\mathsf{U}\}.$$

A proof of a formula φ in $\mathsf{S}$ a finite sequence of formulas ${\phi }_1,\dots ,{\phi }_n$ such that ${\phi }_n=\phi$ and each ${\phi }_i$ is either an axiom or derived from previous formulas by an inference rule. A formula φ is provable (or a theorem) in $\mathsf{S}$ (notation: ${⊢}_{\mathsf{S}}\phi$) if there exists a proof of φ in $\mathsf{S}$. A formula φ is derivable from a set of formulas Γ in $\mathsf{S}$ (notation: $\Gamma {⊢}_{\mathsf{S}}\phi$) if there exists a finite subset $\Delta \subseteq \Gamma$ such that ${⊢}_{\mathsf{S}}\bigwedge \Delta \to \phi$. Here, $\bigwedge \Delta$ is the conjunction of all formulas in Δ. In particular, $\bigwedge ⌀=\top$.

Lemma 2. 

For all formulas φ, ${\psi }_1$ and ${\psi }_2$, if ${⊢}_{\mathsf{S}}{\psi }_1\leftrightarrow {\psi }_2$, then ${⊢}_{\mathsf{S}}\phi \leftrightarrow \phi ({\psi }_1/{\psi }_2)$ where $\phi ({\psi }_1/{\psi }_2)$ is obtained from φ by substituting ${\psi }_2$ for one or more occurrences of ${\psi }_1$ in φ.

Proof. 

The proof proceeds by induction on the complexity $c\left(\phi \right)$. The case $\phi =p\in \mathbb{V}$ is trivial. Suppose that $\phi =\neg \psi$. By induction hypothesis, $⊢\psi \leftrightarrow \psi ({\psi }_1/{\psi }_2)$. By (A1) and (MP), $⊢\neg \psi \leftrightarrow \neg \psi ({\psi }_1/{\psi }_2)$. Suppose that $\phi =\sim \psi$. By induction hypothesis, $⊢\psi \leftrightarrow \psi ({\psi }_1/{\psi }_2)$. By (CP) and (A1), $⊢\sim \psi \leftrightarrow \sim \psi ({\psi }_1/{\psi }_2)$. Suppose that $\phi =\diamond \psi$, $⧫\psi$ or $\mathsf{E}\psi$. These cases are similar, and we show only the first case. By induction hypothesis, $⊢\psi \leftrightarrow \psi ({\psi }_1/{\psi }_2)$. By (A1), $⊢\neg \psi \leftrightarrow \neg \psi ({\psi }_1/{\psi }_2)$. By $\left({\mathrm{Gen}}_{\square }\right)$, (MP) and (A6), $⊢\square \neg \psi \leftrightarrow \square \neg \psi ({\psi }_1/{\psi }_2)$. By (A1), $⊢\neg \square \neg \psi \leftrightarrow \neg \square \neg \psi ({\psi }_1/{\psi }_2)$. Then, $⊢\diamond \psi \leftrightarrow \diamond \psi ({\psi }_1/{\psi }_2)$ by (A5) and (A1). Suppose that $\phi$ is $\psi \vee \chi$. By induction hypothesis, $⊢\psi \leftrightarrow \psi ({\psi }_1/{\psi }_2)$ and $⊢\chi \leftrightarrow \chi ({\psi }_1/{\psi }_2)$. By (A1) and (MP), $⊢\psi \vee \chi \leftrightarrow \psi ({\psi }_1/{\psi }_2)\vee \chi ({\psi }_1/{\psi }_2)$. Hence, $⊢\psi \vee \chi \leftrightarrow (\psi \vee \chi )({\psi }_1/{\psi }_2)$. □

Lemma 3. 

The following hold in $\mathsf{S}$:

$\left(1\right)$

${⊢}_{\mathsf{S}}\neg \odot \sim \phi \leftrightarrow \sim \odot \neg \phi$ where $\odot \in \{\square ,\blacksquare ,\mathsf{U},\diamond ,⧫,\mathsf{E}\}$.

$\left(2\right)$

${⊢}_{\mathsf{S}}\diamond \phi \to \mathsf{E}\phi$ and ${⊢}_{\mathsf{S}}⧫\phi \to \mathsf{E}\phi$.

$\left(3\right)$

if ${⊢}_{\mathsf{S}}\phi \to \psi$, then ${⊢}_{\mathsf{S}}\odot \phi \to \odot \psi$ where $\odot \in \{\square ,\blacksquare ,\mathsf{U},\diamond ,⧫,\mathsf{E}\}$.

$\left(4\right)$

${⊢}_{\mathsf{S}}\diamond \blacksquare \phi \to \phi$ and ${⊢}_{\mathsf{S}}⧫\square \phi \to \phi$.

$\left(5\right)$

${⊢}_{\mathsf{S}}\diamond \phi \to \psi$ if and only if ${⊢}_{\mathsf{S}}\phi \to \blacksquare \psi$.

$\left(6\right)$

${⊢}_{\mathsf{S}}⧫\phi \to \psi$ if and only if ${⊢}_{\mathsf{S}}\phi \to \square \psi$.

Proof. 

For (1), we only prove the case for □. By the definition of □, ${⊢}_{\mathsf{S}}\neg \square \sim \phi \leftrightarrow \neg \sim \diamond \sim \sim \phi$. By (A2) and Lemma 2, ${⊢}_{\mathsf{S}}\neg \square \sim \phi \leftrightarrow \neg \sim \diamond \phi$. By (A3), ${⊢}_{\mathsf{S}}\neg \sim \diamond \phi \leftrightarrow \sim \neg \diamond \phi$. By (A5), (A1) and Lemma 2, ${⊢}_{\mathsf{S}}\sim \neg \diamond \phi \leftrightarrow \sim \square \neg \phi$. By (A1), ${⊢}_{\mathsf{S}}\neg \square \sim \phi \leftrightarrow \sim \square \neg \phi$. For (2), we show only the case for ⋄. By (A10), ${⊢}_{\mathsf{S}}\mathsf{U}\sim \phi \to \square \sim \phi$. By (CP), ${⊢}_{\mathsf{S}}\sim \square \sim \phi \to \sim \mathsf{U}\sim \phi$. By (A2) and Lemma 2, ${⊢}_{\mathsf{S}}\diamond \phi \to \mathsf{E}\phi$. For (3), we show only the case for □. Assume that ${⊢}_{\mathsf{S}}\phi \to \psi$. By $\left({\mathrm{Gen}}_{\square }\right)$, ${⊢}_{\mathsf{S}}\square (\phi \to \psi )$. By (A6) and (MP), ${⊢}_{\mathsf{S}}\square \phi \to \square \psi$. For (4), by (A12) and (CP), ${⊢}_{\mathsf{S}}\sim \square ⧫\sim \phi \to \sim \sim \phi$. Then, ${⊢}_{\mathsf{S}}\sim \sim \diamond \sim ⧫\sim \phi \to \sim \sim \phi$. By (A2) and (MP), ${⊢}_{\mathsf{S}}\diamond \blacksquare \phi \to \phi$. Similarly, ${⊢}_{\mathsf{S}}⧫\square \phi \to \phi$. For (5), assume that ${⊢}_{\mathsf{S}}\diamond \phi \to \psi$. By (3), ${⊢}_{\mathsf{S}}\blacksquare \diamond \phi \to \blacksquare \psi$. By (A13), (A1) and (MP), ${⊢}_{\mathsf{S}}\phi \to \blacksquare \psi$. Assume that ${⊢}_{\mathsf{S}}\phi \to \blacksquare \psi$. By (3), ${⊢}_{\mathsf{S}}\diamond \phi \to \diamond \blacksquare \psi$. By (4), (A1) and (MP), ${⊢}_{\mathsf{S}}\diamond \phi \to \psi$. The item (6) is shown similarly. □

Lemma 4. 

The following hold in $\mathsf{S}$:

$\left(1\right)$

${⊢}_{\mathsf{S}}\neg \diamond \phi \leftrightarrow \square \neg \phi$; ${⊢}_{\mathsf{S}}\neg ⧫\phi \leftrightarrow \blacksquare \neg \phi$ and ${⊢}_{\mathsf{S}}\neg \mathsf{E}\phi \leftrightarrow \mathsf{U}\neg \phi$.

$\left(2\right)$

${⊢}_{\mathsf{S}}\sim (\phi \vee \psi )\leftrightarrow \sim \phi \wedge \sim \psi$ and ${⊢}_{\mathsf{S}}\sim (\phi \wedge \psi )\leftrightarrow \sim \phi \vee \sim \psi$.

$\left(3\right)$

${⊢}_{\mathsf{S}}\odot (\phi \vee \psi )\leftrightarrow \odot \phi \vee \odot \psi$ and ${⊢}_{\mathsf{S}}\odot (\phi \wedge \psi )\to \odot \phi \wedge \odot \psi$ for $\odot \in \{\diamond ,⧫,\mathsf{E}\}$.

$\left(4\right)$

${⊢}_{\mathsf{S}}\odot \phi \vee \odot \psi \to \odot (\phi \vee \psi )$ and ${⊢}_{\mathsf{S}}\odot (\phi \wedge \psi )\leftrightarrow \odot \phi \wedge \odot \psi$ for $\odot \in \{\square ,\blacksquare ,\mathsf{U}\}$.

$\left(5\right)$

${⊢}_{\mathsf{S}}\square \phi \wedge \diamond \psi \to \diamond (\phi \wedge \psi )$; ${⊢}_{\mathsf{S}}\blacksquare \phi \wedge ⧫\psi \to ⧫(\phi \wedge \psi )$ and ${⊢}_{\mathsf{S}}\mathsf{U}\phi \wedge \mathsf{E}\psi \to \mathsf{E}(\phi \wedge \psi )$.

Proof. 

(1) By (A1) and Lemma 2, ${⊢}_{\mathsf{S}}\neg \diamond \phi \leftrightarrow \neg \diamond \neg \neg \phi$. By (A5), (A1) and Lemma 2, ${⊢}_{\mathsf{S}}\neg \diamond \phi \leftrightarrow \square \neg \phi$. Similarly, we have ${⊢}_{\mathsf{S}}\neg ⧫\phi \leftrightarrow \blacksquare \neg \phi$ and ${⊢}_{\mathsf{S}}\neg \mathsf{E}\phi \leftrightarrow \mathsf{U}\neg \phi$.

(2) For ${⊢}_{\mathsf{S}}\sim (\phi \vee \psi )\leftrightarrow \sim \phi \wedge \sim \psi$, it suffices to show ${⊢}_{\mathsf{S}}\sim (\phi \vee \psi )\to \sim \phi \wedge \sim \psi$ by (A4). By (A1), ${⊢}_{\mathsf{S}}\phi \to \phi \vee \psi$ and ${⊢}_{\mathsf{S}}\psi \to \phi \vee \psi$. Then by (CP), ${⊢}_{\mathsf{S}}\sim (\phi \vee \psi )\to \sim \phi$ and ${⊢}_{\mathsf{S}}\sim (\phi \vee \psi )\to \sim \psi$. Hence, ${⊢}_{\mathsf{S}}\sim (\phi \vee \psi )\to \sim \phi \wedge \sim \psi$ by (A1). For ${⊢}_{\mathsf{S}}\sim (\phi \wedge \psi )\leftrightarrow \sim \phi \vee \sim \psi$, clearly ${⊢}_{\mathsf{S}}\sim (\phi \wedge \psi )\leftrightarrow \sim \neg (\neg \phi \vee \neg \psi )$. By (A3), ${⊢}_{\mathsf{S}}\sim \neg (\neg \phi \vee \neg \psi )\leftrightarrow \neg \sim (\neg \phi \vee \neg \psi )$. By Lemma 2 and ${⊢}_{\mathsf{S}}\sim (\neg \phi \vee \neg \psi )\leftrightarrow \sim \neg \phi \wedge \sim \neg \psi$ which we have just proven, ${⊢}_{\mathsf{S}}\neg \sim (\neg \phi \vee \neg \psi )\leftrightarrow \neg (\sim \neg \phi \wedge \sim \neg \psi )$. By (A3), ${⊢}_{\mathsf{S}}\neg (\sim \neg \phi \wedge \sim \neg \psi )\leftrightarrow \neg (\neg \sim \phi \wedge \neg \sim \psi )$. By (A1), ${⊢}_{\mathsf{S}}\neg (\neg \sim \phi \wedge \neg \sim \psi )\leftrightarrow (\sim \phi \vee \sim \psi )$. By (A1), ${⊢}_{\mathsf{S}}\sim (\phi \wedge \psi )\leftrightarrow (\sim \phi \vee \sim \psi )$.

(3) Clearly, ${⊢}_{\mathsf{S}}\phi \to \phi \vee \psi$ and ${⊢}_{\mathsf{S}}\psi \to \phi \vee \psi$. By Lemma 3 (3), ${⊢}_{\mathsf{S}}\diamond \phi \to \diamond (\phi \vee \psi )$ and ${⊢}_{\mathsf{S}}\diamond \psi \to \diamond (\phi \vee \psi )$. By (A1), ${⊢}_{\mathsf{S}}(\diamond \phi \vee \diamond \psi )\to \diamond (\phi \vee \psi )$. Clearly, ${⊢}_{\mathsf{S}}\neg \phi \to (\neg \psi \to \neg (\phi \vee \psi ))$. By $\left({\mathrm{Gen}}_{\square }\right)$, (A6) and (MP), ${⊢}_{\mathsf{S}}\square \neg \phi \to \square (\neg \psi \to \neg (\phi \vee \psi ))$. By (A6), ${⊢}_{\mathsf{S}}\square (\neg \psi \to \neg (\phi \vee \psi ))\to (\square \neg \psi \to \square \neg (\phi \vee \psi ))$. By (A1), ${⊢}_{\mathsf{S}}\square \neg \phi \to (\square \neg \psi \to \square \neg (\phi \vee \psi ))$. By (A1), ${⊢}_{\mathsf{S}}\square \neg \phi \wedge \square \neg \psi \to \square \neg (\phi \vee \psi )$. Again by (A1), ${⊢}_{\mathsf{S}}\neg \square \neg (\phi \vee \psi )\to \neg (\square \neg \phi \wedge \square \neg \psi )$. Again By (A1), ${⊢}_{\mathsf{S}}\neg \square \neg (\phi \vee \psi )\to \neg \square \neg \phi \vee \neg \square \neg \psi$. Hence, by (A5) and Lemma 2, ${⊢}_{\mathsf{S}}\diamond (\phi \vee \psi )\to \diamond \phi \vee \diamond \psi$. Similarly, ${⊢}_{\mathsf{S}}⧫(\phi \vee \psi )\leftrightarrow (⧫\phi \vee ⧫\psi )$ and ${⊢}_{\mathsf{S}}\mathsf{E}(\phi \vee \psi )\leftrightarrow (\mathsf{E}\phi \vee \mathsf{E}\psi )$. Clearly, ${⊢}_{\mathsf{S}}\phi \wedge \psi \to \phi$ and ${⊢}_{\mathsf{S}}\phi \wedge \psi \to \psi$. For $\odot \in \{\diamond ,⧫,\mathsf{E}\}$, by Lemma 3 (3), ${⊢}_{\mathsf{S}}\odot (\phi \wedge \psi )\to \odot \phi$ and ${⊢}_{\mathsf{S}}\odot (\phi \wedge \psi )\to \odot \psi$. Hence, ${⊢}_{\mathsf{S}}\odot (\phi \wedge \psi )\to \odot \phi \wedge \odot \psi$.

(4) Clearly, ${⊢}_{\mathsf{S}}\phi \to (\phi \vee \psi )$ and ${⊢}_{\mathsf{S}}\psi \to (\phi \vee \psi )$. For $\odot \in \{\square ,\blacksquare ,\mathsf{U}\}$, by Lemma 3 (3), ${⊢}_{\mathsf{S}}\odot \phi \to \odot (\phi \vee \psi )$ and ${⊢}_{\mathsf{S}}\odot \psi \to \odot (\phi \vee \psi )$. Then, ${⊢}_{\mathsf{S}}(\odot \phi \vee \odot \psi )\to \odot (\phi \vee \psi )$. By (A5) and (A1), ${⊢}_{\mathsf{S}}\square (\phi \wedge \psi )\leftrightarrow \neg \diamond \neg (\phi \wedge \psi )$. By (A1) and Lemma 2, ${⊢}_{\mathsf{S}}\neg \diamond \neg (\phi \wedge \psi )\leftrightarrow \neg \diamond (\neg \phi \vee \neg \psi )$. By (3), ${⊢}_{\mathsf{S}}\neg \diamond (\neg \phi \vee \neg \psi )\leftrightarrow \neg (\diamond \neg \phi \vee \diamond \neg \psi )$. By (A1), ${⊢}_{\mathsf{S}}\neg (\diamond \neg \phi \vee \diamond \neg \psi )\leftrightarrow (\neg \diamond \neg \phi \wedge \neg \diamond \neg \psi )$. By (A5) and (A1), ${⊢}_{\mathsf{S}}(\neg \diamond \neg \phi \wedge \neg \diamond \neg \psi )\leftrightarrow (\square \phi \wedge \square \psi )$. By (A1), ${⊢}_{\mathsf{S}}\square (\phi \wedge \psi )\leftrightarrow (\square \phi \wedge \square \psi )$. Similarly, ${⊢}_{\mathsf{S}}\blacksquare (\phi \wedge \psi )\leftrightarrow (\blacksquare \phi \wedge \blacksquare \psi )$ and ${⊢}_{\mathsf{S}}\mathsf{U}(\phi \wedge \psi )\leftrightarrow (\mathsf{U}\phi \wedge \mathsf{U}\psi )$.

(5) By (A5) and (A1), ${⊢}_{\mathsf{S}}\square \phi \wedge \diamond \psi \to \square \phi \wedge \neg \square \neg \psi$. By (A1), ${⊢}_{\mathsf{S}}(\square \phi \wedge \neg \square \neg \psi )\to \neg (\square \phi \to \square \neg \psi )$. By (A6) and (A1), ${⊢}_{\mathsf{S}}\neg (\square \phi \to \square \neg \psi )\to \neg \square (\phi \to \neg \psi )$. By (A5) and (A1), ${⊢}_{\mathsf{S}}\neg \square (\phi \to \neg \psi )\to \diamond \neg (\phi \to \neg \psi )$. By (A1) and Lemma 2, ${⊢}_{\mathsf{S}}\diamond \neg (\phi \to \neg \psi )\to \diamond (\phi \wedge \psi )$. Hence, ${⊢}_{\mathsf{S}}\square \phi \wedge \diamond \psi \to \diamond (\phi \wedge \psi )$ by (A1). Similarly, ${⊢}_{\mathsf{S}}\blacksquare \phi \wedge ⧫\psi \to ⧫(\phi \wedge \psi )$ and ${⊢}_{\mathsf{S}}\mathsf{U}\phi \wedge \mathsf{E}\psi \to \mathsf{E}(\phi \wedge \psi )$. □

Now, we prove the completeness of $\mathsf{S}$ by the canonical model method. First, we define deductive filters and use them to define the canonical model.

Definition 7. 

A nonempty set of formulas F is an $\mathsf{S}$-deductive filter if $\phi \in F$ and ${⊢}_{\mathsf{S}}\phi \to \psi$ imply $\psi \in F$. An $\mathsf{S}$-deductive filter F is proper if $\perp \notin F$. The set of all $\mathsf{S}$-deductive filters is denoted by $\mathcal{F}\left(\mathsf{S}\right)$. A proper $\mathsf{S}$-deductive filter F is prime if $\phi \vee \psi \in F$ implies $\phi \in F$ or $\psi \in F$. The set of all prime $\mathsf{S}$-deductive filters is denoted by ${\mathcal{F}}_p\left(\mathsf{S}\right)$.

Lemma 5. 

Let $F\in {\mathcal{F}}_p\left(\mathsf{S}\right)$. For all formulas φ and ψ, the following hold:

$\left(1\right)$

$\phi \wedge \psi \in F$ if and only if $\phi \in F$ and $\psi \in F$.

$\left(2\right)$

$\phi \vee \psi \in F$ if and only if $\phi \in F$ or $\psi \in F$.

$\left(3\right)$

$\neg (\phi \wedge \psi )\in F$ if and only if $\neg \phi \in F$ or $\neg \psi \in F$.

$\left(4\right)$

$\neg (\phi \vee \psi )\in F$ if and only if $\neg \phi \in F$ and $\neg \psi \in F$.

$\left(5\right)$

$\sim (\phi \wedge \psi )\in F$ if and only if $\sim \phi \in F$ or $\sim \psi \in F$.

$\left(6\right)$

$\sim (\phi \vee \psi )\in F$ if and only if $\sim \phi \in F$ and $\sim \psi \in F$.

Proof. 

For (1), assume that $\phi \wedge \psi \in F$. By ${⊢}_{\mathsf{S}}\phi \wedge \psi \to \phi$ and ${⊢}_{\mathsf{S}}\phi \wedge \psi \to \psi$, we obtain $\phi \in F$ and $\psi \in F$. Conversely, assume that $\phi \in F$ and $\psi \in F$. By ${⊢}_{\mathsf{S}}\phi \to (\psi \to \phi \wedge \psi )$, we obtain $\phi \wedge \psi \in F$. For (2), assume that $\phi \vee \psi \in F$. Since F is prime, we have $\phi \in F$ or $\psi \in F$. Assume that $\phi \in F$ or $\psi \in F$. By ${⊢}_{\mathsf{S}}\phi \to (\phi \vee \psi )$ and ${⊢}_{\mathsf{S}}\psi \to (\phi \vee \psi )$, we have $\phi \vee \psi \in F$. The items (3) and (4) are shown similarly. By Lemma 4(2) and items (1) and (2), we obtain (5) and (6). □

For a nonempty set of formulas $\Phi$, let $[\Phi )=\{\psi \mid \exists {\phi }_1,\dots ,{\phi }_n\in \Phi ({⊢}_{\mathsf{S}}{\phi }_1\wedge \dots \wedge {\phi }_n\to \psi )\}$. Clearly, $[\Phi )$ is an $\mathsf{S}$-deductive filter. If $\Phi =\left\{\phi \right\}$, we write $\left[\phi \right)$ for $\left[\right\{\phi \left\}\right)$.

Lemma 6. 

The following hold in $\mathsf{S}$:

(1)

If $F\in \mathcal{F}\left(\mathsf{S}\right)$ and $\psi \notin F$, there exists $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F\subseteq G$ and $\psi \notin G$.

(2)

If $\phi {⊬}_{\mathsf{S}}\psi$, then there exists $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $\phi \in G$ and $\psi \notin G$.

Proof. 

For (1), assume that $F\in \mathcal{F}\left(\mathsf{S}\right)$ and $\psi \notin F$. Consider the set $\mathfrak{X}=\{H\in \mathcal{F}(\mathsf{S})\mid F\subseteq H\&\psi \notin H\}$. Note that $\mathfrak{X}\ne ⌀$ since $F\in \mathfrak{X}$. Then, $(\mathfrak{X},\subseteq )$ is a partially ordered set. Let $\mathfrak{Y}$ be any ⊆-chain in $\mathfrak{X}$. It is easily shown that $G^{\prime }=\bigcup \mathfrak{Y}\in \mathfrak{X}$ is a ⊆-upper bound of $\mathfrak{Y}$. By Zorn’s lemma, there exists a ⊆-maximal element G in $\mathfrak{X}$. Clearly, $F\subseteq G$ and $\psi \notin G$. It suffices to show that G is prime. For a contradiction, suppose that ${\psi }_1\vee {\psi }_2\in G$, ${\psi }_1\notin G$ and ${\psi }_2\notin G$. Let $H_1=[G\cup \left\{{\psi }_1\right\})$ and $H_2=[G\cup \left\{{\psi }_2\right\})$. Since G is ⊆-maximal, $H_1\notin \mathfrak{X}$ and $H_2\notin \mathfrak{X}$. Then, $\psi \in H_1$ and $\psi \in H_2$. Then, there exist ${\chi }_1,{\chi }_2\in G$ such that ${⊢}_{\mathsf{S}}{\chi }_1\wedge {\psi }_1\to \psi$ and ${⊢}_{\mathsf{S}}{\chi }_2\wedge {\psi }_2\to \psi$. By (A1), ${⊢}_{\mathsf{S}}{\chi }_1\wedge {\chi }_2\wedge {\psi }_1\to \psi$ and ${⊢}_{\mathsf{S}}{\chi }_1\wedge {\chi }_2\wedge {\psi }_2\to \psi$. Again by (A1), ${⊢}_{\mathsf{S}}({\chi }_1\wedge {\chi }_2)\wedge ({\psi }_1\vee {\psi }_2)\to \psi$. By Lemma 5 (1), $({\chi }_1\wedge {\chi }_2)\wedge ({\psi }_1\vee {\psi }_2)\in G$. Then, $\psi \in G$ which contradicts $\psi \notin G$. For (2), let $F=\left[\phi \right)$. Then, $\psi \notin F$ and $F\in \mathcal{F}\left(\mathsf{S}\right)$. By (1), there exists $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $\phi \in G$ and $\psi \notin G$. □

Definition 8. 

For a nonempty set of formulas Φ, let ${\odot }^{-}\Phi =\{\phi \mid \odot \phi \in \Phi \}$ and $\odot \Phi =\{\odot \phi \mid \phi \in \Phi \}$ for $\odot \in \{\square ,\blacksquare ,\diamond ,⧫,\mathsf{U},\mathsf{E}\}$. The canonical AAF for $\mathsf{S}$ is defined as the structure ${\mathfrak{F}}_{\mathsf{S}}=(W_{\mathsf{S}},R_{\mathsf{S}},R_{\mathsf{E}})$ where

• $W_{\mathsf{S}}={\mathcal{F}}_p\left(\mathsf{S}\right)$.
• $F{R}_{\mathsf{S}}G$ if and only if ${\square }^{-}F\subseteq G\subseteq {\diamond }^{-1}F$ and ${\blacksquare }^{-}G\subseteq F\subseteq {⧫}^{-}G$.
• $F{R}_{\mathsf{E}}G$ if and only if ${\mathsf{U}}^{-}F\subseteq G\subseteq {\mathsf{E}}^{-}F$.

The canonical model for $\mathsf{S}$ is defined as the model ${\mathfrak{M}}_{\mathsf{S}}=({\mathfrak{F}}_{\mathsf{S}},l_{\mathsf{S}})$ where $l_{\mathsf{S}}$ is a labeling given by $l_{\mathsf{S}}^{+}\left(F\right)=\{p\in \mathbb{V}\mid p\in F\}$ and $l_{\mathsf{S}}^{-}\left(F\right)=\{p\in \mathbb{V}\mid \sim p\in F\}$ for every $F\in {\mathcal{F}}_p\left(\mathsf{S}\right)$.

The canonical AAF ${\mathfrak{F}}_{\mathsf{S}}$ consists of two relations $R_{\mathsf{S}}$ and $R_{\mathsf{E}}$, and so it is not an AAF in the sense of Definition 2. Thus, the proof of completeness is not standard. Using the following Lemma 7, we obtain a submodel ${\mathfrak{M}}_{\mathsf{S}}\left(F\right)$ generated by a point $F\in W_{\mathsf{S}}$ and so it will be a model in the sense of Definition 4.

Lemma 7. 

$R_{\mathsf{S}}\subseteq R_{\mathsf{E}}$ and $\breve{R_{\mathsf{S}}}\subseteq R_{\mathsf{E}}$.

Proof. 

Assume that $F{R}_{\mathsf{S}}G$. We show ${\mathsf{U}}^{-}F\subseteq G$ and $G\subseteq {\mathsf{E}}^{-}F$. Suppose that $\mathsf{U}\phi \in F$. By (A10), $\square \phi \in F$. By $F{R}_{\mathsf{S}}G$, we have $\phi \in G$. Hence, ${\mathsf{U}}^{-}F\subseteq G$. Suppose that $\phi \in G$. By $F{R}_{\mathsf{S}}G$, we have $\diamond \phi \in F$. By Lemma 3 (2), $\mathsf{E}\phi \in F$. Hence, $G\subseteq {\mathsf{E}}^{-}F$. Hence, $R_{\mathsf{S}}\subseteq R_{\mathsf{E}}$. Similarly, we have $\breve{R_{\mathsf{S}}}\subseteq R_{\mathsf{E}}$. □

Definition 9. 

For the canonical model ${\mathfrak{M}}_{\mathsf{S}}=(W_{\mathsf{S}},R_{\mathsf{S}},R_{\mathsf{E}},l_{\mathsf{S}})$ and $F\in W_{\mathsf{S}}$, the generated submodel ${\mathfrak{M}}_{\mathsf{S}}\left(F\right)=(W_F,R_F,l_F)$ is defined as follows:

(1)

$W_F={\bigcup }_{n\in \mathbb{N}}{R}_{\mathsf{E}}^n\left(F\right)$ where $R_{\mathsf{E}}^0\left(F\right)=\left\{F\right\}$ and $R_{\mathsf{E}}^{n+1}\left(F\right)=R_{\mathsf{E}}\left[R_{\mathsf{E}}^n\left(F\right)\right]$.

(2)

$R_F=R_{\mathsf{S}}\bigcap (W_F\times W_F)$.

(3)

$l_F\left(G\right)=(l_{\mathsf{S}}^{+}\left(G\right)\bigcap W_F,l_{\mathsf{S}}^{-}\left(G\right)\bigcap W_F)$ for every $G\in W_F$.

Lemma 8. 

Let $\phi \in Fm$ and $G\in W_F$. The following hold:

(1)

${\mathfrak{M}}_{\mathsf{S}}\left(F\right),G{\vDash }^{+}\phi$ if and only if ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{+}\phi$.

(2)

${\mathfrak{M}}_{\mathsf{S}}\left(F\right),G{\vDash }^{-}\phi$ if and only if ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{-}\phi$.

Proof. 

We prove (1) and (2) simultaneously by induction on the the complexity of $\phi$. The case $\phi =p,\neg \psi ,\sim \psi$ or $\psi \vee \chi$ is trivial. Suppose that $\phi =\diamond \psi$. For (1), assume ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),G{\vDash }^{+}\diamond \psi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),H{\vDash }^{+}\psi$ for some $H\in R_F\left(G\right)$. By induction hypothesis, ${\mathfrak{M}}_{\mathsf{S}}\left(H\right),H{\vDash }^{+}\psi$. By induction hypothesis and Lemma 7, ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),H{\vDash }^{+}\psi$. Hence, ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{+}\diamond \psi$. Conversely, assume that ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{+}\diamond \psi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),H{\vDash }^{+}\psi$ for some $H\in R_G\left(G\right)$. By induction hypothesis, ${\mathfrak{M}}_{\mathsf{S}}\left(H\right),H{\vDash }^{+}\psi$. By induction hypothesis and $H\in W_F$, we have ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),H{\vDash }^{+}\psi$. By $G{R}_{G}H$ and Lemma 7, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),G{\vDash }^{+}\diamond \psi$. Similarly, we can prove (2). The case for $\phi =⧫\psi$ or $\mathsf{E}\psi$ is shown similarly. □

Lemma 9 

(Existence Lemma). For every $F\in {\mathcal{F}}_p\left(\mathsf{S}\right)$, the following hold:

(1)

$\diamond \phi \in F$ if and only if $\phi \in G$ for some $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$.

(2)

$⧫\phi \in F$ if and only if $\phi \in G$ for some $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $G{R}_{\mathsf{S}}F$.

(3)

$\mathsf{E}\phi \in F$ if and only if $\phi \in G$ for some $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{E}}G$.

(4)

$\sim \diamond \phi \in F$ if and only if $\sim \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$.

(5)

$\sim ⧫\phi \in F$ if and only if $\sim \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $G{R}_{\mathsf{S}}F$.

(6)

$\sim \mathsf{E}\phi \in F$ if and only if $\sim \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{E}}G$.

(7)

$\neg \diamond \phi \in F$ if and only if $\neg \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$.

(8)

$\neg ⧫\phi \in F$ if and only if $\neg \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $G{R}_{\mathsf{S}}F$.

(9)

$\neg \mathsf{E}\phi \in F$ if and only if $\neg \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $G{R}_{\mathsf{E}}F$.

Proof. 

(1) The right-to-left direction follows from the definition of $R_{\mathsf{S}}$. Assume that $\diamond \phi \in F$. Let $F^{\prime }=[{\square }^{-}F\cup ⧫F\cup \left\{\phi \right\})$. Consider $\mathfrak{X}=\{H\in \mathcal{F}\left(\mathsf{S}\right)\mid F^{\prime }\subseteq H\&\diamond H\subseteq F\&{\blacksquare }^{-}H\subseteq F\}$.

Next, we show $F^{\prime }\in \mathfrak{X}$. Suppose that $\chi \in F^{\prime }$. Then, there exist ${\psi }_1,\dots ,{\psi }_m\in {\square }^{-}F$ and $⧫{\delta }_1,\dots ,⧫{\delta }_n\in ⧫F$ such that ${⊢}_{\mathsf{S}}\left({\bigwedge }_{1\le i\le m}{\psi }_i\right)\wedge ({\bigwedge }_{1\le k\le n}⧫{\delta }_k)\wedge \phi \to \chi$. By Lemma 3 (3), ${⊢}_{\mathsf{S}}\diamond (\left({\bigwedge }_{1\le i\le m}{\psi }_i\right)\wedge ({\bigwedge }_{1\le k\le n}⧫{\delta }_k)\wedge \phi )\to \diamond \chi$. By Lemma 4 (5), ${⊢}_{\mathsf{S}}\square (\left({\bigwedge }_{1\le i\le m}{\psi }_i\right)\wedge ({\bigwedge }_{1\le k\le n}⧫{\delta }_k))\wedge \diamond \phi \to \diamond \chi$. By Lemma 4 (4), ${⊢}_{\mathsf{S}}({\bigwedge }_{1\le i\le m}\square {\psi }_i)\wedge ({\bigwedge }_{1\le k\le n}\square ⧫{\delta }_k)\wedge \diamond \phi \to \diamond \chi$. For $1\le k\le n$, by $⧫{\delta }_k\in ⧫F$ and (A12), $\square ⧫{\delta }_k\in F$. Hence, $\diamond \chi \in F$ since ${\psi }_i\in {\square }^{-}F$ and $\diamond \phi \in F$. Hence, $\diamond F^{\prime }\subseteq F$. Furthermore, by Lemma 3 (2), $\mathsf{E}\chi \in F$ and so $\mathsf{E}{F}^{\prime }\subseteq F$. To show ${\blacksquare }^{-}{F}^{\prime }\subseteq F$, suppose that $\blacksquare {\chi }^{\prime }\in F^{\prime }$. Then, $\diamond \blacksquare {\chi }^{\prime }\in F$ since $\diamond F^{\prime }\subseteq F$. By Lemma 3 (4), ${\chi }^{\prime }\in F$. Hence, ${\blacksquare }^{-}{F}^{\prime }\subseteq F$. Thus, $F^{\prime }\in \mathfrak{X}$, i.e., $\mathfrak{X}\ne ⌀$.

Let $\mathfrak{Y}$ be a ⊆-chain in $(\mathfrak{X},\subseteq )$. Let $H^{\prime }=\bigcup \mathfrak{Y}$. Clearly, $H^{\prime }\in \mathfrak{X}$ is a ⊆-upper bound of $\mathfrak{Y}$. By Zorn’s lemma, there exists a maximal ⊆-element G in $\mathfrak{X}$. Suppose that $\perp \in G$. Then, $\mathsf{E}\perp \in F$ by $G\in \mathfrak{X}$ and Lemma 3(2). Clearly, ${⊢}_{\mathsf{S}}\mathsf{E}\perp \to \perp$. Then, $\perp \in F$ which contradicts $F\in {\mathcal{F}}_p\left(\mathsf{S}\right)$. Hence, $\perp \notin G$. Clearly, ${\square }^{-}F\subseteq G$, $⧫F\subseteq G$, $\diamond G\subseteq F$ and ${\blacksquare }^{-}G\subseteq F$. It suffices to show that G is prime.

Assume that ${\chi }_1\vee {\chi }_2\in G$ and ${\chi }_1\notin G$ and ${\chi }_2\notin G$. For a contradiction, let $F_1=[G\cup \left\{{\chi }_1\right\})$ and $F_2=[G\cup \left\{{\chi }_2\right\})$. Clearly, $G⊊F_1$ and $G⊊F_2$. By the maximality of G, $F_1\notin \mathfrak{X}$ and $F_2\notin \mathfrak{X}$. By $F^{\prime }\subseteq G$, we have, for $i=1,2$, $\diamond F_i⊈F$ or ${\blacksquare }^{-}{F}_i⊈F$. We have the following cases:

(1.1) There exist ${\beta }_1\in F_1$ and ${\beta }_2\in F_2$ with $\diamond {\beta }_1\notin F$ and $\diamond {\beta }_2\notin F$. By ${\beta }_1\in F_1$ and ${\beta }_2\in F_2$, there exist ${\alpha }_1,{\alpha }_2\in G$ such that ${⊢}_{\mathsf{S}}{\alpha }_1\wedge {\chi }_1\to {\beta }_1$ and ${⊢}_{\mathsf{S}}{\alpha }_2\wedge {\chi }_2\to {\beta }_2$. Let $\alpha ={\alpha }_1\wedge {\alpha }_2$. Clearly, $\alpha \in G$. Then, ${⊢}_{\mathsf{S}}\alpha \wedge {\chi }_1\to {\beta }_1$ and ${⊢}_{\mathsf{S}}\alpha \wedge {\chi }_2\to {\beta }_2$. Then, ${⊢}_{\mathsf{S}}\alpha \wedge ({\chi }_1\vee {\chi }_2)\to {\beta }_1\vee {\beta }_2$. Clearly, $\alpha \wedge ({\chi }_1\vee {\chi }_2)\in G$. Then, ${\beta }_1\vee {\beta }_2\in G$. Then, $\diamond ({\beta }_1\vee {\beta }_2)\in F$. By Lemma 4 (3), $\diamond {\beta }_1\vee \diamond {\beta }_2\in F$. Hence, $\diamond {\beta }_1\in F$ or $\diamond {\beta }_2\in F$, which contradicts $\diamond {\beta }_1,\diamond {\beta }_2\notin F$.

(1.2) There exist $\blacksquare {\beta }_1\in F_1$ and $\blacksquare {\beta }_2\in F_2$ such that ${\beta }_1\notin F$ and ${\beta }_2\notin F$. By $\blacksquare {\beta }_1\in F_1$ and $\blacksquare {\beta }_2\in F_2$, there exist ${\alpha }_1,{\alpha }_2\in G$ such that ${⊢}_{\mathsf{S}}{\alpha }_1\wedge {\chi }_1\to \blacksquare {\beta }_1$ and ${⊢}_{\mathsf{S}}{\alpha }_2\wedge {\chi }_2\to \blacksquare {\beta }_2$. Let $\alpha ={\alpha }_1\wedge {\alpha }_2$. Clearly, $\alpha \in G$. Then, ${⊢}_{\mathsf{S}}\alpha \wedge {\chi }_1\to \blacksquare {\beta }_1$ and ${⊢}_{\mathsf{S}}\alpha \wedge {\chi }_2\to \blacksquare {\beta }_2$. Then, ${⊢}_{\mathsf{S}}\alpha \wedge ({\chi }_1\vee {\chi }_2)\to \blacksquare {\beta }_1\vee \blacksquare {\beta }_2$. Clearly, $\alpha \wedge ({\chi }_1\vee {\chi }_2)\in G$. Then, $\blacksquare {\beta }_1\vee \blacksquare {\beta }_2\in G$. Therefore, $\diamond (\blacksquare {\beta }_1\vee \blacksquare {\beta }_2)\in F$ since $G\in \mathfrak{X}$. Hence, $\diamond \blacksquare {\beta }_1\vee \diamond \blacksquare {\beta }_2\in F$ by Lemma 4 (3). Note that ${⊢}_{\mathsf{S}}\diamond \blacksquare {\beta }_1\vee \diamond \blacksquare {\beta }_2\to {\beta }_1\vee {\beta }_2$ by Lemma 3 (4). Then, ${\beta }_1\vee {\beta }_2\in F$. Hence, ${\beta }_1\in F$ or ${\beta }_2\in F$ which contradicts ${\beta }_1,{\beta }_2\notin F$.

(1.3) There exist ${\beta }_1\in F_1$ and $\blacksquare {\beta }_2\in F_2$ such that $\diamond {\beta }_1\notin F$ and ${\beta }_2\notin F$. In the same way of case (1.1), we can show that $\diamond {\beta }_1\in F$ or $\diamond \blacksquare {\beta }_2\in F$. The latter implies that ${\beta }_2\in F$ by Lemma 3 (4). Hence, $\diamond {\beta }_1\in F$ or ${\beta }_2\in F$ which contradicts $\diamond {\beta }_1,{\beta }_2\notin F$.

(1.4) There exist $\blacksquare {\beta }_1\in F_1$ and ${\beta }_2\in F_2$ such that ${\beta }_1\notin F$ and $\diamond {\beta }_2\notin F$. This case can be shown in the same way of the case (1.3).

The proofs of (2) and (3) are similar to that of (1), and we omit the details.

(4) Assume that $\sim \diamond \phi \in F$. Then, $\square \sim \phi \in F$. By definition of the canonical model, $\sim \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$. To show the other direction, assume that $\sim \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$. For a contradiction, suppose that $\sim \diamond \phi \notin F$. Then, $\neg \sim \diamond \phi \in F$. Then, $\diamond \neg \sim \phi \in F$. By (1), $\neg \sim \phi \in G$ for some $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$. Then, $\sim \phi \notin G$ which leads to a contradiction.

(5)–(6) are similar to case (4).

(7) Assume that $\neg \diamond \phi \in F$. Then, $\square \neg \phi \in F$ by (A5). By definition of canonical model, $\neg \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$. To show the other direction, assume that $\neg \phi \in G$ for all $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$. For a contradiction, suppose that $\neg \diamond \phi \notin F$. Then, $\diamond \phi \in F$. By (1), $\phi \in G$ for some $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $F{R}_{\mathsf{S}}G$. Then, $\neg \phi \notin G$ which leads to a contradiction.

(8) and (9) are similar to (7). □

Lemma 10 

(Truth Lemma). For all $F\in W_{\mathsf{S}}$ and formula φ, the following hold:

(1)

${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\phi$ if and only if $\phi \in F$.

(2)

${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\phi$ if and only if $\sim \phi \in F$.

Proof. 

We prove (1) and (2) simultaneously by induction on the complexity of $\phi$. The case that $\phi$ is atomic is trivial. We have the following cases:

(i) $\phi =\diamond \psi$. For (1), assume that ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\diamond \psi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),G{\vDash }^{+}\psi$ for some $G\in W_F$ such that $F{R}_{F}G$. Thus, ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{+}\psi$ by Lemma 8(1). By induction hypothesis, $\phi \in G$. By Lemma 9 (1), $\diamond \psi \in F$. Conversely, assume that $\diamond \psi \in F$. By Lemma 9 (1), $\psi \in G$ for some $G\in W_{\mathsf{S}}$ such that $F{R}_{\mathsf{S}}G$. By induction hypothesis, ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{+}\psi$. By Lemma 7, $G\in W_F$. By Lemma 8 (1), ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),G{\vDash }^{+}\psi$. Hence, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\diamond \psi$. For (2), assume that ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\diamond \psi$. For all $G\in W_F$ such that $F{R}_{F}G$, we have ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),G{\vDash }^{-}\psi$. By Lemma 8 (2), ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{-}\psi$. By induction hypothesis, $\sim \psi \in G$. Then, by Lemma 7, $\sim \psi \in G$ for all $G\in W_{\mathsf{S}}$ such that $F{R}_{\mathsf{S}}G$. By Lemma 9 (4), $\sim \diamond \psi \in F$. The other direction is shown similarly.

(ii) $\phi =⧫\psi$ or $\mathsf{E}\psi$. This case is similar to the case (i).

(iii) $\phi =\sim \psi$. For (1), assume that ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\sim \psi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\psi$. By induction hypothesis, $\sim \psi \in F$. The other direction is shown similarly. For (2), assume that ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\sim \psi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\psi$. By induction hypothesis, $\psi \in F$. By (A2), we have $\sim \sim \psi \in F$. The other direction is shown similarly.

(iv) $\phi =\neg \psi$. For (1), assume that ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\neg \psi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{⊭}^{+}\psi$. By induction hypothesis, $\psi \notin F$. Then, $\neg \psi \in F$ since F is prime. Conversely, assume that $\neg \psi \in F$. Then, $\psi \notin F$ since F is proper. By induction hypothesis, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{⊭}^{+}\psi$. Hence, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\neg \psi$. For (2), assume ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\neg \psi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{⊭}^{-}\psi$. By induction hypothesis, $\sim \psi \notin F$. Then, $\neg \sim \psi \in F$ since F is prime. By (A3), $\sim \neg \psi \in F$. The other direction is shown similarly.

(v) $\phi =\psi \vee \chi$. For (1), assume that ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\psi \vee \chi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\psi$ or ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{+}\chi$. By induction hypothesis, $\psi \in F$ or $\chi \in F$. By Lemma 5 (2), $\psi \vee \chi \in F$. The other direction is shown similarly. For (2), assume ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\psi \vee \chi$. Then, ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\psi$ and ${\mathfrak{M}}_{\mathsf{S}}\left(F\right),F{\vDash }^{-}\chi$. By induction hypothesis, $\sim \psi \in F$ and $\sim \chi \in F$. By Lemma 5 (1), $\sim \psi \wedge \sim \chi \in F$. By (A4), $\sim (\psi \vee \chi )\in F$. The other direction is shown similarly. □

Theorem 1 

(Completeness). $\Gamma {⊢}_{\mathsf{S}}\psi$ if and only if $\Gamma \vDash \psi$.

Proof. 

The soundness can be checked as usual. Assume that $\Gamma {⊬}_{\mathsf{S}}\psi$. Then, $\psi \notin [\Gamma )$. By Lemma 6(1), there exists $G\in {\mathcal{F}}_p\left(\mathsf{S}\right)$ such that $[\Gamma )\subseteq G$ and $\psi \notin G$. By Lemma 10 (1), ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{\vDash }^{+}\Gamma$ but ${\mathfrak{M}}_{\mathsf{S}}\left(G\right),G{⊭}^{+}\psi$. Hence, $\Gamma ⊭\psi$. □

4. Discussion

In an AAF, consider different arguments a and b which have the same relations to other arguments. The following Example 2 gives such a scenario. The problem is how a and b can be distinguished from each other. The semantics given by Dung [5] can not tell the difference between arguments a and b since an argument is completely determined by its relations to other arguments. However, using the semantics presented in this paper, we can achieve this. For an argument a, it has not only the attack relationship to other arguments, for example, the argument b attacks a and a attacks c, but also can accept or reject some properties. For example, a accepts the property p and rejects q. Thus, from this semantical perspective, an argument is an abstract entity whose role is determined both by its relations to other arguments and its semantical relations to propositions.

Example 2. 

Marry and John both oppose presidential candidate A. However, they oppose him for different reasons. Marry opposes them because she thinks that he is not honest; and John opposes them because he thinks that his policies can not support economic growth.

The two arguments in Example 2 (Marry and John’s arguments) both attack the argument that presidential candidate A should be elected, but they are different arguments. Using the labeling semantics, a formula $\phi$ can be interpreted as a property of arguments or a set of all arguments accepting $\phi$. The formula $\sim \phi$ is interpreted as a set of all arguments rejecting $\phi$. The formula $\diamond \phi$ is interpreted as a set of all arguments which attack some arguments supporting $\phi$. The formula $\square \phi$ is interpreted as a set of all arguments which attack only arguments supporting $\phi$. The formulas $⧫\phi$ and $\blacksquare \phi$ are interpreted similarly. The formula $\mathsf{E}\phi$ is interpreted as that there is an argument accepting $\phi$, and $\mathsf{U}\phi$ as that all arguments accept $\phi$. By the labeling semantics, arguments are distinguished by properties.

Furthermore, many arguments are based on incomplete and inconsistent information. Dung [5] said that “all forms of reasoning with incomplete information rest on the simple intuitive idea that a defeasible statement can be believed only in the absence of any evidence to the contrary which is very much like the principle of argumentation.”. Since information is usually not only incomplete but also inconsistent based on multiple information sources, the labeling semantics given in the present paper works naturally since it introduces the acceptance and rejection semantical relations.

Grossi [23,24] introduced the doing argumentation theory to study abstract argumentation. In this framework, an argument a belonging to $\mathfrak{I}\left(p\right)$ in a given model means that a has the property p or that p is true of a. Thus, either a has the property p or a does not have p, but not both. This approach is essentially bivalent. In our paraconsistent labeling semantics, we have the following four cases:

(1)

a accepts p (p is true of a).

(2)

a rejects p (p is false of a).

(3)

a both accepts and rejects p (p is both true and false of a).

(4)

a neither accepts nor rejects p (p is neither true nor false of a).

Grossi’s doing argumentation theory can not express the inconsistency or lacking information of arguments. For example, the arguments which attack an argument supporting $\phi$ and rejecting $\phi$ can be expressed by the formula $\diamond (\phi \wedge \sim \phi )$ under our labeling semantics.

Caminada [25] proposed an alternative labeling semantics for abstract argumentation. In their framework, every argument is labeled (or be valued) by in, out or undec, which means, respectively, the argument is accepted, rejected and illegally undec.

A Caminada Labeling is a function $\lambda$ from the set of all arguments to the set of labels (or propositional variables), in, out and undec, satisfying the following conditions.

(1)

If $R\left(a\right)=⌀$ (i.e., there is no argument attacking a), then $\lambda \left(a\right)=in$.

(2)

If $b\in R\left(a\right)$ (i.e., the argument b attacking a) and $\lambda \left(b\right)=in$, then $\lambda \left(a\right)=out$.

(3)

If all $b\in R\left(a\right)$, $\lambda \left(b\right)=out$, then $\lambda \left(a\right)=in$.

(4)

Otherwise, $\lambda \left(a\right)=undec$.

Caminada’s labeling demands consistency, i.e., an argument a is rejected if it is attacked by an accepted argument b. It also demands maximal acceptance, i.e., an argument a which is not attacked by no argument is necessarily accepted. However, in our paraconsistent approach, neither consistency nor maximal acceptance is assumed.

5. Concluding Remarks and Future Work

This paper develops a paraconsistent labeling semantics for abstract argumentation. Then, we introduces the paraconsistent modal logic $\mathsf{PML}$ and its Hilbert-style axiomatic system $\mathsf{S}$. The system $\mathsf{S}$ is shown to be sound and complete with respect to the paraconsistent labeling semantics. Moreover, we have compared paraconsistent labeling semantics with other semantical approaches to the abstract argumentation.

The present paper leaves some interesting directions which are worth exploring in further work. One direction is that paraconsistency at the level of accessibility relation may be generalized in two different ways: one is the four-valued accessibility relation, and the other is the birelational frame semantics. In the latter way, we have the attack relation and support relation so that an argument can both attack and support the same arguments. Some logicians have given a sort of four-valued paraconsistent modal logic based on birelational frame semantics, but the resulting logic is not a temporal logic (cf., e.g., [26]).

Another approach is using the modal hybrid logic that can enrich the expressiveness of language on structures. We may add names of arguments to the language so that we can talk about properties of arguments in a direct way. Some logicians have considered this kind of modal hybrid logic (cf., e.g., [27]), but the used logic is not a temporal one.

The last approach is the study of measures of inconsistency in abstract argumentation (AAF) that can enable us to compare in a direct way two different AAFs with respect of the number of inconsistencies. For example, the arguments from a debate among the candidates consist of an argumentation; then, the less inconsistency there is in the argumentation, the clearer the candidate’s policy. Measures of inconsistency in the context of argumentation theory are worth exploring further; although, this kind of work has been done in other contexts (cf., e.g., [27,28,29]).