Reliability of Partitioning Metric Space Data
Abstract
1. Introduction
- The distance from a data point to itself is zero: d(x, x) = 0.
- The distance between two distinct points x and y is always positive: d(x, y) > 0.
- The distance from x to y is always the same as the distance from y to x: d(x, y) = d(y, x).
- There is a triangle inequality: d(x, y) + d(y, z) ≤ d(x, z).
2. Preliminary Materials: Some Definitions and Separation Power (SP) Calculation Method
2.1. Some Definitions
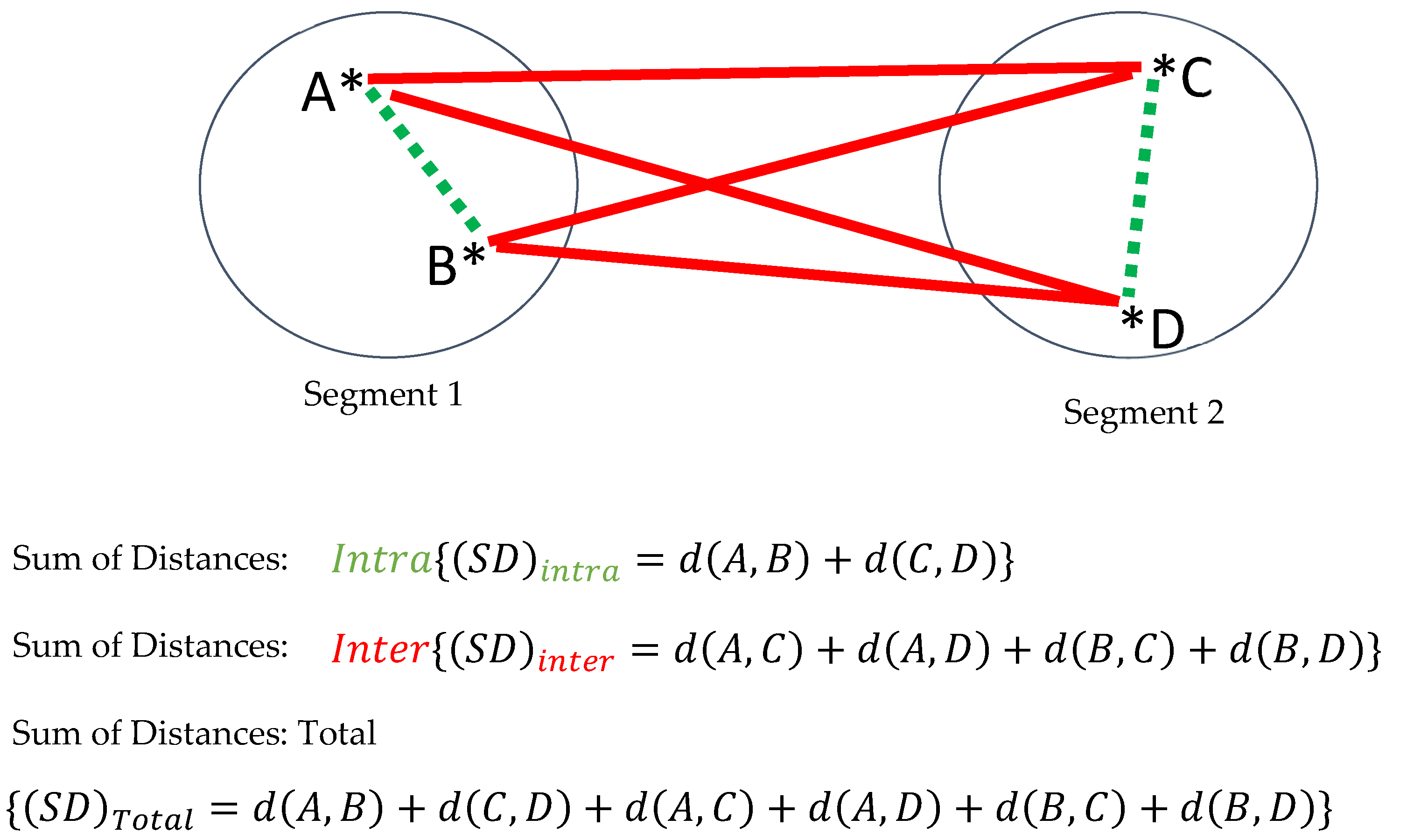
- Intra degrees of connection : The sum of data pairs belonging to the same groups, i.e.,
- Inter degrees of connection : The sum of data pairs belonging to the different groups, i.e.,
- .
- Total degrees of connection : The sum of all data pairs, i.e.,
- . Obviously,
- .
- Intra sum of distances : The sum of distances between data pairs belonging to the same groups.
- Inter sum of distances : The sum of distances between data pairs belonging to the different groups.
- Total sum of distances : The sum of distances between all data pairs. Obviously (see Figure 3 for an example),
- .
- Intra mean distance : The sum of distances between data pairs belonging to the same groups divided by the intra degrees of connection——i.e., ;
- Inter mean distance : The sum of distances between data pairs belonging to the different groups divided by the inter degrees of connection——i.e., .
- Separation/segregation power—SP divided by , i.e.,
2.2. Some Illustrative Examples of SP Calculation for the Different Kinds of Data
2.2.1. Data Represented by Real Numbers
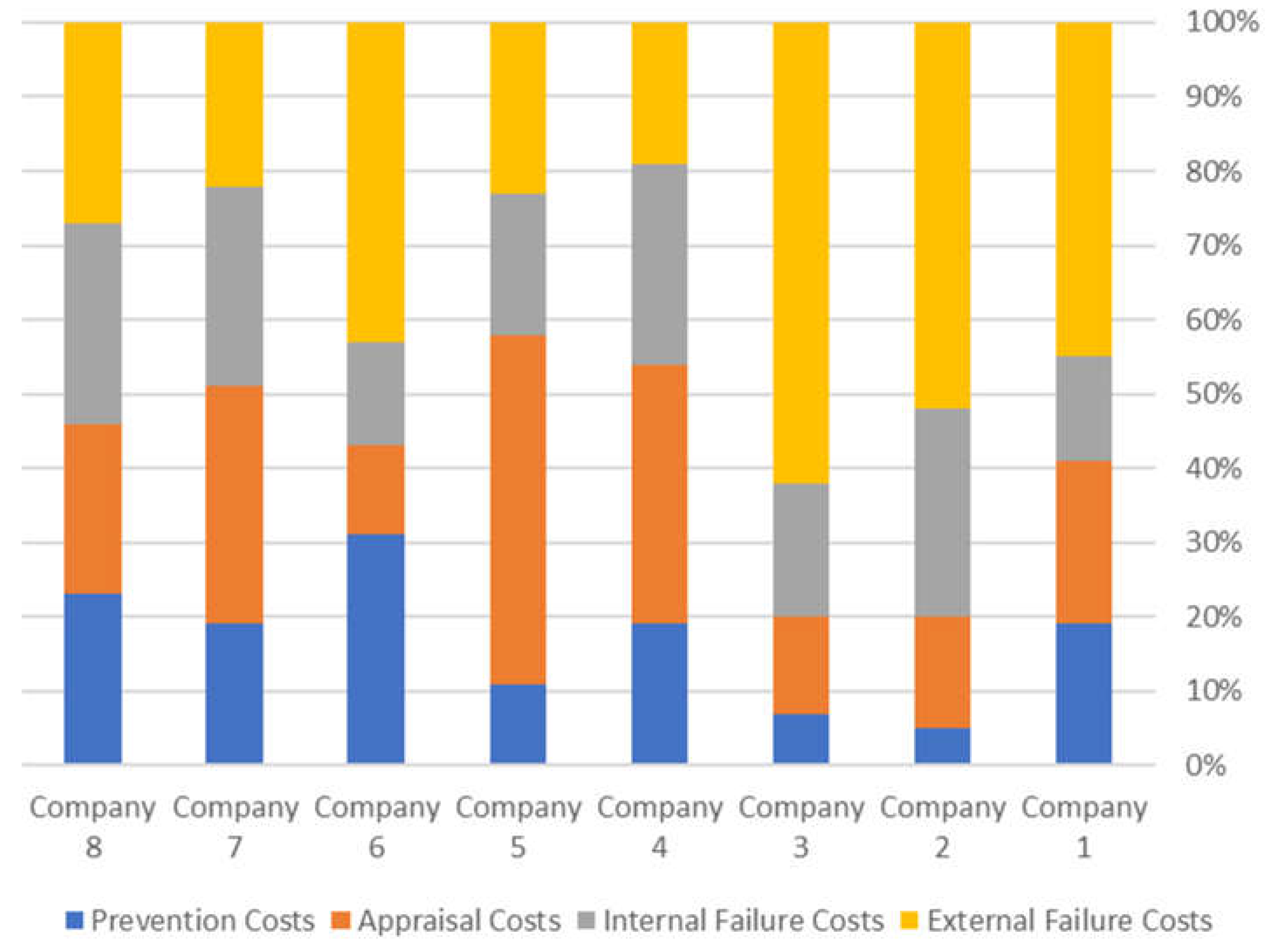
2.2.2. Each Datum Is a Discrete Distribution over Categories (as in a Pie Chart)
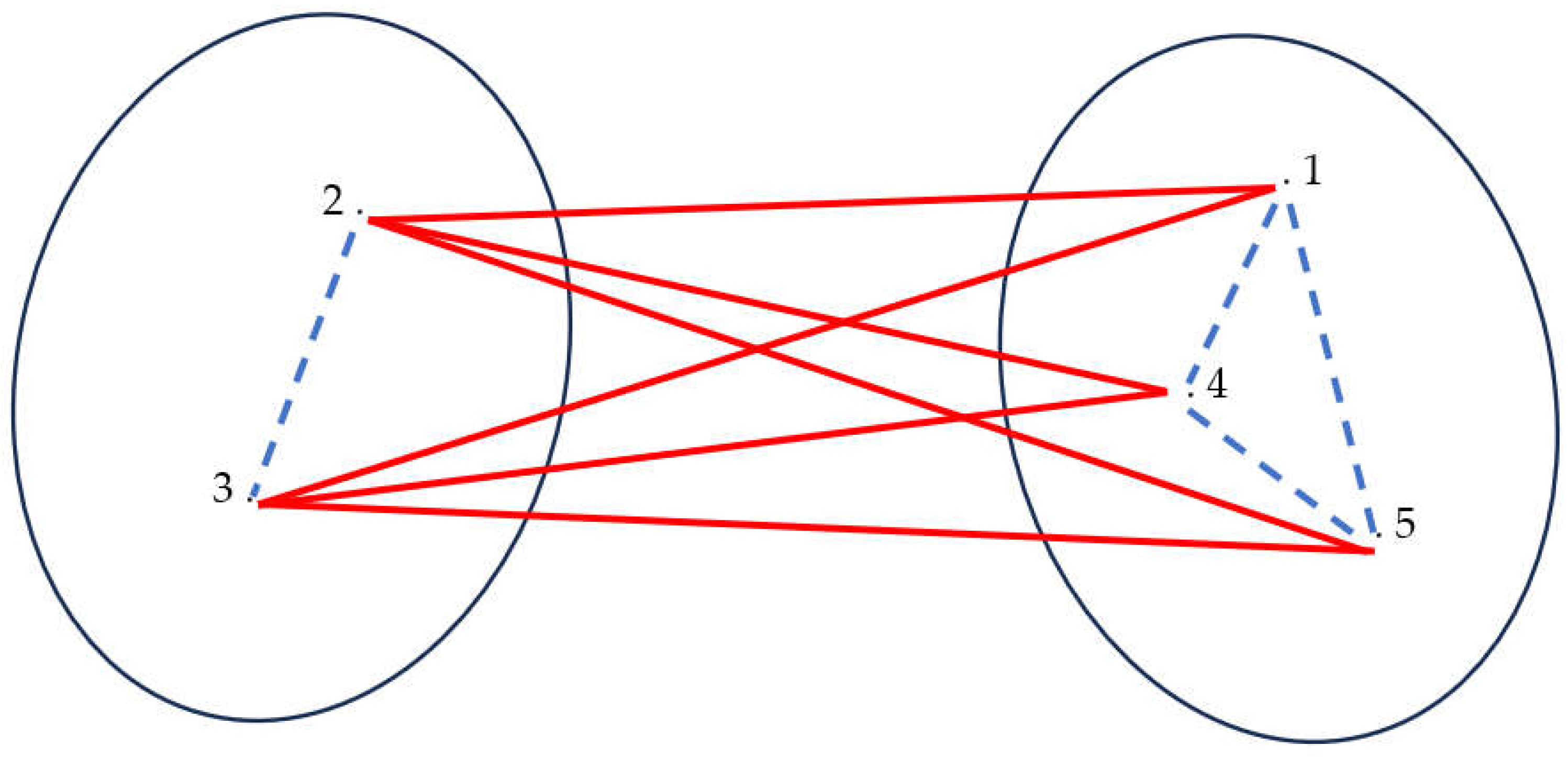
2.2.3. Each Datum Is a Preference Chain of Alternatives
2.3. Checking the Homogeneity Hypothesis H0
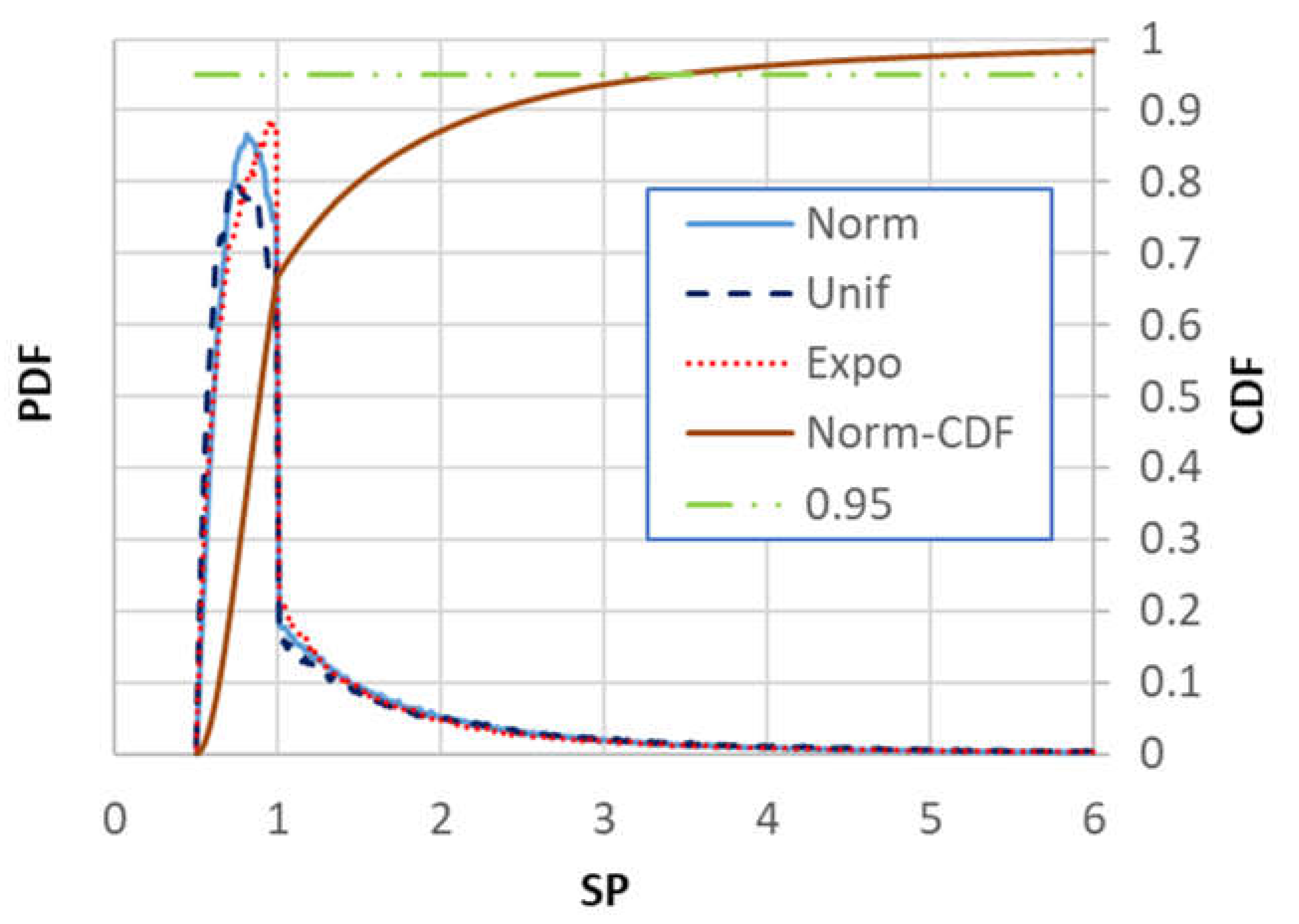
2.4. Some Simple Examples of Distance Metric Distribution
2.4.1. Normal Distribution
2.4.2. Uniform Distribution
2.4.3. Exponential Distribution
2.4.4. Conclusions Derived from the above Examples
3. Results of the Theoretical and Simulation Studies
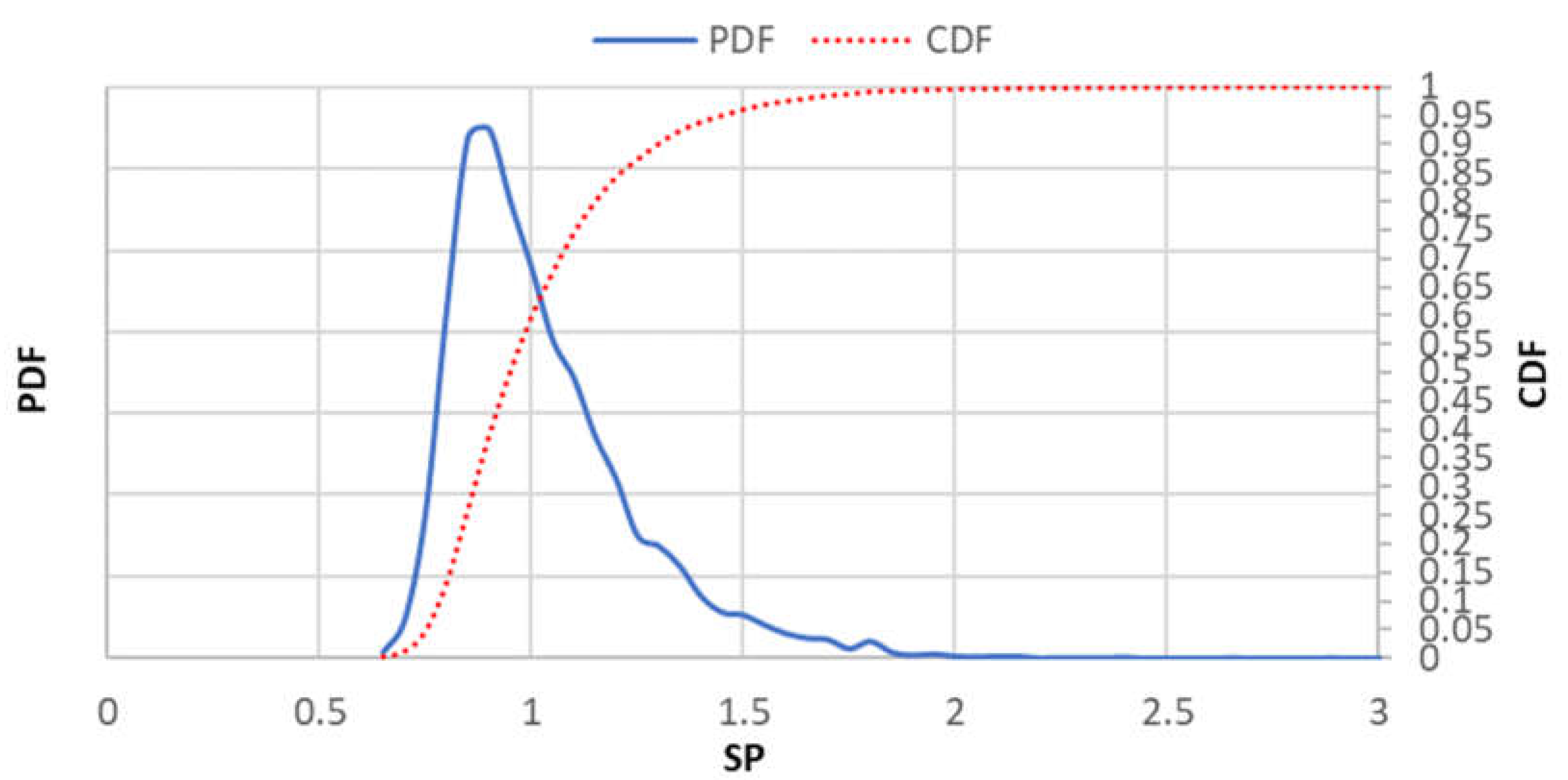
3.1. Some General Considerations Regarding SP Distribution under H0
3.2. Some Remarks on Deriving the SP Distribution from a Simulation Process under H0
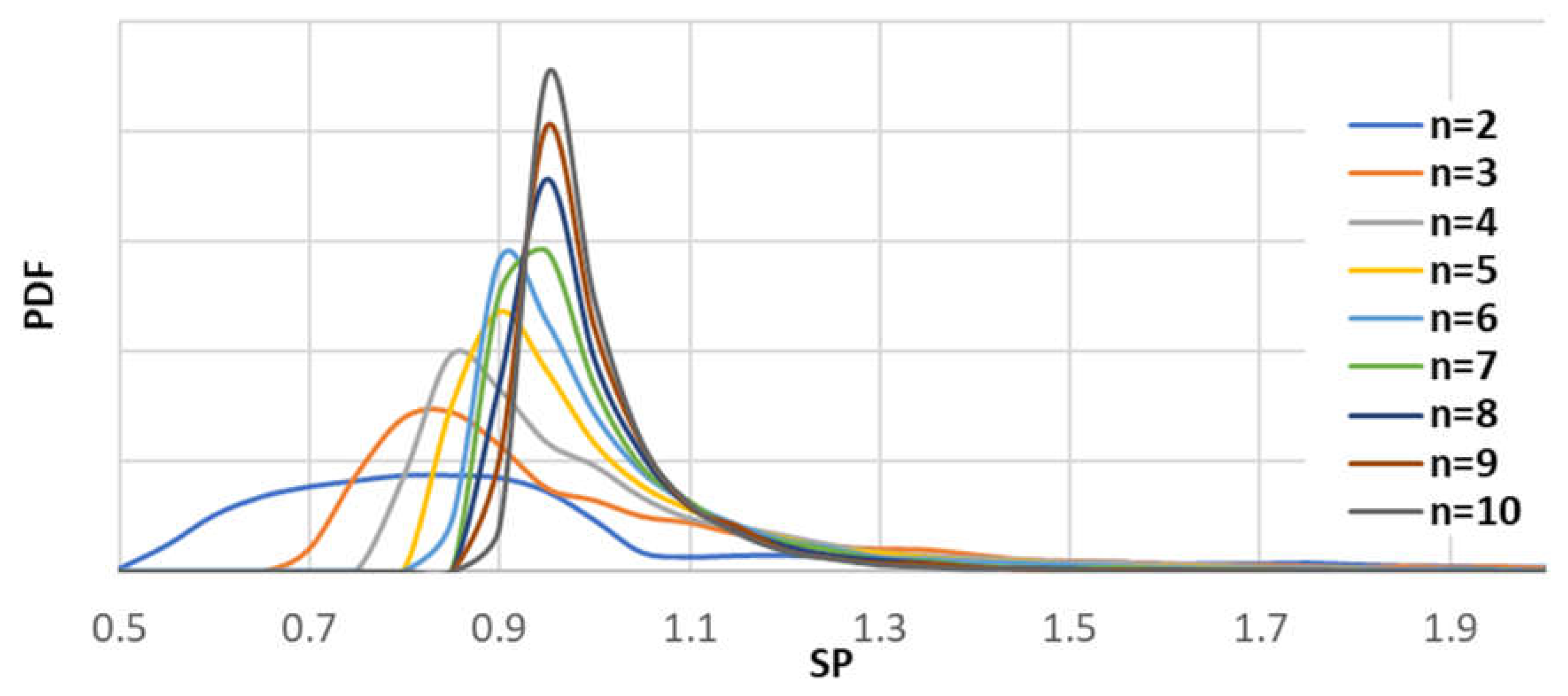
3.2.1. The Case Described in Section 2.2.1
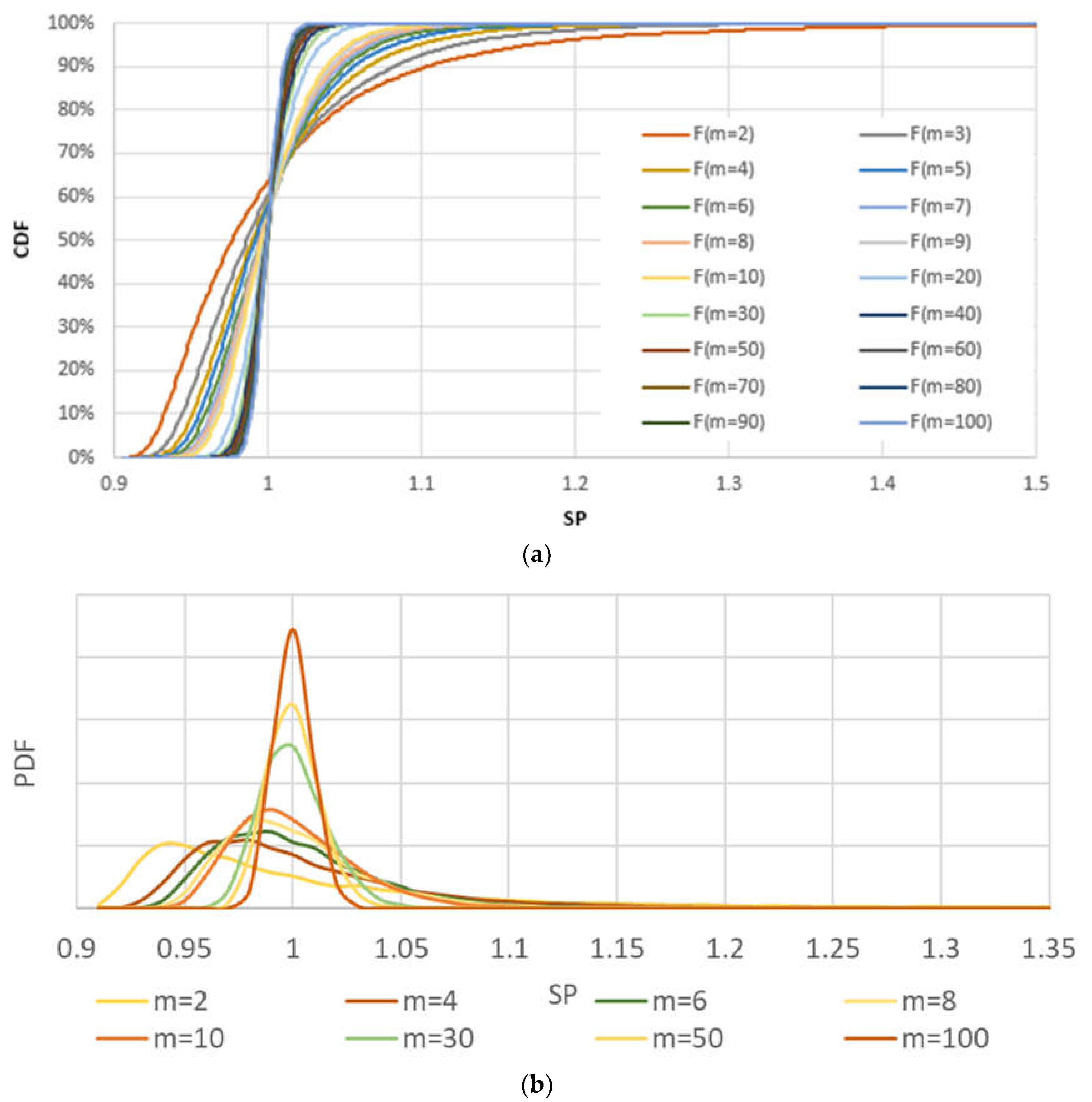
3.2.2. The Case Described in Section 2.2.2
3.2.3. The Case Described in Section 2.2.3
3.3. General Methodology: Modus Operandi for Analyzing a Metric Data Partition (10 Steps)
- Decide on the OUS population.
- Make an assumption about the type of the expected distribution of these objects within a homogeneous population.
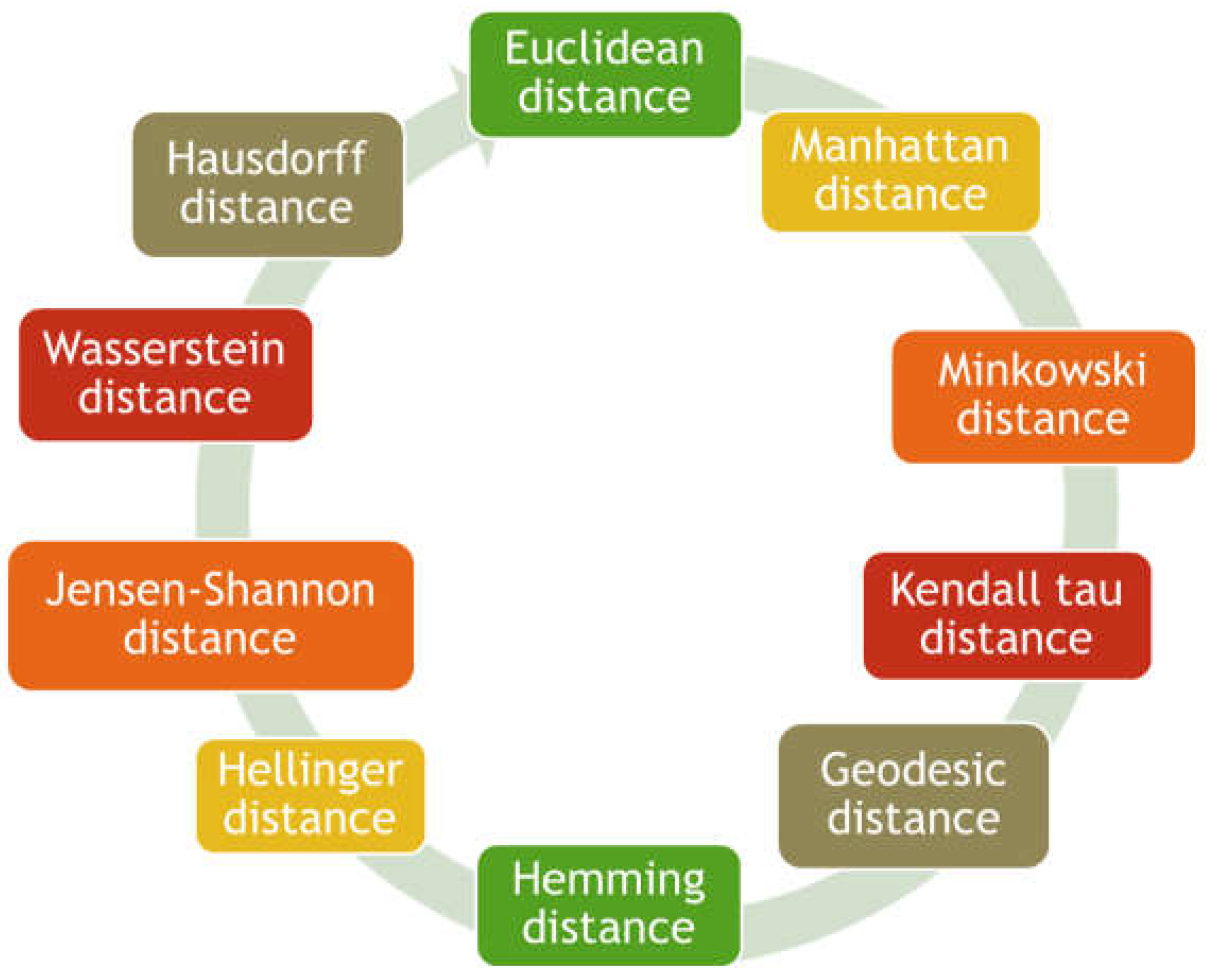
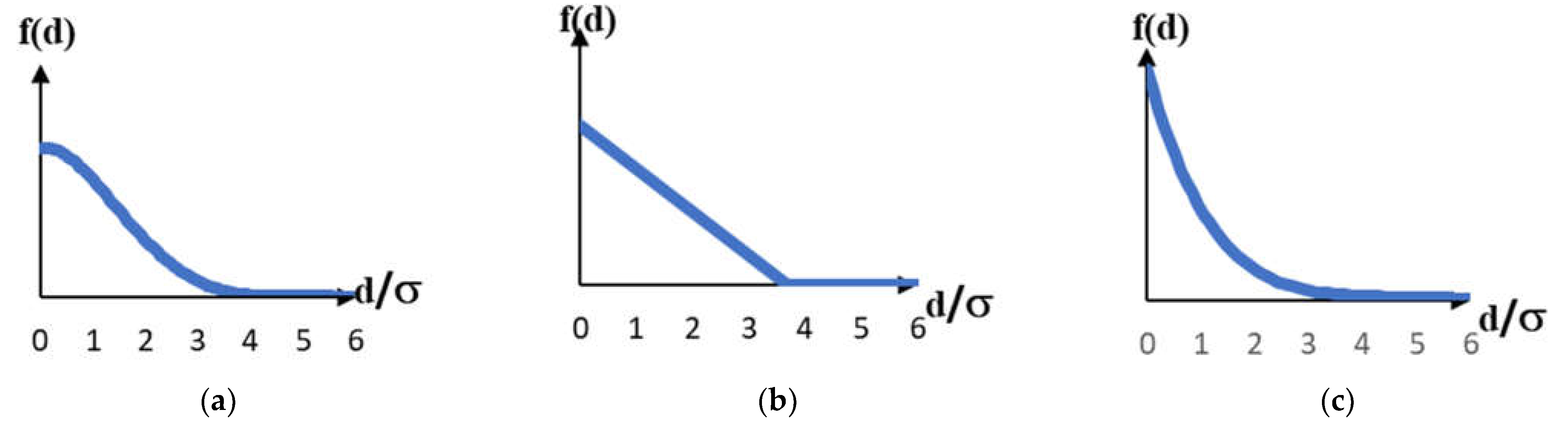
- Choose a distance metric suitable for this distribution (see Figure 1).
- Decide on the factor that, in your opinion, can discriminate/distinguish between the OUSs (heterogeneity hypothesis), and which levels serve as the basis for dividing/separating objects into groups (partitioning).
- Provide a corresponding data partitioning/division.
- Calculate the SP (as in Section 3, for example)
- Simulate the SP distribution under H0 in accordance with the vector of the partition just made and the chosen distance metric. Every simulation process cycle includes:
- (a)
- Random generation of N data from a population of OUS (as per step 1) characterized by the assumed distribution (as per step 2).
- (b)
- Distance matrix calculation (as per step 3).
- (c)
- Partitioning these distances into their inter and intra components (as per steps 4 and 5).
- (d)
- SP calculation, which ends the cycle and returns us to (a).
- Determine the alpha risk α of homogeneity hypothesis H0 rejection.
- Find the (1 − α) percentile of the simulated SP distribution, or alternatively, the p–value of the calculated SP.
- Make a final decision according to the results of step 9.
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. How Does the Scale Parameter Influence the Sum of Distances (SD) and the SP Distributions?
Appendix A.2. How Does the Scale Parameter Influence the SD Distribution?
Appendix A.3. How Does the Scale Parameter Influence the SP Distribution?
Appendix B
Why Is There a Correlation between Two Distances with a Common Vertex Datum?
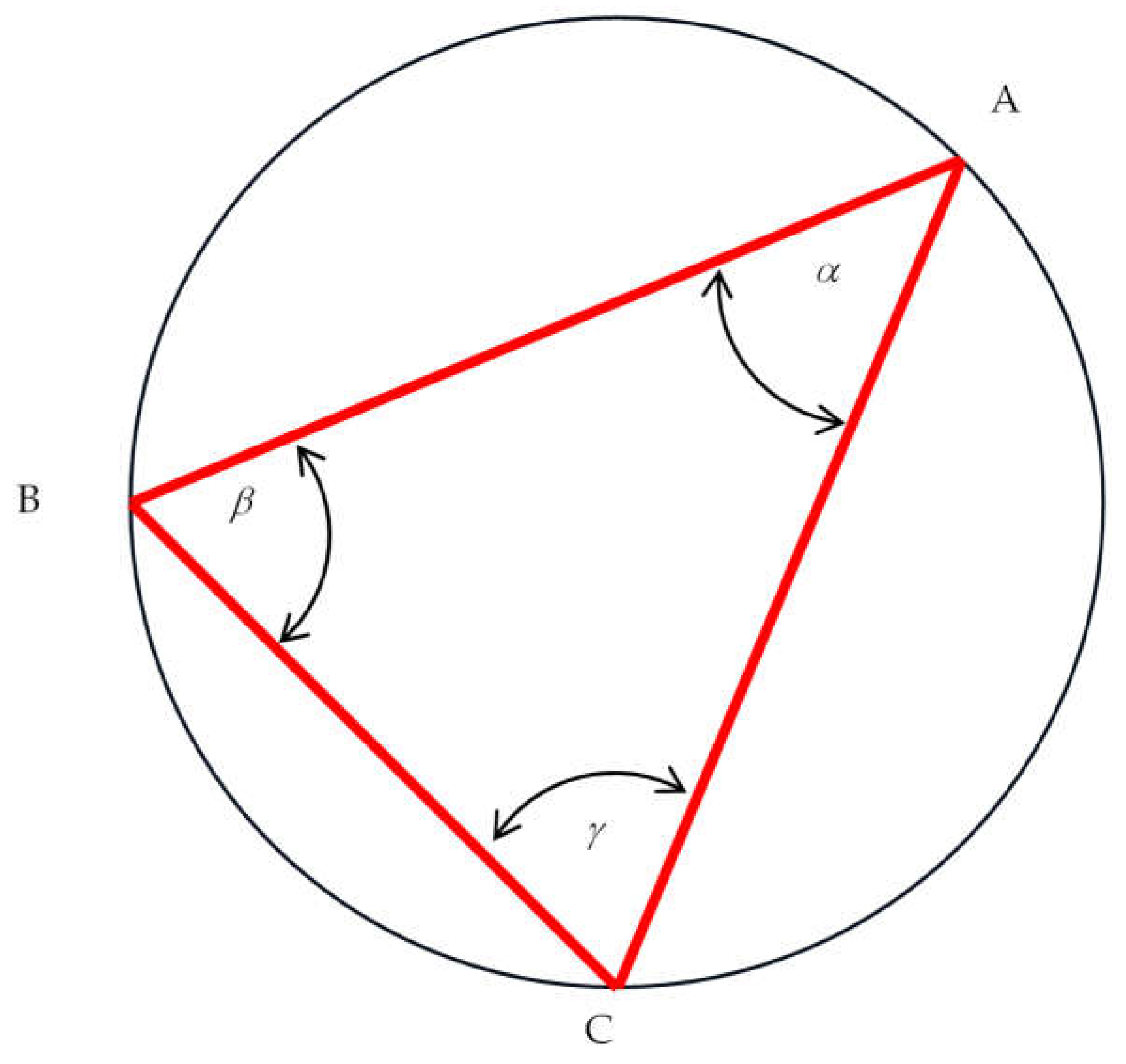
Appendix C
Asymptotical Behavior of the SP Distribution
References
- Marmor, Y.N.; Bashkansky, E. Processing new types of quality data. Qual. Reliab. Eng. Int. 2020, 36, 2621–2638. [Google Scholar] [CrossRef]
- Song, W.; Zheng, J. A new approach to risk assessment in failure mode and effect analysis based on engineering textual data. Qual. Eng. 2024. [Google Scholar] [CrossRef]
- González del Pozo, R.; Dias, L.C.; García-Lapresta, J.L. Using Different Qualitative Scales in a Multi-Criteria Decision-Making Procedure. Mathematics 2020, 8, 458. [Google Scholar] [CrossRef]
- Weiß, C.H. On some measures of ordinal variation. J. Appl. Stat. 2019, 46, 2905–2926. [Google Scholar] [CrossRef]
- Grzybowski, A.Z.; Starczewski, T. New look at the inconsistency analysis in the pairwise-comparisons-based prioritization problems. Expert. Syst. Appl. 2020, 159, 113549. [Google Scholar] [CrossRef]
- Yang, W.; Chen, J.; Zhang, C.; Paynabar, K. Online detection of cyber-incidents in additive manufacturing systems via analyzing multimedia signals. Qual. Reliab. Eng. Int. 2022, 38, 1340–1356. [Google Scholar] [CrossRef]
- Gadrich, T.; Bashkansky, E.; Zitikis, R. Assessing variation: A unifying approach for all scales of measurement. Qual. Quant. 2015, 49, 1145–1167. [Google Scholar] [CrossRef]
- Feigenbaum, A.V. Total Quality Control, 3rd ed.; McGraw Hill: New York, NY, USA, 1991. [Google Scholar]
- Rosenfeld, Y.; Jabrin, H.; Baum, H. Costs of Non-Qualiy in Residential Construction in Israel; National Institute for Construction Research: Haifa, Israel, 2019. Available online: https://www.gov.il/BlobFolder/reports/research_1077/he/r1077.pdf (accessed on 16 July 2023). (In Hebrew)
- Le Cam, L.M.; Yang, G.I. Asymptotics in Statistics: Some Basic Concepts; Springer Science & Business Media: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Vanacore, A.; Marmor, Y.N.; Bashkansky, E. Some metrological aspects of preferences expressed by prioritization of alternatives. Measurement 2019, 135, 520–526. [Google Scholar] [CrossRef]
- Marmor, Y.N.; Gadrich, T.; Bashkansky, E. Accuracy of multiexperts’ prioritization under Mallows’ model of errors creation. Qual. Eng. 2021, 33, 286–299. [Google Scholar] [CrossRef]
- McKay, A.T.; Pearson, E.S. A note on the distribution of range in samples of n. Biometrika 1933, 25, 415–420. [Google Scholar] [CrossRef]
- Hartley, H.O. The range in random samples. Biometrika 1942, 32, 334–348. [Google Scholar] [CrossRef]
- Crooks, G.E. Field Guide to Continuous Probability Distributions; Berkeley Institute for Theoretical Science: Berkeley, CA, USA, 2019; Available online: https://threeplusone.com/pubs/FieldGuide.pdf (accessed on 16 July 2023).
- Johnson, H.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Gadrich, T.; Bashakansky, E. A Bayseian approach to evaluating uncertainty of inaccurate categorical measurements. Measurement 2016, 91, 186–193. [Google Scholar] [CrossRef]
- Gadrich, T.; Marmor, Y.N. Two-way ORDANOVA:Analyzing ordinal variation in a cross-balanced design. J. Stat. Plan. Inference 2021, 215, 330–343. [Google Scholar]
- Kumar, P.; Kumar, A. Quantifying Reliability Indices of Garbage Data Collection IOT-based Sensor Systems using Markov Birth-death Process. Int. J. Math. Eng. Manag. Sci. 2023, 8, 1255–1274. [Google Scholar] [CrossRef]
- Seltman, H. Approximations for Mean and Variance of a Ratio. Available online: https://www.stat.cmu.edu/~hseltman/files/ratio.pdf (accessed on 19 July 2019).
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 6000 | 7000 | 5000 |
| B | 6000 | 0 | 13,000 | 11,000 |
| C | 7000 | 13,000 | 0 | 2000 |
| D | 5000 | 11,000 | 2000 | 0 |
| Company 1 | Company 2 | Company 3 | Company 4 | Company 5 | Company 6 | Company 7 | Company 8 | |
|---|---|---|---|---|---|---|---|---|
| Prevention costs | 0.19 | 0.05 | 0.07 | 0.19 | 0.11 | 0.31 | 0.19 | 0.23 |
| Appraisal costs | 0.22 | 0.15 | 0.13 | 0.35 | 0.47 | 0.12 | 0.32 | 0.23 |
| Internal failure costs | 0.14 | 0.28 | 0.18 | 0.27 | 0.19 | 0.14 | 0.27 | 0.27 |
| External failure costs | 0.45 | 0.52 | 0.62 | 0.19 | 0.23 | 0.43 | 0.22 | 0.27 |
| Total | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Company 1 | Company 2 | Company 3 | Company 4 | Company 5 | Company 6 | Company 7 | Company 8 | |
|---|---|---|---|---|---|---|---|---|
| Company 1 | 0.000 | 0.198 | 0.169 | 0.214 | 0.222 | 0.122 | 0.189 | 0.152 |
| Company 2 | 0.198 | 0.000 | 0.094 | 0.290 | 0.290 | 0.265 | 0.265 | 0.240 |
| Company 3 | 0.169 | 0.094 | 0.000 | 0.328 | 0.320 | 0.230 | 0.302 | 0.266 |
| Company 4 | 0.214 | 0.290 | 0.328 | 0.000 | 0.120 | 0.269 | 0.030 | 0.104 |
| Company 5 | 0.222 | 0.290 | 0.320 | 0.120 | 0.000 | 0.317 | 0.127 | 0.191 |
| Company 6 | 0.122 | 0.265 | 0.230 | 0.269 | 0.317 | 0.000 | 0.244 | 0.178 |
| Company 7 | 0.189 | 0.265 | 0.302 | 0.030 | 0.127 | 0.244 | 0.000 | 0.077 |
| Company 8 | 0.152 | 0.240 | 0.266 | 0.104 | 0.191 | 0.178 | 0.077 | 0.000 |
| Judge j | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Judge i | 1 | 0 | 0.59 | 0.73 | 0.33 | 0.38 |
| 2 | 0.59 | 0 | 0.46 | 0.45 | 0.44 | |
| 3 | 0.73 | 0.46 | 0 | 0.65 | 0.61 | |
| 4 | 0.33 | 0.45 | 0.65 | 0 | 0.37 | |
| 5 | 0.38 | 0.44 | 0.61 | 0.37 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marmor, Y.N.; Bashkansky, E. Reliability of Partitioning Metric Space Data. Mathematics 2024, 12, 603. https://doi.org/10.3390/math12040603
Marmor YN, Bashkansky E. Reliability of Partitioning Metric Space Data. Mathematics. 2024; 12(4):603. https://doi.org/10.3390/math12040603
Chicago/Turabian StyleMarmor, Yariv N., and Emil Bashkansky. 2024. "Reliability of Partitioning Metric Space Data" Mathematics 12, no. 4: 603. https://doi.org/10.3390/math12040603
APA StyleMarmor, Y. N., & Bashkansky, E. (2024). Reliability of Partitioning Metric Space Data. Mathematics, 12(4), 603. https://doi.org/10.3390/math12040603








