Abstract
Images captured under low-light conditions often suffer from serious degradation due to insufficient light, which adversely impacts subsequent computer vision tasks. Retinex-based methods have demonstrated strong potential in low-light image enhancement. However, existing approaches often directly design prior regularization functions for either illumination or reflectance components, which may unintentionally introduce noise. To address these limitations, this paper presents an enhancement method by integrating a Plug-and-Play strategy into an extended decomposition model. The proposed model consists of three main components: an extended decomposition term, an iterative reweighting regularization function for the illumination component, and a Plug-and-Play refinement term applied to the reflectance component. The extended decomposition enables a more precise representation of image components, while the iterative reweighting mechanism allows for gentle smoothing near edges and brighter areas while applying more pronounced smoothing in darker regions. Additionally, the Plug-and-Play framework incorporates off-the-shelf image denoising filters to effectively suppress noise and preserve useful image details. Extensive experiments on several datasets confirm that the proposed method consistently outperforms existing techniques.
MSC:
68U10; 94A08
1. Introduction
Images captured in low-light environments typically suffer from severe degradation issues, including low contrast, unknown noise, color distortions, and so on. These significantly impact subsequent tasks in computer vision applications [1,2,3]. However, many image enhancement techniques have primarily focused on improving contrast alone [4,5,6]. Some methods applied uniform enhancement across the entire image, which often led to overexposed bright areas and underexposed dark areas. Additionally, noise was often amplified during the enhancement process, deriving unsatisfactory enhancement results. To address the noise issue, some approaches have employed filtering methods post-enhancement [7,8]. Unfortunately, this often caused further blurring of important image details such as textures and edges. Despite numerous efforts in this domain, achieving high-quality noise-free enhancement remains a persistent challenge.
Recently, many advanced algorithms have been developed [9,10,11,12,13,14,15,16]. Among the model-based approaches, histogram equalization and Retinex-based decomposition methods have been widely adopted. Histogram equalization enhances contrast by adjusting the distribution of pixel values [9,10,11], expanding the dynamic range or redistributing brightness to modify image contrast. While these techniques can improve the visibility of dark areas, they tend to amplify noise to some degree.
Alternatively, one of the most extensively used methods is based on Retinex decomposition. Retinex methods are inspired by the human visual system and decompose the image into illumination and reflectance components. Gamma correction is often applied afterward to enhance the image. Illumination refers to the distribution of light, while reflectance pertains to the inherent properties and colors of objects within the scene. Due to their ability to separately optimize illumination and reflectance, Retinex methods have been widely adopted in low-light image enhancement, dehazing, and object detection [13,14,15,16,17].
More recently, deep learning-based methods have shown remarkable success in image enhancement, significantly advancing the field [18,19,20,21,22,23,24,25,26]. Many of these methods learn the mapping between low-light images and their normal-light counterparts, or design new pyramid structures consisting of branches for brightness perception and feature extraction [19]. Others enhance images by learning depth curve estimations, while lightweight networks predict higher-order curves for pixel-level adjustments [20]. Some studies have explored network unfolding techniques for low-light image enhancement. However, learning-based methods are not without limitations. First, the challenge of acquiring paired low-light and normal-light images under identical conditions often leads to poor generalization in uneven lighting scenarios. Additionally, these methods are often criticized for their lack of interpretability, as they function as black-box systems with little insight into their underlying mechanisms. Moreover, the parameters in such models are typically fixed after training, which limits their adaptability to diverse image scenes.
Due to insufficient light condition, low-light images are often affected by various types of noise. Although many image enhancement methods have been developed to tackle noise in low-light environments, their effectiveness remains constrained. Therefore, developing an algorithm that can significantly enhance brightness while effectively suppressing noise continues to be a key research challenge. It is noted that a Plug-and-Play (PnP) framework has been developed to incorporate various denoisers into multi-task image problems. By splitting variables, PnP decomposes the objective function into data fidelity and prior knowledge subproblems to improve the quality and robustness of denoising. One of the advantages of the PnP framework is that it requires no predefined noise distribution, supports data-driven denoiser training, and effectively combines with noise synthesis schemes to better meet the demands of multi-task image processing. It can directly embed existing state-of-the-art denoising techniques to address multi-task image problems such as image restoration, inpainting, enhancement, and super-resolution [27,28,29,30,31,32].
In this paper, we tackle the image enhancement problem by integrating a Plug-and-Play strategy into an extended decomposition model. Our approach introduces an enhanced decomposition scheme that splits the input image into three components: illumination, reflectance, and color layer. The extended decomposition model offers a more precise representation of these image components. To address the illumination component, we employ an iterative reweighting regularization mechanism, which dynamically adjusts the penalty using spatially adaptive weight functions. This allows for gentle smoothing near edges and bright areas, while applying more aggressive smoothing in darker regions, and enhancing visual quality. For the reflectance component, we incorporate the Plug-and-Play framework, leveraging state-of-the-art image denoising filters to effectively remove noise while preserving important image details. This framework is highly adaptable, as it can integrate different filters to handle various types of noise, providing a robust and flexible solution for achieving superior image restoration. Our contributions are summarized as follows:
- We decompose the input image into three layers: illumination, reflectance, and color layer, allowing for a more precise and detailed representation of each component.
- Instead of traditional penalty functions, an adaptive iterative reweighting method is used to regularize the illumination component, allowing gentle smoothing near edges and bright areas while stronger smoothing in darker regions.
- The Plug-and-Play framework is incorporated into the reflectance restoration process, utilizing several off-the-shelf image denoising filters to retain essential details and eliminate noise during image enhancement.
The paper is structured as follows: Section 2 provides an overview of related work. In Section 3, we present a detailed description of the proposed model and the corresponding numerical algorithm. Extensive experimental results and discussions are provided in Section 4, and Section 5 concludes the paper.
2. Related Work
2.1. Retinex-Based Methods
The Retinex decomposition methods operate on the fundamental principle of separating an image into illumination and reflectance components, followed by applying suitable regularization functions. These functions aim to smooth the illumination component while retaining useful details in the reflectance, achieving a precise distinction between illumination and reflectance during the optimization process. The strength of this approach lies in its ability to handle complex lighting variations effectively, leading to enhanced images that appear more natural. One of the most well-known Retinex methods is introduced in [12], where a total variation-based Retinex decomposition model is proposed. Building on this foundational work, several modifications and variations have emerged [13,14,15,16,17,33,34]. Some of these works focused on directly designing regularization functions for either the illumination or reflectance component. For instance, Guo et al. [13] applied an norm to the illumination component while using an norm to measure the difference between the maximum intensity and the adjusted illumination map across all channels, improving the overall enhancement quality. Similarly, Park et al. [14] suggested a method to enhance low-light images by incorporating an norm for the illumination and an norm for the reflectance. Several other studies aimed to modify the regularization terms or improve the decomposition process. For example, the work in [15] introduced a weighted variational regularization technique to enhance image quality, while [16] employed structure and texture-aware weights to more accurately estimate illumination and reflectance. Additionally, Jia et al. [17] proposed a novel decomposition model that applied a weighted regularization scheme, helping to better preserve significant edges during the enhancement process.
2.2. Simultaneous Enhancement and Denoising
Noise hidden in dark areas is a significant issue in image enhancement tasks, particularly in low-light conditions [35,36,37,38]. Many methods have improved regularization strategies to mitigate the negative impact of noise on image quality. For instance, Ren et al. [35] utilized a low-rank regularization technique for noise control within reflectance estimates, resulting in a robust low-rank enhancement approach. Considering the inherent characteristics of both illumination and reflectance, Kurihara et al. [36] explored a joint optimization strategy using an norm on the reflectance to preserve textures and details. Chien et al. [37] introduced a shadow-up function within the Retinex framework, which is particularly sensitive to noise. This method not only improves contrast in dark regions but also reduces noise, thus enhancing visibility of details under low-light conditions. The balance between contrast enhancement and noise reduction results in high-quality images across various lighting scenarios. The authors in [38] proposed a fractional derivative-based weighted regularization technique on the reflectance component. Their approach sought to restore enhanced image details while minimizing noise and artifacts, achieving superior image enhancement. By applying weighted regularization, their method better preserves details, delivering higher contrast and richer visual features. Moreover, in [3], the authors presented a strategy combining domain-specific knowledge with hybrid enhancement techniques to achieve improved detail preservation and noise reduction, thus yielding high-quality images.
2.3. Plug-and-Play Framework
The Plug-and-Play (PnP) algorithm is a widely developed framework in recent years, primarily utilized for solving multi-task image problems. The main idea of ADMM-based Plug-and-Play is reviewed as follows [27,28,29]. Firstly, the composite problem
can be converted into a constrained problem and solved by the operator splitting scheme as
where is the scaled Lagrange multiplier, and . Secondly, it is observed that the v-subproblem in (2) is a proximity operator at the point . Inspired by the work in [28], it can be seen as a denoising step. For example, if we select , the minimization problem corresponds to the well-known ROF denoising model. Based on the understanding, ref. [28] presented a variant form of the above scheme by suggesting that one does not need to specify . Instead, it can be replaced by an off-the-shelf image denoising algorithm, i.e., , to form a denoiser
Finally, by substituting (3) in (2), it forms the Plug-and-Play framework
which enables the integration of various denoisers. Its advantage lies in its ability to directly utilize existing state-of-the-art denoising techniques, enabling integration into multi-task image problems, such as image inpainting, image super-resolution, image enhancement, and so on [29,30,31].
3. Proposed Model and Algorithm
Building on the foundation of previous work, we developed a novel image enhancement model. This model introduces an extended decomposition technique, applies an iterative reweighting method to the illumination component, and integrates a Plug-and-Play framework for the reflectance component. These combined approaches aim to deliver superior image enhancement results. The structure of the model is illustrated in Figure 1, in which the illumination component and the reflectance component possess the same sizes as the inputting .
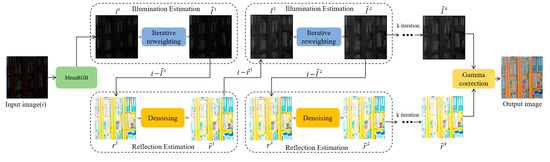
Figure 1.
The architecture of the proposed model.
3.1. Extended Decomposition Approach
Inspired by the work in [17,39], an observed image is decomposed in three components: the illumination layer, the reflectance layer, and the color layer. Based on the decomposition scheme, we design the enhancement model as the following minimization problem
where the image domain is denoted as Ω, which is an open and bounded domain with a Lipschitz boundary. The image intensity function satisfies the Neumann bounded condition. Furthermore, the denotations of the variables in (5) are defined or described in the following constructions of each term. The minimization problem in (5) is regarded as the extended decomposition model.
The fidelity functional is designed to measure the discrepancy between the original image and the sum of its illumination and reflectance components. Additionally, the illumination component is encouraged to align with the average value across all channels of the input image. Thus, the fidelity term can be expressed as follows:
where denotes the logarithmic conversion of observed image . and are the logarithms of illumination and reflectance layer, respectively. is an intermediate variable, which is expected to apply piecewise smoothing priors in each channel.
For the regularization functional , it is expected to perform mild smoothing around edges or bright regions, while employing more aggressive smoothing in dark areas, so a weighted scheme is introduced and the regularization is designed as
where the operator “” refers to the element-wise product and is the weight map. Specifically, is desired to preserve important edges, i.e., should be allocated smaller weight and imposed mild smoothing operation in the regions with larger gradients, and the larger weight in the smooth areas. Moreover, during the smoothing process, it is crucial to preserve the edges with the larger gradients across any of the three-color channels. The denominator of the weight is calculated based on the maximum gradient across the color channels. Synthesizing the above analysis, the weight is represented as an edge-aware smoothing map
It is noted that when we solve in the numerical algorithm, we just utilize which was calculated by Equation (8) with the information of . The algorithm formed in this way is classified as the iterative reweighting method.
For the functional , it is desired to restore texture and details effectively, eliminate noise in shadowed areas, and improve the enhancement and restoration results. Based on the Plug-and-Play algorithm, it will be addressed in the form of a denoiser.
3.2. Numerical Algorithm with the Plug-and-Play Framework
It is evident that the optimal choice for the variable in problem (5) is the average values of among , which simplifies the problem to solving only two variables and . These can be addressed through a block coordinate descent algorithm, resulting in the following two subproblems
- -subproblem
On the one hand, the functional in (9) can be reformulated as
Therefore, the minimization problem in (9) can be rewritten as
with . It has a closed form solution as
where and are defined as the horizontal and vertical components of operator , respectively, whereas and are the horizontal and vertical vectorized forms of , respectively.
With the solution of (13), and by the conversion of Equation (6), can be solved in the following explicit expression
- -subproblem
By introducing auxiliary variable , the minimization problem (10) can be expressed as a constrained optimization problem with respect to ,
Similar to Equation (11), the functional can be simplified as
where is the average of , and is the and functions, which can be ignored in minimizing solutions for . Substituting Equation (16) into (15), it formulates the optimization problem as
It is noted that, the parameter here is actually 1/3 of in Equation (15). Following the Plug-and-Play framework in (4), (17) can be solved as
where is the scaled Lagrange multiplier, and
Summarizing the above solving processing, we formulate the Plug-and-Play framework based numerical algorithm in Algorithm 1. It is noted that the parameters in the algorithm are discussed in the experimental section.
| Algorithm 1 The numerical algorithm for the minimization problem (5) |
| 1. Input: convert the input image into the logarithmic domain and denote it as , initialize , choose a group of initial parameters. 2. Conduct the following alternating iterative process. For k = 1, 2……, do update by (13); update by (14); update by (18); End above iteration when the stopping criterion is satisfied. 3. Gamma correct. 4. Output: and . |
4. Experimental Results and Discussions
4.1. Experiment Setting
To assess the effectiveness of the proposed model, we conducted extensive experiments using three datasets. The first dataset is LIME, consisting of nine widely referenced images [14]. The second dataset LOL [40], which contains approximately 500 images captured in low-light conditions, along with their corresponding normal-light versions. The third dataset, Nikon, is a subset of the Huawei dataset and includes 20 low-light images, each paired with its corresponding normal-light counterpart. We compared our method with several existing approaches, including the joint intrinsic-extrinsic prior model (JIEP) [33], the extended variational image decomposition model for color image enhancement (EVID) [17], the structure and texture-aware Retinex model (STAR) [16], the Retinex-based variational framework (RBVF) [41], the sequential decomposition with Plug-and-Play framework (SDPF) [29], and the Retinex-based extended decomposition model (REDM) [39].
To evaluate the enhancement performance, we employed objective metrics peak signal-to-noise ratio (PSNR), structural similarity index (SSIM) [42], natural image quality evaluator (NIQE) [43], and the autoregressive-based image sharpness metric (ARISM) [44]. The index PSNR is defined as
where denotes the number of pixels in the image, represents the clean image, and represents the restored result. The index SSIM is defined as
where and represent the average intensities of image and , and represent the variances of image and , and represents the covariance between image and . The index NIQE is defined as
where and are the mean vectors and covariance matrices of the natural multivariate Gaussian model and the distorted image’s multivariate Gaussian model [43]. Finally, ARISM is a no-reference blind sharpness evaluation metric proposed in [44], which is established by analyzing the parameters of the autoregressive (AR) model. It first calculates the energy and contrast differences of locally estimated AR coefficients in a pointwise manner, then quantifies image sharpness using percentile pooling to predict the overall score. Furthermore, it considers the influence of color information on the visual perception of sharpness and extends the metric to the widely used YIQ color space. It is important to note that higher SSIM and PSNR values indicate better image quality, while lower NIQE and ARISM values represent that image contrasts have been more improved.
Regarding parameter setting, the parameters and in Equation (5) were empirically chosen from the intervals [0.06, 0.14] and [0.15, 0.25], respectively, following the guidelines from our previous work [39]. The denoising parameter is predominantly influenced by the choice of denoising filters , which we will discuss in conjunction with the experimental results.
4.2. Experimental Results
4.2.1. Qualitative Comparison
In this section, we present several experimental results. Figure 2 and Figure 3 show the visual outputs for the images “cars.bmp” and “building.bmp” using various comparison methods. As illustrated in Figure 2, the JIEP, EVID, and SDPF methods struggle to capture small details effectively, while the STAR, RBVF, and REDM methods fail to adequately suppress noise in dark areas. In contrast, our method not only enhances the dark regions while maintaining the original colors, but also effectively minimizes noise amplification in those darker areas.


Figure 2.
Visual comparison of the 7 methods on the LIME dataset. (a) is the original image, (b–g) are the results of the methods we compared, and (h) is the result of our method.

Figure 3.
Visual comparison of the 7 methods on the LIME dataset. (a) is the original image, (b–g) are the results of the methods we compared, and (h) is the result of our method.
In Figure 3, although all methods yield reasonable results, a detailed inspection shows that the enhanced results generated by JIEP, EVID, STAR, RBVF, and REDM exhibit increased noise in the shadowed regions. While SDPF manages to slightly brighten the dark regions, its overall improvement remains limited. Notably, our proposed method not only provides superior image enhancement but also significantly reduces noise in the shadowed areas, ensuring better overall image quality.
To further validate the effectiveness of our method, we evaluate its performance on low-light images from the LOL dataset. Two representative images, “5.png” and “9.png”, were selected for comparison. Figure 4 and Figure 5 present the visual comparison results. As seen in these figures, our method consistently demonstrates superior visual quality compared to other techniques. Specifically, our approach successfully reproduces images with more detailed features and vibrant colors. In contrast, the enhanced results produced by competing methods often fail to preserve the natural appearance of the original low-light scenes, frequently showing signs of excessive noise amplification or unnatural color shifts.

Figure 4.
Visual comparison of the 7 methods on the LOL dataset. (a) is the original image, (b–g) are the results of the methods we compared, and (h) is the result of our method.


Figure 5.
Visual comparison of the 7 methods on the LOL dataset. (a) is the original image, (b–g) are the results of the methods we compared, and (h) is the result of our method.
Additionally, we assessed the performance of various methods using low-light images from the Nikon dataset. For this analysis, we selected two representative images, “3002.jpg” and “3007.jpg”. The visual comparisons presented in Figure 6 and Figure 7 clearly demonstrate that our method outperforms others in terms of overall image quality. Moreover, our approach performs better in enhancing contrast, preserving fine details, and rendering true-to-life colors.

Figure 6.
Visual comparison of the 7 methods on the Nikon dataset. (a) is the original image, (b–g) are the results of the methods we compared, and (h) is the result of our method.


Figure 7.
Visual comparison of the 7 methods on the Nikon dataset. (a) is the original image, (b–g) are the results of the methods we compared, and (h) is the result of our method.
Lastly, taking the resulting images of Figure 4 as an example, we plotted the histograms of all the images in Figure 8. Compared to the original low-light image and the enhancement results of other methods, the histogram of our method shows a uniform gray-level distribution, covering the entire gray-scale range (from 0 to 255). Its peak is centered, with a balanced brightness distribution that naturally presents image details while avoiding any bias toward dark or bright areas.
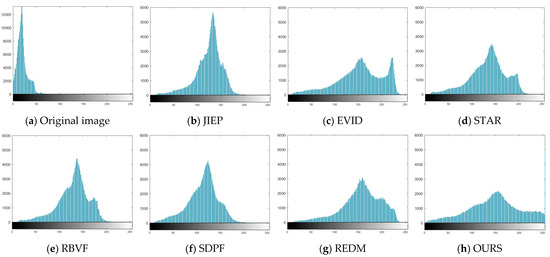
Figure 8.
Histograms for all the resulting images of Figure 4.
4.2.2. Quantitative Comparison
In this subsection, we present a quantitative comparison of our method against other approaches on the LOL and Nikon datasets. As shown by the metrics in Table 1 and Table 2, our method outperforms several other approaches, achieving higher PSNR and SSIM scores while yielding lower NIQE and ARISM values. These results further validate that the proposed model is capable of significantly enhancing image brightness while effectively suppressing unknown noise.

Table 1.
Quantitative analysis of different methods for images of the LOL dataset.

Table 2.
Quantitative analysis of different methods for images of the Nikon dataset.
4.3. Discussions
4.3.1. The Effectiveness of Denoiser
To assess the performance of various denoisers, we evaluated four filtering methods: block-batching and 3D filtering (BM3D), total variation (TV), non-local means (NLM), and recursive edge-preserving filter (RF). Image enhancement experiments were conducted using each of these methods, and the results are presented in Table 3. The table shows the average metrics for these four denoising techniques across the LOL and Nikon datasets. The results indicate that all four methods yield comparable performance, with the BM3D-based method showing a certain degree of superiority. Therefore, for consistency, we presented the results of the BM3D-based method in the comparative experiments discussed earlier.

Table 3.
Average results of different denoising methods on LOL and Nikon datasets.
4.3.2. Evaluations on the Extended Decomposition Method
To assess the performance of the extended decomposition method, we introduce the correlation coefficient (denoted as “Corr”) to measure the relationship between the illumination and reflectance components, as detailed below
where represents the covariance, and denotes the variance of the variables in question. The correlation between illumination and reflectance can be quantified using the “Corr” metric, where lower values indicate better image decomposition quality. To verify the effectiveness of the extended decomposition method, we compare our approach with Retinex-based variational methods, including JIEP and STAR methods. The former applies edge-preserving regularization through local variation deviation, and the latter incorporates adaptive weights to enhance structure and texture perception based on Retinex decomposition. Figure 9 shows the visualization results of these decomposition methods. From the results, we observe that JIEP retains more content in the illumination component, while STAR preserves some image details in the reflectance component. In contrast, our proposed method better maintains the details in the reflectance component while ensuring that the illumination component remains piecewise smooth. In Table 4, we list the “Corr” values of the results corresponding to that in Figure 9. It is clear that the proposed method holds the least “Corr” metrics, which indicates our method outperforms other methods in decomposition performance.

Figure 9.
Comparisons of illumination and reflectance components by different methods on the image of the LIME dataset.

Table 4.
The “Corr” metric results of Figure 9.
5. Conclusions
In this paper, we propose an extended decomposition based image enhancement algorithm, introducing significant advancements in methodology and performance. First, we improve the decomposition mode into an extended framework that provides a more flexible and effective description of the illumination and reflectance components. Second, we apply iterative reweighting regularization on the illumination layer, enabling adaptive smoothing—allowing for gentle smoothing around edges or bright areas, while applying stronger smoothing in darker regions. Simultaneously, we integrate the Plug-and-Play framework in the restoration process of the reflectance layer, incorporating existing image denoising filters to preserve essential details and remove noise. These extensive experiments demonstrate that our method outperforms state-of-the-art techniques in both qualitative and quantitative evaluations, achieving significant improvements in metrics such as PSNR, SSIM, NIQE, and ARISM. Visual comparisons further validate that the proposed approach consistently produces sharper and more visually appealing results.
Author Contributions
Conceptualization, C.Z. and J.W.; writing—original draft preparation, C.Z. and W.Y.; methodology, C.Z. and Y.W. (Yingjun Wang); software, W.Y. and Y.W. (Yan Wang); investigation and data curation, S.L. and H.C.; writing—review and editing, C.Z. and J.W.; funding acquisition, C.Z., H.C., S.L., and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the China Postdoctoral Science Foundation under Grant No. 2019M652545, the National Natural Science Foundation of China under Grant 62001158, 12371429, and 62202513, the Key Scientific and Technological Research Projects in Henan Province under Grant 242102211072, Key R&D projects in Henan Province under Grant 24111121180.
Data Availability Statement
The data presented in this study are publicly available data (sources stated in the citations). Please contact the corresponding author regarding data availability.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable and helpful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lozano-Vázquez, L.V.; Miura, J.; Rosales-Silva, A.J.; Luviano-Juárez, A.; Mújica-Vargas, D. Analysis of different image enhancement and feature extraction methods. Mathematics 2022, 10, 2407. [Google Scholar] [CrossRef]
- Kumar, A.; Rastogi, P.; Srivastava, P. Design and FPGA implementation of DWT, image text extraction technique. Procedia Comput. Sci. 2015, 57, 1015–1025. [Google Scholar] [CrossRef]
- Muslim, H.S.M.; Khan, S.A.; Hussain, S.; Jamal, A.; Qasim, H.S.A. A knowledge-based image enhancement and denoising approach. Comput. Math. Organ. Theory 2019, 25, 108–121. [Google Scholar] [CrossRef]
- Wang, W.; Wu, X.; Yuan, X.; Gao, Z. An experiment-based review of low-light image enhancement methods. IEEE Access 2020, 8, 87884–87917. [Google Scholar] [CrossRef]
- Wu, W.; Weng, J.; Zhang, P.; Wang, X.; Yang, W.; Jiang, J. Uretinex-net: Retinex-based deep unfolding network for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5901–5910. [Google Scholar]
- Yang, S.; Zhou, D.; Cao, J.; Guo, Y. LightingNet: An integrated learning method for low-light image enhancement. IEEE Trans. Comput. Imaging 2023, 9, 29–42. [Google Scholar] [CrossRef]
- Bharati, S.; Khan, T.Z.; Podder, P.; Hung, N.Q. A comparative analysis of image denoising problem: Noise models, denoising filters and applications. Cogn. Internet Med. Things Smart Healthc. Serv. Appl. 2021, 311, 49–66. [Google Scholar]
- Chen, X.; Zhan, S.; Ji, D.; Xu, L.; Wu, C.; Li, X. Image denoising via deep network based on edge enhancement. J. Ambient Intell. Humaniz. Comput. 2023, 14, 14795–14805. [Google Scholar] [CrossRef]
- Dhal, K.G.; Das, A.; Ray, S.; Gálvez, J.; Das, S. Histogram equalization variants as optimization problems: A review. Arch. Comput. Methods Eng. 2021, 28, 1471–1496. [Google Scholar] [CrossRef]
- Patel, S.; Bharath, K.P.; Balaji, S.; Muthu, R.K. Comparative study on histogram equalization techniques for medical image enhancement. In Soft Computing for Problem Solving: SocProS 2018; Springer: Singapore, 2020; Volume 1, pp. 657–669. [Google Scholar]
- Jha, K.; Sakhare, A.; Chavhan, N.; Lokulwar, P.P. A Review on Image Enhancement Techniques using Histogram Equalization. Grenze Int. J. Eng. Technol. 2024, 497–502. [Google Scholar]
- Ng, M.K.; Wang, W. A total variation model for retinex. SIAM J. Imaging Sci. 2011, 4, 345–365. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Ling, H. LIME: Low-light image enhancement via illumination map estimation. IEEE Trans. Image Process. 2016, 26, 982–993. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Yu, S.; Moon, B.; Ko, S.; Paik, J. Low-light image enhancement using variational optimization-based retinex model. IEEE Trans. Consum. Electron. 2017, 63, 178–184. [Google Scholar] [CrossRef]
- Fu, X.; Zeng, D.; Huang, Y.; Zhang, X.P.; Ding, X. A weighted variational model for simultaneous reflectance and illumination estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2782–2790. [Google Scholar]
- Xu, J.; Hou, Y.; Ren, D.; Liu, L.; Zhu, F.; Yu, M.; Wang, H.; Shao, L. Star: A structure and texture aware retinex model. IEEE Trans. Image Process. 2020, 29, 5022–5037. [Google Scholar] [CrossRef]
- Jia, X.; Feng, X.; Wang, W.; Zhang, L. An extended variational image decomposition model for color image enhancement. Neurocomputing 2018, 322, 216–228. [Google Scholar] [CrossRef]
- Zheng, C.; Shi, D.; Shi, W. Adaptive unfolding total variation network for low-light image enhancement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 4439–4448. [Google Scholar]
- Li, J.; Li, J.; Fang, F.; Li, F.; Zhang, G. Luminance-aware pyramid network for low-light image enhancement. IEEE Trans. Multimed. 2020, 23, 3153–3165. [Google Scholar] [CrossRef]
- Liu, R.; Ma, L.; Zhang, J.; Fan, X.; Luo, Z. Retinex-inspired unrolling with cooperative prior architecture search for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10561–10570. [Google Scholar]
- Guo, C.; Li, C.; Guo, J.; Loy, C.C.; Hou, J.; Kwong, S.; Cong, R. Zero-reference deep curve estimation for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1780–1789. [Google Scholar]
- Li, C.; Guo, J.; Porikli, F.; Pang, Y. LightenNet: A convolutional neural network for weakly illuminated image enhancement. Pattern Recognit. Lett. 2018, 104, 15–22. [Google Scholar] [CrossRef]
- Pan, Z.; Yuan, F.; Lei, J.; Li, W.; Ling, N.; Kwong, S. MIEGAN: Mobile image enhancement via a multi-module cascade neural network. IEEE Trans. Multimed. 2021, 24, 519–533. [Google Scholar] [CrossRef]
- Liang, L.; Zharkov, I.; Amjadi, F.; Joze, H.R.V.; Pradeep, V. Guidance network with staged learning for image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 836–845. [Google Scholar]
- Yu, W.; Zhao, L.; Zhong, T. Unsupervised Low-Light Image Enhancement Based on Generative Adversarial Network. Entropy 2023, 25, 932. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Liu, R.; Zhang, J.; Fan, X.; Luo, Z. Learning deep context-sensitive decomposition for low-light image enhancement. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 5666–5680. [Google Scholar] [CrossRef] [PubMed]
- Venkatakrishnan, S.V.; Bouman, C.A.; Wohlberg, B. Plug-and-play priors for model based reconstruction. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; pp. 945–948. [Google Scholar]
- Chan, S.H.; Wang, X.; Elgendy, O.A. Plug-and-play ADMM for image restoration: Fixed-point convergence and applications. IEEE Trans. Comput. Imaging 2016, 3, 84–98. [Google Scholar] [CrossRef]
- Wu, T.; Wu, W.; Yang, Y.; Fan, F.L.; Zeng, T. Retinex image enhancement based on sequential decomposition with a plug-and-play framework. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 14559–14572. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Li, Y.; Zuo, W.; Zhang, L.; Van Gool, L.; Timofte, R. Plug-and-play image restoration with deep denoiser prior. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 6360–6376. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, K.; Liang, J.; Cao, J.; Wen, B.; Timofte, R.; Van Gool, L. Denoising diffusion models for plug-and-play image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1219–1229. [Google Scholar]
- Lin, Y.H.; Lu, Y.C. Low-light enhancement using a plug-and-play Retinex model with shrinkage mapping for illumination estimation. IEEE Trans. Image Process. 2022, 31, 4897–4908. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; Xu, X.; Guo, K.; Jia, K.; Hu, B.; Tao, D. A joint intrinsic-extrinsic prior model for retinex. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4000–4009. [Google Scholar]
- Du, S.; Zhao, M.; Liu, Y.; You, Z.; Shi, Z.; Li, J.; Xu, Z. Low-light image enhancement and denoising via dual-constrained Retinex model. Appl. Math. Model. 2023, 116, 1–15. [Google Scholar] [CrossRef]
- Ren, X.; Yang, W.; Cheng, W.H.; Liu, J. LR3M: Robust low-light enhancement via low-rank regularized retinex model. IEEE Trans. Image Process. 2020, 29, 5862–5876. [Google Scholar] [CrossRef] [PubMed]
- Kurihara, K.; Yoshida, H.; Iiguni, Y. Low-light image enhancement via adaptive shape and texture prior. In Proceedings of the 2019 15th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Sorrento, Italy, 26–29 November 2019; pp. 74–81. [Google Scholar]
- Chien, C.C.; Kinoshita, Y.; Shiota, S.; Kiya, H. A retinex-based image enhancement scheme with noise aware shadow-up function. Int. Workshop Adv. Image Technol. (IWAIT) 2019, 11049, 501–506. [Google Scholar]
- Ma, Q.; Wang, Y.; Zeng, T. Retinex-based variational framework for low-light image enhancement and denoising. IEEE Trans. Multimed. 2022, 25, 5580–5588. [Google Scholar] [CrossRef]
- Zhao, C.; Yue, W.; Xu, J.; Chen, H. Joint Low-Light Image Enhancement and Denoising via a New Retinex-Based Decomposition Model. Mathematics 2023, 11, 3834. [Google Scholar] [CrossRef]
- Wei, C.; Wang, W.; Yang, W.; Liu, J. Deep retinex decomposition for low-light enhancement. arXiv 2018, arXiv:1808.04560. [Google Scholar]
- Ma, Q.; Wang, Y.; Zeng, T. Variational Low-Light Image Enhancement Based on Fractional-Order Differential. Commun. Comput. Phys. 2024, 35, 139–159. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a completely blind image quality analyzer. IEEE Signal Process 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Gu, K.; Zhai, G.; Lin, W.; Yang, X.; Zhang, W. No-reference image sharpness assessment in autoregressive parameter space. IEEE Trans. Image Process. 2015, 24, 3218–3231. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).