Testing Spherical Symmetry Based on Statistical Representative Points
Abstract
1. Introduction
2. The Construction of the RP Chisquare and the Equiprobable Chisquare Tests
3. An Empirical Comparison Between the RP Chisquare and the Equiprobable Chisquare Tests
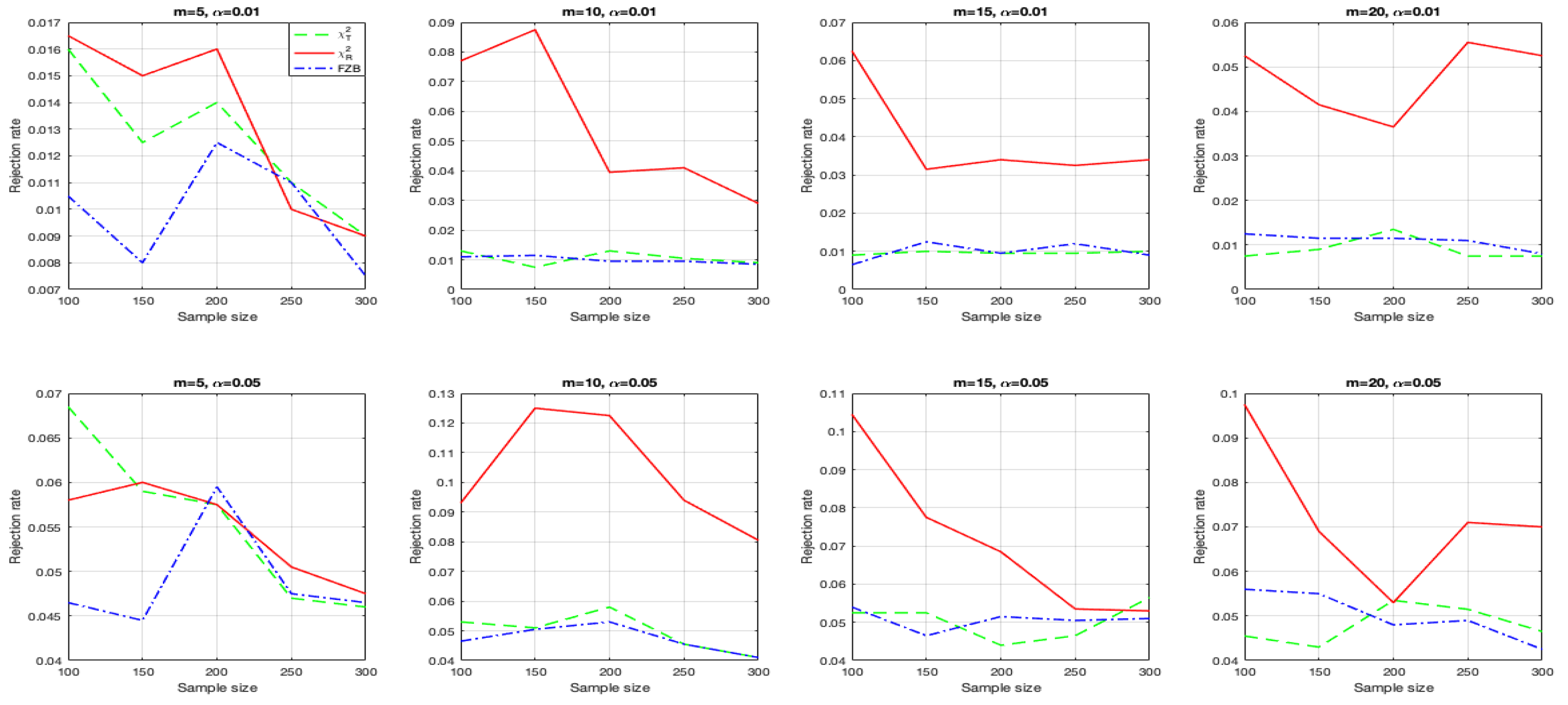
3.1. Empirical Type I Error Rates
- (1)
- The standard normal distribution ;
- (2)
- The multivariate t-distribution , with degrees of freedom ;
- (3)
- The Kotz-type distribution with parameters , , and .
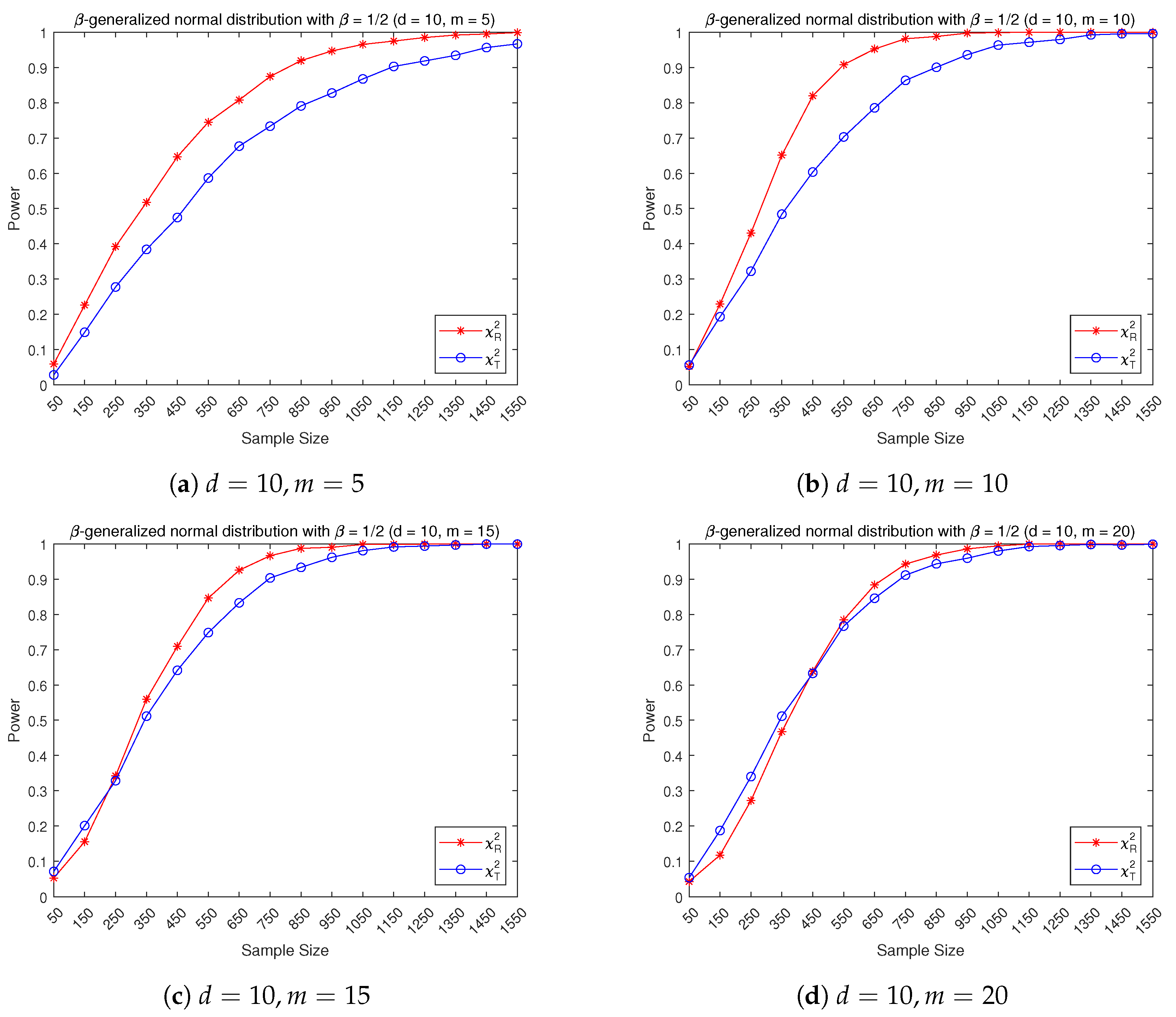
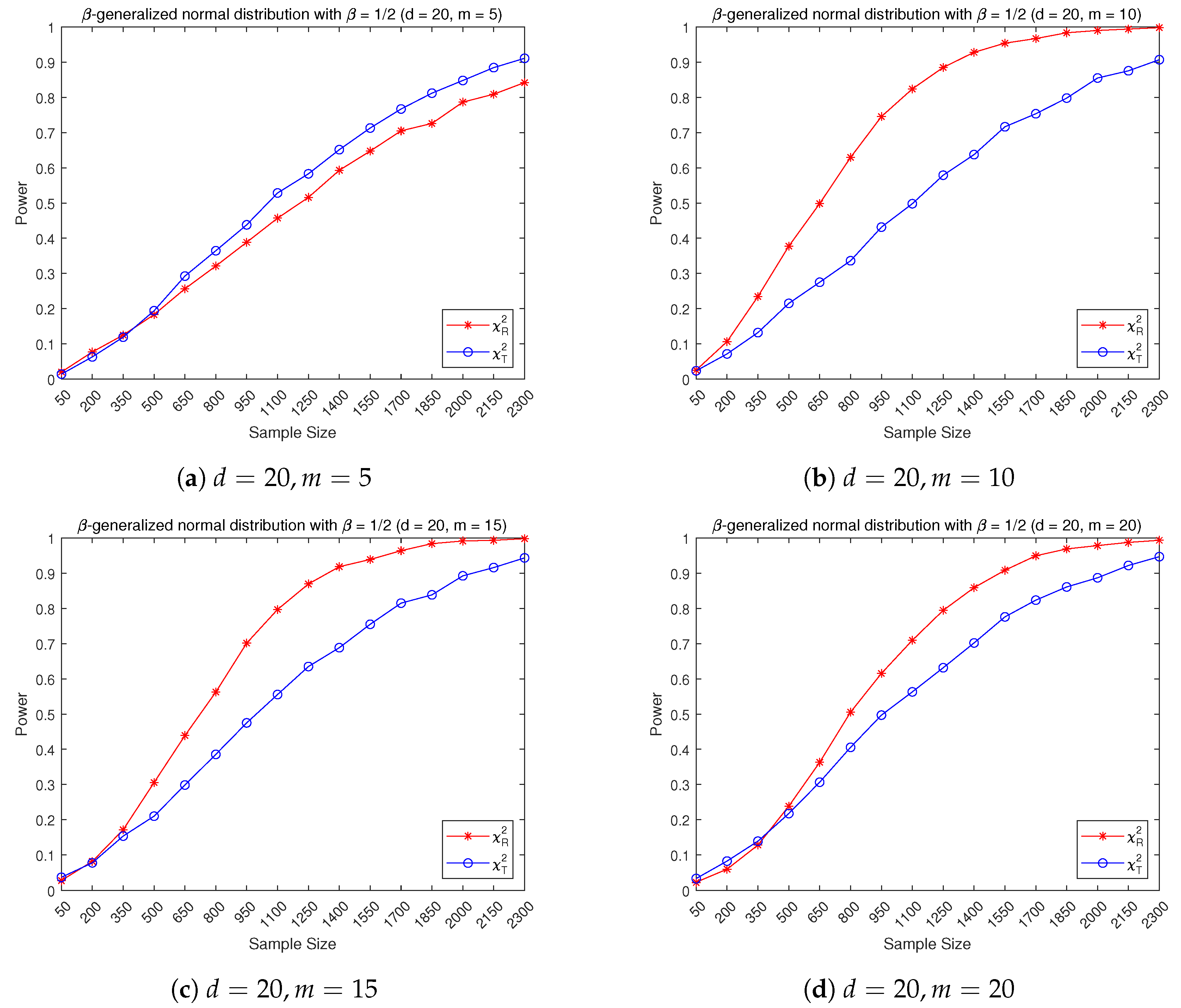
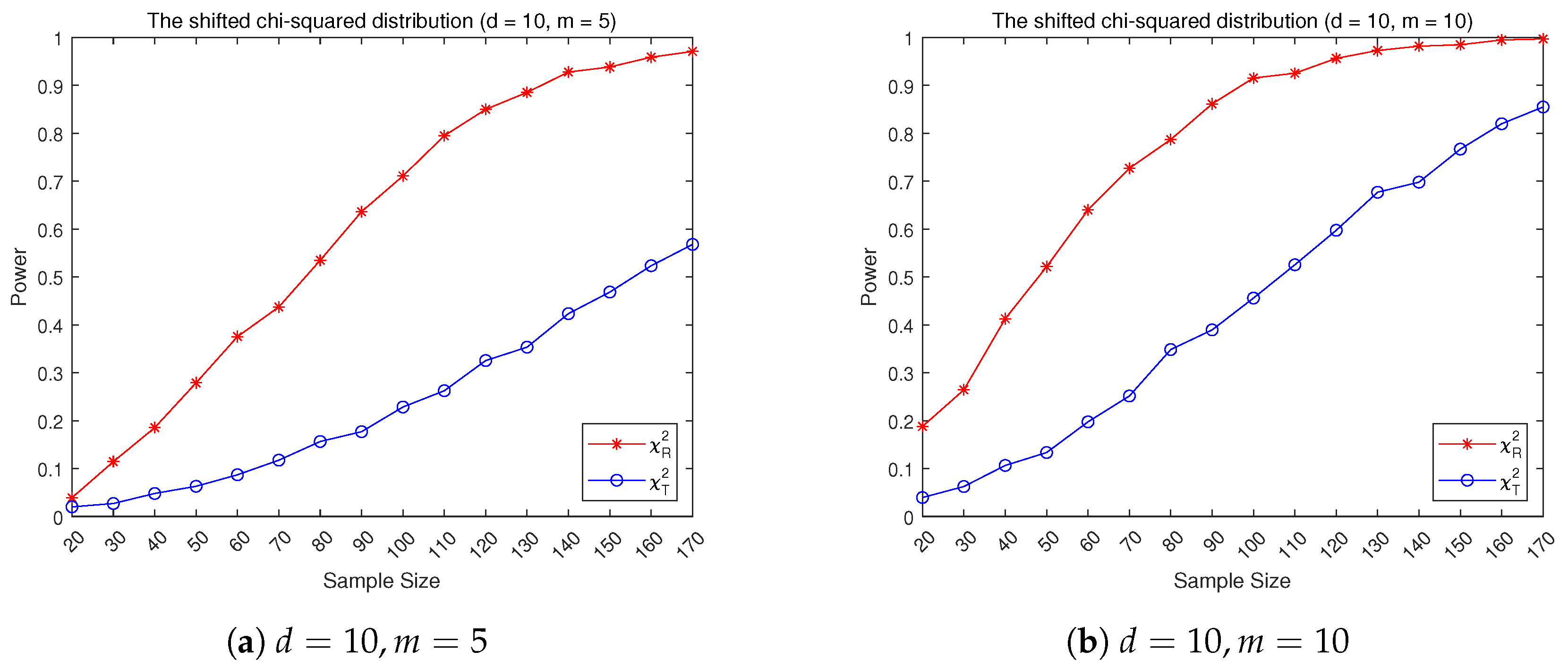
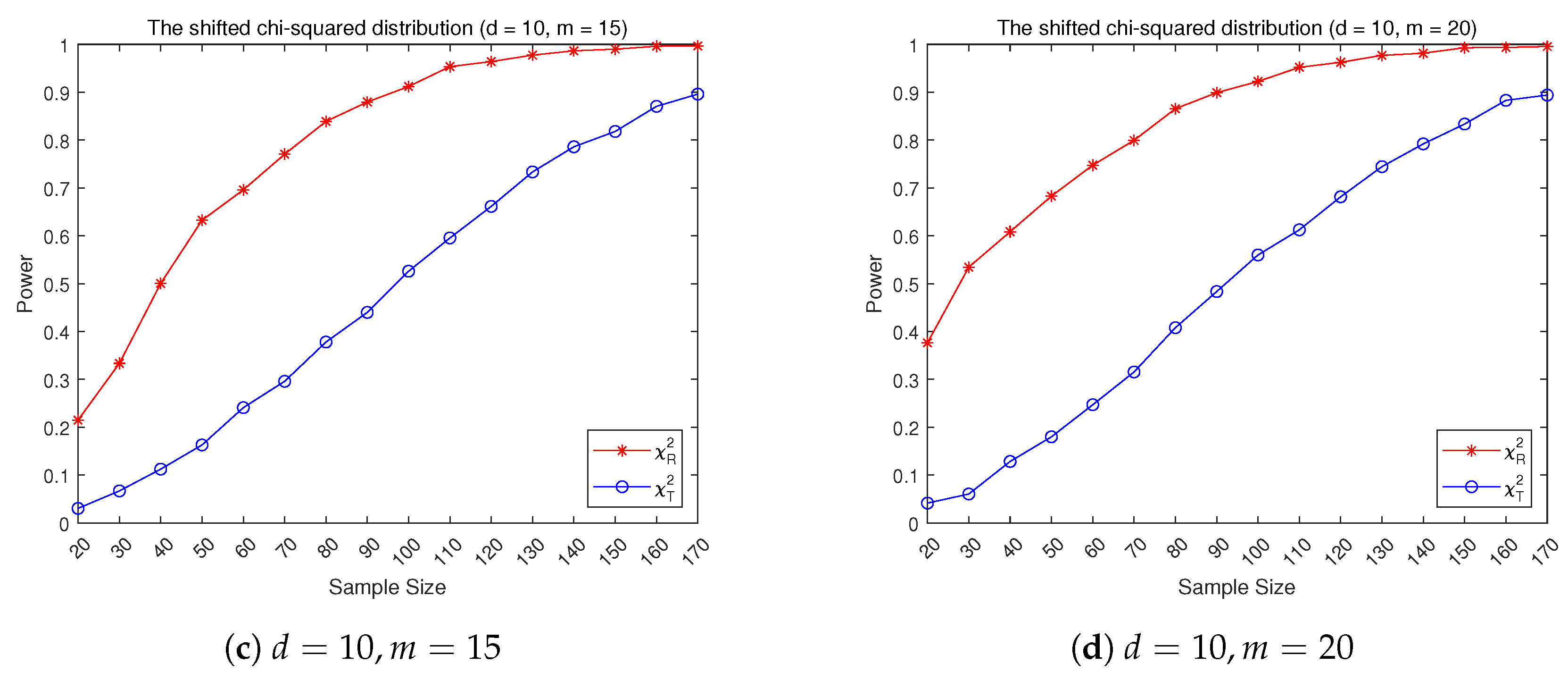
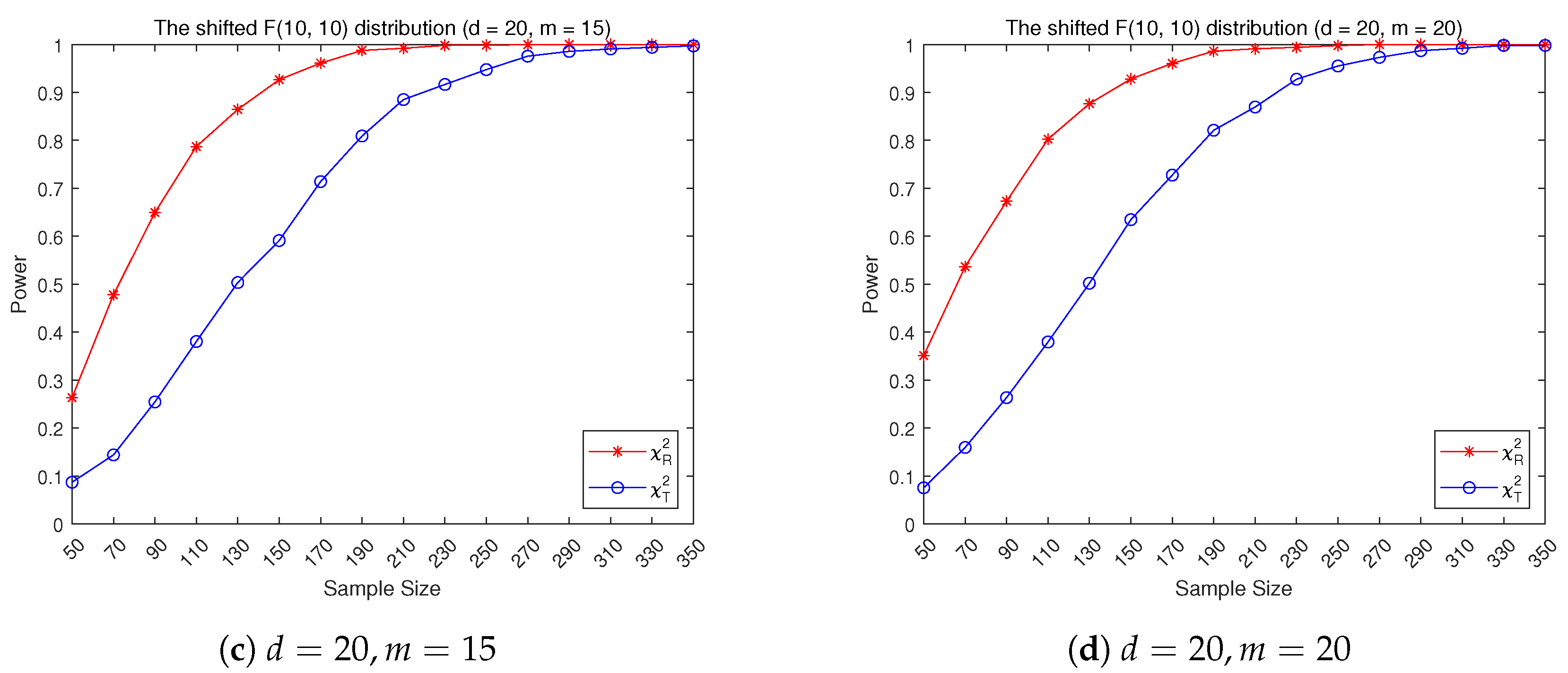
3.2. Empirical Power Performance
- (1)
- The multivariate -generalized normal distribution constructed from the i.i.d. one-dimensional marginal -generalized normal distribution with the density function given byWe take .
- (2)
- Shifted -distribution: constructed from i.i.d. one-dimensional marginal chisquare with .
- (3)
- Shifted F-distribution ; constructed from i.i.d. one-dimensional marginal with .
3.3. A Simple Comparison with Two Existing Tests
3.3.1. A Simple Comparison with a Necessary Test
3.3.2. A Simple Comparison with a Necessary-And-Sufficient Test
- (1)
- The FZB test is completely ineffective in testing spherical symmetry in the low-dimensional () case when randomly choosing the orthogonal directions to approximate the statistic in (15). This implies that the FZB test is very sensitive for the choice of the orthogonal projection directions for approximating the null distribution of the test.
- (2)
- Among the six tests in Table 4, only has better performance in testing spherical symmetry for the two symmetric alternative distributions and (the generalized beta distribution with and , respectively).
- (3)
- All six tests have similar power performance for the non-symmetric alternative distributions: the shifted chisquare distribution and the shifted F-distribution , as described in Section 3.2.
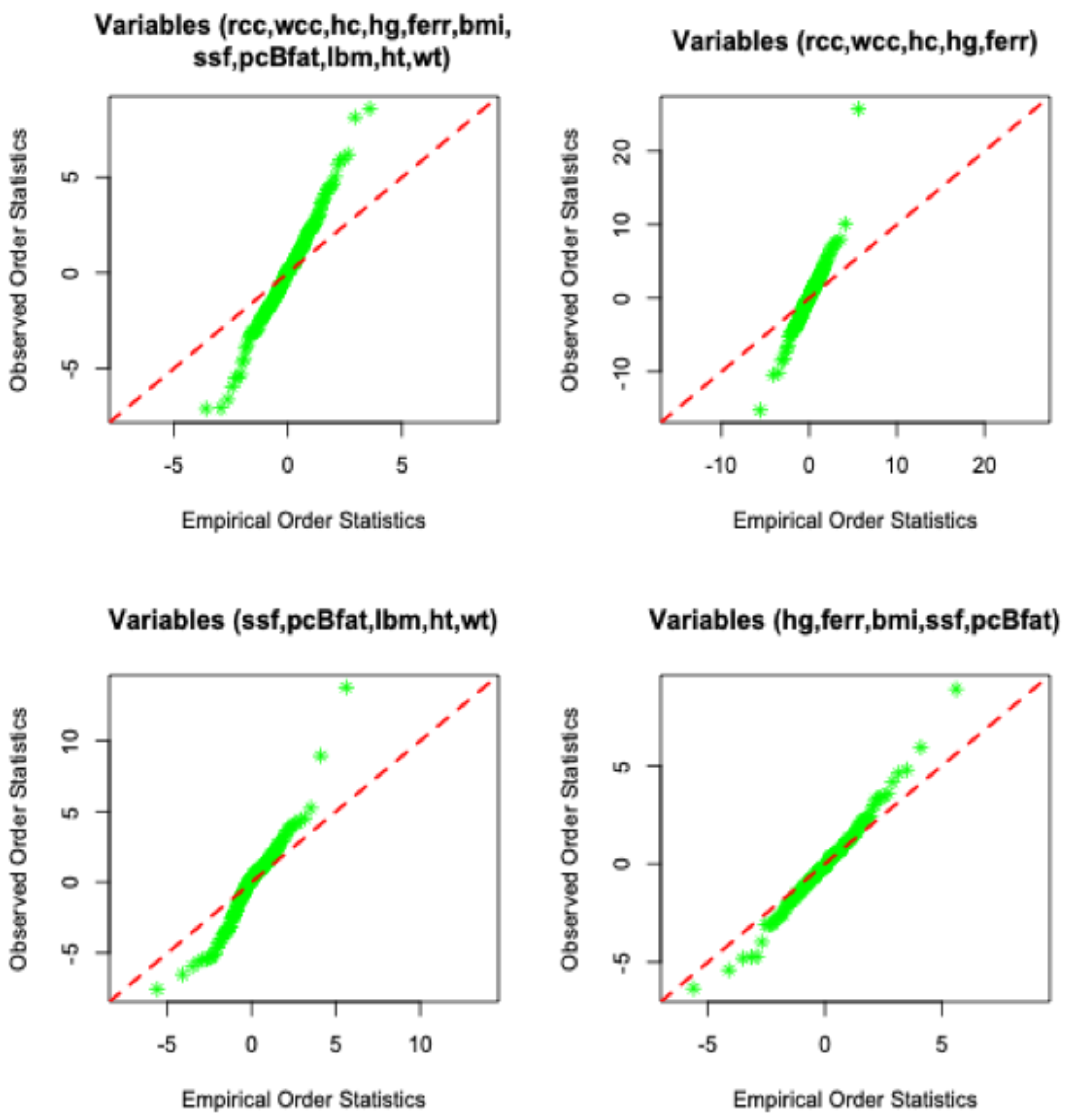
3.4. An Illustrative Example
4. Conclusions and a Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, K.T.; Kotz, S.; Ng, K.W. Symmetric Multivariate and Related Distributions; Chapman and Hall: London, UK; New York, NY, USA, 1990. [Google Scholar]
- Fang, K.T.; Zhang, Y. Generalized Multivariate Analysis; Springer: Berlin, Germany; Beijing, China, 1990. [Google Scholar]
- Läuter, J. Exact t and F tests for analyzing studies with multiple endpoints. Biometrics 1996, 52, 964–970. [Google Scholar] [CrossRef]
- Läuter, J.; Glimm, E.; Kropf, S. New multivariate tests for data with an inherent structure. Biom. J. 1996, 38, 5–23. [Google Scholar] [CrossRef]
- Läuter, J.; Glimm, E.; Kropf, S. Multivariate tests based on left-spherically distributed linear scores. Ann. Statist. 1998, 26, 1972–1988. [Google Scholar]
- Li, R.; Fang, K.T.; Zhu, L.X. Some Q-Q probability plots to test spherical and elliptical symmetry. J. Comput. Graph. Statist. 1997, 6, 435–450. [Google Scholar] [CrossRef]
- Liang, J.; Fang, K.T. Some applications of Läuter’s technique in tests for spherical symmetry. Biom. J. 2000, 42, 923–936. [Google Scholar] [CrossRef]
- Liang, J.; Li, R.; Fang, H.B.; Fang, K.T. Testing multinormality based on low-dimensional projection. J. Statist. Plann. Infer. 2000, 86, 129–141. [Google Scholar] [CrossRef]
- Glimm, E.; Läuter, J. On the admissibility of stable spherical multivariate tests. J. Multivar. Anal. 2003, 86, 254–265. [Google Scholar] [CrossRef]
- Liang, J.; Tang, M.L. Generalized F-tests for the multivariate normal mean. Comput. Statist. Data Anal. 2009, 57, 1177–1190. [Google Scholar] [CrossRef]
- Liang, J.; Tang, M.L.; Chan, P.S. A generalized Shapiro-Wilk W Statistic for testing high-dimensional normality. J. Comput. Graph. Statist. 2009, 53, 3883–3891. [Google Scholar] [CrossRef]
- Liang, J.; Ng, K.W. A multivariate normal plot to detect non-normality. J. Comput. Graph. Statist. 2009, 18, 52–72. [Google Scholar] [CrossRef]
- Zellner, A. Bayesian and non-Bayesian analysis of the regression model with multivariate Student-t error terms. J. Amer. Statist. Assoc. 1976, 71, 400–405. [Google Scholar] [CrossRef]
- Owen, J.; Rabinovitch, R. On the class of elliptical distributions and their applications to the theory of portfolio choice. J. Financ. 1983, 38, 745–752. [Google Scholar] [CrossRef]
- Lange, K.L.; Little, R.J.A.; Taylor, J.M.G. Robust statistical modeling using the t-distribution. J. Amer. Statist. Assoc. 1989, 84, 881–896. [Google Scholar] [CrossRef]
- Fang, K.T.; Anderson, T.W. Statistical Inference in Elliptically Contoured and Related Distributions; Allerton Press: New York, NY, USA, 1990. [Google Scholar]
- Kariya, T.; Kurata, H. Generalized Least Squares; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Gupta, A.K.; Varga, T.; Bodnar, T. Elliptically Contoured Models in Statistics and Portfolio Theory; Springer: New York, NY, USA, 2013. [Google Scholar]
- Bura, E.; Forzani, L. Sufficient reductions in regressions with elliptically contoured inverse predictors. J. Amer. Statist. Assoc. 2015, 110, 420–434. [Google Scholar] [CrossRef]
- Dewick, P.R.; Liu, S.; Liu, Y.; Ma, T. Elliptical and skew-elliptical regression models and their applications to financial data analytics. J. Risk Fin. Manag. 2023, 16, 310. [Google Scholar] [CrossRef]
- Gupta, A.K.; Varga, T. Elliptically Contoured Models in Statistics; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Sakhanenko, L. Testing for ellipsoidal symmetry: A comparison study. Comput. Statist. Data Anal. 2008, 53, 565–581. [Google Scholar] [CrossRef]
- Babic, S.; Ley, C.; Palangetic, M. Elliptical symmetry tests in R. R J. 2021, 13, 661–672. [Google Scholar] [CrossRef]
- Kariya, T.; Eaton, M.L. Robust tests for spherical symmetry. Ann. Statist. 1977, 5, 206–215. [Google Scholar] [CrossRef]
- Beran, R. Testing for elliptical symmetry of a multivariate density. Ann. Statist. 1979, 7, 150–162. [Google Scholar] [CrossRef]
- Baringhaus, L. Testing for spherical symmetry of a multivariate distribution. Ann. Statist. 1991, 19, 899–917. [Google Scholar] [CrossRef]
- Fang, K.T.; Zhu, L.X.; Bentler, P.M. A necessary test for sphericity of a high-dimensional distribution. J. Multivar. Anal. 1993, 44, 34–55. [Google Scholar] [CrossRef]
- Zhu, L.X.; Fang, K.T.; Zhang, J.T. A projection NT-type test for spherical symmetry of a multivariate distribution. In New Trends in Probability and Statistics; VSP: Utrecht, The Netherland; Tokyo, Japan; TEV: Uilnius, Lithuania, 1995; Volume 3, pp. 109–122. [Google Scholar]
- Koltchinskii, V.I.; Li, L. Testing for spherical symmetry of a multivariate distribution. J. Multivar. Anal. 1998, 65, 228–244. [Google Scholar] [CrossRef]
- Huffer, F.W.; Park, C. A test for elliptical symmetry. J. Multivar. Anal. 2007, 98, 256–281. [Google Scholar] [CrossRef]
- Liang, J.; Fang, K.T.; Hickernell, F.J. Some necessary uniform tests for spherical symmetry. Ann. Instit. Statist. Math. 2008, 60, 679–696. [Google Scholar] [CrossRef]
- Henze, N.; Hlávka, Z.; Meintanis, S.G. Testing for spherical symmetry via the empirical characteristic function. Stat.—A J. Theor. Appl. Stat. 2014, 48, 1282–1296. [Google Scholar] [CrossRef]
- Albisetti, I.; Balabdaoui, F.; Holzmann, H. Testing for spherical and elliptical symmetry. J. Multivar. Anal. 2020, 180, 104667. [Google Scholar] [CrossRef]
- Fang, K.T.; He, S.D. The Problem of Selecting a Given Number of Representative Points in a Normal Population and a Generalized Mills Ratio; Stanford Technical Report No. 327; Department of Statistics, Stanford University: Stanford, CA, USA, 1982. [Google Scholar]
- Flury, B.A. Principal points. Biometrika 1990, 77, 33–41. [Google Scholar] [CrossRef]
- Liang, J.; He, P.; Yang, J. Testing multivariate normality based on t-representative points. Axioms 2022, 11, 587. [Google Scholar] [CrossRef]
- Cao, Y.; Liang, J.; Xu, L.; Kang, J. Testing multivariate normality based on beta-representative points. Mathematics 2024, 12, 1711. [Google Scholar] [CrossRef]
- Voinov, V.; Nikulin, M.S.; Balakrishnan, N. Chisquared Goodness of Fit Tests with Applications; Academic Press: Cambridge, UK, 2013. [Google Scholar]
- Fang, K.T. Spherical and elliptical symmetry, test of. In Encyclopedia of Statistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2006; Volume 12, pp. 7924–7930. [Google Scholar]
- D’Agostino, R.B.; Stephens, M.A. Goodness-of-Fit Techniques. Marcel Dekker, Inc.: New York, NY, USA; Basel, Switzerland, 1986. [Google Scholar]
- Tashiro, D. On methods for generating uniform points on the surface of a sphere. Ann. Instit. Statist. Math. 1977, 29, 295–300. [Google Scholar] [CrossRef]
- Fang, K.T.; Wang, Y. Number-Theoretic Methods in Statistics; Chapman and Hall: London, UK, 1994. [Google Scholar]





| n | m | ||||||
|---|---|---|---|---|---|---|---|
| 0.0130 | 0.0115 | 0.0095 | 0.0115 | 0.0135 | |||
| 0.0165 | 0.0135 | 0.0090 | 0.0080 | 0.0170 | |||
| 0.0410 | 0.0200 | 0.0165 | 0.0155 | 0.0210 | |||
| 0.0235 | 0.0165 | 0.0240 | 0.0170 | 0.0205 | |||
| 0.0600 | 0.0365 | 0.0290 | 0.0310 | 0.0230 | |||
| 0.0315 | 0.0205 | 0.0255 | 0.0275 | 0.0235 | |||
| 0.0830 | 0.0505 | 0.0325 | 0.0335 | 0.0325 | |||
| 0.0265 | 0.0265 | 0.0230 | 0.0285 | 0.0205 | |||
| 0.0085 | 0.0115 | 0.0070 | 0.0135 | 0.0115 | |||
| 0.0130 | 0.0160 | 0.0100 | 0.0130 | 0.0170 | |||
| 0.0465 | 0.0200 | 0.0230 | 0.0180 | 0.0165 | |||
| 0.0225 | 0.0190 | 0.0235 | 0.0215 | 0.0245 | |||
| 0.0830 | 0.0310 | 0.0250 | 0.0230 | 0.0200 | |||
| 0.0245 | 0.0235 | 0.0205 | 0.0250 | 0.0240 | |||
| 0.0550 | 0.0320 | 0.0295 | 0.0275 | 0.0230 | |||
| 0.0335 | 0.0245 | 0.0230 | 0.0190 | 0.0275 | |||
| 0.0120 | 0.0135 | 0.0130 | 0.0125 | 0.0110 | |||
| 0.0135 | 0.0145 | 0.0115 | 0.0145 | 0.0210 | |||
| 0.0250 | 0.0190 | 0.0200 | 0.0210 | 0.0215 | |||
| 0.0180 | 0.0190 | 0.0200 | 0.0185 | 0.0225 | |||
| 0.0740 | 0.0345 | 0.0235 | 0.0210 | 0.0205 | |||
| 0.0225 | 0.0285 | 0.0225 | 0.0260 | 0.0235 | |||
| 0.0595 | 0.0325 | 0.0320 | 0.0240 | 0.0325 | |||
| 0.0255 | 0.0255 | 0.0420 | 0.0260 | 0.0275 | |||
| 0.0140 | 0.0085 | 0.0100 | 0.0110 | 0.0120 | |||
| 0.0200 | 0.0090 | 0.0125 | 0.0115 | 0.0120 | |||
| 0.0255 | 0.0245 | 0.0185 | 0.0250 | 0.0190 | |||
| 0.0205 | 0.0225 | 0.0200 | 0.0195 | 0.0170 | |||
| 0.0400 | 0.0250 | 0.0285 | 0.0265 | 0.0265 | |||
| 0.0270 | 0.0245 | 0.0205 | 0.0260 | 0.0225 | |||
| 0.0760 | 0.0240 | 0.0265 | 0.0290 | 0.0250 | |||
| 0.0235 | 0.0240 | 0.0250 | 0.0325 | 0.0255 |
| n | m | ||||||
|---|---|---|---|---|---|---|---|
| 0.0160 | 0.0135 | 0.0095 | 0.0105 | 0.0125 | |||
| 0.0110 | 0.0115 | 0.0130 | 0.0135 | 0.0105 | |||
| 0.0465 | 0.0210 | 0.0205 | 0.0140 | 0.0185 | |||
| 0.0225 | 0.0220 | 0.0155 | 0.0135 | 0.0170 | |||
| 0.0570 | 0.0330 | 0.0350 | 0.0180 | 0.0220 | |||
| 0.0250 | 0.0265 | 0.0285 | 0.0245 | 0.0265 | |||
| 0.0945 | 0.0600 | 0.0340 | 0.0295 | 0.0235 | |||
| 0.0230 | 0.0250 | 0.0280 | 0.0295 | 0.0245 | |||
| 0.0135 | 0.0140 | 0.0155 | 0.0180 | 0.0150 | |||
| 0.0165 | 0.0205 | 0.0165 | 0.0145 | 0.0160 | |||
| 0.0530 | 0.0255 | 0.0215 | 0.0240 | 0.0205 | |||
| 0.0215 | 0.0195 | 0.0235 | 0.0215 | 0.0205 | |||
| 0.0750 | 0.0340 | 0.0335 | 0.0230 | 0.0265 | |||
| 0.0285 | 0.0275 | 0.0205 | 0.0300 | 0.0240 | |||
| 0.0570 | 0.0405 | 0.0335 | 0.0370 | 0.0285 | |||
| 0.0325 | 0.0270 | 0.0235 | 0.0330 | 0.0365 | |||
| 0.0155 | 0.0110 | 0.0090 | 0.0130 | 0.0075 | |||
| 0.0120 | 0.0165 | 0.0160 | 0.0120 | 0.0100 | |||
| 0.0295 | 0.0220 | 0.0210 | 0.0245 | 0.0165 | |||
| 0.0220 | 0.0210 | 0.0235 | 0.0330 | 0.0190 | |||
| 0.0885 | 0.0320 | 0.0300 | 0.0245 | 0.0220 | |||
| 0.0285 | 0.0245 | 0.0220 | 0.0320 | 0.0215 | |||
| 0.0630 | 0.0395 | 0.0425 | 0.0280 | 0.0250 | |||
| 0.0305 | 0.0285 | 0.0290 | 0.0315 | 0.0325 | |||
| 0.0135 | 0.0130 | 0.0125 | 0.0115 | 0.0160 | |||
| 0.0145 | 0.0165 | 0.0140 | 0.0115 | 0.0155 | |||
| 0.0285 | 0.0200 | 0.0190 | 0.0265 | 0.0185 | |||
| 0.0195 | 0.0230 | 0.0255 | 0.0175 | 0.0265 | |||
| 0.0485 | 0.0295 | 0.0385 | 0.0285 | 0.0265 | |||
| 0.0260 | 0.0220 | 0.0235 | 0.0255 | 0.0270 | |||
| 0.0770 | 0.0340 | 0.0400 | 0.0300 | 0.0310 | |||
| 0.0325 | 0.0310 | 0.0245 | 0.0305 | 0.0255 |
| n | m | ||||||
|---|---|---|---|---|---|---|---|
| 0.0160 | 0.0120 | 0.0105 | 0.0130 | 0.0080 | |||
| 0.0105 | 0.0130 | 0.0145 | 0.0115 | 0.0155 | |||
| 0.0330 | 0.0175 | 0.0205 | 0.0235 | 0.0150 | |||
| 0.0205 | 0.0130 | 0.0230 | 0.0220 | 0.0210 | |||
| 0.0520 | 0.0370 | 0.0310 | 0.0210 | 0.0275 | |||
| 0.0220 | 0.0325 | 0.0230 | 0.0215 | 0.0250 | |||
| 0.0765 | 0.0535 | 0.0440 | 0.0265 | 0.0330 | |||
| 0.0220 | 0.0250 | 0.0265 | 0.0260 | 0.0245 | |||
| 0.0080 | 0.0090 | 0.0125 | 0.0080 | 0.0120 | |||
| 0.0105 | 0.0140 | 0.0155 | 0.0180 | 0.0150 | |||
| 0.0390 | 0.0220 | 0.0240 | 0.0145 | 0.0195 | |||
| 0.0165 | 0.0185 | 0.0195 | 0.0220 | 0.0210 | |||
| 0.0800 | 0.0275 | 0.0335 | 0.0255 | 0.0285 | |||
| 0.0155 | 0.0275 | 0.0215 | 0.0215 | 0.0245 | |||
| 0.0525 | 0.0365 | 0.0445 | 0.0385 | 0.0235 | |||
| 0.0250 | 0.0205 | 0.0225 | 0.0255 | 0.0260 | |||
| 0.0115 | 0.0125 | 0.0120 | 0.0110 | 0.0095 | |||
| 0.0115 | 0.0125 | 0.0180 | 0.0130 | 0.0135 | |||
| 0.0285 | 0.0225 | 0.0230 | 0.0130 | 0.0260 | |||
| 0.0200 | 0.0220 | 0.0190 | 0.0145 | 0.0175 | |||
| 0.0765 | 0.0315 | 0.0300 | 0.0255 | 0.0270 | |||
| 0.0275 | 0.0250 | 0.0275 | 0.0265 | 0.0245 | |||
| 0.0665 | 0.0375 | 0.0365 | 0.0285 | 0.0210 | |||
| 0.0320 | 0.0335 | 0.0245 | 0.0325 | 0.0270 | |||
| 0.0130 | 0.0065 | 0.0110 | 0.0160 | 0.0095 | |||
| 0.0125 | 0.0120 | 0.0115 | 0.0075 | 0.0155 | |||
| 0.0195 | 0.0205 | 0.0195 | 0.0195 | 0.0200 | |||
| 0.0210 | 0.0215 | 0.0185 | 0.0235 | 0.0235 | |||
| 0.0375 | 0.0240 | 0.0295 | 0.0205 | 0.0270 | |||
| 0.0300 | 0.0230 | 0.0185 | 0.0245 | 0.0280 | |||
| 0.0775 | 0.0300 | 0.0405 | 0.0255 | 0.0265 | |||
| 0.0270 | 0.0260 | 0.0310 | 0.0265 | 0.0285 |
| m | n | Test | t-distr. | ||||
|---|---|---|---|---|---|---|---|
| 0.0510 | 0.2225 | 0.6130 | 0.9985 | 0.9185 | |||
| 0.0145 | 0 | 0.0005 | 0.9960 | 0.7550 | |||
| FZB | 0 | 0 | 0 | 0 | 0 | ||
| 0.0405 | 0.0765 | 0.1530 | 1.0000 | 0.9985 | |||
| 0.0385 | 0.0775 | 0.1635 | 1.0000 | 0.9980 | |||
| 0.0450 | 0.0525 | 0.0595 | 1.0000 | 0.9985 | |||
| 0.0475 | 0.4790 | 0.9295 | 0.9960 | 0.9995 | |||
| 0.0170 | 0.0270 | 0.1420 | 0.9940 | 0.9750 | |||
| FZB | 0 | 0 | 0 | 0 | 0 | ||
| 0.0375 | 0.1165 | 0.4000 | 1.0000 | 1.0000 | |||
| 0.0355 | 0.1210 | 0.4305 | 1.0000 | 1.0000 | |||
| 0.0405 | 0.0655 | 0.0715 | 1.0000 | 1.0000 | |||
| 0.0455 | 0.6840 | 0.9930 | 0.9450 | 0.9345 | |||
| 0.0645 | 0.0390 | 0.0135 | 0.8580 | 0.7060 | |||
| FZB | 0 | 0 | 0 | 0 | 0 | ||
| 0.0355 | 0.0720 | 0.1525 | 0.9990 | 0.9985 | |||
| 0.0360 | 0.0725 | 0.1630 | 0.9990 | 0.9980 | |||
| 0.0410 | 0.0490 | 0.0570 | 0.9990 | 0.9985 | |||
| 0.0510 | 0.9590 | 1.0000 | 1.0000 | 1.0000 | |||
| 0.0310 | 0.0060 | 0.0085 | 0.9915 | 0.9505 | |||
| FZB | 0 | 0 | 0 | 0 | 0 | ||
| 0.0465 | 0.1055 | 0.3730 | 1.0000 | 1.0000 | |||
| 0.0485 | 0.1135 | 0.4100 | 1.0000 | 1.0000 | |||
| 0.0500 | 0.0510 | 0.0620 | 1.0000 | 1.0000 |
| Full 11 Variables, | V = (rcc, wcc, hc, hg, ferr), | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| m | 5 | 10 | 15 | 20 | m | 5 | 10 | 15 | 20 |
| 178 | 427 | 749 | 1176 | 323 | 918 | 1832 | 2978 | ||
| p-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | p-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 96 | 220 | 275 | 349 | 123 | 207 | 304 | 355 | ||
| p-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | p-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| V = (ssf, pcBfat, lbm, ht, wt), | V = (hg, ferr, bmi, ssf, pcBfat), | ||||||||
| 142 | 457 | 936 | 1693 | 16 | 85 | 186 | 256 | ||
| p-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | p-value | 0.0003 | 0.0000 | 0.0000 | 0.0000 |
| 83 | 116 | 150 | 193 | 16 | 38 | 44 | 49 | ||
| p-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | p-value | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; He, P.; Liu, Q. Testing Spherical Symmetry Based on Statistical Representative Points. Mathematics 2024, 12, 3939. https://doi.org/10.3390/math12243939
Liang J, He P, Liu Q. Testing Spherical Symmetry Based on Statistical Representative Points. Mathematics. 2024; 12(24):3939. https://doi.org/10.3390/math12243939
Chicago/Turabian StyleLiang, Jiajuan, Ping He, and Qiong Liu. 2024. "Testing Spherical Symmetry Based on Statistical Representative Points" Mathematics 12, no. 24: 3939. https://doi.org/10.3390/math12243939
APA StyleLiang, J., He, P., & Liu, Q. (2024). Testing Spherical Symmetry Based on Statistical Representative Points. Mathematics, 12(24), 3939. https://doi.org/10.3390/math12243939





