Particle Swarm Optimization Algorithm for Determining Global Optima of Investment Portfolio Weight Using Mean-Value-at-Risk Model in Banking Sector Stocks

Abstract

Computational algorithms are systematically written instructions or steps used to solve logical and mathematical problems with computers. These algorithms are crucial to rapidly and efficiently analyzing complex data, especially in global optimization problems like portfolio investment optimization. Investment portfolios are created because investors seek high average returns from stocks and must also consider the risk of loss, which is measured using the value at risk (VaR). This study aims to develop a computational algorithm based on the metaheuristic particle swarm optimization (PSO) model, which can be used to solve global optimization problems in portfolio investment. The data used in the simulation of the developed computational algorithm consist of daily stock returns from the banking sector traded in the Indonesian capital market. The quantitative research methodology involves formulating an algorithm to solve the global optimization problem in portfolio investment with mathematical calculations and quantitative data analysis. The objective function is to maximize the mean-value-at-risk model for portfolio investment, with constraints on the capital allocation weights in each stock within the portfolio. The results of this study indicate that the adapted PSO algorithm successfully determines the optimal portfolio weight composition, calculates the expected return and VaR in the optimal portfolio, creates an efficient frontier surface graph, and establishes portfolio performance measures. Across 50 trials, the algorithm records an average expected return of 0.000737, a return standard deviation of 0.00934, a value at risk of 0.01463, and a Sharpe ratio of 0.0504. Further evaluation of the PSO algorithm’s performance shows high consistency in generating optimal portfolios with appropriate parameter selection. The novelty of this research lies in developing an accurate computational algorithm for determining the global optima of mean-value-at-risk portfolio investments, yielding precise, consistent results with relatively fast computation times. The contribution to users is an easy-to-use tool for computational analysis that can assist in decision-making for portfolio investment formation.

1. Introduction

Algorithms are well-defined computational steps that play a crucial role in solving a wide range of problems, from simple to complex ones. For example, algorithms are employed to solve differential equations, non-convex optimization problems, and numerical optimization problems [1,2,3]. This asserts that optimization, as the effort to find the best solution to a problem, can be simplified through computational algorithms [4].

Global optimization is a critical research field focusing on finding the best solution from the entire solution set for a given problem [5]. However, solving global optimum issues, even for simple cases, can take hours or even days [6]. In this context, computational algorithms are pivotal to enhancing the speed and accuracy of global optimum searches for various problems [7,8].

One of the frequently encountered issues today is the problem of investment portfolio selection. Investment involves allocating capital to a company or project with the expectation of obtaining optimal returns within a specified period. Faced with market fluctuations, investors must select a portfolio that maximizes the expected returns and manages the risks at an acceptable level [9].

Globally optimized investment portfolios are an essential aspect of financial management, aiming to balance risk and return effectively. Proper portfolio optimization, with accurate assessment, focuses on asset allocation strategies that can address uncertainty and maximize the expected returns at an acceptable risk level [10].

One approach to selecting an optimal portfolio is the mean-value-at-risk (mean-VaR) model. The value at risk (VaR) is a method for measuring risk by estimating the maximum potential loss that could occur in an investment portfolio over a given period at a certain confidence level [11]. VaR calculations utilize potential loss estimates based on historical data and statistical models, considering volatility and asset correlations [12]. The VaR offers a simple approach to measuring and managing portfolio risk, making it a frequently used tool in portfolio selection. However, the VaR has limitations that may affect its effectiveness in risk estimation. These limitations arise from the reliance on historical data, assumptions concerning the return distribution, and the need for more information about the magnitude of potential losses. Computational algorithms can comprehensively address these limitations and account for additional risk factors [11].

Research on optimal portfolios using the mean-VaR model has been discussed by Tsao, focusing on portfolio selection based on the efficient frontier of the mean-VaR model. Tsao (2010) found that risk-averse investors may allocate their wealth inefficiently if their decisions are based on the mean variance framework. Therefore, investors should base their investment decisions on the efficient frontier of the mean-VaR model [13]. Furthermore, Zhang and Liu researched a firework algorithm for the mean-VaR/CVaR model. Zhang and Liu demonstrated that the algorithm outperformed the genetic algorithm regarding accuracy, speed, and solution stability. However, further testing is required to evaluate the improved algorithm’s efficiency and application to general optimization problems [14].

Jiang et al. explored a multi-objective bat algorithm based on credibility for a multi-period mean-VaR portfolio optimization problem. Jiang et al. (2021) found that the bat algorithm had better accuracy, diversity, and distribution than others. However, the algorithm may not apply to all market conditions [15]. Moreover, Babazadeh and Esfahanipour investigated a new multi-period mean-VaR optimization model that considers practical constraints and transaction costs. Their study revealed that the developed NSGA-II algorithm outperformed the original NSGA-II in terms of well-known metaheuristic performance metrics. Although metaheuristic algorithms are efficient, optimal design and customization are still required for successful implementation [16].

Several gaps exist based on previous research, such as the need for further development of the algorithms used. To address these gaps and fill the identified research gaps, this study aims to develop an efficient computational algorithm for determining the global optima of an investment portfolio using the mean-VaR model, which is applicable to various market conditions. The computational algorithm developed in this research is expected to effectively decide the global optimization of mean-value-at-risk investment portfolios and could serve as a reference for investors.

2. Literature Review

2.1. Computational Algorithms

A computational algorithm is a set of logical, structured, and systematic steps used to solve a problem or complete a specific task in computation or computer programming. Computational algorithms are at the core of every computer program, as they determine how tasks are processed and completed [17].

The key characteristics of computational algorithms include the following:

• Input: The algorithm accepts the input data or information required to solve the problem.
• Process: The algorithm applies a series of logical steps and operations to process the input and generate the desired output.
• Output: The algorithm produces an output or final result representing the solution to the problem.
• Efficiency: A good algorithm should efficiently use time, memory, and storage space.
• Correctness: The algorithm must produce accurate and correct results that align with the given problem.
• Termination: The algorithm must terminate after a finite number of steps; it should not run indefinitely without an end.

Computational algorithms can be written in various forms, such as pseudocode, flowcharts, or specific programming languages. These algorithms are applied across multiple fields, including data processing, image processing, cryptography, artificial intelligence, and scientific computing. Each representation helps clarify the algorithm’s logic and steps, making it easier to implement and analyze in different contexts.

Algorithms help organize, analyze, and extract valuable insights from large datasets. In image processing, they are used for tasks such as image enhancement, recognition, and compression. Cryptography relies on algorithms to secure communication and protect sensitive data. Artificial intelligence and machine learning algorithms enable systems to learn from data and make decisions autonomously. Lastly, in scientific computing, algorithms are fundamental to solving complex mathematical models and simulations in physics, biology, and engineering.

2.2. Particle Swarm Optimization

Particle swarm optimization (PSO) is based on the behavior of a flock of birds or a school of fish. The PSO algorithm mimics the social behavior of these organisms. Social behavior consists of individual actions and the influence of other individuals within a group. The term “particle” refers to, for example, a bird in a flock of birds. Each individual, or particle, behaves by using its intelligence and is also influenced by the collective behavior of the group [18].

In the context of PSO, particles move through a multi-dimensional search space, adjusting their positions based on both their own previous experiences (personal best) and the experiences of other particles (global best). This process is repeated iteratively, allowing the particles to converge toward the optimal solution for a given problem, with the collective intelligence of the swarm guiding the search process.

Thus, the behavior of a flock of birds is based on a combination of three factors: cohesion, separation, and alignment. PSO is developed based on the following three models:

• When an object approaches the target (minimum or maximum of an objective function), it quickly sends information to other objects in a particular group.
• Other objects will follow the direction toward the target rather than directly.
• A component that depends on each object’s behavior is its memory of past events.

In the PSO algorithm, the search for solutions is conducted by several particles from a population. The population is randomly initialized with a specified maximum and minimum values range. Each particle represents a position or solution to the problem at hand. Each particle seeks the optimal solution by moving through the search space, adjusting its position toward the best position it has encountered (local best) and the best position found by the entire swarm (global best). Thus, the spread of experience or information occurs within each particle and between a particle and the best particle of the whole swarm during the search process. Subsequently, the search continues to find the best position for each particle over several iterations until a relatively stable position is reached or the predefined iteration limit is reached. In each iteration, the performance of each solution, represented by the particle’s position, is evaluated by inserting that solution into a fitness function. Each particle is treated as a point in a specific dimensional space. Two factors define the particle’s status in the search space: the particle’s position and the particle’s velocity [18].

The mathematical formulation that describes the position and velocity of a particle in a specific dimensional space is as follows:

$$X_i\left(t\right)=x_{i1}\left(t\right),x_{i2}\left(t\right),\dots ,x_{iN}\left(t\right),$$

$$V_i\left(t\right)=v_{i1}\left(t\right),v_{i2}\left(t\right),\dots ,v_{iN}\left(t\right),$$

where $X$ represents the particle’s position, $V$ is the particle’s velocity, $i$ is the particle index, and $N$ is the dimensional space size. The mathematical model that describes the calculation of particle iteration is as follows:

$$V_i\left(t\right)=V_i\left(t-1\right)+c_1{r}_1\left(pbes{t}_i-X_i\left(t-1\right)\right)+c_2{r}_2\left(gbest-X_i\left(t-1\right)\right),$$

(1)

$$X_i\left(t\right)=V_i\left(t\right)+X\left(t-1\right),$$

(2)

where $pbest$ represents the best position of the i-th particle, while $gbest$ represents the best position of the entire swarm. $c_1$ and $c_2$ are constants known as learning factors, while $r_1$ and $r_2$ are random numbers with values between 0 and 1.

In the particle swarm optimization algorithm, $c_1$ and $c_2$ control the influence of the particle’s best position (local best) and the swarm’s best position (global best) on the particle’s movement. $c_1$ (cognitive coefficient) regulates how much the particle’s best position affects its movement, while $c_2$ (the social coefficient) controls how much the swarm’s best position influences the particle’s movement. Additionally, $r_1$ and $r_2$ are random numbers between 0 and 1 that introduce an element of uncertainty and variation into the particle’s movement. These random numbers add an exploration element to the search for solutions, allowing particles to avoid getting trapped in local solutions and enhancing their ability to explore the search space more effectively.

Equations (3) and (4) can be used to update each particle’s best position and the entire swarm’s best position.

$$pbes{t}_i\left(t+1\right)=\left\{\begin{array}{cc}pbes{t}_i\left(t\right),\hfill & \mathrm{if} f\left(X_i\left(t+1\right)\right)\le f\left(pbes{t}_i\left(t\right)\right)\hfill \\ pbes{t}_i\left(t+1\right),\hfill & \mathrm{if} f\left(X_i\left(t+1\right)\right)>f\left(pbes{t}_i\left(t\right)\right)\hfill \end{array}\right.,$$

(3)

$$gbest\left(t+1\right)=\max \left\{x_{i1}\left(t+1\right),x_{i2}\left(t+1\right),\dots ,x_{iN}\left(t+1\right)\right\}.$$

(4)

The iteration of each particle continues until the stopping criteria are met. In this case, the stopping criteria used are when the particle converges to a value or after reaching the predefined iteration limit. The convergence criterion of the particle can be checked using the formula in Equation (5).

$$\left|f\left(X_i\left(t+1\right)\right)-f\left(X_i\left(t\right)\right)\right|<{ϵ}_f, \forall i,$$

(5)

where $f\left(X_i\left(t\right)\right)$ is the fitness value of the i-th particle at iteration $t$, and ${ϵ}_f$ is the convergence threshold for the fitness value. The fundamental steps of the particle swarm optimization (PSO) algorithm are summarized in Algorithm 1. This pseudocode outlines the initialization process, the update of particle velocities and positions, and the termination criteria commonly used in PSO implementations.

Algorithm 1. Pseudocode for basic particle swarm optimization algorithm

Initialize parameters, such as the inertia weight (w), cognitive coefficient (c1), social coefficient (c2), and convergence criteria Initialize each particle: - Assign a random initial position within the search space - Assign a random initial velocity - Set the initial personal best position (pbest) to the particle’s starting position - Evaluate the fitness of each particle’s pbest Determine the initial global best (gbest) - Set gbest as the best pbest among all the particles Loop until the stopping criteria are met (e.g., maximum iterations or convergence): - For each particle: Update the particle’s velocity using Equation (1) Update the particle’s position using Equation (2) Evaluate the fitness of the particle’s new position. If the new position is better than the current pbest, update pbest - Update gbest if any particle’s pbest is better than the current gbest, as in Equation (3). Return gbest as the optimal solution

Several key challenges are commonly encountered when designing and implementing computational algorithms. One is the algorithmic complexity in terms of both the computational time and the memory requirements, where inefficient algorithms can lead to poor performance when faced with large-scale problems. Scalability also becomes a challenge, as the algorithm must scale well when handling the growth of data or problems [19]. Algorithm optimization to improve the computational time efficiency, memory usage, or other resources is another challenge that often requires in-depth analysis and the application of specialized techniques [7].

2.3. Global Optimization

Optimization models are a systematic approach to decision-making aimed at finding the best or optimal solution to a problem while considering existing constraints [20]. The primary objective of optimization is to maximize the benefits obtained with minimal effort. As shown in Figure 1, if the point $x$ corresponds to the minimum value of a function $f\left(x\right)$, then that point also corresponds to the maximum value of the negative of the function, $-f\left(x\right)$ [21].

In general, an optimization problem is formulated as follows:

Find,

$$x=\left[\begin{array}{c}{x}_1\\ x_2\\ \begin{array}{c}⋮\\ x_n\end{array}\end{array}\right],$$

which can minimize or maximize the value of a function $f\left(x\right)$, such that the following constraint equations are satisfied:

$$g_j\left(x\right)\le 0, j=1,2,\dots ,m,$$

$$h_i\left(x\right)=0, i=1,2,\dots ,p.$$

Global optimization is a branch of mathematical optimization focused on finding the overall (global) optimal solution of a given objective function by considering all the possible solutions within the search space. This contrasts with local optimization, which only focuses on finding an optimal solution within a local region or around a specific initial value [22].

Definition 1 

(global maximum [23]). A global maximum $\widehat{x}\in \mathbb{X}$ of an objective function $f:\mathbb{X}\to \mathbb{R}$ is an input element such that $f\left(\widehat{x}\right)\ge f\left(x\right)$ for every $x\in \mathbb{X}$.

Definition 2 

(global minimum [23]). A global minimum $\check{x}\in \mathbb{X}$ of an objective function $f:\mathbb{X}\to \mathbb{R}$ is an inout element such that $f\left(\check{x}\right)\le f\left(x\right)$ for every $x\in \mathbb{X}$.

Definition 3 

(global optimum [23]). A global optimum $x^{*}\in \mathbb{X}$ of an objective function $f:\mathbb{X}\to \mathbb{R}$ is either a global maximum or a global minimum.

2.4. Portfolio Investment Model

An investment portfolio model is a theoretical framework and methodology used to construct and manage a collection of investment assets to achieve an optimal balance between the expected risk and return. These models provide guidance and techniques for determining optimal asset allocation, assessing portfolio risk, and measuring investment performance [24]. Generally, investment portfolio models are built upon certain assumptions about the characteristics and behaviors of financial markets, such as the asset return distribution, asset correlations, and factors affecting asset returns.

The primary goal of an investment portfolio model is to maximize the expected returns for a given level of risk or to minimize the risk for a given expected return [10]. The risk in an investment portfolio is typically measured using metrics like the variance, standard deviation, or other risk measures consistent with the assumptions and characteristics of the model employed.

Investors can benefit from stock investments through capital gains (the difference between the selling price and the purchase price of the stock) and dividends (a company’s profit distribution to shareholders) [9].

Return and Risk

The stock return is the rate of return that investors receive from their stock investments. Generally, stock returns have two main components: capital gains and dividends. The capital gain is the profit earned from the positive difference between a stock’s buying and selling prices. The higher the selling price relative to the purchase price, the larger the investor’s capital gain. Meanwhile, dividends are portions of a company’s profits distributed to shareholders. The amount of dividend paid depends on the company’s policy and is typically disbursed periodically. There are several types of stock return rates, but this research primarily emphasizes simple returns and continuous compound returns [25].

The calculation of the asset return for a single period, from period $t-1$ to period $t$, results in the gross return as follows:

$$1+R_t={\displaystyle \frac{P_t}{P_{t-1}}} \mathrm{atau} P_t=P_{t-1}\left(1+R_t\right).$$

(6)

From Equation (6), the simple return is obtained as follows:

$$R_t={\displaystyle \frac{P_t}{P_{t-1}}}-1={\displaystyle \frac{P_t-P_{t-1}}{P_{t-1}}},$$

(7)

where $P_t$ represents the gross return for a single period and $R_t$ represents the simple return for a single period. Meanwhile, the continuous compound return (log return) is derived from the natural logarithm of the gross simple return of an asset.

$$r_t=\ln \left(1+R_t\right)=\ln \left({\displaystyle \frac{P_t}{P_{t-1}}}\right)=p_t-p_{t-1},$$

(8)

where $p_t=ln ln \left(P_t\right)$, and $r_t$ represents the continuous compound return (log return).

Risk is the likelihood of experiencing loss or unfavorable outcomes in any activity, including investments. Generally, risk can arise from various sources, such as changes in economic conditions, political events, natural disasters, and human error. In finance, risk refers to the potential variation in investment returns, whether positive or negative. Investors face risk when aiming for higher returns, making risk management essential to minimize possible losses.

In investment management, risk reflects how much the actual return deviates from the expected return. The more significant the difference between the actual and expected returns, the higher the risk [26]. To understand the risks resulting from uncertainty, investors need to grasp probability distributions:

$$Variance \left({\sigma }^2\right)=\sum _{i=1}^n{\left\{\left(R_i-E\left(R\right)\right)\right\}}^2·X_i,$$

(9)

where $R_i$ represents the actual of asset $i$, $E\left(R\right)$ denotes the expected return, and $X_i$ represents the probability of event $i$.

Stock returns can be modeled as random variables at time $t$. If $R_t$ is the distribution with a probability density function denoted by $f\left(r_t\right)$, the expected return of a stock can be defined as shown in Equation (10):

$${\mu }_A=E\left[R_{A,t}\right]=\underset{-\infty }{\overset{\infty }{\int }}{r}_{A,t}f\left(r_{A,t}\right)d{r}_{A,t},$$

(10)

where ${\mu }_A$ is the expected return of stock $A$, $r_{\left\{A,t\right\}}$ is the return of stock $A$ at time $t$, and $f\left(r_{\left\{A,t\right\}}\right)$ is the probability density function of stock A’s return distribution.

The estimation of the variance of a stock can be defined as in Equation (11):

$$\begin{array}{c}{\mu }_A=E\left[R_{A,t}\right]=\underset{-\infty }{\overset{\infty }{\int }}{r}_{A,t}f\left(r_{A,t}\right)d{r}_{A,t}\\ =E\left[R_{A,t}^2\right]-{\left\{E\left[R_{A,t}^2\right]\right\}}^2,\end{array}$$

(11)

where ${\sigma }_A^2$ is the variance of stock A.

The covariance is a statistical measure that indicates the extent to which two random variables are related [27]. In the context of investments, the covariance is used to evaluate how closely the changes in one investment’s value are related to the changes in the value of another asset. This helps to explain how fluctuations in individual investment returns occur together [28]. The covariance between stocks A and B is defined as follows:

$$\begin{array}{cc}{\sigma }_{AB}\hfill & =E\left[\left(R_{A,t}-{\mu }_A\right)\left(R_{B,t}-{\mu }_B\right)\right],\hfill \\ & =\underset{-\infty }{\overset{\infty }{\int }}\left(r_{A,t}-{\mu }_A\right)\left(r_{B,t}-{\mu }_B\right)f\left(r_{A,t},r_{B,t}\right)d{r}_{A,t}d{r}_{B,t}\hfill \\ & =E\left[R_{A,t},R_{B,t}\right]-{\mu }_A{\mu }_B, \hfill \end{array}$$

(12)

where ${\sigma }_{AB}$ is the covariance between stock $A$ and stock $B$, ${\mu }_A$ is the expected return of stock $B$, $r_{A,t}$ is the return of stock $A$ at time $t$, $r_{B,t}$ is the return of stock B at time $t$, $f\left(r_{A,t}\right)$ is the probability density function of stock $A$’s return distribution, and $f\left(r_{B,t}\right)$ is the probability density function of stock $B$’s return distribution.

2.5. Burr (4P) and Log-Logistic (3P) Distribution

2.5.1. Burr (4P) Distribution

The Burr (4P) distribution is a versatile statistical model widely used in fields like finance, engineering, and actuarial science due to its ability to model complex data patterns, including bimodal and heavy-tailed distributions. This flexible distribution accommodates various data shapes, and its parameters can be estimated using methods like the maximum likelihood [29]. Its applications include modeling income data and reliability analysis, particularly for lifetime data and failure rates. However, some researchers suggest that its complexity may lead to overfitting in more straightforward datasets, where simpler models can sometimes remain effective. A continuous non-negative random variable $X$ is considered to follow a Burr (4P) distribution if its probability density function $\left(f\left(x\right)\right)$ and cumulative distribution function $\left(F\left(x\right)\right)$ are defined as given in Equations (13) and (14) [30].

$$f\left(x\right)={\displaystyle \frac{\alpha k{\left(\frac{x-\gamma }{\beta }\right)}^{\alpha -1}}{\beta {\left(1+{\left(\frac{x-\gamma }{\beta }\right)}^{\alpha }\right)}^{k+1}}},$$

(13)

$$F\left(x\right)=1-{\left(1+{\left({\displaystyle \frac{x-\gamma }{\beta }}\right)}^{\alpha }\right)}^{-k},$$

(14)

where $k,\alpha ,\beta ,$ and $\gamma$ are parameters.

To calculate the expectation and variance of data following a Burr distribution, Equations (15) and (16) can be used [31,32].

$$E\left(X\right)=\gamma +k\beta B\left(1+{\displaystyle \frac{1}{\alpha }},k-{\displaystyle \frac{1}{\alpha }}\right),$$

(15)

$$E\left[X^2\right]-{\left(E\left[X\right]\right)}^2=k{\beta }^2 B\left(1+{\displaystyle \frac{2}{\alpha }},k-{\displaystyle \frac{2}{\alpha }}\right)-k^2{\beta }^2 B^2\left(1+{\displaystyle \frac{1}{\alpha }},k-{\displaystyle \frac{1}{\alpha }}\right),$$

(16)

where $0<{\displaystyle \frac{1}{\alpha }}<k,k,\alpha ,\beta >0,-\mathrm{\infty }<\gamma <+\mathrm{\infty }$, and $B\left(b,c\right)$ represents the beta function.

2.5.2. Log-Logistic (3P) Distribution

The log-logistic (3P) distribution, initially developed by Verhulst (1838) for modeling population growth and later known as the Fisk distribution in economics, is widely used across various fields. It applies to non-negative random variables as a continuous distribution with an unimodal failure rate. Its applications include modeling wealth and income, economic and actuarial science, hydrology flow data, biostatistics for post-transplant survival times, seismic risk estimation, reliability analysis, and daily water consumption forecasting [33]. The probability density function $\left(f\left(x\right)\right)$ and cumulative distribution function $\left(F\left(x\right)\right)$ for the log-logistic distribution are given in Equations (17) and (18).

$$f\left(x\right)={\displaystyle \frac{\alpha }{\beta }}{\left({\displaystyle \frac{x-\gamma }{\beta }}\right)}^{\alpha -1}{\left(1+{\left({\displaystyle \frac{x-\gamma }{\beta }}\right)}^{\alpha }\right)}^{-2},$$

(17)

$$F\left(x\right)={\left(1+{\left({\displaystyle \frac{x-\gamma }{\beta }}\right)}^{\alpha }\right)}^{-1},$$

(18)

where $\alpha ,\beta ,$ and $\gamma$ are parameters.

To calculate the expectation and variance of the data following a Burr distribution, Equations (19) and (20) can be used [31].

$$E\left(X\right)=\gamma +\beta \mathrm{B}\left(1+{\displaystyle \frac{1}{\alpha }},1-{\displaystyle \frac{1}{\alpha }}\right),$$

(19)

$$E\left[X^2\right]-{\left(E\left[X\right]\right)}^2={\beta }^2\left[B\left(1+{\displaystyle \frac{2}{\alpha }},k-{\displaystyle \frac{2}{\alpha }}\right)-B^2\left(1+{\displaystyle \frac{1}{\alpha }},1-{\displaystyle \frac{1}{\alpha }}\right)\right],$$

(20)

where $\alpha ,\beta >0,-\mathrm{\infty }<\gamma <+\mathrm{\infty }$, and $B\left(b,c\right)$ represents the beta function.

2.6. Maximum Likelihood Estimation

The maximum likelihood estimation (MLE) method is one of the most popular and frequently used parameter estimation techniques. The main principle of the MLE is to find the parameters that maximize the likelihood function, which is the probability of the observed data given the estimated parameters. The likelihood function is defined as the product of the probability density functions for each data point in the sample equation:

$$L\left(\theta \right)=\prod _{i=1}^{n}f\left(x_i|\theta \right).$$

(21)

To simplify the calculations, the log-likelihood is often used, which is the logarithm of the likelihood function:

$$\mathcal{l}\left(\theta \right)=\log L\left(\theta \right)=\sum _{i=1}^n\log f\left(x_i|\theta \right).$$

(22)

The MLE estimate for the parameter $\theta$ is the value $\underset{\_}{\theta }$ that maximizes the log-likelihood function $l\left(\theta \right)$. This process typically involves solving the first derivative $l\left(\theta \right)$ concerning $\theta$ and finding the value of $\theta$ that makes this derivative zero [34]. Parameter estimation using the MLE method is efficient because it assumes the data distribution.

2.7. Portfolio

Modern portfolio theory (MPT) provides a more specific framework for understanding risk preferences within the investment context. MPT employs the concepts of the efficient frontier and indifference curves to illustrate how investors with varying risk preferences can select an optimal portfolio aligned with their risk tolerance levels [25]. This theory emphasizes the importance of diversification to mitigate risk without reducing the expected returns while acknowledging the inherent trade-off between risk and return. Through MPT, investors’ risk preferences can be translated into concrete asset allocation strategies, enabling the construction of portfolios that match each investor’s attitude toward uncertainty and potential losses [35]. Thus, understanding risk preferences, as grounded in utility theory and applied through MPT, is crucial for effective investment decision-making that is aligned with an investor’s unique characteristics.

The expected return of a portfolio can be calculated as the sum of the expected returns of each asset, where each return is weighted according to the asset’s proportion within the portfolio. The expected return is calculated using Equation (23):

$${\mu }_{pt}=\sum _{i=1}^n{w}_i{\mu }_{it},$$

(23)

where ${\mu }_{pt}$ represents the expected portfolio return, $w_i$ denotes the portfolio weights, and $\mu$ is the vector of expected returns within the investment portfolio, which is expressed as follows:

$$\mathsf{\mu }=\left[\begin{array}{c}{\mu }_1\\ {\mu }_2\\ ⋮\\ {\mu }_n\end{array}\right].$$

The portfolio risk is a statistical measure known as variance, which describes risk as the variance of returns within a portfolio of stocks. The variance of portfolio returns is defined in Equation (24):

$${\sigma }_{pt}^2={\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w},$$

(24)

The covariance between stocks $i$ and $j$ can be determined using Equation (25):

$$\begin{array}{cc}{\sigma }_{ij}\hfill & =E\left[\left(r_{it}-{\mu }_{it}\right)\left(r_{jt}-{\mu }_{jt}\right)\right]\hfill \\ & ={\rho }_{ij}{\sigma }_{it}{\sigma }_{jt}; i\ne j.\hfill \end{array}$$

(25)

The covariance of the portfolio returns can be expressed in matrix form, incorporating an identity matrix, as shown in Equations (26) and (27):

$$\mathbf{\Sigma }=\left(\begin{array}{cccc}{\sigma }_{11}^2& {\sigma }_{12}& \dots & {\sigma }_{1n}\\ {\sigma }_{21}& {\sigma }_{22}^2& \dots & {\sigma }_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ {\sigma }_{n1}& {\sigma }_{n2}& \dots & {\sigma }_{nn}^2\end{array}\right),$$

(26)

and

$$\mathbf{I}=\left(\begin{array}{cccc}1& 0& \dots & 0\\ 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & 1\end{array}\right).$$

(27)

2.8. Portfolio Optimization Mean-VaR Model

The value at risk (VaR) model is a statistical method for measuring potential losses in an investment with a specified confidence level and over a given time horizon [36]. In other words, it is used to determine the minimum level of potential loss at a certain confidence level.

According to Sukono et al. [37], a normal distribution approach can be used to calculate the value at risk with a weight vector $w$, as shown in Equation (28):

$$Va{R}_{pt}=-W_0\left({\mu }_{pt}+z_{\alpha }{\sigma }_{pt}\right),$$

(28)

or

$$Va{R}_{pt}=-W_0\left({\mathbf{w}}^{\mathrm{T}}\mathit{\mu }+z_{\alpha }{\left({\mathbf{w}}^T\sum \mathbf{w}\right)}^{{\displaystyle \frac{1}{2}}}\right),$$

(29)

where $W_0$ represents the initial weight, and $z_{\alpha }$ is the percentile of the distribution $(\alpha =0.05)$.

The multitude of potential portfolios that can be formed from the available risky assets in the market presents a challenge for investors. Since the number of possible combinations is theoretically infinite, selecting an optimal portfolio becomes a significant challenge for investors. Typically, investors aim to choose an optimal portfolio [38].

When the risk level is measured using the value at risk, the solution sought for the optimization problem becomes:

$$\mathrm{maximize}\left\{2\tau {\mu }_{pt}-Va{R}_{pt}\right\}.$$

(30)

$$\mathrm{Subject} \mathrm{to}, {\sum }_{i=1}^N{w}_i=1,$$

Using the constraint ${\mathbf{e}}^T\mathbf{w}=1$, vector Equations (23) and (29), with the assumption that $W_0=1$ unit, the optimization problem in Equation (30) can be rewritten as follows:

$$\begin{array}{c}\mathrm{maximize}\left\{2\tau {\mathsf{\mu }}^T\mathbf{w}+\left({\mathsf{\mu }}^T\mathbf{w}+z_{\alpha }{\left({\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}\right)}^{{\displaystyle \frac{1}{2}}}\right)\right\},\\ \mathrm{subject} \mathrm{to}, {\mathbf{e}}^T\mathbf{w}=1.\end{array}$$

(31)

The mean variance model, introduced by Markowitz, uses the variance or standard deviation as a measure of the portfolio risk. This approach assumes that the asset returns follow a normal distribution, making it more suitable for investors who focus on symmetric risk volatility. However, in practice, asset return distributions often exhibit non-normal characteristics, such as skewness and kurtosis, making this approach less accurate in addressing extreme risks [32].

In contrast, the mean-VaR model uses the value at risk (VaR) as the risk measure, specifically assessing the maximum loss at a given confidence level. The VaR is more appropriate for investors who want to understand the downside risks (worst-case losses) rather than the general volatility. In other words, the VaR provides a more realistic perspective in risk management, especially for portfolios exposed to significant risks under extreme market conditions.

The advantages of the mean-VaR model in risk management are as follows:

• Focus on downside risk: The VaR considers potential losses, offering a more relevant tool for conservative risk management.
• Adaptability to non-normal markets: This model is more flexible in handling asset return distributions that are asymmetric or non-normal.
• Application in financial regulation: The VaR is widely used by financial institutions and regulators as a standard for measuring portfolio risk exposure.

Reasons for Choosing the Mean-VaR Model

In this study, the mean-VaR model was chosen because it provides a more comprehensive framework for measuring and optimizing the portfolio risk in real-world scenarios. By using this approach, this research offers a more accurate solution for investors facing downside risks, which are often a primary concern, particularly in high-risk assets such as banking stocks.

It is essential to evaluate the portfolio performance to increase the likelihood of achieving investment objectives. Portfolio performance measurement can be conducted either before or after making investment decisions [25]. In uncertain conditions, investors can only consider the level of return offered while accounting for risk factors. Therefore, the performance of an investment portfolio is measured based on the return and risk variables.

When the portfolio risk is measured using the value at risk (VaR) ratio, the RVaR metric represents the ratio of the portfolio’s risk premium to its value at risk (VaR). Mathematically, the RVaR is expressed as follows:

$$RVaR={\displaystyle \frac{{\mu }_{pt}-{\mu }_f}{Va{R}_{pt}}},$$

(32)

where ${\mu }_{pt}$ is the average return of portfolio $p$ at time $t$, ${\mu }_f$ is the average return of the risk-free asset, and $Va{R}_{pt}$ represents the portfolio’s value at risk $p$ at time $t$. The highest value of the RVaR ratio determines the portfolio performance.

2.9. Integration of Reinforcement Learning and Generative Approaches in Portfolio Optimization

2.9.1. Relevance of Reinforcement Learning in Investment Portfolios

Research by Jiang et al. (2017) introduced a reinforcement learning (RL)-based framework designed to manage financial portfolios optimally without relying on traditional economic models [39]. This approach leverages deep neural networks such as the CNN, RNN, and LSTM to predict and evaluate portfolio weight adjustments continuously. Its focus on the cryptocurrency market highlights RL’s ability to handle high volatility and non-linear market environments. The framework demonstrated significant returns despite the high transaction costs.

However, a major challenge in RL implementation lies in its reliance on historical market data, which can introduce bias if the data fail to accurately represent current market conditions. Furthermore, RL algorithms often require extensive training time to achieve convergence.

The integration of this concept into portfolio optimization highlights the need to address these challenges, particularly in ensuring that the algorithms adapt to rapidly changing market dynamics. Exploring reinforcement learning can significantly enhance the ability to optimize financial decisions dynamically.

2.9.2. The Role of Generative Models in Investment Portfolios

Cheng and Chen (2023) proposed an alternative framework based on generative models for portfolio construction. This framework applies multi-armed bandit techniques to combine portfolio strategies, including probabilistic approaches and blending methods. The findings showed that strategies incorporating generative copula-based models with objective functions like the Sharpe ratio outperformed individual portfolio strategies. This is particularly relevant in cryptocurrency markets, where the high asset correlations and unstable covariance matrices often pose challenges [40].

Generative models excel in accommodating diverse market conditions through simulations based on historical data and probabilistic parameterization. Moreover, they enhance risk mitigation compared to traditional methods by accurately processing multivariate distributions. Integrating this approach into portfolio management underscores its potential to provide more robust and flexible optimization strategies.

2.9.3. Integration in the Context of Current Research

This concept aligns closely with portfolio optimization using PSO and the mean-VaR model. The RL framework can refine PSO parameterization by incorporating reward mechanisms based on portfolio returns, while generative models can support risk estimation in the mean-VaR framework.

Combining RL and generative methods creates a hybrid approach that addresses market volatility and the limitations of relying solely on historical data. By utilizing RL for dynamic decision-making and generative models for precise risk distribution estimation, portfolio strategies can become more adaptive and resilient. This integration reflects a modernized approach to balancing return maximization and risk management, particularly in environments prone to sudden changes.

3. Materials and Method

3.1. Materials

The focal point of this research is the development and application of computational algorithms aimed at optimizing investment portfolio selection through the mean-value-at-risk (MVaR) model. This study addresses the challenge of creating a practical computational approach regarding the processing speed, accuracy, and reliability when generating optimal portfolios. By focusing on global optima, the proposed algorithm seeks to enhance portfolio performance by balancing the potential returns against the associated risks in a structured manner, thereby offering a robust solution to the complex problem of portfolio optimization.

The empirical data utilized in this study consist of the daily closing prices of stocks from companies in Indonesia’s banking sector. The selection of this dataset is intended to provide a comprehensive view of stock performance within a key economic industry, reflecting both the volatility and the return potential unique to banking stocks in emerging markets. The data were sourced from www.finance.yahoo.com, with data collection commencing on 1 August 2024 to ensure a complete and up-to-date dataset for analysis. For analytical consistency, the data utilized in the optimization span from 1 August 2022 to 1 July 2024, offering a two-year window for studying market trends, seasonal effects, and volatility patterns that may impact portfolio decisions.

3.2. Method

3.2.1. Research Method

The research method employed in this study is a quantitative approach, emphasizing numerical analysis through the application of mathematical and statistical techniques. This research aims to develop a computational algorithm based on particle swarm optimization (PSO) for global portfolio optimization using the mean-value-at-risk (mean-VaR) model.

The research method includes the following steps:

• Data Collection
  Daily closing price data of banking sector stocks are obtained from reliable sources. These data are then processed to calculate the stock returns, the variances, and the covariance matrix, which will be used in the mean-VaR model.
• Mean-Value-at-Risk (Mean-VaR) Modelling
  The mean-VaR objective function is formulated using a vector- and matrix-based approach. This model aims to minimize the VaR risk while maximizing the portfolio returns, referring to the distribution parameters of the stock return data.
• Development of the PSO Algorithm
  The PSO algorithm is employed as a heuristic method to find the optimal portfolio weights. Parameters such as the inertia weight, the learning constants (c1 and c2), and the number of particles are adjusted to achieve the optimal solution.
• Evaluation of the Algorithm and Optimal Portfolio
  The algorithm’s results are evaluated based on the speed, accuracy, and consistency. The performance of the optimal portfolio is measured using financial metrics such as the expected return, the volatility, and the Sharpe ratio.

This method provides a systematic foundation for producing optimal, data-driven investment decisions.

3.2.2. Research Flow

The research flow is divided into three systematic main stages to achieve the research objectives: developing the PSO algorithm, applying the PSO algorithm using banking sector data, and evaluating the PSO algorithm’s results. The steps for each stage are as follows:

• Stage 1: Developing the PSO Algorithm for Global Portfolio Optimization

The first stage involves developing a PSO-based computational algorithm to determine global portfolio optimization for banking sector stocks. The steps are as follows:

• Identify Key Variables for the Computational Algorithm
  Determine the variables used in the algorithm, such as the mean vector $\left(\mathsf{\mu }\right)$, unit vector $\left(\mathbf{e}\right)$, and covariance matrix.
• Formulate the Objective Function Using the Mean-VaR Model
  The objective function for the mean-VaR model is formulated using vector- and matrix-based equations to optimize the portfolio returns with controlled risk.
• Develop the Heuristic PSO Algorithm
  The PSO algorithm is developed to find the optimal solution for the portfolio. This step includes adjusting the PSO parameters, such as the inertia weight $\left(w\right)$, the learning constants $(c_1, c_2)$, and the number of particles.
• The Mean-VaR
  Implement the Algorithm to Determine the Global Portfolio Optimization

The PSO algorithm is implemented to find the optimal portfolio weights that minimize the VaR risk and maximize the desired returns.

• Stage 2: Applying the PSO Algorithm Using Banking Sector Data

In the second stage, the developed PSO algorithm is applied using banking sector stock data to determine the portfolio optimization. The steps are as follows:

• Input Daily Closing Price Data of Stocks
  The daily closing price data of banking sector stocks collected earlier are input into the algorithm to calculate the stock returns.
• Calculate Stock Return Values
  The stock returns are calculated based on the daily closing price data obtained, using the appropriate formula (e.g., log-return).
• Test the Distribution Model for Stock Return
  The stock return distribution model is tested using a histogram, and the distribution parameters are calculated. A goodness-of-fit test is conducted to ensure the distribution aligns with the data. Stocks that do not meet the distribution criteria are excluded from the analysis.
• Calculate Expected Return, Variance, and Covariance
  The expected return, variance, and covariance of the selected banking sector stocks are calculated.
• Implement the Computational Algorithm for Portfolio Optimization
  The developed PSO algorithm is applied to find the optimal portfolio weights that minimize the risk and maximize the returns for the selected banking sector stocks.
• Measure the Performance of the Optimal Portfolio
  The portfolio performance is measured using the return levels, the volatility, and the Sharpe ratio to evaluate the efficiency of the generated portfolio.

• Stage 3: Evaluating the Results of the PSO Algorithm

The final stage involves evaluating the results of the implemented PSO algorithm. In this stage, the PSO algorithm’s performance is measured based on its speed, accuracy, and consistency in generating an optimal portfolio. The steps are as follows:

• Input Stock Data
  Banking sector stock data are input into the existing program to determine the optimal portfolio using the mean-VaR approach.
• Experiment with the Developed PSO Algorithm
  Two experiments are conducted to evaluate the algorithm’s performance:
  • Experiment 1: The PSO algorithm is tested by conducting 50 trials to assess the consistency of its results. This experiment aims to ensure the algorithm reliably converges to a similar optimal solution across multiple runs.
  • Experiment 2: The impact of different parameter settings for the PSO algorithm is investigated. Several values of key parameters, such as the cognitive coefficient $\left(c_1\right)$, social coefficient $\left(c_2\right)$, and inertia weight $\left(w\right)$, are tested to observe how they affect the optimization process and the quality of the portfolio generated.
• Analyze Performance Results
  The experimental results are evaluated based on three main metrics: speed, accuracy, and consistency. Insights from the two experiments are analyzed to identify the best parameter settings and ensure reliable algorithm performance. If any weaknesses are identified, improvements will be made to enhance the algorithm’s efficiency and effectiveness.

4. Results

4.1. PSO Algorithm in Determining the Optimal Portfolio Weight Based on the Mean-VaR Model

In determining the optimal portfolio weights based on the mean-VaR model, the particle swarm optimization (PSO) algorithm offers a population-based approach capable of exploring solutions globally, making it suitable for application in portfolio investment contexts requiring asset weight optimization.

To understand how PSO functions in searching for optimal solutions in portfolio optimization problems, one can start by manually simulating its process. A manual simulation illustrates the essential workings of the PSO algorithm, in which particles are randomly initialized and subsequently move toward the optimal solution based on velocities and positions updated iteratively. This manual simulation provides insights into the mechanisms behind the PSO algorithm in determining the optimal portfolio weights, as demonstrated in Algorithm 2.

Algorithm 2. PSO algorithm for determining the global optima of the investment portfolio weight using the mean-value-at-risk model

Parameter initialization 1.1. Initialize PSO parameters - Number of particles (NW) - Maximum iteration (Imax) - Inertia (w) - Cognitive coefficient (c1) - Social coefficient (c2) - Initial tolerance value, τ = 0 1.2. Initialize parameters in the optimization problem - Mean vector (μ) - Covariance matrix $\left(\mathbf{\Sigma }\right)$ - Unit vector (e) - Distribution percentile value $\left(z_{\alpha }\right)$ 1.3. Calculate the inverse of matrix $\mathbf{\Sigma }$, denoted as ${\mathbf{\Sigma }}^{\mathbf{-}\mathbf{1}}$ 1.4. Define the objective function as a combination of the return, risk, and constraints Looping for τ values 2.1. For$(\tau =0;\tau <1.6;\tau =\tau +0.05):$ - Calculate λ using the quadratic equation: $$\left({\mathbf{e}}^T{\mathbf{\Sigma }}^{-1}\mathbf{e}\right){\lambda }^2+\left(\left(2\tau +1\right)\left({\mathbf{e}}^T{\mathbf{\Sigma }}^{-1}\mathsf{\mu }+{\mathsf{\mu }}^T{\mathbf{\Sigma }}^{-1}\mathbf{e}\right)\right)\lambda +\left({\left(2\tau +1\right)}^2{\mathsf{\mu }}^T{\mathbf{\Sigma }}^{-1}\mathsf{\mu }-z_{\alpha }^2\right)=0,$$ From this equation, obtain: $$\begin{array}{c}a:={\mathbf{e}}^T{\mathbf{\Sigma }}^{-1}\mathbf{e}\\ b:=\left(2\tau +1\right)\left({\mathbf{e}}^T{\mathbf{\Sigma }}^{-1}\mathsf{\mu }+{\mathsf{\mu }}^T{\mathbf{\Sigma }}^{-1}\mathbf{e}\right)\\ c:={\left(2\tau +1\right)}^2{\mathsf{\mu }}^T{\mathbf{\Sigma }}^{-1}\mathsf{\mu }-z_{\alpha }^2\end{array}$$ - If $(b^2-4ac<0): \mathit{set} \lambda :=0$ 2.1.1. PSO initialization - Initialize the particle position $${\mathbf{w}}_{\mathit{i}}\left(0\right)={\left[r_{{\mathbf{w}}_i}^{\left(1\right)},r_{{\mathbf{w}}_{\mathbf{i}}}^{\left(2\right)},\dots ,r_{{\mathbf{w}}_i}^{\left(9\right)}\right]}^T$$ using random numbers with a Dirichlet distribution, $$r_{{\mathbf{w}}_i}^{\left(j\right)}, j=1,2,\dots ,9$$ - Initialize the particle velocity, $${\mathbf{v}}_{\mathit{i}}\left(0\right)={\left[r_{{\mathbf{v}}_i}^{\left(1\right)},r_{{\mathbf{v}}_{\mathbf{i}}}^{\left(2\right)},\dots ,r_{{\mathbf{v}}_i}^{\left(9\right)}\right]}^T$$ using random numbers with a uniform distribution, $$r_{{\mathbf{v}}_i}^{\left(j\right)}, j=1,2,\dots ,9$$ 2.1.2. Calculate and evaluate the objective function 2.1.2.1. For $(i=1$; $i<N_{\mathbf{W}}$; $i=i+1$): calculate, $$f\left({\mathbf{w}}_{\mathrm{i}}\left(0\right)\right)=\left(2\tau +1\right){\mathsf{\mu }}^T{\mathbf{w}}_{\mathrm{i}}(0)+z_{\alpha }{\left({\mathbf{w}}_{\mathrm{i}}{\left(0\right)}^{\mathit{T}}\mathbf{\Sigma }{\mathbf{w}}_{\mathrm{i}}\left(0\right)\right)}^{{\displaystyle \frac{1}{2}}}+\lambda \left({\mathbf{w}}_{\mathrm{i}}{\left(0\right)}^{\mathit{T}}\mathbf{e}-1\right)$$ 2.1.2.2. Set the personal best position (pbest) $$pbest={\left[{\mathbf{w}}_1\left(0\right),{\mathbf{w}}_2\left(0\right),\dots ,{\mathbf{w}}_{N_{\mathbf{W}}}\left(0\right)\right]}^{\mathit{T}}$$ 2.1.2.3. Set the global best position (gbest) $$gbest={\mathbf{w}}_{\mathrm{best}}, \mathrm{where},$$ $${\mathbf{w}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}=\mathit{arg}\underset{{\mathbf{w}}_{\mathbf{i}} }{\max }\left\{f\left({\mathit{w}}_1\left(0\right)\right),f\left({\mathit{w}}_2\left(0\right)\right),\dots ,f\left({\mathit{w}}_{N_{\mathbf{W}}}\left(0\right)\right)\right\}$$ 2.1.2.4. Set the global best score (Gbest) $$Gbest=f\left({\mathbf{w}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}\right)$$ 2.1.3. Update the velocity and position of particles Initialize: $condition1=False, iter=1$ While $\left(condition1==False \mathit{o}\mathit{r} iter<I_{max}\right)$ - Generate random number $r_1,r_2\in \left(0,1\right)$ 2.1.3.1. For $(i=1; i<N_{\mathbf{W}}$; $i=i+1$): - Update the particle velocity, $${\mathbf{v}}_{\mathbf{i}}\left(iter\right)=w{\mathbf{v}}_{\mathbf{i}}\left(iter-1\right)+c_1{r}_1\left(pbes{t}_i-{\mathbf{w}}_{\mathbf{i}}\left(iter-1\right)\right)+c_2{r}_2\left(gbest-{\mathbf{w}}_{\mathbf{i}}\left(iter-1\right)\right)$$ - Update the particle position, $${\mathbf{w}}_{\mathbf{i}}\left(iter\right)={\mathbf{v}}_{\mathbf{i}}\left(iter\right)+{\mathbf{w}}_{\mathbf{i}}\left(iter-1\right)$$ - Define ${\mathbf{w}}_{\mathbf{i}}\left(iter\right):={\mathbf{w}}_{\mathbf{i}}\left(iter\right)\times {\displaystyle \frac{1}{Tota{l}_{{\mathbf{w}}_{\mathbf{i}}\left(iter\right)}}}$ - Update the pbest value and position If $\left({\mathbf{w}}_{\mathbf{i}}\left(iter\right)\right)>f\left(pbes{t}_i\right)$; $pbes{t}_i:={\mathbf{w}}_{\mathbf{i}}\left(iter\right)$; - Update the gbest position and Gbest value $$gbest\left(iter\right):={\mathbf{w}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}$$ where $${\mathbf{w}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}=\mathit{arg}\underset{{\mathit{pbest}}_{\mathbf{i}} }{\max }\left\{f\left(pbes{t}_1\right),f\left(pbes{t}_2\right),\dots ,f\left(pbes{t}_{N_{\mathbf{w}}}\right)\right\}$$ $$Gbest\left(iter\right):=f\left({\mathbf{w}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}\right)$$ 2.1.3.2. If $\left|Gbest\right(iter)-Gbest(iter-1\left)\right|\le {10}^{-16}$ - $condition1=True$ - Calculate the portfolio expected return $\left({\mu }_{pt}\right)$ $${\mu }_{pt}={\mathbf{w}}^T\mathsf{\mu }$$ - Calculate the portfolio risk $\left({\sigma }_{pt}\right)$ $${\sigma }_{pt}=\sqrt{{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}}$$ where $\mathbf{w}=gbest$ - Calculate the value at risk $\left(Va{R}_{pt}\right)$ $$Va{R}_{pt}=-W_0\left({\mu }_{pt}+z_{\alpha }{\sigma }_{pt}\right)$$ $\mathrm{with} W_0=1$ - Calculate the portfolio performance (ratio) $$ratio={\displaystyle \frac{{\mu }_{pt}}{Va{R}_{pt}}}$$ - Save the iteration results into a results list (iteration_results) 2.1.3.3. Update the iteration, iter = iter + 1 Output 3.1 Convert the iteration results list into a DataFrame 3.2 Display the iteration results DataFrame 3.3 Export the DataFrame to a .csv file

4.2. Application of the PSO Algorithm Using Banking Sector Stock Data

4.2.1. Banking Sector Stock Data

The data analyzed in this study consist of closing stock prices obtained from the website www.finance.yahoo.com. These data were accessed from 1 August 2022 to 30 July 2024. From this source, 33 stocks classified under the banking sector were retrieved. The list of analyzed stocks is presented in Appendix A.

Figure 2 displays the closing price movement of BBCA stock. Overall, the stock price shows a stable upward trend despite some fluctuations. These fluctuations at specific points reflect typical market volatility, possibly caused by changes in economic conditions, monetary policies, or internal company factors. The dotted trend line illustrates a general tendency of positive price movement, although temporary declines occasionally occur. This chart suggests that BBCA stock offers good long-term growth potential, yet caution is necessary due to the risk of short-term fluctuations.

4.2.2. Calculating Stock Return

The daily stock returns are calculated using Equation (8). For example, the return calculation for BBCA stock on 2 August 2022 is as follows:

$$r_t=\ln \left({\displaystyle \frac{P_t}{P_{t-1}}}\right)=\ln \left({\displaystyle \frac{7600}{7500}}\right)=\ln \left(1.01333\right)=0.01324.$$

The daily return calculations for BBCA stock can be performed using the data in

Table 1. BBCA stock return.

Date	Close Price	Return
8/1/2022	7500	-
8/2/2022	7600	0.01324
8/3/2022	7625	0.00328
⋮	⋮	⋮
7/29/2024	10,250	−0.00729
7/30/2024	10,175	−0.00734

.

Return calculations are conducted for all the banking stocks used in this study.

Figure 3 shows the daily return chart for BBCA stock over the specified period. This chart illustrates the volatility of the returns fluctuating over time. It reveals periods of high volatility with significant positive and negative spikes. At specific points, the stock return experiences sharp increases, reflecting positive momentum in BBCA’s stock price, while other points display sharp declines, indicating intense selling pressure affecting the stock price.

This fluctuation pattern suggests that BBCA stock undergoes dynamic price movements, reflecting both risks and potential returns for investors. This chart is essential in analyzing the stock risk and return, particularly for determining the optimal strategies for portfolio management.

4.2.3. Fitting and Testing the Stock Return Distribution Model

Next, by using histogram charts of the daily return data for each banking stock, we can determine the distribution model assumption for each stock.

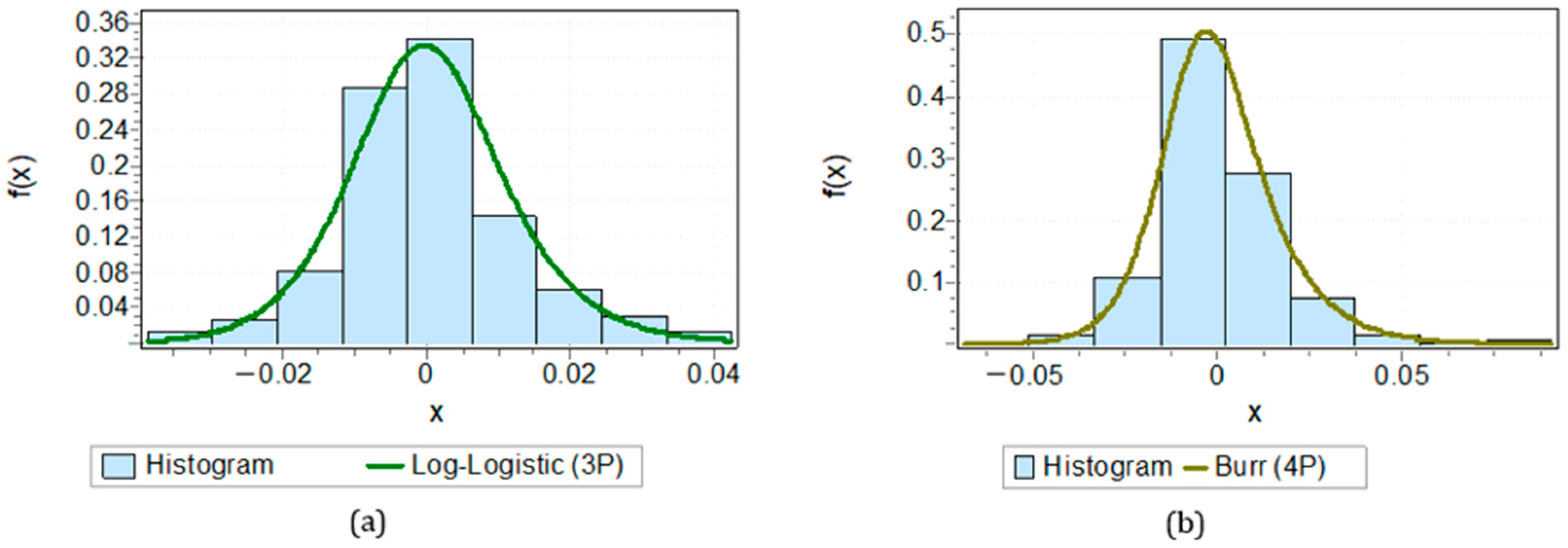
Based on the histogram visualization results, each daily stock return data point approximates a specific distribution model. For example, in Figure 4a, the histogram of BBCA’s stock return chart displays a symmetrical pattern, with most data concentrated around the central value and long tails on both sides, characteristic of the log-logistic distribution.

Meanwhile, in Figure 4b, the histogram of BBTN’s daily return chart shows a symmetric distribution pattern around zero, with most observations concentrated at the center value. This aligns with the characteristics of the Burr distribution, which can model data with a sharp peak and broader tails.

Next, the parameter estimation process for maximizing the values for each stock’s distribution model is performed using the maximum likelihood estimation (MLE) by substituting the probability density function of each distribution model into the likelihood function. For the log-logistic distribution model, the parameter estimation is conducted using the maximum likelihood estimation (MLE). For example, the parameter estimation for BBCA stock is carried out by substituting the log-logistic distribution’s probability density function in Equation (16) into the likelihood function, resulting in:

$$\begin{array}{cc}L\left(x|\alpha ,\beta ,\gamma \right)\hfill & =\ln {\displaystyle \prod _{i=1}^n}{\displaystyle \frac{\alpha }{\beta }}{\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha -1}{\left(1+{\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha }\right)}^{-2},\hfill \\ & ={\displaystyle \sum _{i=1}^n}\ln \left({\displaystyle \frac{\alpha }{\beta }}\right)+\left(\alpha -1\right)\ln \left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)-2\ln \left[1+{\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha }\right].\hfill \end{array}$$

To ensure the results of each maximum parameter, the first derivative of the log-likelihood function must equal zero for each parameter. The first derivatives concerning each parameter are provided as follows:

• Derivative for $\alpha$

  $${\displaystyle \frac{\partial \left(\ln L\left(x|\alpha ,\beta ,\gamma \right)\right)}{\partial \alpha }}=0,$$

  $$\sum _{i=1}^n{\displaystyle \frac{1}{\alpha }}+\ln \left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)-2\left({\displaystyle \frac{1}{1+{\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }}}\right){\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha }\ln \left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)=0.$$
• Derivative for $\beta$

  $${\displaystyle \frac{\partial \left(\ln L\left(x|\alpha ,\beta ,\gamma \right)\right)}{\partial \beta }}=0,$$

  $$\sum _{i=1}^n-{\displaystyle \frac{1}{\beta }}-{\displaystyle \frac{\left(\alpha -1\right)}{\beta }}+{\displaystyle \frac{2\alpha }{\beta }}\left({\displaystyle \frac{{\left(\frac{\left(x_i-\gamma \right)}{\beta }\right)}^{\alpha }}{1+{\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }}}\right)=0.$$
• Derivative for $\gamma$

  $${\displaystyle \frac{\partial \left(\ln L\left(x|\alpha ,\beta ,\gamma \right)\right)}{\partial \gamma }}=0,$$

  $$\sum _{i=1}^n-{\displaystyle \frac{\left(\alpha -1\right)}{\left(x_i-\gamma \right)}}+{\displaystyle \frac{2\alpha }{\left(x_i-\gamma \right)}}\left({\displaystyle \frac{{\left(\frac{x_i-\gamma }{{\beta }^{\alpha }}\right)}^{\alpha }}{1+{\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }}}\right)=0.$$

Meanwhile, for the parameter estimation in the Burr (4P) distribution model for BBTN stock, the probability density function of the Burr distribution is substituted into Equation (12) for the likelihood function, yielding:

$$\begin{array}{ll}L\left(x|k,\alpha ,\beta ,\gamma \right)& =\ln {\displaystyle \prod _{i=1}^n}{\displaystyle \frac{ak{\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha -1}}{\beta {\left(1+{\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }\right)}^{k+1} }},\\ & =\ln {\displaystyle \prod _{i=1}^n}{\displaystyle \frac{ak}{\beta }}{{\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha -1}\left(1+{\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha }\right)}^{1-k},\\ & ={\displaystyle \sum _{i=1}^n}\ln \left({\displaystyle \frac{\alpha k}{\beta }}\right)+\left(\alpha -1\right)\ln \left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)+(1-k)\ln \left[1+{\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha }\right].\end{array}$$

To ensure the maximum result for each parameter, the first derivative of the log-likelihood function must be equal to zero for each parameter. The first derivatives concerning each parameter are given as follows:

• Derivative for $k$

  $${\displaystyle \frac{\partial \left(\ln L\left(x|k,\alpha ,\beta ,\gamma \right)\right)}{\partial k}}=0,$$

  $$\sum _{i=1}^n{\displaystyle \frac{1}{k}}-\ln \left({\left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)}^{\alpha }+1\right)=0.$$
• Derivative for $\alpha$

  $${\displaystyle \frac{\partial \left(\ln L\left(x|k,\alpha ,\beta ,\gamma \right)\right)}{\partial \alpha }}=0,$$

  $$\sum _{i=1}^n{\displaystyle \frac{1}{\alpha }}+{\displaystyle \frac{\left(1-k\right)\ln \left(\frac{x_i-\gamma }{\beta }\right){\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }}{{\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }+1}}+\ln \left({\displaystyle \frac{x_i-\gamma }{\beta }}\right)=0.$$
• Derivative for $\beta$

  $${\displaystyle \frac{\partial \left(\ln L\left(x|k,\alpha ,\beta ,\gamma \right)\right)}{\partial \beta }}=0,$$

  $$\sum _{i=1}^n-{\displaystyle \frac{1}{\beta }}-{\displaystyle \frac{\left(\alpha -1\right)}{\beta }}-{\displaystyle \frac{\left(1-k\right)\alpha {\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }}{\left({\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }+1\right)\beta }}=0.$$
• Derivative for $\gamma$

  $${\displaystyle \frac{\partial \left(\ln L\left(x|k,\alpha ,\beta ,\gamma \right)\right)}{\partial \gamma }}=0,$$

  $$\sum _{i=1}^n-{\displaystyle \frac{\left(\alpha -1\right)}{x_i-\gamma }}-{\displaystyle \frac{\left(1-k\right)\alpha {\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }}{\left({\left(\frac{x_i-\gamma }{\beta }\right)}^{\alpha }+1\right)(x_i-\gamma )}}=0.$$

The first derivatives for $k$, $\alpha$, $\beta$, and $\gamma$ do not yield direct values for the parameter estimation. Therefore, the parameter estimation is performed using EasyFit 5.6 software. The estimated parameter values are shown in Appendix B.

After obtaining the parameter values, the next step is to conduct a distribution test using the Anderson–Darling (AD) method. The hypotheses used for distribution testing are as follows:

H₀. 

Stock returns follow the assumed distribution model.

H₁. 

Stock returns do not follow the assumed distribution model.

The criteria for the hypothesis testing state that ${\mathrm{H}}_0$ is accepted if a stock meets the requirement, i.e., the test statistic $A^2$ value $<$ the critical table value $\left(3.9074\right)$. Conversely, if none of the distribution tests meet this requirement (test statistic > table value), for example, using EasyFit, the following test results were obtained for BBCA stock: an AD test statistic of 0.93494 with a table value of 3.9074 at a significance level $\alpha =0.01$. Based on these results, it can be seen that for all three distribution tests, BBCA stock meets the requirement test statistic $<$ table value, confirming that BBCA stock follows a log-logistic distribution.

From the distribution model testing results, 14 out of 33 stocks met the test criteria, i.e., test statistic $<$ table value, so ${\mathrm{H}}_0$ is accepted. These 14 stocks are thus candidates for inclusion in the stock portfolio selection, as they have been verified to follow a specific distribution, either the Burr (4P) or log-logistic distribution.

4.2.4. Determining the Mean Vector, Unit Vector, and Covariance Matrix Among Selected Stock Returns

The expected return for each stock can be calculated by utilizing the stock returns using the formulas in Equations (14) and (18). Meanwhile, the formulas in Equations (15) and (19) are used to estimate the variance for each stock. The expected return and variance calculations for each stock are adjusted according to their respective distribution models. For example, for BBCA stock with a log-logistic distribution, the expected return is obtained as follows:

• Log-logistic expected return

  $$\begin{array}{cc}E\left(X\right)\hfill & =\gamma +\beta \mathrm{B}\left(1+{\displaystyle \frac{1}{\alpha }},1-{\displaystyle \frac{1}{\alpha }}\right),\hfill \\ & =\left(-0.19579\right)+\left(0.19599\right)B\left(1+{\displaystyle \frac{1}{29.145}},1-{\displaystyle \frac{1}{29.145}}\right)\hfill \\ & =0.00058.\hfill \end{array}$$

  and the variance of return for the log-logistic distribution can be calculated as:

  $$\begin{array}{cc}E\left[X^2\right]-{\left(E\left[X\right]\right)}^2\hfill & ={\beta }^2 \left[B\left(1+{\displaystyle \frac{2}{\alpha }},1-{\displaystyle \frac{2}{\alpha }}\right)-B^2\left(1+{\displaystyle \frac{1}{\alpha }},1-{\displaystyle \frac{1}{\alpha }}\right)\right],\hfill \\ & ={\left(0.19599\right)}^2\left[B\left(1+{\displaystyle \frac{2}{29.145}},1-{\displaystyle \frac{2}{29.145}}\right)-B^2\left(1+{\displaystyle \frac{1}{29.145}},1-{\displaystyle \frac{1}{29.145}}\right)\right],\hfill \\ & =0.000150.\hfill \end{array}$$
  For the BBTN stock, which follows the Burr (4P) distribution, the following is obtained:
• The expected return for the Burr (4P) distribution

  $$\begin{array}{cc}E\left(X\right)\hfill & =\gamma +k\beta B\left(1+{\displaystyle \frac{1}{\alpha }},k-{\displaystyle \frac{1}{\alpha }}\right),\hfill \\ & =\left(-2.5887\right)+\left(0.60647\right)\left(2.582\right) B\left(1+{\displaystyle \frac{1}{353.49}},0.60647-{\displaystyle \frac{1}{353.49}}\right),\hfill \\ & =0.00023.\hfill \end{array}$$

  and the variance of return for the Burr (4P) distribution can be calculated as:

  $$\begin{array}{cc}E\left[X^2\right]-{\left(E\left[X\right]\right)}^2\hfill & =k{\beta }^2 B\left(1+{\displaystyle \frac{2}{\alpha }},k-{\displaystyle \frac{2}{\alpha }}\right)-k^2{\beta }^2 B^2\left(1+{\displaystyle \frac{1}{\alpha }},k-{\displaystyle \frac{1}{\alpha }}\right),\hfill \\ & =\left(0.60647 \right){\left(2.582\right)}^2 B\left(\left(1+{\displaystyle \frac{2}{353.49}}\right),\left(0.60647-{\displaystyle \frac{2}{353.49}}\right)\right)\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\left(0.60647\right)}^2{\left(2.582\right)}^2 B^2\left(1+{\displaystyle \frac{1}{353.49}},0.60647-{\displaystyle \frac{1}{353.49}}\right),\hfill \\ & =0.00028.\hfill \end{array}$$
  The results of the expected return and variance calculations for each stock are presented in

  Table 2. Expected returns and variance of returns for the banking sector stocks that meet the distribution model assumptions.

  Stock	Expected Return	Varian Return	Stock	Expected Return	Varian Return
  BBCA	$5.80\times {10}^{-4}$	$1.50\times {10}^{-4}$	BRIS	$5.04\times {10}^{-4}$	$5.22\times {10}^{-4}$
  BBNI	$5.18\times {10}^{-4}$	$4.31\times {10}^{-4}$	NISP	$0.00131$	$2.40\times {10}^{-4}$
  BBRI	$2.97\times {10}^{-4}$	$3.78\times {10}^{-4}$	PNBN	$-7.11\times {10}^{-4}$	$7.21\times {10}^{-4}$
  BBTN	$2.30\times {10}^{-4}$	$2.81\times {10}^{-4}$	ARTO	$-0.00283$	$0.00174$
  BDMN	$1.60\times {10}^{-4}$	$2.10\times {10}^{-4}$	AGRO	$-0.00246$	$7.89\times {10}^{-4}$
  BMRI	$0.00126$	$8.05\times {10}^{-4}$	BBYB	$-0.00402$	$0.00148$
  BNGA	$7\times {10}^{-4}$	$1.81\times {10}^{-4}$	BANK	$-0.00116$	$8.48\times {10}^{-4}$

  .

Based on Table 2, nine stocks show a positive expected return, meaning they are projected to generate profits. For example, BBCA stock has an expected return of $5.80\times {10}^{-4}$, indicating potential profitability. On the other hand, five stocks show a negative expected return, meaning they are projected to incur losses.

The variance of the returns presented provides insight into the volatility or risk associated with each stock. A higher variance means more significant uncertainty regarding the actual return, while a lower variance indicates more stable and predictable returns.

Based on this, stocks with positive expected returns are selected as candidates for investment portfolio selection.

Table 3. Selected stocks.

Stock	Expected Return	Varian Return
BBCA	$5.80\times {10}^{-4}$	$1.50\times {10}^{-4}$
BBNI	$5.18\times {10}^{-4}$	$4.31\times {10}^{-4}$
BBRI	$2.97\times {10}^{-4}$	$3.78\times {10}^{-4}$
BBTN	$2.30\times {10}^{-4}$	$2.81\times {10}^{-4}$
BDMN	$1.60\times {10}^{-4}$	$2.10\times {10}^{-4}$
BMRI	$0.00126$	$8.05\times {10}^{-4}$
BNGA	$7\times {10}^{-4}$	$1.81\times {10}^{-4}$
BRIS	$5.04\times {10}^{-4}$	$5.22\times {10}^{-4}$
NISP	$0.00131$	$2.40\times {10}^{-4}$

shows the selected stocks.

Next, the covariance of the returns between stocks is calculated using Equation (24). The results of the covariance calculation between stock returns are presented in

Table 4. The covariance of the stock returns values.

	Covariance
Stock	BBCA	BBNI	BBRI	BBTN	BDMN	BMRI	BNGA	BRIS	NISP
BBCA	$0.000150$	$0.000076$	$0.000078$	$0.000068$	$0.000041$	$0.000090$	$0.000042$	$0.000042$	$0.000056$
BBNI	0.000076	0.000431	0.000122	0.000105	0.000067	0. 000134	0.000050	0.000097	0.000058
BBRI	0.000078	0.000122	0.000378	0.000109	0.000057	0.000110	0.000064	0.000099	0.000073
BBTN	0.000068	0.000105	0.000109	0.000281	0.000068	0.000092	0.000076	0.000107	0.000074
BDMN	0.000041	0.000067	0.000057	0.000068	0.000210	0.000062	0.000073	0.000063	0.000058
BMRI	0.000090	0.000134	0.000110	0.000092	0.000062	0.000805	0.000047	0.000091	0.000063
BNGA	0.000042	0.000050	0.000064	0.000076	0.000073	0.000047	0.000181	0.000055	0.000093
BRIS	0.000042	0.000097	0.000099	0.000107	0.000063	0.000091	0.000055	0.000522	0.000066
NISP	0.000056	0.000058	0.000073	0.000074	0.000058	0.000063	0.000093	0.000066	0.000240

.

Based on Table 4, it can be observed that the covariance of the returns between all the stocks is positive. Positive covariance values indicate that the two stocks tend to move in the same direction, meaning that when one stock experiences a return increase, the other stock also tends to rise. For example, the covariance between BBCA and BBNI is 0.000076, indicating a positive but relatively low relationship between the two stocks. This means that the two stocks tend to move together in a similar trend.

Forming the Vectors μ, e, and Σ

The vector $\mu$ is a vector with entries that represent the expected return values for each of the selected portfolio stocks, as presented in Table 3, and it is formed as shown in Equation (22). The vector $e$ is a vector with all the entries equal to one, and it is the same size as the vector $\mu$. The vectors $\mu$ and $e$ are defined as follows:

$$\mathsf{\mu }=\left[\begin{array}{c}0.0005844\\ 0.0005183\\ 0.0002974\\ 0.0001388\\ 0.0001603\\ 0.0012600\\ 0.0007985\\ 0.0005044\\ 0.0013100\end{array}\right], \mathbf{e}=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\end{array}\right]$$

Next, the calculated covariance values of the stock returns presented in Table 4 are formed as in Equation (25), referred to as the vector $\Sigma$. This vector can be seen in Appendix C.

4.2.5. Determining the Optimal Portfolio Weight Proportion Based on the Mean-VaR Model

The PSO algorithm is simulated for several values $\tau$, starting from zero and incrementally increasing until the algorithm stops at the last iteration when at least one stock weight is harmful to a particular value $\tau$. This simulation aims to find the optimal portfolio with positive stock weights, ensuring the portfolio is feasible for implementation. Furthermore, several calculations are performed to support the evaluation of the portfolio performance. The portfolio’s expected return $\left({\mu }_{pt}\right)$ is calculated using Equation (22), which measures the portfolio’s average return. Next, the portfolio volatility $\left({\sigma }_{pt}\right)$ is calculated using Equation (23), which represents the total risk associated with the portfolio. The portfolio risk is also assessed using the value at risk ($Va{R}_{pt}$), calculated using Equation (28), which estimates the maximum loss that may occur at a certain confidence level. Lastly, the portfolio performance is evaluated using the Sharpe ratio, derived from Equation (31), to assess the portfolio’s efficiency in generating returns relative to the risk taken. The complete results of the simulation and calculations can be found in Appendix D, which shows how variations $\tau$ affect the stock weights and overall portfolio performance. The optimal portfolio weights calculation results using the mean-VaR model and PSO can be found in Appendix D.

Appendix D presents the results of the portfolio stock weight optimization using the PSO method for various values $\tau$, representing different calculation scenarios in the optimization process. The first column displays the values of $\tau$ and the number of iterations, where each value of τ corresponds to a different iteration count in the PSO. In this study, the first simulation selected $\tau$ values in the range $0\le \tau \le 2$ with an increment of 0.1, and it stopped when at least one weight became negative for a specific value $\tau$. In this simulation, a negative weight for BBTN stock was found at $\tau =1.6$. The $\tau$ scale was then refined to determine the optimal solution. The second simulation was conducted with $\tau$ values in the range of $1.5\le \tau \le 1.6$, with an increment of 0.01. The trials continued this way until a precise value $\tau$ was obtained with four decimal places.

Based on the results in Appendix D, it can be seen that for a risk tolerance value of $\tau =0$, the portfolio’s average return $\left({\mu }_{pt}\right)$ is 0.00063, and the risk level $\left(Va{R}_{pt}\right)$ is 0.01447, as achieved after 331 iterations in the PSO algorithm. These values represent the minimum average return and $VaR$ of the portfolio. For a risk tolerance value of $\tau =1.5224$, the portfolio’s average return is 0.00074, with a risk level of 0.01463. These values correspond to the maximum average return and VaR of the portfolio. $\tau >1.5224$ Negative weights were found for the values of BBTN stock, such as the weight for BBTN stock is $-0.0008$ at $\tau =1.5225$, rendering it unsuitable for portfolio selection.

Overall, the values provided in Appendix D indicate that an increase in the risk tolerance value leads to an increase in the portfolio’s average return, accompanied by a rise in the risk level.

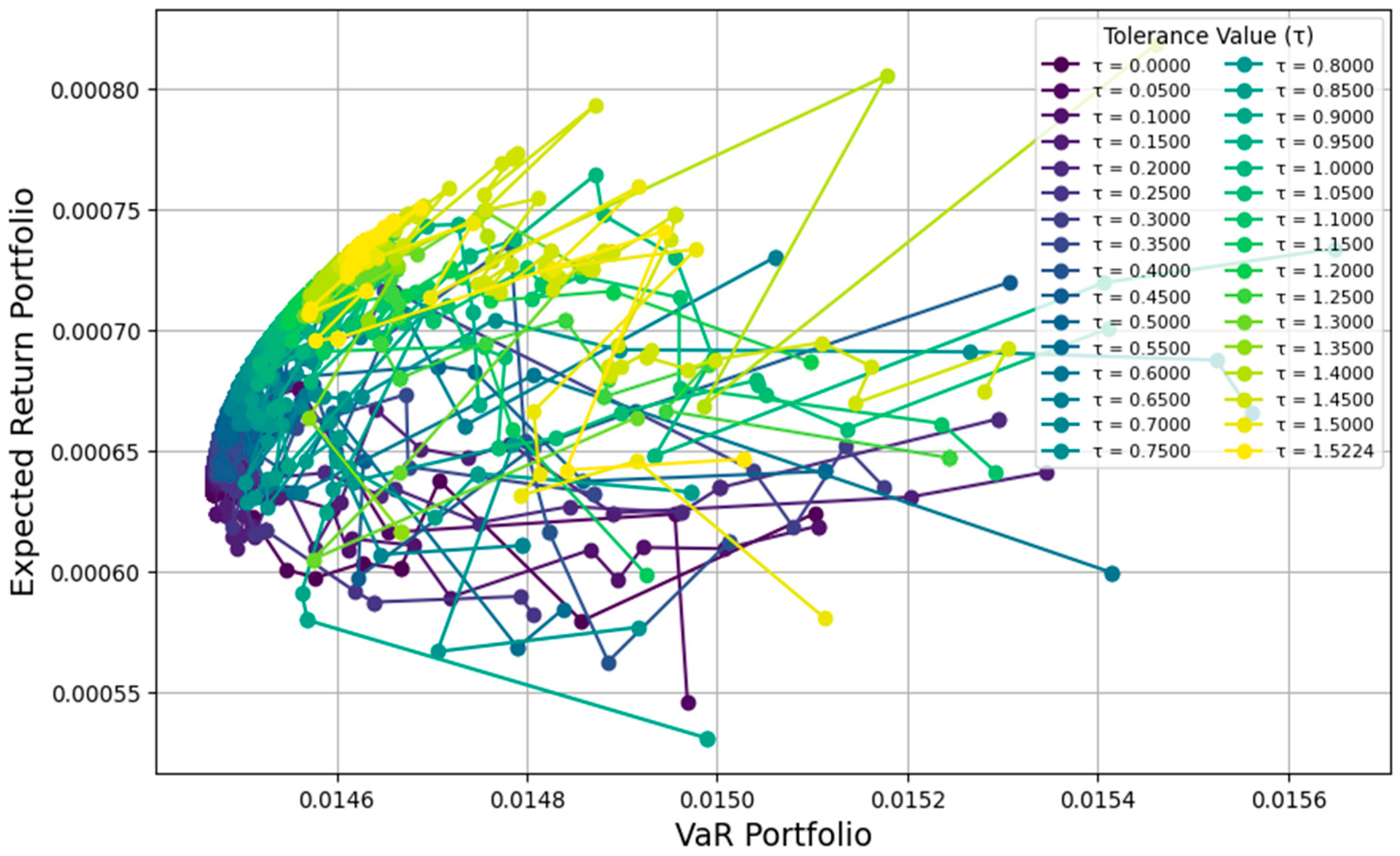
Figure 5 displays the iteration plot for each value $\tau$ in the portfolio optimization process using the PSO method. The horizontal axis represents the VaR of the portfolio, which measures the maximum risk that the portfolio might incur, while the vertical axis shows the portfolio’s expected return $\left({\mu }_{pt}\right)$. Each point on the plot corresponds to the portfolio outcome at a specific iteration for each value $\tau$. The colors in the plot indicate the risk tolerance values $\tau$, ranging from $\tau =0$ (purple) to $\tau =1.5224$ (yellow).

Based on the plot in Figure 5, the evolution pattern of the portfolio is observed as $\tau$ changes. As $\tau$ increases, the portfolio moves toward the upper right, indicating an increase in the expected return and an increase in the risk (VaR) simultaneously. Iterations for lower values $\tau$ (from purple to green) are spread out toward the lower part of the graph, showing portfolios with lower returns and relatively controlled risk. In contrast, iterations for higher values of $\tau$ (yellow) tend to result in higher returns but with a significant increase in risk. This plot shows how the PSO method iterates and balances the two main factors in portfolio decision-making: the expected return and the risk, as measured through the VaR.

This graph reveals the evolutionary pattern of the portfolio as the risk tolerance parameter $\left(\tau \right)$ changes. Investors can observe that portfolios with lower $\tau$ values (represented by purple to green colors) tend to offer lower risks but also lower expected returns, while portfolios with higher $\tau$ values (yellow colors) achieve higher returns but with significantly greater risks. Understanding this pattern allows investors to determine their portfolio preferences based on their risk tolerance levels.

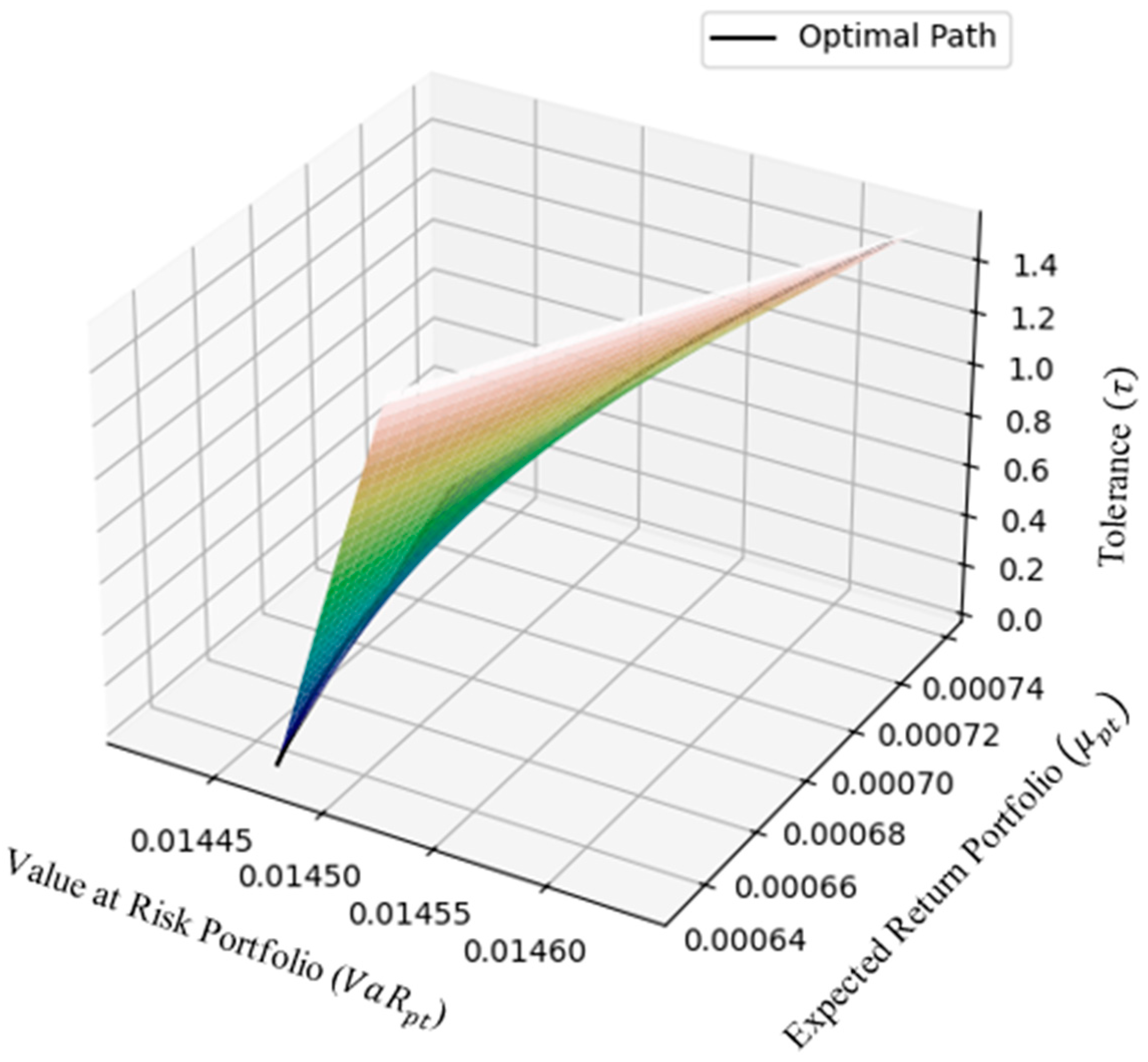
Figure 6 represents the efficient portfolio surface in the three-dimensional space, with three main axes: portfolio value at risk $\left(Va{R}_{pt}\right)$, expected return portfolio $\left({\mu }_{pt}\right)$, and tolerance $\left(\tau \right)$. This surface illustrates the optimal path of the portfolio generated through the particle swarm optimization (PSO) algorithm for various risk tolerance values $\left(\tau \right)$ within the range $0\le \tau \le 1.40$. Each point on this surface represents a combination of the expected return $\left({\mu }_{pt}\right)$ and risk $\left(Va{R}_{pt}\right)$ associated with a specific risk tolerance value. The optimal path displayed shows the points of efficient solutions, where each portfolio offers the best combination of return and risk according to the investor’s preferences.

Investors can select the optimal portfolio that provides the highest ratio between the expected return and risk, often referred to as the Sharpe ratio, which is the main target of the optimization strategy. Once a set of efficient portfolios has been identified, the next crucial step is determining which portfolio composition will yield the highest benefit. Investors typically seek a portfolio that can offer the highest average return while minimizing the level of risk as much as possible. For decision-making, the optimal portfolio is identified as the one that delivers the best trade-off, particularly the portfolio with the highest Sharpe ratio.

This efficient frontier chart further aids in simplifying the process of portfolio selection. It visually guides investors by highlighting the efficient portfolios across various risk tolerance levels. To identify the optimal portfolio, investors can focus on points along the frontier with the maximum Sharpe ratio, representing the most favorable combination of return and risk. For instance, in this study, the optimal portfolio achieves the highest Sharpe ratio at $\tau =1.5224$, offering a balance between acceptable risk levels and attractive returns. This visualization underscores the effectiveness of PSO in addressing portfolio optimization challenges.

The Sharpe ratio is a widely recognized metric that evaluates the efficiency of a portfolio by measuring its ability to generate a return relative to the amount of risk taken. The ratio considers volatility as a proxy for risk, with higher values of the Sharpe ratio indicating a more efficient portfolio in terms of return generation. Portfolios with higher Sharpe ratios are better at rewarding investors for the level of risk they assume. Therefore, the portfolio with the highest Sharpe ratio is deemed optimal, as it offers the most favorable trade-off between the expected return and the risk investors are willing to undertake. This selection method ensures that investors choose a portfolio that not only maximizes the return potential but also minimizes the volatility or uncertainty associated with that return. The results of the Sharpe ratio calculations can be seen in Appendix D, and a visual representation of these ratios is provided in Figure 7, allowing for a comprehensive understanding of how the portfolios compare in terms of the risk-adjusted returns.

Based on Figure 7 and Appendix D, the analysis reveals that the optimal portfolio achieves the highest performance relative to the risk with a ratio of average return $\left({\mu }_{pt}\right)$ to risk $\left(Va{R}_{pt}\right)$ of 0.050378, which occurs at a risk tolerance value of $\tau =1.5224$. This optimal portfolio composition results from carefully balancing the return expectations and the risk using the mean-VaR optimization approach.

The optimal portfolio comprises nine banking stocks: BBCA, BBNI, BBRI, BBTN, BDMN, BMRI, BNGA, BRIS, and NISP. The corresponding stock weight vector, which represents the proportion of each stock in the portfolio, is as follows: $w=$ $(0.3314, 0.0366, 0.0062, 2\times {10}^{-7}, 0.1147, 0.036, 0.232, 0.054,$ and $0.1891)$. This distribution of weights indicates that BBCA has the most significant weight in the portfolio at 33.14%, followed by BNGA and NISP with 23.2% and 18.91%, respectively. The remaining stocks, such as BBNI, BBRI, and BDMN, contribute smaller portions to the portfolio.

This optimal portfolio composition yields an average return of 0.00074, representing the expected return over the given investment horizon. Additionally, the portfolio’s risk level, as measured by the value at risk (VaR), is 0.01463. This means that the maximum potential loss in the portfolio, at a specified confidence level, is approximately 1.463% of the portfolio’s value.

A VaR of 1.463% indicates that, under normal market conditions, the likelihood of experiencing losses beyond this percentage is minimal. This risk level is particularly appealing to risk-averse investors, as it signifies that the portfolio exhibits stability and limited exposure to extreme market fluctuations. In practical terms, such a VaR aligns well with investors aiming for predictable returns without significant deviations from the expected performance.

The combination of a relatively high return and manageable risk level makes this portfolio a strong candidate for investors seeking an efficient balance between return and risk. However, it is important to note that the VaR does not account for extreme or rare market conditions, which could result in losses exceeding the estimated threshold.

The results of this optimization process suggest that the chosen portfolio strikes a favorable balance, offering the potential for steady returns while maintaining a level of risk that is within acceptable limits. The analysis further demonstrates the effectiveness of the PSO-based optimization method in selecting an optimal portfolio that meets the investor’s objectives in the context of banking sector stocks.

5. Discussion

The execution of the PSO algorithm was evaluated to assess its performance in solving the optimization problem. A total of 50 algorithm trials were conducted using different initial guesses. For the implementation of the PSO algorithm in portfolio weight optimization, the following device specifications were used:

• Processor: Intel(R) Core(TM) i3-7020U CPU @ 2.30 Ghz
• RAM: 4.00 GB
• Operating system: Windows 11 Pro, 64-bit OS, x64-based processor
• Storage: SSD WD Green 240 GB dan HDD WD Blue 1 TB
• GPU: Intel(R) HD Graphics 620

For programming and executing the algorithm, this study utilized Google Compute Engine with the following specifications:

• Programming language: Python 3
• Virtual machine RAM: 12.7 GB
• Storage capacity: 107.7 GB

The specifications of the devices used in this study played a significant role in the success and efficiency of the PSO algorithm. While the primary device had limitations in terms of the physical RAM (4.00 GB), the use of Google Compute Engine, which provided a more powerful virtual machine with 12.7 GB of RAM and ample storage, allowed for faster computation and accommodated the high computational demands of the algorithm. These enhanced resources were significant in handling the large dataset of banking sector stocks and ensuring that the algorithm could perform many iterations without performance degradation.

To evaluate the accuracy of the developed PSO algorithm in optimizing the portfolio using the mean-value-at-risk model, a series of trials with various initial values were conducted. These trials aimed to assess the consistency of the results obtained from the algorithm, particularly in generating an expected return, standard deviation, and the value at risk (VaR) of the optimized portfolio. The results of these trials are presented in

Table 5. PSO algorithm trial table.

Trial	Iteration	${\mathit{\mu }}_{\mathit{p}\mathit{t}}$	${\mathit{\sigma }}_{\mathit{p}\mathit{t}}$	$\mathit{V}\mathit{a}{\mathit{R}}_{\mathit{p}\mathit{t}}$	Sharpe Ratio	Time
1	486	0.0007369986	0.0093421661	0.0146294972	0.0503775742	27.02
2	418	0.0007369983	0.0093421655	0.0146294964	0.0503775598	26.58
3	437	0.0007369984	0.0093421656	0.0146294966	0.0503775628	26.14
4	483	0.0007369946	0.0093421563	0.0146294851	0.0503773449	26.26
5	631	0.0007369984	0.0093421657	0.0146294967	0.0503775659	26.54
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
49	394	0.0007369984	0.0093421656	0.0146294966	0.0503775629	26.70
50	788	0.0007370152	0.0093422070	0.0146295478	0.0503785369	26.98
Average		0.0007369986	0.0093421662	0.0146294973	0.0503775769	26.40
Std. Deviation		0.000000003	0.000000007	0.000000009	0.000000168

.

Table 5 presents the results of the accuracy tests for the computational algorithm developed using the particle swarm optimization (PSO) method. The tests were carried out 50 times, each with different initial values, to evaluate the accuracy and stability of the algorithm. The primary outcomes from each trial included three critical parameters: portfolio expected return, portfolio standard deviation, and portfolio value at risk (VaR). These values were averaged to overview the algorithm’s performance comprehensively. At the same time, the trial results’ standard deviations indicated how consistently the algorithm produced similar outcomes in each repetition. This evaluation process was essential to ensure the reliability of the PSO method in optimizing the portfolio weights and to assess the algorithm’s robustness under different initial conditions.

The table demonstrates that the average values of the parameters are as follows: the expected return $\left({\mu }_{pt}\right)$ is 0.0007369986, the portfolio standard deviation $\left({\sigma }_{pt}\right)$ is 0.0093421662, the VaR is 0.0146294973, and the Sharpe ratio is 0.0503775769. These results indicate that the algorithm consistently generates stable outcomes with minimal fluctuations. This is further supported by the minimal standard deviations: $3\times {10}^{-9}$ for ${\mu }_{pt}$, $7\times {10}^{-9}$ for ${\sigma }_{pt}$, $9\times {10}^{-9}$ for $Va{R}_{pt}$, and $1.68\times {10}^{-7}$ for the Sharpe ratio, demonstrating that the PSO algorithm has a high level of accuracy and precision when optimizing the portfolio. The minimal variation in the results between trials suggests that the algorithm is not highly sensitive to changes in the initial values, thereby increasing its reliability in finding the optimal solution.

When evaluating the consistency of the PSO algorithm, it is essential to consider both the execution time and the optimization results. In this study, the consistency was measured from two key perspectives: the stability of the execution time and the consistency of the optimization results. The results show that the PSO algorithm demonstrates stable performance across all the trials in terms of both the execution speed and the quality of the optimized portfolio. These findings suggest that the PSO algorithm, in the context of the mean-value-at-risk model, is reliable and consistent in solving complex optimization problems, which is crucial for practical applications in portfolio management.

Furthermore, the table also provides the execution times for each of the 50 trials, showing the variation in the time required to complete the PSO algorithm for solving the optimization problem. The time for each trial was recorded in seconds, offering insight into the computational efficiency of the algorithm. From the data, it is clear that there is some variation in the execution time across the trials, with the shortest execution time recorded at 25.69 s in trial 15 and the longest time at 27.48 s in trial 30. Despite these variations, the average execution time across all the trials was 26.40 s, reflecting the algorithm’s efficiency in performing the optimization task. While there were some fluctuations in the execution time between trials, the overall consistency in the average time suggests that the PSO algorithm operates with good stability, ensuring that it is both efficient and reliable for large-scale optimization tasks.

The PSO algorithm employs different initial position and velocity values for particles in each experiment. This variation influences the number of iterations needed to converge to the optimal solution for portfolio optimization. As a result, the execution time for each iteration fluctuates, depending on the total iterations required in each trial. This inherent variability highlights the dynamic nature of the PSO algorithm in addressing optimization problems.

In conclusion, the evaluation of the PSO algorithm in terms of its accuracy and speed confirms its capability to optimize the portfolio based on the mean-value-at-risk model. The results from the 50 trials demonstrate that the algorithm can reliably produce stable and efficient solutions with minimal variation in both the optimization outcomes and the execution times. This makes the PSO algorithm a viable tool for portfolio optimization in financial applications, where accuracy and computational efficiency are crucial.

The parameter values used in the PSO algorithm are also crucial to evaluate as they can impact the portfolio optimization results. Experiments were conducted with various variations of the inertia weight ($w$), cognitive learning coefficient $\left(c_1\right)$, and social learning coefficient $\left(c_2\right)$, each performed five times. The results of these experiments can be seen in

Table 6. PSO parameter testing.

Parameter Value	Iteration	Portfolio Weight									Ratio
		BBCA	BBNI	BBRI	BBTN	BDMN	BMRI	BNGA	BRIS	NISP
$w=0.1$ $c_1=2,$ $c_2=2$	224	0.20798	0.08588	0.05671	0.02131	0.11048	0.04757	0.23516	0.06165	0.17327	0.047813
	206	0.30039	0.03936	0.02966	0.03258	0.12183	0.03635	0.20863	0.06708	0.16412	0.047491
	212	0.30052	0.03897	0.03330	0.02383	0.10907	0.03215	0.21381	0.05764	0.19071	0.049096
	198	0.30077	0.06131	0.01043	0.04467	0.10639	0.03460	0.19798	0.06827	0.17558	0.048052
	224	0.28784	0.05404	0.03913	0.01822	0.10496	0.04290	0.21963	0.04052	0.19276	0.049728
$w=0.25$ $c_1=0.1$ $c_2=0.1$	67	0.33895	0.03153	0.02867	−0.00273	0.14730	0.02802	0.17589	0.05387	0.19851	0.048468
	75	0.33445	0.03286	0.00672	0.00235	0.14346	0.03672	0.18337	0.05435	0.20573	0.049639
	73	0.33516	0.03649	0.01103	−0.00299	0.11175	0.03580	0.23141	0.05170	0.18963	0.050445
	78	0.32218	0.03453	−0.00069	0.00432	0.12086	0.03667	0.23498	0.05875	0.18840	0.050260
	57	0.33231	0.03694	0.00618	−0.00032	0.11458	0.03583	0.23133	0.05417	0.18897	0.050365
$w=0.75$ $c_1=2$ $c_2=2$	591	0.33144	0.03659	0.00620	0.00000	0.11473	0.03600	0.23199	0.05395	0.18909	0.050378
	351	0.33145	0.03659	0.00620	0.00000	0.11473	0.03599	0.23200	0.05395	0.18909	0.050378
	392	0.33145	0.03659	0.00620	0.00000	0.11473	0.03599	0.23200	0.05395	0.18909	0.050378
	413	0.33144	0.03659	0.00620	0.00000	0.11473	0.03600	0.23200	0.05395	0.18909	0.050378
	725	0.33144	0.03659	0.00620	0.00000	0.11473	0.03599	0.23200	0.05396	0.18909	0.050378
$w=0.75$ $c_1=0.1$ $c_2=0.1$	253	0.30849	0.03772	0.00362	0.00719	0.11989	0.03749	0.24261	0.05447	0.18850	0.050282
	271	0.31229	0.04230	0.00030	0.01022	0.12808	0.04027	0.21952	0.05372	0.19330	0.050072
	257	0.32544	0.03751	0.01007	0.00002	0.12312	0.03759	0.21417	0.05369	0.19840	0.050321
	234	0.33127	0.03661	0.00625	−0.00015	0.11479	0.03601	0.23234	0.05392	0.18896	0.050377
	241	0.33169	0.03535	0.00656	0.00331	0.12302	0.03629	0.22344	0.05191	0.18842	0.049985
$w=1$ $c_1=2$ $c_2=2$	576	0.32976	0.03652	0.00482	0.00319	0.11823	0.03673	0.22729	0.05207	0.19139	0.050323
	336	0.33608	0.03950	0.01062	−0.00689	0.12155	0.03659	0.22448	0.06214	0.17592	0.049572
	531	0.33028	0.03667	0.00630	−0.00001	0.11868	0.03678	0.22161	0.05177	0.19793	0.050555
	999	0.33360	0.03509	0.00744	0.00176	0.11689	0.03597	0.22730	0.05411	0.18783	0.050158
	452	0.33088	0.03662	0.00551	0.00328	0.11071	0.03603	0.23670	0.05373	0.18655	0.050372

. This discussion aims to examine how changes in the parameters can affect the distribution of the weights on the stocks and assess the stability and effectiveness of the parameter combinations used.

The results of the experiments with various parameter values in the PSO algorithm, as shown in Table 6, indicate that changes in the parameter values have a significant impact on the portfolio weight distribution. The inertia weight is a parameter that determines how much the particle’s velocity influences its new best position. In contrast, the cognitive $\left(c_1\right)$ and social $\left(c_2\right)$ learning coefficients determine the extent of the search space used in the PSO algorithm. Lower inertia values $(w=0.1$ $w=0.25)$ generally result in inconsistent weights, as observed after five trials with wide and narrow search spaces. Furthermore, a tremendous inertia value $(w=1)$, which implies that the velocity entirely determines the particle’s position, also leads to inconsistent results.

In contrast, an inertia value $w=0.75$, which suggests that velocity does not entirely dominate the discovery of new particle positions, produces consistent results when combined with a vast search space $\left(c_1=2, c_2=2\right)$. This combination supports the stability and reliability of the portfolio’s decision-making process for stock weight allocation. Thus, this parameter combination effectively generates consistent solutions, which is crucial for portfolio optimization in an investment context.

6. Conclusions

This research successfully developed an effective computational algorithm for determining the global optima of an investment portfolio based on the mean-value-at-risk (mean-VaR) model by adapting the particle swarm optimization (PSO) algorithm. This modified PSO algorithm addressed the challenge of determining the optimal portfolio weights by adjusting the parameters to account for the return distribution of banking sector stocks. When applied to Indonesian banking sector stock data from 1 August 2022 to 30 July 2024, 9 out of 33 stocks were selected based on the positive expected returns and distributions aligned with the model. The stock selection considered the risk characteristics and return potential, yielding the optimal portfolio weights and enabling PSO to produce a portfolio composition that aligns with investment objectives in the mean-VaR context. This application’s success indicates that PSO can be a reliable computational method for processing accurate capital market data and providing relevant recommendations for investment decisions in the banking sector.

Further evaluation of the PSO algorithm’s performance demonstrated high consistency in generating optimal portfolios with appropriate parameter selection. Across 50 trials, the algorithm recorded an average expected return of 0.000737, a return standard deviation of 0.00934, a value at risk of 0.01463, and a Sharpe ratio of 0.0504. The low standard deviation across these trials highlights the algorithm’s accuracy, stability, and robustness against variations in the initial values. With an average execution time of 26.4 s, the PSO algorithm demonstrated stable performance in terms of the speed, accuracy, and consistency in the optimization results.

Several experiments have been conducted, showing that variations in the VaR parameter values consistently result in well-calibrated portfolio weights (summing to one). This indicates that the PSO algorithm demonstrates reliable and adaptive performance, making it suitable for application across various market conditions.

In this study, the stock selection method utilized a data distribution model based on the closing prices of banking sector stocks. However, this method has limitations since not all the data conform to the applied distribution model. Consequently, the range of data used in the simulation becomes a critical aspect to consider. For future research, alternative methods, such as Monte Carlo simulation or the ARMA-GARCH method, are recommended to allow for more flexible data ranges and to optimize the stock selection process for investment portfolios.

Additionally, for a more comprehensive risk analysis, it is suggested to explore supplementary risk models, such as the conditional value at risk (CVaR) or expected shortfall (ES), particularly when addressing highly volatile market conditions. Adopting these alternative risk models can provide broader perspectives in portfolio risk measurement and support more comprehensive investment decision-making.