Optimizing a Machine Learning Algorithm by a Novel Metaheuristic Approach: A Case Study in Forecasting
Abstract
1. Introduction
2. Methodology
2.1. XGBoost Algorithm
2.2. Genetic Algorithm
2.3. Grey Wolf Optimizer
2.4. White Shark Optimizer
2.5. Artificial Rabbits Optimization
2.6. Artificial Bee Colony
| Algorithm 1 Pseudocode of Artificial Bee Colony Algorithm |
| 1. Initialize parameters (number of food sources, employed bees, onlooker bees, and scout bees). 2. Randomly generate an initial population of food sources (possible solutions). 3. Evaluate the fitness of each food source. 4. Repeat until the termination condition is met: 4.1 For each employed bee: - Explore the neighborhood of the associated food source to discover new solutions. - If a new solution is better than the current one, replace the old solution with the new one. 4.2 Calculate the probability of each food source based on its fitness. 4.3 For each onlooker bee: - Select a food source probabilistically based on fitness. - Explore the neighborhood of the chosen food source. - If a new solution is better, update the food source. 4.4 If a food source has not improved for a predetermined number of cycles: - Abandon the food source. - Send a scout bee to explore a new random location. 5. Memorize the best solution found so far. 6. End. |
2.7. Fire Hawk Optimizer
| Algorithm 2 Pseudocode of Fire Hawk Optimizer Algorithm |
| 1. Initialization of the population: Initialize a population of fire hawks and prey (possible solutions). 2. Re-reading and evaluation: Evaluate the fitness of each prey (solution). 3. Sending the fire hawks to hunt prey: - Fire hawks move towards the prey based on their fitness (distance from the prey). - If a fire hawk finds a better prey, it updates its position to that new prey. 4. Sending other fire hawks to improve exploration: - Fire hawks that are far from the best prey are sent to explore new regions of the search space. - Fire hawks adapt their positions to explore areas with high potential. 5. Sending the scout fire hawks to discover new prey: - If a fire hawk doesn’t find better prey within a certain number of moves, it is repositioned to a new location. - Scout fire hawks are used to explore unknown areas to avoid local optima. 6. Memorizing the best prey found so far and updating the position of the fire hawks accordingly. 7. Repeating the steps until the termination condition is met. |
2.8. Hybrid ABC-FHO Algorithm
| Algorithm 3 Text Pseudocode of Hybrid ABC-FHO Algorithm |
| 1. Initialize population of agents randomly in the search space. 2. Evaluate the fitness of all agents. 3. Repeat until maximum iterations are reached: 3.1 ABC: Employed Bee Phase - For each agent: - Generate a new solution by modifying the current agent’s position. - If the new solution is better, update the agent’s position and reset its trial counter. - If not, increase the trial counter for that agent. 3.2 ABC: Onlooker Bee Phase - Select agents probabilistically based on their fitness. - Generate new solutions as in the employed bee phase. 3.3 FHO: Fire Hawk Search - For each agent: - Determine whether to perform a global or local search based on the distance to the best solution. - If performing a global search, make larger steps in the search space. - If performing a local search, make smaller steps for fine-tuning. 3.4 ABC: Scout Bee Phase - Replace agents that have not improved after a certain number of attempts with new random solutions. 4. Return the best solution and its fitness. |
2.8.1. Statistical Metrics
Shapiro–Wilk
Mann–Whitney U Test
3. Case Study
- Dataset 1: This dataset, sourced from COVID-19-related sales data, highlights volatile sales dynamics caused by pandemic-induced consumer behavior changes. It includes 13 features, such as the date, sales, and region, reflecting the impact of lockdown measures and recovery phases on sales.
- Dataset 2: This dataset provides weekly Walmart sales data across multiple stores, including features like the store, weekly sales, and holiday flags. Its structure allows for an in-depth evaluation of forecasting models in a multi-regional retail context, making it ideal for testing the adaptability of the proposed algorithms.
- Dataset 3: Focused on Amazon UK sales, this dataset spans from 2019 to 2021 and includes 21 features, such as the weekly sales, product category, and promotional discounts. Its temporal coverage captures critical patterns in e-commerce growth during the pandemic era.
3.1. Experimental Setup
3.2. Parameter Settings
3.3. Evaluation Metrics
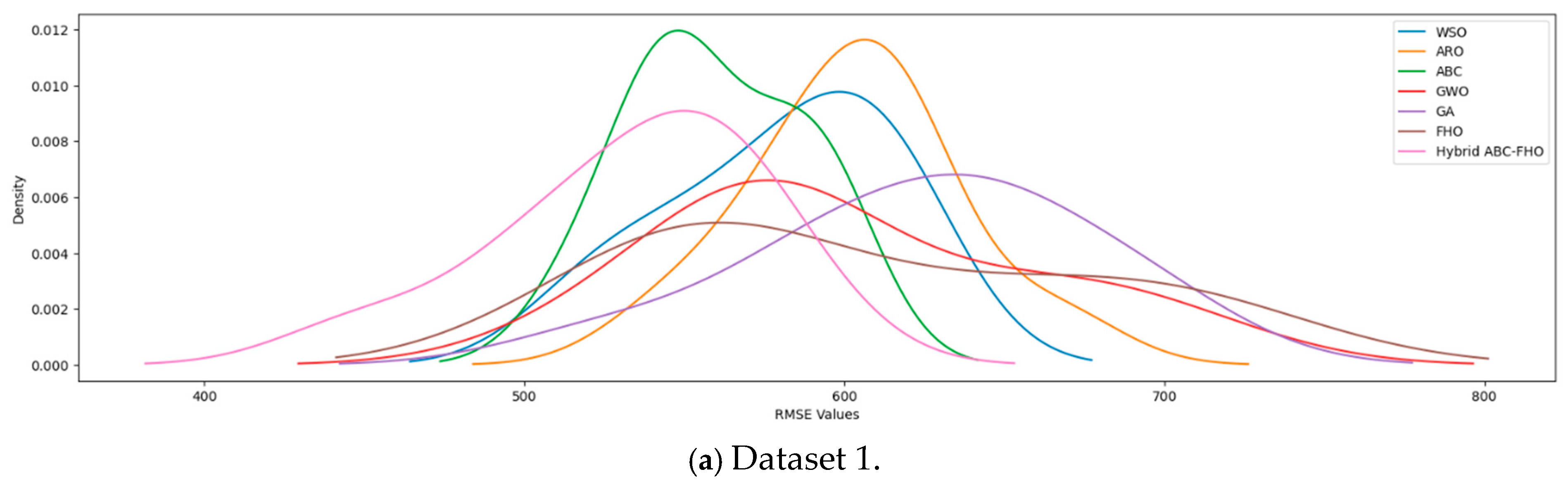
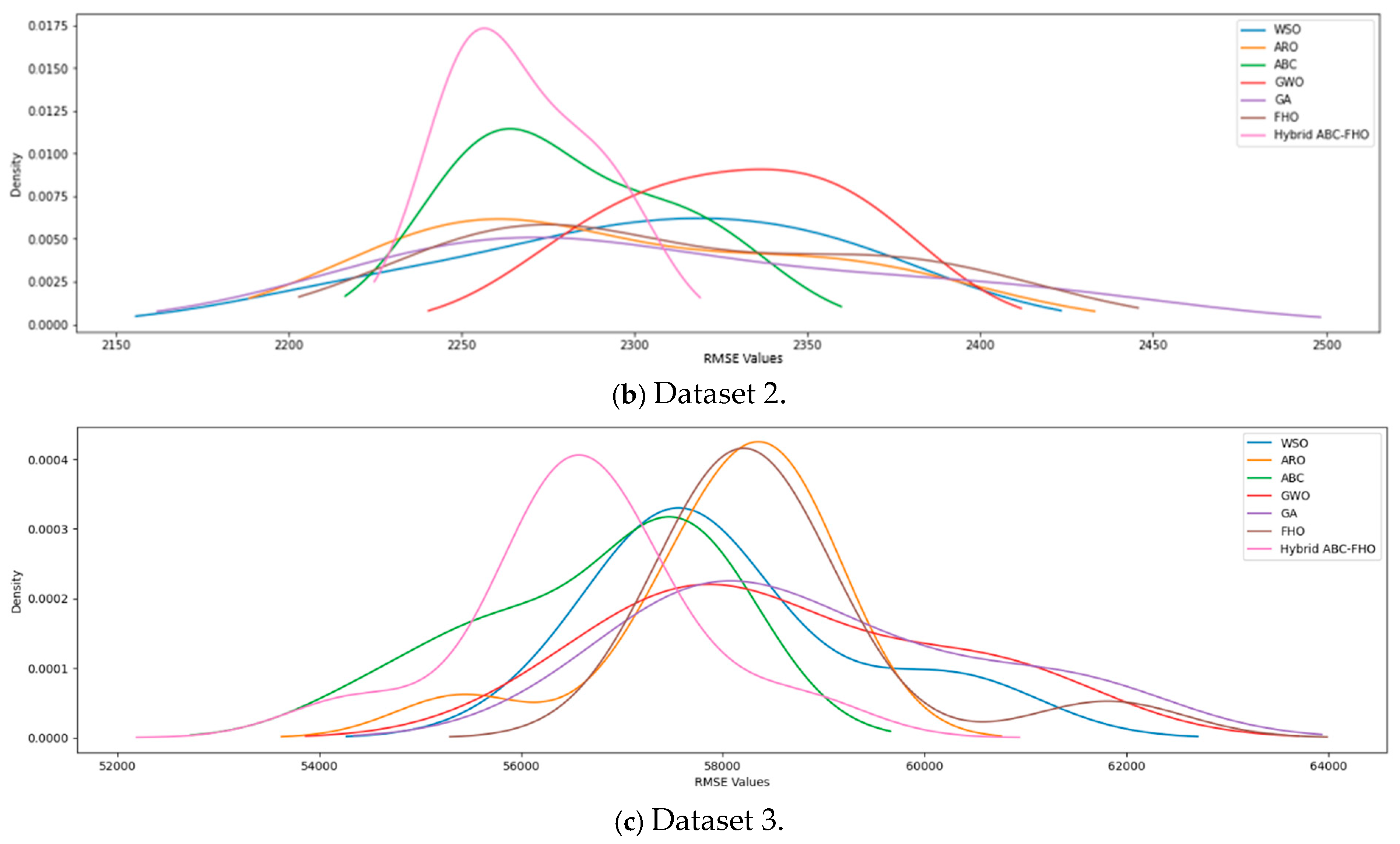
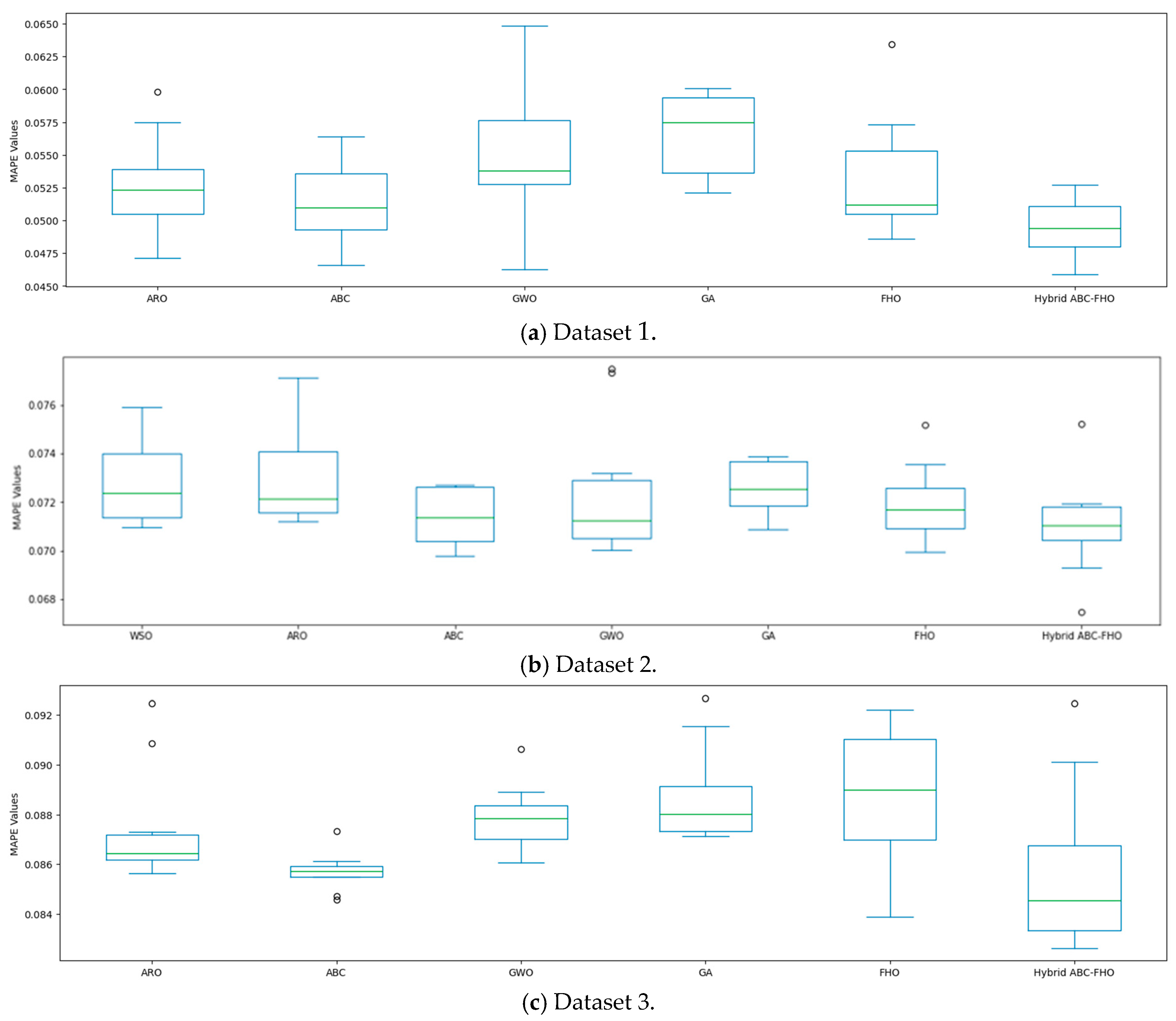
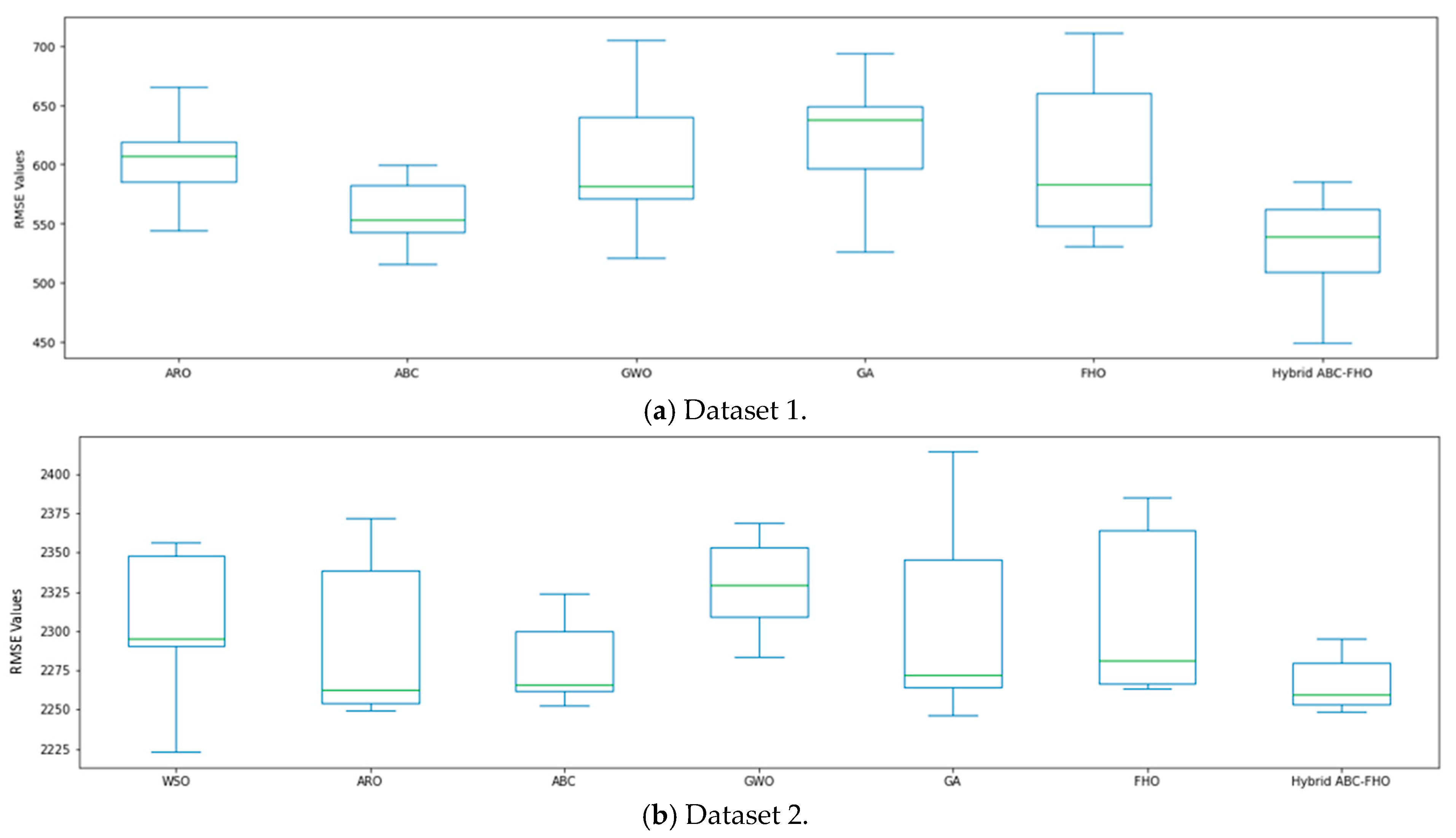
3.4. Results and Analysis
Performance Results
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huber, J.; Stuckenschmidt, H. Advances in seasonal and promotional sales forecasting using machine learning models. J. Bus. Res. 2020, 117, 452–461. [Google Scholar] [CrossRef]
- Choi, Y.; Seo, S.; Lee, J.; Kim, T.W.; Koo, C. A machine learning-based forecasting model for personal maximum allowable exposure time under extremely hot environments. Sustain. Cities Soc. 2024, 101, 105140. [Google Scholar] [CrossRef]
- Singh, A.R.; Kumar, R.S.; Bajaj, M.; Khadse, C.B.; Zaitsev, I. Machine learning-based energy management and power forecasting in grid-connected microgrids with multiple distributed energy sources. Sci. Rep. 2024, 14, 19207. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Wang, X.; Band, S.S.; Bagherzadeh, S.A.; Taherifar, S.; Abdollahi, A.; Bahrami, M.; Karimipour, A.; Chau, K.-W.; et al. Energetic thermo-physical analysis of MLP-RBF feed-forward neural network compared with RLS fuzzy to predict CuO/liquid paraffin mixture properties. Eng. Appl. Comput. Fluid Mech. 2022, 16, 764–779. [Google Scholar] [CrossRef]
- Ben Jabeur, H.; Bouzidi, M.; Malek, J. XGBoost outperforms traditional machine learning models in retail demand forecasting. J. Retail. Consum. Serv. 2024, 67, 102859. [Google Scholar]
- Mishra, P.K.; Singh, S.; Kumar, A.; Gupta, V. Evaluating the performance of machine learning models in rainfall forecasting: A comparison of XGBoost, ARIMA, and state space models. Environ. Earth Sci. 2024, 83, 11481. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Li, Z. A comparison of XGBoost and ARIMA in demand forecasting of e-commerce platforms. Electron. Commer. Res. Appl. 2021, 45, 101030. [Google Scholar]
- Massaro, M.; Dumay, J.; Garlatti, A. A hybrid XGBoost-ARIMA model for improving sales forecasting accuracy in retail. J. Bus. Econ. Manag. 2021, 22, 512–526. [Google Scholar]
- Panarese, P.; Vasile, G.; Zambon, E. Sales forecasting using XGBoost: A case study in the e-commerce sector. Expert Syst. Appl. 2021, 177, 114934. [Google Scholar] [CrossRef]
- Arnold, C.; Biedebach, L.; Küpfer, A.; Neunhoeffer, M. The role of hyperparameters in machine learning models and how to tune them. Political Sci. Res. Methods 2024, 12, 841–848. [Google Scholar] [CrossRef]
- Ali, A.; Zain, A.M.; Zainuddin, Z.M.; Ghani, J.A. A survey of swarm intelligence and evolutionary algorithms for hyperparameter tuning in machine learning models. Swarm Evol. Comput. 2023, 56, 100–114. [Google Scholar]
- Tani, L.; Rand, D.; Veelken, C.; Kadastik, M. Evolutionary algorithms for hyperparameter optimization in machine learning for application in high energy physics. Eur. Phys. J. C 2021, 81, 170. [Google Scholar] [CrossRef]
- Yin, X.; Cheng, S.; Yu, H.; Pan, Y.; Liu, Q.; Huang, X.; Gao, F.; Jing, G. Probabilistic assessment of rockburst risk in TBM-excavated tunnels with multi-source data fusion. Tunn. Undergr. Space Technol. 2024, 152, 105915. [Google Scholar] [CrossRef]
- Du, X.; Xu, H.; Zhu, F. Understanding the effect of hyperparameter optimization on machine learning models for structure design problems. Comput. Aided Des. 2021, 135, 103013. [Google Scholar] [CrossRef]
- Dhake, P.S.; Patil, A.D.; Desai, R.R. Genetic algorithm for optimizing hyperparameters in LSTM-based solar energy forecasting. Renew. Energy 2023, 198, 75–84. [Google Scholar] [CrossRef]
- Zulfiqar, U.; Rehman, M.U.; Khan, A. Adaptive differential evolution and support vector machines for load forecasting. Electr. Power Syst. Res. 2022, 208, 107976. [Google Scholar] [CrossRef]
- Kaya, E.; Gorkemli, B.; Akay, B.; Karaboga, D. A review on the studies employing artificial bee colony algorithm to solve combinatorial optimization problems. Eng. Appl. Artif. Intell. 2022, 115, 105311. [Google Scholar] [CrossRef]
- Mohakud, B.; Dash, R. Grey wolf optimization-based convolutional neural network for skin cancer detection. J. King Saud Univ. Comput. Inf. Sci. 2021, 34, 3717–3729. [Google Scholar] [CrossRef]
- Tran, Q.A.; Nguyen, D.K.; Le, T.H. Enhancing long-term meteorological predictions with genetic algorithms and LSTM networks. IEEE Access 2020, 8, 29832–29843. [Google Scholar]
- Azizi, M.; Talatahari, S.; Gandomi, A.H. Fire Hawk Optimizer: A novel metaheuristic algorithm. Artif. Intell. Rev. 2023, 56, 287–363. [Google Scholar] [CrossRef]
- Çetinbaş, M.; Özcan, E.; Bayramoğlu, S. Hybrid White Shark Optimizer and Artificial Rabbits Optimization for photovoltaic parameter extraction. Renew. Energy 2023, 180, 1236–1249. [Google Scholar] [CrossRef]
- Al-Shourbaji, I.; Hassan, M.M.; Mohamed, M.A. Hybrid ant colony optimization and reptile search algorithm for solving complex optimization problems. Expert Syst. Appl. 2022, 192, 116331. [Google Scholar]
- Bindu, M.G.; Sabu, M.K. A hybrid feature selection approach using artificial bee colony and genetic algorithm. In Proceedings of the IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 2–4 July 2020; pp. 1–6. [Google Scholar]
- Abd Elaziz, M.; Hosseinzadeh, M.; Elsheikh, A.H. A novel hybrid of Fire Hawk Optimizer and Artificial Rabbits Optimization for complex optimization problems. J. Intell. Fuzzy Syst. 2023, 36, 125–139. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Shabani, M.; Yousefi, M. A novel hybrid machine learning model to forecast electricity prices using XGBoost, ELM, and LSTM. Energy 2023, 263, 125546. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, J.; Liu, F. A hybrid model of XGBoost and LSTM for electricity load forecasting. J. Energy Storage 2022, 46, 103568. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, 2nd ed.; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2024, 69, 46–61. [Google Scholar] [CrossRef]
- Makhadmeh, Z.; Al Momani, M.; Mohammed, A. An enhanced Grey Wolf Optimizer for solving real-world optimization problems. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar]
- Braik, M.; Awadallah, M.A.; Mousa, A. White Shark Optimizer: A novel meta-heuristic algorithm for global optimization problems. Appl. Soft Comput. 2022, 110, 107625. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, X.S. A XGBoost risk model via feature selection and Bayesian hyper-parameter optimization. arXiv 2019, arXiv:1901.08433. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Kaya, M.; Karaboga, D.; Basturk, B. A comprehensive review of artificial bee colony algorithm variants and their applications. Swarm Evol. Comput. 2022, 72, 101069. [Google Scholar] [CrossRef]
- Jahangir, H.; Eidgahe, D.R. A new and robust hybrid artificial bee colony algorithm—ANN model for FRP-concrete bond strength evaluation. Constr. Build. Mater. 2020, 264, 113160. [Google Scholar]
- Lee, W.W.; Hashim, M.R. A hybrid algorithm based on artificial bee colony and artificial rabbits optimization for solving economic dispatch problem. In Proceedings of the 2023 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 17 June 2023; pp. 298–303. [Google Scholar] [CrossRef]
- Moosavi, S.K.R.; Saadat, A.; Abaid, Z.; Ni, W.; Li, K.; Guizani, M. Feature selection based on dataset variance optimization using Hybrid Sine Cosine—Firehawk Algorithm (HSCFHA). Future Gener. Comput. Syst. 2024, 141, 1–15. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Jurečková, J.; Picek, J. Robust Statistical Methods with R; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- MacFarland, T.W.; Yates, J.M. Introduction to Nonparametric Statistics for the Biological Sciences Using R; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Arcuri, A.; Fraser, G. Parameter tuning or default values? An empirical investigation in search-based software engineering. Empir. Softw. Eng. 2023, 18, 594–623. [Google Scholar] [CrossRef]
- Kapoor, S.; Perrone, V. A simple and fast baseline for tuning large XGBoost models. arXiv 2021, arXiv:2111.06924. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Advanced hyperparameter optimization for improved spatial prediction of shallow landslides using extreme gradient boosting (XGBoost). Bull. Eng. Geol. Environ. 2022, 81. [Google Scholar] [CrossRef]
- Tao, M.; Hong, Z.; Liu, L.; Zhao, M.; Wu, C. An intelligent approach for predicting overbreak in underground blasting operation based on an optimized XGBoost model. Eng. Appl. Artif. Intell. 2023, 6, 100279. [Google Scholar]
- Vivas, E.; Allende-Cid, H.; Salas, R. A systematic review of statistical and machine learning methods for electrical power forecasting with reported MAPE score. Entropy 2020, 22, 1412. [Google Scholar] [CrossRef] [PubMed]
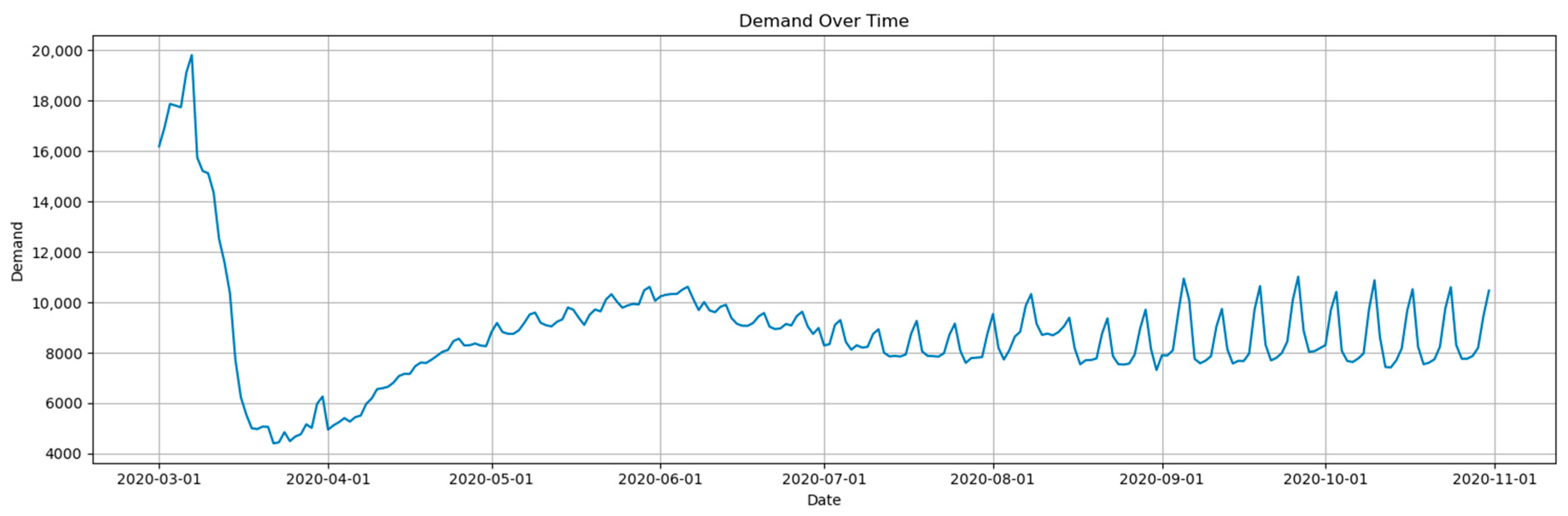

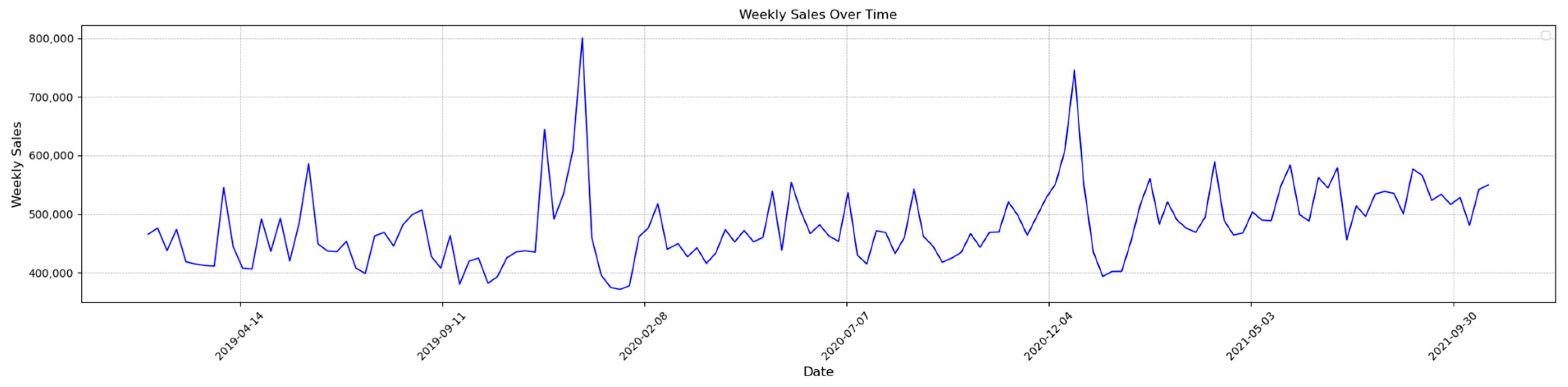


| Dataset | Source | No. of Instances | No. of Features |
|---|---|---|---|
| Dataset 1 | https://github.com/ashfarhangi/COVID-19/ (accessed on 8 October 2024) | 30,264 | 13 |
| Dataset 2 | https://www.kaggle.com/datasets/aslanahmedov/walmart-sales-forecast (accessed on 8 October 2024) | 8190 | 12 |
| Dataset 3 | https://data.world/revanthkrishnaa/amazon-uk-sales-forecasting-2018-2021/workspace/project-summary (accessed on 8 October 2024) | 8661 | 21 |
| Hyperparameters | Lower Bound | Upper Bound | Default Value |
|---|---|---|---|
| Colsample Bytree | 0 | 1 | 1 |
| N Estimators | 30 | 1000 | 100 |
| Max Depth | 0 | ∞ | 6 |
| Learning Rate | 0 | 1 | 0.3 |
| Min Child Weight | 0 | ∞ | 1 |
| Reg Alpha | 0 | ∞ | 0 |
| Reg Lambda | 0 | ∞ | 1 |
| Subsample | 0 | 1 | 1 |
| Max Leaves | 0 | ∞ | 0 |
| Hyperparameters | Lower Bound | Upper Bound |
|---|---|---|
| Colsample Bytree | 0.5 | 1 |
| N Estimators | 50 | 1000 |
| Max Depth | 2 | 15 |
| Learning Rate | 0.1 | 0.5 |
| Min Child Weight | 0.001 | 10 |
| Reg Alpha | 0 | 1 |
| Reg Lambda | 0 | 1 |
| Subsample | 0.5 | 1 |
| Max Leaves | 10 | 900 |
| Dataset | Metric | GA | ARO | WSO | GWO | ABC | FHO | ABC-FHO |
|---|---|---|---|---|---|---|---|---|
| Dataset 1 | MAPE | 0.057 | 0.053 | 0.052 | 0.055 | 0.051 | 0.053 | 0.049 |
| RMSE | 624.90 | 602.96 | 580.21 | 601.93 | 559.80 | 607.50 | 532.96 | |
| Dataset 2 | MAPE | 0.073 | 0.073 | 0.073 | 0.072 | 0.071 | 0.072 | 0.071 |
| RMSE | 2308.38 | 2295.41 | 2302.68 | 2328.83 | 2296.83 | 2312.16 | 2279.23 | |
| Dataset 3 | MAPE | 0.0887 | 0.0874 | 0.0871 | 0.0878 | 0.0856 | 0.0887 | 0.0855 |
| RMSE | 58,878.51 | 57,974.10 | 58,054.78 | 58,578.09 | 56,733.30 | 58,564.27 | 56,614.05 |
| Dataset | Metric | GA | ARO | WSO | GWO | ABC | FHO | ABC-FHO | |
|---|---|---|---|---|---|---|---|---|---|
| Dataset 1 | Best | MAPE | 0.052 | 0.047 | 0.045 | 0.046 | 0.047 | 0.049 | 0.046 |
| Worst | MAPE | 0.060 | 0.060 | 0.059 | 0.065 | 0.056 | 0.063 | 0.053 | |
| Dataset 2 | Best | MAPE | 0.072 | 0.071 | 0.070 | 0.070 | 0.070 | 0.070 | 0.068 |
| Worst | MAPE | 0.075 | 0.077 | 0.075 | 0.077 | 0.073 | 0.074 | 0.074 | |
| Dataset 3 | Best | MAPE | 0.0968 | 0.0975 | 0.0908 | 0.0943 | 0.0958 | 0.0929 | 0.0920 |
| Worst | MAPE | 0.1048 | 0.1045 | 0.1061 | 0.1043 | 0.1000 | 0.1028 | 0.0985 |
| Dataset | Metric | GA | ARO | WSO | GWO | ABC | FHO | ABC-FHO | |
|---|---|---|---|---|---|---|---|---|---|
| Dataset 1 | Best | RMSE | 527.4 | 484.9 | 540.5 | 470.0 | 482.1 | 485.1 | 475.1 |
| Worst | RMSE | 714.91 | 716.40 | 692.78 | 724.93 | 689.39 | 663.79 | 638.41 | |
| Dataset 2 | Best | RMSE | 2246.1 | 2249.8 | 2222.7 | 2283.3 | 2280.8 | 2263.6 | 2267.2 |
| Worst | RMSE | 2414.2 | 2338.4 | 2356.4 | 2368.9 | 2323.9 | 2384.9 | 2295.4 | |
| Dataset 3 | Best | RMSE | 56,740.1 | 55,407.8 | 56,378.2 | 56,323.6 | 54,457.2 | 57,468.1 | 54,375.3 |
| Worst | RMSE | 61,537.1 | 58,974.6 | 60,597.3 | 61,244.5 | 57,925.9 | 61,815.3 | 58,751.6 |
| Dataset | GA | ARO | WSO | GWO | ABC | FHO | ABC-FHO |
|---|---|---|---|---|---|---|---|
| Dataset 1 | 15.882 | 16.677 | 15.275 | 11.694 | 21.536 | 17.110 | 23.442 |
| Dataset 2 | 45.413 | 48.612 | 45.193 | 48.987 | 60.380 | 41.552 | 68.350 |
| Dataset 3 | 18.190 | 18.068 | 17.379 | 16.512 | 20.440 | 16.256 | 22.130 |
| Dataset | Algorithms | Hypothesis (MAPE) | Hypothesis (RMSE) |
|---|---|---|---|
| Dataset 1 | GA | Rejected | Rejected |
| ARO | Rejected | Rejected | |
| WSO | Rejected | Rejected | |
| GWO | Rejected | Rejected | |
| ABC | Rejected | Not Rejected | |
| FHO | Rejected | Rejected | |
| Dataset 2 | GA | Rejected | Rejected |
| ARO | Rejected | Rejected | |
| WSO | Rejected | Rejected | |
| GWO | Not Rejected | Rejected | |
| ABC | Not Rejected | Rejected | |
| FHO | Rejected | Rejected | |
| Dataset 3 | GA | Rejected | Rejected |
| ARO | Rejected | Rejected | |
| WSO | Rejected | Rejected | |
| GWO | Rejected | Rejected | |
| ABC | Rejected | Rejected | |
| FHO | Rejected | Rejected |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gülsün, B.; Aydin, M.R. Optimizing a Machine Learning Algorithm by a Novel Metaheuristic Approach: A Case Study in Forecasting. Mathematics 2024, 12, 3921. https://doi.org/10.3390/math12243921
Gülsün B, Aydin MR. Optimizing a Machine Learning Algorithm by a Novel Metaheuristic Approach: A Case Study in Forecasting. Mathematics. 2024; 12(24):3921. https://doi.org/10.3390/math12243921
Chicago/Turabian StyleGülsün, Bahadır, and Muhammed Resul Aydin. 2024. "Optimizing a Machine Learning Algorithm by a Novel Metaheuristic Approach: A Case Study in Forecasting" Mathematics 12, no. 24: 3921. https://doi.org/10.3390/math12243921
APA StyleGülsün, B., & Aydin, M. R. (2024). Optimizing a Machine Learning Algorithm by a Novel Metaheuristic Approach: A Case Study in Forecasting. Mathematics, 12(24), 3921. https://doi.org/10.3390/math12243921





