1. Introduction
In machine learning, data classification plays a very important role. Up to now, a large number of data classification methods have emerged and powered the development of machine learning and its practical applications in different domains [
1], such as image detection [
2], speech recognition [
3], text understanding [
4], disease diagnosis [
5,
6], and financial prediction [
7].
Currently, popular data classification methods include the Support Vector Machine (SVM) [
8,
9], Decision Tree (DT) [
10,
11], Naive Bayes (NB) [
12], K-Nearest Neighbors (KNN) [
13], Random Forest (RF) [
14], Deep Learning (DL) [
15], and Deep Reinforcement Learning (DRL) [
16]. SVM is based on optimization theory [
17]. DL is implemented through a multilayer neural network under the guidance of optimization techniques, such as the stochastic gradient descent algorithm [
18]. DRL combines DL with Reinforcement Learning, and it is effective in real-time scenarios [
16]. The others fall in the title of statistical methods [
19,
20].
Many comparative studies are employed to evaluate these classification methods by analyzing their accuracies, time costs, stability, and sensitivity, as well as their advantages and disadvantages [
21,
22,
23]. SVM is efficient when there is a clear margin of separation between the classes, but the choice of its kernel function is difficult, and it does not work with noisy datasets [
23,
24]. DL is developing rapidly, but its training is a very time-consuming process because a large number of parameters need to be optimized through the stochastic gradient descent algorithm. In addition, some hyperparameters in DL are set empirically, such as the number of layers in the neural network, the number of nodes in each layer, and the learning rate, resulting in high sensitivity in the performance, dependent on the hyperparameters and specific problems [
25,
26]. KNN and DT are easy to apply. However, KNN requires the calculation of the Euclidean distance between all the points, leading to a high computation cost. DT is unsuitable for continuous variables, and it has a problem of overfitting [
23]. Other classical methods also obtained great successes [
27,
28]. In order to improve classification accuracy, an ensemble learning scheme, such as AdaBoost [
29,
30], Bagging [
31], Stacking [
32] and Gradient Boosting [
33], is usually adopted to solve an intricate or large-scale problem [
34,
35].
Inspired by the ability of our brain to recognize the musical notes played by any musical instrument in a noisy environment, this paper proposes an optimization method for constructing feature coordinates for data classification by simulating a non-uniform membrane structure model. No matter how complex a musical instrument’s structure is, or how different its vibration patterns are, when we listen to a piece of music played by an instrument, our brain can extract the fundamental tone of its vibration at every moment, and can recognize the beautiful melody as time goes by. Mathematically, this can be clearly explained. The vibration of the musical instrument at every moment is adaptively expanded on its own eigenfunction system, and our brain can grasp the lowest eigenvalue and its eigenfunction components corresponding to the musical notes every moment, and enjoy the beautiful melody over time. In order to extract the data features from complex samples, we simulate the adaptively generating process of the eigenfunction coordinate system of a musical instrument and build the mapping from data features to the low-frequency subspace of the eigenfunction system. Through analyzing the solution space and the eigenfunctions of the partial differential equations describing the vibration of a non-uniform membrane, which is a simple musical instrument, the mutual-energy inner product is defined and is used to extract data features. The introduction of the mutual-energy inner product can not only avoid generating an eigenfunction system to reduce the computational complexity, but also can enhance the feature information and filter out data noise, furthermore, it can benefit the simplification of the data classifier training.
The full paper is divided into six sections.
Section 1 briefly introduces popular data classification methods and the research background.
Section 2 analyzes the solution space of the partial differential equations describing a non-uniform membrane, and defines the concept of the mutual-energy inner product.
Section 3, by making use of the eigenvalues and the eigenfunctions of the non-uniform membrane vibration equations, the mutual-energy inner product is expressed as a series of eigenfunctions, and its potential in data classification is pointed out for enhancing feature information and filtering out data noise.
Section 4 builds a mutual-energy inner product optimization model and discusses the convexity and concavity properties of its objective function.
Section 5 designs a sequential linearization algorithm to solve the optimization model by combing the finite element method (FEM).
Section 6, the mutual-energy inner product optimization method for constructing feature coordinates is applied to a 2-D image classification problem, and numerical examples are given in combination with Gaussian classifiers and the handwritten digit MINST dataset.
Section 7, we summarize the full paper and introduce the future scope of the work.
2. Mutual-Energy Inner Product
Consider the linear partial differential equations
where
is a homogeneous linear self-adjoint differential operator;
is a piecewise continuous function;
is the domain of definition, with a boundary
; and
is a homogeneous linear differential operator on the boundary
, describing the Robin boundary condition.
Expression (2) can be regarded as static equilibrium equations of a simple elastic structure, such as a 1-D string and a 2-D membrane, and can be expanded to an n-dimensional problem. For a 2-dimensional problem, is a domain occupied by a membrane with its boundary ; and stand for the elastic modulus and distributed support elastic coefficient of the membrane, respectively; is the support elastic coefficient on the boundary; is an external force acting on the membrane; is the deformations of the membrane due to , and has a piecewise continuous first-order derivative; is the derivative of the deformations in the outward-pointing normal direction of . In this research, it is required that, , , are piecewise continuous functions, and , , .
A structure subjected to an external force
will generate the deformation
, and its deformation energy
can be expressed as
If the structure is simultaneously subjected to another external force
, then it will generate an additional deformation
. The total deformation
satisfies the superposition principle due to the linearity of Expression (1). The deformation
can cause additional work performed by
. Generally, the additional deformation energy
is called the mutual energy between
and
or the mutual work between
and
. The mutual energy describes the correlation of the two external forces, and can be expressed as
Substituting Expression (1) into Expression (4), by integrating by parts, we obtain
Expression (5) is a bilinear functional. Comparing Expressions (3) and (4), we have
Due to
,
,
, according to the Expressions (5) and (6), the mutual energy satisfies
Expression (7) describes a simple physical phenomenon: when the elastic modulus of the structural material is positive, if the structure deforms, deformation energy is generated; otherwise, the deformation energy is zero.
Expression (5) also shows that the mutual energy is symmetrical and satisfies the commutative law. Combined with Expression (7), it can be inferred that the mutual energy satisfies the Cauchy–Schwarz inequality
The Expressions (7) and (8) show that the mutual energy can be regarded as an inner product of the structural deformation functions. For simplicity, we use
and
to represent the mutual-energy inner product and the Euclidean inner product, respectively; that is,
We define
as the norm derived from
, and
as the norm derived from
. Based on Expression (6),
satisfies
is proportional to the square root of the deformation energy, and is also the energy norm. According to the Cauchy–Schwarz inequality (8),
satisfies the triangle inequality
Based on Expression (1), when a structure is subjected to a piecewise continuous external force, its deformation function has piecewise continuous first-order derivatives on the domain and satisfies the boundary condition . The set of these deformation functions can span a space , which can be equipped either with the Euclidean inner product or with the mutual-energy inner product .
In addition, applying the variational principle, Expression (1) can also be rewritten as the minimum energy principle expression
Here, the feasible domain of has piecewise continuous first-order derivatives on , and does not need to satisfy homogeneous boundary conditions.
3. Signal Processing Property of Mutual-Energy Inner Product
The eigenequation of
can be written as
For Expression (13), its non-zero solutions
and the corresponding coefficients
are called eigenfunctions and eigenvalues, respectively. These eigenfunctions and eigenvalues have the following properties due to
,
,
[
36].
- (1)
Expression (13) has infinite eigenvalues and eigenfunctions , i.e., . If all the eigenvalues are ranked like then they satisfy and . Meanwhile, has continuous dependence on , and , and will increase with the increase in , and .
- (2)
Normalized eigenfunctions
satisfy the orthogonality condition (14), and can form a set of orthogonal and complete basis functions to span the deformation function space
.
Therefore, the solutions of Expression (1) can be expressed by
. For
,
can be presented as a series of eigenfunctions satisfying absolute and uniform convergence, i.e.,
Expression (15) has profound physical meaning. and are the order structural natural frequency and the order vibration mode. If is regarded as a vibration amplitude function, it can be decomposed into a superposition of the vibration modes at each order natural frequency, where the coefficient is the vibration magnitude at . This is equivalent to spectral decomposition. Imagine such a scene. When we enjoy a piece of music, our brains constantly decompose the instantaneous vibration amplitude according to Expression (15), and meanwhile, perceive the vibration coefficients and mark them with . For a musical instrument, is its fundamental frequency (tone) and the remaining eigenvalues are overtones. Different musical instruments have different vibration patterns, and their eigenfunctions are also different. However, after tuning the tone of the different musical instruments, the fundamental frequency of each note is consistent.
The eigenfunctions and eigenvalues satisfy Expression (13), so we have
Multiplying both sides of Expression (16) by
and integrating by parts, we can yield
Expression (17) shows that the eigenfunctions also satisfy the orthogonal condition with respect to the mutual-energy inner product. So, these eigenfunctions can also be used as basis functions to span the mutual-energy inner product space .
Substituting Expression (15) into Expression (5) and applying Expression (17), we have
If
satisfies the normalization condition
or
, based on the Expressions (14) and (18), the eigenvalue
satisfies
where the optimal solution of
is the eigenfunction
.
Similarly, the deformation
caused by
can be expressed as
where
is the amplitude coefficient and can be interpreted as the component of
at the
vibration mode
. Substituting Expression (20) into Expression (12) and using the orthogonal condition (17), we have
where the coefficient
is the projection of
on
with respect to the Euclidean inner product
Enforcing the derivative of
in Expression (21) with respect to
to zero, we have
According to the series representation of
in Expression (15), if
is the deformation caused by
, the coefficient
satisfies
Substituting the Expressions (15), (20), (23) and (24) into Expression (5) and using the orthogonal condition (17), we have
Generally speaking, the external force
, because
does not satisfy the homogeneous boundary conditions, i.e.,
. In this case,
is equal to the projection of
on
or the optimal approximation of
in
. Of course, in order to make
, we may expand the design domain and simplify the boundary condition. For example, after expanding the design domain, we can set a fixed boundary and let
, or set a mirror boundary and let
. In these cases,
and
. Then, applying the orthogonal condition (14) yields
After and are expressed as a superposition of the eigenfunctions of the operator , through comparing the mutual-energy inner product in Expression (25) and the Euclidean inner product in Expression (26), it can be found that the mutual-energy inner product has the advantage of enhancing the low-frequency coordinate components () and suppressing the high-frequency coordinate components (). In other words, if and are regarded as signals, the mutual-energy inner product can augment the low-frequency eigenfunction components and filter out the high-frequency eigenfunction components of the signals, with the help of a structural model.
4. Mutual-Energy Inner Product Optimization Model for Feature Extraction
Assume that is a training dataset with samples, and each sample is represented as , while represents the class labels. For example, the samples are divided into two classes, and includes two subsets and , where . Generally, the samples in different classes are assumed to be random variables, which are independent and have identical distributions.
We hope to find an appropriate feature coordinate system to represent and use fewer coordinate components to classify the samples. If there is no further information, we may select the means of the probability distribution of and as reference features. In order to design a feature extraction model, two points should be considered: one to enhance the feature information, and the other to suppress the effect of random noise. We resort to a structural model and use the mutual-energy inner product to extract the features. Its main idea is to map the data features to a low-frequency eigenfunction space of the structural model.
If
and
are used to represent the means of the probability distribution of
and
, respectively, their unbiased estimates can be written as
We regard , and as external forces acting on the structural model, and use , and to represent their corresponding deformations, respectively. If we represent the selected reference feature in as , we can use the mutual-energy inner product to extract the feature coordinate component of . In order to construct the feature extraction optimization model, we first select as the reference feature and try to explore the physical meanings of the structural model when is the maximum, the minimum or equal to zero.
In order to enhance the feature information of the samples in
, a high statistical mean value
should be given
with a primary objective
In Expression (29), the mutual-energy inner product and deformations are functions of and , and its physical meaning is not intuitive. So, next, we will conduct a quantitative analysis to reveal the structural characteristics hidden in Expression (29).
According to the minimum energy principle (12), if an optimal solution of
is obtained, the derivative of the objective at the optimal solution in any direction
is zero, satisfying
Through calculating Expression (30), we obtain the relationship between
and
Expression (31) is a structural static equilibrium equation, and is also a constraint on
in optimization problem (29). In Expression (31), letting
yields
Substituting Expression (32) into Expression (12) yields the optimal value
of the objective
Through substituting Expressions (12) and (33) into the optimization problem (29), Expression (29) is transformed into an unconstrained optimization problem
If and are given, in Expression (34) is a quadratic and concave functional with respect to , due to and . If is given, is a linear function with respect to and .Through using the Univariate Search Method to solve Expression (34), if and are given, the maximum value of can be found by solving Expression (31) for , and if is given, the maximum value of will be reached on the lower bounds of and . So, the lower bounds of and must be larger than zero to ensure that Expression (29) has a finite optimal solution. In addition, the upper bounds of and should also be constrained to avoid the trivial solution . Therefore, when the optimization objective is to maximize the mutual-energy inner product, as shown in Expression (29), its optimal structural model would be the minimum stiffness structure, and the selected feature belongs to a low-frequency eigenfunction subspace. On the contrary, if the optimization objective is to minimize the mutual-energy inner product, the optimal structural model would be the maximum stiffness, and the selected feature would be mapped to a high-frequency eigenfunction subspace.
In addition, when using the mutual-energy inner product to extract feature information
of the samples in
, the feature information
of the samples in
should be suppressed. So, a small statistical mean value
is given
Here, we may set
to be zero or even negative, and impose constraints on the structural model
In Expression (31), setting
yields
. Replacing
with
, and exchanging
,
, we have
If Expression (36) satisfies
, then
and
are required to be orthogonal with respect to the mutual-energy inner product. Although the means of the two classes of the samples are generally not orthogonal in the continuous function space
, i.e.,
, the orthogonality of
and
can be easily realized according to Expression (37). For example, if setting
and dividing the domain
into two sub-regions according to the same or opposite signs of
and
, we can adjust
in the two sub-regions and control the positive and negative work performed by the external forces
on the deformations
, so as to make the total work
in Expression (37) zero. According to Expression (25), this can also be understood as designing a structural model and adjusting its eigenfunctions and eigenvalues, so as to use these eigenvalues as weights to achieve the weighted orthogonality of
and
. Further,
can be regarded as the relaxation of the orthogonal constraints on the mutual-energy inner product, which can be realized by adjusting
and
to make
. Geometrically, this means that the angle between
and
in the mutual-energy inner product space
is not an acute angle. If
is required to be minimal
based on Expression (12), similar to the discussion on Expression (29), the optimization problem (38) can be transformed into an unconstrained form
where
is a slack variable introduced to relax the constraint, which is the constraint of the static equilibrium equation describing the structural deformation due to
and
acting on the structure simultaneously. The objective can be expressed as
Obviously, if and are given, is a quadratic functional of , , and . is convex with respect to and , and is concave with respect to . If , and are given, is linear with respect to and .
In order to design a feature coordinate to classify the samples in
, the objective is to maximize
first. By combining the Expressions (28) and (35), the optimization objective can be expressed as
Then, to improve the classification accuracy, the distributions of the samples in and along the feature coordinate should also be considered, and their variances should be small. The variances of and are high-order functions of , , and , so putting them into the optimization objective function (41) will destroy its low-order characteristics.
In order to improve the computational efficiency, the sum of the absolute values of the sample deviations from the mean are used to replace the variances, and only some samples in
and
are selected for calculation. In the subset
, we only select
samples
, whose components on
are less than
, and calculate their mean absolute deviation
. In the subset
, we only select
samples
, whose components on
are larger than
, and calculate their mean absolute deviation
.
and
can be expressed as
Through using Expressions (41) and (42), and considering the means and the mean absolute deviations of the samples, the optimization objective can be written as
where
is a weight variable, satisfying
. To simplify Expression (42), the auxiliary deformation function
is defined as
where
can be regarded as an external force corresponding to
, satisfying
By substituting Expressions (41), (42), (44) and (45) into Expression (43), the optimization objective is simplified as
Here,
is a combination of the deformation functions, and can be expressed as
In order to improve the generalization of the data classifier, regularizers should be added to the optimization model. Here,
and
stand for the 1-norms of
and
, respectively, and are used as regularizers to avoid increasing the order of the optimization model. Meanwhile, these regularizers are treated as two constraints by directly setting the values of
and
. Due to
and
,
and
can be simply written as
It should be noted that objective (46) is built by taking the mean
of
as the reference feature and selecting the deformation
as the reference feature coordinate axis. If other deformation functions
are selected as the reference feature coordinate axis, the results are similar. For example,
can be set as
,
,
, or others. Through setting
as the reference feature coordinate axis, the optimization model can be summarized as
Here,
,
and
are arbitrary continuous functions on
;
and
, are lower bounds of
and
;
and
are two constants;
,
,
and
are given in Expressions (27), (45) and (47).
and
should be determined according to the reference feature coordinate axis, and can be rewritten as
5. Mutual-Energy Inner Product Feature Coordinate Optimization Algorithm
The EFM is used to solve the differential Equation (1) to realize the mapping from
,
, and
to
,
, and
in the optimization model (49). We divide the domain
into
elements
, and assume the
element
has
nodes. For the
node in
, its global coordinate in
, deformation value
, and interpolation basis function are denoted as
,
,
, respectively, where
, is the local coordinate of the element
. In this way, for an element, its global and local coordinate relationship
and the element deformation function
can be expressed as [
37]
It is assumed that
is an
-dimensional row vector with the
component
;
is an
matrix with the entry
, where
is the
component of the local coordinate
; and
is an
matrix with the entry
, where
is the
component of the element node coordinates
. Applying Expression (51), the
Jacobi matrix
for the transformation between the global and local coordinates, the deformation function
and its
-dimensional gradient vector
, can be expressed in the concise and compact form
where
is a vector with the component
, which is the deformation value of the
node in the
element, and
is an
matrix. In the optimization model (49), the design variables are
and
. We assume
and
in each element are constants
and
. So, the design variables can be expressed as
and
in
.
Substituting Expression (52) into the mutual-energy expressions (5) and (9) yields
Here,
is an
element stiffness matrix, which is a positive semidefinite symmetric matrix and can be expressed as
In Expression (54),
is a linear function of
and
;
and
are corresponding coefficient matrices; and
is the contribution of the boundary constraint to the element stiffness matrix. If the element boundary does not overlap with the design domain boundary, then
. Here,
,
,
can be calculated by
In Expression (53),
is the equivalent node input vector, resulting from the equivalent action between the force
on the element and the force
on the node, and satisfies
It is assumed that the design domain comprises element nodes. We number these nodes globally, and use two -dimension vectors and to denote the values of and at all the nodes. The components of and are and , where the subscript is the global node number. The component can be calculated through Expression (56). Expression (56) is calculated for each element adjacent to the global node, and is the superposition of the element node corresponding to the global node.
Based on the relationship between the local and global node numbers, Expression (53) can be rewritten as
where
is the global stiffness matrix, an
positive definite symmetric matrix. Substituting Expression (57) into Expression (12) yields
Based on Expression (58), the solution of the differential Equation (1) satisfies
Similarly, assume that the input of Expression (1) is
and the corresponding solution is
;
is the global node vector corresponding to
on
, and
is the element node vector corresponding to
on
; and
is the equivalent node input vector corresponding to
. We have
Similarly to the derivation of Expression (57), through using Expressions (59) and (60), the mutual-energy expression of
and
can be derived
In Expression (61), the first equation is used for model optimization, and the second equation is used for data classifier training and prediction, avoiding the need to solve for the Expressions (59) and (60).
After discretizing the design domain by finite elements, the differential Equation (1) is converted into a system of linear equations, and the mutual-energy definition (5) can be expressed by the matrix and vector product. In this way, the optimization model (49) can be rewritten in the vector form
Here,
is the finite element node vector corresponding to the selected reference feature coordinate, and can be the statistical features of the sample sets or their combination; for example,
Meanwhile,
,
, and
are the finite element node vectors corresponding to the mean and deviation of the samples, and
is the temporary node vector generated by the mean and deviation. Expression (47) can be rewritten as
The significant advantage of the optimization model (62) is that
is a positive definite symmetric matrix and is linear with respect to the design variables
and
, and meanwhile, the coefficient matrices corresponding to the components of the design variables are positive semidefinite matrices, convenient for the algorithm design. Intermediate variables
,
,
are functions of the design variables and can be calculated by using the linear equations, and the optimization model (62) can be solved by the sequential linearization algorithm. The objective
and the constraint
are nonlinear, and their derivatives with respect to the design variables need to be calculated. The derivative of
with respect to
is
where
and
are determined by taking the derivative of
and
with respect to
Substituting Expression (66) into Expression (44) yields
Substituting Expression (54) into Expression (67) yields
. Similarly,
can also be computed
The Expressions (63) and (64) show that
and
are linear combinations of
,
, and
. According to the superposition principle,
and
also satisfy equations similar to Expression (66), and have exactly the same derivation as Expression (68). So, we obtain
Optimization Algorithm 1: Mutual-energy inner product feature coordinate optimization algorithm
Based on Expressions (68) and (69), the optimization model (62) can be solved by the sequential linearization algorithm. The algorithm steps are summarized as follows:
- (1)
Use vectors to represent the sample data
Convert the sample data
in the training subsets
and
into the finite element node vectors
. Based on Expression (70), first calculate the element node vectors
, and then use them to assemble the global node vector
.
- (2)
Set the optimization constants and initial values of the design variables
- ①
Set the optimization constants
Set , the weight of the mean and deviation, with the requirement ; set the total amount , and the lower bounds , of the design variables; set the moving limit of the design variables for the linear programming; set the design variable minimum increment and the objective function minimum increment , which are used to determine if the optimization ends or not.
- ②
Set the initial values of the design variables
Set , . Generally, set , .
- (3)
Calculate the current value of the objective function
- ①
Calculate the element stiffness matrices and assemble the global stiffness matrix
Based on Expressions (54) and (55), calculate the element stiffness matrices . The element stiffness matrix is linear with respect to and , and the coefficient matrices are determined only by the element interpolation basis functions, so the calculation can be performed prior to the optimization to speed up the optimization process. Then, assemble the global stiffness matrix according to the node numbers. Since is a positive definite symmetric matrix, through performing Cholesky decomposition on it, we can have , where is a lower triangular matrix.
- ②
Compute the mean vectors and , and select the reference feature coordinate axis
where
and
represent the means of the sample data in
and
;
and
are the sample numbers in
and
;
can be selected and calculated by Expression (63).
- ③
Compute the deviation vector and the intermediate vector
where
is the deviation of the sample data and only the sample data in
and
are calculated.
and
represent the projections of the means of the sample data in
and
on
. After
,
,
are obtained,
can be obtained by Expression (64).
- ④
Calculate the current values of the objective function and the constraint
Based on the optimization model (62), the current values of
and
can be calculated by
- (4)
Calculate the gradient vectors of the objective function and the constraint
Apply Expressions (68) and (69) to calculate , , and . Then, express them as the compact gradient vectors , , and . Here, is defined as and the other gradient vector definitions are similar. In Expressions (68) and (69), and are only determined by the element interpolation basis functions and are constant matrices independent of the design variables. So, and can be calculated prior to the optimization, and the gradient vectors of and can be achieved through the mapping relationship between the local and global node numbers.
- (5)
Obtain increments of the design variables by solving the sequential linearization optimization model
- ①
Construct the sequential linearization optimization model
where the design variables
,
;
and
are increments of the design variables, and their
components are
and
;
,
, and
,
can be calculated by
- ②
Solve the sequential linearization optimization model (74) to obtain and
When solving Expression (74), slack variables are added to to facilitate the initial feasible solution construction.
- (6)
Determine whether to end the optimization iteration
- ①
Store the design variables, the objective function, and the constraint function of the previous step of the sequential linearization optimization.
Store the design variables , , the objective function value , and the constraint function value .
- ②
Update the design variables and the objective function value.
Let , , then execute step (3) to update the objective function value .
- ③
Determine whether to end the iteration.
If or , then end the iteration. Otherwise, if , go to step (4) to continue the iteration; if , reduce the moving limits of the design variables by letting ; here, , then go to step (5) to iteratively calculate the design variable increments and .
6. Algorithm Implementation and Image Classifier
Image classification is used to determine if an image has certain given features and can be realized by algorithms for extracting the feature information of the image. Applying the mutual-energy inner product to extract the image features has the advantage of enhancing the feature information and suppressing other high-frequency noise. If we select multiple features of an image, we can design multiple mutual-energy inner products, and each mutual-energy inner product can be regarded as one feature coordinate of the image. Using multiple mutual-energy inner products to characterize an image is equivalent to using multiple feature coordinates to describe the image, or equivalent to representing the high-dimensional image in a low-dimensional space, reducing the dimensionality of image data.
This part will discuss the implementation of Optimization Algorithm 1 and its application in 2-D grayscale image classification. Assume that each sample in the training datasets and is a 2-D grayscale image; the domain occupied by the image is rectangular; each image is expressed by pixels; and each pixel is a square with a side length of 1. In this case, and .
6.1. Vectorized Implementation of Optimization Algorithm 1
While using FEM to discretize the design domain, we regard each pixel as a finite element and divide the domain
into
quadrilateral elements
, i.e.,
and
. In
, the global element numbering uses column priority, where the upper left corner element is numbered 1 and the lower right corner element is numbered
. A planar quadrilateral element is used to interpolate the deformation functions. Each element has four nodes, so the total number of nodes is
, and the total number of boundary nodes is
. The global node numbering also uses column priority, where the upper left corner node is numbered 1 and the lower right corner node is numbered
. The interpolation basis functions of the quadrilateral element are
where the domain of the definition is square and is expressed as
. The element nodes are four corner points of the quadrilateral. The node with the coordinate
is numbered 1, in counter-clockwise order, and the other nodes with the coordinates
,
,
are numbered 2, 3, and 4, respectively. The interpolation basis function
corresponds to the
node, where
is the corresponding node coordinate. The mapping relationship between the element node numbers and the global node numbers can be described by an
matrix
, and its
row corresponds to the
element. If
denotes its entry at the
row and the
column, then
,
,
,
are the global node numbers corresponding to the element node numbers 1, 2, 3 and 4 of the
element. So, we have
where
is a module when
is divided by
. Since all the elements are same squares, the isoparametric transformation
in Expression (51) is actually a scaling transformation. Through substituting
into Expressions (52) and (55), we can find that the coefficient matrices
and
are independent of the element node numbers. So, we use
and
to express
and
, and calculate them directly by
When a side of an element overlaps with the boundary of the domain
, the influence of the boundary conditions
in Expression (1) on
should be considered, so a
matrix
should be calculated. Assume that the
side of the element overlaps with the boundary of
and the entry in the
row and
column of
is
. Then, the non-zero entries in
can be calculated by
In Expression (78), the subscripts and stand for the starting and end points of the side of the element, where the starting point is the element node numbered and the end point is determined along the side in counterclockwise order; is a constant, equal to the approximate value of on the side. In this paper, we handle the influence of on while assembling the global stiffness matrix. We just simply replace the subscripts and of in Expression (78) with global node numbers, then directly use them to assemble the global stiffness matrix.
Because each element corresponds to a pixel, we can assume that its grayscale value is a constant
. In this way, a sample image
can be expressed as
. Through substituting Expression (75) into Expression (70), the relationship between element node vectors and image grayscale values can be obtained
where
, which can be regarded as mapping coefficients from the image grayscale to the element node vector.
While using element stiffness matrices and element node vectors to assemble the global stiffness matrix and the global node vector , the functions for generating a sparse matrix in MATLAB R2020a or the Python 2.7 SciPy module can be used, and the input arguments include the row index vector, the column index vector, and the values of the non-zero entries. More importantly, these sparse matrix generation functions can sum the non-zero entries with the same indexes, which is consistent with the process of assembling and .
In order to convert the image grayscale vector
to the global node vector
, a
matrix
should first be calculated, whose
column corresponds to the element node vector
. Then,
is converted to a
-dimensional column vector
in column-major order. Obviously, if we divide the components of
into multiple groups in sequence and each group includes four components, then the
group corresponds to the element node vector
.
can be calculated by
where the function
can convert the dimension of the matrix
into
while keeping the total number of the entries unchanged.
Through the mapping matrix
, the position indexes of components of
in the global node vector
can be obtained. We transpose the
matrix
to the
matrix
, whose
column corresponds to global node numbers of the
element, and then convert
to a
-dimensional column vector
in the column-major order.
can be figured out by
is the row index vector for generating by a sparse matrix generation function. Since has only one column, we use to denote a -dimensional column index vector and set all the components of to 1. Through substituting , , into the sparse matrix generation function, we can yield .
Similarly, the global stiffness matrix
can be assembled by using the sparse matrix generation function. A vector
related to
should be first calculated by
where the operator
denotes the Kronecker product of the matrices;
is a
matrix;
and
are the design variables. If
is divided into multiple blocks from left to right and each block is a
matrix, the
block is the calculation result of the first two terms of
in Expression (54), without including
. Therefore, if
are divided into multiple blocks in sequence and each block includes 16 components, the
block will correspond to a 1-dimensional vector converted from the
element stiffness matrix in the column priority. We set
, and use
,
to denote the row indexes and column indexes of the entries in the global stiffness matrix. Then,
,
corresponding to the components of
can be calculated by
As mentioned above, the constraint on the design boundary can generate additional stiffness for the adjacent elements. If we regard an element side overlapping with as a 2-node line element, then its stiffness matrix will be a matrix , which can be figured out by Expression (78). Similarly, these line element stiffness matrices can be assembled into the global stiffness matrix. While designing an image classifier based on the mutual-energy inner products, we set a fixed boundary for Expression (1), i.e., . This boundary condition can be handled by adding a relatively large number to the diagonal entries of , where its diagonal entries correspond to the boundary node numbers. The sparse matrix generation function is used to implement this boundary condition. First, we set the dimension of the vector as , which is the total number of the boundary nodes, and set all the components of to . Meanwhile, we let the -dimensional row and column index vectors be the same, i.e., , and set their components to be the boundary node numbers. Finally, we combine and , and , and , respectively, and input them into the sparse matrix generation function to obtain .
Based on Expressions (68) and (69), the gradients of the objective and the constraint can be efficiently obtained by using
. For example, if we have two
-dimensional global node vectors
and
, we can adopt fancy indexing to generate two
matrices
and
whose
rows correspond to the node vectors of the
element. According to Expression (69), the objective function gradients
,
can be calculated by
where
stands for multiplying the corresponding entries of the matrices, and
is summing the rows of a matrix to obtain a column vector. Mathematically, Expression (84) can be written as
and
, where the function
is used to extract the main diagonal entries from a square matrix. Similarly, the constraint function gradients
,
can be calculated by replacing
,
with
,
.
6.2. Image Classifier
For a given training dataset
, in order to use Optimization Algorithm 1 to construct the mutual-energy inner product coordinate axes
, we select the subset
of
as the reference training set and select the mean of samples of the class “0” or the class “1” in
or a combination of these means as the reference feature
. The subset
is gradually generated as the coordinate
is generated. Prior to generating the coordinate
,
mutual-energy inner product coordinate axes
have been generated and there are
subsets
. One of the
subsets is selected as a subset
to generate the coordinate
. In order to explain how the generation of new axes work, we use a set
to manage the
generated subsets, i.e.,
. If
has
samples of the class “0” and
samples of the class “1”, the subset
in
is taken as the reference training sample set
to generate
and its index
satisfies
After determining the subset and the reference feature , can be obtained by Optimization Algorithm 1. Next, we divide into two subsets. First, for each sample in , we calculate its coordinate component on the axis by ; we calculate and , the means of samples of the class “0” and the class “1” and set a threshold . Second, according to and , we divide into two subsets satisfying and . Finally, we add and into , and delete from . At this time, contains training sample subsets, and one of them will be selected to calculate the coordinate axis .
The following summarizes the detailed steps of generating mutual-energy inner product feature coordinates.
Algorithm 2: Mutual-energy inner product feature coordinates generation
- (1)
Let and ;
- (2)
According to Expression (85), select in to generate the coordinate axis and delete from ;
- (3)
Adopt Optimization Algorithm 1 to calculate based on the determined reference subset and the selected reference feature ;
- (4)
For each sample in , calculate its coordinate components on the axis , the means and of the class “0” and the class “1”, as well as the threshold ;
- (5)
According to and , divide into two subsets and , and add them into ;
- (6)
Judge if , set and go to Step (2); otherwise, stop.
After generating mutual-energy inner product coordinate axes
by Algorithm 2, the coordinate components
of each sample in
can be calculated and are represented by a feature vector
. Based on
, a simple Gaussian classifier is used to classify the images. We use
to represent a training dataset comprising
samples, where the subscript
is the class index of the samples. A Gaussian classifier can be used to classify the samples into multiple classes. We use
to indicate the class of a sample and use
to denote the total number of classes. In
, the probability of the class
is
Furthermore, it is assumed that, for the samples in the same class, their feature vectors
follow the Gaussian distribution
where
is the mean of
;
is the covariance matrix of
; and the subscript
corresponds to the class
. Using the training sample dataset
, their maximum likelihood estimates can be calculated by [
38]
Here,
. Based on Expressions (86) and (87), when giving the feature vector of a sample, the posterior probability of the sample belonging to the class
is
where
is the posterior probability, and
can be expressed as
Finally, the class of the sample is determined based on the posterior probability
6.3. Numerical Examples
The MNIST dataset has become one of the benchmark datasets in machine learning. It comprises 60,000 sample images in the training set and 10,000 sample images in the test set, and each one is a 28-by-28-pixel grayscale image of the handwritten digits 0–9. In this section, we will use the MNIST to design Gaussian image classifiers based on Optimization Algorithm 1.
Before designing Gaussian image classifiers, image preprocessing is conducted to align the image centroids and normalize the sample images. In Optimization Algorithm 1, the selected parameters are , , , , , , and .
6.3.1. Binary Gaussian Classifier: Identify Digits “0” and “1”
The MINST training set comprises 6742 samples “1” and 5923 samples “0”. We select the difference between the means of samples “1” and “0” as the reference feature, i.e.,
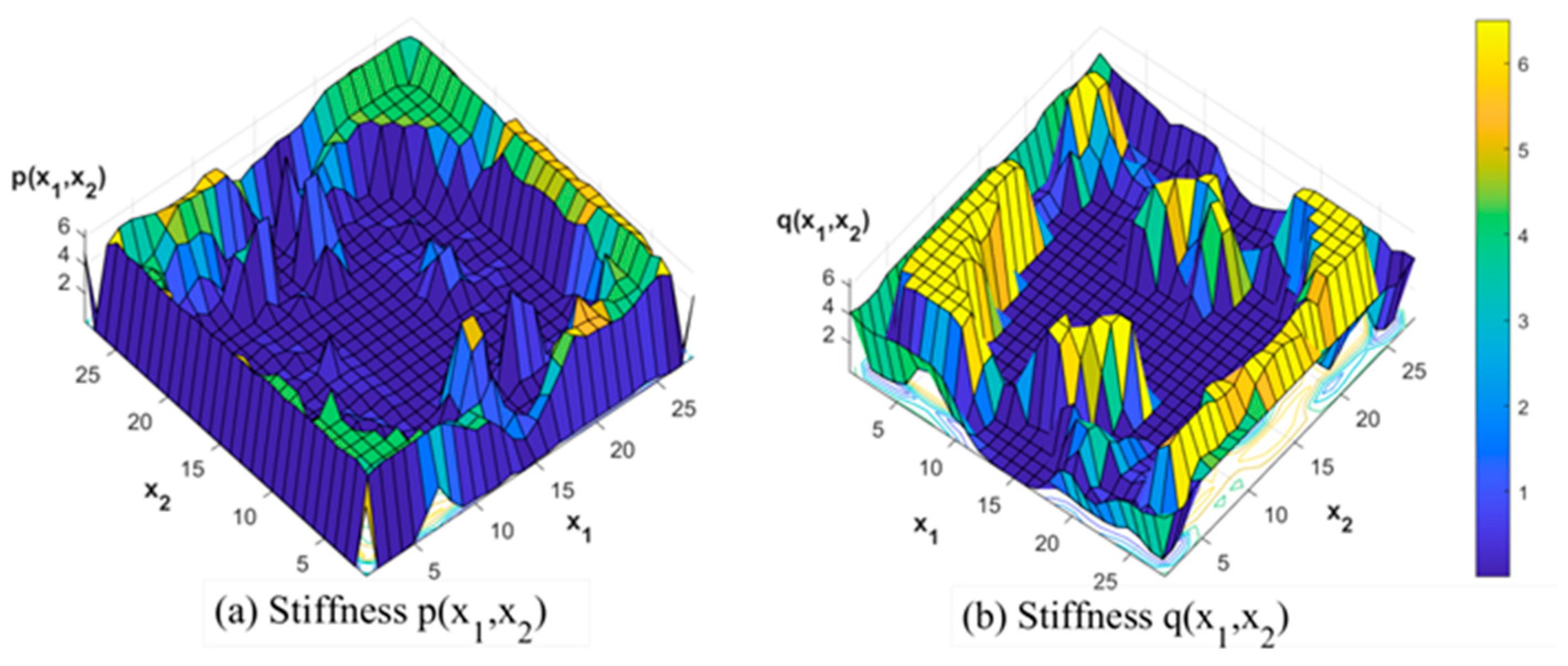
. Optimization Algorithm 1 converges after 166 iterations. The means of samples “1” and “0”, the design variables, and the reference feature coordinate
, are visualized in
Figure 1,
Figure 2 and
Figure 3. Due to obvious differences in the mean feature, digits “0” and “1” can be identified using only one mutual-energy inner product coordinate
.
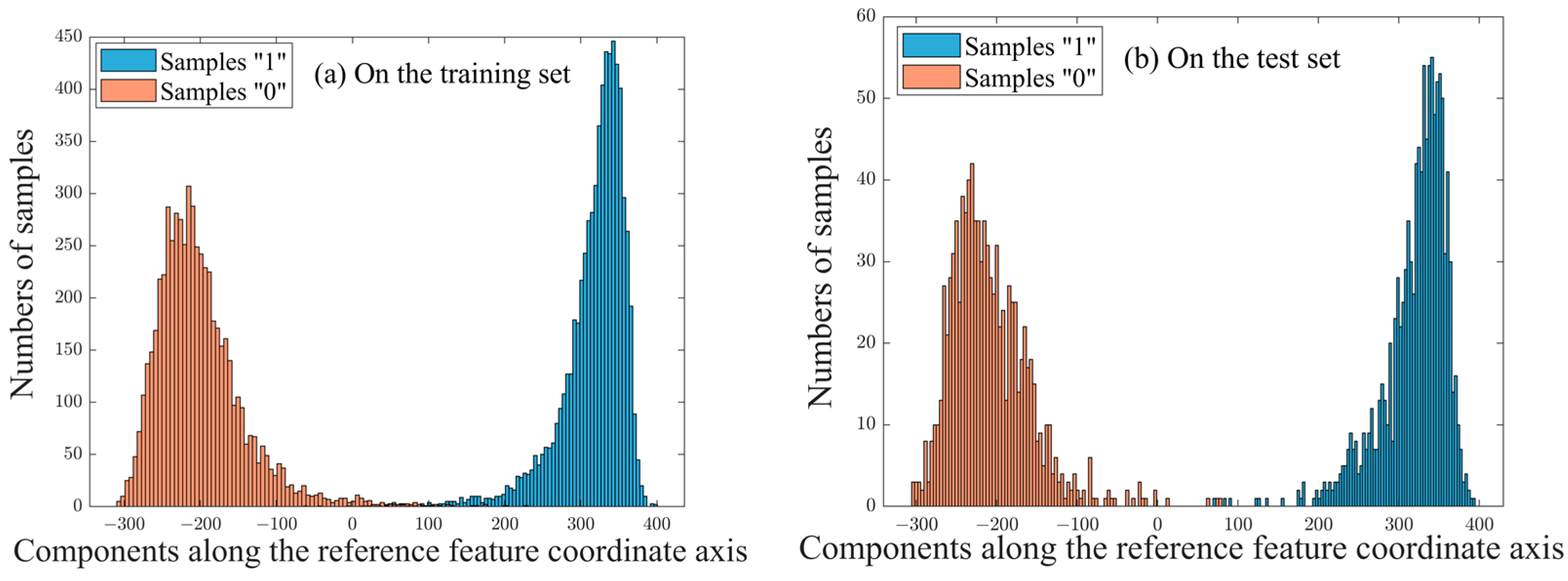
Figure 4a shows the training sample distribution in accordance with the components on
.
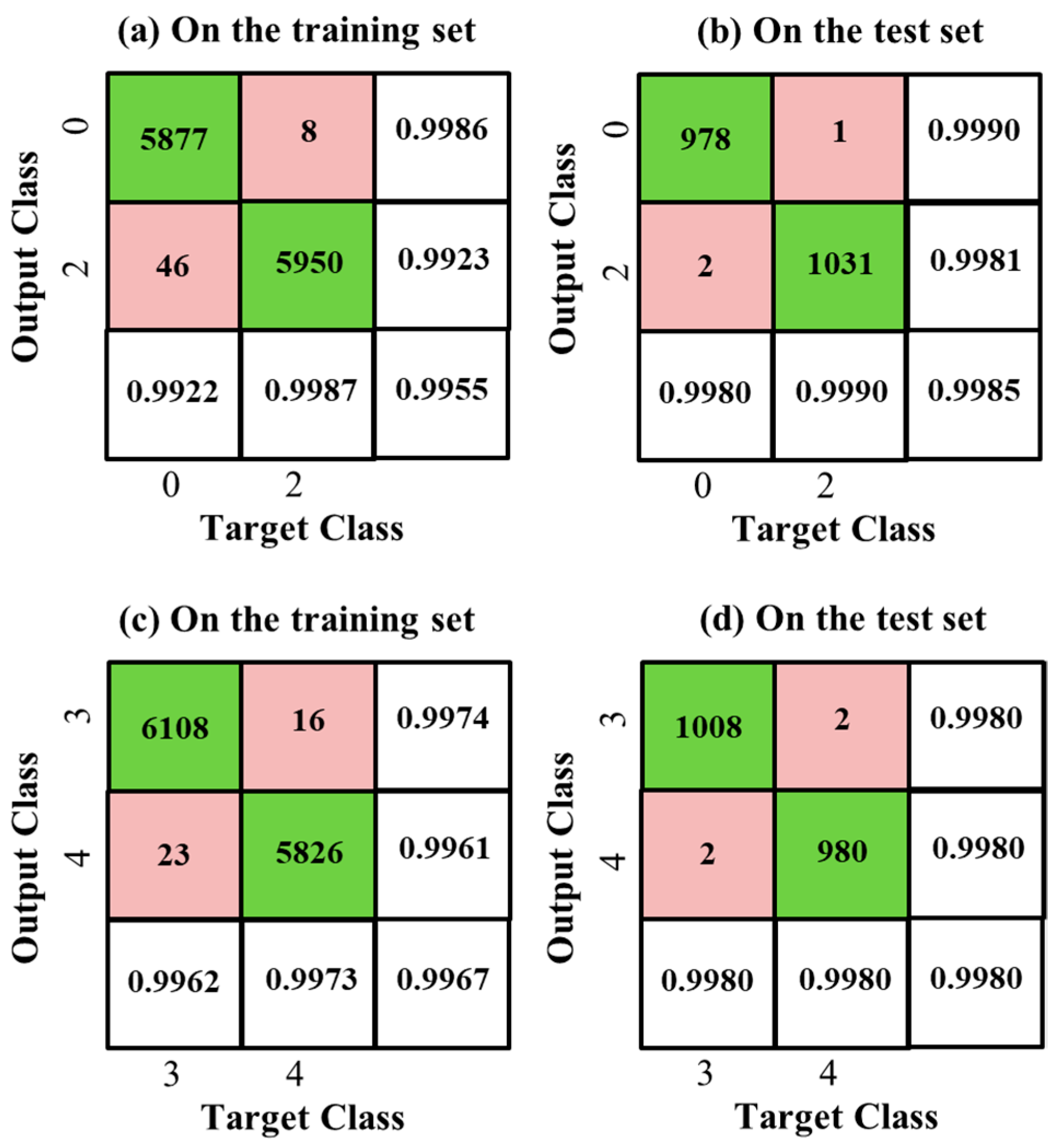
Figure 5a gives the Confusion Matrix of the classification results, where the horizontal and vertical axes correspond to the target class and the output class of the classifier, respectively. In the Confusion Matrix, the column on the far right shows the precision of all the examples predicted to belong to each class, and the row at the bottom shows the recall of all the examples belonging to each class; the entry in the bottom right shows the overall accuracy; the diagonal entries are the correctly classified numbers of digits “0” and “1” and the off-diagonal entries correspond to the wrong classifications. This binary Gaussian classifier on the training set achieves a very high overall accuracy of 99.66%, shown at the bottom right of the Confusion Matrix.
The binary Gaussian classifier is tested on the MINST test set, which comprises 1135 samples “1” and 980 samples “0”. The test results are visualized in
Figure 4b and
Figure 5b. Its overall accuracy can reach 99.91%, higher than that on the training set.
6.3.2. Binary Gaussian Classifier: Identify Digits “0” and “2”
The MINST training set comprises 5958 samples “2” and 5923 samples “0”, and the MINST test set comprises 1032 samples “2” and 980 samples “0”. Similarly to the previous classifier, the reference feature is also selected as
. The difference in the mean features of digits “2” and “0” is not as significant as that of digits “1” and “0”. If only one mutual-energy inner product coordinate is used for classification, the accuracy is only 96.72% on the training set and 97.81% on the test set. In order to improve the classification accuracy, we use Algorithm 2 to generate 60 mutual-energy inner product coordinates based on the training sample set and its subsets, and construct a 60-dimensional Gaussian classifier. The Confusion Matrices of the classification results are given in
Figure 6a,b, showing an overall accuracy of 99.55% on the training set and a higher overall accuracy of 99.85% on the test set.
6.3.3. Binary Gaussian Classifier: Identify Digits “3” and “4”
The MINST training set comprises 6131 samples of “3” and 5842 samples of “4”, and the MINST test set comprises 1010 samples of “3” and 982 samples of “4”. Here, we select the means of samples “3” and “4” as reference features, i.e.,
and
, and then use Algorithm 2 to generate 50 mutual-energy inner product coordinates, respectively, finally forming 100 classification coordinates. Because these coordinates are not linearly independent, we use matrix singular value decomposition to construct a 50-dimensional Gaussian classifier.
Figure 6c,d is the Confusion Matrices, showing an overall accuracy of 99.67% on the training set and a higher overall accuracy of 99.80% on the test set.
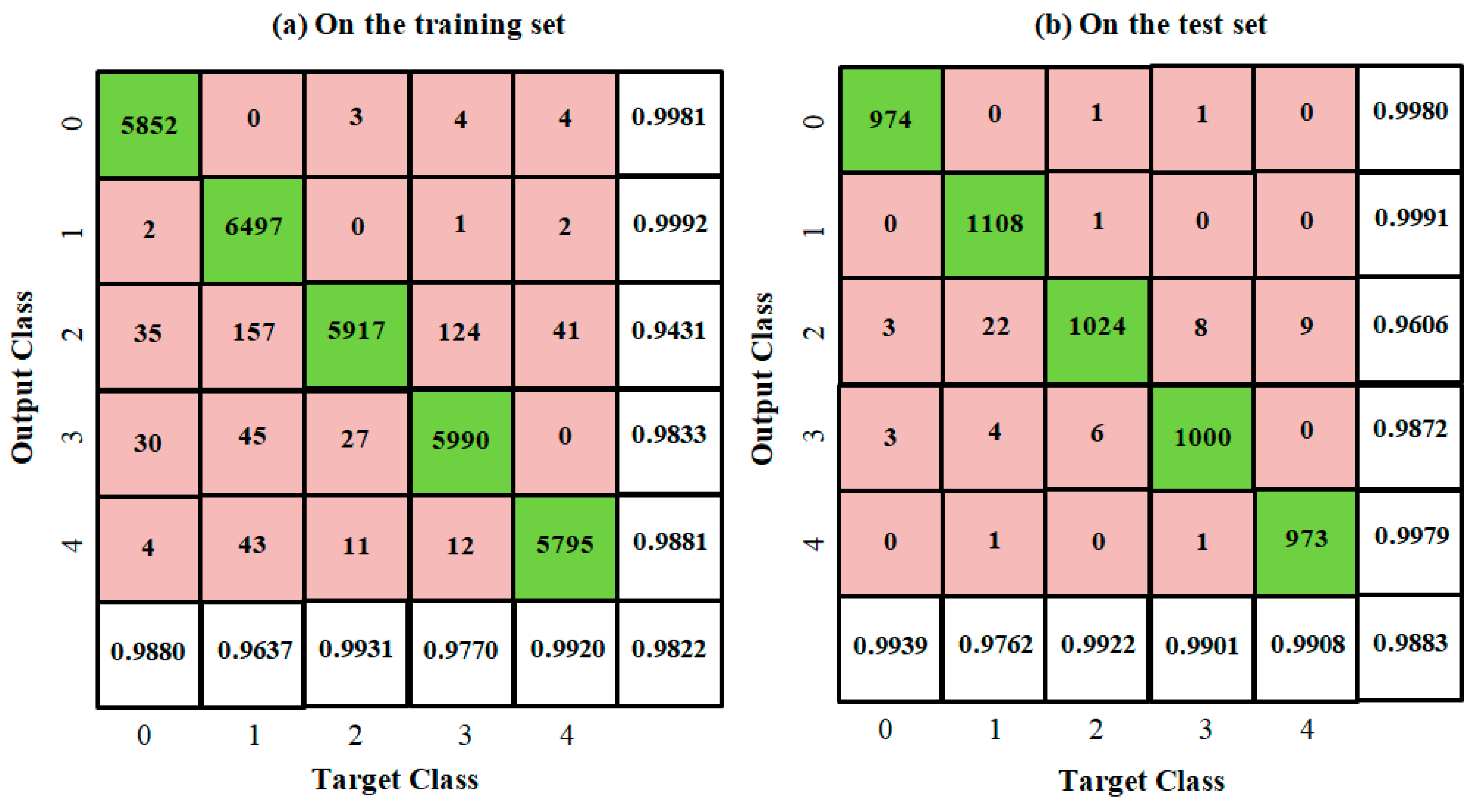
6.3.4. Multiclass Gaussian Classifier: Identify Digits “0”, “1”, “2”, “3” and “4”
In the training set, we select one digit from samples “0”, “1”, “2”, “3” and “4” as the first class and the other training samples of the five digits as the second class, and we take the two classes as the training sample set. Then, we select the difference between the means of the samples in the two classes as the reference feature, i.e.,
, and use Algorithm 2 to generate 120 mutual-energy inner product coordinates. In this way, we construct 5 training sample sets and finally generate 600 coordinates. However, many of them are linearly dependent; in order to identify the digits “0”, “1”, “2”, “3” and “4”, we use matrix singular value decomposition to reduce its dimensions from 600 to 60 and construct a 60-dimensional multiclass Gaussian classifier.
Figure 7 shows an overall accuracy of 98.22% on the training set and a higher overall accuracy of 98.83% on the test set.
7. Discussion
Based on the solution space of the partial differential equations describing the vibration of a non-uniform membrane, the concept of the mutual-energy inner product is defined. By expending the mutual-energy inner product as a superposition of the eigenfunctions of the partial differential equations, an important property is found: the mutual-energy inner product has the significant advantage of enhancing the low-frequency eigenfunction components and suppressing the high-frequency eigenfunction components, compared to the Euclidean inner product.
In data classification, if the reference data features of the samples belong to a low-frequency subspace of the set of the eigenfunctions, these data features can be extracted through the mutual-energy inner product, which can not only enhance feature information but also filter out high-frequency data noise. As a result, a mutual-energy inner product optimization model is built to extract the feature coordinates of the samples, which can enhance the data features, reduce the sample deviations, and regularize the design variables. We make use of the minimum energy principle to eliminate the constraints of the partial differential equations in the optimization model and obtain an unconstrained optimization objective function. The objective function is a quadratic functional, which is convex with respect to the variables that minimize the objective function, is concave with respect to the variables that maximize the objective function, and is linear with respect to the design variables. These properties facilitate the design of optimization algorithms.
FEM is used to discrete the design domain, and the design variables of each element are set as constants. Based on these finite elements, the gradients of the mutual-energy inner product relative to the element design variables are analyzed, and a sequential linearization algorithm is constructed to solve the mutual-energy inner product optimization model. Algorithm implementation only involves solving equations with the positive definite symmetric matrix when calculating the intermediate variables and only needs to handle a few constraints in the nested linear optimization module, guaranteeing the stability and effectiveness of the algorithm.
The mutual-energy inner product optimization model is applied to extract the feature coordinates of the sample images and construct a low-dimensional coordinate system to represent the sample images. Multiclass Gaussian classifiers are trained and tested to classify the 2-D images. Here, only the means of the training sample set and its subsets are selected as reference features in Optimization Algorithm 1, and the vectorized implementation of Optimization Algorithm 1 is discussed. Generating mutual-energy inner product coordinates via the optimization model and training or testing Gaussian classifiers are two independent steps. In training or testing Gaussian classifiers, calculating mutual-energy inner products can be converted into calculating the Euclidean inner products between the reference feature coordinates and the sample data, not adding computational complexity to the Gaussian classifiers.
In the MINST dataset, the mutual-energy inner product feature coordinate extraction method is used to train a 1-dimensional two-class Gaussian classifier, a 50-dimensional two-class Gaussian classifier, a 60-dimensional two-class Gaussian classifier, and a 60-dimensional five-class Gaussian classifier, and good prediction results are achieved. The feature coordinate extraction method achieves a higher overall accuracy on the test set than that on the training set, indicating that the classification model is experiencing underfitting. This shows large potential in the achievable accuracy of this method that has not yet been explored.
From the view of theory and algorithm, this feature extraction method is obviously different from the existing techniques in machine learning. Its limitation is the need of the given reference features in advance. In this paper, only the mean features of a sample dataset and its subsets are selected as the reference features to construct Gaussian classifiers. In the future, convolution operation can be adopted to construct other image reference features, such as image edge features, local features, textures [
39], and multi-scale features, and these image features can be combined to generate a mutual-energy inner product feature coordinate system. In addition, other ensemble classifiers, such as Bagging and AdaBoost, can be introduced to improve the performances of the image classifiers. Meanwhile, the feasibility of applying the mutual-energy inner product optimization method to the neural network will also be explored.