Performance Analysis of Reconfigurable Intelligent Surface (RIS)-Assisted Satellite Communications: Passive Beamforming and Outage Probability
Abstract
1. Introduction
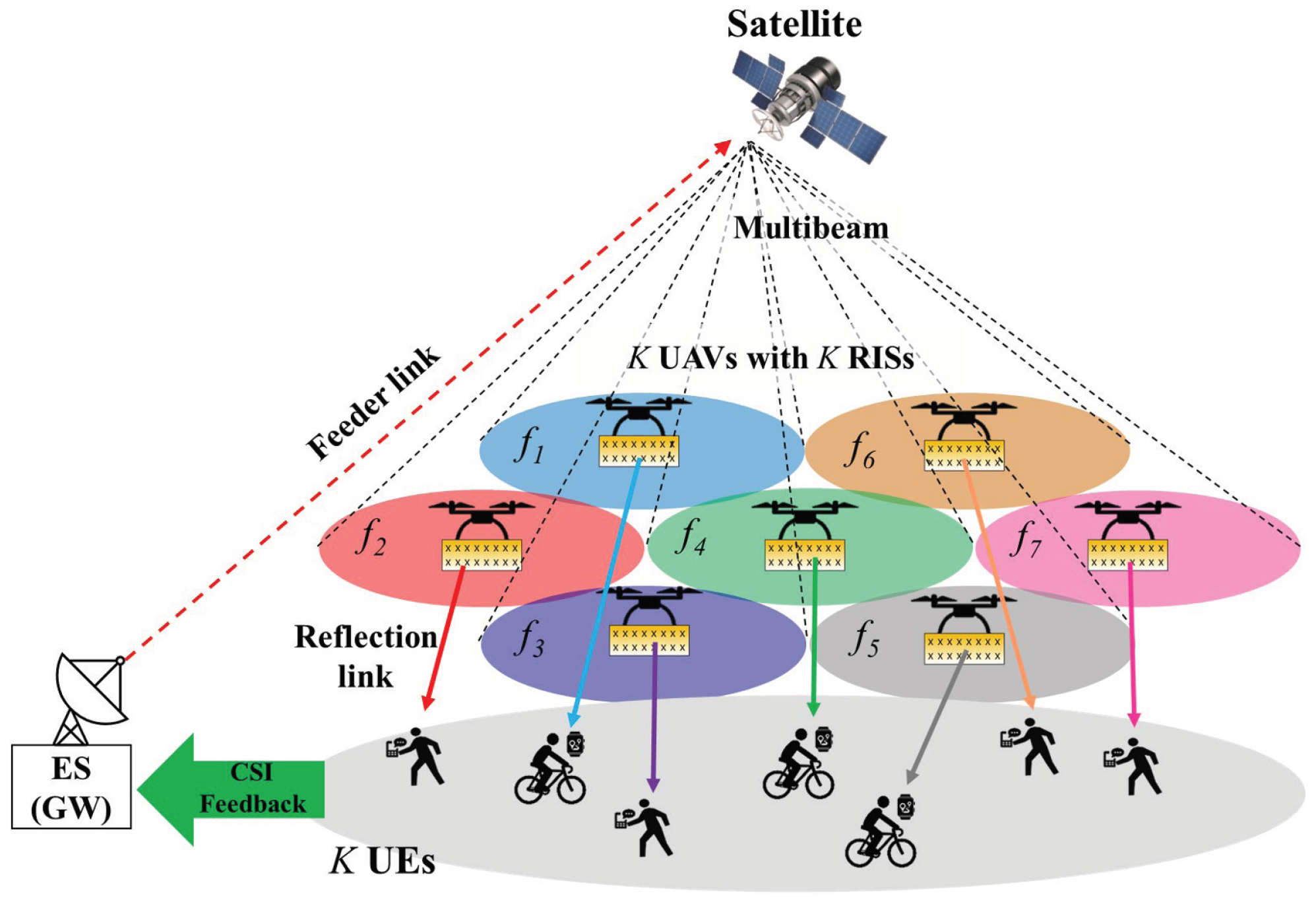
2. System Model
3. Asymptotic Performance Analysis in Unicast System
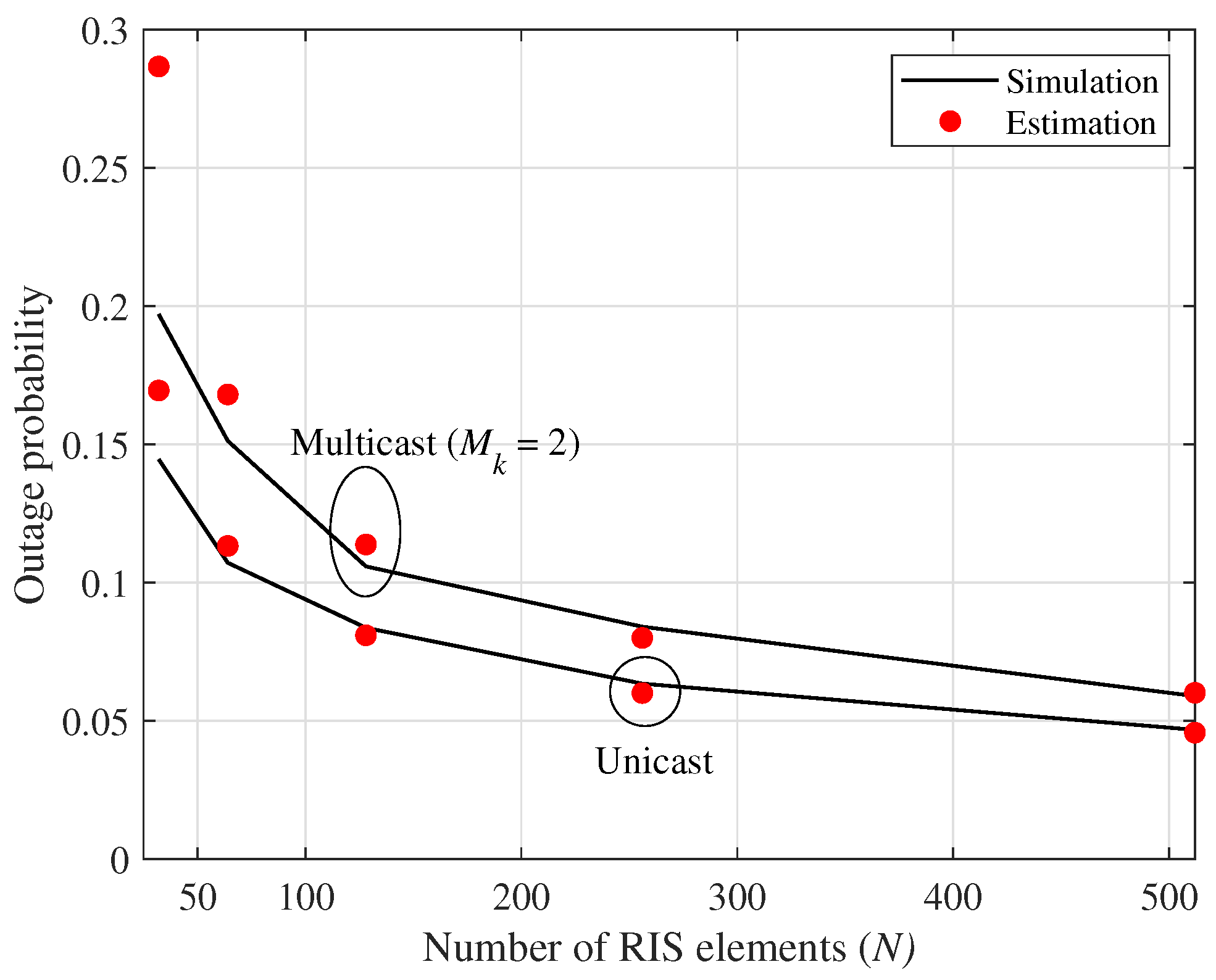
4. Asymptotic Performance Analysis in a Multicast System
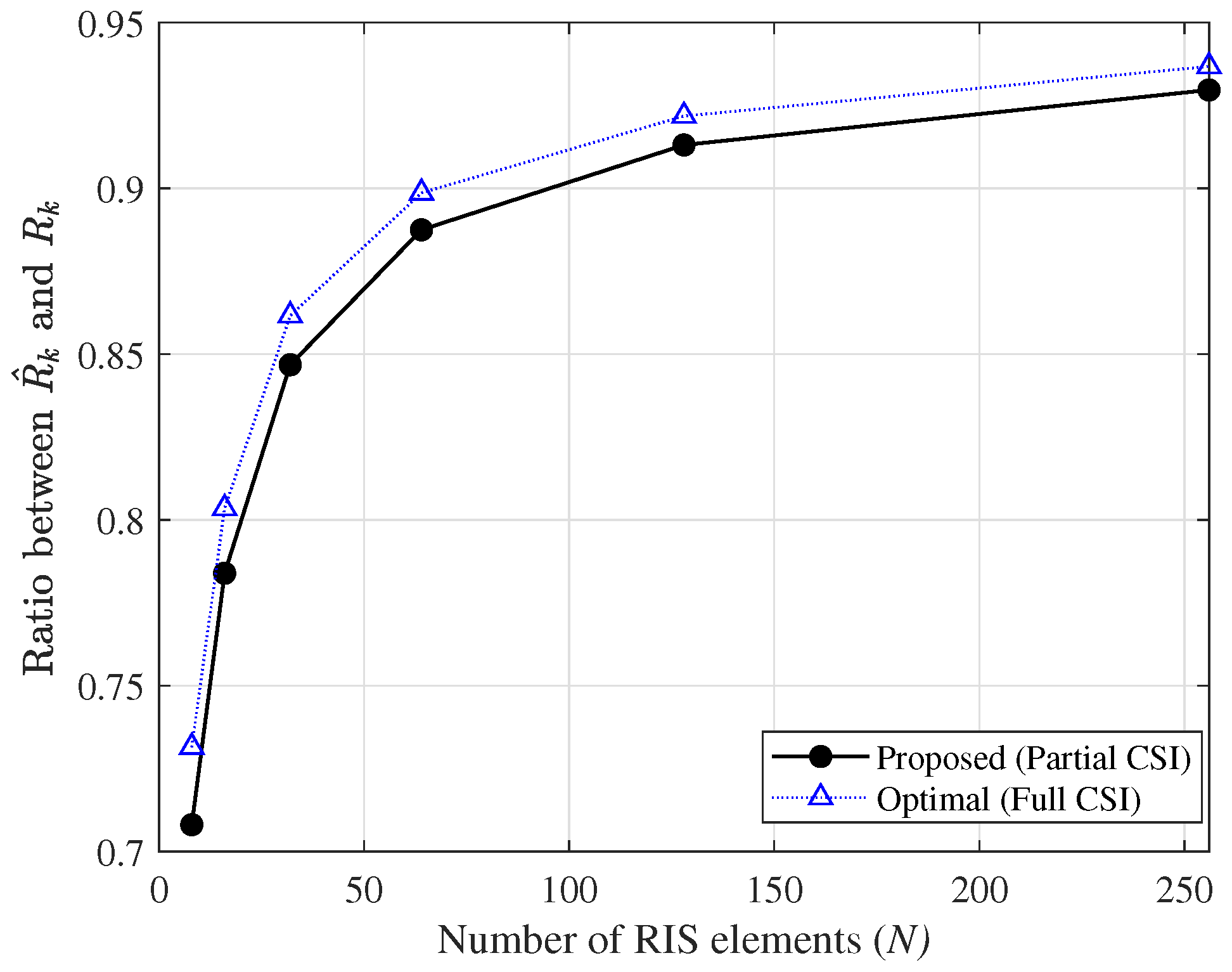
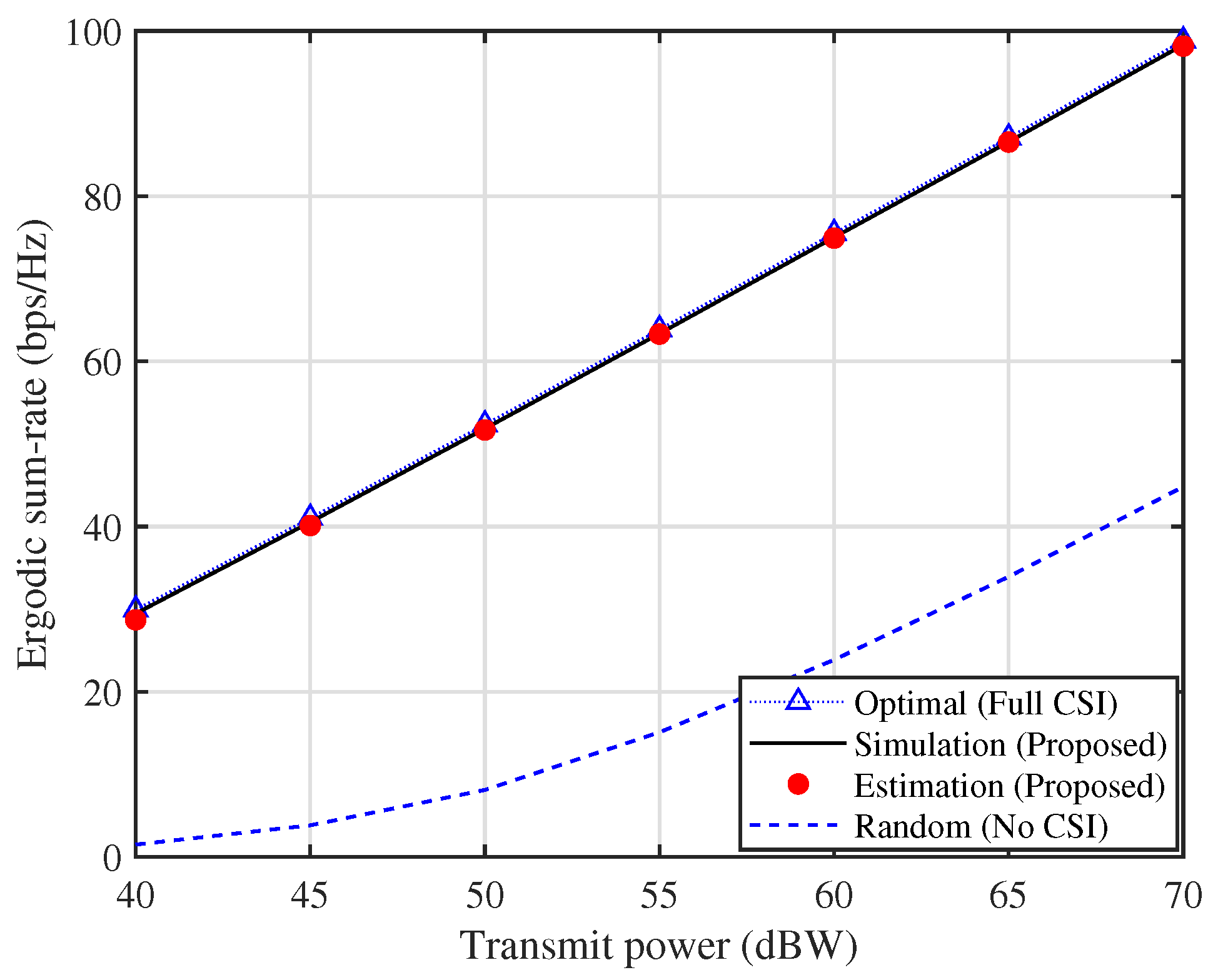
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Q.; Zhang, R. Beamforming Optimization for Wireless Network Aided by Intelligent Reflecting Surface with Discrete Phase Shifts. IEEE Trans. Commun. 2020, 68, 1838–1851. [Google Scholar] [CrossRef]
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Mozaffari, M.; Kasgari, A.T.Z.; Saad, W.; Bennis, M.; Debbah, M. Beyond 5G with UAVs: Foundations of a 3D Wireless Cellular Network. IEEE Trans. Wirel. Commun. 2019, 18, 357–372. [Google Scholar] [CrossRef]
- Lin, Z.; Niu, H.; An, K.; Wang, Y.; Zheng, G.; Chatzinotas, S.; Hu, Y. Refracting RIS-Aided Hybrid Satellite-Terrestrial Relay Networks: Joint Beamforming Design and Optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar] [CrossRef]
- Tekbıyık, K.; Kurt, G.K.; Yanikomeroglu, H. Energy-Efficient RIS-Assisted Satellites for IoT Networks. IEEE Internet Things J. 2022, 9, 14891–14899. [Google Scholar] [CrossRef]
- Khan, W.U.; Lagunas, E.; Mahmood, A.; ElHalawany, B.M.; Chatzinotas, S.; Ottersten, B. When RIS Meets GEO Satellite Communications: A New Sustainable Optimization Framework in 6G. In Proceedings of the IEEE Vehicular Technology Conference, Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Jung, M.; Kim, T.; Son, H. Performance Analysis of RIS-Assisted SatComs Based on a ZFBF and Co-Phasing Scheme. Mathematics 2024, 12, 1257. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Jung, M.; Saad, W.; Debbah, M.; Hong, C.S. On the Optimality of Reconfigurable Intelligent Surfaces (RISs): Passive Beamforming, Modulation, and Resource Allocation. IEEE Trans. Wirel. Commun. 2021, 20, 4347–4363. [Google Scholar] [CrossRef]
- Jung, M.; Saad, W.; Jang, Y.; Kong, G.; Choi, S. Reliability analysis of large intelligent surfaces (LISs): Rate distribution and outage probability. IEEE Wirel. Commun. Lett. 2019, 8, 1662–1666. [Google Scholar] [CrossRef]
- Ramaccia, D.; Sounas, D.L.; Alù, A.; Toscano, A.; Bilotti, F. Phase-Induced Frequency Conversion and Doppler Effect with Time-Modulated Metasurfaces. IEEE Trans. Antennas Propag. 2020, 68, 1607–1617. [Google Scholar] [CrossRef]
- He, J.; Wymeersch, H.; Juntti, M. Leveraging Location Information for RIS-Aided mmWave MIMO Communications. IEEE Wirel. Commun. Lett. 2021, 10, 1380–1384. [Google Scholar] [CrossRef]
- Long, H.; Chen, M.; Yang, Z.; Wang, B.; Li, Z.; Yun, X.; Shikh-Bahaei, M. Reflections in the Sky: Joint Trajectory and Passive Beamforming Design for Secure UAV Networks with Reconfigurable Intelligent Surface. arXiv 2020, arXiv:2005.10559. [Google Scholar]
- Zhang, Q.; Saad, W.; Bennis, M.; Lu, X.; Debbah, M.; Zuo, W. Predictive Deployment of UAV Base Stations in Wireless Networks: Machine Learning Meets Contract Theory. IEEE Trans. Wirel. Commun. 2021, 20, 637–652. [Google Scholar] [CrossRef]
- Joo, C.; Choi, J. Low-delay broadband satellite communications with high-altitude unmanned aerial vehicles. J. Commun. Netw. 2018, 20, 102–108. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, F.; Wu, Q.; Jin, S.; Wu, Y.; Jia, W. Beam Tracking for UAV Mounted SatCom on-the-Move with Massive Antenna Array. IEEE J. Sel. Areas Commun. 2018, 36, 363–375. [Google Scholar] [CrossRef]
- Singya, P.K.; Alouini, M.S. Performance of UAV-Assisted Multiuser Terrestrial-Satellite Communication System Over Mixed FSO/RF Channels. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 781–796. [Google Scholar] [CrossRef]
- Kim, C.; Saad, W.; Jung, M. Performance Analysis of RIS-aided Multibeam Satellite Communication Systems. IEEE Trans. Aerosp. Electron. Syst. 2024, 1–11. [Google Scholar] [CrossRef]
- Jia, M.; Zhang, X.; Gu, X.; Guo, Q.; Li, Y.; Lin, P. Interbeam Interference Constrained Resource Allocation for Shared Spectrum Multibeam Satellite Communication Systems. IEEE Internet Things J. 2019, 6, 6052–6059. [Google Scholar] [CrossRef]
- Jia, M.; Gu, X.; Guo, Q.; Xiang, W.; Zhang, N. Broadband Hybrid Satellite-Terrestrial Communication Systems Based on Cognitive Radio toward 5G. IEEE Wirel. Commun. 2016, 23, 96–106. [Google Scholar] [CrossRef]
- Li, Y.; Yin, C.; Do-Duy, T.; Masaracchia, A.; Duong, T.Q. Aerial Reconfigurable Intelligent Surface-Enabled URLLC UAV Systems. IEEE Access 2021, 9, 140248–140257. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge Univ. Press: Cambridge, UK, 2005. [Google Scholar]
- Ahmad, I.; Nguyen, K.D.; Letzepis, N.; Lechner, G.; Joroughi, V. Zero-Forcing Precoding with Partial CSI in Multibeam High Throughput Satellite Systems. IEEE Trans. Veh. Technol. 2021, 70, 1410–1420. [Google Scholar] [CrossRef]
- Ahmad, I.; Nguyen, K.D.; Letzepis, N. Performance Analysis of High Throughput Satellite Systems with Optical Feeder Links. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Arnau, J.; Christopoulos, D.; Chatzinotas, S.; Mosquera, C.; Ottersten, B. Performance of the Multibeam Satellite Return Link with Correlated Rain Attenuation. IEEE Trans. Wirel. Commun. 2014, 13, 6286–6299. [Google Scholar] [CrossRef]
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO networks: Spectral, energy, and hardware efficiency. Found. Trends® Signal Process. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Cai, X.; Song, J.; Rodríguez-Piñeiro, J.; Mogensen, E.P.; Tufvesson, F. Characterizing the Small-Scale Fading for Low Altitude UAV Channels. In Proceedings of the International Conference on Wireless and Mobile Communications, Tumkur, India, 3–4 December 2021; pp. 16–19. [Google Scholar]
- Lohan, P.; Mishra, D. Utility-Aware Optimal Resource Allocation Protocol for UAV-Assisted Small Cells with Heterogeneous Coverage Demands. IEEE Trans. Wirel. Commun. 2020, 19, 1221–1236. [Google Scholar] [CrossRef]
- Hochwald, B.M.; Marzetta, T.L.; Tarokh, V. Multiple-antenna channel hardening and its implications for rate feedback and scheduling. IEEE Trans. Inf. Theory 2004, 50, 1893–1909. [Google Scholar] [CrossRef]
- Li, Q.; Feng, Z.; Li, W.; Gulliver, T.A. A New Multicast Scheduling Scheme for Cellular Networks. IEEE Wirel. Commun. Lett. 2014, 3, 26–29. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Orbit | LEO (2520 km) |
| Carrier frequency | 2 GHz (L-band) |
| Bandwidth per beam, | 20 MHz, 50 dBW |
| K, , | 7, dB, |
| UE antenna gain | dB |
| Boltzmann’s constant | J/K |
| Noise temperature at UE | 207 K |
| RIS element layout | 2D square lattice (spacing m) |
| Average rain attenuation | 3 dB |
| , , | 10, 1 km, km |
| , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, M.; Son, H. Performance Analysis of Reconfigurable Intelligent Surface (RIS)-Assisted Satellite Communications: Passive Beamforming and Outage Probability. Mathematics 2024, 12, 3781. https://doi.org/10.3390/math12233781
Jung M, Son H. Performance Analysis of Reconfigurable Intelligent Surface (RIS)-Assisted Satellite Communications: Passive Beamforming and Outage Probability. Mathematics. 2024; 12(23):3781. https://doi.org/10.3390/math12233781
Chicago/Turabian StyleJung, Minchae, and Hyukmin Son. 2024. "Performance Analysis of Reconfigurable Intelligent Surface (RIS)-Assisted Satellite Communications: Passive Beamforming and Outage Probability" Mathematics 12, no. 23: 3781. https://doi.org/10.3390/math12233781
APA StyleJung, M., & Son, H. (2024). Performance Analysis of Reconfigurable Intelligent Surface (RIS)-Assisted Satellite Communications: Passive Beamforming and Outage Probability. Mathematics, 12(23), 3781. https://doi.org/10.3390/math12233781







