Abstract
This article is devoted to the practical application of multi-operations theory to the construction of decision-making systems and the description of the subsequent research results. Unlike classical multi-valued and fuzzy logic, where events are described by only two logical values, namely, “true” and “false”, when there are various types of uncertainty between these two states, the theory of multi-operations can be used to describe events using a larger number of logical values for the uncertainties between these states. This article demonstrates a new approach to processing input information using rank 3 multi-operations, i.e., considering input information for a set of three logical values and five values of uncertainty. This approach allows for saving time and resources when forming a subject area model for decision-making systems and when working with specific users. The application of this approach is illustrated in the article by using the example of determining the area of human disease. When testing this system, which is built on the basis of rank 3 multi-operations, we show that applying multi-operations theory allows for significant expansion of the range of accepted decisions; this makes the system more flexible for the construction of human–machine interfaces and organizes the integration of efforts in the development of humans and machines with a common goal.
Keywords:
intelligence system; property of explainability; theory of multi-operations; system of inclusions MSC:
68T27
1. Introduction
Decision intelligence is a practical field that covers a wide range of decision-making techniques, combining many traditional and advanced disciplines to develop, model, agree, align, execute, monitor, and tune decision-making models and processes [].
The methods of formal logic and probability theory are often used in the construction of decision-making systems. These methods assume rational principles of judgment and reasoning [,].
One of the directions of building decision-making systems is their creation on the basis of co-evolutionary hybrid intelligence []. These are systems that continuously interact with humans and have the functions of self-analysis, adapting to humans, and taking into account the human state. These systems are aimed not just at combining the efforts of humans and machines in solving an applied task but at developing themselves and the human as a single organism. In such systems, a general model of the subject domain is built by taking into account the knowledge obtained from different agents, including different humans and AI systems. Along with the general model, the system builds a private model of an individual participant in interaction. With the help of the private model, the system is adapted to the specific perception of the second participant of interaction and to the specific conditions of solving a private problem.
Such systems can be used to create new drugs and organize the schedule of patients taking drugs in clinical and medical research to determine the psycho-physiological state of a person, e.g., make a medical diagnosis.
In such systems, there is an increasing number of different states of the problem object and a significantly increasing number of uncertainties. In life, it is often impossible to make an unambiguous decision about the state of the object in the presence of uncertainties. Today, decision-making systems often use very different approaches from mathematical apparatus. These include classical Boolean logic, various modifications of multi-valued and fuzzy logic, and others. They are used in combination with artificial neural networks, genetic algorithms, and statistical methods. Descriptions of such systems are given, for example, in [,,]. Multi-valued logic is often used in decision-making systems for an expressive formal representation of relations between objects and their attributes. In these systems, the number of values depends on a particular attribute []. Therefore, the application of logic models based on multi-valued and fuzzy logic in situations with many values and uncertainties between them is difficult or leads to a “wrong” decision. For decision-making, it is often necessary to undertake a number of additional activities to clarify the details of the problem (additional data collection, additional definitions of the task conditions, adding new task conditions, etc.). All these activities represent kinds of solutions, too.
To represent uncertainties, non-Bayesian decision-making methods and nonprobabilistic methods [,] are often used. Noncommutative logic is used to model preference relations in decision-making processes as a possible tool for modeling “irrational decisions” [,,].
Another very important factor is the existence of the property of explainability in such systems. Most such systems are “black boxes” today, which produce a result but do not provide any explanation of how the result was obtained. Explanation is important for reducing errors and inaccuracies in solving critical issues, increasing human acceptance of AI systems, and increasing confidence in AI systems.
The theory of multi-operations can be used for the problems described above. The theory of multi-operations is a nonlinear multi-valued logic that allows for working with a number of logical values greater than two and considering the uncertainties between any logical values. Each element in multi-operations is a set. If the set consists of one element, it is a logical value; otherwise, it is uncertain. Uncertainty is a set that can be empty or includes several logical values. Uncertainty is understood as knowledge about information within a certain set. This idea is similar to nondeterministic models, where uncertainty is an element for which only the area in which it can be located is known. Existing theories that model uncertainties use a linear approach, i.e., different degrees of uncertainty are in a linear order. However, in some practical situations, different uncertainties may be incomparable, and for these, models with a linear truth scale are simply not applicable. Our approach is aimed at solving this problem.
In addition, the theory of multi-operations can provide explainability for decision-making systems. The theory of multi-operations is a subtype of multi-valued logic and belongs to the theory of functional systems; it is a quite new direction and actively started to be studied in the 21st century. The following are some studies in the theory of multi-operations: [] is devoted to the study of the lattice of closed classes of partial multi-operations (partial hyperclones); in [], a complete list of maximal closed classes of partial multi-operations is obtained; in [] a partition of all minimal closed classes of functions into five types is achieved; in [], this classification is extended to closed classes of multi-operations; in [,,], hyperclones on a two-element set are studied; and in [,], ultraclones of rank 2 are studied.
Currently, computer calculations are applied in various studies of the theory of multi-operations. For example, in [], all algebras of rank 3 unary multi-operations are listed. In [], all rank 4 unary Schaeffer multi-operations are calculated. The works [,,] are devoted to studying all the minimal and superminimal algebras of rank 3 operations. In [,,,], they consider the issue of pre-complete closed sets of multi-operations using E-operator on a two-element set.
In our article, we present the results of our research on the construction of a decision-making system based on the theory of multi-operations, which allows for an arbitrary number of logical values of the object under study and the uncertainties between these values.
We have chosen the field of medicine to illustrate the possibilities of a decision-making system based on the theory of multi-operations. In this field, it is most relevant to make an explainable decision, taking into account many uncertainties, based on the set of expert knowledge. In medical decision-making systems, the process of knowledge accumulation, the constant analysis of this knowledge and the correction of the general model of the object under study (for example, a disease), and the personalization of the system for a particular patient, environmental conditions, etc., are all important. Decision-making systems based on multi-operations allow for explaining the cause–effect relationship that leads to a particular decision. They are capable of self-analysis, optimization, and scaling.
The article is organized in the following way: Section 2 presents the basic concepts of the theory of multi-operations, on which the proposed method of solving inclusion systems and the decision-making system are based. In the Section 3, the advantages of applying the theory of multi-operations over other mathematical apparatuses are described. The Section 4 is focused on demonstrating how the theory of multi-operations can be applied to decision-making systems. This section first describes a method for solving inclusion systems in natural language. Next, the general idea of the decision system itself is given, the knowledge model that has been created for the decision system is demonstrated, and an example of how the program works is described. First, the work of the decision-making system in the formation of the model of the subject area is demonstrated, and then the work of the decision-making system for a particular patient is shown. At the end of the section, a description of system testing is given. Section 5 presents a discussion of the main advantages and disadvantages of applying the theory of multi-operations to the construction of decision-making systems and gives directions for future research.
2. Basic Statements of the Theory of Multi-Operations
Let A be an arbitrary set and be the set of all subsets of A. The mapping f of the Cartesian degree from to is called a n-local multi-operation on A. The set of all n-local multi-operations for A is designated as . The rank of a multi-operation is the cardinality of the set A. When = k, we use the designation .
The multi-operation for the arbitrary set can be represented as mappings:
using the following encoding:
Moreover, the n-ary multi-operation f can be represented as a vector of all its values, , where and are the representations of in the base k calculus using an n-digit number.
Let us define the superposition operator for the set of n-local multi-operations as follows: if and , then
The notion of a term with a set of variables, X, and a set of constants, K, over a set of multi-operations, , is defined as follows:
- if , then is a term, and ;
- if and are terms, then is a term, and ;
- if is a term and and are terms, then is a term, and .
3. Advantages of the Theory of Multi-Operations
Let us consider the assignment of multi-operations at rank 3 and 4 to illustrate how uncertainty can be described in the theory of multi-operations.
With a rank of 3, the set A = {1, 2, 4}. This means that the multi-operation can be represented as a mapping, , using the following encoding:
From the encoding, it can be seen that a system based on rank 3 multi-operations will consist of three logical elements (1, 2, and 4). In fact, this system will describe three different values and five uncertainties between them, which are set on the logic elements (0, 3, 5, 6, and 7). Figure 1 illustrates the three values and the uncertainties between them for a system based on rank 3 multi-operations. The colored circles are the logic elements corresponding to the values, and the uncolored circles are the uncertainties between the values:
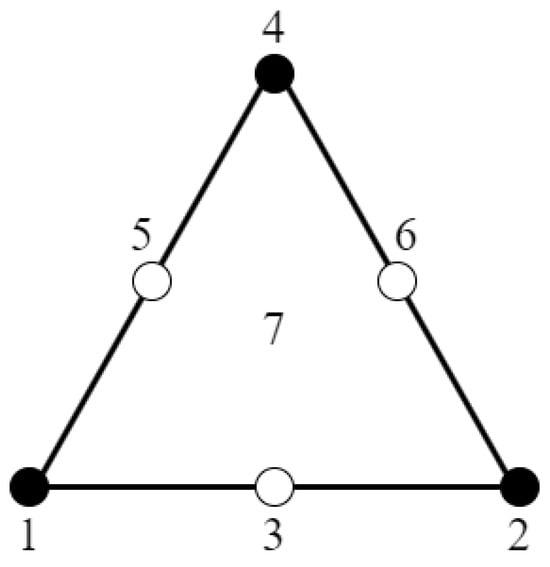
Figure 1.
The logic of constructing rank 3 multi-operations.
It is worth noting that logical element 0 is not in Figure 1 because logical element 0 means an empty set.
A system based on rank 4 multi-operations can be represented as a system of four values corresponding to the set of logical elements . Then, the whole set of states together with the uncertainties is a mapping of multi-operations, , of the following form:
using the following encoding:
Figure 2 illustrates such a system.
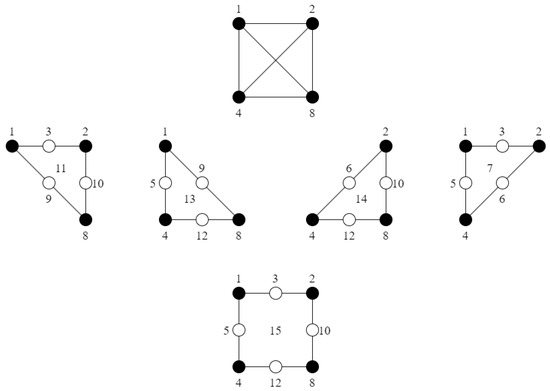
Figure 2.
Illustration of a four-state system with uncertainties based on rank 4 multi-operations.
The existence of uncertainties in classical multi-valued and fuzzy logic is schematically represented in Figure 3.
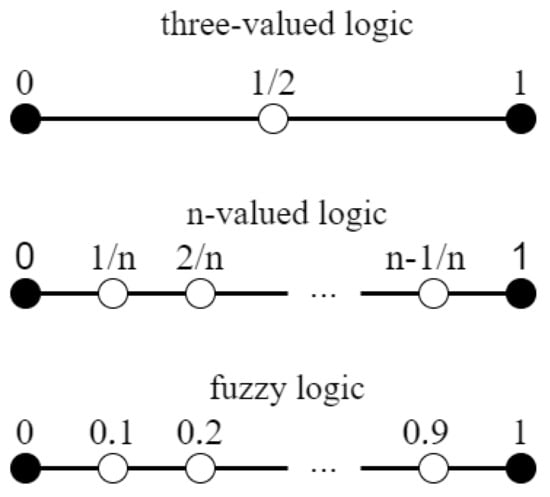
Figure 3.
Uncertainties in nonclassical logic.
In Figure 1 and Figure 2, we try to show the main idea of multi-operations. The theory of multi-operations uses nonlinear logic and considers not only the information between two logical values, e.g., “true” and “false”, but also other logical values. The number of logical values depends on the rank of the multi-operations. We also consider uncertainty between any logical values. Such a structure lets us consider the different uncertainties between different logical values. This approach allows us to process input information; otherwise, the input information can be considered from k positions, where k is the rank of the multi-operations. Figure 3 shows the classical multi-valued and fuzzy logic, but these consider only the information between two logical values: “true” and “false”.
4. Application of the Theory of Multi-Operations for Building an Intelligent System
4.1. The Method for Solving Systems of Inclusions
We use systems of inclusions, which are defined using multi-operations, to build domain models for the decision-making system.
The general form of the system of inclusions with unknowns in multi-operations is as follows:
where and are terms with variables and constants of .
The solution of system (1) is the set of multi-operations such that for all i, the inclusions are satisfied under the standard definition of the value of the terms by means of the introduced superposition operator:
The method for solving systems of inclusions with unknowns in multi-operations consists of four steps []:
- Entering the inclusions system;
- Transition from a system of inclusions to a system of Boolean inequalities using spatial matrices;
- Finding a solution in a system of Boolean inequalities;
- The solution obtained in step 3 is converted into multi-operations.
4.2. Description of the Disease Domain Detection System
In order to show how the theory of multi-operations can be applied, consider a self-learning intelligent system with the property of explainability [], which defines a disease domain by using a set of symptoms and a description of each of the disease domains.
The system is based on three sets of parameters: the physiological parameters of the patient, the symptoms of the disease, and the parameters of the disease domains. Based on the patient’s physiological parameters, it is determined which symptoms the patient has, and based on the symptoms, it is determined which disease domain the disease belongs to.
At the start of the intelligent system, the expert forms a model (inclusion system) using the human–machine interface. In order to form the model, the expert needs to define a set of physiological parameters, a set of symptoms, and a set of domains, on the basis of which the model will be built. After forming the model and, subsequently, after each edit of the model, the intelligence system searches for a general solution for the system of inclusions and further analyzes the obtained solution. When analyzing the solution, the system searches for deficiencies in the considered model. If there are deficiencies, an explanation is formed about what deficiencies the model has and how they can be solved. If there are no deficiencies, the system accepts the new model.
In order to analyze the general solution, conditions for the model are introduced into the system in advance. These conditions can be different and have different purposes. For example, a condition could be a check for data sufficiency in the model, i.e., how unambiguous the expert inputs are for each domain. Another example of a condition might be to minimize the model for certain domains, i.e., how many and which symptoms are sufficient to address a certain number of domains.
The expert can enter the physiological parameters of the patient into the database itself when the model satisfies all the given conditions and is accepted by the system. Such data include the following:
- One-time measurements that can be recorded in the form of numbers or text (temperature, pulse, etc.);
- Data that are pre-processed and/or analyzed (sleep quality, facial expressions, etc.) are collected over a period.
This may be data processed using AI techniques. For example, the intelligent system may include a module for assessing a patient’s heart rate in real time using a camera. In this case, the data are not entered into the system by the doctor but are substituted automatically by this embedded module.
The examiner can obtain an explanation from the intelligent system for each decision after all the patient’s physiological parameters have been entered. For example, they can find out why a certain domain is or is not suitable. The explanation is constructed as follows: each symptom in the inclusion system has a state for a particular patient according to the symptom model. Therefore, specific values are substituted instead of symptoms. The intelligent assistant then constructs a partial solution to the inclusion system. Based on this partial solution, an explanation is formed.
Next, the following options are possible:
- The expert agrees with the system’s decision.
- The expert does not agree with the decision of the system. In this case, it is necessary to analyze the solution of the system of inclusions and the model itself. It is possible that the model may need to be modified: a change in the physiologic parameter set, the symptom set and domain set, and/or a change in the system of inclusions in the model.
- The expert is not qualified to assess some symptoms or physiologic parameters. In this case, the intelligent assistant needs a new expert who is qualified for these symptoms. Additionally, in this case, the new expert can add new information to the model.
- Not all symptoms have a valid value in the data source. This case means that the expert made a mistake, or the AI methods gave an incorrect value based on incorrect initial data. The reasons can be very different.
The conditions of case 1 are necessary for a successful solution in terms of the selection of the disease domain. If another case has been obtained, it is necessary to modify the system with the help of an expert. If a suitable expert is not available, then the data that are stored in the system are not sufficient to determine the patient’s disease domain.
The proposed decision-making system based on the theory of multi-operations has the following advantages:
- It gives a detailed patient-specific explanation for each disease domain;
- When analyzing the overall solution, the system can automatically identify deficiencies in the model that the expert may not have foreseen or may have forgotten. The system can also provide new knowledge that the expert may not have been aware of because, sometimes, nonobvious aspects are quite difficult to foresee when designing the model.
4.3. Knowledge Representation Model Based on the Theory of Multi-Operations
We developed two knowledge representation models based on the theory of multi-operations (the symptom model and the domain model) in order to correctly interpret input and output data.
Symptom model:
- 0—⌀: the expert is not qualified for the given symptom;
- 1—{1}: there is no symptom;
- 2—{2}: there is a symptom;
- 3—{1,2}: uncertain (contradiction between the expert and the measuring device);
- 4—{4}: the measurement device gives a nonvalid value;
- 5—{1,4}: the measurement device gives a nonvalid value, and the expert makes an assumption on the basis of experience that there is no symptom;
- 6—{2,4}: the measurement device gives a nonvalid value, and the expert makes an assumption on the basis of experience that there is a symptom;
- 7—{1,2,4}: it is necessary to clarify.
A measuring device refers to some device, such as a thermometer, tonometer, etc., for measuring data in relation to a physiological parameter.
Model of disease domains:
- 0—⌀: the person is not an expert in the current domain;
- 1—{1}: the domain does not fit the symptoms;
- 2—{2}: the domain fits the symptoms;
- 3—{1,2}: due to the contradiction between the expert and the measuring device, it is impossible to determine the exact state of the domain;
- 4—{4}: it is not possible to determine the condition of the domain because information about all symptoms is not available;
- 5—{1,4}: based on the expert’s experience, it is concluded that the domain is not suitable;
- 6—{2,4}: based on the expert’s experience, it is concluded that the domain fits the symptoms;
- 7—{1,2,4}: it is necessary to clarify the symptoms in order to determine the state of the domain.
In order to specify a system of inclusions, the following multi-operations are defined:
- Logical AND (&) = (111 124 144);
- Logical OR (∨) = (124 222 424);
- Logical negation (¬) = (214).
4.4. Demonstration of System Work
Before starting to work with the system, it is necessary to determine what disease domains will be considered in the system, what symptoms are needed to define the domains, and what physiological parameters of the patient are needed to define the symptoms. Suppose that the expert has specified the following sets:
Multiple disease domains , where —Cardiology; —Neurology; —Therapy.
Set of symptoms , where —increased heart rate; —increased pressure; —SGR-anxiety; —increased eye blinking; and —increased temperature.
Set of physiological parameters , where —pulse; —pressure; —SGR values; —blink rate; and —temperature.
The conditions under which a symptom is considered to be present in a patient are as follows:
is true when the index is greater than 90;
is true when the index is greater than 140/90;
is true when the index showed anxiety;
is true when the index is greater than 25;
is true when the index is greater than 37.0.
Next, the expert needs to form a model for the intelligent system. Suppose that the expert has specified the following model based on inclusion systems:
In order to test a new model, it is necessary to find a general solution, analyze it, and provide an explanation for the expert. In this explanation, the system agrees with the new model or explains the deficiencies of the new model.
Let us demonstrate the solution of the system of inclusions. For this purpose, we use the method described at the beginning of the section but without the last step. This is due to the fact that the transition from Boolean functions to multi-operations is not always easy, and it is easier to analyze the solution in Boolean functions.
Step 1. The system of inclusions (2) is given as input.
Step 2. In order to go from the system of inclusions to the system of Boolean inequalities, it is necessary to represent all input data in the form of spatial matrices.
Since the inclusion system is solved at rank 3, we obtain the following matrices:
Multi-operations from the basis:
Symptoms:
Domains:
Next, it is necessary to represent each operation from the inclusion system as a spatial matrix:
Now, by using the following matrices , , it is possible to compose a system of Boolean inequalities:
Step 3: Finding a solution to the system of Boolean inequalities.
It is possible to find a general solution to the system of inequalities (3) using any algorithm from the theory of Boolean functions [,].
The general solution will have the following form:
where are arbitrary Boolean functions of variables .
Now, it is necessary to analyze the obtained solution. Since the work is initially carried out using the theory of multi-operations, during the analysis of the solution, it is necessary to group the obtained solutions. In more detail, expressions refer to , expressions refer to , and expressions refer to . The same is true for symptoms.
As an example, let us analyze the solution for the sufficiency of the input data, i.e., how the input data are unambiguous for each domain. When considering the expressions , it is clear that the summands in them (which do not contain arbitrary functions) indicate the set of those variables (symptoms) that significantly affect the choice of the domain. Moreover, this can be seen if we compare the obtained result with the original system of inequalities in Boolean functions. However, the obtained solution cannot be called unambiguous because in each expression, , there is an arbitrary function. Let us consider the expression in detail. If the variable is equal to 0, the expression will depend on 1, which is determined by variables ; that is, the domain may be influenced by symptoms and in the general decision, although the original model does not have this logic. This suggests that the model needs to be edited.
In order to rid the model of the above disadvantages, it is necessary to introduce constraints into the model. As a result, there will be no arbitrary functions in the general solution. Let us consider an example for the first inclusion: . If the value of or is 4 according to the knowledge representation model for symptoms, the result is as follows: . In this case, can be equal to {4}, {1,4}, {2,4}, {1,2,4}. To make the solution unambiguous, we introduce the following constraint: . Then, the result will have the following form: and . In this case, is uniquely equal to {4}. Let us introduce a constraint for each inclusion and obtain a new model (5):
For the new model, we obtain a general solution (6):
It can be seen that there are no arbitrary functions in the general solution. This indicates that the model has passed the input data sufficiency condition.
After the model has been accepted by the system, it is possible to start working with users. Four examples of expert’s work with patients and an intelligent system are described below. To test the developed approach, we generate data. An example of the data can be found here (accessed on 1 October 2024): https://drive.google.com/file/d/1KZz689gZ4hSPGNVWG8cnsMe2B1TwG5hv/view?usp=sharing.
The physiological parameters of patient 1 are as follows:
= 110; is unknown because the blood pressure device is not working; = SGR is normal; = 20; and = 36.6.
Let us define the meaning of each symptom according to the knowledge representation model for symptoms:
- .
Now let us replace the symptoms with their values according to the symptom knowledge representation model in the inclusion system (4) and obtain the values for each domain:
From this, it can be concluded that the domains “Neurology” and “Therapy” are not suitable. For the “Cardiology” domain, it is impossible to determine the value of the domain because the symptom “High blood pressure” cannot be defined. In this case, we cut off two of the three domains, and for the last one, the patient’s blood pressure must be accurately determined.
The physiologic parameters of patient 2 are as follows:
- = 98; = 130/80; = SGR is normal; = 30; and = 36.5; however, the expert disagrees with this parameter and believes that the patient has a temperature and that the temperature measuring device is not working correctly.
Let us define the meaning of each symptom according to the knowledge representation model for symptoms:
- .
Now let us replace the symptoms with their values according to the symptom knowledge representation model in the inclusion system (4) and obtain the values for each domain:
In this case, it is possible to conclude that the domain “Neurology” is not suitable. The value of the domains “Cardiology” and “Therapy” cannot be determined precisely because there is a contradiction between the expert and the symptom measurement devices . In this case, we cut off one of the three domains, and for the remaining two, it is necessary to accurately determine the patient’s temperature.
The physiologic parameters of patient 3 are as follows:
- is not known because the heart rate monitor is not working, but the expert believes it is equal to 110; = 150/98; = SGR is normal; = 20; and = 36.8.
Let us define the meaning of each symptom according to the knowledge representation model for symptoms:
- .
Now, let us replace the symptoms with their values according to the symptom knowledge representation model in the inclusion system (4) and obtain the values for each domain:
In this case, it is possible to conclude that the domains “Neurology” and “Therapy” are not suitable. The Cardiology domain may be appropriate, as the examiner believes that the patient has an elevated pulse rate. In this case, we eliminate two of the three domains, and the Cardiology domain requires an accurate determination of the patient’s heart rate.
The physiologic parameters of patient 4 are as follows:
- = 88; = 120/80; = SGR is normal; = 20; and = 36.7.
Let us define the meaning of each symptom according to the knowledge representation model for symptoms:
- .
Obviously, in this case, none of the disease domains will fit. In this case, it is necessary to consider a new or expanded current model. In this case, new experts may be involved. If the expansion of the model is not possible, it means that there are not enough data in the intelligent system to define the disease domain.
Suppose the expert decides to extend the model by adding a new domain called “Pulmonology”, which requires two new symptoms ( is an active cough, and is an increased dyspnea) and two new physiologic parameters ( is cough and is breath).
The conditions under which and symptoms are considered to be present in a patient are as follows:
- is true when parameter is greater than 3;
- is true when parameter is greater than 20.
The modified model will look as follows:
The new model also undergoes validation by the system, which is described above. In order not to describe the search for a general solution again, we skip this point and say that the new model has no drawbacks and is accepted by the system.
Let us determine the parameters and for patient 4:
- .
Now, let us replace the symptoms with their values according to the symptom knowledge representation model in the inclusion system (10) and obtain the values for each domain:
As a result, it is possible to conclude that the domains “Cardiology”, “Neurology”, and “Therapeutics” are not suitable, while the domain “Pulmonology” is suitable.
4.5. Testing of System
Synthetic data are generated for 54 patients to test the system described above. The generated data can be divided into three groups: patients with accurate data, patients with uncertain data, and patients with missing data. Figure 4 shows the result of testing the system based on this data.
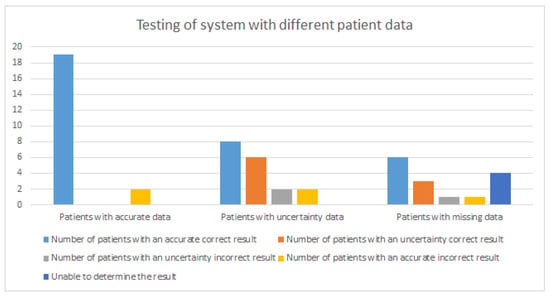
Figure 4.
Testing of system with different patient data.
Incorrect result is the case where the results of the expert and the system do not match. Unable to determine the result is the case where both the expert and the system cannot determine the result. After obtaining these results, the work of the expert is simulated to improve the performance of the system. This work consists of redefining the data that the system points out to the expert and that the system considers missing or incorrect. Figure 5 shows the results of the system after the data improvement iteration.
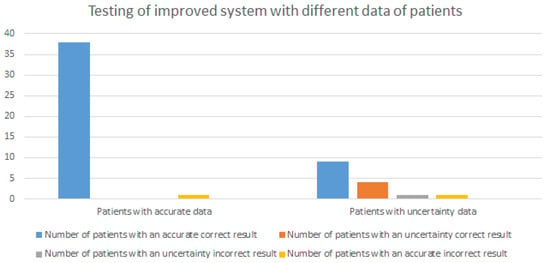
Figure 5.
Testing of improved system with different patient data.
The number of accurate correct results is increased significantly after the system improvement and redefinition of the generated data. This approach can provide new opportunities compared to existing solutions. Such a system can handle other uncertainties in the input data and provide an explanation for the obtained result.
5. Discussion
We have considered an intelligent medical system, but the same approach can be used in other areas. The theory of multi-operations can be applied not only to decision-making systems. The main task is to determine what the third, fourth, and other logical values are that are different from the values of the true and false mean. Determining the meaning of another logical value is quite a nontrivial task. In most practical domains, all events are considered between true and false because of the application of Boolean logic, and it is quite difficult to translate the workflow to more states. In our case, the third logical value is responsible for the event when it is impossible to obtain the physiological parameters of the patient, and the system itself is based on the joint work of the system and the expert.
It should also be noted that the application of the theory of multi-operations makes sense only for systems with a large amount of data and complex logic. In a system that is designed to solve small problems, it makes no sense to transfer such a system to the theory of multi-operations, as it may negatively affect the system’s performance. It can lead to an increase in time in terms of receiving a response from the system.
In addition, it is not an easy task to work with the theory of multi-operations from a programming point of view. To program multi-valued logic, it is necessary to develop special solutions that will not decrease the speed of program execution and preserve the rules on which the theory of multi-operations is based at the same time.
The authors do not reject other mathematical solutions, including fuzzy theory. We say that there is a theory of multi-operations that can work with such quantities that fuzzy logic cannot. However, to build hybrid solutions in the field of intelligent systems, we need all solutions. They are not mutually exclusive; they are complementary to each other.
6. Conclusions
Our research has shown that the application of the theory of multi-operations for the construction of decision-making systems allows for not only considering the basic states of the object but also building decisions based on the absence of some data or taking into account the incorrectness of the data. These systems allow the input of various forms of uncertainties.
Using this approach provides the following advantages:
- When forming a domain model, the system analyzes the new model to identify inaccuracies or errors in the new rules and optimizes the new model. While the system is analyzing the new model, an explanation is being built for the expert, which allows the expert to immediately and exactly understand what the current model’s problem is. This saves time and resources when setting up the domain model in the system.
- When working with the end user, the system can make recommendations for each individual option (in our case, the disease area) within the domain model, even with high uncertainty in the input data. In addition, the system can reduce the overall list by excluding options that are definitely not suitable for the user. This also saves time and resources when working with end users.
Models can be embedded in each other. Thus, a more general model can be built on the basis of submodels. Another advantage of these systems is the possibility of self-analysis, searches for contradictory rules, and optimization of the system of rules. When building a system of rules, it is possible to give weight to each rule on the basis of different approaches. Such approaches can be the statistical processing of existing and tested decisions on the basis of these rules or on the basis of expert rating, using one of the types of voting, etc. Decision-making methods based on the theory of multi-operations can be embedded in the cognitive architecture [] in modules such as knowledge management, comprehensive modules, decision-making, action planning, reflection, and self-analysis. The disadvantage of this approach is the high computational complexity of analyzing the built inclusion system. This disadvantage is smoothed by the fact that the analysis is performed episodically when the inclusion system is changed.
Author Contributions
Methodology, project administration, software, visualization and writing—original draft, S.T.; conceptualization, supervision, investigation, Y.S.; formal analysis, validation, writing—review and editing, N.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
To test the developed approach, we generated data. An example of the data can be found here (accessed on 1 October 2024): https://drive.google.com/file/d/1KZz689gZ4hSPGNVWG8cnsMe2B1TwG5hv/view?usp=sharing.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Decision Intelligence. American Mathematical Society. Available online: https://www.gartner.com/en/information-technology/glossary/decision-intelligence (accessed on 19 September 2024).
- Yun, Y.; Ma, D.; Yang, M. Human–computer interaction-based Decision Support System with Applications in Data Mining. Future Gener. Comput. Syst. 2021, 114, 285–289. [Google Scholar] [CrossRef]
- Kagan, E.; Novoselsky, A.; Ramon, D.; Rybalov, A. Non-Commutative Logic for Collective Decision-Making with Perception Bias. Robotics 2023, 12, 76. [Google Scholar] [CrossRef]
- Krinkin, K.; Schichkina, Y.; Ignatyev, A. Co-evolutionary hybrid intelligence is a key concept for the world intellectualization. Kybernetes, 2022; ahead-of-print. [Google Scholar]
- Villalonga, A.; Negri, E.; Biscardo, G.; Castano, F.; Haber, R.E.; Fumagalli, L.; Macchi, M. A Decision-making Framework for Dynamic Scheduling of Cyber-physical Production Systems Based on Digital Twins. Annu. Rev. Control 2021, 51, 357–373. [Google Scholar] [CrossRef]
- Souza, M.L.H.; da Costa, C.A.; Ramos, G.d.; Righi, R.d.R. A survey on decision-making based on system reliability in the context of Industry 4.0. J. Manuf. Syst. 2020, 56, 133–156. [Google Scholar] [CrossRef]
- Ma, J.; Harstvedt, J.D.; Jaradat, R.; Smith, B. Sustainability driven multi-criteria project portfolio selection under uncertain decision-making environment. Comput. Ind. Eng. 2020, 140, 106236. [Google Scholar] [CrossRef]
- Lyutikova, L.A. Using multivalued logic for qualitative data analysis. J. Phys. Conf. Ser. 2021, 2131, 032046. [Google Scholar] [CrossRef]
- Aliev, R.A.; Huseynov, O.H. Decision Theory with Imperfect Information; World Scientific: Singapore, 2014. [Google Scholar]
- Massimiliaon, A. A Unified Framework for Bayesian and Non-Bayesian Decision Making and Inference. Math. Oper. Res. 2022, 47, 2721–2742. [Google Scholar] [CrossRef]
- Ruggeri, K.; Alí, S.; Berge, M.L.; Bertoldo, G.; Bjørndal, L.D.; Cortijos-Bernabeu, A.; Davison, C.; Demi’c, E.; Esteban-Serna, C.; Friedemann, M.; et al. Replicating patterns of prospect theory for decision under risk. Nat. Hum. Behav 2020, 4, 622–633. [Google Scholar] [CrossRef] [PubMed]
- Kahneman, D.; Tversky, A.A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Doroslovacki, R.; Pantovic, J.; Vojvodic, G. One Interval in the Lattice of Partial Hypeclones. Czech Math J. 2005, 55, 719–724. [Google Scholar] [CrossRef]
- Romov, B.A. Partial hyperclones on a finite set. In Proceedings of the 32nd IEEE International Symposium on Multiple-Valued Logic, Boston, MA, USA, 15–18 May 2002; pp. 17–22. [Google Scholar] [CrossRef]
- Rosenberg, I.G. Minimal clones I: The five types. In Lectures in Universal Algebra; Elsevier: Amsterdam, The Netherlands, 1986; pp. 405–427. [Google Scholar] [CrossRef]
- Pouzet, M.; Rosenberg, I.G. Small clones and projection property. Algebra Universalis 2007, 63, 37–44. [Google Scholar] [CrossRef][Green Version]
- Machida, H. Hyperclones on a two-element set. Mult.-Valued Logic. Int. J. 2002, 8, 495–501. [Google Scholar] [CrossRef]
- Machida, H.; Pantovic, J. On maximal hyperclones on 0, 1—A new approach. In Proceedings of the 38th IEEE International Symposium on Multiple-Valued Logic (ISMVL 2008), Dallas, TX, USA, 22–24 May 2008; pp. 32–37. [Google Scholar]
- Pantovic, J.; Vojvodic, G. Minimal partial hyperclones on a two-element set. In Proceedings of the 34th IEEE International Symposium on Multiple-Valued Logic (ISMVL 2004), Toronto, ON, Canada, 19–22 May 2004; pp. 115–119. [Google Scholar]
- Badmaev, S.A.; Duragov, A.E.; Fomina, I.V.; Sharankhaev, I.K. On Some Intervals In The Lattice Of Ultraclones Of Rank 2. Sib. Electron. Math. Rep. 2021, 18, 1210–1218. [Google Scholar] [CrossRef]
- Badmaev, S.A.; Sharankhaev, I.K. On Minimal Bases In Full Partial Ultraclones Of Rank 2. Sib. Electron. Math. Rep. 2021, 17, 1478–1487. [Google Scholar] [CrossRef]
- Kazimirov, A.S.; Peryazev, N.A. Algebras of unary multioperations. In Proceedings of the International Conference “Mal’tsev Reading”, Novosibirst, Russia, 12–15 November 2013; p. 156. [Google Scholar]
- Malina, A.V.; Peryazev, N.A. Schaeffer multioperations in the complete algebra of unary multioperations of rank 4. Proceedings of the Southwestern State University. Series: Management, Computer Technology, Computer Science. Med. Instrum. 2016, 18, 29–32. (In Russian) [Google Scholar]
- Eremenko, D.A. Algebras of Unary Multioperation of Rank 3. Available online: https://izv.etu.ru/en/archive/2019/7/14-18 (accessed on 2 September 2024).
- Eremenko, D.A. Minimal algebras of binary operations of rank 3. Comput. Tools Educ. 2020, 1, 38–48. [Google Scholar] [CrossRef]
- Eremenko, D.A. Upminimal algebras of binary operations of rank 3. Comput. Tools Educ. 2021, 4, 72–87. [Google Scholar] [CrossRef]
- Panteleev, V.I.; Ryabets, L.V. The Completeness Criterion for Closure Operator with the Equality Predicate Branching on the Set of Multioperations on Two-Element Set. Bull. Irkutsk State Univ. Ser. Math. 2019, 29, 68–85. [Google Scholar] [CrossRef]
- Panteleev, V.I.; Ryabets, L.V. E-closed Sets of Hyperfunctions on Two-Element Set. J. Sib. Fed. Univ. Math. Phys. 2020, 13, 231–241. [Google Scholar] [CrossRef]
- Panteleev, V.I.; Ryabets, L.V. Classification of Multioperations of Rank 2 by E-precomplete Sets. Bull. Irkutsk State Univ. Ser. Math. 2020, 34, 93–108. [Google Scholar] [CrossRef]
- Panteleev, V.I.; Taglasov, E.S. On the Lattice of ESI-closed Classes of Multifunctions on Two-elements Set. Bull. Irkutsk State Univ. Ser. Math. 2021, 38, 96–111. [Google Scholar] [CrossRef]
- Peryazev, N.A. Systems of Inclusions with Unknowns in Multioperations. Bull. Irkutsk State Univ. Ser. Math. 2023, 38, 112–123. [Google Scholar] [CrossRef]
- Todikov, S.I. The possibility of Applying the Theory of Multioperations to Build Self-learning Artificial Intelligence Systems with the Explainabilitry Property. In Proceedings of the IV International Conference on Neural Networks and Neurotechnologies (NeuroNT), St. Petersburg, Russia, 16 June 2023; pp. 56–59. [Google Scholar] [CrossRef]
- Levchenkov, V.S. Analytical form of the solution of Boolean equations. Dokl. RAN 1999, 369, 325–328. [Google Scholar]
- Levchenkov, V.S. Boolean Equations; VMiK MGU Publication: Moscow, Russia, 1999; p. 69. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).