Probabilistic Topology Optimization Framework for Geometrically Nonlinear Structures Considering Load Position Uncertainty and Imperfections
Abstract
1. Introduction
2. Problem Statement
2.1. Exploring Finite Element Analysis
2.2. Deterministic Approach
2.3. Introducing Probabilistic Approaches to Topology Optimization
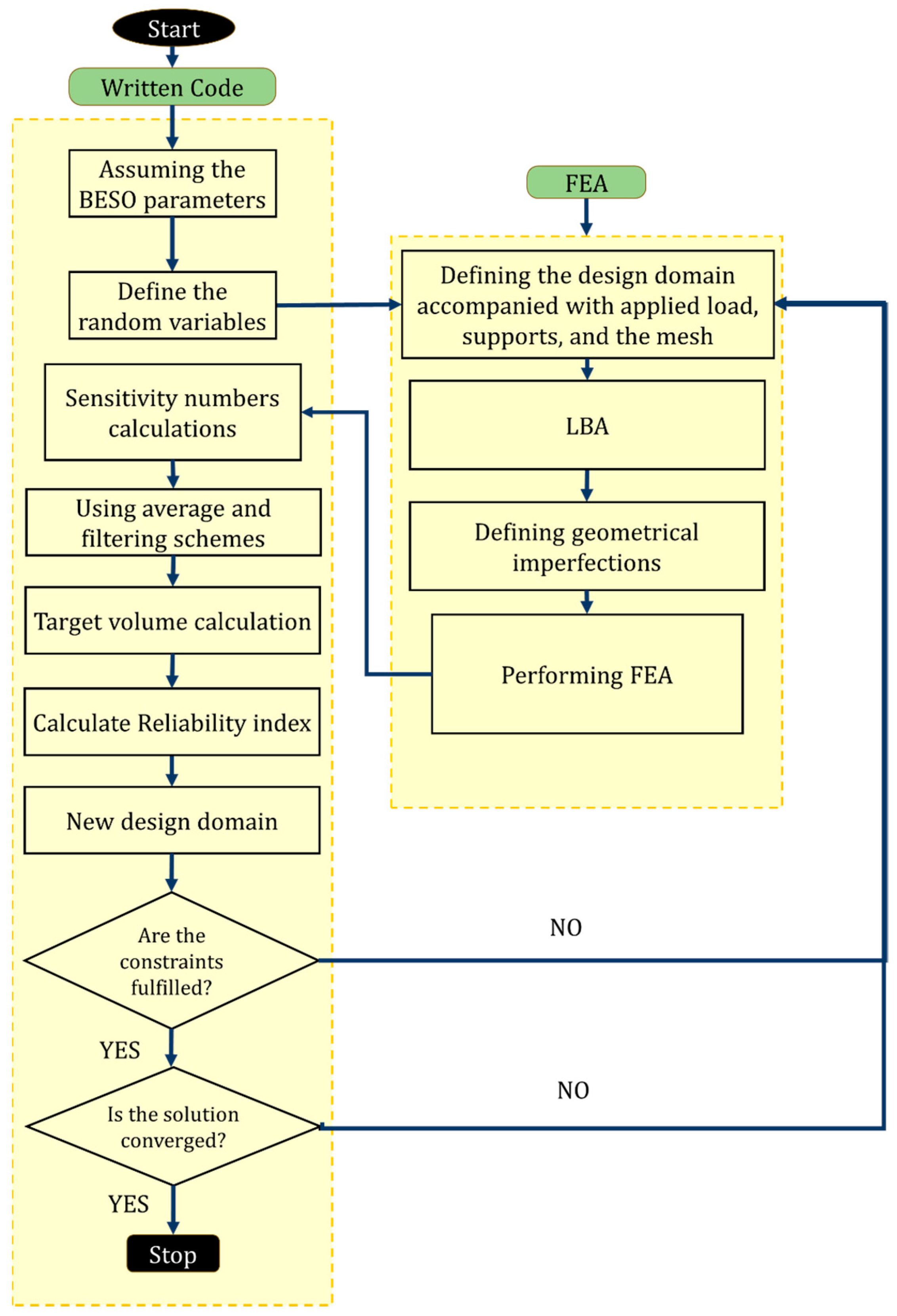
3. The Developed Algorithm Based on BESO
- Material properties, boundary conditions, and loading scenarios are defined using ABAQUS 2021 software for initial simulations.
- A custom MATLAB code utilizes the BESO method to iteratively refine the material distribution by removing inefficient elements based on sensitivity analysis. Each iteration evaluates the objective function subject to constraints, continuing until the predefined constraints and convergence criteria are met.
4. Results and Discussion
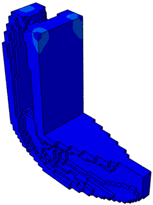
4.1. Example #1: U-Shaped Plate
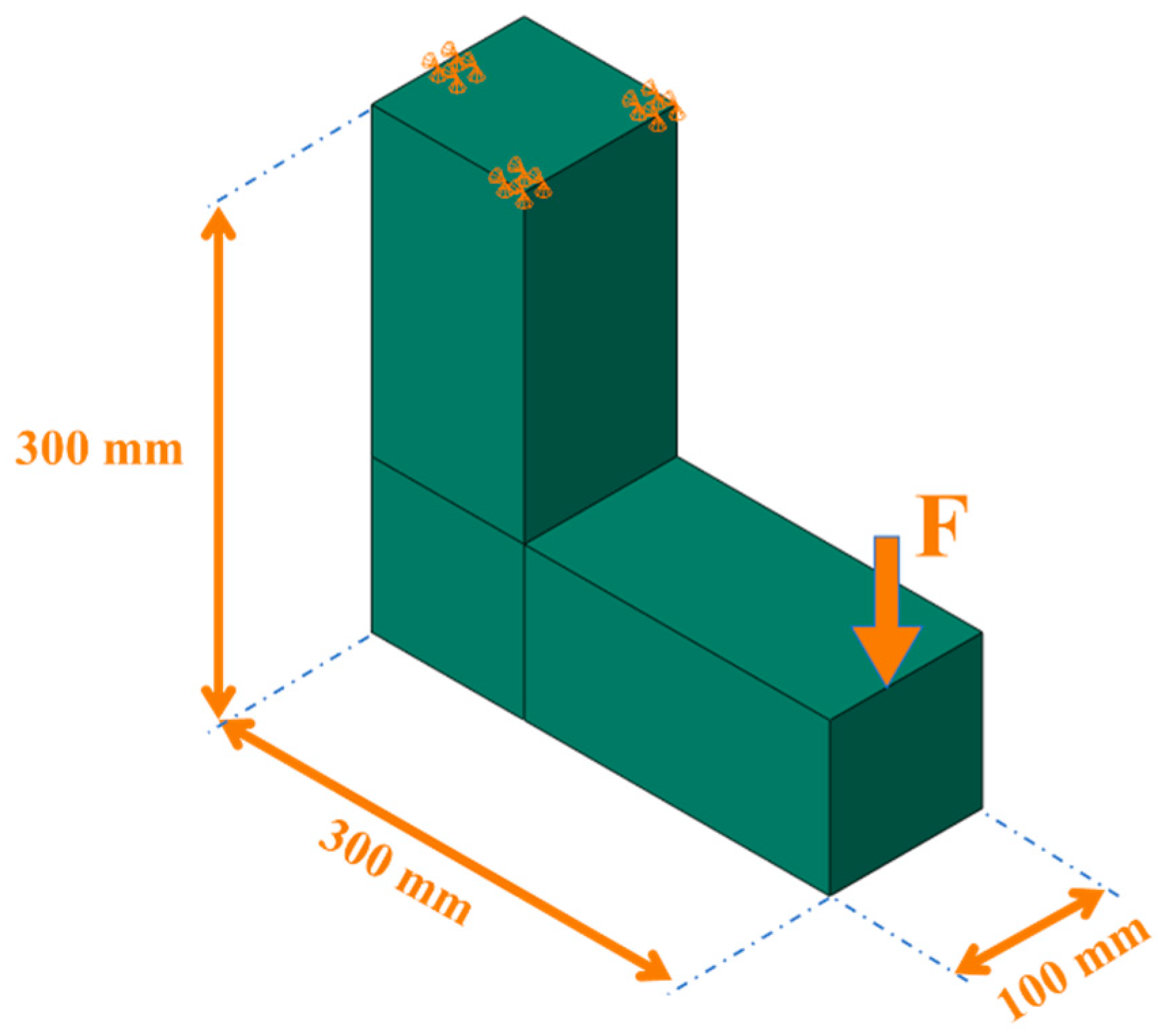
4.2. Example #2: 3D L-Shaped Beam
4.3. Example #3: Steel I-Beam
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, D.; Chen, J.; Tang, Y.; Cao, J. Topology Optimization of Die Weight Reduction for High-Strength Sheet Metal Stamping. Int. J. Mech. Sci. 2012, 59, 73–82. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient Topology Optimization in MATLAB Using 88 Lines of Code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef]
- Qiu, Y.; Xu, C.; Peng, J.; Song, Y. Isogeometric Topology Optimization of Multi-Material Structures under Thermal-Mechanical Loadings Using Neural Networks. Mathematics 2024, 12, 2350. [Google Scholar] [CrossRef]
- Xiao, P.; Zhou, C.; Qu, Y.; Luo, Y.; Li, Q. Topology Optimization for Quasi-Periodic Cellular Structures Using Hybrid Moving Morphable Components and the Density Approach. Mathematics 2024, 12, 2401. [Google Scholar] [CrossRef]
- Hurtado-Pérez, A.B.; Pablo-Sotelo, A.d.J.; Ramírez-López, F.; Hernández-Gómez, J.J.; Mata-Rivera, M.F. On Topology Optimisation Methods and Additive Manufacture for Satellite Structures: A Review. Aerospace 2023, 10, 1025. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P.; Querin, O.M. Bidirectional Evolutionary Method for Stiffness Optimization. AIAA J. 1999, 37, 1483–1488. [Google Scholar] [CrossRef]
- Radman, A. Combination of BESO and Harmony Search for Topology Optimization of Microstructures for Materials. Appl. Math. Model. 2021, 90, 650–661. [Google Scholar] [CrossRef]
- Zhu, Q.; Han, Q.; Liu, J. Topological Optimization Design on Constrained Layer Damping Treatment for Vibration Suppression of Thin-Walled Structures via Improved BESO Method. Aerosp. Sci. Technol. 2023, 142, 108600. [Google Scholar] [CrossRef]
- Querin, O.M.; Young, V.; Steven, G.P.; Xie, Y.M. Computational Efficiency and Validation of Bi-Directional Evolutionary Structural Optimisation. Comput. Methods Appl. Mech. Eng. 2000, 189, 559–573. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, Q.; Hong, J.; Yang, N. Bidirectional Evolutionary Optimization Design of Material Stiffness for the Uniformity of the Contact Stress. Eur. J. Mech.—A/Solids 2021, 89, 104288. [Google Scholar] [CrossRef]
- Habashneh, M.; Movahedi Rad, M. Optimizing Structural Topology Design through Consideration of Fatigue Crack Propagation. Comput. Methods Appl. Mech. Eng. 2024, 419, 116629. [Google Scholar] [CrossRef]
- Li, Y.; Chang, T.; Kong, W.; Wu, F.; Kong, X. Topological Optimization of Bi-Directional Progressive Structures with Dynamic Stress Constraints under Aperiodic Load. Appl. Sci. 2023, 14, 322. [Google Scholar] [CrossRef]
- Habashneh, M.; Cucuzza, R.; Domaneschi, M.; Movahedi Rad, M. Advanced Elasto-Plastic Topology Optimization of Steel Beams under Elevated Temperatures. Adv. Eng. Softw. 2024, 190, 103596. [Google Scholar] [CrossRef]
- Zhao, F. A Nodal Variable ESO (BESO) Method for Structural Topology Optimization. Finite Elem. Anal. Des. 2014, 86, 34–40. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, F.; Luo, Y.; Li, Q. Concurrent Topology Optimization of Curved-Plate Structures with Double-Sided Stiffeners. Mathematics 2024, 12, 2213. [Google Scholar] [CrossRef]
- Tang, Y.; Kurtz, A.; Zhao, Y.F. Bidirectional Evolutionary Structural Optimization (BESO) Based Design Method for Lattice Structure to Be Fabricated by Additive Manufacturing. Comput.-Aided Des. 2015, 69, 91–101. [Google Scholar] [CrossRef]
- Kazakis, G.; Lagaros, N.D. Multi-Scale Concurrent Topology Optimization Based on BESO, Implemented in MATLAB. Appl. Sci. 2023, 13, 10545. [Google Scholar] [CrossRef]
- Kiusalaas, J. Optimal Design of Structures with Buckling Constraints. Int. J. Solids Struct. 1973, 9, 863–878. [Google Scholar] [CrossRef]
- Khot, N.S.; Venkayya, V.B.; Berke, L. Optimum Structural Design with Stability Constraints. Int. J. Numer. Methods Eng. 1976, 10, 1097–1114. [Google Scholar] [CrossRef]
- Zhou, M. Difficulties in Truss Topology Optimization with Stress and Local Buckling Constraints. Struct. Optim. 1996, 11, 134–136. [Google Scholar] [CrossRef]
- Gao, X.; Ma, H. Topology Optimization of Continuum Structures under Buckling Constraints. Comput. Struct. 2015, 157, 142–152. [Google Scholar] [CrossRef]
- Ferrari, F.; Sigmund, O. Revisiting Topology Optimization with Buckling Constraints. Struct. Multidiscip. Optim. 2019, 59, 1401–1415. [Google Scholar] [CrossRef]
- Wang, Y.; Sigmund, O. Multi-Material Topology Optimization for Maximizing Structural Stability under Thermo-Mechanical Loading. Comput. Methods Appl. Mech. Eng. 2023, 407, 115938. [Google Scholar] [CrossRef]
- Habashneh, M.; Movahedi Rad, M. Plastic-Limit Probabilistic Structural Topology Optimization of Steel Beams. Appl. Math. Model. 2024, 128, 347–369. [Google Scholar] [CrossRef]
- Zhang, G.; Khandelwal, K.; Guo, T. Topology Optimization of Stability-Constrained Structures with Simple/Multiple Eigenvalues. Int. J. Numer. Methods Eng. 2024, 125, e7387. [Google Scholar] [CrossRef]
- Movahedi Rad, M.; Habashneh, M.; Lógó, J. Reliability Based Bi-Directional Evolutionary Topology Optimization of Geometric and Material Nonlinear Analysis with Imperfections. Comput. Struct. 2023, 287, 107120. [Google Scholar] [CrossRef]
- Kharmanda, G.; Olhoff, N.; Mohamed, A.; Lemaire, M. Reliability-Based Topology Optimization. Struct. Multidiscip. Optim. 2004, 26, 295–307. [Google Scholar] [CrossRef]
- dos Santos, R.B.; Torii, A.J.; Novotny, A.A. Reliability-Based Topology Optimization of Structures under Stress Constraints. Int. J. Numer. Methods Eng. 2018, 114, 660–674. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Jensen, H.A. Computational Methods in Optimization Considering Uncertainties—An Overview. Comput. Methods Appl. Mech. Eng. 2008, 198, 2–13. [Google Scholar] [CrossRef]
- Wang, L.; Xia, H.; Yang, Y.; Cai, Y.; Qiu, Z. A Novel Approach of Reliability-Based Topology Optimization for Continuum Structures under Interval Uncertainties. Rapid Prototyp. J. 2019, 25, 1455–1474. [Google Scholar] [CrossRef]
- Van Huynh, T.; Tangaramvong, S.; Do, B.; Gao, W.; Limkatanyu, S. Sequential Most Probable Point Update Combining Gaussian Process and Comprehensive Learning PSO for Structural Reliability-Based Design Optimization. Reliab. Eng. Syst. Saf. 2023, 235, 109164. [Google Scholar] [CrossRef]
- Maute, K.; Frangopol, D.M. Reliability-Based Design of MEMS Mechanisms by Topology Optimization. Comput. Struct. 2003, 81, 813–824. [Google Scholar] [CrossRef]
- Meng, Z.; Pang, Y.; Pu, Y.; Wang, X. New Hybrid Reliability-Based Topology Optimization Method Combining Fuzzy and Probabilistic Models for Handling Epistemic and Aleatory Uncertainties. Comput. Methods Appl. Mech. Eng. 2020, 363, 112886. [Google Scholar] [CrossRef]
- Lógó, J.; Ghaemi, M.; Rad, M.M. Optimal Topologies in Case of Probabilistic Loading: The Influence of Load Correlation. Mech. Based Des. Struct. Mach. 2009, 37, 327–348. [Google Scholar] [CrossRef]
- Nishino, T.; Kato, J. Robust Topology Optimization Based on Finite Strain Considering Uncertain Loading Conditions. Int. J. Numer. Methods Eng. 2021, 122, 1427–1455. [Google Scholar] [CrossRef]
- Jung, H.S.; Cho, S. Reliability-Based Topology Optimization of Geometrically Nonlinear Structures with Loading and Material Uncertainties. Finite Elem. Anal. Des. 2004, 41, 311–331. [Google Scholar] [CrossRef]
- Csébfalvi, A. Structural Optimization under Uncertainty in Loading Directions: Benchmark Results. Adv. Eng. Softw. 2018, 120, 68–78. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, X.; Zhang, W.; Yan, J.; Sun, G. Multi-Scale Robust Design and Optimization Considering Load Uncertainties. Comput. Methods Appl. Mech. Eng. 2015, 283, 994–1009. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2009. [Google Scholar]
- Yang, X.Y.; Xie, Y.M.; Liu, J.S.; Parks, G.T.; Clarkson, P.J. Perimeter Control in the Bidirectional Evolutionary Optimization Method. Struct. Multidiscip. Optim. 2002, 24, 430–440. [Google Scholar] [CrossRef]
- Li, Q.; Steven, G.P.; Xie, Y.M. A Simple Checkerboard Suppression Algorithm for Evolutionary Structural Optimization. Struct. Multidiscip. Optim. 2001, 22, 230–239. [Google Scholar] [CrossRef]
- Habashneh, M.; Rad, M.M. Reliability Based Topology Optimization of Thermoelastic Structures Using Bi-Directional Evolutionary Structural Optimization Method. Int. J. Mech. Mater. Des. 2023, 19, 605–620. [Google Scholar] [CrossRef]
- Movahedi Rad, M.; Habashneh, M.; Lógó, J. Elasto-Plastic Limit Analysis of Reliability Based Geometrically Nonlinear Bi-Directional Evolutionary Topology Optimization. Structures 2021, 34, 1720–1733. [Google Scholar] [CrossRef]



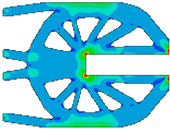
| Applied External Force | Movahedi et al. [43] | Proposed Algorithm | |
|---|---|---|---|
 |  |  | |
 | 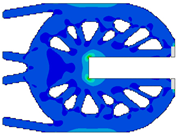 | ||
 |  | ||
 | 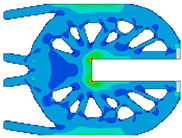 |
| Applied External Force | Movahedi et al. [43] | Proposed Algorithm | |
|---|---|---|---|
 |  |  | |
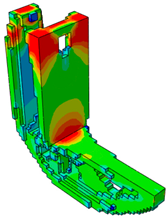 |  | ||
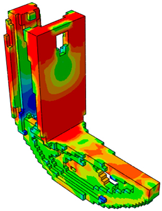 | 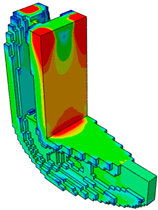 | ||
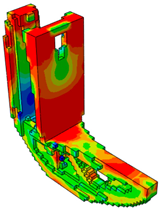 | 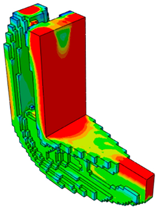 |
| Variable | Mean Value | Standard Deviation |
|---|---|---|
| (KN) | |||||
|---|---|---|---|---|---|
| Applied Load | Habashneh et al. [24] | Proposed Algorithm |
|---|---|---|
 | ||
 | ||
 | ||
 | ||
 | ||
| Applied Load | Habashneh et al. [24] | Proposed Algorithm |
|---|---|---|
 | ||
 | ||
 | ||
 | ||
 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habashneh, M.; Ghodousian, O.; Fathnejat, H.; Movahedi Rad, M. Probabilistic Topology Optimization Framework for Geometrically Nonlinear Structures Considering Load Position Uncertainty and Imperfections. Mathematics 2024, 12, 3686. https://doi.org/10.3390/math12233686
Habashneh M, Ghodousian O, Fathnejat H, Movahedi Rad M. Probabilistic Topology Optimization Framework for Geometrically Nonlinear Structures Considering Load Position Uncertainty and Imperfections. Mathematics. 2024; 12(23):3686. https://doi.org/10.3390/math12233686
Chicago/Turabian StyleHabashneh, Muayad, Oveys Ghodousian, Hamed Fathnejat, and Majid Movahedi Rad. 2024. "Probabilistic Topology Optimization Framework for Geometrically Nonlinear Structures Considering Load Position Uncertainty and Imperfections" Mathematics 12, no. 23: 3686. https://doi.org/10.3390/math12233686
APA StyleHabashneh, M., Ghodousian, O., Fathnejat, H., & Movahedi Rad, M. (2024). Probabilistic Topology Optimization Framework for Geometrically Nonlinear Structures Considering Load Position Uncertainty and Imperfections. Mathematics, 12(23), 3686. https://doi.org/10.3390/math12233686







