Abstract
Image classification is a fundamental task in deep learning, and recent advances in quantum computing have generated significant interest in quantum neural networks. Traditionally, Convolutional Neural Networks (CNNs) are employed to extract image features, while Multilayer Perceptrons (MLPs) handle decision making. However, parameterized quantum circuits offer the potential to capture complex image features and define sophisticated decision boundaries. In this paper, we present a novel Hybrid Quantum–Classical Neural Network (H-QNN) for image classification, and demonstrate its effectiveness using the MNIST dataset. Our model combines quantum computing with classical supervised learning to enhance classification accuracy and computational efficiency. In this study, we detail the architecture of the H-QNN, emphasizing its capability in feature learning and image classification. Experimental results demonstrate that the proposed H-QNN model outperforms conventional deep learning methods in various training scenarios, showcasing its effectiveness in high-dimensional image classification tasks. Additionally, we explore the broader applicability of hybrid quantum–classical approaches in other domains. Our findings contribute to the growing body of work in quantum machine learning, and underscore the potential of quantum-enhanced models for image recognition and classification.
MSC:
81P99
1. Introduction
Image classification [1] is a cardinal task in computer vision, which involves the assignment of images to predefined categories or labels. Accurate object recognition is critical in various applications, including medical imaging, social media analytics [2], and autonomous driving systems [3]. Traditionally, binary classification (i.e., distinguishing between two distinct categories) has been achieved using handcrafted features or, more recently, deep learning methods such as Convolutional Neural Networks (CNNs), which automatically learn hierarchical features from images.
In recent years, the emergence of quantum machine learning (QML) [4,5] has opened new avenues for improving data processing, optimization, and classification tasks. The relevance of QML has grown significantly in the Noisy Intermediate-Scale Quantum (NISQ) era, which bridges machine learning principles [6,7,8] with the computational advantages of quantum systems [9,10,11]. Quantum computing’s ability to handle complex, high-dimensional data efficiently makes it particularly suitable for applications requiring probabilistic and computationally intensive operations like image interpretation.
While several models leveraging parameterized quantum circuits (PQCs) [12,13] and quantum annealers have been proposed, the potential of quantum neural networks (QNNs) [14,15] to surpass conventional machine learning models remains an open question. Despite advancements in quantum computing, the practical applicability of QML is currently constrained by hardware limitations, including qubit coherence and fault tolerance, which have restricted most quantum algorithms to small-scale simulations.
The ongoing development of hybrid quantum–classical models (e.g., Hybrid Quantum Neural Networks (H-QNNs) [16]) offers a promising approach to overcoming these limitations. By combining classical deep learning techniques with quantum computational advantages, H-QNNs aim to enhance both the efficiency and performance of image classification tasks. This hybrid approach is particularly well-suited for energy-efficient and computational resource-efficient applications. This hybrid approach make it a strong candidate for deployment in real-world scenarios as quantum technology matures. To evaluate the efficacy of H-QNNs in binary image classification, we apply our model to the MNIST dataset, which is a widely-used benchmark in machine learning. The dataset consists of grayscale images of handwritten digits. We focus specifically on the binary classification of the digits ‘0’ and ‘1’. This study demonstrates how H-QNNs can effectively extract features and classify these digits, thereby offering potential improvements over classical models. Our results add to the growing quantum machine learning literature and highlight the potential of hybrid quantum–classical methods in image recognition and beyond.
The synergy between classical and quantum techniques in image classification has shown promise not only in enhancing accuracy but also in improving computational efficiency for large-scale datasets. Recent studies have explored the application of Quantum Support Vector Machines (QSVMs) and Quantum k-Nearest Neighbors (QkNN) networks [17,18,19] in classifying high-dimensional image data. These quantum-inspired models leverage the unique properties of quantum states and operations, such as superposition and entanglement, to improve data separability, particularly in binary and multi-class classification tasks. Additionally, optimization methods such as Quantum Gradient Descent and Quantum Approximate Optimization Algorithms (QAOAs) are contributing to the robustness and scalability of hybrid approaches [20,21,22]. Integrating these quantum techniques with classical image processing methods, as in H-QNNs, is anticipated to accelerate the development of practical, scalable solutions for image classification tasks in domains like medical diagnostics, autonomous driving, and smart surveillance systems. As quantum hardware continues to improve, hybrid models are expected to play a central role in bridging the gap between classical limitations and quantum capabilities.
1.1. Motivation and Contribution
Recent research works have demonstrated the potential of leveraging quantum computing in conjunction with classical machine learning methods for various tasks [16,23,24]. Although these applications show promise, further optimization and comprehensive testing are required to achieve peak performance. Future research should focus on improving quantum circuit architectures, expanding to larger qubit systems, and exploring diverse quantum algorithms to fully capitalize on quantum computing’s potential in enhancing machine learning models.
The primary contributions of this work are as follows:
- We presents a novel Hybrid Quantum–Classical Neural Network (H-QNN) model. This architecture integrates fundamentals feature mapping with a classical neural network to effectively improve image classification tasks, with a specific focus on binary classification using the MNIST dataset.
- The proposed work refines the quantum layer by using parameterized quantum circuits (VQCs) that contain RY rotation gates and CX entanglement gates, in conjunction with the ZZFeature Map for efficient data encoding. This design reduces the circuit depth while maintaining favorable computational efficiency.
- By obtaining a score of 99.7% on the binary MNIST classification task, the proposed H-QNN model shows that it is more accurate and needs a lot less computing power than traditional CNNs and QCNNs.
- This paper underscores the broader applicability of hybrid quantum–classical models in different domains like finance, cybersecurity, and medical diagnostics and highlights the potential for scaling these models to handle more complex data and tasks.
1.2. Organization
This article is organized as follows: Section 2 reviews related work on quantum computing for image classification. Section 3 introduces quantum computing’s fundamental concepts. Section 4 details the architecture of the H-QNN model and proposed methodology. Section 5 covers the experimental setup. Section 6 provides the experimental analysis of the model’s performance. Finally, Section 7 concludes with insights and future directions.
2. Related Work
2.1. Convolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNNs) were introduced by LeCun in 1989 and have since become a cornerstone in the field of image recognition, e.g., handwritten digit classification tasks [25]. CNNs have evolved and been widely used in different artificial intelligence (AI) domains such as image segmentation, classification, object detection, and noise reduction. In fact, various canonical CNN architectures have been systematically devised over time, e.g., LeNet [26], AlexNet [27], VGG [28], GoogLeNet [29,30], and ResNet [31,32]. Notably, in 2012, AlexNet won the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC), thereby marking CNNs’ breakthrough into mainstream computer vision tasks.
CNNs are capable of automatically learning hierarchical features from raw data through a sequence of layers, which include convolutional, activation, and pooling layers. To generate feature maps, the convolutional layer performs feature extraction by applying filters (kernels) to the input image. The activation layer introduces non-linearity into the model. Pooling layers then perform down-sampling operations to reduce the spatial dimensions of the feature maps. The pooling process attempts to retain essential information, and improves computational efficiency and reduces the risk of overfitting. Overfitting can be mitigated by techniques such as dropout and data augmentation, as demonstrated by Levi and Hassner [33]. They showed that such strategies can achieve strong performance even on small and unconstrained datasets for gender and age classification.
CNNs have also proven effective in large-scale image classification tasks. Karpathy et al. [34] trained a CNN on a dataset of 1 million YouTube videos spanning 487 classes. This demonstrated CNNs’ ability to learn robust features from vast and often poorly labeled data. Their model showed substantial improvements, with a reported performance boost of up to 63.3% on the UCF-101 Action Recognition dataset. Jmour et al. [35] explored CNNs for traffic sign classification. They trained a CNN on the ImageNet dataset and showed that the accuracy of the model was sensitive to hyperparameters like mini-batch size. They achieved an accuracy of 93.33% on the test set with a mini-batch size of ten. Kang et al. [36] applied CNNs to document image classification by using rectified linear units and dropout for improved generalization. Their model outperformed previously established methods by attaining a median accuracy of 65.37% on the Tobacco dataset and a perfect median accuracy of 100% on the NIST tax-form dataset. Sermanet et al. [37] applied CNNs to house number digit classification. They employed multi-stage feature extraction and Lp pooling to reduce error rates by 45.2%. Their work on the SVHN dataset increased classification accuracy to 94.85%. Wu [38] applied CNNs to the MNIST handwritten digit dataset using the LeNet-5 architecture. The network consists of an input layer of neurons that also corresponds to the image dimensions, a hidden layer with 100 neurons, and an output layer for classifying digits. The framework was trained using the Stochastic Gradient Descent (SGD) algorithm, and achieved a testing accuracy of 94.00% after 100 epochs. Palvanov and Cho [39] achieved a testing accuracy of 98.10% on the MNIST dataset using a CNN with two convolutional layers and two fully connected layers, employing a mini-batch size of 50.
2.2. Quantum Neural Networks (QNNs)
In recent years, QNNs, widely used methods in QML, have garnered significant attention. Most of the work in this area has focused on designing quantum networks, which mimic the structure of classical neural networks, with the goal of achieving competitive results. Despite numerous challenges (e.g., hardware limitations and algorithmic complexities), research on QNNs has made notable progress. Jeswal and Chakraverty [40] provide a comprehensive overview of recent QNN applications like breast cancer prediction, image compression, and pattern recognition.
A significant body of work has also explored the efficacy of QNNs for image data classification. For instance, Nguyen et al. [41] proposed a QNN architecture optimized for current quantum hardware, and showed that QNNs can classify images with reduced noise, even with shallow circuits and optimized gate usage. One of the pioneering models in the development of QNNs is the Quantum M-P Neural Network by Zhou and Ding [42]. This model extends the classical M-P Neural Network by using qubits as inputs, and each neuron computed the weighted sum of the connected qubits. The network employs a weighted learning algorithm for training like classical neural structures for quantum computation.
In addition to image classification, QNNs have been applied to various domains. Safari et al. [43] explored the use of QNNs for weather prediction within smart systems. Their research highlighted the benefits of combining QNNs with classical models to form hybrid architectures. Any such procedure could be advantageous for processing large-scale data like the high-dimensional datasets required for weather forecasting in smart grids. Paquet and Soleymani [44] introduced QuantumLeap, a hybrid quantum–classical model designed for financial time series analysis. The model utilizes a quantum encoder to transform financial data into density matrices, a quantum network to forecast future matrices, and a classical network to predict optimal security prices. Another innovative quantum model is the quantum convolutional neural network (QCNN), which was presented by Wei et al. [45]. The QCNN mimics the architecture of classical CNNs [46] by employing quantum convolutional layers, pooling layers, and fully connected layers. To replicate classical pooling operations, the QCNN reduces the dimensionality of quantum states by eliminating qubits at the pooling layers. Furthermore, a parameterized Hamiltonian is used in the fully connected layer, and its expectation value is computed and passed through a non-linear activation function to introduce nonlinearity into the quantum model. The Hamiltonian represents the total energy of the quantum system and is parameterized to allow for dynamic adjustments during training. In terms of performance, classical CNN models and QCNN have achieved an average accuracy of 97.2% and 96%, respectively, on the MNIST-2 dataset. It is worth noting that QCNN operates with reduced computational overhead and fewer parameters but is still able to deliver satisfactory outcomes.
2.3. Hybrid Quantum–Classical Neural Networks (HQNNs)
Hybrid Quantum–Classical Neural Networks (HQNNs) have gained significant attention due to their potential to outperform classical approaches across different complex problem domains. These models blend quantum algorithms with classical neural networks, and enhance performance in domains like image recognition, finance, molecular dynamics, and cybersecurity. This section highlights recent advancements and key contributions in the development of HQNNs with a focus on classification problems.
HQNNs leverage the computational power of quantum algorithms while maintaining the stability and reliability of classical architectures. For example, Xia et al. [47] demonstrated the utility of HQNNs in quantum chemistry to determine molecular ground state energies. The hybrid approach exhibited notable improvements over classical models in certain scenarios. Similarly, Drain and Senderowicz’s expanded the use of HQNNs in several machine learning tasks to showcase their adaptability and problem-solving efficacy across domains. Hellstem [48] proposed a hybrid quantum–classical architecture for the classification of both structured financial data and unstructured datasets, including MNIST digits. The study also highlighted the versatility of HQNNs in solving both classical and quantum classification tasks. While, Fan et al. [24] explored the integration of quantum layers within conventional CNN architectures to process large-scale image datasets. Their findings revealed that hybrid models can match or even surpass the efficiency of pure CNNs while utilizing fewer computational resources. Likewise, Bokhan et al. [49] applied quantum convolutional layers alongside classical learning algorithms for multiclass image classification tasks and indicated the suitability of quantum models for high-dimensional image data. Xu et al. [50] further investigated parallel quantum circuits to optimize the performance of hybrid models in image classification and demonstrated improved scalability and efficiency. Furthermore, Ling et al. [51] examined the fusion of quantum and classical backpropagation techniques within HQNNs, and achieved competitive results on standard large-scale image datasets. Finally, Islam et al. [52] proposed a hybrid quantum–classical model to detect cyberattacks on cloud-supported vehicular networks, and demonstrated that the hybrid architecture effectively enhances anomaly detection. The techniques used along with the highlights and limitations of the various discussed schemes are summarized in Table 1.

Table 1.
Summarized related work.
3. Basic Preliminaries
3.1. Superposition
Superposition is a foundational principle of quantum mechanics, describing the phenomenon where a quantum system can exist in multiple states simultaneously. It arises from the linearity of the Schrödinger equation, where if two solutions and exist, any linear combination of these solutions, given by
is also a valid solution. Here, and are complex coefficients. More generally, for wave equations with multiple solutions, combinations of all such solutions remain legitimate.
This principle underpins many quantum phenomena, including interference and entanglement. Superposition is not limited to quantum computing; it applies broadly across quantum physics, from atomic and molecular systems to quantum fields [58,59,60]. In essence, superposition enables quantum systems to exhibit behaviors that have no classical analog, such as the simultaneous existence of multiple pathways in quantum interference experiments.
3.2. Qubits
In quantum computing, a qubit is the fundamental unit of quantum information that directly applies the principle of superposition. Unlike classical bits, which exist solely in one of two states, 0 or 1, a qubit can simultaneously represent both states. Mathematically, the state of a qubit is expressed as follows:
where and are the basis states, and and are complex numbers known as probability amplitudes. These amplitudes satisfy the normalization condition:
The coefficients and determine the probabilities of measuring the qubit in the or state. Upon measurement, the qubit collapses to one of these basis states, with probabilities and , respectively. Qubits are realized using various technologies, such as superconducting circuits, trapped ions, and photonic systems [61,62,63]. Their ability to exist in superposition enables quantum computers to perform complex computations, such as searching databases or factoring large numbers, exponentially faster than classical computers in certain cases.
3.3. Quantum Gates
Quantum gates serve as the rudimentary building blocks of quantum circuits like conventional logic gates. They operate on qubits to perform functions such as state flipping, entanglement, and superposition creation. Key quantum gates include the Pauli-X gate that acts like a classical NOT gate by flipping a qubit’s state, the Hadamard gate that generates superposition, and the CNOT (Controlled-NOT) gate that entangles two qubits. Quantum circuits often involve a combination of these gate operations to manipulate the quantum states of qubits [64,65].
3.4. Entanglement
Entanglement is a fundamental property of quantum mechanics, where two or more quantum systems become linked such that their states cannot be described independently. This phenomenon is mathematically represented by a quantum state of multiple particles. For instance, a general two-qubit state can be expressed as follows:
where , , , and are complex coefficients satisfying the normalization condition .
A key characteristic of entanglement is the inseparability of the quantum state. For a state to be entangled, it must not be expressible as a tensor product of the individual states of the subsystems. Mathematically, the state is separable (not entangled) if and only if it can be written in the form:
where and are states of the individual subsystems (qubits).
To determine entanglement, the partial transpose criterion (Peres–Horodecki criterion) provides a necessary condition [66,67]. For the density matrix of a two-qubit system, if the partial transpose has any negative eigenvalues, the state is entangled. This can be summarized as follows:
where are the elements of the original density matrix .
For example, the Bell state
is an entangled state because it cannot be expressed as a product of individual qubit states. Its density matrix
has a partial transpose with negative eigenvalues, confirming entanglement.
3.5. Measurement
In quantum computing, measurement is the process of extracting information from a qubit, which leads to the collapse of its superposition into a definitive state of either 0 or 1. The qubit’s superposition coefficients determine the probabilities of these outcomes. Measurement alters the operational state of the qubit and is typically confined to a computational basis like the Z-basis [68]. For instance, in IBM quantum computers, measurements are performed along the Z-axis of the Bloch sphere to determine whether the qubit collapses to or . To measure in other bases, such as the X-basis or Y-basis, additional quantum gates are required to rotate the qubit states into the desired computational basis. This approach simplifies the measurement process while enabling flexibility in basis selection. The architecture of a quantum neural network (QNN) is illustrated in Figure 1.
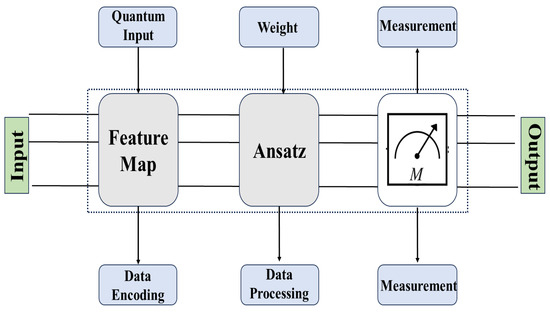
Figure 1.
The architecture of QNNs.
3.6. CNNs and QNNs: Foundations, Architectures, and Recent Advancements in Quantum Machine Learning
A CNN has convolutional layers, pooling layers, and a fully connected layer that determines the image’s class. The convolution operation involves applying a convolving kernel to the image, and sliding it according to a specified step size (e.g., often set to 1). Mathematically, if the input image A is of size and the kernel P is , the convolution can be expressed as follows:
where represents the nonlinear function. Padding is often employed in the convolutional layer to match the dimensions of feature maps with the input image. Following convolution, the feature map is passed to the pooling layer for dimensionality reduction by employing techniques like max pooling or average pooling. The final classification is performed in the fully connected layer.
Recent years have seen significant momentum for QNNs as a key method in QML. The predominant focus has been on designing quantum networks that emulate classical neural networks while delivering similar performance [69,70,71]. While challenges and ongoing refinement are necessary, significant advancements have been made in the development and application of QNNs. For instance, recent work by Waris et al. (2024) explored a diverse array of applications for QNNs, including breast cancer prediction, image compression, and pattern recognition. The architecture of CNNs is depicted in Figure 2.
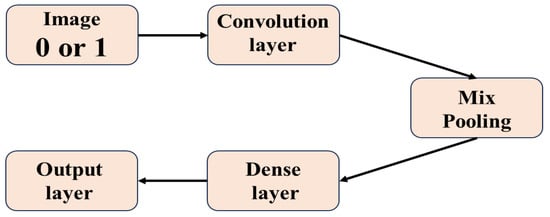
Figure 2.
The architecture of CNNs.
4. Materials and Methodology for Proposed Method
4.1. MNIST Dataset Description
In this work, we utilized the MNIST dataset, which has been considered as a benchmark for evaluating machine learning algorithms in handwritten digit classification. It consists of 60,000 training examples and 10,000 test examples of grayscale images of digits (0 to 9). For our experiments, we selected a subset comprising 10,000 training images and 2000 test images. Each image is a pixel grayscale matrix, with pixel intensity values ranging from 0 to 255. There are 784 pixels per image. The dataset is balanced across the ten digit classes, and ensures even representation of each class. Figure 3 provides sample images from the MNIST dataset.

Figure 3.
Sample images from the MNIST dataset.
4.2. Hybrid Quantum-Classical Architecture
The proposed hybrid quantum–classical model consists of three parts: the quantum layer, variational quantum circuit (VQC), and classical layer. They work together to address two-class classification problems using both classical and quantum computing. A simplified structure is shown in Figure 4.
Figure 4.
Hybrid Quantum–Classical Neural Network model.
In Figure 4, is a nonlinear function, is the value of neuron n in each hidden layer, and is a rotation gate that rotates by . The final prediction value from the hybrid network is denoted by y. Table 2 and Table 3 show the layer type, output shape, and number of parameters in the PyTorch and quantum neural networks.

Table 2.
Structure of the PyTorch neural network.

Table 3.
Structure of the quantum neural network (QNN).
- Quantum Layer: The quantum layer serves as a bridge between classical and quantum processing by transforming classical data into quantum states. Using quantum feature maps, it encodes data into a higher-dimensional quantum space, enabling complex relationships to be captured that might be hidden in classical representation. This mapping enhances the model’s ability to identify intricate patterns by leveraging quantum properties, ultimately improving the performance of hybrid quantum–classical algorithms. Through this transformation, classical inputs gain access to the computational advantages of quantum mechanics.Quantum Feature Mapping: We use the ZZFeature map to encode the conventional feature vector into a quantum state. Quantum states process information through unitary gates by enabling the model to learn more complex and non-linear patterns than classical models. After encoding, the quantum state is passed to the variational quantum circuit (VQC) for further processing.
- Variational Quantum Circuit (VQC): A VQC is a quantum circuit with parameterized quantum gates, forming the foundation of the quantum layer in hybrid quantum–classical models. These gates contain trainable variables, allowing the circuit’s parameters to be adjusted. During training, these parameters are iteratively optimized based on a cost function, enabling the VQC to learn patterns or solutions. This iterative process allows VQCs to approximate complex functions and contribute to quantum machine learning and optimization tasks.
- Parametric Quantum Gates: The VQC employs RY rotation gates to rotate qubit states on the Y-axis of the Bloch sphere and CX entanglement gates to establish qubit correlations.
- Real Amplitudes Ansatz: This ansatz is employed in our VQC design, which includes RY rotations and CX gates in sequential layers. The circuit depth and number of trainable parameters can be adjusted based on the complexity of the problem. For efficiency and to capture complex patterns, only one repetition of the circuit is used. During training, classical optimization methods such as the Adam optimizer are applied to minimize the loss function and align the VQC’s output with the target labels.
- Classical Layer: The VQC produces quantum measurements, which are then processed by a classical layer to make decisions:
- Measurement: Quantum circuits are measured to collapse quantum states into classical data, which yield the system’s state probabilities. These probabilities are then fed into the classical model for further processing.
- Classical Neural Network: A feed-forward neural network (or another classifier like SVM) takes the quantum probabilities as input, and produces a binary output (‘0’ or ‘1’). It allows the model to combine quantum feature encoding with classical decision-making.
4.3. Dataset Preprocessing
As mentioned above, the MNIST dataset contains 70,000 handwritten digits (0–9) at pixels, and considered as a benchmark for image classification. We used 10,000 training and 2000 testing records focused on digits 0 and 1 for binary classification. Its simplicity and common use in hybrid quantum–classical modeling showcase the benefits of quantum machine learning. All simulations were performed using the Jupyter Notebook environment, which permitted efficient and dynamic exploration.
After choosing the dataset, preprocessing was performed in order to prepare the data for quantum computing as well as to increase the learning efficiency of the quantum model.
4.3.1. Data Splitting
We divided the dataset into two parts. The Training Set (80%) comprises 800 samples. This set has features and labels to use for model training. The Testing Set (20%) features 200 samples. This set includes only features for the sake of validating model generalization to new data. This splitting strategy is crucial to assess the model’s performance on previously unseen data and its overall effectiveness.
4.3.2. Standard Scaling
Following the data split, we applied standard scaling to normalize the pixel intensity values to ensure they have zero mean and unit variance. This step is important because most machine learning models, including quantum models, assume that input features are normally distributed. Standard scaling is useful to prevent issues like vanishing or exploding gradients. It allows the learning algorithm to remain robust against variations in feature distribution, ultimately improving performance.
4.4. Quantum Circuit Design
We then focus on the quantum circuit layout by first discussing state preparation to represent the preprocessed data in quantum form. Figure 5 shows the quantum circuit design. The idea is to employ quantum-based techniques to extract features and thereby enhance the learning algorithm’s efficiency through quantum parallelism.
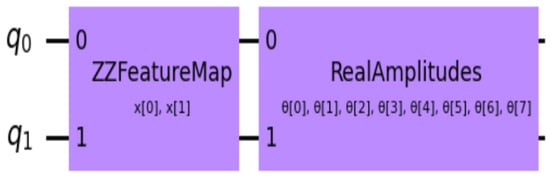
Figure 5.
Quantum circuit.
4.4.1. State Preparation (ZZFeature Map)
State preparation is an important step in quantum machine learning, as it involves mapping classical data onto quantum states.
- To encode data, the ZZFeature Map was used, inspired by traditional machine learning kernel methods. This approach non-linearly transforms classical datasets into a higher-dimensional quantum space.
- The feature map generates quantum states. The function states describe a larger feature space that enables the classifier to spot a separating hyperplane in the extended quantum area. The unitary operation creates a circuit of circuit of Hadamard gates (H) interleaved with entangling gates to achieve the encoding.
- This approach improves the learning of non-linear data patterns through the use of quantum feature mapping.
4.4.2. Real Amplitudes Ansatz
The Real Amplitudes Ansatz from the Qiskit library was utilized to generate the variational quantum circuit in our hybrid model.
- This ansatz is made of single-qubit rotation gates and two-qubit entanglement gates . First, the parameterized gates are applied to each qubit, and then the entangling gates are executed.
- A second parameterized rotation is performed as a fourth step after the entanglement wall. This setup allows for slow and accurate encoding of data into the quantum states. Moreover, circuit depth was reduced by selecting a single repetition of the gates and rotations.
Algorithm 1 illustrates the hybrid quantum–classical cricuits.
| Algorithm 1 Hybrid quantum–classical module. |
|
4.5. Optimization
We used the Adam optimizer to fine-tune the model parameters. This highly efficient optimization method is efficient for large-scale problems with extensive data and numerous parameters. Adam combines two optimization algorithms, i.e., ‘gradient descent with momentum’ and ‘RMSProp’. The momentum component in gradient descent accelerates convergence to minima by considering the exponentially weighted average of past gradients, whereas RMSProp adjusts the learning rate utilizing the exponential moving average of squared gradients leading to enhanced AdaGrad’s performance. These features together make Adam a powerful optimization tool in machine learning.
5. Experimental Setup
Figure 6 illustrates the flowchart of a quantum–classical hybrid model pipeline for binary classification of the MNIST dataset with sub-sampling of only classes 0 and 1. Below is a step-by-step explanation of the components and the process flow:
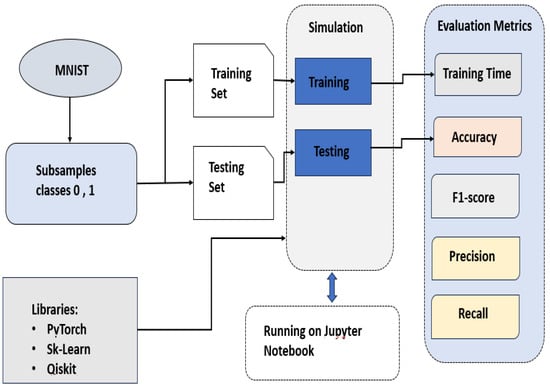
Figure 6.
Experimental Setups.
- MNIST Dataset: It starts with MNIST, which consists of handwritten digit images.Subsampling Classes 0 and 1: A portion of the MNIST data is chosen, composed solely of images of the digits “0” and “1”. This simplifies the classification task to a binary classification. Labeled and predicted images from the MNIST dataset are shown in Figure 7.
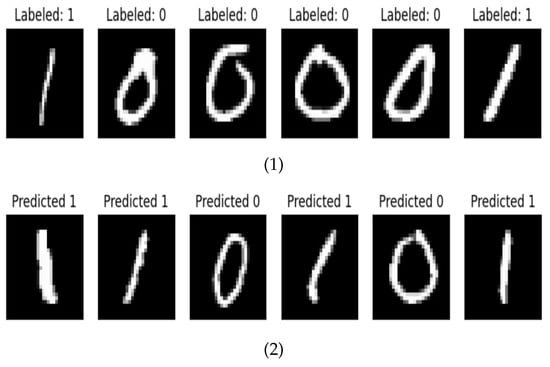 Figure 7. Labeled (1) and Predicted (2) images of MNIST.
Figure 7. Labeled (1) and Predicted (2) images of MNIST. - Data Splitting: The subsampled dataset is divided into two sets: training set (i.e., this includes all records used to train the model) and testing set (i.e., a portion is used for validations and other part is reserved for model validation after construction and development).
- Simulation (Training and Testing): The training set introduces the hybrid quantum classical model. It refines weights and quantum circuit parameters to improve image classification. After that, the test set evaluates the model’s generalization by running it on new data to assess its accuracy in predicting images as “0” or “1”.
- Libraries used: The following libraries were used for the simulation:PyTorch: A classical framework widely used for training neural networks data processing tasksScikit-Learn (Sk-Learn): A Python 13.11.0 library for dataset splitting, model evaluation, and classical machine learning.Qiskit: It is an IBM programming framework utilized to build and simulat quantum circuits in a hybrid quantum–classical architecture.
- Running on Jupyter Notebook: All computation, data processing, training, testing, and evaluation were conducted in Jupyter Notebook, which is widely used for running Python code interactively.
- Evaluation Metrics: After testing the model, several evaluation metrics were computed to assess the model’s performance:Training Time: measures the duration taken to complete the model training.Accuracy: The proportion of correctly identified images by classifier out of total testing set.F1-Score: The average mean of precision and recall that is useful for handling class imbalance.Precision: The percentage of true positive identifications, e.g., correctly identifying images of “1”.Recall: The ratio of true positive identifications to all actual positive cases in the testing dataset.
6. Results and Discussion
This section evaluates the performance of the Hybrid Quantum-Classical Neural Network (H-QNN) on focusing on classifying digits 0 and 1 in the MNIST dataset. The 10,000 training images and 2000 testing images were used. Due to current quantum hardware limitations, we resized the images to pixel images for practical quantum simulation. Here, we outline the experiment’s configuration and compare the results to standard CNNs.
6.1. Performance Metrics
We evaluated the performance of our H-QNN model over ten epochs for training and validation. We used a test set to calculate accuracy and loss. Figure 8 and Figure 9 represent the efficiency and loss as a function of the number of epochs. Training loss is shown in Figure 9. The training loss steadily decreased from −4.5 to −7.5 over the epochs, which indicates that the model was learning effectively. Validation loss loss decreased from −4.8 to −7.7 that demonstrates that the model not only learned from the training data but also adapted well to new data. Both training and validation losses are falling and this reflects that the model was reliable and detected valuable data patterns.
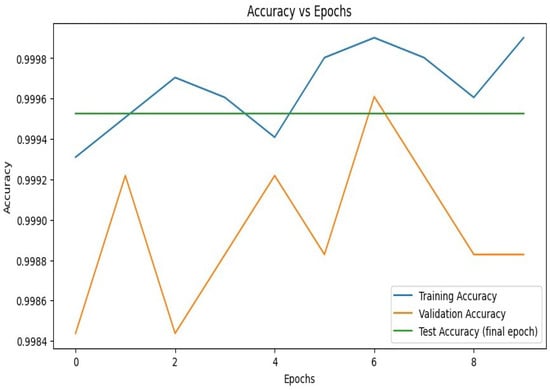
Figure 8.
Accuracy vs. Epochs.
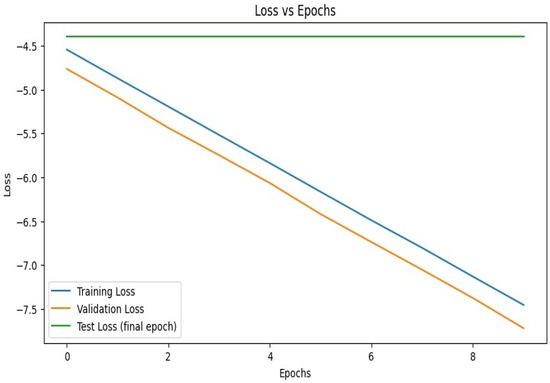
Figure 9.
Loss vs. Epochs.
6.2. Accuracy Metrics
The training accuracy consistently improved, and reached a peak of 99.96%. Validation accuracy showed minor shifts across epochs, while consistently remaining high between 99.84% and 99.96%. These outcomes indicate that the model effectively distinguished between the digits 0 and 1.
6.3. Confusion Matrix
The model’s performance is shown using the confusion matrix in Figure 10. It displays the true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) for the binary classification task. With a precision of 99%, recall of 99%, and an F1-score of 98.9%, the metrics indicate that the model effectively identified a significant proportion of digit images while maintaining a low rate of false positives and negatives. All in all, these results demonstrate the model’s excellent accuracy and recall, as also reflected in its strong F1-score.
Figure 10.
Confusion matrix.
6.4. Comparison with CNN and QCNN
The H-QNN architecture was evaluated against a standard CNN model for the binary MNIST classification task. As shown in Table 4 and Figure 11, the H-QNN outperformed both traditional CNNs and QCNNs. Using the simulation’s limited quantum hardware, our H-QNN produced superior results with fewer parameters and minimal computational effort. The most important finding of this work is that the H-QNN model has higher performance compared with other state-of-art models when applied to the MNIST dataset, including CNNs, ResNet, DenseNet, Vision Transformer (ViT), and Capsule Network (CapNet). A comparison as to these models is presented below demonstrating the advantage of H-QNN. The performance of the different models, including their accuracies and strengths are summarized in Table 4. In Figure 11, we show the accuracy comparison of the above mentioned models and the performance of H-QNN against it peers.

Table 4.
Performance comparison of models on MNIST dataset.
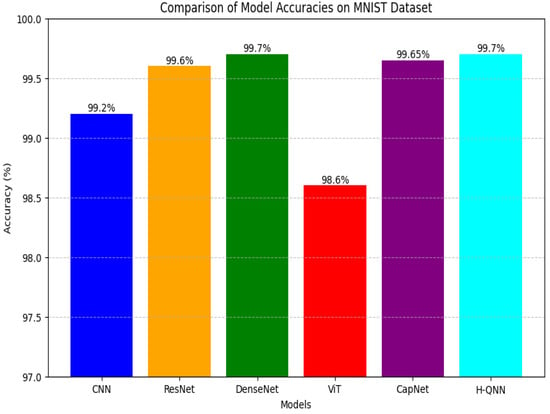
Figure 11.
Comparison of accuracy.
- CNNs have been reported to give very good results when used with MNIST dataset with an accuracy of 99.2% with LeNet architecture [54]. Although CNNs easily learn stacked features using convolutional layers, they may be brittle to other forms of features compared to these more complex networks. However, to overcome this limitation H-QNN uses the concept of the quantum feature mapping so that it can learn the complex representations effectively.
- ResNet, which uses residual connection, gives a 99.6% accuracy of the MNIST. It performs well in training deep networks due to helping solve the vanishing gradient problem but is precluded by classical computation that limits its ability to learn intricate data representation patterns [53]. Like other quantum neural networks, H-QNN takes advantage of parallelism within the quantum computer, thus making it capable of solving more complex patterns in a shorter time than is possible in classical computers.
- DenseNet achieves an accuracy of 99.7% by dense connections enabled with efficient feature reuse and gradient flow. While this architecture is very powerful in many ways, it requires more memory and more computation than the network depth grows [53,54]. By allowing quantum circuits to perform more effective complex feature mapping, H-QNN obtains similar accuracy with fewer resources.Furthermore, self-attention mechanisms are used in Vision Transformers (ViT) and are able to work better with larger datasets. Despite such accuracy ranges between 98.6% and 99.2% on MNIST. ViT is computationally expensive and lacks specialization to smaller datasets [55,56]. Compared to datasets of medium size, H-QNN is particularly efficient at extracting rich information using quantum features.
- CapNet preserves spatial hierarchies and has strong performance, which achieves 99.65% accuracy on MNIST. Despite that, CapNet’s dynamic routing is a hindrance to training and adds computational load [57]. Its hybrid approach, similar to H-QNN, achieves the same accuracy in a lower complexity.
Overall, the H-QNN model outperforms all classical alternatives because it takes advantage of quantum parallelism and feature mapping to learn complex patterns quickly with fewer resources than the classical alternatives. Once H-QNN scales, it should scale effectively as quantum hardware advances and could make use of large, high-dimensional datasets.
6.5. Discussion
Experimental results indicate that hybrid quantum–classical approaches may enhance the reliability and performance of image classification tasks. The use of quantum feature encoding and variational quantum circuits enabled the H-QNN model to recognize complex patterns compared to classical CNNs. Low loss and high accuracy reveal that the hybrid model benefits from quantum parallelism in its quantum layers while reducing resources needed for effective learning. Nonetheless, the trend in validation accuracy indicates potential for more improvements, e.g., through learning rate scheduling or higher regularization. Despite minor differences in results, the overall performance remains good, thus proving that quantum computing can help improve the conventional machine learning models. Overall, the proposed H-QNN model exhibits robust performance in image classification. It produced high accuracy, precision, and recall. Thus, this work further supports recent findings on the effectiveness of quantum–classical hybrid generative models in machine learning.
7. Conclusions and Future Work
This paper presented a new Hybrid Quantum–Classical Neural Network (H-QNN) for binary image classification using the MNIST dataset. By integrating quantum technology within traditional neural network structures, we showed some significant opportunities to enhance classification accuracy and efficiency. The H-QNN achieved an accuracy of 99.7% and outperformed conventional CNNs and QCNNs. The hybrid model proficiently applied quantum feature encoding to transform classical data into a transform space, which facilitated the discovery of complex patterns that conventional models typically have trouble recognizing. The consistent performance observed in both training and validation datasets emphasize the unique advantages of quantum computation in machine learning for complex datasets. High precision and recall demonstrate the H-QNN’s capability in correctly recognizing digits while ensuring minimal false positive and negative rates. It is appropriate for critical applications such as medical diagnostics and autonomous systems. All in all, there are still certain limitations like reduced image resolution and variations in validation accuracy. Future efforts should focus on addressing these challenges through improved data resolution and refined quantum circuit designs.
Author Contributions
D.R.: Conceptualization, writing, validation; S.P.: Software, validation, writing, visualization, data curation; Z.A.: Editing, writing, validation; P.K.: Reviewing and editing, investigation; A.V.V.: Reviewing and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Wang, S.Y.; Liao, W.S.; Hsieh, L.C.; Chen, Y.Y.; Hsu, W.H. Learning by expansion: Exploiting social media for image classification with few training examples. Neurocomputing 2012, 95, 117–125. [Google Scholar] [CrossRef]
- Turay, T.; Vladimirova, T. Toward performing image classification and object detection with convolutional neural networks in autonomous driving systems: A survey. IEEE Access 2022, 10, 14076–14119. [Google Scholar] [CrossRef]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 2015, 56, 172–185. [Google Scholar] [CrossRef]
- Ciliberto, C.; Herbster, M.; Ialongo, A.D.; Pontil, M.; Rocchetto, A.; Severini, S.; Wossnig, L. Quantum machine learning: A classical perspective. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170551. [Google Scholar] [CrossRef]
- Alpaydin, E. Machine Learning; MIT Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. Quantum computation. Science 1995, 270, 255–261. [Google Scholar] [CrossRef]
- Vedral, V.; Plenio, M.B. Basics of quantum computation. Prog. Quantum Electron. 1998, 22, 1–39. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sim, S.; Johnson, P.D.; Aspuru-Guzik, A. Expressibility and entangling capability of parameterized quantum circuits for hybrid quantum-classical algorithms. Adv. Quantum Technol. 2019, 2, 1900070. [Google Scholar] [CrossRef]
- Leyton-Ortega, V.; Perdomo-Ortiz, A.; Perdomo, O. Robust implementation of generative modeling with parametrized quantum circuits. Quantum Mach. Intell. 2021, 3, 17. [Google Scholar] [CrossRef]
- Gupta, S.; Zia, R. Quantum neural networks. J. Comput. Syst. Sci. 2001, 63, 355–383. [Google Scholar] [CrossRef]
- Kiss, O.; Tacchino, F.; Vallecorsa, S.; Tavernelli, I. Quantum neural networks force fields generation. Mach. Learn. Sci. Technol. 2022, 3, 035004. [Google Scholar] [CrossRef]
- Hafeez, M.A.; Munir, A.; Ullah, H. H-QNN: A Hybrid Quantum–Classical Neural Network for Improved Binary Image Classification. AI 2024, 5, 1462–1481. [Google Scholar] [CrossRef]
- Cheng, D.; Chen, L.; Lv, C.; Guo, L.; Kou, Q. Light-guided and cross-fusion U-Net for anti-illumination image super-resolution. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 8436–8449. [Google Scholar] [CrossRef]
- Yu, S.; Guan, D.; Gu, Z.; Guo, J.; Liu, Z.; Liu, Y. Radar Target Complex High-Resolution Range Profile Modulation by External Time Coding Metasurface. IEEE Trans. Microw. Theory Tech. 2024, 72, 6083–6093. [Google Scholar] [CrossRef]
- Wang, G.; Li, R. DSolving: A novel and efficient intelligent algorithm for large-scale sliding puzzles. J. Exp. Theor. Artif. Intell. 2017, 29, 809–822. [Google Scholar] [CrossRef]
- Guo, T.; Yuan, H.; Hamzaoui, R.; Wang, X.; Wang, L. Dependence-Based Coarse-to-Fine Approach for Reducing Distortion Accumulation in G-PCC Attribute Compression. IEEE Trans. Ind. Inform. 2024, 20, 11393–11403. [Google Scholar] [CrossRef]
- Xu, Y.; Ding, L.; He, P.; Lu, Z.; Zhang, J. A Memory-Efficient Tri-Stage Polynomial Multiplication Accelerator Using 2D Coupled-BFUs. IEEE Trans. Circuits Syst. Regul. Pap. 2024. [Google Scholar] [CrossRef]
- Mi, B.; Huang, D.; Wan, S.; Hu, Y.; Choo, K.K.R. A post-quantum light weight 1-out-n oblivious transfer protocol. Comput. Electr. Eng. 2019, 75, 90–100. [Google Scholar] [CrossRef]
- Li, W.; Chu, P.C.; Liu, G.Z.; Tian, Y.B.; Qiu, T.H.; Wang, S.M. An image classification algorithm based on hybrid quantum classical convolutional neural network. Quantum Eng. 2022, 2022, 5701479. [Google Scholar] [CrossRef]
- Fan, F.; Shi, Y.; Guggemos, T.; Zhu, X.X. Hybrid quantum-classical convolutional neural network model for image classification. IEEE Trans. Neural Netw. Learn. Syst. 2023. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Zhang, C.W.; Yang, M.Y.; Zeng, H.J.; Wen, J.P. Pedestrian detection based on improved LeNet-5 convolutional neural network. J. Algorithms Comput. Technol. 2019, 13, 1748302619873601. [Google Scholar] [CrossRef]
- Yuan, Z.W.; Zhang, J. Feature extraction and image retrieval based on AlexNet. In Proceedings of the Eighth International Conference on Digital Image Processing (ICDIP 2016), Chengu, China, 20–22 May 2016; SPIE: Bellingham, WA, USA, 2016; Volume 10033, pp. 65–69. [Google Scholar]
- Sengupta, A.; Ye, Y.; Wang, R.; Liu, C.; Roy, K. Going deeper in spiking neural networks: VGG and residual architectures. Front. Neurosci. 2019, 13, 95. [Google Scholar] [CrossRef]
- Al-Qizwini, M.; Barjasteh, I.; Al-Qassab, H.; Radha, H. Deep learning algorithm for autonomous driving using googlenet. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 89–96. [Google Scholar]
- Zhu, C. Computational intelligence-based classification system for the diagnosis of memory impairment in psychoactive substance users. J. Cloud Comput. 2024, 13, 119. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, C.; Van Den Hengel, A. Wider or deeper: Revisiting the resnet model for visual recognition. Pattern Recognit. 2019, 90, 119–133. [Google Scholar] [CrossRef]
- Song, W.; Wang, X.; Jiang, Y.; Li, S.; Hao, A.; Hou, X.; Qin, H. Expressive 3D Facial Animation Generation Based on Local-to-global Latent Diffusion. IEEE Trans. Vis. Comput. Graph. 2024, 30, 7397–7407. [Google Scholar] [CrossRef] [PubMed]
- Levi, G.; Hassner, T. Age and gender classification using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 34–42. [Google Scholar]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1725–1732. [Google Scholar]
- Jmour, N.; Zayen, S.; Abdelkrim, A. Convolutional neural networks for image classification. In Proceedings of the 2018 International Conference on Advanced Systems and Electric Technologies (IC_ASET), Hammamet, Tunisia, 22–25 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 397–402. [Google Scholar]
- Kang, L.; Kumar, J.; Ye, P.; Li, Y.; Doermann, D. Convolutional neural networks for document image classification. In Proceedings of the 2014 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3168–3172. [Google Scholar]
- Sermanet, P.; Chintala, S.; LeCun, Y. Convolutional neural networks applied to house numbers digit classification. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3288–3291. [Google Scholar]
- Wu, H. CNN-Based Recognition of Handwritten Digits in MNIST Database. In Research School of Computer Science; The Australia National University: Canberra, Australia, 2018. [Google Scholar]
- Palvanov, A.; Im Cho, Y. Comparisons of deep learning algorithms for MNIST in real-time environment. Int. J. Fuzzy Log. Intell. Syst. 2018, 18, 126–134. [Google Scholar] [CrossRef]
- Jeswal, S.; Chakraverty, S. Recent developments and applications in quantum neural network: A review. Arch. Comput. Methods Eng. 2019, 26, 793–807. [Google Scholar] [CrossRef]
- Nguyen, T.; Paik, I.; Watanobe, Y.; Thang, T.C. An evaluation of hardware-efficient quantum neural networks for image data classification. Electronics 2022, 11, 437. [Google Scholar] [CrossRef]
- Zhou, R.; Ding, Q. Quantum mp neural network. Int. J. Theor. Phys. 2007, 46, 3209–3215. [Google Scholar] [CrossRef]
- Safari, A.; Ghavifekr, A.A. Quantum neural networks (QNN) application in weather prediction of smart grids. In Proceedings of the 2021 11th Smart Grid Conference (SGC), Tabriz, Iran, 7–9 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Paquet, E.; Soleymani, F. QuantumLeap: Hybrid quantum neural network for financial predictions. Expert Syst. Appl. 2022, 195, 116583. [Google Scholar] [CrossRef]
- Wei, S.; Chen, Y.; Zhou, Z.; Long, G. A quantum convolutional neural network on NISQ devices. AAPPS Bull. 2022, 32, 2. [Google Scholar] [CrossRef]
- Kadam, S.S.; Adamuthe, A.C.; Patil, A.B. CNN model for image classification on MNIST and fashion-MNIST dataset. J. Sci. Res. 2020, 64, 374–384. [Google Scholar] [CrossRef]
- Xia, R.; Kais, S. Hybrid quantum-classical neural network for calculating ground state energies of molecules. Entropy 2020, 22, 828. [Google Scholar] [CrossRef]
- Hellstem, G. Hybrid quantum network for classification of finance and MNIST data. In Proceedings of the 2021 IEEE 18th International Conference on Software Architecture Companion (ICSA-C), Stuttgart, Germany, 22–26 March 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Bokhan, D.; Mastiukova, A.S.; Boev, A.S.; Trubnikov, D.N.; Fedorov, A.K. Multiclass classification using quantum convolutional neural networks with hybrid quantum-classical learning. Front. Phys. 2022, 10, 1069985. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, Y.; Yang, T.; Cai, P.; Shen, K.; Lv, B.; Chen, S.; Wang, J.; Zhu, Y.; Wu, Z.; et al. Parallel Structure of Hybrid Quantum-Classical Neural Networks for Image Classification. Res. Sq. 2024; preprint. [Google Scholar]
- Ling, Y.Q.; Zhang, J.H.; Zhang, L.H.; Li, Y.R.; Huang, H.L. Image Classification Using Hybrid Classical-Quantum Neutral Networks. Int. J. Theor. Phys. 2024, 63, 125. [Google Scholar] [CrossRef]
- Islam, M.; Chowdhury, M.; Khan, Z.; Khan, S.M. Hybrid quantum-classical neural network for cloud-supported in-vehicle cyberattack detection. IEEE Sensors Lett. 2022, 6, 1–4. [Google Scholar] [CrossRef]
- Sarmah, J.; Saini, M.L.; Kumar, A.; Chasta, V. Performance Analysis of Deep CNN, YOLO, and LeNet for Handwritten Digit Classification. In Proceedings of the International Conference on Artificial Intelligence on Textile and Apparel, Bangalore, India, 11–12 August 2023; Springer: Singapore, 2023; pp. 215–227. [Google Scholar]
- Choudhuri, A.R.; Thakurata, B.G.; Debnath, B.; Ghosh, D.; Maity, H.; Chattopadhyay, N.; Chakraborty, R. MNIST Image Classification Using Convolutional Neural Networks. In Modeling, Simulation and Optimization: Proceedings of CoMSO 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 255–266. [Google Scholar]
- Zhang, L.; Lu, J.; Zheng, S.; Zhao, X.; Zhu, X.; Fu, Y.; Xiang, T.; Feng, J.; Torr, P.H. Vision transformers: From semantic segmentation to dense prediction. Int. J. Comput. Vis. 2024, 132, 6142–6162. [Google Scholar] [CrossRef]
- Hwang, E.E.; Chen, D.; Han, Y.; Jia, L.; Shan, J. Multi-Dataset Comparison of Vision Transformers and Convolutional Neural Networks for Detecting Glaucomatous Optic Neuropathy from Fundus Photographs. Bioengineering 2023, 10, 1266. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, S.; Saurav, S.; Saini, R.; Singh, S. Capsule networks for computer vision applications: A comprehensive review. Appl. Intell. 2023, 53, 21799–21826. [Google Scholar] [CrossRef]
- Zhou, G.; Li, H.; Song, R.; Wang, Q.; Xu, J.; Song, B. Orthorectification of fisheye image under equidistant projection model. Remote Sens. 2022, 14, 4175. [Google Scholar] [CrossRef]
- Prajapat, S.; Kumar, P.; Kumar, D.; Das, A.K.; Hossain, M.S.; Rodrigues, J.J. Quantum secure authentication scheme for internet of medical things using blockchain. IEEE Internet Things J. 2024, 11, 38496–38507. [Google Scholar] [CrossRef]
- Prajapat, S.; Gautam, D.; Kumar, P.; Jangirala, S.; Das, A.K.; Park, Y.; Lorenz, P. Secure lattice-based aggregate signature scheme for vehicular Ad Hoc networks. IEEE Trans. Veh. Technol. 2024, 73, 12370–12384. [Google Scholar] [CrossRef]
- Prajapat, S.; Thakur, G.; Kumar, P.; Das, A.K.; Hossain, M.S. A blockchain-assisted privacy-preserving signature scheme using quantum teleportation for metaverse environment in Web 3.0. Future Gener. Comput. Syst. 2024, 164, 107581. [Google Scholar] [CrossRef]
- Prajapat, S.; Kumar, P.; Kumar, S. A privacy preserving quantum authentication scheme for secure data sharing in wireless body area networks. Clust. Comput. 2024, 27, 9013–9029. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, Q.; Huang, Y.; Tian, J.; Li, H.; Wang, Y. True2 orthoimage map generation. Remote Sens. 2022, 14, 4396. [Google Scholar] [CrossRef]
- Pan, H.; Wang, Y.; Li, Z.; Chu, X.; Teng, B.; Gao, H. A complete scheme for multi-character classification using EEG signals from speech imagery. IEEE Trans. Biomed. Eng. 2024, 71, 2454–2462. [Google Scholar] [CrossRef]
- Kumar, P.; Bharmaik, V.; Prajapat, S.; Thakur, G.; Das, A.K.; Shetty, S.; Rodrigues, J.J. A Secure and Privacy-Preserving Signature Protocol Using Quantum Teleportation in Metaverse Environment. IEEE Access 2024, 12, 96718–96728. [Google Scholar] [CrossRef]
- Xu, X.; Fu, X.; Zhao, H.; Liu, M.; Xu, A.; Ma, Y. Three-Dimensional Reconstruction and Geometric Morphology Analysis of Lunar Small Craters within the Patrol Range of the Yutu-2 Rover. Remote Sens. 2023, 15, 4251. [Google Scholar] [CrossRef]
- Prajapat, S.; Kumar, D.; Kumar, P. Quantum image encryption protocol for secure communication in healthcare networks. Clust. Comput. 2025, 28, 3. [Google Scholar] [CrossRef]
- Prajapat, S.; Dhiman, A.; Kumar, S.; Kumar, P. A practical convertible quantum signature scheme with public verifiability into universal quantum designated verifier signature using self-certified public keys. Quantum Inf. Process. 2024, 23, 331. [Google Scholar] [CrossRef]
- Yao, F.; Zhang, H.; Gong, Y. DifSG2-CCL: Image Reconstruction Based on Special Optical Properties of Water Body. IEEE Photonics Technol. Lett. 2024, 36, 1417–1420. [Google Scholar] [CrossRef]
- Shi, H.; Hayat, M.; Cai, J. Unified open-vocabulary dense visual prediction. IEEE Trans. Multimed. 2024, 26, 8704–8716. [Google Scholar] [CrossRef]
- Hu, C.; Dong, B.; Shao, H.; Zhang, J.; Wang, Y. Toward purifying defect feature for multilabel sewer defect classification. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).