Efficient Quantum Private Comparison with Unitary Operations

Abstract

Quantum private comparison (QPC) is a crucial component of quantum multiparty computing (QMPC), allowing parties to compare their private inputs while ensuring that no sensitive information is disclosed. Many existing QPC protocols that utilize Bell states encounter efficiency challenges. In this paper, we present a novel and efficient QPC protocol that capitalizes on the distinct characteristics of Bell states to enable secure comparisons. Our method transforms private inputs into unitary operations on shared Bell states, which are then returned to a third party to obtain the comparison results. This approach enhances efficiency and decreases the reliance on complex quantum resources. A single Bell state can compare two classical bits, achieving a qubit efficiency of 100%. We illustrate the feasibility of the protocol through a simulation on the IBM Quantum Cloud Platform. The security analysis confirms that our protocol is resistant to both eavesdropping and attacks from participants.

1. Introduction

Secure multiparty computation (MPC), a cryptographic paradigm, allows multiple parties to collaboratively compute a function using their private inputs while maintaining the confidentiality of those inputs [1]. Recently, MPC has garnered significant attention due to its enhanced privacy protections and applicability across various domains. These include functions of secret-sharing [2,3], private set intersection [4,5], making private queries [6,7], and private comparison [8,9,10]. In this paper, we primarily concentrate on the development of protocols for private comparison. We aim to develop efficient and secure techniques that enable parties to compare their private data while keeping sensitive information confidential. This effort contributes to the wider domain of secure multiparty computation.

Private comparison protocols originate from the need to allow the parties to compare their private data without revealing the actual values to each other, which was first introduced in the millionaires’ problem [11]. Boudot et al. [12] expanded the millionaires’ problem to address the specific issue known as the socialist millionaires’ problem, where two millionaires wish to determine if they have equal wealth without revealing their actual amounts. This problem has since attracted considerable interest in the cryptographic community, leading to various solutions that enhance privacy and security. In the context of designing private comparison protocols, Lo [13] highlighted a crucial limitation: securely evaluating a two-party computational function in a purely two-party setting is fundamentally impossible without compromising privacy. To overcome this challenge, the introduction of a semi-honest third party (TP) becomes essential. The TP assists the users in securely comparing their private data, acting as an intermediary that can facilitate the computation while ensuring that the individual inputs remain confidential.

The security of private comparison protocols hinges on unproven mathematical assumptions, making them vulnerable to threats posed by quantum computers, which leverage the principles of quantum mechanics for powerful parallel computation. Notably, the Shor algorithm [14] can factor large integers in polynomial time, rendering classical public-key cryptographic systems like RSA insecure against quantum attacks. Furthermore, the Grover algorithm [15] poses a significant threat to symmetric-key cryptography by allowing for faster search and function inversion, effectively halving the effective key length for symmetric algorithms. Therefore, quantum private comparison (QPC) came into being. It leverages quantum mechanics to provide enhanced security features, ensuring that sensitive information remains confidential during the comparison process.

The first quantum private comparison (QPC) protocol was introduced by Yang and Wen [16], who employed EPR pairs to transmit quantum information, alongside decoy photons and a one-way hash function to ensure security. Subsequently, Chen et al. [17] developed an efficient QPC protocol utilizing triplet entangled states, enhancing qubit efficiency by partitioning the secrets into multiple groups. Tseng et al. [18] took advantage of EPR pairs to facilitate comparisons, resulting in a more straightforward implementation and achieving 50% qubit efficiency. Lang et al. [19] introduced a QPC protocol that utilizes Bell states, also attaining 50% qubit efficiency. This protocol utilized quantum gates rather than classical exclusive-OR operations to perform the private calculations regarding the secrets, thereby improving security by minimizing reliance on classical computational methods. Hou et al. [20] employed rotation operations and Bell states for comparison, achieving 50% qubit efficiency. In their approach, two participants encoded their inputs into the angles of the rotation operations applied to the Bell states. Huang et al. [21] developed a QPC protocol utilizing entanglement swapping among three Bell states, also with 50% qubit efficiency. Similarly, Hou and Wu [22] encoded their private inputs as bit flip and phase shift operators applied to shared Bell states, also attaining 50% qubit efficiency. In contrast, Huang et al. [23] utilized GHZ-type states for private comparisons, where each could compare two-bit information, which led to a qubit efficiency of 67%. Moreover, other quantum states have been explored as information carriers in the design of QPC protocols, including multiple-qubit entangled states [24,25,26,27,28], multiple-qubit cluster states [29,30,31,32], and d-dimensional quantum states [33,34,35,36,37,38,39,40,41,42]. However, the QPC protocols that utilize easily implementable quantum states—such as single photon, Bell state, and GHZ state—facilitate higher practical implementation compared to those using d-dimensional quantum states. Despite this advantage, protocols based on single photons, Bell states, and GHZ states often face challenges related to lower qubit efficiency, with many achieving only 50% efficiency.

To tackle this challenge, we put forward an efficient QPC protocol that takes advantage of the distinctive characteristics of Bell states to enable secure comparisons. Our approach involves transforming private inputs into unitary operations applied to shared Bell states. After these operations, the states are returned to a third party, who can then obtain the comparison results. The primary contributions of this paper include the following:

(1) We introduce an efficient QPC protocol that enables two participants to compare their secrets by encoding their inputs as unitary operations applied to shared Bell states.

(2) Our protocol employs Bell states and unitary operations as fundamental components, which are easier to implement than QPC protocols based on d-dimensional quantum states. We illustrate the feasibility of the protocol through a simulation on the IBM Quantum Cloud Platform.

(3) Our protocol achieves 100% qubit efficiency since a single Bell state can compare two bits of classical information.

(4) A comprehensive security analysis verifies that our protocol is resilient against eavesdropping and participant attacks, ensuring robust protection of private information.

The remaining sections are organized as follows: Section 2 introduces the unitary operations. Section 3 and Section 4 present the detailed steps of the proposed QPC protocol and its correctness, respectively. Section 5 conducts a simulation, while Section 6 discusses the security analysis of the protocol. Section 7 provides an efficiency analysis and comparison. Finally, Section 8 concludes with a summary of our contributions.

2. Unitary Operations

The bit flip and phase shift operations are

$$X=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),Z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$

(1)

The two operations described above are unitary operations as they satisfy the conditions $X{X}^{†}=XX=I$ and $Z{Z}^{†}=ZZ=I$, where I represents the 2 × 2 identity matrix.

The four Bell states can be expressed as follows:

$$|{\psi }_{00}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle |0\rangle +|1\rangle |1\rangle \right)$$

(2)

$$|{\psi }_{01}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle |0\rangle -|1\rangle |1\rangle \right)$$

(3)

$$|{\psi }_{10}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle |1\rangle +|1\rangle |0\rangle \right)$$

(4)

$$|{\psi }_{11}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\rangle |1\rangle -|1\rangle |0\rangle \right)$$

(5)

We applied the operation $X^a{Z}^b\left(\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} a,b\in \left\{\mathrm{0,1}\right\}\right)$ to the first qubit of the four Bell states; the resulting states are presented in

Table 1. The resulting Bell states.

Bell States	${\mathit{X}}^0{\mathit{Z}}^0$	${\mathit{X}}^1{\mathit{Z}}^0$	${\mathit{X}}^0{\mathit{Z}}^1$	${\mathit{X}}^1{\mathit{Z}}^1$
$\left|{\psi }_{00}\right.⟩$	$\left|{\psi }_{00}\right.⟩$	$\left|{\psi }_{10}\right.⟩$	$\left|{\psi }_{01}\right.⟩$	$\left|{\psi }_{11}\right.⟩$
$\left|{\psi }_{01}\right.⟩$	$\left|{\psi }_{01}\right.⟩$	$\left|{\psi }_{11}\right.⟩$	$\left|{\psi }_{00}\right.⟩$	$\left|{\psi }_{10}\right.⟩$
$\left|{\psi }_{10}\right.⟩$	$\left|{\psi }_{10}\right.⟩$	$\left|{\psi }_{00}\right.⟩$	$\left|{\psi }_{11}\right.⟩$	$\left|{\psi }_{01}\right.⟩$
$\left|{\psi }_{11}\right.⟩$	$\left|{\psi }_{11}\right.⟩$	$\left|{\psi }_{01}\right.⟩$	$\left|{\psi }_{10}\right.⟩$	$\left|{\psi }_{00}\right.⟩$

.

The Bell states in Table 1 do not include the global phase factor, as measurements performed using the Bell basis do not affect the measurement outcomes.

3. The Proposed QPC Protocol

The goal of the QPC protocol was to determine whether the secrets X and Y held by two users, Alice and Bob, were equal. They sought assistance from a semi-trusted third party (TP), who acted as an intermediary that needed to adhere to the protocol steps and could not collude with the participants, who were considered honest but curious. The binary representations of X and Y could be represented as $X=\left(x_{L-1}, x_{L-2},\cdots ,x_1,x_0\right)$ and $Y=\left(y_{L-1}, y_{L-2},\cdots ,y_1{,y}_0\right)$, where $x_i,y_i\in \left\{\mathrm{0,1}\right\}$ for $i=\mathrm{0,1},\cdots ,L-1$. The protocol assumed a quantum channel that was free from noise and loss, while the classical channel was authenticated during transmission.

The specific steps are outlined as follows:

Step 1. Alice and Bob divide their secret integers X and Y into $⌈L/2⌉$ groups, respectively, with each group containing two-bit classical information. If $L\mathit{mod}2=1$, they add a 0 to the last group. Consequently, we can rewrite X and Y as $X^{\prime }=\left(x_{⌈L/2⌉-1}^{\prime },x_{⌈L/2⌉-2}^{\prime },\cdots ,x_1^{\prime },x_0^{\prime }\right)$ and $Y^{\prime }=\left(y_{⌈L/2⌉-1}^{\prime },y_{⌈L/2⌉-2}^{\prime },\cdots ,y_1^{\prime },y_0^{\prime }\right)$, respectively, where $x_j^{\prime }=x_{2j+1}{x}_{2j}$ and $y_j^{\prime }=y_{2j+1}{y}_{2j}$ for $j=\mathrm{0,1},\cdots ,⌈L/2⌉-2,⌈L/2⌉-1.$

Step 2. TP prepares $⌈L/2⌉$ Bell states and takes the first and second qubits of all Bell states to form two ordered quantum sequences, $S_{TA}$ and $S_T$. To detecting eavesdropping, TP prepares a set of decoy states $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ and inserts them into $S_{TA}$ at random positions to generate a sequence $S_{TA}^{\prime }$, which is sent to Alice via a quantum channel. The sequence $S_T$ is kept by TP.

Step 3. Upon receiving $S_{TA}^{\prime }$, Alice informs TP that she has received the sequence. TP then announces the positions of the decoy states and the measurement basis to Alice. Alice measures the corresponding qubits using the correct basis and returns the measurement results to TP, who compares the consistency of the measurement results with the prepared decoy states to determine whether the quantum channel has been compromised by eavesdropping. TP calculates the error rate; if this rate falls below a predefined threshold, the quantum channel is deemed secure, allowing the protocol to advance to the next step. If the error rate exceeds the threshold, the protocol is terminated and restarted.

Step 4. Alice discards all decoy states from $S_{TA}^{\prime }$ to cover $S_{TA}$ and performs the following operations:

(1)

She applies $U_{x_j^{\prime }}=X^{x_{2j+1}}{Z}^{x_{2j}}$ on each j-th qubit in $S_{TA}$ to produce a transformed sequence denoted as $S_A$.

(2)

She generates her own secret key $K_A=\left(a_{⌈L/2⌉-1},a_{⌈L/2⌉-2},\cdots ,a_1,a_0\right)$, where $a_j\in \left\{\mathrm{00,01,10,11}\right\}$ for $j=\mathrm{0,1},\cdots ,⌈L/2⌉-2,⌈L/2⌉-1$.

(3)

She performs $U_{a_j}\left(\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} U_{a_j}\in \left\{X^0{Z}^0,X^0{Z}^1,X^1{Z}^0,X^1{Z}^1\right\} \mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{o} a_j\right)$ on each j-th qubit in $S_A$ to produce a transformed sequence denoted as $S_A^{\prime }$.

(4)

She prepares decoy states chosen from $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ and inserts them into $S_A^{\prime }$ to create a sequence $S_A^{″}$.

(5)

She sends $S_A^{″}$ to Bob via a quantum channel.

Step 5. Upon receiving $S_A^{\prime },$ Bob interacts with Alice to detect eavesdropping in the quantum channel in the same manner as TP and Alice did. If the quantum channel is secure, Bob discards all decoy states from $S_A^{″}$ to cover $S_A^{\prime }$ and performs the following operations:

(1)

He applies $U_{y_j^{\prime }}=X^{y_{2j+1}}{Z}^{y_{2j}}$ on each j-th qubit in $S_A^{\prime }$ to produce a transformed sequence denoted as $S_B$.

(2)

He generates his own secret key $K_B=\left(b_{⌈L/2⌉-1},b_{⌈L/2⌉-2},\cdots ,b_1,b_0\right)$, where $b_j\in \left\{\mathrm{00,01,10,11}\right\}$ for $j=\mathrm{0,1},\cdots ,⌈L/2⌉-2,⌈L/2⌉-1$.

(3)

He performs $U_{b_j}\left({\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} U}_{b_j}\in \left\{X^0{Z}^0,X^0{Z}^1,X^1{Z}^0,X^1{Z}^1\right\} \mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{o} b_j\right)$ on each j-th qubit in $S_B$ to produce a transformed sequence denoted as $S_B^{\prime }$.

(4)

He prepares decoy states chosen from $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ and inserts them into $S_B^{\prime }$ to create a sequence $S_B^{″}$.

(5)

He sends $S_B^{″}$ to TP through a quantum channel.

Step 6. TP detects eavesdropping by interacting with Bob upon receiving $S_B^{″}$, similar to the process in Step 3. Alice and Bob then announce their respective secret keys $K_A$ and $K_B$ to TP.

Step 7. TP discards all decoy states from $S_B^{″}$ to cover $S_B^{\prime }$, and performs the following operations:

(1)

TP applies $U_{a_j}$ and $U_{b_j}$ on each j-th qubit in $S_B^{\prime }$ to produce a transformed sequence denoted as $S_{TAB}$.

(2)

TP performs a Bell basis measurement on the qubits in $S_{TAB}$ and $S_T$ to obtain the measurement results.

(3)

TP compares the measurement results with the prepared Bell states to determine whether $X=Y$. If they are identical, $X=Y$; otherwise, $X\ne Y$.

(4)

TP conveys the outcomes of the comparison to Alice and Bob.

4. Correctness

In our designed protocol, decoy states are ignored when demonstrating correctness, as they are only used for eavesdropping detection. When performing $U_{x_j^{\prime }}$ on each j-th qubit in $S_{TA}$, the resulting sequence $S_A$ can be given by

$$S_A=\left(U_{{x^{\prime }}_j}\right)S_{TA}=\left(X^{x_{2j+1}}{Z}^{x_{2j}}\right)S_{TA}$$

(6)

When performing $U_{a_j}\left({\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} U}_{a_j}\in \left\{X^0{Z}^0,X^0{Z}^1,X^1{Z}^0,X^1{Z}^1\right\} \mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{o} a_j\right)$ on each j-th qubit in $S_A$, the resulting sequence $S_A^{\mathrm{’}}$ can be written as

$${S^{\prime }}_A=\left(U_{a_j}\right)S_A=\left(U_{a_j}{X}^{x_{2j+1}}{Z}^{x_{2j}}\right)S_{TA}$$

(7)

When performing $U_{y_j^{\prime }}$ on each j-th qubit in $S_A^{\prime }$, the resulting sequence $S_B$ can be given by

$$S_B=\left(U_{{y^{\prime }}_j}\right){S^{\prime }}_A=\left(X^{y_{2j+1}}{Z}^{y_{2j}}{U}_{a_j}{X}^{x_{2j+1}}{Z}^{x_{2j}}\right)S_{TA}$$

(8)

When performing $U_{b_j}\left({\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} U}_{b_j}\in \left\{X^0{Z}^0,X^0{Z}^1,X^1{Z}^0,X^1{Z}^1\right\} \mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{o} b_j\right)$ on each j-th qubit in $S_B$, the resulting sequence $S_B^{\mathrm{’}}$ can be given by

$${S^{\prime }}_B=\left(U_{b_j}\right){S^{\prime }}_A=\left(U_{b_j}{X}^{y_{2j+1}}{Z}^{y_{2j}}{U}_{a_j}{X}^{x_{2j+1}}{Z}^{x_{2j}}\right)S_{TA}$$

(9)

When performing $U_{a_j}$ and $U_{b_j}$ on each j-th qubit in $S_B^{\prime }$, the resulting sequence $S_{TAB}$ can be given by

$$S_{TAB}=\left(U_{b_j}{U}_{a_j}\right){S^{\prime }}_B=\left(U_{b_j}{U}_{a_j}{U}_{b_j}{X}^{y_{2j+1}}{Z}^{y_{2j}}{U}_{a_j}{X}^{x_{2j+1}}{Z}^{x_{2j}}\right)S_{TA}=\left(X^{y_{2j+1}}{Z}^{y_{2j}}{X}^{x_{2j+1}}{Z}^{x_{2j}}\right)S_{TA}$$

(10)

From Equation (10), we can deduce that the initial sequence $S_{TA}$ remains unchanged if and only if both the 2j-th and (2j + 1)-th bits in secrets X and Y are identical. Consequently, TP can ascertain the comparison results by juxtaposing the prepared Bell states with the measurement results obtained from performing a Bell basis measurement on the qubits in $S_{TAB}$ and $S_T$.

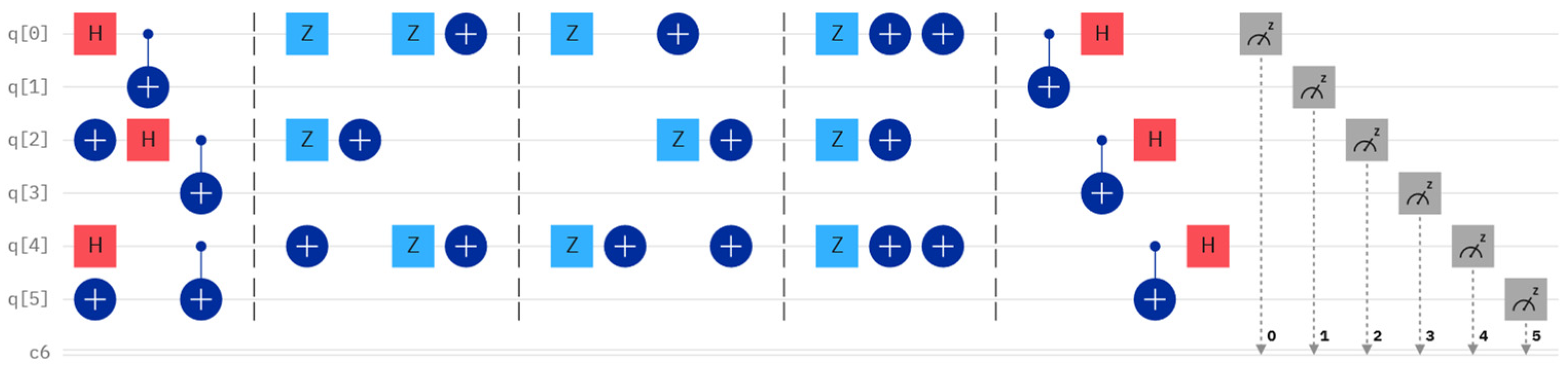
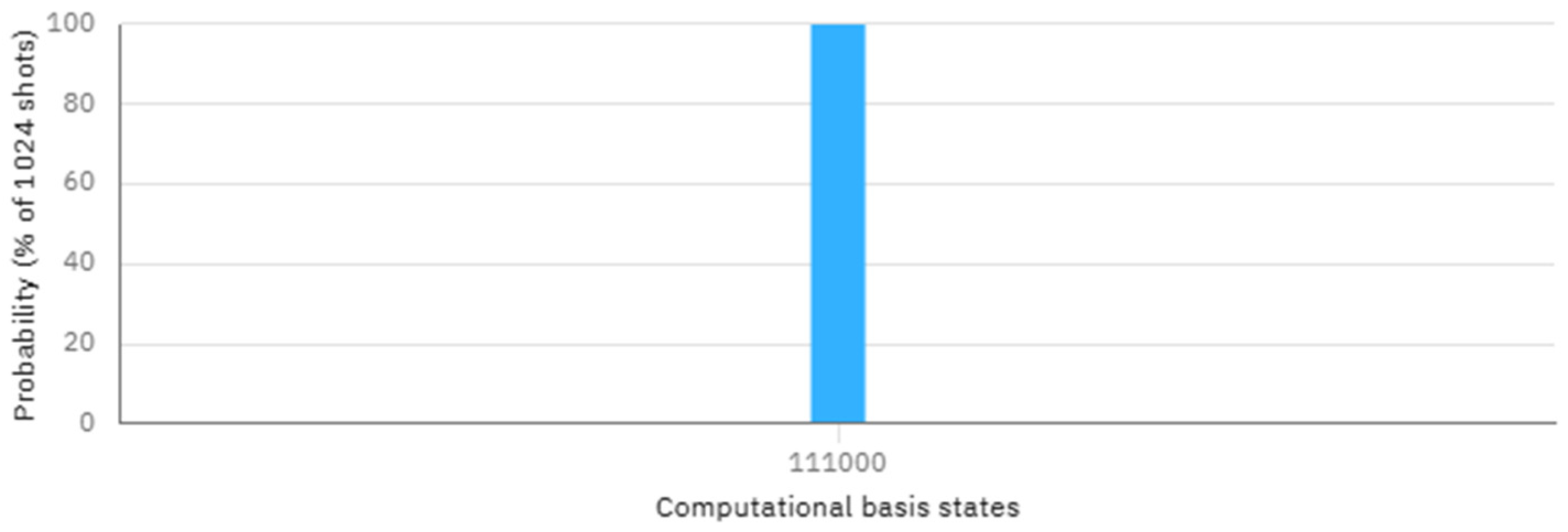
5. Simulation

In this section, we illustrate the feasibility of the protocol through a simulation on the IBM Quantum Cloud Platform.

Consider the case in which Alice possesses a secret $X=45$ and Bob has a secret $Y=49$. The binary representations of X and Y are $X=\left(x_5, x_4,\cdots ,x_1,x_0\right)=(10, 11, 01)$ and $Y=\left(y_5, y_4,\cdots ,y_1{,y}_0\right)=(11, 00, 01)$, respectively. When dividing X and Y into three groups, we obtain $X^{\prime }=\left(x_2^{\prime },x_1^{\prime },x_0^{\prime }\right)=\left(\mathrm{10,11,01}\right)$ and $Y^{\prime }=\left(y_2^{\prime },,y_1^{\prime },y_0^{\prime }\right)=\left(\mathrm{11,00,01}\right)$. We assume that the initially prepared three Bell states are $S_A=\left\{\left|{\psi }_{00}\right.⟩,\left|{\psi }_{01}\right.⟩,\left|{\psi }_{10}\right.⟩\right\}$ and the secret keys are $K_A=\left(a_2,a_1,a_0\right)=\left(\mathrm{11,00,11}\right)$ and $K_B=\left(b_2,b_1,b_0\right)=\left(\mathrm{10,11,10}\right)$. When performing a Bell measurement, equivalent to applying the CNOT and Hadamard gates once on the three initially prepared Bell states, the measurement results correspond to 00, 01, and 10. Additionally, when performing a Bell measurement on $\left|{\psi }_{11}\right.⟩$, the measurement result corresponds to 11. Without considering eavesdropping detection, the quantum circuit for comparing $X$ and $Y$, along with the measurement results obtained from executing this quantum circuit in the IBM Quantum Experience, are presented in Figure 1 and Figure 2, respectively.

From Figure 2, we observe that the measurement outcomes in the computational basis states were 00, 10, 11, which corresponded to $\left|{\psi }_{00}\right.⟩,\left|{\psi }_{10}\right.⟩,\left|{\psi }_{11}\right.⟩$. This indicated that the final measurement results differed from the prepared Bell states, leading to the conclusion that $X\ne Y$.

6. Security Analysis

In this section, we present a comprehensive security analysis that verifies our protocol’s resilience against eavesdropping and participant attacks, providing strong safeguards for private information.

6.1. External Attacks

External attacks refer to any attempts by an eavesdropper, Eve, to uncover the secrets of Alice and Bob by intercepting or eavesdropping on the quantum channel during the transmission of quantum sequences between the participating entities. However, the proposed protocol employs decoy photon technology, which is designed to detect eavesdropping and provides unconditional security. This technology has been proven effective in resisting external attacks, primarily including intercept–resend and entangle–measure attacks. We demonstrate that our protocol can effectively counter both intercept–resend and entangle–measure attacks as follows.

6.1.1. Intercept–Resend Attack

The intercept–resend attack involves Eve intercepting the quantum sequence during transmission, measuring it using her guessed Z-basis or X-basis, generating a new sequence where each state corresponds to the measurement results, and then sending this new sequence to the original receiver [43,44,45]. If a quantum state remains in the state $\left|1\right.⟩$, measuring it with the Z-basis yields a measurement result of $\left|1\right.⟩$, resulting in a new state that is identical to the initial state, thereby introducing no error. Conversely, when measuring with the X-basis, the measurement result can be either $\left|+\right.⟩$ or $\left|-\right.⟩$, each with a probability of 50%, leading to a new state that is not identical to the initial state. This means that there is a 50% probability of introducing no error and a 50% probability of introducing an error. Consequently, for a randomly chosen decoy state, the errors introduced by performing measurements with the guessed basis during eavesdropping detection are calculated as $\left(1-{\displaystyle \frac{1}{2}}\times 1-{\displaystyle \frac{1}{2}}\times {\displaystyle \frac{1}{2}}\right)={\displaystyle \frac{1}{4}}$. Given this, the probability that d newly generated decoy states will be detected is $1-{\left({\displaystyle \frac{3}{4}}\right)}^d$. When d is sufficiently large, the detection rate of the introduced decoy states approaches 1, which means that Eve’s eavesdropping behavior will be detected, leading to the termination of the protocol and a return to the first step for re-execution. Therefore, Alice’s and Bob’s secrets remain confidential from Eve, even if she attempts the intercept–resend attack.

6.1.2. Entangle–Measure Attack

The entangle–measure attack involves Eve first intercepting the quantum sequence during transmission and then entangling her auxiliary state sequence $E=\left\{\left|E_0\right.⟩,\left|E_1\right.⟩,\cdots ,\left|E_{n-1}\right.⟩\right\}$ with the intercepted states using specific unitary operations. The unitary operations performed on the intercepted states $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$ and the auxiliary state can be expressed as follows:

$$U|0\rangle |E_i\rangle =a_0|0\rangle |e_{00}\rangle +b_0|1\rangle |e_{01}\rangle$$

(11)

$$U|1\rangle |E_i\rangle =a_1|1\rangle |e_{10}\rangle +b_1|1\rangle |e_{11}\rangle$$

(12)

$$\begin{array}{ll}U|+\rangle |E_i\rangle & ={\displaystyle \frac{1}{2}}|+\rangle \left(a_0|e_{00}\rangle +b_0|e_{01}\rangle +a_1|e_{10}\rangle +b_1|e_{11}\rangle \right)\hfill \\ & +{\displaystyle \frac{1}{2}}|-\rangle \left(a_0|e_{00}\rangle -b_0|e_{01}\rangle +a_1|e_{10}\rangle -b_1|e_{11}\rangle \right)\hfill \end{array}$$

(13)

$$\begin{array}{ll}U|-\rangle |E_i\rangle & ={\displaystyle \frac{1}{2}}|+\rangle \left(a_0|e_{00}\rangle +b_0|e_{01}\rangle -a_1|e_{10}\rangle -b_1|e_{11}\rangle \right)\hfill \\ & +{\displaystyle \frac{1}{2}}|-\rangle \left(a_0|e_{00}\rangle -b_0|e_{01}\rangle -a_1|e_{10}\rangle +b_1|e_{11}\rangle \right)\hfill \end{array}$$

(14)

The parameters $a_0$, $b_0$, $a_1$, and $b_1$ should satisfy

$${\left|a_0\right|}^2+{\left|b_0\right|}^2=1$$

(15)

$${\left|a_1\right|}^2+{\left|b_1\right|}^2=1$$

(16)

During the transmission of quantum sequences between two parties, eavesdropping detection is always a consideration. If the prepared decoy state is chosen to be $\left|0\right.⟩$ or $\left|1\right.⟩$, and Eve is able to bypass detection, she must set $a_1=b_0=0$. Similarly, if the prepared decoy state is chosen to be $\left|+\right.⟩$ or $\left|-\right.⟩$, and Eve can bypass detection, the following condition must be satisfied:

$$a_0|e_{00}\rangle -b_0|e_{01}\rangle +a_1|e_{10}\rangle -b_1|e_{11}\rangle =\mathbf{0}$$

(17)

$$a_0|e_{00}\rangle +b_0|e_{01}\rangle -a_1|e_{10}\rangle -b_1|e_{11}\rangle =\mathbf{0}$$

(18)

Combining $a_1=b_0=0$, we can deduce that $a_0\left|e_{00}\right.⟩=b_1\left|e_{11}\right.⟩$. Substituting this result into Equations (11)–(14), we obtain

$$U|0\rangle |E_i\rangle =a_0|0\rangle |e_{00}\rangle$$

(19)

$$U|1\rangle |E_i\rangle =b_1|1\rangle |e_{11}\rangle =a_0|0\rangle |e_{00}\rangle$$

(20)

$$U|+\rangle |E_i\rangle ={\displaystyle \frac{1}{2}}|+\rangle \left(a_0|e_{00}\rangle +0+0+b_1|e_{11}\rangle \right)=a_0|+\rangle |e_{00}\rangle$$

(21)

$$U|-\rangle |E_i\rangle ={\displaystyle \frac{1}{2}}|-\rangle \left(a_0|e_{00}\rangle -0-0+b_1|e_{11}\rangle \right)=a_0|-\rangle |e_{00}\rangle$$

(22)

From Equations (19)–(22), we can conclude that the auxiliary states prepared by Eve do not entangle with the intercepted states. Therefore, performing the entangle–measure attack cannot succeed in acquiring the private information of Alice and Bob.

6.1.3. Trojan Horse Attacks

Since the proposed protocol utilizes a bidirectional quantum channel for transmitting the quantum sequence, it is inevitably susceptible to Trojan horse attacks, which include invisible photon attacks and delay photon attacks [46]. Each participant can affix a filter that allows only wavelengths close to the operating wavelength to resist the invisible photon attack, while photon number splitting can be used to counter the delay photon attack. Upon detecting these attacks, the discoverer will restart the protocol.

6.2. Participant Attacks

Participants can receive immediate results regarding the encoded quantum sequence, which poses a higher security risk for obtaining the private information of other participants compared to outsider attacks. A security analysis of participant attacks is presented below.

6.2.1. TP’s Attacks

In our protocol, TP is regarded as semi-honest. This indicates that while TP cannot conspire with Alice and Bob, they may still try to access their confidential information. If TP seeks to gather insights into Alice’s or Bob’s private data, they might execute an intercept attack on the quantum sequence being transmitted, akin to the methods used by external attackers. However, this activity will be identified during the eavesdropping detection phase without knowing the exact locations and associated measurement bases of the decoy states. Additionally, while preparing the quantum sequences used to facilitate private comparison and knowing the secret keys $K_A$ and $K_B$, TP may exploit this information to try to learn additional details about the participants’ private information. It is evident that TP can establish whether a single bit of Alice’s and Bob’s secrets is equal. However, TP cannot completely determine their secrets, as identical results may emerge from two distinct scenarios. Consequently, our protocol remains secure against attacks from TP.

6.2.2. Alice’s Attacks

Alice may perform an intercept–resend attack on $S_B^{″}$. By utilizing the information regarding the locations of the inserted decoy particles that Bob discloses during the eavesdropping detection phase, Alice is able to recover $S_B^{\prime }$, even though this attack will ultimately be detected. Knowing the sequence $S_A^{\prime }$, Alice can deduce the encoding operations performed on $S_A^{\prime }$. However, in our protocol, when Bob receives the sequence $S_A^{\prime }$ sent from Alice, he applies $U_{y_j^{\prime }}=X^{y_{2j+1}}{Z}^{y_{2j}}$ corresponding to his secrets, followed by $U_{b_j}$ corresponding to his own secret key $K_B$ on $S_A^{\prime }$. For Alice, she cannot know the secret key $K_B$ since the eavesdropping detection has not been confirmed to have passed, meaning that the secret key $K_B$ will not be announced. Therefore, Alice cannot obtain Bob’s private information.

6.2.3. Bob’s Attack

When Bob receives $S_A^{″}$ and discards all decoy states to recover $S_A^{″}$, he can compare the states in $S_A^{\prime }$ and $S_{TA}$ to deduce the operations performed by Alice, thus gaining access to her private information according to the encoding rules. However, Bob is unable to accomplish this. On one hand, TP does not reveal the prepared Bell states to anyone due to their semi-honesty. If Bob intends to learn $S_{TA}$, he would need to intercept $S_{TA}^{\prime }$ in the same manner as external attackers, which would prevent him from passing the eavesdropping detection, resulting in his inability to obtain $S_{TA}$. Additionally, the sequence $S_A^{\prime }$ is encoded with $X^{\prime }$ and $K_A$. Even if $K_A$ is announced, Bob still cannot deduce $X^{\prime }$ due to his lack of knowledge regarding the secret sequence $S_{TA}$. Therefore, Bob attempts to ascertain Alice’s secret would ultimately be unsuccessful.

7. Efficiency Analysis and Comparison

The qubit efficiency serves as a crucial metric for assessing the utilization rate of qubits, which can be defined as follows:

$${\eta }_e={\displaystyle \frac{{\eta }_c}{{\eta }_t}}$$

(23)

where ${\eta }_c$ represents the total number of classical bits compared, while ${\eta }_t$ denotes the total number of qubits used, excluding those allocated for eavesdropping detection, which is treated as a separate process within the quantum communication protocol. In our approach, L Bell states act as the carriers of quantum information to enable private comparisons, facilitating the comparison of 2L classical bits. This results in 100% qubit efficiency.

Table 2. Comparison between our protocol and several existing QPC protocols.

Protocol	Quantum Resource	Unitary Operation	Entanglement Swapping	Quantum Measurement	QKD	Qubit Efficiency
Ref. [16]	EPR pairs	Yes	No	Bell-basis	No	25%
Ref. [17]	GHZ state	Yes	No	Single-particle	No	33%
Ref. [18]	EPR pairs	No	No	Single-particle	No	50%
Ref. [19]	Bell states	Yes	No	$\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$ basis	No	50%
Ref. [20]	Bell states	Yes	No	Bell-basis	Yes	50%
Ref. [21]	Bell state	No	Yes	GHZ-basis	Yes	50%
Ref. [22]	Bell states	Yes	No	Bell-basis	Yes	50%
Ours	Bell states	Yes	No	Bell-basis	No	100%

provides a comparison between our protocol and several existing QPC protocols. While protocols discussed in Refs. [16,17,18,19,20,21,22] and ours utilize quantum resources that are easier to prepare, exhibiting better practicality, our protocol achieves 100% qubit efficiency. Additionally, our protocol does not require a quantum key distribution (QKD) [47,48,49,50] protocol for sharing a secret key, unlike the methods described in Refs. [20,21,22]. Unlike Ref. [19], which utilizes entanglement swapping to achieve private comparison, our protocol is easier to implement using unitary operations.

8. Conclusions

In this paper, we presented a quantum private comparison protocol that harnesses the distinctive properties of Bell states to facilitate secure comparisons. Users encode their private information using bit flip and phase shift operators and utilize a circular transmission mode to send the quantum sequence, achieving 100% qubit efficiency. We demonstrated the protocol’s feasibility through a simulation conducted on the IBM Quantum Cloud Platform. Additionally, the security analysis verified that our method is resilient against both eavesdropping and attacks from participants. Compared to existing QPC protocols, our protocol demonstrates enhanced performance in terms of both qubit efficiency and practical implementation by employing easier-to-implement Bell states, unitary operations, and Bell measurements as fundamental components.