Aperiodic Optimal Chronotherapy in Simple Compartment Tumour Growth Models Under Circadian Drug Toxicity Conditions
Abstract
1. Introduction
2. The Cost Function
3. Existence of Aperiodic Solutions in Chronotherapy
3.1. Cytotoxic Drugs
- Constant drug administration, specifically with no treatment () or MTD ();
- Bang–bang aperiodic solutions, with two switches per day and a non-decreasing daily drug administration interval;
- An order 1 singular arc with a duration h that satisfiesA necessary condition for the singular arc to exist is .
- Comment: Bang–bang solutions can be constructed, and thus one can determine if they intersect the singular arc, a segment of a circle in the plane, with , , satisfying the above arc condition. The singular arc only needs to be considered if there is an intersection.
- Comment: The singular arc has a log tumour size change of less than , so it cannot contribute to substantial tumour decay.
- when ; i.e., .
- when ; i.e., .
- A singular arc if holds for an extended period; i.e., .
3.2. Drugs Targeting Growth
- Constant drug administration, specifically with no treatment () or MTD ();
- Bang–bang aperiodic solutions, with two switches per day and a non-decreasing daily drug administration interval;
- An order 1 singular arc with a duration of h that satisfiesA necessary condition for the singular arc to exist is that monotonically decreases on the arc, which requires that .
- Comment: The singular arc has a log tumour size range less than and thus cannot contribute to substantial tumour decay.
- when ; i.e., .
- when ; i.e., .
- A singular arc if holds for an extended period; i.e., .
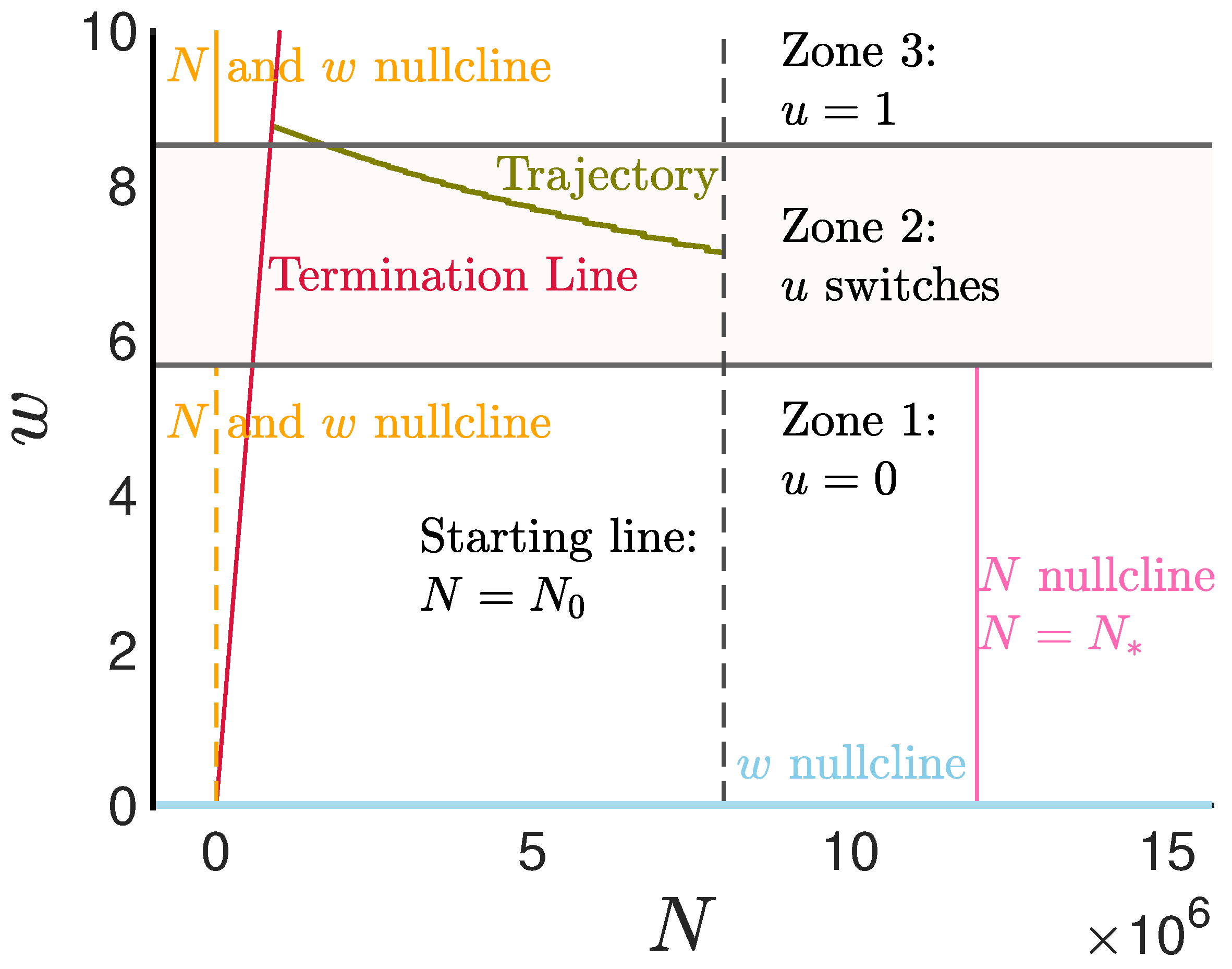
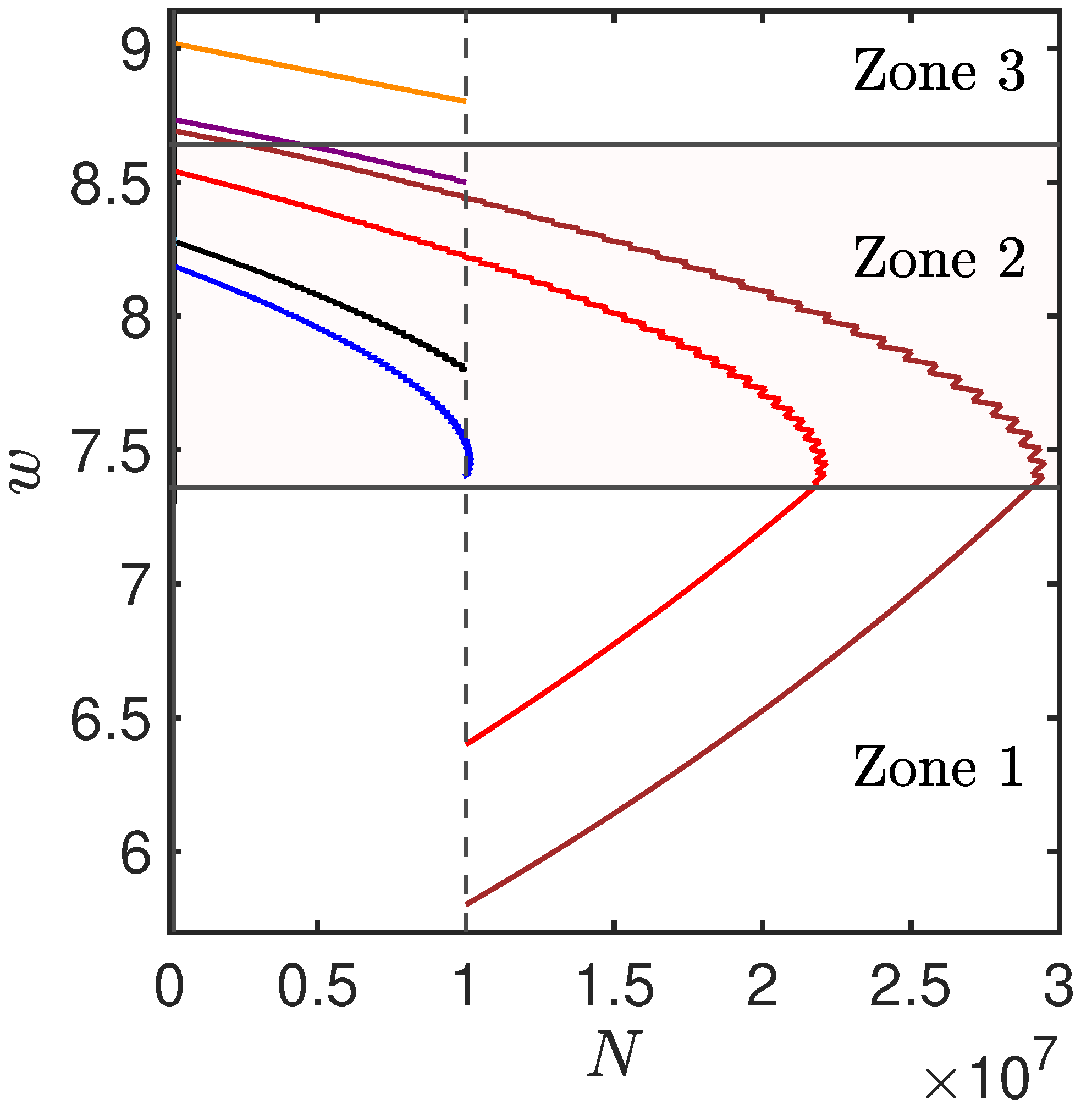
4. Optimal Solutions for Logistic Tumor Growth
- zone 1: : The control , and the number of cancer cells undergoes logistic growth;
- zone 2: : The control switches between one and zero depending on if or . This area is called the “switching zone”; since is periodic, there will typically be two switches per day;
- zone 3: : The control , and the tumor size decays in a manner in accordance with logistic dynamics.
The Cost and Treatment Time of Optimal Solutions
5. Gompertz Model
- zone 1:
- Here, w is less than ; the control is equal to zero, and the tumor size increases.
- zone 2:
- Here, ; the control switches between one and zero.
- zone 3:
- Here, w is greater than ; the control is equal to one, and the tumor size decreases.
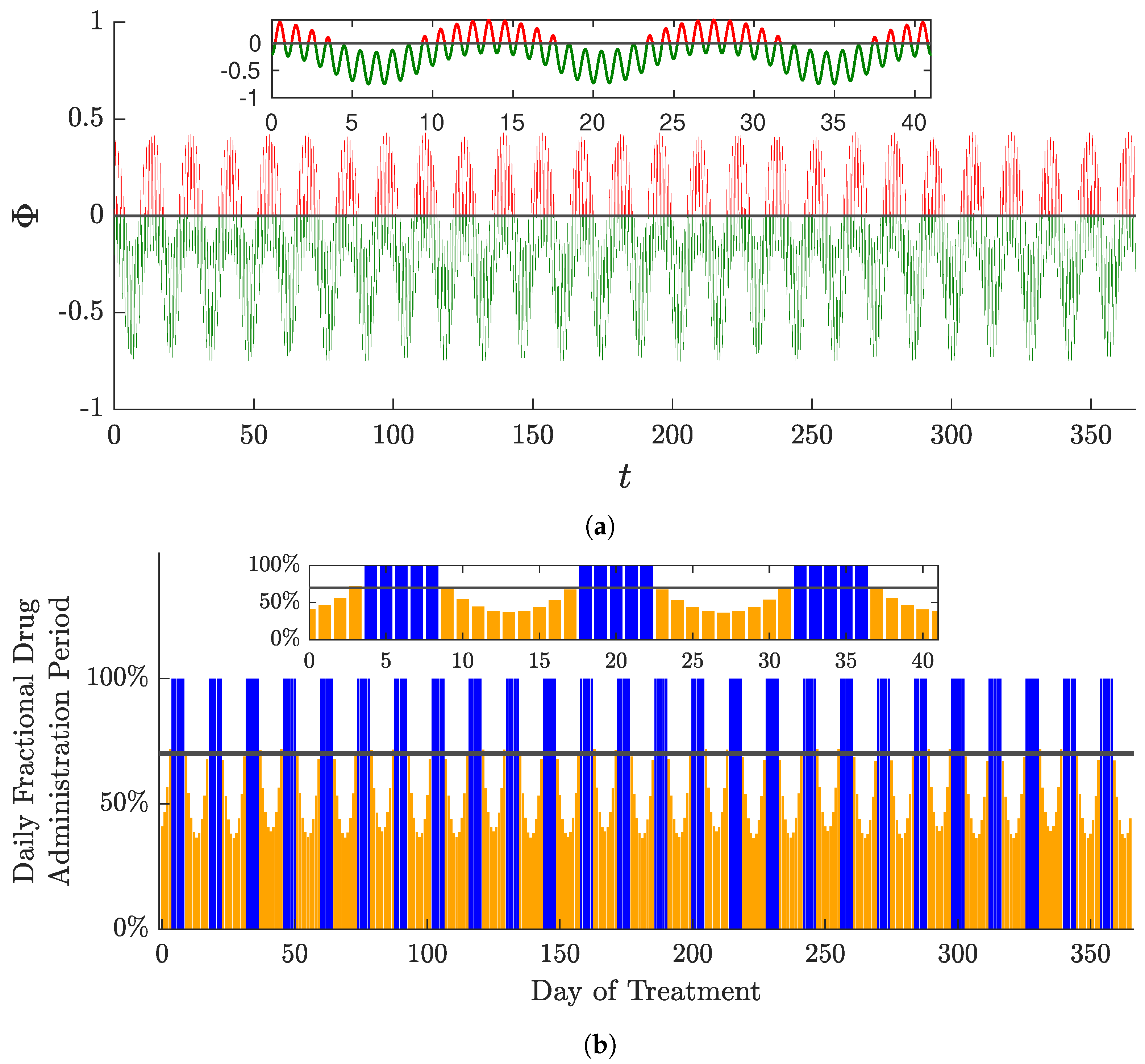
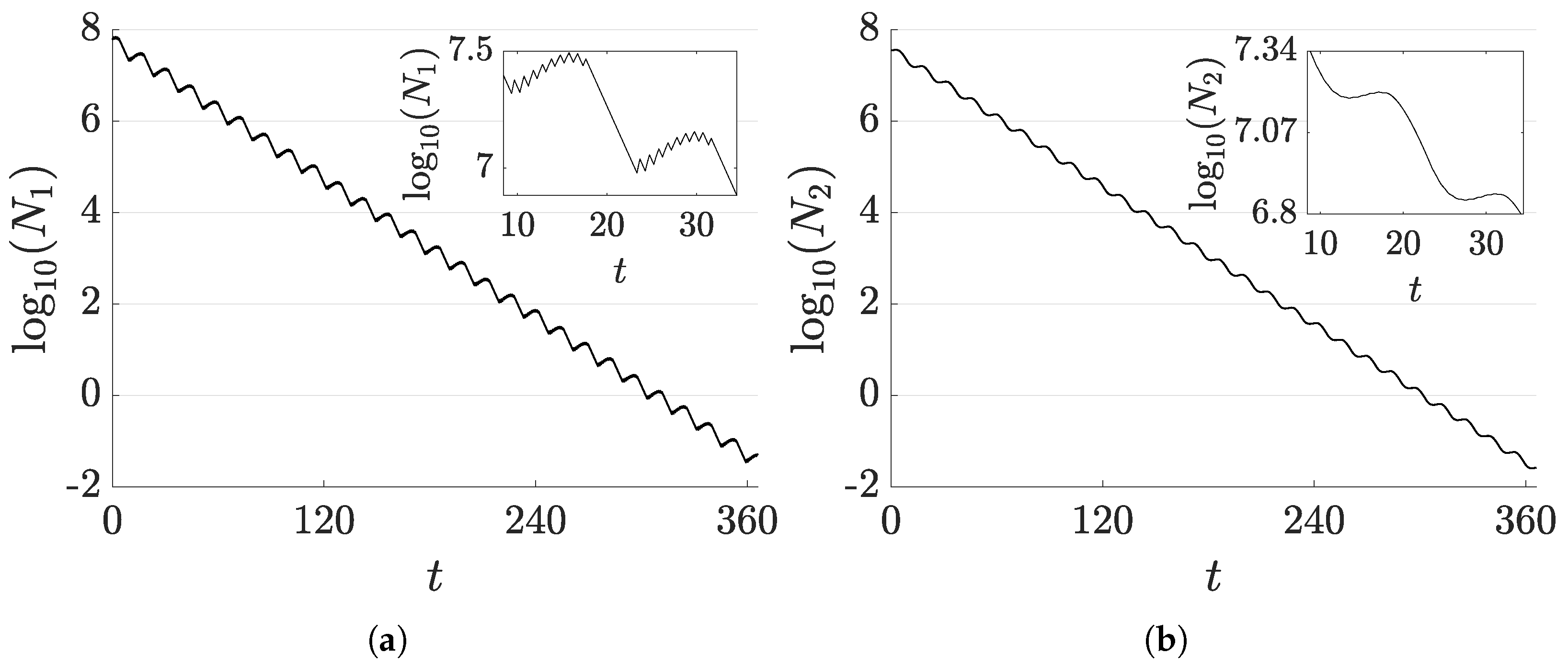
6. Aperiodic Solutions in Multi-Compartment Models
- A drug regimen that satisfies PMP, hereafter referred to as PMP drug regimen (PMPDR);
- A drug regimen that minimises the objective function when restricted to bang–bang periodic solutions and a period of one day. This solution is hereafter referred to as the optimal periodic drug regimen (OPDR).
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
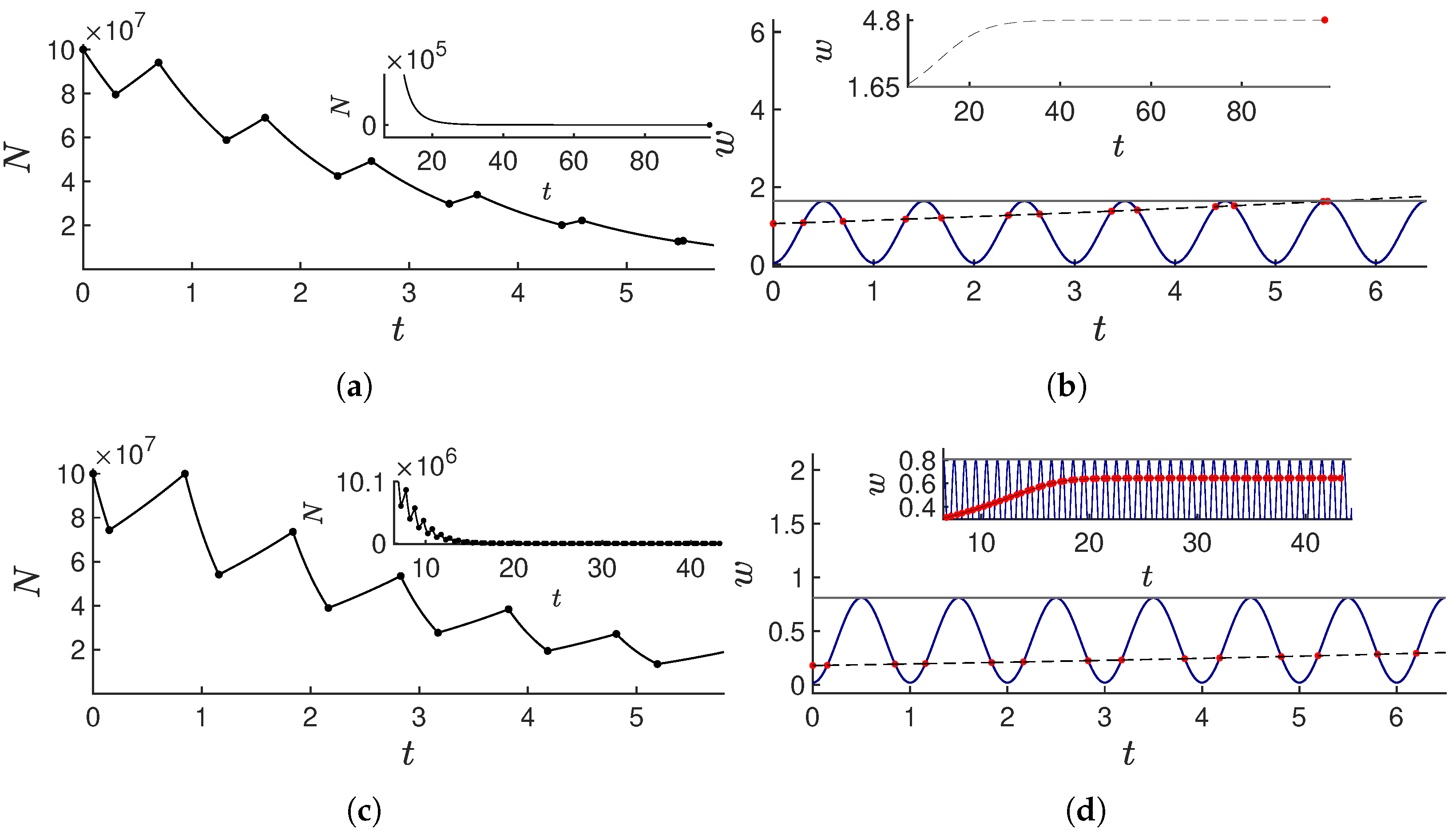
Appendix A. Optimal Solutions for the Exponential Growth Model
- I.
- Large tumours. Case: . The switching function is negative, so treatment comprises MTD for the full horizon, , giving from Equation (A1). Thus, , giving the tumour size constraint
- II.
- Small tumours. Case: . The switching function is positive; therefore, for the full horizon, and we have , and thus , giving the tumour size constraint
- III.
- Intermediate-sized tumours. Case: . In this case, the control switches from 1 to 0 and vice versa. Let be the switching times in increasing order. Observe that , and so ; then, by solving for , , the equation becomeswith a first switching time of . Drug administration is periodic thereafter until T, with the drug being administered around noon between , and, on the last day zero beyond . The tumour size decays by per day, so it decays if . By taking the limits and , we can obtain the initial tumour size range for this case between that of small and large tumours as defined above.
Appendix B. The Pontryagin Minimum Principle for Non-Autonomus Systems
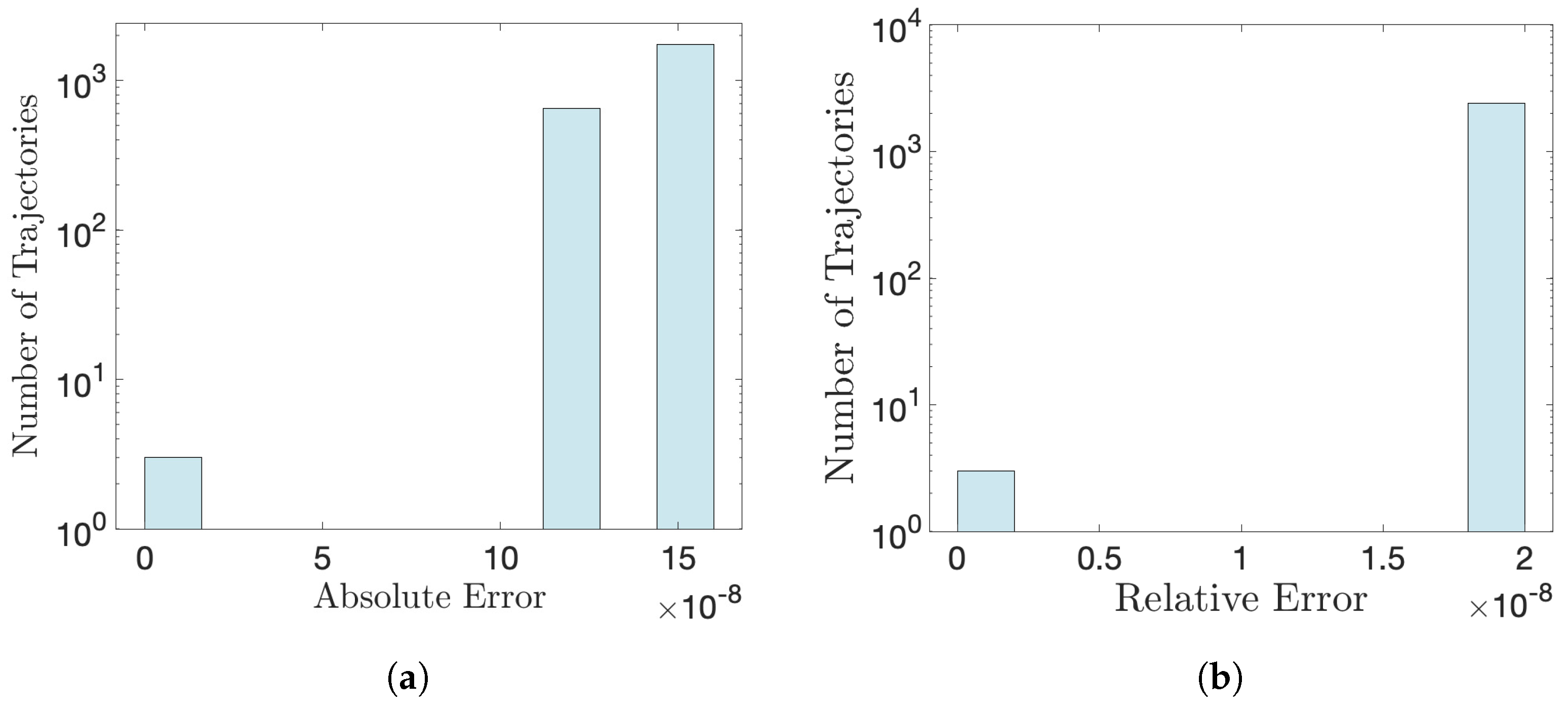
Appendix C. Accuracy of Numerical Calculation

Appendix D. Multi Compartment Cell Division Model
- iff ,
- iff .
- Generate trajectories in the space (for a given time horizon T) using Equations (A8)–(A13)
- Minimise the cost functional (1) with weights and for drug regimens that are constrained to be periodic
- Compare the cost of the generated trajectory to the optimised periodic drug regimen
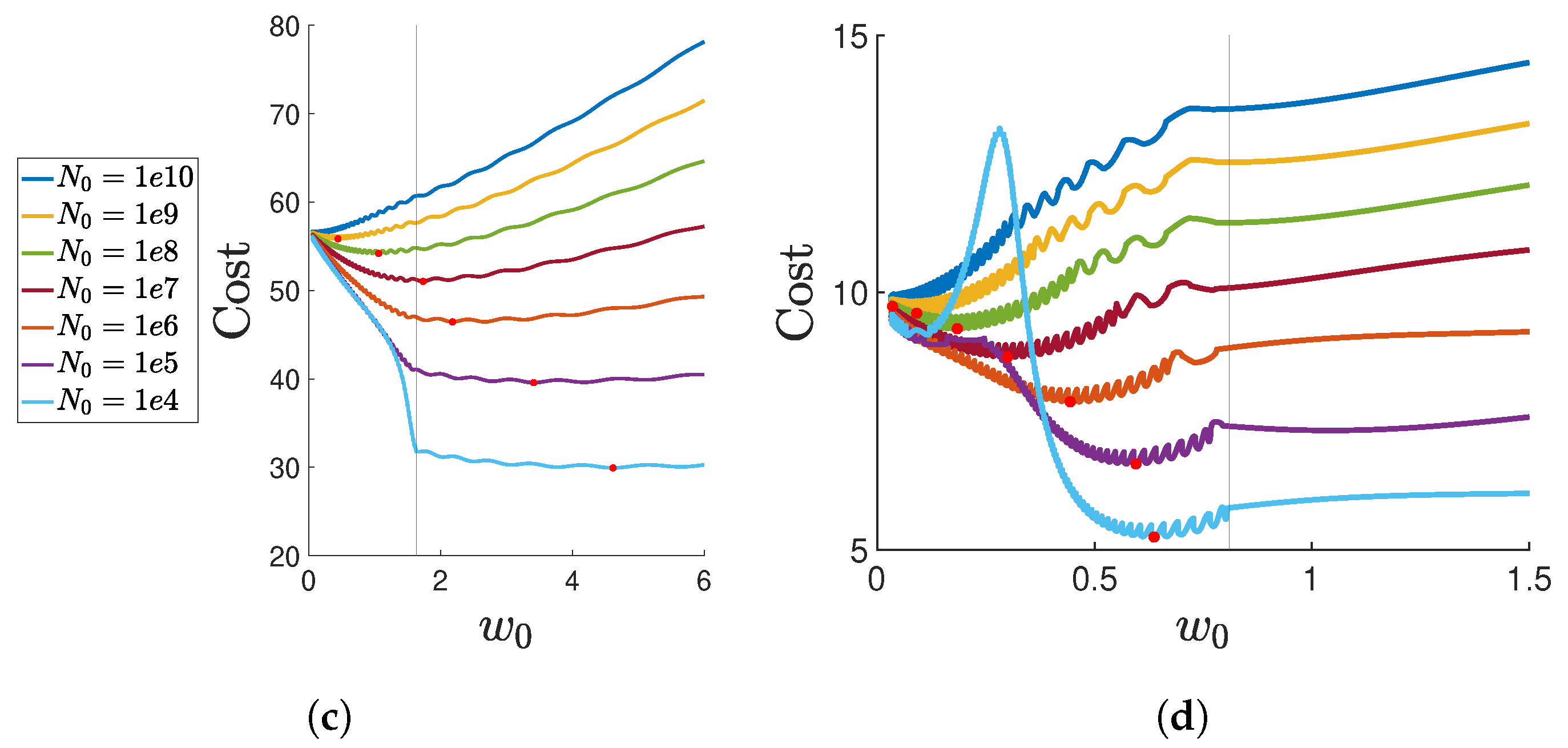
Appendix E. Realistic Parameter Analysis


Appendix F. Proof of Aperiodic Optimal Bang–Bang Solutions with Metastatic Risk
References
- Ayyar, V.S.; Sukumaran, S. Circadian rhythms: Influence on physiology, pharmacology, and therapeutic interventions. J. Pharmacokinet. Pharmacodyn. 2021, 48, 321–338. [Google Scholar] [CrossRef] [PubMed]
- Mohawk, J.A.; Green, C.B.; Takahashi, J.S. Central and peripheral circadian clocks in mammals. Annu. Rev. Neurosci. 2012, 35, 445–462. [Google Scholar] [CrossRef] [PubMed]
- Farshadi, E.; van Der Horst, G.T.; Chaves, I. Molecular links between the circadian clock and the cell cycle. J. Mol. Biol. 2020, 432, 3515–3524. [Google Scholar] [CrossRef]
- Gérard, C.; Goldbeter, A. Entrainment of the mammalian cell cycle by the circadian clock: Modeling two coupled cellular rhythms. PLoS Comput. Biol. 2012, 8, e1002516. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Lahens, N.F.; Ballance, H.I.; Hughes, M.E.; Hogenesch, J.B. A circadian gene expression atlas in mammals: Implications for biology and medicine. Proc. Natl. Acad. Sci. USA 2014, 111, 16219–16224. [Google Scholar] [CrossRef]
- Feillet, C.; Krusche, P.; Tamanini, F.; Janssens, R.C.; Downey, M.J.; Martin, P.; Teboul, M.; Saito, S.; Lévi, F.A.; Bretschneider, T.; et al. Phase locking and multiple oscillating attractors for the coupled mammalian clock and cell cycle. Proc. Natl. Acad. Sci. USA 2014, 111, 9828–9833. [Google Scholar] [CrossRef]
- Savvidis, C.; Koutsilieris, M. Circadian rhythm disruption in cancer biology. Mol. Med. 2012, 18, 1249–1260. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, Z.; Nice, E.; Huang, C.; Zhang, W.; Tang, Y. Circadian rhythms and cancers: The intrinsic links and therapeutic potentials. J. Hematol. Oncol. 2022, 15, 21. [Google Scholar] [CrossRef]
- Lee, Y. Roles of circadian clocks in cancer pathogenesis and treatment. Exp. Mol. Med. 2021, 53, 1529–1538. [Google Scholar] [CrossRef]
- Tsuchiya, Y.; Ushijima, K.; Noguchi, T.; Okada, N.; Hayasaka, J.I.; Jinbu, Y.; Ando, H.; Mori, Y.; Kusama, M.; Fujimura, A. Influence of a dosing-time on toxicities induced by docetaxel, cisplatin and 5-fluorouracil in patients with oral squamous cell carcinoma; a cross-over pilot study. Chronobiol. Int. 2018, 35, 289–294. [Google Scholar] [CrossRef]
- Lee, Y.; Fong, S.Y.; Shon, J.; Zhang, S.L.; Brooks, R.; Lahens, N.F.; Chen, D.; Dang, C.V.; Field, J.M.; Sehgal, A. Time-of-day specificity of anticancer drugs may be mediated by circadian regulation of the cell cycle. Sci. Adv. 2021, 7, eabd2645. [Google Scholar] [CrossRef] [PubMed]
- Shafi, A.A.; Knudsen, K.E. Cancer and the circadian clock. Cancer Res. 2019, 79, 3806–3814. [Google Scholar] [CrossRef] [PubMed]
- Ballesta, A.; Innominato, P.F.; Dallmann, R.; Rand, D.A.; Lévi, F.A. Systems chronotherapeutics. Pharmacol. Rev. 2017, 69, 161–199. [Google Scholar] [CrossRef] [PubMed]
- Dallmann, R.; Okyar, A.; Lévi, F. Dosing-time makes the poison: Circadian regulation and pharmacotherapy. Trends Mol. Med. 2016, 22, 430–445. [Google Scholar] [CrossRef]
- Printezi, M.I.; Kilgallen, A.B.; Bond, M.J.G.; Štibler, U.; Putker, M.; Teske, A.J.; Cramer, M.J.; Punt, C.J.A.; Sluijter, J.P.G.; Huitema, A.D.R.; et al. Toxicity and efficacy of chronomodulated chemotherapy: A systematic review. Lancet 2022, 23, E129–E143. [Google Scholar] [CrossRef]
- Amiama-Roig, A.; Verdugo-Sivianes, E.M.; Carnero, A.; Blanco, J.R. Chronotherapy: Circadian Rhythms and Their Influence in Cancer Therapy. Cancers 2022, 14, 5071. [Google Scholar] [CrossRef]
- Squire, T.; Buchanan, G.; Rangiah, D.; Davis, I.; Yip, D.; Chua, Y.J.; Rich, T.; Elsaleh, H. Does chronomodulated radiotherapy improve pathological response in locally advanced rectal cancer? Chronobiol. Int. 2017, 34, 492–503. [Google Scholar] [CrossRef]
- Lévi, F.; Altinok, A.; Clairambault, J.; Goldbeter, A. Implications of circadian clocks for the rhythmic delivery of cancer therapeutics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 3575–3598. [Google Scholar] [CrossRef]
- Bernard, S.; Čajavec Bernard, B.; Lévi, F.; Herzel, H. Tumor growth rate determines the timing of optimal chronomodulated treatment schedules. PLoS Comput. Biol. 2010, 6, e1000712. [Google Scholar] [CrossRef]
- Powathil, G.G.; Gordon, K.E.; Hill, L.A.; Chaplain, M.A.J. Modelling the effects of cell-cycle heterogeneity on the response of a solid tumour to chemotherapy Biological insights from a hybrid multiscale cellular automaton model. J. Theor. Biol. 2012, 308, 1–19. [Google Scholar] [CrossRef]
- Powathil, G.G.; Adamson, D.J.; Chaplain, M.A. Towards predicting the response of a solid tumour to chemotherapy and radiotherapy treatments: Clinical insights from a computational model. PLoS Comput. Biol. 2013, 9, e1003120. [Google Scholar] [CrossRef] [PubMed]
- Altinok, A.; Lévi, F.; Goldbeter, A. Identifying mechanisms of chronotolerance and chronoefficacy for the anticancer drugs 5-fluorouracil and oxaliplatin by computational modeling. Eur. J. Pharm. Sci. 2009, 36, 20–38. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Alagoz, O.; Erenay, F.S.; Su, Q. A survey of optimization models on cancer chemotherapy treatment planning. Ann. Oper. Res. 2014, 221, 331–356. [Google Scholar] [CrossRef]
- Rojas, C.; Belmonte-Beitia, J. Optimal control problems for differential equations applied to tumor growth: State of the art. Appl. Math. Nonlinear Sci. 2018, 3, 375–402. [Google Scholar] [CrossRef]
- Jarrett, A.M.; Faghihi, D.; Hormuth, D.A.; Lima, E.A.; Virostko, J.; Biros, G.; Patt, D.; Yankeelov, T.E. Optimal control theory for personalized therapeutic regimens in oncology: Background, history, challenges, and opportunities. J. Clin. Med. 2020, 9, 1314. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Clairambault, J.; Volpert, V. Improving cancer treatments via dynamical biophysical models. Phys. Life Rev. 2021, 39, 1–48. [Google Scholar] [CrossRef]
- Swan, G.W. Optimization of Human Cancer Radiotherapy; Interdisciplinary Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Martin, R.; Te, K.L. Optimal Control of Drug Administration in Cancer Chemotherapy; World Scientific Publishing Company Pte. Ltd.: Singapore, 1994. [Google Scholar] [CrossRef]
- Schattler, H.; Ledzewicz, U. Optimal Control for Mathematical Models of Cancer Therapies an Application of Geometric Methods; Lecture Notes in Biomathematics v 42; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Dömény, M.F.; Puskás, M.; Kovács, L.; Drexler, D.A. A Review of Multi-Objective Optimization Algorithms in the Field of Chemotherapy Optimization. In Proceedings of the 2024 IEEE 18th International Symposium on Applied Computational Intelligence and Informatics (SACI), Siófok, Hungary, 21–25 May 2024; pp. 345–350. [Google Scholar]
- Barbolosi, D.; Iliadis, A. Optimizing drug regimens in cancer chemotherapy: A simulation study using a PK–PD model. Comput. Biol. Med. 2001, 31, 157–172. [Google Scholar] [CrossRef]
- Ballesta, A.; Dulong, S.; Abbara, C.; Cohen, B.; Okyar, A.; Clairambault, J.; Levi, F. A combined experimental and mathematical approach for molecular-based optimization of irinotecan circadian delivery. PLoS Comput. Biol. 2011, 7, e1002143. [Google Scholar] [CrossRef]
- Basdevant, C.; Clairambault, J.; Lévi, F. Optimisation of time-scheduled regimen for anti-cancer drug infusion. Esaim Math. Model. Numer. Anal.—Modélisation Mathématique et Analyse Numérique 2005, 39, 1069–1086. [Google Scholar] [CrossRef][Green Version]
- Clairambault, J.; Fercoq, O. Physiologically structured cell population dynamic models with applications to combined drug delivery optimisation in oncology. Math. Model. Nat. Phenom. 2016, 11, 45–70. [Google Scholar] [CrossRef]
- Angaroni, F.; Graudenzi, A.; Rossignolo, M.; Maspero, D.; Calarco, T.; Piazza, R.; Montangero, S.; Antoniotti, M. An optimal control framework for the automated design of personalized cancer treatments. Front. Bioeng. Biotechnol. 2020, 8, 523. [Google Scholar] [CrossRef] [PubMed]
- Gamkrelidze, R. Selected Research Papers: L. S. Pontryagin Select Works; CRC Press: Boca Raton, FL, USA, 2019; Volume 1. [Google Scholar]
- Locatelli, A. Optimal Control: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Robbins, H. A generalized Legendre-Clebsch condition for the singular cases of optimal control. IBM J. Res. Dev. 1967, 11, 361–372. [Google Scholar] [CrossRef]
- Rao, A.V. A survey of numerical methods for optimal control. Adv. Astronaut. Sci. 2009, 135, 497–528. [Google Scholar]
- Crozier, L.; Foy, R.; Adib, R.; Kar, A.; Holt, J.A.; Pareri, A.U.; Valverde, J.M.; Rivera, R.; Weston, W.A.; Wilson, R.; et al. CDK4/6 inhibitor-mediated cell overgrowth triggers osmotic and replication stress to promote senescence. Mol. Cell 2023, 83, 4062–4077.e5. [Google Scholar] [CrossRef]
- Murphy, H.; Jaafari, H.; Dobrovolny, H.M. Differences in predictions of ODE models of tumor growth: A cautionary example. BMC Cancer 2016, 16, 163. [Google Scholar] [CrossRef]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.; Hlatky, L.; Hahnfeldt, P. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef]
- Kimmel, M.; Swierniak, A. Control Theory Approach to Cancer Chemotherapy: Benefiting from Phase Dependence. Lect. Notes Math. 2006, 1872, 185–221. [Google Scholar]
- Ledzewicz, U.; Bratton, K.; Schattler, H. A 3-Compartment Model for Chemotherapy of Heterogeneous Tumor Populations. Acta Appl. Math. 2015, 135, 191–207. [Google Scholar] [CrossRef]
- Ledzewicz, U.; Schättler, H. Optimal bang–bang controls for a two-compartment model in cancer chemotherapy. J. Optim. Theory Appl. 2002, 114, 609–637. [Google Scholar] [CrossRef]
- Faivre, C.; Barbolosi, D.; Pasquier, E.; André, N. A mathematical model for the administration of temozolomide: Comparative analysis of conventional and metronomic chemotherapy regimens. Cancer Chemother. Pharmacol. 2013, 71, 1013–1019. [Google Scholar] [CrossRef]
- Basse, B.; Ubezio, P. A generalised age-and phase-structured model of human tumour cell populations both unperturbed and exposed to a range of cancer therapies. Bull. Math. Biol. 2007, 69, 1673–1690. [Google Scholar] [CrossRef] [PubMed]
- Swierniak, A.; Ledzewicz, U.; Schättler, H. Optimal control for a class of compartmental models in cancer chemotherapy. Int. J. Appl. Math. Comput. Sci. 2003, 13, 357–368. [Google Scholar]
- Michor, F.; Beal, K. Improving Cancer Treatment via Mathematical Modeling: Surmounting the Challenges Is Worth the Effort. Cell 2015, 163, 1059–1063. [Google Scholar] [CrossRef] [PubMed]
- Magi, S.; Iwamoto, K.; Okada-Hatakeyama, M. Current status of mathematical modeling of cancer â From the viewpoint of cancer hallmarks. Regulatory and metabolic networks ⢠Cancer and systemic diseases. Curr. Opin. Syst. Biol. 2017, 2, 39–48. [Google Scholar] [CrossRef]
- Jarrett, A.M.; Lima, E.A.B.F.; Hormuth, D.A.n.; McKenna, M.T.; Feng, X.; Ekrut, D.A.; Resende, A.C.M.; Brock, A.; Yankeelov, T.E. Mathematical models of tumor cell proliferation: A review of the literature. Expert Rev. Anticancer. Ther. 2018, 18, 1271–1286. [Google Scholar] [CrossRef]
- Bekisz, S.; Geris, L. Cancer modeling: From mechanistic to data-driven approaches, and from fundamental insights to clinical applications. J. Comput. Sci. 2020, 46, 101198. [Google Scholar] [CrossRef]
- Yin, A.; Moes, D.J.A.; van Hasselt, J.G.; Swen, J.J.; Guchelaar, H.J. A review of mathematical models for tumor dynamics and treatment resistance evolution of solid tumors. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 720–737. [Google Scholar] [CrossRef]
- Hill, R.J.; Innominato, P.F.; Lévi, F.; Ballesta, A. Optimizing circadian drug infusion schedules towards personalized cancer chronotherapy. PLoS Comput. Biol. 2020, 16, e1007218. [Google Scholar] [CrossRef]
- Clairambault, J. Modeling oxaliplatin drug delivery to circadian rhythms in drug metabolism and host tolerance. Adv. Drug Deliv. Rev. 2007, 59, 1054–1068. [Google Scholar] [CrossRef]
- Borzì, A.; Schulz, V. Multigrid Methods for PDE Optimization. SIAM Rev. 2009, 51, 361–395. [Google Scholar] [CrossRef]
- Bensoussan, A.; Da Prato, G.; Delfour, M.C.; Mitter, S. (Eds.) Representation and Control of Infinite Dimensional Systems, 2nd ed.; Birkhauser: Boston, MA, USA, 2007. [Google Scholar]



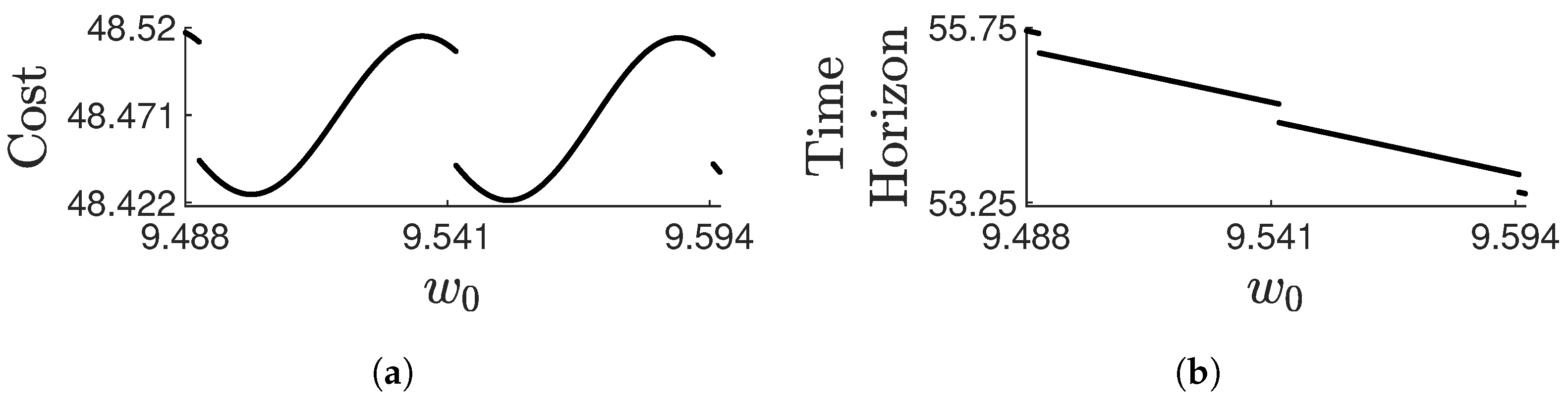

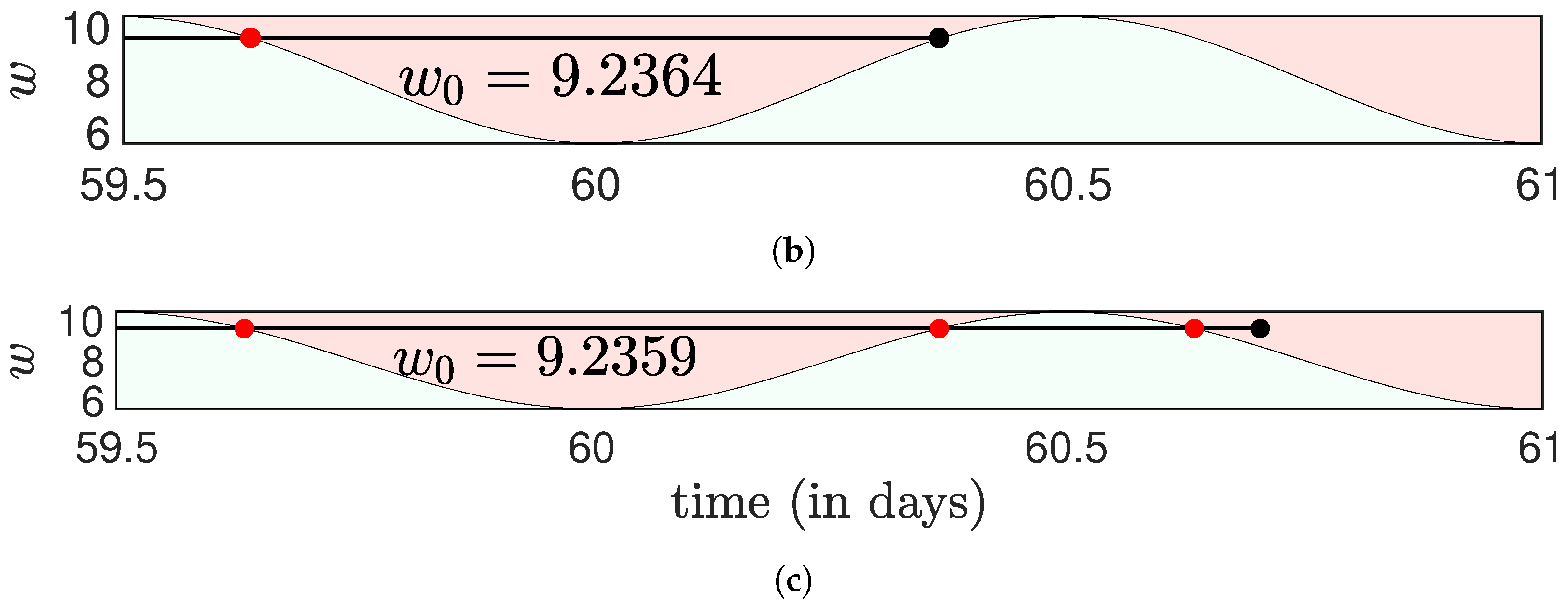
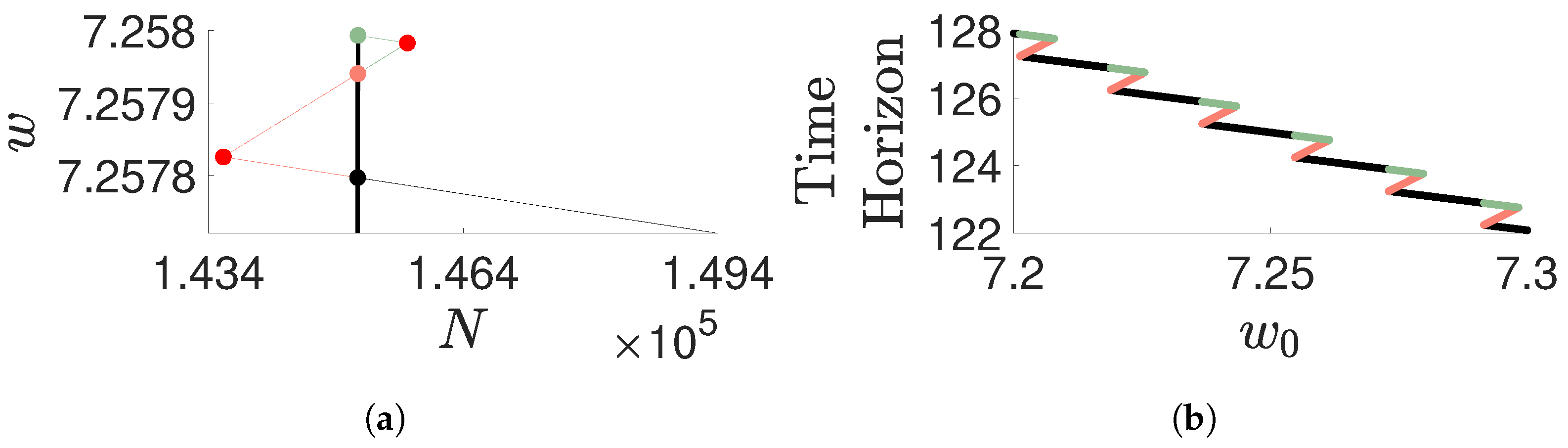



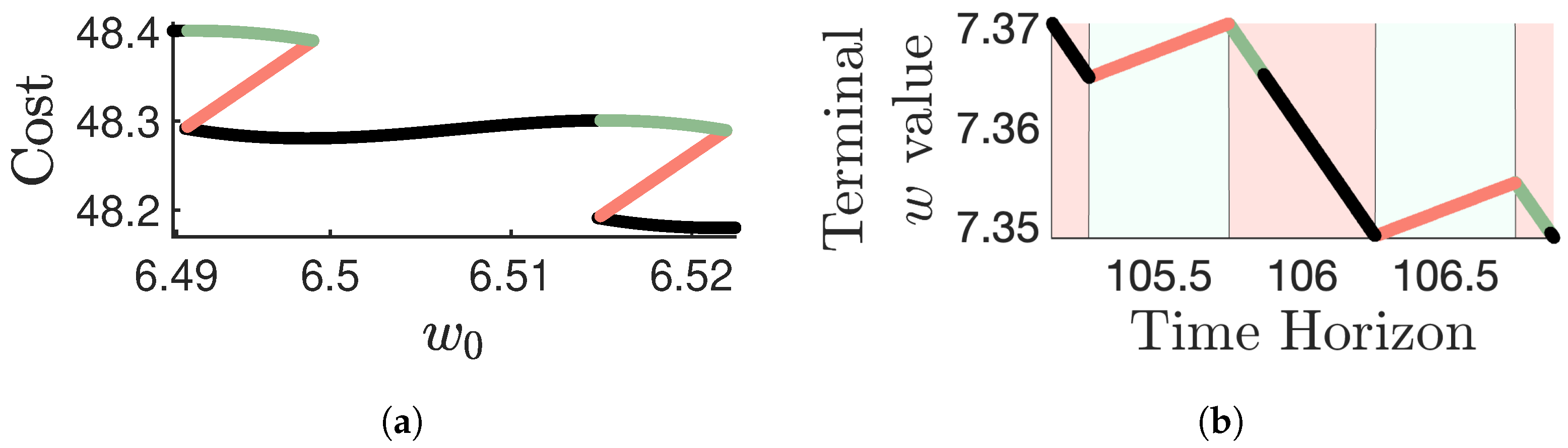


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzamarias, B.D.E.; Ballesta, A.; Burroughs, N.J. Aperiodic Optimal Chronotherapy in Simple Compartment Tumour Growth Models Under Circadian Drug Toxicity Conditions. Mathematics 2024, 12, 3516. https://doi.org/10.3390/math12223516
Tzamarias BDE, Ballesta A, Burroughs NJ. Aperiodic Optimal Chronotherapy in Simple Compartment Tumour Growth Models Under Circadian Drug Toxicity Conditions. Mathematics. 2024; 12(22):3516. https://doi.org/10.3390/math12223516
Chicago/Turabian StyleTzamarias, Byron D. E., Annabelle Ballesta, and Nigel John Burroughs. 2024. "Aperiodic Optimal Chronotherapy in Simple Compartment Tumour Growth Models Under Circadian Drug Toxicity Conditions" Mathematics 12, no. 22: 3516. https://doi.org/10.3390/math12223516
APA StyleTzamarias, B. D. E., Ballesta, A., & Burroughs, N. J. (2024). Aperiodic Optimal Chronotherapy in Simple Compartment Tumour Growth Models Under Circadian Drug Toxicity Conditions. Mathematics, 12(22), 3516. https://doi.org/10.3390/math12223516





