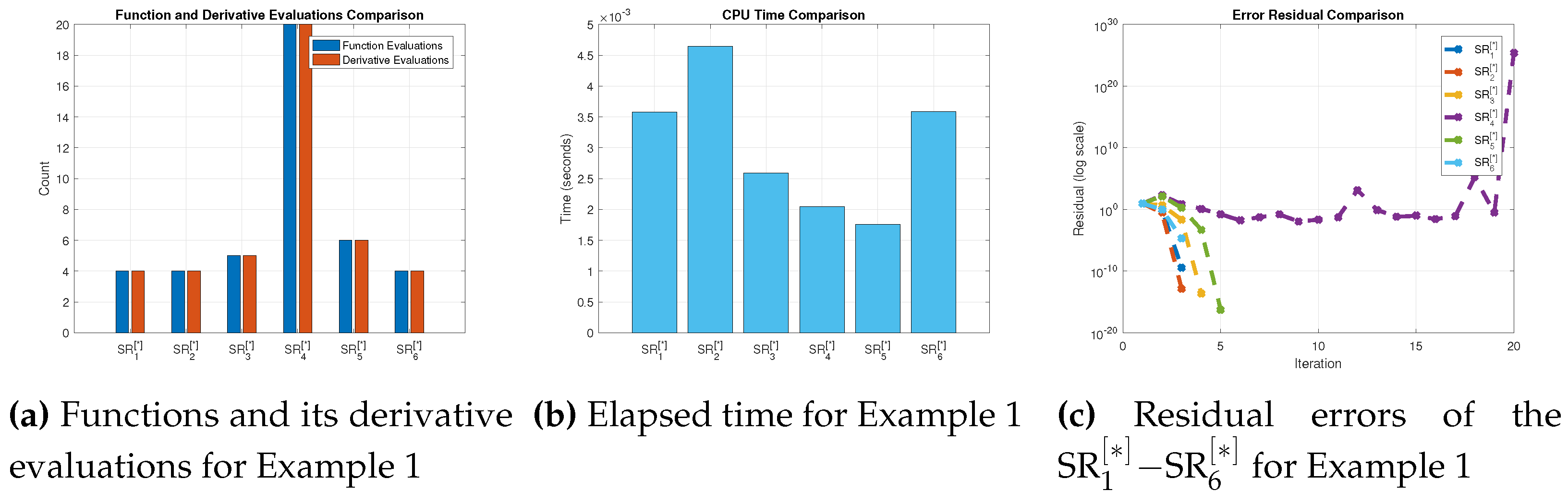
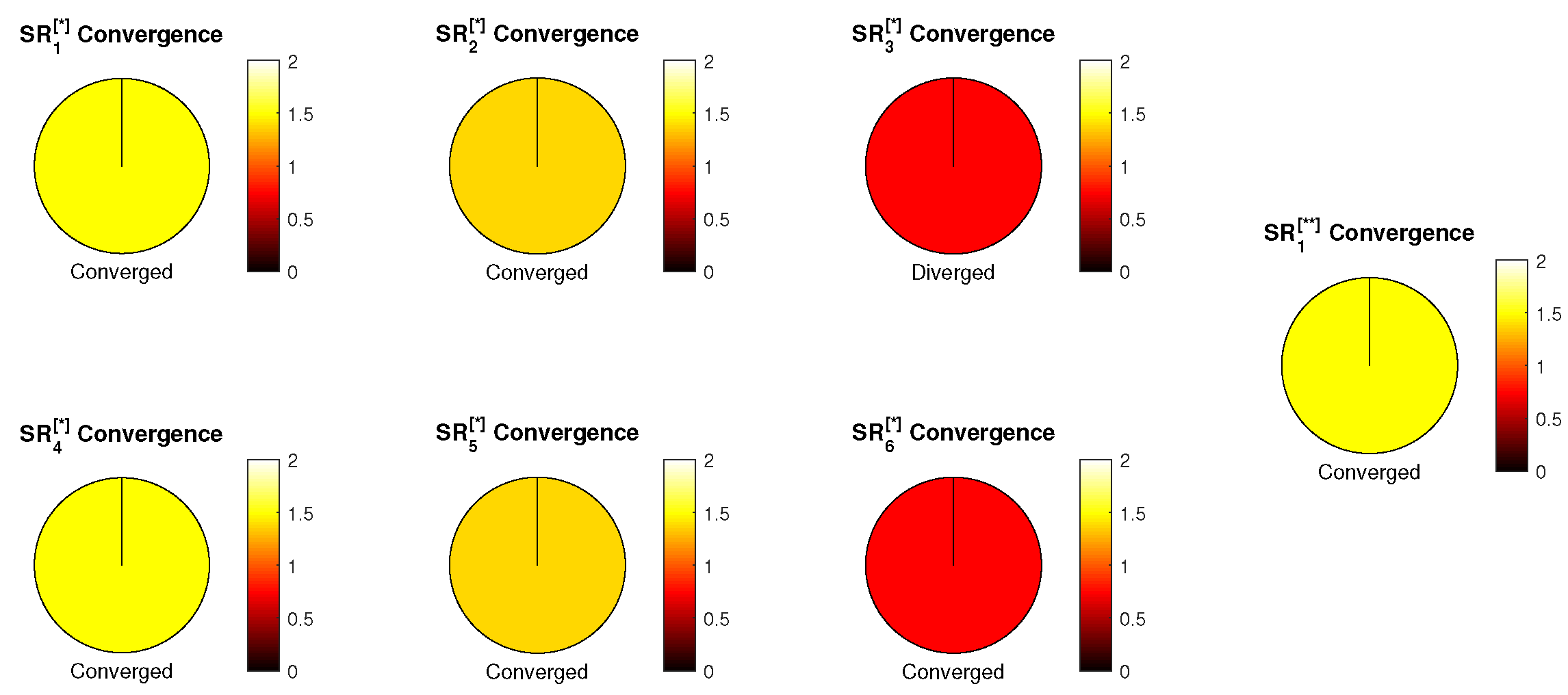
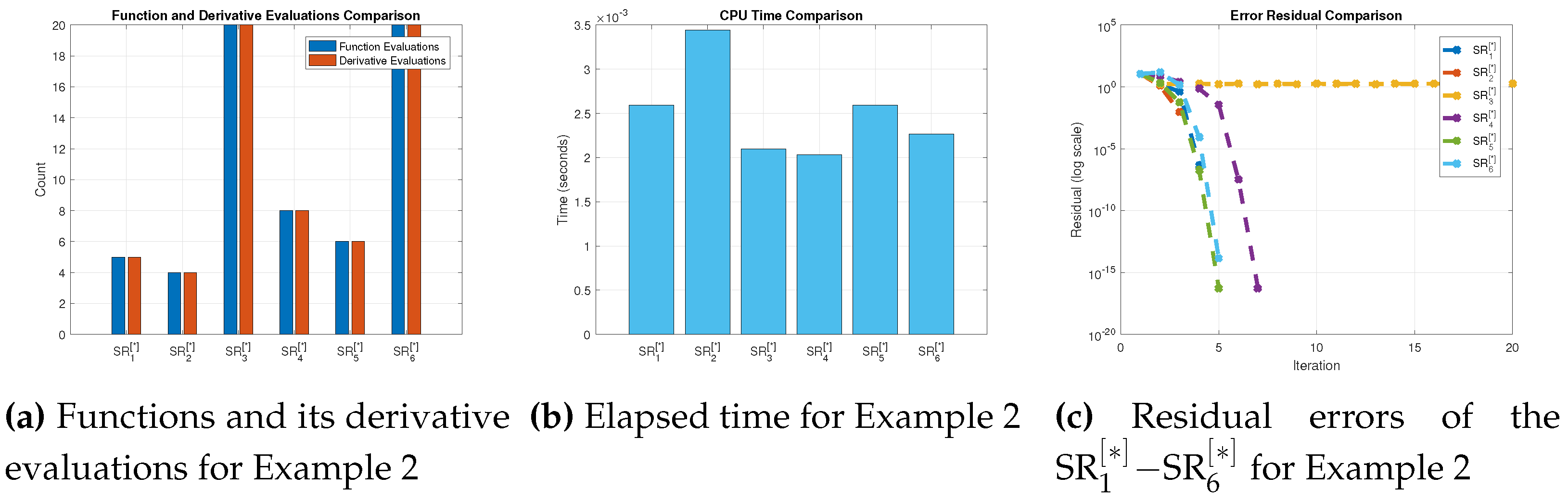
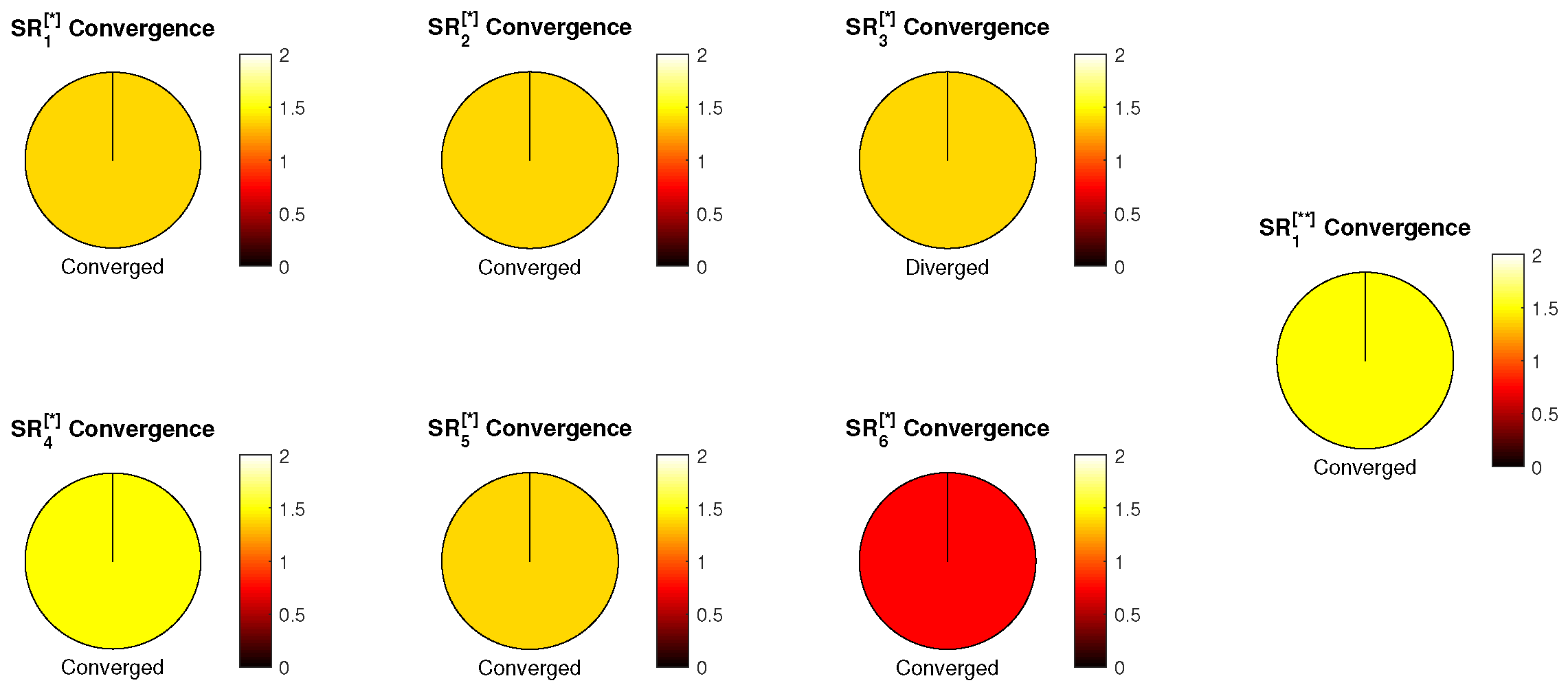
Proof. Let
be a root of
and assume
. Using multiplicative Taylor series expansion of
around
we obtain
Using the natural logs on both sides of (
18), we obtain
where
Taking the derivative of (
21), we have
Taking inverse of (
26), we obtain
Multiplying (
25) with (
27), we have
where
,
,
,
,
,
where
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Thus,
where
,
,
,
,
,
,
,
where
,
,
,
,
,
,
,
,
,
,
where
,
,
,
,
,
,
,
,
,
,
where
Thus, the theorem is proven. □