2.1. Formulation of the Problem
The governing equations for the propagation of disturbances in elastic isotropic media are as follows [
9]:
where
is the displacement vector field at a point
r and time
t, the double dot denotes the second partial derivative with respect to time,
is the mass density, ∇ is the gradient operator in space, and
is the stress tensor in the medium. It is a symmetric 2-tensor that depends on Lamé coefficients denoted by
and
, and the displacement field
as
where
I is the unit tensor. Here and in what follows, the conventional tensor notations are used, e.g.,
and
(Einstein’s rule of summation over repeated indices is always implied, unless stated otherwise), and the superscript
T stands for transposition of tensor indices. For homogeneous media,
,
, and
are constant, and Equation (
1) admits plane-wave solutions with three polarization modes. The two transverse polarization modes are known as shear waves, and the longitudinal mode describes compression waves. The transverse and longitudinal waves propagate with different speeds, denoted by
and
, respectively, that depend on the media parameters. Any inhomogeneity in the media causes scattering of the elastic waves.
An inhomogeneity is described by the relative mass density and Lamé coefficients, denoted by
. For example,
, where
is the constant mass density of the background media so that
only in regions where the mass density differs from that of the background media, and similarly for
. A solution to the scattering problem is sought in the form
, where
is the frequency of incident and scattered waves. The amplitude
is then shown to satisfy the following equation:
The relative Lamé coefficients and vanish in the bulk. They are piecewise continuous, having jump discontinuities at the boundary of a region occupied by the scattering structure. A solution is sought as a regular distribution that is required to be continuous everywhere and has a continuous normal traction where is a unit normal to the boundary of . These conditions result from the continuity of the elastic displacement and mechanical equilibrium of the scattering structure, respectively. The normal traction boundary condition induces a coupling of different elastic polarization modes at the interface separating two elastic media. A standard approach to solving the problem is to convert the differential equation into an integral equation using a suitable Green’s function for the operator , whose solution is then analyzed by methods for integral equations (e.g., von Neumann series).
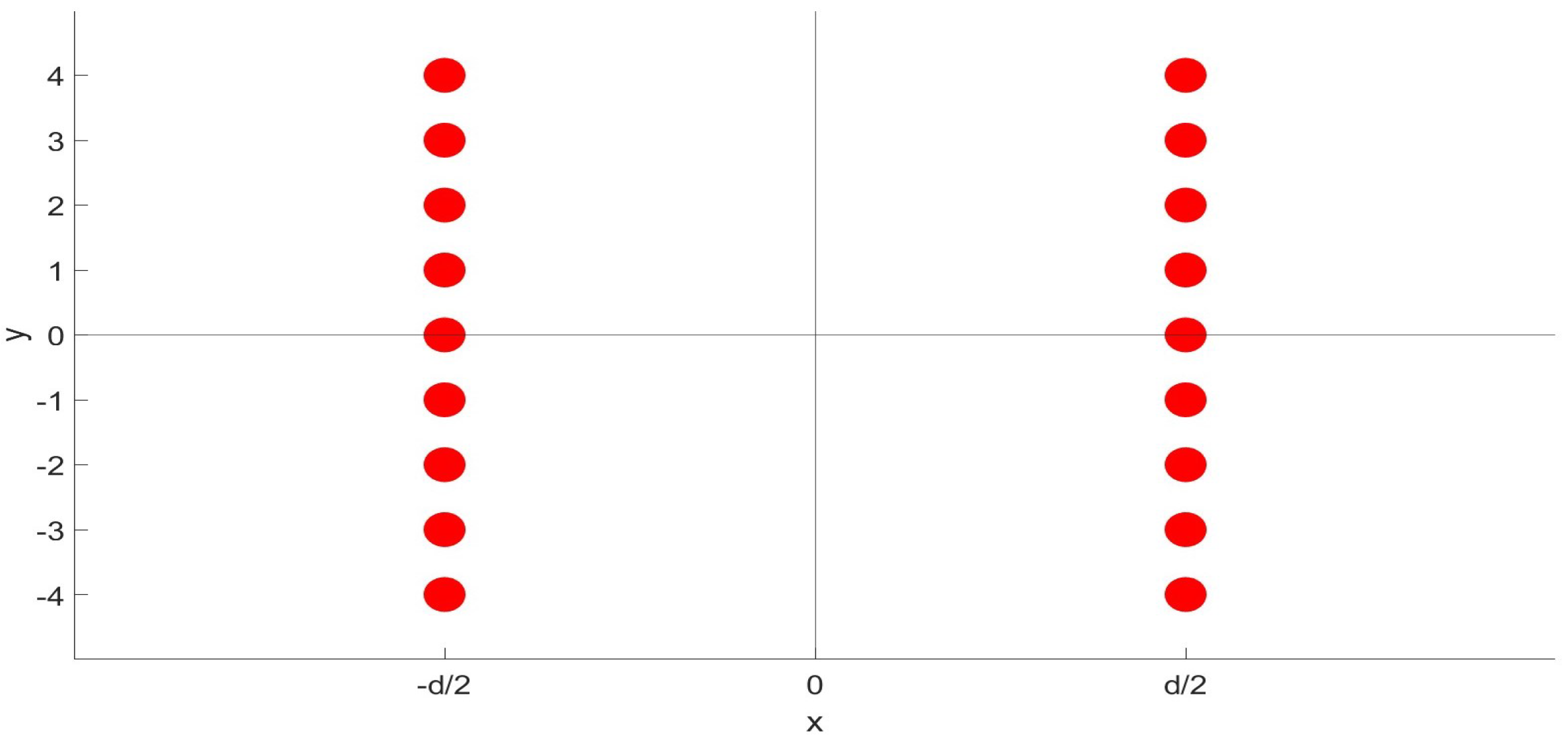
Here, the scattering problem is studied for the following elastic structures: The first structure consists of one array of infinite parallel cylindrical defects that are periodically arranged in a plane. The second structure has two such arrays separated by a distance, as depicted in
Figure 1. Finally, the structure with two parallel arrays shifted relative each other is studied. In the latter case, the parity symmetry in the direction normal to the arrays is broken.
The systems have a translational symmetry in the direction parallel to the cylinders and are periodic in the direction perpendicular to the cylinders. The cylinders are set parallel to the
z axis. Due to the translational symmetry along the
z axis, the field
u is independent of the variable
z so
in what follows. The wave vector of an incident plane wave lies in the
plane. So, one shear mode is polarized along the
z axis, and the vector field
u of the other shear mode and longitudinal mode lies in the
plane. The former and latter modes are called
out-of-plane and
in-plane modes, respectively. The solution is the sum
of the scattered wave
and an incident wave that satisfies the associated homogeneous equation
Equation (
3) has three linearly independent plane-wave solutions of the form
, where
and
are components of the wave vector for a wave polarized parallel to a unit vector
. The polarization vector
is perpendicular to the wave vector for the shear modes (as the field is divergence free in this case) and parallel to it for the compression mode. The components of the wave vector are not independent and must satisfy the dispersion relation for each polarization mode
, where
and
are the magnitudes of wave vectors of the longitudinal and transverse modes, respectively. Thus, each independent solution is uniquely determined by the polarization state and a pair of spectral parameters
, whereas
is determined by the dispersion relation for each polarization mode. The necessity to choose
as an independent spectral parameter will become clear shortly, when the Bloch periodicity condition is introduced for periodic scattering structures (see Equation (
5)). So, an incident wave is chosen to be a superposition of the above three independent plane-wave solutions to (
3). It is convenient to write it as the following sum of a longitudinal (compression) wave, a transverse (shear) wave polarized in the
plane, and a transverse (shear) wave polarized parallel to the
z axis:
where
is a unit vector parallel to the
z axis,
and
are scalar amplitudes of the in-plane longitudinal and transverse incident waves, respectively,
is the scalar amplitude of the out-of-plane mode, and
and
are the
x components of the wave vectors for the transverse and longitudinal modes, respectively. They are positive solutions to the dispersion relations for each polarization mode so that the incident wave propagates in the direction of increasing
x.
Similarly, in the asymptotic region
, the scattered wave is a superposition (
4) of plane waves with the parameters
and unknown scalar amplitudes of three independent polarization modes. The components
and
in the scattered-wave modes are positive and negative roots of the dispersion relation for the transmitted (
) and reflected (
) waves, respectively. To solve the scattering problem, one has to find the scalar amplitudes of reflected and transmitted waves for each polarization mode and the corresponding
in terms of scalar amplitudes of the incident wave and its spectral parameters.
The system in question is periodic along the
y axis with a period of a unit length. Therefore, any solution must satisfy the Bloch condition
This is the reason for choosing
as an independent spectral parameter of the incident and scattered waves. In what follows, the parameter
will often be referred to as a Bloch phase. It follows from (
5) that
can change only by integer multiples of
in the scattering modes, that is,
, where
n is an integer. The range of
n is determined by the condition that the corresponding roots
,
, of the dispersion relation are real:
where
As a consequence, each incident wave
can scatter into finitely many
open diffraction channels, defined by (
6). The number of open channels depends on
. The radiation continuum for each mode is defined as
. It consists of intervals in which one or two or three (and so on) diffraction channels are open.
Owing to the Bloch condition, the scattered field should be sought in the strip
D:
and
. The scattered wave (in any open diffraction channel) must carry an energy flux away from the array in the asymptotic region
and, hence, satisfy the Sommerfeld radiation condition
where
labels the three polarization modes, and
is the positive root of the dispersion relation (
6). Therefore, the scattered elastic field that satisfies the Bloch and Sommerfeld conditions must be the following superposition of plane waves in the far-field region:
where the sums are taken over open diffraction channels for each polarization mode defined by (
6), and the signs ± are taken for reflected
) and transmitted
) waves. The scattering amplitudes
are functions of the spectral parameters of the incident wave and also depend on geometrical and material parameters of the system. The objective is to calculate these amplitudes.
If the incident wave is set to zero, , then there can still exist solutions that satisfy the Bloch and Sommerfeld conditions that are localized, meaning that they are square integrable in the region D. They are called bounded states. The square integrability implies that bound states cannot have an oscillatory behavior with a constant amplitude in the far region as propagating waves. They are stationary states (or standing waves), and their energy is not carried away from the structure in which they are localized. This also implies that bound states are decoupled from the radiation continuum and, hence, cannot be excited by an incident wave. If the frequency of bound states lies below the radiation continuum, then they are regular bound states. If lies in an open diffraction channel, then such solutions are known as bound states in the radiation continuum (BSC). BSC do not generally exist for any values of physical and geometrical parameters of a scattering structure. If the scattering amplitudes exhibit resonances, or poles in the complex plane with a positive imaginary part (the width of resonances) and with the real part in an open diffraction channel, then the existence of BSC can be detected by analyzing the resonance width as a function of physical and geometrical parameters. If the width can be driven to zero by varying these parameters, then there exist BSC as resonances with the vanishing width.
Physically, an excited resonance decays in time that is reciprocal of the resonance width, and, hence, the same time is needed to excite the resonance by an incident (incoming) wave. The resonance initial energy is carried away to the asymptotic region by outgoing radiation waves whose frequency is determined by the real part of the pole. If the width can reach zero at certain values of the parameters, then the resonant state can live an infinitely long time and becomes a stationary (bound) state. It also decouples from the radiation continuum in the limit of the zero width.
In what follows, the resonant properties of the scattering amplitudes will be investigated to show that a double array can have resonances in open diffraction channels whose width vanishes for certain material, geometrical, and spectral parameters, and the corresponding BSC will be found. The key difference between BSC analytically found in similar electromagnetic systems is that elastic BSC for the in-plane modes do not have any particular polarization because the longitudinal and transverse polarization modes are coupled through the normal traction boundary condition at the cylinders. If one makes an analogy with Maxwell’s theory, then such elastic BSC correspond to electromagnetic BSC in which two transverse polarization modes are coupled in the scattering system and have different dispersions (like in anisotropic background media).
2.2. Lippmann–Schwinger Equation
Suppose that the scatterers are homogeneous so that the relative mass density and Lamé coefficients are constant in the region occupied by the scatterers. Then,
,
, and
are piecewise constant and vanish outside of the scatterers. The differential equation for the elastic field satisfying the Sommerfeld condition is proved to be equivalent to the Lippmann–Schwinger integral equation
where
is the Green’s function for the operator
that satisfies the Sommerfeld radiation conditions, and the star stands for the convolution defined in the distributional sense. It is shown in
Appendix A.1 that
where
,
, and
is the Hankel function of the first kind. It is easy to see from the asymptotic behavior of the Hankel functions for
that the Green’s function satisfies the Sommerfeld condition (
8). For a small
r,
, and, hence, the singular distributional part of second partials is canceled due to
so that
is locally integrable. Thus, the Green’s function is a regular distribution defined by a smooth function for
. The support of the region occupied by the scatterers is not bounded in the plane, and, hence, the existence of the convolution should be investigated. It was shown in [
2] that the convolution
exists in the sense of distributions for any regular tempered distribution
f that satisfies the Bloch periodicity condition and has support on bounded non-overlapping scatterers. Owing to the existence of the convolution, its derivatives can be applied to either of the distributions in the convolution in the last term on the right-hand side of (
9).
If
r in (
9) is restricted to support the scatterers, e.g.,
, where
is defined in the caption of
Figure 1 and
R is the radius of cylinders, then the equation is a Fredholm-type integral equation whose solution defines the scattered field within the scattering structure. This field is induced by an incident wave. By (
9), the induced field defines the scattered field outside the scattering structure. In particular, the scattering amplitudes are obtained from (
9) by taking the limits
. Here, the said integral equation is solved in the leading order of the long wavelength limit, when the wavelength of the incident wave is much larger than the radius of cylinders
. It is proved in
Appendix A.2 that, in this approximation, the elastic field
and the corresponding stress tensor
can be assumed to have constant values across each scatterer, that is,
and
, where
are the positions of the scatterers. Therefore, the scattered wave is a superposition of outgoing waves produced by point sources of strength
and
located at the positions of the scatterers:
where
is the area of the cross section of each cylinder and
for any
n. Thus, the scattering problem is reduced to finding the induced field
and the induced stress tensor
on the scatterers.
A peculiarity of the problem is that, if one sets
,
, and
for
in integral Equation (
9), then it gives a relation between two unknowns,
and
, that is not sufficient to uniquely determine them, in full contrast to electromagnetic or acoustic scattering problems in the same approximation (for small scatterers) where the induced field on the scatterers uniquely determines the scattered field. The second equation comes from the normal traction boundary condition in elasticity theory. The implementation of this condition turns out to be a tedious technical problem.
2.2.1. A Solution for a Single Array in the Long-Wavelength Approximation
Consider first the single array case. The centers of the cylinder are at
, where
n ranges over all integers. Owing to the Bloch condition,
. Therefore, the induced sources are determined by unknowns
and
. Here and in what follows,
,
, and
stand for the constant values of
,
, and
on the scatterers. In
Appendix A.2, it is proved that if the wavelength is much larger than the radius of cylinders, then the convolutions in the Lippmann–Schwinger equation can be calculated in the approximation of
and
by constant values on the scatterers so that Equation (
9) is reduced to
Equation (
12) shows that the induced field
and stress
define the strength of point sources for the scattered field. To find them, first,
is calculated by substituting (
12) into (
2). Next, it is demanded that the field
and the normal traction
are continuous across the boundary of each cylinder
. In the long wavelength limit (
), the continuity conditions are equivalent to continuity of
and the stress tensor
at
.
A substitution of (
12) into (
2) yields for
where
is the stress tensor of the incident wave. By the Bloch condition,
. So, it is sufficient to satisfy the continuity conditions only at
. Let
This limit is to be calculated in the leading order of a small parameter
of the long wavelength approximation. For example, owing to the local integrability of
,
in the leading order of
, where the series converges by Abel’s test.
If the relative Lamé coefficients vanish, then
and
is found by setting
in (
12) so that the induced sources are determined only by
. If
, then the limit of the derivatives of
must be calculated. Derivatives of Green’s functions
are not regular distributions, and a calculation of the limit is not a straightforward task that can be accomplished by a term-by-term differentiation of the series (
13) [
39]. In
Appendix A.3,
and
are proved to exist and their explicit form is found in the leading order of
. So, taking the limit
in (
12) and in (
14), the continuity conditions for the field and stress tensor yield the following system of linear equations for the unknowns
and
:
where
and
are the incident field and its stress tensor at
, respectively. No summation over
i is implied in
. The system (
16) and (
17) define the induced sources of scattered elastic waves. It is drastically different from similar electromagnetic or acoustic cases due to the normal traction boundary condition that is unique to elastic theory. The additional unknown
also makes an analysis of the system technically more involved when the relative Lamé coefficients are not zero.
Equations (
16) and (
17) can be cast in the following matrix form:
where the column vectors are defined by
It follows from the explicit form of
,
, and
given at the end of
Appendix A.3 that the
matrix
is block diagonal. Its blocks are
and there is a
block,
. Equation (
18) is decoupled into three matrix equations and one scalar equation associated with the block structure of
:
By Equation (
12), the S-matrix coefficients are given by linear combinations of the components of
; hence, the poles of the S-matrix are determined by analytic properties of the inverse of
in the complex
plane. In particular, the positions of bound states and resonances are roots of the equation
. An analysis of this equation is given in
Section 3.
2.2.2. The Double Array Case
For a double array, the origin of the coordinate system is set so that the system is symmetric under reflection in the
plane,
, as shown in
Figure 1. In the long wavelength approximation, the convolution in the Lippmann–Schwinger equation is computed in the same way as in the single array case using the values of
and
at the centers of the cylinders. The Bloch condition shows that these values are determined only by their values at
, that is, by
and
.
Let
be the parity index. Then, by
Appendix A.2 (see also (
11)), the Lippmann–Schwinger Equation (
9) is equivalent to
in the long-wavelength approximation, where
are defined by (
13). The unknowns
and
are found from the continuity of
and
at
, just like in the single array case. The field (
23) is used to calculate the stress tensor
given in (
2). Then, the limits
are taken in (
23) and (
2) to obtain the following system of equations:
where
, and
is the stress tensor for the incident field at
. Each of the above equations stands for two equations: one for the top parity indices in each term and another for the bottom parity indices in each term.
Equations (
24) and (
25) can be cast in the matrix form (
18), where the vector
has 16 components that are 16 unknowns,
and
,
is a 16-vector with components that are the corresponding components of
and
, and the matrix
becomes a
matrix. The pole structure of the scattering matrix is determined by analytic properties of the inverse of
.
2.3. Resonances and BSC
To find scattering resonances and BSC in the studied systems, one should find square integrable solutions to the associated homogeneous Lippmann–Schwinger equation when
. The square integrability is understood in the
x direction because any solution is Bloch periodic in the
y direction. This is an eigenvalue problem where
plays the role of the spectral parameter. The eigenfunctions are known as Siegert states. They exist at generally complex-valued solutions
to the equation
. If
is a root, then the associated homogeneous system of linear equations for the induced sources (either (
16) and (
17) or (
24) and (
25) with
) has a non-trivial solution. This solution is to be substituted into (
12) (for the single array case) or into (
23) (for the double array case), and the square integrability of the obtained field
is to be verified.
If the real part of a root
lies in an open diffraction channel, then
defines the position of a resonance in the scattered field (or the resonant frequency
), and the imaginary part
determines the width of the resonance. In this case, the equations for the induced sources have a unique solution for any incident wave (
) of a frequency
near
because the matrix
is not singular for a real
. The amplitude of the scattered field (
12) or (
23) exhibits a typical Lorentzian profile as a function of the frequency
due to the complex pole at
coming from the inverse of
.
A Siegert state associated with a real root that lies in an open diffraction channel is a Bound State in the Continuum. By construction, it is a standing-wave solution to the elastic-wave equation that is localized in the vicinity of the scattering structure and whose frequency lies in the radiation continuum (in an open diffraction channel). In this case, the matrix is singular at and a non-trivial solution for the induced sources exists without any incident wave, . Naturally, the induced sources are determined up to an arbitrary factor in this case, which can be fixed by normalizing a BSC solution, e.g., by demanding that a BSC solution has a certain elastic energy per one period of the structure. So, the objective is to find the conditions on geometrical and material parameters under which the studied systems have resonances with the vanishing width in open diffraction channels. Technically, the problem is reduced to solving the equation and identifying the roots corresponding to Siegert states with desired properties.