Abstract
The scattering problem of elastic waves impinging on periodic single and double arrays of parallel cylindrical defects is considered for isotropic materials. An analytic expression for the scattering matrix is obtained by means of the Lippmann–Schwinger formalism and analyzed in the long-wavelength approximation. It is proved that, for a specific curve in the space of physical and geometrical parameters, the scattering is dominated by resonances. The shear mode polarized parallel to the cylinders is decoupled from the other two polarization modes due to the translational symmetry along the cylinders. It is found that a relative mass density and relative Lamé coefficients of the scatterers give opposite contributions to the width of resonances in this mode. A relation between the Bloch phase and material parameters is found to obtain a global minimum of the width. The minimal width is shown to vanish in the leading order of the long wavelength limit for the single array. This new effect is not present in similar acoustic and photonic systems. The shear and compression modes in a plane perpendicular to the cylinders are coupled due to the normal traction boundary condition and have different group velocities. For the double array, it is proved that, under certain conditions on physical and geometrical parameters, there exist resonances with the vanishing width, known as Bound States in the Continuum (BSC). Necessary and sufficient conditions for the existence of BSC are found for any number of open diffraction channels. Analytic BSC solutions are obtained. Spectral parameters of BSC are given in terms of the Bloch phase and group velocities of the shear and compression modes.
Keywords:
bound states in the continuum; elastic wave scattering; scattering theory; scattering resonances MSC:
74J05; 74J20
1. Introduction
Elastic and photonic metamaterial structures have been of great interest in the field of wave physics, both mathematically and experimentally. Exotic wave properties can be seen across the field of scattering theory, including scalar theory, such as in acoustic wave guides [1] and photonic structures [2,3,4]. The unusual properties of elastic waves have also been a field of interest because structures made of elastic metamaterials [5,6,7,8] have the ability to achieve atypical elastic moduli that cannot be obtained in conventional elastic structures. From a mathematical point of view, the structure of the wave equation is quite different for electromagnetic, acoustic, and elastic waves. An electromagnetic wave has two transverse polarization modes that have the same group velocity in isotropic media. Acoustic waves are scalar (compression) waves, whereas elastic waves have three polarizations, two transverse or shear modes, and a longitudinal or compression mode. The shear and compression modes have different group velocities even in isotropic media. In addition, shear and compression modes are coupled at an interface separating two different isotropic materials via the so-called normal traction boundary conditions [9]. The coupling of modes with different dispersion relations merits an extensive mathematical analysis of the scattering properties of elastic structures as compared to similar structures in photonics or acoustics which have been studied previously. In this paper, the scattering problem is analyzed for elastic waves impinging on a periodic single and double array of cylindrical elastic scatterers made of an isotropic material and embedded into isotropic background elastic media. The photonic counterpart is known for its ability to support standing electromagnetic waves that are localized in the vicinity of the structure and whose frequency lies in the radiation continuum (in an open diffraction channel) [3]. One of the objectives of the present work is to investigate elastic BSC in this system for most general material and geometrical parameters. These unconventional standing-wave solutions, whose spectrum lies in the spectrum of asymptotic (scattered) waves, were first discovered by von Neumann and Wigner [10] for the Schrödinger equation via an inverse design of the potential and are called Bound States in the Continuum (BSC). The results were further extended and corrected by Stillinger and Herrick [11].
Since their advent, BSC have been studied in much more depth. There has been a classification of different types of BSC, which has revealed the main mechanisms that allow for the existence of such modes [12]. In addition, these modes have also seen experimental realizations in acoustic wake-shedding experiments [13] and acoustic wave guides [1]. Layered structures and anisotropic acoustic structures have also seen realizations of BSC [14,15]. Of the few types of BSC that have been analyzed, the one of concern in this paper has been commonly referred to as the Fabry–Pérot type. The mechanism behind a formation of these BSC is a perfect destructive interference of the far-field radiation outgoing from two identical resonators. It is achieved by means of fine-tuning material, geometrical, and spectral parameters and results in a localization of the wave field in one or more dimensions.
For example, an array of infinite parallel identical dielectric cylinders positioned periodically in a plane is a resonator for an incident wave polarized parallel to the cylinders. The quality factor depends on the dielectric constant and the radius of the cylinders. If two such arrays are positioned to be parallel at some distance, then the combined system contains two coupled resonators [3]. Each resonator emits waves in the two opposite directions that are normal to the arrays, and the outgoing waves are also scattered by the neighboring array. So, the far-field radiation is a superposition of emitted waves with multiple reflections like in a Fabry–Pérot interferometer. The difference with the latter is that the interferometer interfaces are resonating and their reflection coefficients have a standard Lorentzian profile as functions of the incident wave frequency. By tuning the distance between the arrays, one can achieve perfect destructive interference of the radiation outgoing from the two resonators in the asymptotic region at the resonant frequency of each array. This implies that an electromagnetic wave emitted by resonating interfaces can no longer escape to the asymptotic region. It becomes a standing wave localized in the vicinity of the resonators [3], despite the wave frequency lying in an open diffraction channel of the system. This analysis has to be amended in a significant way in order to achieve BSC in the elastic counterpart by means of this mechanism. The reason is that the shear and compression modes propagate with different speeds, so the round-trip phase gained by these waves by traveling back and forth between the interfaces is not the same. Since the modes are coupled and must be both present in the asymptotic region, the destructive interference is impossible to achieve simultaneously for the shear and compression modes by merely adjusting the distance between the arrays.
There is extensive literature on numerical studies of the scattering problem for similar layered periodic structures in fluids ([16,17,18]), acoustics ([19,20]), elastics ([21,22,23,24,25,26,27]), and electromagnetism ([2,3,4,28,29,30,31,32,33]). In particular, the scattering problem was numerically studied in [21] for elastic waves impinging a periodic array of cylinders and containing only the shear mode polarized parallel to the cylinders which is decoupled from the compression mode. In this sense, the problem is analogous to the aforementioned electromagnetic one. A coupling of different wave modes was investigated in [34], where it was proposed to couple elastic BSC to photonic resonances to exploit opto-mechanical effects in crystal slabs. Resonances and BSC have been analyzed in periodic wave guides connected to side-coupled pillared resonators [35] and in architected beams [36]. Devices such as these can be utilized in order to perform elastic mode conversion. Additionally, there has been experimental evidence of BSC in layered structures consisting of solids and liquids [37]. Topological standing waves have been analyzed in elastic honeycomb plates with pentagonal disinclination [38].
The first analysis of elastic BSC that contain coupled shear and compression modes was carried out in [39]. The scattering system consisted of two identical parallel arrays of elastic cylinders. Each array consisted of infinite parallel cylinders that were periodically arranged in a plane. The system had a parity symmetry in the direction normal to the arrays and a translational symmetry in the direction parallel to the cylinders, and it was periodic in the direction along the arrays and perpendicular to the cylinders. Owing to the symmetries, the shear mode polarized parallel to the cylinders was decoupled from the other two polarization modes. The shear mode polarized in the plane perpendicular to the cylinders was coupled to the compression mode so that these wave modes were mixed by the scattering process. It was shown in [39] that if the distance between the arrays is much larger than the period of the arrays and there is just one open diffraction channel for each polarization mode, then BSC exist in both scattering channels. In this approximation, evanescent fields of each array can be neglected in the vicinity of the other array so that the arrays can interact only via propagating wave modes like in the aforementioned Fabry–Pérot interferometer with resonating interfaces. In the case of coupled shear and compression modes, an additional condition of the Bloch phase of the waves is required in order for BSC to exist due to the destructive interference mechanism [39]. For zero relative Lamé coefficients, BSC in the decoupled shear mode were shown to have the same structure as in the electromagnetic counterpart reported in [2]. The result was established in the long-wavelength approximation (also called a dipole approximation in scattering theory) when the wavelength was much larger than the radius of the cylinders.
In this paper, the results of [39] are extended in several ways. First, a complete solution for the scattering problem for single arrays is given in the case of arbitrary Lamé coefficients (Section 2.2.1). Second, ultra-narrow resonances (or quasi-BSC) are shown to be present in the decoupled transverse mode for the single array structure. The effect is due to opposite contributions of variations in the mass density and Lamé coefficients to the resonance width (Section 3.2.1). With a suitable choice of these material parameters, one can tune the resonance width even lower than is possible in the electromagnetic counterpart studied in [2]. In fact, in the long-wavelength approximation, these resonances appear as BSC (as resonances with the vanishing width). However, whether or not this conclusion holds beyond this perturbative approach remains to be seen. This is a new phenomenon that is shown to be unique to elastic-wave systems and has not been reported in the literature. From an applied perspective, this implies that it is possible to construct an elastic single array that has extremely narrow resonances, the likes of which would be impossible in the corresponding photonic or acoustic structure. Such arrays can be made of elastic metamaterials and used as narrow filters.
Third, the scattering problem is solved for a double array system in which one array is shifted relative to the other so that the parity symmetry is broken (Section 4). The solution is given for an arbitrary separation of the arrays, an arbitrary relative shift, and an arbitrary number of open diffraction channels. Necessary and sufficient conditions for the existence of BSC with coupled polarization modes and with spectral parameters in higher-order open diffraction channels are found (Section 4.1). They contain an equation for BSC frequencies and conditions of the Bloch phase that depend on the number of open diffraction channels. Explicit analytic solutions to the elastic wave equation describing BSC are also given (Section 4.2.1). Finally, the effect of evanescent fields on the spectral parameters of BSC is fully investigated (Section 4.2). It is shown that the conditions of the Bloch phase are not affected by evanescent fields, while there is a drastic change in the spectrum of BSC for separations of the arrays comparable with the wavelength. In particular, in the case of the symmetric double array studied in [39] in the Fabry–Pérot approximation for one open diffraction channel, BSC that are symmetric under the parity transformation no longer exist below a certain array separation, while antisymmetric BSC still exist. Above this separation threshold, BSC of different parities have different frequencies, whereas they have the same frequency in the Fabry–Pérot approximation.
The paper is organized as follows: In Section 2, the scattering problem is formulated for most general settings and then reduced to the Lippmann–Schwinger integral equation. In the case of periodically arranged parallel elastic cylinders, open diffraction channels are defined for all scattering elastic wave modes. Then, the Lippmann–Schwinger equation is solved in the limit when the wavelength of an incident wave is significantly larger than the radius of cylinders (in the dipole approximation). The solution is given in terms of the partial wave series, and the scattering matrix is extracted from the solution. Then, the incident field is set to zero so that the Lippmann–Schwinger equation becomes an eigenvalue problem where the squared frequency plays the role of a spectral parameter and solutions are demanded to be square integrable. The eigenfunctions are called Siegert states. They exist generally only for complex eigenvalues of the spectral parameter. The eigenvalues define the poles of the scattering matrix. An equation for the spectrum of Siegert states is found for single and double arrays with no restrictions on geometrical and material parameters. A resonance in the scattered field corresponds to a pole whose real part determines the resonant frequency, whereas the imaginary part determines the width. BSC are Siegert states corresponding to real poles that lie in an open diffraction channel. Therefore, the system can have BSC if its geometrical and material parameters can fulfill conditions under which the width of one or more resonances vanishes.
In Section 3, the equation for the spectrum of Siegert states is solved in the case when the distance between the arrays is large compared to the wavelength, that is, when the effects of evanescent fields can be neglected, but there is no restriction on the material parameters (the mass density and Lamé coefficients). It is proved that there exists a curve in the space of parameters along which BSC exist (as resonances with the vanishing width). For the decoupled shear mode in the single array, a relation between the material parameters and the Bloch phase of the wave is found, under which resonances have a nearly vanishing width (the width vanishes in the leading order of the dipole approximation). This shows that the width of resonances in this system has a global minimum in the space of parameters due to opposite contributions of the relative mass density and Lamé coefficients of the scatterers to the resonance width. This new scattering phenomenon does not exist in similar photonic or acoustic systems.
In Section 4, the scattering problem is solved for the double array with an arbitrary separation of the arrays and an arbitrary relative asymmetric shift (to break the reflection symmetry of the double array). The solution includes multiple open diffraction channels for all scattering modes. The analysis goes essentially along the same lines as given in Section 2, but it is technically much more involved than in Section 3. For the sake of technical simplicity, only the case of zero relative Lamé coefficients is analyzed in detail. It is proved that BSC exist only if the relative shift is either equal to zero or half a period of the arrays. Although the parity symmetry is broken in the latter case, another discrete symmetry is found that protects BCS. In each case, the necessary and sufficient conditions for BSC to exist in higher-order open diffraction channels are found. Spectral parameters of BSC are given in terms of group velocities of the elastic modes and their Bloch phases. The effect of evanescent fields on the spectrum of BSC is investigated. The main results here are that the frequency degeneracy of BSC with different parities is removed and symmetric BSC no longer exist when the distance between the arrays is below a certain threshold. Finally, explicit analytic solutions for BSC are given as the corresponding Siegert eigenstates in some special cases.
In the dipole approximation, the scattered field for any type of waves is determined by the so-called induced dipole moment of the scatterers. In a generic elastic system, the induced dipole moment depends on the induced elastic wave field and the induced stress tensor. So, the analysis in Section 3 and Section 4 requires an explicit form of the induced field and the induced stress tensor for each cylinder. They are found by solving the system of linear equations derived in Section 2 using normal traction boundary conditions on the surface of the cylinders and the Lippmann–Schwinger equation. All technical results needed for calculating coefficients in this system for each studied case have been moved to the Appendix A to separate the analysis of resonances and BSC from the in-part overwhelming and lengthy technicalities. Appendix A.1 contains a derivation of the Green’s function for the tensor Helmholtz operator describing elastic waves of a fixed frequency in isotropic media. Appendix A.2 is devoted to solving the Lippmann–Schwinger equation in the long-wavelength approximation. Appendix A.3 contains calculations of coefficients in the aforementioned system of linear equations for the induced dipole moments of the scatterers. The polylogarithm subtraction method [30,31] for Schlömilch series of derivatives of Hankel’s functions is modified and used, in combination with the Poisson summation formula, for this purpose.
2. Lippmann–Schwinger Formalism for a Single and Double Array of Elastic Cylinders
2.1. Formulation of the Problem
The governing equations for the propagation of disturbances in elastic isotropic media are as follows [9]:
where is the displacement vector field at a point r and time t, the double dot denotes the second partial derivative with respect to time, is the mass density, ∇ is the gradient operator in space, and is the stress tensor in the medium. It is a symmetric 2-tensor that depends on Lamé coefficients denoted by and , and the displacement field as
where I is the unit tensor. Here and in what follows, the conventional tensor notations are used, e.g., and (Einstein’s rule of summation over repeated indices is always implied, unless stated otherwise), and the superscript T stands for transposition of tensor indices. For homogeneous media, , , and are constant, and Equation (1) admits plane-wave solutions with three polarization modes. The two transverse polarization modes are known as shear waves, and the longitudinal mode describes compression waves. The transverse and longitudinal waves propagate with different speeds, denoted by and , respectively, that depend on the media parameters. Any inhomogeneity in the media causes scattering of the elastic waves.
An inhomogeneity is described by the relative mass density and Lamé coefficients, denoted by . For example, , where is the constant mass density of the background media so that only in regions where the mass density differs from that of the background media, and similarly for . A solution to the scattering problem is sought in the form , where is the frequency of incident and scattered waves. The amplitude is then shown to satisfy the following equation:
The relative Lamé coefficients and vanish in the bulk. They are piecewise continuous, having jump discontinuities at the boundary of a region occupied by the scattering structure. A solution is sought as a regular distribution that is required to be continuous everywhere and has a continuous normal traction where is a unit normal to the boundary of . These conditions result from the continuity of the elastic displacement and mechanical equilibrium of the scattering structure, respectively. The normal traction boundary condition induces a coupling of different elastic polarization modes at the interface separating two elastic media. A standard approach to solving the problem is to convert the differential equation into an integral equation using a suitable Green’s function for the operator , whose solution is then analyzed by methods for integral equations (e.g., von Neumann series).
Here, the scattering problem is studied for the following elastic structures: The first structure consists of one array of infinite parallel cylindrical defects that are periodically arranged in a plane. The second structure has two such arrays separated by a distance, as depicted in Figure 1. Finally, the structure with two parallel arrays shifted relative each other is studied. In the latter case, the parity symmetry in the direction normal to the arrays is broken.
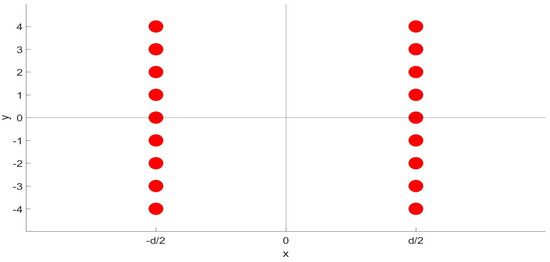
Figure 1.
The cross section of the double array of cylinders in a plane perpendicular to the cylinders. The cylinders are infinite and parallel to the z axis. The figure displays the cross section of the cylinders in the plane. The x axis is horizontal, and the y axis is vertical (the arrays are periodic in this direction). The length is measured in units of the period of the array. The origin is set so that the system is symmetric under the reflection . The axis of each cylinder is parallel to the z axis and passes through the points in the plane, where d is the distance between the arrays, n ranges over all integers, and and are unit vectors parallel to the coordinate axes.
The systems have a translational symmetry in the direction parallel to the cylinders and are periodic in the direction perpendicular to the cylinders. The cylinders are set parallel to the z axis. Due to the translational symmetry along the z axis, the field u is independent of the variable z so in what follows. The wave vector of an incident plane wave lies in the plane. So, one shear mode is polarized along the z axis, and the vector field u of the other shear mode and longitudinal mode lies in the plane. The former and latter modes are called out-of-plane and in-plane modes, respectively. The solution is the sum
of the scattered wave and an incident wave that satisfies the associated homogeneous equation
Equation (3) has three linearly independent plane-wave solutions of the form , where and are components of the wave vector for a wave polarized parallel to a unit vector . The polarization vector is perpendicular to the wave vector for the shear modes (as the field is divergence free in this case) and parallel to it for the compression mode. The components of the wave vector are not independent and must satisfy the dispersion relation for each polarization mode , where and are the magnitudes of wave vectors of the longitudinal and transverse modes, respectively. Thus, each independent solution is uniquely determined by the polarization state and a pair of spectral parameters , whereas is determined by the dispersion relation for each polarization mode. The necessity to choose as an independent spectral parameter will become clear shortly, when the Bloch periodicity condition is introduced for periodic scattering structures (see Equation (5)). So, an incident wave is chosen to be a superposition of the above three independent plane-wave solutions to (3). It is convenient to write it as the following sum of a longitudinal (compression) wave, a transverse (shear) wave polarized in the plane, and a transverse (shear) wave polarized parallel to the z axis:
where is a unit vector parallel to the z axis, and are scalar amplitudes of the in-plane longitudinal and transverse incident waves, respectively, is the scalar amplitude of the out-of-plane mode, and and are the x components of the wave vectors for the transverse and longitudinal modes, respectively. They are positive solutions to the dispersion relations for each polarization mode so that the incident wave propagates in the direction of increasing x.
Similarly, in the asymptotic region , the scattered wave is a superposition (4) of plane waves with the parameters and unknown scalar amplitudes of three independent polarization modes. The components and in the scattered-wave modes are positive and negative roots of the dispersion relation for the transmitted () and reflected () waves, respectively. To solve the scattering problem, one has to find the scalar amplitudes of reflected and transmitted waves for each polarization mode and the corresponding in terms of scalar amplitudes of the incident wave and its spectral parameters.
The system in question is periodic along the y axis with a period of a unit length. Therefore, any solution must satisfy the Bloch condition
This is the reason for choosing as an independent spectral parameter of the incident and scattered waves. In what follows, the parameter will often be referred to as a Bloch phase. It follows from (5) that can change only by integer multiples of in the scattering modes, that is, , where n is an integer. The range of n is determined by the condition that the corresponding roots , , of the dispersion relation are real:
where
As a consequence, each incident wave can scatter into finitely many open diffraction channels, defined by (6). The number of open channels depends on . The radiation continuum for each mode is defined as . It consists of intervals in which one or two or three (and so on) diffraction channels are open.
Owing to the Bloch condition, the scattered field should be sought in the strip D: and . The scattered wave (in any open diffraction channel) must carry an energy flux away from the array in the asymptotic region and, hence, satisfy the Sommerfeld radiation condition
where labels the three polarization modes, and is the positive root of the dispersion relation (6). Therefore, the scattered elastic field that satisfies the Bloch and Sommerfeld conditions must be the following superposition of plane waves in the far-field region:
where the sums are taken over open diffraction channels for each polarization mode defined by (6), and the signs ± are taken for reflected ) and transmitted ) waves. The scattering amplitudes are functions of the spectral parameters of the incident wave and also depend on geometrical and material parameters of the system. The objective is to calculate these amplitudes.
If the incident wave is set to zero, , then there can still exist solutions that satisfy the Bloch and Sommerfeld conditions that are localized, meaning that they are square integrable in the region D. They are called bounded states. The square integrability implies that bound states cannot have an oscillatory behavior with a constant amplitude in the far region as propagating waves. They are stationary states (or standing waves), and their energy is not carried away from the structure in which they are localized. This also implies that bound states are decoupled from the radiation continuum and, hence, cannot be excited by an incident wave. If the frequency of bound states lies below the radiation continuum, then they are regular bound states. If lies in an open diffraction channel, then such solutions are known as bound states in the radiation continuum (BSC). BSC do not generally exist for any values of physical and geometrical parameters of a scattering structure. If the scattering amplitudes exhibit resonances, or poles in the complex plane with a positive imaginary part (the width of resonances) and with the real part in an open diffraction channel, then the existence of BSC can be detected by analyzing the resonance width as a function of physical and geometrical parameters. If the width can be driven to zero by varying these parameters, then there exist BSC as resonances with the vanishing width.
Physically, an excited resonance decays in time that is reciprocal of the resonance width, and, hence, the same time is needed to excite the resonance by an incident (incoming) wave. The resonance initial energy is carried away to the asymptotic region by outgoing radiation waves whose frequency is determined by the real part of the pole. If the width can reach zero at certain values of the parameters, then the resonant state can live an infinitely long time and becomes a stationary (bound) state. It also decouples from the radiation continuum in the limit of the zero width.
In what follows, the resonant properties of the scattering amplitudes will be investigated to show that a double array can have resonances in open diffraction channels whose width vanishes for certain material, geometrical, and spectral parameters, and the corresponding BSC will be found. The key difference between BSC analytically found in similar electromagnetic systems is that elastic BSC for the in-plane modes do not have any particular polarization because the longitudinal and transverse polarization modes are coupled through the normal traction boundary condition at the cylinders. If one makes an analogy with Maxwell’s theory, then such elastic BSC correspond to electromagnetic BSC in which two transverse polarization modes are coupled in the scattering system and have different dispersions (like in anisotropic background media).
2.2. Lippmann–Schwinger Equation
Suppose that the scatterers are homogeneous so that the relative mass density and Lamé coefficients are constant in the region occupied by the scatterers. Then, , , and are piecewise constant and vanish outside of the scatterers. The differential equation for the elastic field satisfying the Sommerfeld condition is proved to be equivalent to the Lippmann–Schwinger integral equation
where is the Green’s function for the operator that satisfies the Sommerfeld radiation conditions, and the star stands for the convolution defined in the distributional sense. It is shown in Appendix A.1 that
where , , and is the Hankel function of the first kind. It is easy to see from the asymptotic behavior of the Hankel functions for that the Green’s function satisfies the Sommerfeld condition (8). For a small r, , and, hence, the singular distributional part of second partials is canceled due to so that is locally integrable. Thus, the Green’s function is a regular distribution defined by a smooth function for . The support of the region occupied by the scatterers is not bounded in the plane, and, hence, the existence of the convolution should be investigated. It was shown in [2] that the convolution exists in the sense of distributions for any regular tempered distribution f that satisfies the Bloch periodicity condition and has support on bounded non-overlapping scatterers. Owing to the existence of the convolution, its derivatives can be applied to either of the distributions in the convolution in the last term on the right-hand side of (9).
If r in (9) is restricted to support the scatterers, e.g., , where is defined in the caption of Figure 1 and R is the radius of cylinders, then the equation is a Fredholm-type integral equation whose solution defines the scattered field within the scattering structure. This field is induced by an incident wave. By (9), the induced field defines the scattered field outside the scattering structure. In particular, the scattering amplitudes are obtained from (9) by taking the limits . Here, the said integral equation is solved in the leading order of the long wavelength limit, when the wavelength of the incident wave is much larger than the radius of cylinders . It is proved in Appendix A.2 that, in this approximation, the elastic field and the corresponding stress tensor can be assumed to have constant values across each scatterer, that is, and , where are the positions of the scatterers. Therefore, the scattered wave is a superposition of outgoing waves produced by point sources of strength and located at the positions of the scatterers:
where is the area of the cross section of each cylinder and for any n. Thus, the scattering problem is reduced to finding the induced field and the induced stress tensor on the scatterers.
A peculiarity of the problem is that, if one sets , , and for in integral Equation (9), then it gives a relation between two unknowns, and , that is not sufficient to uniquely determine them, in full contrast to electromagnetic or acoustic scattering problems in the same approximation (for small scatterers) where the induced field on the scatterers uniquely determines the scattered field. The second equation comes from the normal traction boundary condition in elasticity theory. The implementation of this condition turns out to be a tedious technical problem.
2.2.1. A Solution for a Single Array in the Long-Wavelength Approximation
Consider first the single array case. The centers of the cylinder are at , where n ranges over all integers. Owing to the Bloch condition, . Therefore, the induced sources are determined by unknowns and . Here and in what follows, , , and stand for the constant values of , , and on the scatterers. In Appendix A.2, it is proved that if the wavelength is much larger than the radius of cylinders, then the convolutions in the Lippmann–Schwinger equation can be calculated in the approximation of and by constant values on the scatterers so that Equation (9) is reduced to
Equation (12) shows that the induced field and stress define the strength of point sources for the scattered field. To find them, first, is calculated by substituting (12) into (2). Next, it is demanded that the field and the normal traction are continuous across the boundary of each cylinder . In the long wavelength limit (), the continuity conditions are equivalent to continuity of and the stress tensor at .
A substitution of (12) into (2) yields for
where is the stress tensor of the incident wave. By the Bloch condition, . So, it is sufficient to satisfy the continuity conditions only at . Let
This limit is to be calculated in the leading order of a small parameter of the long wavelength approximation. For example, owing to the local integrability of ,
in the leading order of , where the series converges by Abel’s test.
If the relative Lamé coefficients vanish, then and is found by setting in (12) so that the induced sources are determined only by . If , then the limit of the derivatives of must be calculated. Derivatives of Green’s functions are not regular distributions, and a calculation of the limit is not a straightforward task that can be accomplished by a term-by-term differentiation of the series (13) [39]. In Appendix A.3, and are proved to exist and their explicit form is found in the leading order of . So, taking the limit in (12) and in (14), the continuity conditions for the field and stress tensor yield the following system of linear equations for the unknowns and :
where and are the incident field and its stress tensor at , respectively. No summation over i is implied in . The system (16) and (17) define the induced sources of scattered elastic waves. It is drastically different from similar electromagnetic or acoustic cases due to the normal traction boundary condition that is unique to elastic theory. The additional unknown also makes an analysis of the system technically more involved when the relative Lamé coefficients are not zero.
Equations (16) and (17) can be cast in the following matrix form:
where the column vectors are defined by
It follows from the explicit form of , , and given at the end of Appendix A.3 that the matrix is block diagonal. Its blocks are
and there is a block, . Equation (18) is decoupled into three matrix equations and one scalar equation associated with the block structure of :
By Equation (12), the S-matrix coefficients are given by linear combinations of the components of ; hence, the poles of the S-matrix are determined by analytic properties of the inverse of in the complex plane. In particular, the positions of bound states and resonances are roots of the equation . An analysis of this equation is given in Section 3.
2.2.2. The Double Array Case
For a double array, the origin of the coordinate system is set so that the system is symmetric under reflection in the plane, , as shown in Figure 1. In the long wavelength approximation, the convolution in the Lippmann–Schwinger equation is computed in the same way as in the single array case using the values of and at the centers of the cylinders. The Bloch condition shows that these values are determined only by their values at , that is, by and .
Let be the parity index. Then, by Appendix A.2 (see also (11)), the Lippmann–Schwinger Equation (9) is equivalent to
in the long-wavelength approximation, where are defined by (13). The unknowns and are found from the continuity of and at , just like in the single array case. The field (23) is used to calculate the stress tensor given in (2). Then, the limits are taken in (23) and (2) to obtain the following system of equations:
where , and is the stress tensor for the incident field at . Each of the above equations stands for two equations: one for the top parity indices in each term and another for the bottom parity indices in each term.
Equations (24) and (25) can be cast in the matrix form (18), where the vector has 16 components that are 16 unknowns, and , is a 16-vector with components that are the corresponding components of and , and the matrix becomes a matrix. The pole structure of the scattering matrix is determined by analytic properties of the inverse of .
2.3. Resonances and BSC
To find scattering resonances and BSC in the studied systems, one should find square integrable solutions to the associated homogeneous Lippmann–Schwinger equation when . The square integrability is understood in the x direction because any solution is Bloch periodic in the y direction. This is an eigenvalue problem where plays the role of the spectral parameter. The eigenfunctions are known as Siegert states. They exist at generally complex-valued solutions to the equation . If is a root, then the associated homogeneous system of linear equations for the induced sources (either (16) and (17) or (24) and (25) with ) has a non-trivial solution. This solution is to be substituted into (12) (for the single array case) or into (23) (for the double array case), and the square integrability of the obtained field is to be verified.
If the real part of a root lies in an open diffraction channel, then defines the position of a resonance in the scattered field (or the resonant frequency ), and the imaginary part determines the width of the resonance. In this case, the equations for the induced sources have a unique solution for any incident wave () of a frequency near because the matrix is not singular for a real . The amplitude of the scattered field (12) or (23) exhibits a typical Lorentzian profile as a function of the frequency due to the complex pole at coming from the inverse of .
A Siegert state associated with a real root that lies in an open diffraction channel is a Bound State in the Continuum. By construction, it is a standing-wave solution to the elastic-wave equation that is localized in the vicinity of the scattering structure and whose frequency lies in the radiation continuum (in an open diffraction channel). In this case, the matrix is singular at and a non-trivial solution for the induced sources exists without any incident wave, . Naturally, the induced sources are determined up to an arbitrary factor in this case, which can be fixed by normalizing a BSC solution, e.g., by demanding that a BSC solution has a certain elastic energy per one period of the structure. So, the objective is to find the conditions on geometrical and material parameters under which the studied systems have resonances with the vanishing width in open diffraction channels. Technically, the problem is reduced to solving the equation and identifying the roots corresponding to Siegert states with desired properties.
3. The Fabry–Pérot Approximation
Following the strategy outlined in Section 2.3, the first objective is to solve the equation in the complex plane of . Unfortunately, this task is not analytically tractable for general parameters of the theory and only numerical methods apply. However, if the equation can be solved for a single array, either analytically or numerically, then the equation for the double array can be studied analytically in the so-called Fabry–Pérot approximation that was used to find electromagnetic and elastic BSC in [3,39], respectively. In this approximation, the distance d between the arrays is assumed to be much larger than the wavelength of the incident wave . If the distance between the arrays is large enough, then the scattering on the double array is dominated by the resonances of each array that are coupled only via propagating modes, while evanescent fields generated by each array can be neglected in the vicinity of the other array because evanescent fields decay exponentially with increasing distance from the array. The latter follows immediately from the explicit form of given in (A4). So, in this approximation, each array emits a wave that also scatters on the neighboring array so that the outgoing wave in the asymptotic regions is a superposition of multiply scattered waves like in a Fabry–Pérot interferometer. If, in addition, the scattering on a single array is proved to be resonance dominated (a background scattering can be neglected), then the amplitudes of the scattered waves are uniquely determined by the position and width of the single array resonance just like in the partial wave summation for a Fabry–Pérot interferometer. Let us investigate resonances and BSC in the double array using this approximation.
3.1. Spectral Range and the S-Matrix
The first objective is to calculate the scattering matrix for the single array. Throughout this section, the analysis is carried out in the case where each of the elastic modes has only one open diffraction channel [39]. The case with an arbitrary number of open diffraction channels will be studied in Section 4. Recall that the diffraction thresholds for each mode are defined by with n being an integer. So, the range of spectral parameters is restricted as
where (see, e.g., [9]), and the upper bound on is necessary so that the second open transverse channel lies above the first longitudinal channel, . Due to the parity symmetry , can be taken as strictly positive. In what follows, it is also assumed that is bounded from below by some positive threshold value in order to keep the diffraction thresholds from merging; for a below this lower bound, the problem becomes indistinguishable from normal incidence. The normal incidence will be discussed in Section 4.3.
Let us define the S-matrix. It is assumed that an incident plane wave is propagating in the direction of increasing x and has the form (4). In the asymptotic region , the solution to the Lippmann–Schwinger equation must have the form
where are the amplitudes for the transmitted in-plane modes, and is the amplitude of the transmitted out-of-plane mode. Similarly, when , the solution reads
where the superscript R denotes the amplitudes of the corresponding reflected waves.
The transmission and reflection amplitudes are linear combinations of the incident amplitudes and with the coefficients being the S-matrix elements. They can be extracted from the solution to the Lippmann–Schwinger Equation (12) in the limit . In this limit, only the terms corresponding to open diffraction channels in the Bloch wave expansion (A4) of must be retained because the terms corresponding to closed diffraction channels decay exponentially when . The result for two open diffraction channels (one transverse and one longitudinal) is given by the following:
where (the cross section area of the scatterers, ). Comparing this expression with the stated asymptotic form of the solution, it is inferred that, for the in-plane modes,
and, for the out-of-plane mode,
where
Note that the S-matrix is block diagonal. The in-plane and out-of-plane modes are decoupled.
The energy carried by an elastic wave, which is described by a solution to (1), across an orientable surface per unit time is given by the flux integral of the vector field
over the surface, where the star * stands for complex conjugation. In particular, the energy flux carried by a plane wave in a given polarization mode across a unit area normal to the direction of propagation is proportional to , where is the group velocity and is the amplitude of the wave. Using the asymptotic form of the scattered field, the energy transmission and reflection coefficients are obtained:
So, any pole in the complex plane in the S-matrix elements appears as a resonance in the energy reflection and transmission coefficients as functions of the incident wave frequency.
3.2. Resonances and BSC in the Out-of-Plane Shear Mode
As noted, the scattering matrix for the out-of-plane mode is identical to the scattering matrix for the analogous electromagnetic system studied in [2,3] if . Here, the effects of non-zero relative Lamé coefficients are investigated. The main result is that, in contrast to in the electromagnetic case, a single array can have resonances with the vanishing width in the long-wavelength approximation that occur due to a fine-tuning of mass density and Lamé coefficients. However, whether this assertion holds beyond perturbation theory still remains to be seen. In addition, the existence of BSC in a double array will be reexamined for the out-of-plane mode in the case where are not zero.
3.2.1. The Single Array Case
Solving the system (21) and (22) and substituting the solution into (32), the reflection coefficient for the out-of-plane mode is found for a single array:
Let us prove that the single array has a resonance near the diffraction threshold and extract the standard Breit–Wigner form of the reflection coefficient near the resonance. To this end, consider the following parameter curve:
where is a fixed complex number. Since the real part of is close to the diffraction threshold, for . Throughout the rest of the paper, this parameter curve will be commonly exploited in order to locate BSC and resonances. The focus will be on the oblique incident case. For small scatterers, this sets a lower bound on . As noted in Section 3.1,
because below this bound, and the solution becomes indistinguishable from the normal incident case, , to the leading order in . In other words, the diffraction thresholds “merge” and the following analysis requires a modification (see Section 4.3).
Zeros of the determinant in the complex plane define poles of the reflection coefficient. They are to be found in the leading order when while is fixed. To accomplish the task, the explicit forms of , , and given at the end of Appendix A.3 are used to expand them to the leading order:
where the functions are analytic. By the analyticity of the s, their contribution to zeros of can be neglected in the said limit. For this reason, the explicit form of the s is irrelevant for what follows and is omitted. Next, the determinant and the reflection coefficients are also expanded to the leading order by means of the above equations. After some algebraic transformations, the reflection coefficient is reduced to the Breit–Wigner form
where and
is the x component of the wave vector for the open transverse channel.
The pole describes a scattering resonance if so it is necessary that . An interesting feature of resonances in this system is that the mass density and Lamé coefficients contribute to the width with opposite signs. In contrast to the analogous electromagnetic problem (single array) [2], here it seems possible to bring the width to zero by fine-tuning the material constants. This can be carried out in two ways. First, in the leading order of the approximation if . However, the corresponding solution to the Lippmann–Schwinger equation is not square integrable and, hence, unphysical (it has infinite energy). Indeed, in the limit and , the asymptotic form of the solution is given by
This function is square integrable in x for a finite but its squared norm diverges in the limit . Therefore, this solution cannot correspond to a physical state.
Second, also occurs along the parameter curve
In this case,
and the solution has the form
where , denotes the sign function. It is square integrable (normalizable) and hence is a physical solution describing BSC.
Unfortunately, it is difficult to prove whether there exists a curve in the space of parameters along which in all orders of perturbation theory, which implies that a single array supports BSC that occur due to a fine-tuning of the mass density and Lamé coefficients. It should be emphasized that this state exists only if because, in the leading order,
This implies that the relative mass density must be positive, , as follows from the parameter curve (37), and that .
The observed state gives some insight into the competing effects from variations of the density and Lamé coefficients. In the Lippmann–Schwinger equation , the vector field can be interpreted as the source for the outgoing wave induced by an incident wave. Its z component is given by
This shows that the vanishing width along the curve (37) in the parameter space can be explained as a perfect destructive interference (in the leading order of the dipole approximation) of outgoing waves produced by two terms in the source density, one of which is proportional the relative density and the other to the relative shear Lamé coefficient . This feature is unique to the elastic scattering on a single array of cylinders, and it does not exist for the similar electromagnetic systems studied earlier [3]. From a practical perspective, this artifact can be used to design arrays of elastic defects that have extremely narrow resonances that cannot be achieved in the scattering of electromagnetic and acoustic waves on similar arrays.
3.2.2. The Double Array Case
The reflection coefficient (35) shows that the background scattering in this channel is negligible as compared to the resonance part. So, the scattering is resonance dominated in the leading order of . It is now not difficult to prove that the double array supports BSC at least in the Fabry–Pérot approximation, where . Just like in the electromagnetic case [3], in this approximation, the reflection coefficient for the double array can be computed by the partial wave summation as in a Fabry–Pérot interferometer (neglecting the effects of evanescent fields of each array):
Using the Breit–Wigner form of in the vicinity of a resonance pole, the poles of are found:
The parity index corresponds to even/odd parity states. If the distance between the arrays is tuned so that with being an integer (a large integer in the approximation used), then the width of one of the resonances vanishes and the width of the other doubles as compared to that for the single array. In this case, the position of the resonances is . By construction, lies in the open diffraction channel for the out-of-plane mode, and, hence, the resonance with the vanishing width is a Bound State in the Continuum.
3.3. Mixed Polarization BSC for Arbitrary Lamé Coefficients
It is shown that the in-plane scattering modes are coupled through the normal traction boundary condition. The scattering matrix is calculated for the single array and given in (27)–(30). Owing to the coupling of the shear and compression modes, the reflection and transmission coefficients become the reflection and transmission matrices. For example, the reflection matrix is defined by
where the components on the right-hand side are given in (29) and (30). The transmission matrix is defined similarly. Suppose there are two identical arrays, as shown in Figure 1, at a distance d from one another. If the distance is large enough, then the reflection matrix of the double array can be computed by the summation of all reflected waves produced by multiple bouncing between the arrays. Since the shear and compression modes are coupled, and each mode has its own dispersion relation, the conventional Fabry–Pérot summation for a scalar wave needs a modification.
3.3.1. A Fabry–Pérot Interferometer with Multiple Coupled Wave Modes
Suppose that two interfaces of a Fabry–Pérot interferometer are identical and each interface can can mix N independent modes of an incident wave of frequency that are labeled by index . Each mode has a group velocity . Suppose that the distance d between the interfaces is much larger than , where . In this case, the evanescent fields produced by each interface can be neglected in the vicinity of the other interface, and reflection and transmission fields for the combined structure are determined only by the multiple scattering of propagating waves on each interface. Let the x axis be normal to the interfaces and be the x component of the wave vector of the ith mode. If and are reflection and transmission matrices of the interface, then the reflection and transmission matrices of the combined structure are obtained using the partial wave summation
where is the identity matrix and is a diagonal matrix,
The pole structure of the reflection and transmission matrices of the combined structure are defined by zeros of the determinant
in the complex frequency plane.
Next, suppose the interface is a resonator. This means that the reflection matrix has a pole at , where . Near the pole, the reflection matrix can be written in the form
where is the residue matrix and the matrix is analytic and describes a background scattering. If the background scattering can be neglected and the resonance is sufficiently narrow ( is small enough) that can be approximated by its value at , then Equation (38) is simplified to
The left-hand side is a polynomial of degree N in the variable . Therefore, it has N complex roots, , , which define the positions of new poles, and . So, the combined system has resonances in general. Some of them can become BSC if their widths can be driven to zero by tuning parameters of the system, e.g., the distance d.
3.3.2. Resonances in the Coupled Shear and Compression Modes
For the in-plane modes in the elastic double array, , and the corresponding quadratic Equation (40) is easy to solve:
Recall that this solution is justified under two assumptions. First, the scattering is resonance dominated, and, second, the resonance is sufficiently narrow. These assumptions are verified below by a direct calculation of the reflection matrix in the leading order just like for the out-of-plane mode in Section 3.2.1. In addition, in Section 3.4, it will be shown by numerical studies that do not rely on any perturbation theory approach that all the assumptions made in the process of deriving (41) are justified for the in-plane modes.
Let us calculate the reflection matrix of the in-plane modes for the single array, reduce it to the Breit–Wigner form (39) to find the residue matrix , and extract the resonance position and width . In doing so, one can also verify the aforementioned hypotheses for validity (41) in the leading order of . Then, Equation (41) is solved to find the width and positions of resonances in the double array. Finally, a possibility to drive the width to zero by a fine-tuning of the geometrical and material parameters can be investigated. It is assumed that ; otherwise, no bound states of any kind can be formed. To find the reflection matrix, Equations (19) and (20) must be solved for and the stress . The solutions are substituted into (29) and (30), and the matrix elements of the reflection matrix are extracted. All calculation should be carried out in the leading order in . Technically, the process is similar to the derivation of the reflection coefficient for the out-of-plane mode given in Section 3.2.1, and the difference is that the reflection matrix has four elements, not just one.
First, it should be noted that the matrix in (19) is regular,
in the frequency range defined in (26), and, hence, the inverse is analytic in the complex plane and so and are obtained by solving (19). The relation (42) is proved by using the expansions of , , and given at the end of Appendix A.3 to calculate the components of the matrix to the leading order. Therefore, the induced sources and can only contribute to the background scattering to the leading order. The resonant scattered wave is generated by and , obtained by solving (20). The result reads
The above equations are the analog of the first three equations in Section 3.2.1.
The next objective is to investigate the pole structure of , which is determined by zeros of . As in Section 3.2.1, the parameter curve defined in (33) is used to study the analytic properties of the reflection matrix for a small . This goal is achieved by the same technical method as in Section 3.2.1. The components of the matrix are calculated using the asymptotic expansions given at the end of Appendix A.3. The equation is solved in the leading order in to show that the reflection matrix has a pole at where
and is defined in (36). So, the width of the resonance , which means that the resonance is extremely narrow. Just like in (35), the reflection matrix is also dominated by the pole contribution and the background scattering is of order . The residue matrix in the leading order is found to be
So, the use of (41) is justified in this approximation. It also follows from the above result that the width can vanish if in the single array case. However, the corresponding solution to the Lippmann–Schwinger equation is not normalizable and should be discarded as non-physical as in Section 3.2.1. In addition, it is required that so that the width is strictly non-negative. This condition is fulfilled for all physical materials as far as we know (as long as , as stated earlier) [40,41].
Finally, plugging the residue matrix into Equation (41), the poles (resonances) of the reflection matrix for the double array can be determined. The widths of the resonances are given by
where the signs ± correspond to even and odd parity, as before. One can see that the condition for the existence of BSC is given by
where N and M are either mutually even integers for even parity or mutually odd integers for odd parity. It should be noted that when the even/odd parity state turns into a Bound State in the Continuum, the odd/even parity state becomes a resonance with the double width, much like in the electromagnetic case [3].
Elastic BSC are robust under variations of elasticity parameters because the quantities (36) and (46) in the condition (47) depend only on , determined by the background media and the spectral parameters and . So, with a suitable choice of the spectral parameters and the distance between the arrays satisfying (47), a standing-wave solution (BSC) localized in the vicinity of the double array is always guaranteed to exist for any positive relative mass density and any physical values of Lamé coefficients. The elastic BSC are formed by the same mechanism, which is a destructive interference in the asymptotic region for both the shear and compression modes. Since the modes have different speeds, the simultaneous destructive interference cannot be achieved only by tuning the distance between the arrays. The condition (47) requires that the y component of the wave vector of each mode is also tuned to achieve the desired destructive interference for both the modes.
For the frequency range (26) (two open diffraction channels), the results do not depend on the longitudinal Lamé coefficient . The effect of this parameter can only be seen near the longitudinal diffraction thresholds, which requires an analysis of higher open diffraction thresholds. An analysis of multiple open channels and intermediate distances is even more technical. However, special cases will be analyzed in Section 4.
3.4. Numerical Analysis of the Resonance Dominance
The perturbation theory developed in the previous section shows that the scattering of the in-plane modes is resonance dominated, and the background scattering can be neglected in the leading order. Here, the problem is investigated numerically without using perturbation theory. The objective is to show that the background scattering in the exact theory has little effect and the conclusions about elastic BSC based on (41) remain valid beyond perturbation theory. To avoid unnecessary technical complications, the case is considered. Yet this parameter plays a similar role to and does not affect anything relevant for our objective and in the physics of the system (as will be shown below).
If , and the scattered wave is generated by . Equations (19) and (20) are reduced to
The exact reflection matrix is obtained in the same way as in the previous section:
where the matrix elements read
Let us show that terms proportional to describe the resonance scattering while those proportional to contribute only to the background scattering by investigating the values of along the parameter curve (33). Using the series representations for and given in the end of Appendix A.3,
where and is analytic in and as . Its explicit form reads
where and . Therefore,
Equations (51) and (52) show that the pole of the exact scattering matrix is a pole of and obtained from the equation
In perturbation theory, when , the width is determined by the imaginary part of in the leading order. Therefore,
Next, the perturbation theory is compared with the exact result computed numerically. The exact expression for the resonance factor is computed and plotted in Figure 2 (solid black line) for the parameters specified in the caption. The obtained profile is numerically fitted into a standard Lorentzian profile where with the position of the pole and its width being the fitting parameters (dashed red line). As one can see, the exact resonance factor in the scattering matrix is almost indistinguishable from the standard Lorentzian profile. So, the scattering is indeed resonance dominated. The blue dotted line shows the Lorentzian profile with the position of the pole and its width calculated by the perturbation theory in the leading order in for the same values of the parameters. The relative error of the perturbation theory in the real part of the pole is and in the width it is for the material and geometrical parameters specified in the plot.
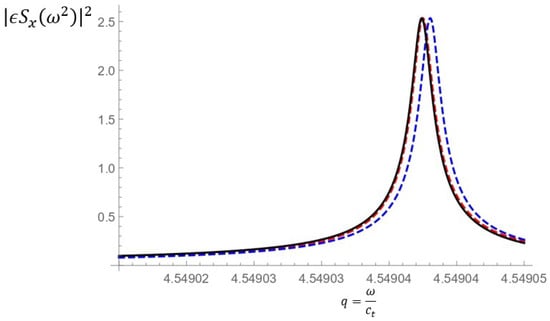
Figure 2.
Plot of vs. q, where for the parameters = (1.73405, 0.001, 29,880, 0.280, 0.59915) (black solid line). The red dashed line corresponds to a numerical Lorentzian fit. The optimal fitting parameters are found to be . The blue dotted line corresponds to the result of the perturbation theory where are computed to the leading order.
It is noteworthy that the distance d used in Figure 2 is much larger than the period (). This is necessary in order to eliminate the effect of evanescent fields and compare the exact results with the theoretical analysis in the Fabry-Perrot approximation. This also implies that evanescent fields decay very slowly with increasing when is small. They decay exponentially but . Therefore their effect on the spectrum of BSC should be significant for d ranging from 1 to in units of period. This is indeed the case as shown in the next section.
4. Asymmetric Double Array
An analysis of resonances in the in-plane polarization modes for a periodic double array of elastic scatterers in the Fabry–Pérot approximation was first presented in [39] in the case of one open diffraction channel for each mode. The major simplification in this limit is that the effect of evanescent fields is totally neglected. From the technical point of view, all terms in the series (A4) that decay exponentially as are neglected, which is reasonable when . On the other hand, it is also known that evanescent fields can have a drastic effect on the spectrum of BSC in similar photonic structures [2]. Here, this effect will be investigated. Moreover, no restriction on the number of open diffraction channel will be imposed. The scattering problem will also be solved for a general double array system in which the single arrays are shifted relative to each other so that the parity symmetry is broken. Necessary and sufficient conditions for the existence of BSC will be found and analyzed.
Consider two periodic identical arrays at a distance d such that one array is shifted parallel relative to the other by a distance so that the centers of the cylinders are at
with n being an integer. The scattering problem for has the same solution as that given in (23), where the sources and are solutions to the system (24) and (25) if are defined by
In addition, when solving the system, the exponentially decaying terms in the tensor (A4) and its partials cannot be neglected for to include the effect of evanescent fields. As before, BSC are determined by non-trivial solutions to the associate homogeneous Equations (24) and (25) in any open diffraction channel, that is, for . The number of open channels is not restricted.
Unfortunately, an analysis for general Lamé coefficients cannot be performed without substantial numerical assistance and will not be presented here. However, a special case can be studied analytically. As explained above, . A further technical assumption is that the lowest closed diffraction channel is transverse. Its threshold is denoted by for an integer N, and, similarly, stands for the threshold for the lowest closed longitudinal diffraction channel for an integer M so that . As before, the scattering of in-plane and out-of-plane polarization modes is decoupled. For the out-of-plane mode, the problem is fully analogous to the electromagnetic counterpart studied in [2] and will not be discussed below in detail.
4.1. BSC for the In-Plane Modes
With , Equation (25) is identically satisfied (since the tensors vanish), and the homogeneous Equation (24) is simplified to
The equation is decoupled for and , as already noted. In what follows, the indices range over x and y (in-plane) components. Equation (55) can be reduced to two separate equations for and :
where for brevity. A non-trivial solution exists if and only if . It follows from (48) and (49) that the latter equation is reduced to in the leading order, or
BSC exist if (56) has a positive real root that lies in an open diffraction channel, that is, for , where is the continuum edge (the lowest frequency squared for all propagating modes in the asymptotic region for a given ). As before, solutions to (56) are sought along the parametric curve (33) where and is the frequency of the lowest closed (transverse) diffraction threshold. The real and imaginary parts of the left- and right-hand sides of (56) are to be expanded to the leading order along this curve. On the left-hand side of (56), the expansions (49) and (50) are used where and has the same form as in (50), in which the diffraction threshold is replaced by and the summation index in the second series cannot take the value N. On the right-hand side of (56), the necessary expansions are obtained by substituting into (A4), and then the latter is calculated in the leading order in :
where is defined in (7), , , and . Thus, to the leading order, the real part of (56) on the curve (33) is given by
Taking the square root of both sides in Equation (58), it is concluded that either or where is the root of the equation
By examining the graphs of functions and , where and , it is not difficult to see that each of the transcendental equations (59) has just one positive root. If the imaginary part of (56) is also satisfied when , then the values define the squared frequencies of two BSC. Equation (58) also shows that are independent of the shift in the leading order. In the next section, the BSC frequencies are obtained explicitly along with the corresponding square integrable solutions of the homogeneous Lippmann–Schwinger equation.
Let satisfy (58). Then, the leading order for the imaginary part of (56) reads
Using the explicit form of the function g, this equation can be reduced to
where denotes the range of n corresponding to open diffraction channels for the polarization mode . Since each term in the series is non-negative, the equation is satisfied only if
The system (61) is a generalization of the phase-matching condition (47) to the case where multiple diffraction channels are open for the in-plane modes.
First, it should be noted that evanescent fields have no effect on the phase conditions (61). The latterare determined only by spectral parameters of the propagating modes in open diffraction channels. Second, the system (61) can have solutions only if , which is possible if either or because . It is then concluded that BSC for the in-plane modes do not exist in a shifted double array if and . The conclusion holds for any separation d and any number of open diffraction channels. If the phase-matching conditions (61) are fulfilled, then frequencies of the BSC are given by the positive roots of (58) that are shown to exist. Thus, the frequencies of BSC depend strongly on evanescent fields. This effect will be investigated in detail in the next section.
In particular, consider the case and the spectral range specified by (26). Then, Equation (60) is reduced to and , which can be written in the form
where for (see (36) and (46)). When there is no offset, , and these equations are nothing but the phase-matching condition given in (47). The solutions with different signs correspond to BSC with even and odd parities. For , these conditions also have solutions for different signs, just as in the case of the symmetric array. However, the corresponding BSC have no specific parity in this case. Their explicit form is given in the next section.
4.2. The Effect of Evanescent Fields on the Spectrum of BSC
Solutions to (58) can be expressed in terms of the product log functions defined by
with n being an integer. Indeed, using the variable , Equation (59) is written in the form
The constant on the right-hand side depends on the number of open transverse diffraction channels. Let be the roots for each of these equations. In the limit , the root becomes negative and, hence, physically unacceptable, as follows from the power expansion of the denominator , while approaches . Let and , then
The graphs of in units of as functions of a dimensionless parameter are shown in Figure 3. By properties of , the root becomes negative if , and, hence, there exists only one bound state in the continuum corresponding to the root when the arrays are sufficiently close. For , there always exist two BSC for sufficiently small scatterers () whose frequencies are given by
The large distance limit corresponds to the Fabry–Pérot approximation which was discussed in the previous section for . In this case, , and there are two BSC with identical frequencies:
If , they coincide with the frequency (53).
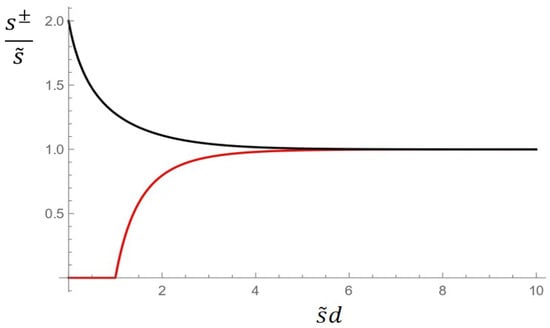
Figure 3.
Plot of vs. . The red (or lower) curve is the graph of , and the black (upper) curve is the graph of .
4.2.1. Explicit BSC Solutions
An explicit form of the solutions to the homogeneous Lippmann–Schwinger equation (Siegert states) is obtained from (23) by setting and (because the Lamé coefficients are set to zero in the case studied) and by substituting the strength of point sources that is a non-trivial solution of (55) where is a root of (56). The latter equation states that and it follows from (55) that . By the analysis in the previous section, a Siegert state becomes a bound state in the continuum only when or 0 (otherwise the phase conditions (61) cannot be fulfilled). Only one equation in the system (55) for is linearly independent and it can be written in the form
as follows from (57). If is taken as a root of (59), then the above equation is reduced to , and if , then . Only the phase difference in matters because an overall phase can always be absorbed into a normalization factor of the Siegert state. So, without loss of generality,
The corresponding field is given by
where are given in (A4) and k is defined by the dispersion relation where . In the asymptotic region ,
up to a phase factor. It is clear that this solution is square integrable and, hence, it is a bound state in the continuum consisting of two coupled polarization modes with different group velocities.
If , then the Lippmann–Schwinger equation is symmetric under the reflection . As a consequence, BSC can have even and odd parity. If , then the equation is symmetric under the affine transformation . Consider the operator
Then, it follows that, for any BSC solution, by the Bloch condition. Therefore, the eigenvalues of T are . The operator T and the integral operator in the Lippmann–Schwinger equation commute and, hence, share the same eigenfunctions. Using the explicit form (A4) for , it is easy to see that are eigenfunctions of T with eigenvalues .
The case is considerably more difficult, at least from an analytic perspective. However, in view of the previous results in Section 3.3, one can surmise that these BSC will persist through a continuity argument. A full analysis will require substantial computational aid and will not be given here.
4.3. Normal Incidence
It turns out that it is impossible to form BSC of mixed polarizations in the spectral range under consideration if is below the lower bound given in (34). This is due to the symmetry of the array structure; the and components of the field become the longitudinal and transverse mode, respectively, when . In this case, the transverse and longitudinal modes are decoupled, and the transverse transmission coefficient tends to unity in the leading order . Any transverse wave passes through the structure with negligible reflection. Therefore, it is impossible to confine a wave polarized along the vector . However, compression-mode BSC polarized along the vector still exist in this case. An explicit construction of these single-mode BSC is analogous to that given in [2] and, for this reason, is omitted here.
5. Conclusions
The scattering problem of elastic waves impinging on an array of periodically arranged parallel infinite cylinders was solved in the long-wavelength approximation. The shear mode parallel to the cylinders (the out-of-plane mode) was decoupled from the other shear mode and the compression mode (the in-plane modes) due to the translational symmetry along the cylinders. It was proved that the scattering matrix for the out-of-plane mode can have extremely narrow resonances. The width of resonances was shown to vanish under a certain condition of the Bloch phase and material parameters of the cylinders so that these resonances became BCS. However, this conjecture still requires a further investigation beyond the perturbation theory used in the present work. The effect is due to opposite contributions of the relative mass density and relative Lamé coefficients of the cylinders to the width of the resonances. This phenomenon does not exist in analogous electromagnetic and acoustic systems; it is unique to elastic systems and has never been reported before.
When the scattering system is made of two parallel arrays of cylinders positioned so that the system has parity symmetry in the direction normal to the arrays, it was shown in [39] in the Fabry–Pérot approximation that BSC with coupled shear and compression polarization modes exist for arbitrary elastic parameters of the scatterers in the case when only one diffraction channel is open for each mode. The required phase-matching condition for the destructive interference is achieved simultaneously for both the modes by tuning the Bloch phase of the wave modes in addition to the distance between the arrays. In the present work, necessary and sufficient conditions for the existence of BSC containing the coupled shear and compression modes were found for arbitrary geometrical and material parameters, an arbitrary number of open diffraction channels, and an arbitrary distance between the arrays to investigate the effect of evanescent fields. The conditions included an equation for frequencies of BSC and conditions of the Bloch phase of BSC that depend on the number of open diffraction channels. Due to the different group velocities of the shear and compression modes, they are more complicated than the Diophantine system found for BSC in higher-order diffraction channels for an analogous photonic system [2]. Examples of solutions were given. Evanescent fields were shown to have a drastic effect on the spectrum of BSC. In particular, BSC with even parity do not exist for separations between the arrays below a certain threshold, and, above this threshold, BSC with even and odd parities have different frequencies, in full contrast to the Fabry–Pérot approximation, in which they have equal frequencies.
The scattering problem was also solved for a double array in which the single arrays are shifted relative each other so that the parity symmetry in the direction normal to the arrays is broken. The existence of BSC was also analyzed for arbitrary separations of the arrays and any number of open channels. BSC were proved to exist only if the relative shift is half a period of the array. Although the parity symmetry is broken, in the latter case, there exists a new symmetry which is a combination of the parity transformation and periodic translations along the arrays. This symmetry protects BSC just like the parity symmetry protects BSC in the case with no relative shift of the arrays. The effect of evanescent fields was shown to be similar to that in the case of a symmetric double array. Explicit analytic BSC solutions were given for some special cases, and their spectral parameters were determined in terms of the Bloch phase and group velocities of elastic modes. BSC with the zero Bloch phase cannot contain coupled shear and compression modes. In this case, BSC can be formed just by the compression mode. The out-of-plane mode was also shown to have BSC in this case. If the relative Lamé coefficients are set to zero, then their spectrum and other properties are similar to those found in [2] for the corresponding electromagnetic system.
For the single array system, in the dipole approximation of the scattering theory, it was shown that the scattering is resonance dominated near each resonance for any scattering mode. In other words, the background scattering can be neglected in this approximation. The resonance dominance is crucial for the destructive interference mechanism for the formation of BSC in the double array scattering system. It was demonstrated numerically that the resonance dominance holds beyond the leading order of perturbation theory.
It is believed that the properties of the elastic BSC and new narrow resonances reported in this work can be used to design elastic wave guides or resonators with high-quality factors in a broad spectral range, especially in view of the fact that elastic systems supporting BSC can be designed using mechanical metamaterials (as materials with desired elastic properties). In particular, owing to a high sensitivity of the quality factor to the geometrical and physical properties of a resonating system, elastic BSC can be used to detect impurities in solids from variations of the density. The energy density of a high-quality resonance (near BSC) has “hot” spots where it exceeds the energy density of the incident wave by orders of magnitudes, which could facilitate studies of non-linear effects in solids.
Author Contributions
Writing—original draft, O.H.; Writing—review & editing, S.V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Green’s Function
The needed Green’s function is a fundamental solution for the differential operator ,
that satisfies the two-dimensional Sommerfeld radiation condition for outgoing waves as . The problem is solved by taking the Fourier transform of the above equation so that the Fourier transform of the Green’s function satisfies the following algebraic equation:
Since is an symmetric 2-tensor, its most general form is
where are tempered distributions that satisfy the scalar equations
where with labeling the transverse (shear) and longitudinal (compression) modes. Since are polynomials, any solution to the first equation can be written in the form
where the symbol stands for a prescription for regularizing the pole at in the k plane so that is a tempered distribution. A distributional regularization is needed because the reciprocal of is not locally integrable in the k plane. The regularization is not unique, but it is proved to exist for any polynomial. Then, any solution to the second equation can be written in the form
Its verification is based on the distributional equality
which, in turn, follows from the identity .
The regularization should be chosen so that the inverse Fourier transform of satisfies the Sommerfeld condition. This is achieved by using the prescription to shift the pole so that
The inverse Fourier transform of the above distributions reads
where and is the Hankel function of the first kind. By taking the inverse Fourier transform in (A1) and using (A2), the final expression (10) for Green’s function is obtained. Owing to the asymptotic form of the Hankel function, the Sommerfeld radiation condition is easily verified.
Appendix A.2. Lippmann–Schwinger Equation in the Long-Wavelength Approximation
Let us investigate the Lippmann–Schwinger Equation (9) for a collection of scatterers positioned at in the long-wavelength approximation. In this case, the functions and are not zero constants in each disk , and the small parameter is where is the frequency of the incident wave. To this end, let us calculate the convolution in (9) in this approximation using the Green’s function found in Appendix A.1.
Let be the characteristic function of that is the union of the disks . The disks are assumed to be non-overlapping. The convolution in the term of (9) that contains the relative mass density is reduced to evaluating the convolution
For any r that is not in , the Grafts formula is used to expand the Hankel function,
and to evaluate the integrals so that
The advantage is that the Bessel functions are analytic so that the behavior of the integrals for a small can be investigated. It will be proved that, in the leading order of , only the term with should be retained in .
In isotropic elastic scattering, the field can be expanded into conservative and rotational parts:
where is the totally skew-symmetric tensor . Inside the scatter positioned at , the potentials satisfy the Helmholtz equation
where a labels the potentials for the three modes, is the magnitude of the wave vector inside the scatter for each mode,
and is the group velocity in the scatter for the mode a, and in the background media. Its regular solution is obtained by separating variables in the polar coordinates
where the coefficients are chosen so that the field is continuous across the circle , that is, the field defined by the potentials for must have a prescribed value at which is determined by the solution outside the scatterer. The analysis for the out-of-plane mode described by the potential is nearly identical to the electromagnetic case studied in [2]. In what follows, only the in-plane modes are investigated, that is, in the field .
The solution inside the scatterer is substituted into the integral , and the latter is then to be estimated for . Let
Then, is a linear combination of the following integrals:
where are a polarization subscript. In the limit of a small , it follows from the power series representation of the Bessel functions that
Next, one should investigate the behavior of when . The in-plane field has only x and y components. Define a matrix as a linear transformation of the Fourier trigonometric coefficients of the field and the coefficients :
where is the field generated by potentials (A3) taken at . By evaluating the integral, the matrix is found to be
The continuity condition at requires that the trigonometric Fourier coefficients of the fields inside and outside the scatterer match. Since the field must be bounded everywhere, the inverse of defines the behavior of in the long-wavelength approximation:
The latter follows from the power expansion of the Bessel functions in . Combining the asymptotic forms of and , it is concluded that
The lowest-order term is at so that
Thus, where .
Next, the same analysis must be carried out for the convolution in the term of (9) that contains the relative Lamé coefficients that are assumed to have constant values inside the scatterers. Therefore, it is necessary to investigate in the leading order of , which is carried out in the same way using the Grafts formula. The integrals now contain the stress tensor in place of . The stress tensor inside a scatterer is calculated from (2) where the field is defined by the potentials (A3) and the asymptotic behavior of is already established. Therefore, there is only a minor modification in estimates of because contains second partials of the potentials instead of the first ones. The leading term is again given by . Therefore, the source of the scattered wave is determined by the stress tensor at the scatterer’s position . Thus, the total scattered field is given by (11) in the leading order of the long-wavelength approximation.
Appendix A.3. Calculation of Πij(r)
In this section, the tensor and its derivatives are calculated both off and on the defects. It follows from the analysis in Appendix A.2 that, if , the integrals in (13) can be approximated by the integral mean value theorem so that
in the leading order in . Evaluations of Schlömilch series of this type have been discussed in a variety of wave theories [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,42,43,44,45,46,47,48,49,50]. However, an analysis of higher-order derivatives requires some special attention since even-order derivatives of Hankel functions are not regular distributions. There are a few methods for evaluating lattice sums. Here, a polylogarithm subtraction method developed in [30,31] will be invoked with some modification in order to handle the singular portion of the distributions .
Using the Poisson summation formula in combination with (A2), one infers that [2]
for , where is defined in (7), , and
The uniform convergence of is guaranteed as as for all for any positive . The series converges conditionally if and y is not an integer. Therefore, in the distributional sense,
where, for brevity,
Since the series also converges uniformly for (for the same reason), the asymptotic scattered field can readily be inferred from the expansion
because only open channels with real contribute in the limit .
The problem of calculating the limit (15) is reduced to evaluating the series of the form
for . Note that and are m-tensors in the plane. Using the above Poisson summation formula, it is concluded that
The method to evaluate these series will be illustrated with the case , while all technical details for the other needed cases will be omitted and only the final results will be stated.
As ,
where is the sign of n and function is given by
By the symmetry of the problem, the off-diagonal components of the tensor vanish. The diagonal components are determined by the symmetric 2-tensor . The latter is inferred by calculating the asymptotic behavior for in the limit ,
and all other components are found to be zero.
The tensor is the difference of two divergent terms in the limit as seen from (A5) for . The asymptotic properties on the Hankel function are known in this limit. Therefore, the next technical objective is to identify the divergent part of the series in the tensor as . To this end, let and define the 2-tensor as
where is the polylogarithm of order p. Then, the tensor can be decomposed into the sum of regular and singular parts when :
where the arguments are omitted for brevity in all functions in the last equation.
By definition of , divergent terms in the series for are canceled for large values and the series converges even for . The distributional derivative (and, hence, the distribution-valued tensor ) is the sum of a singular part that is equal to and a regular distribution (being the corresponding classical derivative wherever it exists). The singular part exactly cancels the singular part of the second distributional derivative of the Hankel function in the expression for . This cancellation occurs for all even-order derivatives. Therefore, the limit can be computed by studying the asymptotic behavior of the polylogarithm near its singular point.
Recall that diverges as for . So, using the asymptotic form of near its singular point and polar coordinates in the plane, one infers that
where is the polar angle counted from the positive x axis counterclockwise and is the Riemann zeta function. Using the above asymptotic equations and the asymptotic form of the Hankel function for a small argument, the limit of components of the tensor is found
where is the Euler constant. Therefore, non-zero components of the tensor are given by the following absolutely convergent series:
where .
The same procedure can be used to evaluate the tensors for . One must first examine the asymptotic behavior of the tensor as . This is accomplished by calculating the expansion
where . The asymptotic coefficients determine the tensor used to define and . The cancellation of the singular distributional part in the tensor is then established, and the asymptotic properties of the polylogarithm function near its singular point are exploited to find the limit of as as an absolutely convergent series:
where p and q are the numbers of the x and y derivatives in , respectively, the series arises from the limit of , and the constant is the sum of and the limit of obtained by the asymptotic expansion of the polylogarithm and Hankel functions, just like in the case given above.
It should be noted that all series involving an odd number of x derivatives will be zero from the parity symmetry of the series. Here are the results up to that are needed to define the scattering amplitudes for the single and double arrays. In particular, representations of the components of tensors via absolutely convergent series are essential when calculating their numerical values for a given k and . For ,
For ,
For ,
Finally, to evaluate the tensors , , and , the following integral must be calculated:
This is accomplished by using the following properties of the cylindrical harmonics defined by :
where
It follows from the above relations that
for . It is clear that all terms with an odd number of partial derivatives in both variables vanish due to the parity symmetry. Now one can easily evaluate , , and :
The above equations along with the interface conditions (continuity of field and normal traction) completely determine both the spectrum and the transmission and reflection coefficients; hence, the scattering problem is completely solved.
References
- Groves, M.D. Examples of embedded eigenvalues for problems in acoustic waveguides. Math. Methods Appl. Sci. 1998, 21, 479. [Google Scholar] [CrossRef]
- Ngandali, R.F.; Shabanov, S.V. Electromagnetic bound states in the radiation continuum for periodic double arrays of subwavelength dielectric cylinders. J. Math. Phys. 2010, 51, 102901. [Google Scholar] [CrossRef]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound states in the continuum in photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef] [PubMed]
- Kavaklioglu, O. Schlömilch series representation for the transverse electric multiple scattering by an infinite grating of insulating dielectric circular cylinders at oblique incidence. J. Phys. A Math. Gen. 2002, 35, 2229. [Google Scholar] [CrossRef]
- Milton, G.W.; Cherkaev, A.V. Which elasticity tensors are realizable? J. Eng. Mater. Technol. 1995, 117, 483. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical metamaterials and their engineering applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics: Theory of Elasticity; Pergamon Press: Oxford, UK, 1959; Volume 7, p. 101. [Google Scholar]
- von Neumann, J.; Wigner, E. Über merkwürdige diskrete Eigenwerte. Phys. Z 1929, 30, 465. [Google Scholar]
- Stillinger, F.H.; Herrick, D.R. Bound states in the continuum. Phys. Rev. A 1975, 11, 446. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačíc, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Parker, R. Resonance effects in wake shedding from parallel plates: Some experimental observations. J. Sound Vib. 1966, 4, 62–72. [Google Scholar] [CrossRef]
- Lim, T.; Farnell, G. Character of pseudo surface waves on anisotropic crystals. J. Acoust. Soc. Am. 1969, 45, 845–851. [Google Scholar] [CrossRef]
- Maznev, A.; Every, A. Bound acoustic modes in the radiation continuum in isotropic layered systems without periodic structures. Phys. Rev. B 2018, 97, 014108. [Google Scholar] [CrossRef]
- Twersky, V. Multiple scattering of radiation by an arbitrary configuration of parallel cylinders. J. Acoust. Soc. Am. 1952, 24, 42–46. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Trapping and near-trapping by arrays of cylinders in waves. J. Eng. Math. 1999, 35, 149–179. [Google Scholar] [CrossRef]
- Moroz, A. Quasi-periodic Green’s functions of the Helmholtz and Laplace equations. J. Phys. A Math. Gen. 2006, 39, 11247. [Google Scholar] [CrossRef]
- Ivansson, S.M. Designing 2D Phononic Crystal Slabs with Transmission Gaps for Solid Angle as well as Frequency Variation. Adv. Acoust. Vib. 2009, 2009, 31790. [Google Scholar] [CrossRef]
- Xu, S.; Qiu, C.; Liu, Z. Acoustic transmission through asymmetric grating structures made of cylinders. J. Appl. Phys. 2012, 111, 094505. [Google Scholar] [CrossRef]
- Platts, S.B.; Movchan, N.V.; McPhedran, R.C.; Movchan, A.B. Elastic waves and homogenization in oblique periodic structures. Proc. R. Soc. Lond. A 2002, 458, 2327. [Google Scholar] [CrossRef]
- Platts, S.B.; Movchan, N.V.; McPhedran, R.C.; Movchan, A.B. Transmission and Polarization of Elastic Waves in Irregular Structures. J. Eng. Mater. Technol. 2003, 125, 2. [Google Scholar] [CrossRef]
- Mei, J.; Liu, Z.; Shi, J.; Tian, D. Theory for elastic wave scattering by a two-dimensional periodical array of cylinders: An ideal approach for band-structure calculations. Phys. Rev. B 2003, 67, 245107. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, Z.; Mei, J.; Ke, M. The layer multiple-scattering method for calculating transmission coefficients of 2D phononic crystals. Solid State Commun. 2005, 134, 765. [Google Scholar] [CrossRef]
- Mei, J.; Liu, Z.; Qiu, C. Multiple-scattering theory for out-of-plane propagation of elastic waves in two-dimensional phononic crystals. J. Phys. Condens. Matter 2005, 17, 3735. [Google Scholar] [CrossRef] [PubMed]
- Robert, S.; Conoir, J.-M.; Franklin, H. Propagation of elastic waves through two-dimensional lattices of cylindrical empty or water-filled inclusions in an aluminum matrix. Ultrasonics 2006, 45, 178–187. [Google Scholar] [CrossRef]
- Sainidou, R.; Stefanou, N. Guided and quasiguided elastic waves in phononic crystal slabs. Phys. Rev. B 2006, 73, 184301. [Google Scholar] [CrossRef]
- García de Abajo, F.J. Colloquium: Light scattering by particle and hole arrays. Rev. Mod. Phys. 2007, 79, 1267–1290. [Google Scholar] [CrossRef]
- Gantzounis, G.; Stefanou, N. Theoretical analysis of three-dimensional polaritonic photonic crystals. Phys. Rev. B 2005, 72, 075107. [Google Scholar] [CrossRef]
- Nicorovici, N.A.; McPhedran, R.C.; Petit, R. Efficient calculation of the Green’s function for electromagnetic scattering by gratings. Phys. Rev. E 1994, 49, 4593. [Google Scholar] [CrossRef]
- Nicorovici, N.A.; McPhedran, R.C.; Petit, R. Lattice sums for off-axis electromagnetic scattering by gratings. Phys. Rev. E 1994, 50, 3143. [Google Scholar] [CrossRef]
- Twersky, V. Scattering by quasi-periodic and quasi-random distributions. IRE Trans. Antennas Propag. 1959, 7, 307–319. [Google Scholar] [CrossRef]
- Lu, Y.W.; Zhou, W.J.; Li, Y.; Li, R.; Liu, J.F.; Wu, L.; Tan, H. Unveiling atom-photon quasi-bound states in hybrid plasmonic-photonic cavity. Nanophotonics 2022, 11, 3307–3317. [Google Scholar] [CrossRef]
- Zhao, M.; Fang, K. Mechanical bound states in the continuum for macroscopic optomechanics. Opt. Express 2019, 27, 10138–10151. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Zhu, Y.; Xu, Y.; Fan, S.W.; Yang, Z.; Assouar, B. Elastic bound state in the continuum with perfect mode conversion. J. Mech. Phys. Solids 2021, 154, 104502. [Google Scholar] [CrossRef]
- Rahman, A.; Pal, R.K. Elastic bound modes in the continuum in architected beams. Phys. Rev. Appl. 2024, 21, 024002. [Google Scholar] [CrossRef]
- Amrani, M.; Quotane, I.; Ghouila-Houri, C.; El Boudouti, E.H.; Krutyansky, L.; Piwakowski, B.; Pernod, P.; Talbi, A.; Djafari-Rouhani, B. Experimental Evidence of the Existence of Bound States in the Continuum and Fano Resonances in Solid-Liquid Layered Media. Phys. Rev. Appl. 2021, 15, 054046. [Google Scholar] [CrossRef]
- Xia, B.; Jiang, Z.; Tong, L.; Zheng, S.; Man, X. Topological bound states in elastic phononic plates induced by disclinations. Acta Mech. Sin. 2022, 38, 521459. [Google Scholar] [CrossRef]
- Haq, O.; Shabanov, S. Bound states in the continuum in elasticity. Wave Motion 2021, 103, 102718. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Structural Analysis with Applications to Aerospace Structures; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Glasser, M.L. The evaluation of lattice sums. I. Analytic procedures. J. Math. Phys. 1973, 14, 409–413. [Google Scholar] [CrossRef]
- Glasser, M.L. The evaluation of lattice sums. III. Phase modulated sums. J. Math. Phys. 1974, 15, 188–189. [Google Scholar] [CrossRef]
- Twersky, V. Scattering theorems for bounded periodic structures. J. Appl. Phys. 1956, 27, 1118–1122. [Google Scholar] [CrossRef]
- Chaba, A.N.; Pathria, R.K. Evaluation of lattice sums using Poisson’s summation formula. IV. J. Phys. A Math. Gen. 1977, 10, 1823. [Google Scholar] [CrossRef]
- Miller, A.R. On certain two-dimensional Schlömilch series. J. Phys. A Math. Gen. 1995, 28, 735. [Google Scholar] [CrossRef]
- Linton, C.M. Schlömilch series that arise in diffraction theory and their efficient computation. J. Phys. A Math. Gen. 2006, 39, 3325. [Google Scholar] [CrossRef]
- Dasgupta, S.; Sen, D.; Sengupta, S. A simple approach to evaluation of lattice sums. Pramana 1985, 25, 597–601. [Google Scholar] [CrossRef]
- Thompson, I.; Linton, C.M. Euler-Maclaurin Summation and Schlömilch Series. Q. J. Mech. Appl. Math. 2010, 63, 39–56. [Google Scholar] [CrossRef][Green Version]
- Hautot, A. A new method for the evaluation of slowly convergent series. J. Math. Phys. 1974, 15, 1722–1727. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).