The Collocation Method Based on the New Chebyshev Cardinal Functions for Solving Fractional Delay Differential Equations
Abstract
1. Introduction
2. Chebyshev Cardinal Polynomials Based on the Lobatto Grid
2.1. Matrix Representation of the Derivative Operator in CCFs Obtained by Lobatto Grids
- If , then we obtainFrom Equation (10), it follows that
- If , then one can obtain
2.2. Matrix Representation of the Fractional Integral Operator in CCFs Obtained by Lobatto Grids
3. Proposed Algorithm
3.1. Convergence Analysis
3.2. Stability Analysis
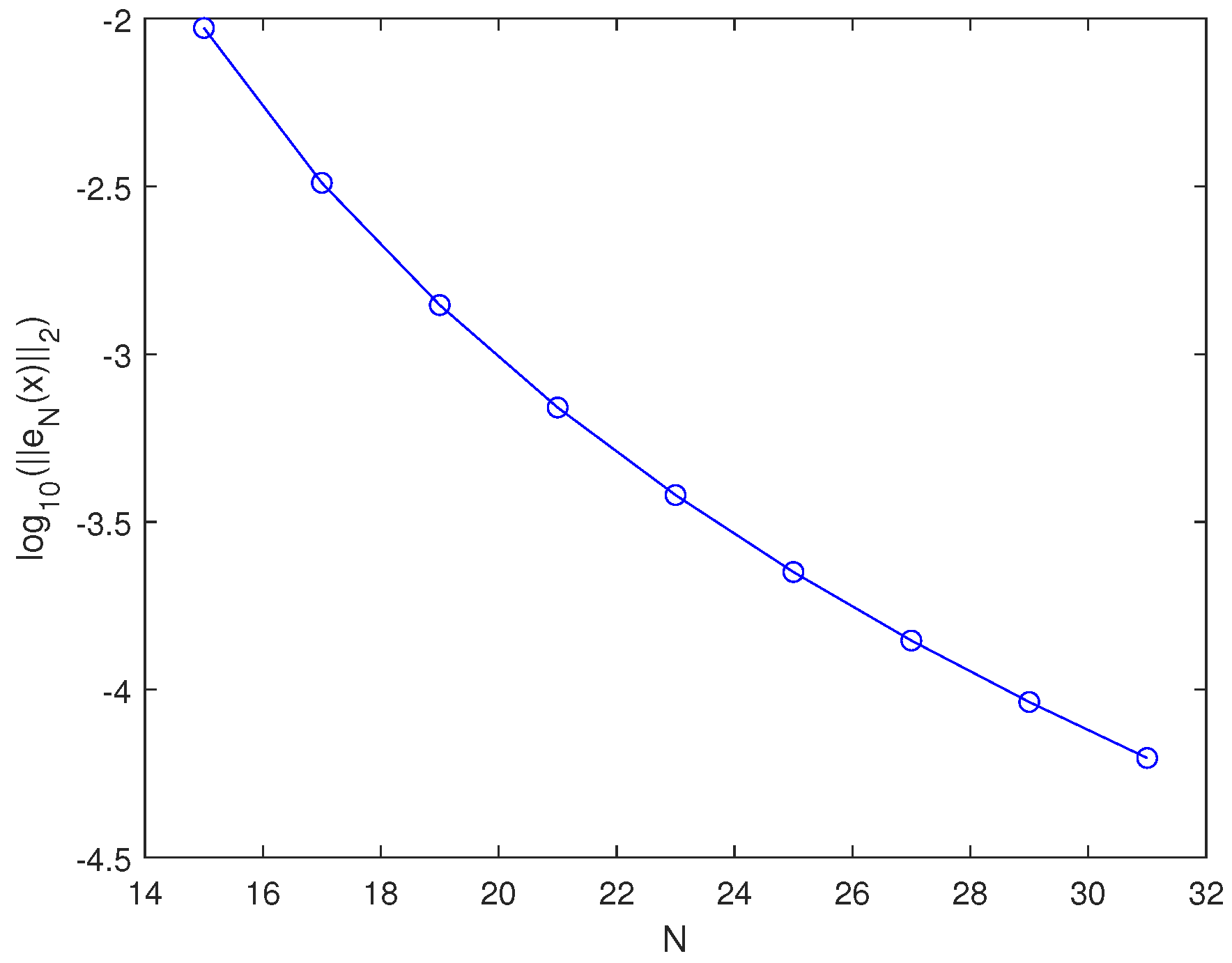
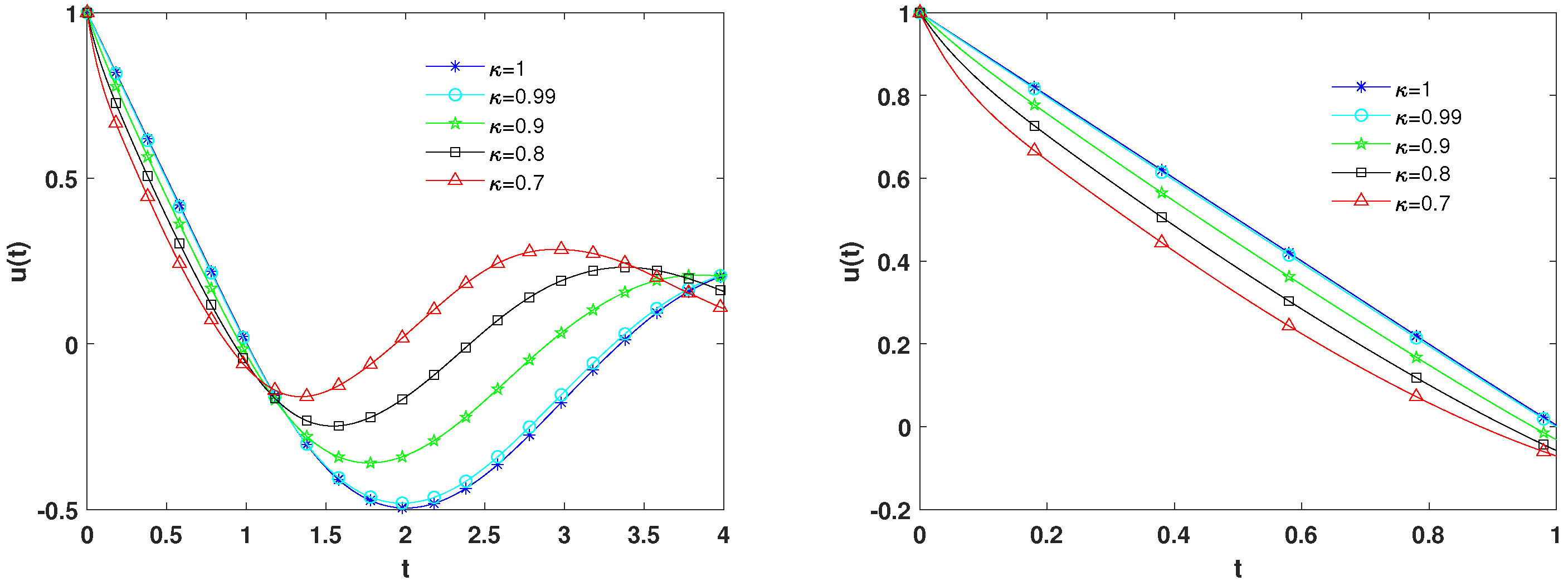
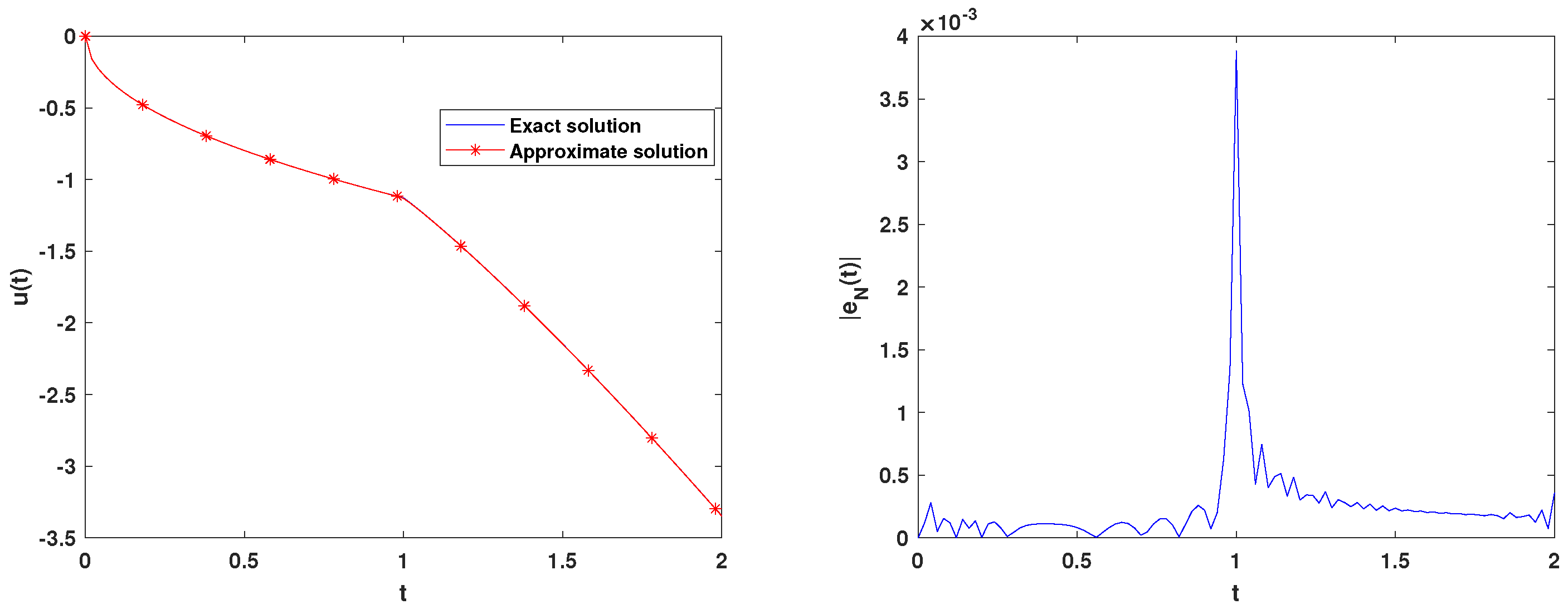
4. Numerical Experiments
5. Conclusions
- The presented algorithm demonstrates efficiency in solving the fractional DDEs.
- Our algorithm demonstrates convergence when tackling these equations.
- The method presented offers reduced computational cost by avoiding integration to find coefficients.
- The CCFs based on the Lobatto grid can efficiently be used as the bases in the spectral methods, especially when studying boundary value equations.
- The proposed algorithm is simple to implement, and it also provides good accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Caputo fractional derivative | |
| L | Lipschitz constant |
| one-parameter Mittag-Leffler function | |
| Chebyshev polynomials | |
| shifted Chebyshev polynomials | |
| Chebyshev cardinal functions | |
| Sobolev space | |
| projection operator | |
| derivative operator with respect to t | |
| fractional integral operator |
References
- Arif, M.; Ali, F.; Khan, I.; Nisar, K.S. A time fractional model with non-singular kernel the generalized couette flow of couple stress nanofluid. IEEE Access 2020, 8, 77378–77395. [Google Scholar] [CrossRef]
- Chang, A.; Sun, H.; Zheng, C.; Bingqing, L.; Chengpeng, L.; Rui, M.; Yong, Z. A Time Fractional Convection-Diffusion Equation to Model Gas Transport through Heterogeneous Soil and Gas Reservoirs. Physica A 2018, 502, 356–369. [Google Scholar] [CrossRef]
- Tenreiro, M.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis Cecília, M.; Marcos, M.G.; Galhano, A.F. Some Applications of Fractional Calculus in Engineering. Math. Probl. Eng. 2010, 2010, 639801. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Asadzadeh, M.; Saray, B.N. On a multiwavelet spectral element method for integral equation of a generalized Cauchy problem. BIT 2022, 62, 383–1416. [Google Scholar] [CrossRef]
- Shi, L.; Saray, B.N.; Soleymani, F. Sparse wavelet Galerkin method: Application for fractional Pantograph problem. J. Comput. Appl. Math. 2024, 451, 116081. [Google Scholar] [CrossRef]
- Thanh Toan, P.; Vo, T.N.; Razzaghi, M. Taylor wavelet method for fractional delay differential equations. Eng. Comput. 2021, 37, 231–240. [Google Scholar] [CrossRef]
- Afarideh, A.; Dastmalchi Saei, F.; Lakestani, M.; Saray, B.N. Pseudospectral method for solving fractional Sturm-Liouville problem using Chebyshev cardinal functions. Phys. Scr. 2021, 96, 125267. [Google Scholar] [CrossRef]
- Afarideh, A.; Dastmalchi Saei, F.; Saray, B.N. Eigenvalue problem with fractional differential operator: Chebyshev cardinal spectral method. J. Math. Model. 2021, 11, 343–355. [Google Scholar]
- Shahriari, M.; Saray, B.N.; Mohammadalipour, B.; Saeidian, S. Pseudospectral method for solving the fractional one-dimensional Dirac operator using Chebyshev cardinal functions. Phys. Scr. 2023, 98, 055205. [Google Scholar] [CrossRef]
- Garrappa, R. On some explicit Adams multistep methods for fractional differential equations. J. Comput. Appl. Math. 2009, 229, 392–399. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, D.; Qi, D.; Deng, L. A Petrov–Galerkin finite element-meshfree formulation for multi-dimensional fractional diffusion equations. Comput. Mech. 2020, 66, 323–350. [Google Scholar] [CrossRef]
- Lakestani, M.; Dehghan, M. The use of Chebyshev cardinal functions for the solution of a partial differential equation with an unknown time-dependent coefficient subject to an extra measurement. J. Comput. Appl. Math. 2010, 235, 669–678. [Google Scholar] [CrossRef][Green Version]
- Daftardar-Gejji, V.; Jafari, A. Adomian decomposition: A tool for solving a system of fractional differential equations. J. Math. Anal. Appl. 2005, 301, 508–518. [Google Scholar] [CrossRef]
- Fix, G.J.; Roop, J.P. Least squares finite element solution of a fractional order two-point boundary value problem. Comput. Math. Appl. 2004, 48, 1017–1033. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhu, P.; Gu, X.M.; Zhao, X.; Jian, H.Y. An implicit integration factor method for a kind of spatial fractional diffusion equations. J. Phys. Conf. Ser. 2019, 1324, 012030. [Google Scholar] [CrossRef]
- Maji, S.; Natesan, S. Adaptive-grid technique for the numerical solution of a class of fractional boundary-value-problems. Comput. Methods Differ. Equ. 2010, 12, 338–349. [Google Scholar]
- Epstein, I.R.; Luo, Y. Differential delay equations in chemical kinetics. Nonlinear models: The cross-shaped phase diagram and the oregonator. J. Chem. Phys. 1991, 95, 244–254. [Google Scholar] [CrossRef]
- Davis, L. Modifications of the optimal velocity traffic model to include delay due to driver reaction time. Phys. A Stat. Mech. Appl. 2003, 319, 557–567. [Google Scholar] [CrossRef]
- Fridman, E.; Fridman, L.; Shustin, E. Steady modes in relay control systems with time delay and periodic disturbances. J. Dyn. Syst. Meas. Control 2000, 122, 732–737. [Google Scholar] [CrossRef]
- Kuang, Y. Delay Differential Equations: With Applications in Population Dynamics; Academic Press: London, UK, 1993; Volume 191. [Google Scholar]
- Saray, B.N.; Lakestani, M. On the sparse multi-scale solution of the delay differential equations by an efficient algorithm. Appl. Math. Comput. 2020, 381, 125291. [Google Scholar] [CrossRef]
- Mohammadzade, R.; Lakestani, M. Analysis of time-varying delay systems by hybrid of block-pulse functions and biorthogonal multiscaling functions. Int. J. Control. 2015, 88, 2444–2456. [Google Scholar] [CrossRef]
- Marzban, H.R.; Razzaghi, M. Analysis of time-delay systems via hybrid of block-pulse functions and taylor series. J. Vib. Control 2005, 11, 1455–1468. [Google Scholar] [CrossRef]
- Huang, C.; Fu, H.; Li, S.; Chen, G. Stability analysis of Runge-Kutta methods for non-linear delay differential equations. BIT 1999, 39, 270–280. [Google Scholar]
- Kuang, J.; Cong, Y. Stability of Numerical Methods for Delay Differential Equations; Science Press: Beijing, China, 2005. [Google Scholar]
- Li, D.; Zhang, C. Nonlinear stability of discontinuous Galerkin methods for delay differential equations. Appl. Math. Lett. 2010, 23, 457–461. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q.; Chen, H. Local Superconvergence vergence of continuous Galerkin solutions for delay differential equations of pantograph type. J. Comput. Math. 2016, 34, 2664–2684. [Google Scholar]
- Zennaro, M. P-stability of Runge-Kutta methods for delay differential equations. Numer. Math. 1986, 49, 305–318. [Google Scholar] [CrossRef]
- Zennaro, M. Asymptotic stability analysis of Runge-Kutta methods for nonlinear systems of delay differential equations. Numer. Math. 1997, 77, 549–563. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V. Fractional Calculus: Theory and Applications; Narosa Publishing House: New Delhi, India, 2014. [Google Scholar]
- Zhen, W.; Xia, H.; Guodong, S. Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput. Math. Appl. 2011, 62, 1531–1539. [Google Scholar]
- Singh, H. Numerical simulation forfractional delay differential equations. Int. J. Dynam. Control 2021, 9, 463–474. [Google Scholar] [CrossRef]
- Liao, C.; Ye, H. Existence of positive solutions of nonlinear fractional delay differential equations. Positivity 2009, 13, 601–609. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Sukale, Y.; Bhalekar, S. Solving fractional delay differential equations: A new approach. Fract. Calc. Appl. Anal. 2015, 18, 400–418. [Google Scholar] [CrossRef]
- Dehestani, H.; Ordokhani, Y.; Razzaghi, M. On the applicability of Genocchi wavelet method for different kinds of fractional-order differential equations with delay. Numer. Linear. Algebr. 2019, 26, e2259. [Google Scholar] [CrossRef]
- Singh, H.; Pandey, R.K.; Baleanu, D. Stable Numerical Approach for Fractional Delay Differential Equations. Few-Body Syst. 2017, 58, 156. [Google Scholar] [CrossRef]
- Jhinga, A.; Daftardar-Gejji, V. A new numerical method for solving fractional delay differential equations. Comput. Appl. Math. 2019, 38, 166. [Google Scholar] [CrossRef]
- Gande, N.R.; Madduri, H. Higher order numerical schemes for the solution of fractional delay differential equations. J. Comput. Appl. Math. 2022, 402, 113810. [Google Scholar] [CrossRef]
- Amin, R.; Shah, K.; Asif, M.; Khan, I. A computational algorithm for the numerical solution of fractional order delay differential equations. Appl. Math. Comput. 2021, 402, 125863. [Google Scholar] [CrossRef]
- Morgado, M.L.; Ford, N.J.; Lima, P. Analysis and numerical methods for fractional differential equations with delay. J. Comput. Appl. Math. 2013, 252, 159–168. [Google Scholar] [CrossRef]
- Xu, M.; Lin, Y. Simplified reproducing kernel method for fractional differential equations with delay. Appl. Math. Lett. 2016, 52, 156–161. [Google Scholar] [CrossRef]
- Kucche, K.D.; Sutar, S.T. On existence and stability results for nonlinear fractional delay differential equations. Bol. Soc. Parana. Mat. 2018, 36, 55–75. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Fariborzi Araghi, M.A.; Sidorov, D. Dynamical strategy on homotopy perturbation method for solving second kind integral equations using the CESTAC method. J. Comput. Appl. Math. 2022, 411, 114226. [Google Scholar] [CrossRef]
- Saray, B.N. Sparse multiscale representation of Galerkin method for solving linear-mixed Volterra-Fredholm integral equations. Math. Method. Appl. Sci. 2020, 43, 2601–2614. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Sidorov, D.; Wawaz, A.-M.; Sidorow, N.; Sizikov, V. The Numerical Validation of the Adomian Decomposition Method for Solving Volterra Integral Equation with Discontinuous Kernels. Mathematics 2021, 9, 260. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover Publications: New York, NY, USA, 2001. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms. Analysis, Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherland, 2006. [Google Scholar]
- Saray, B.N. Abel’s integral operator: Sparse representation based on multiwavelets. BIT 2021, 61, 587–606. [Google Scholar] [CrossRef]
- Shi, L.; Chen, Z.; Ding, X.; Ma, Q. A new stable collocation method for solving a class of nonlinear fractional delay differential equations. Numer. Algor. 2020, 85, 1123–1153. [Google Scholar] [CrossRef]
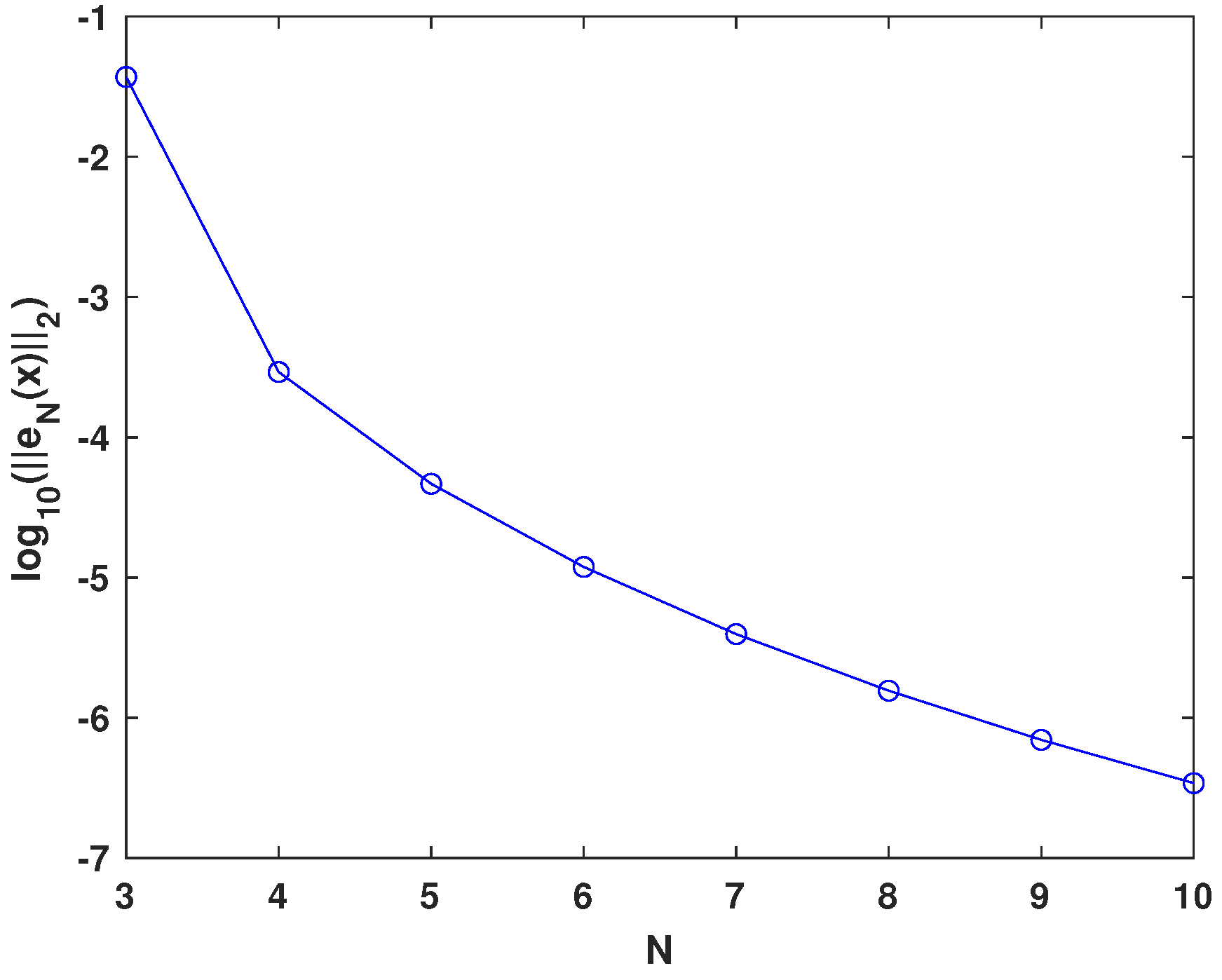
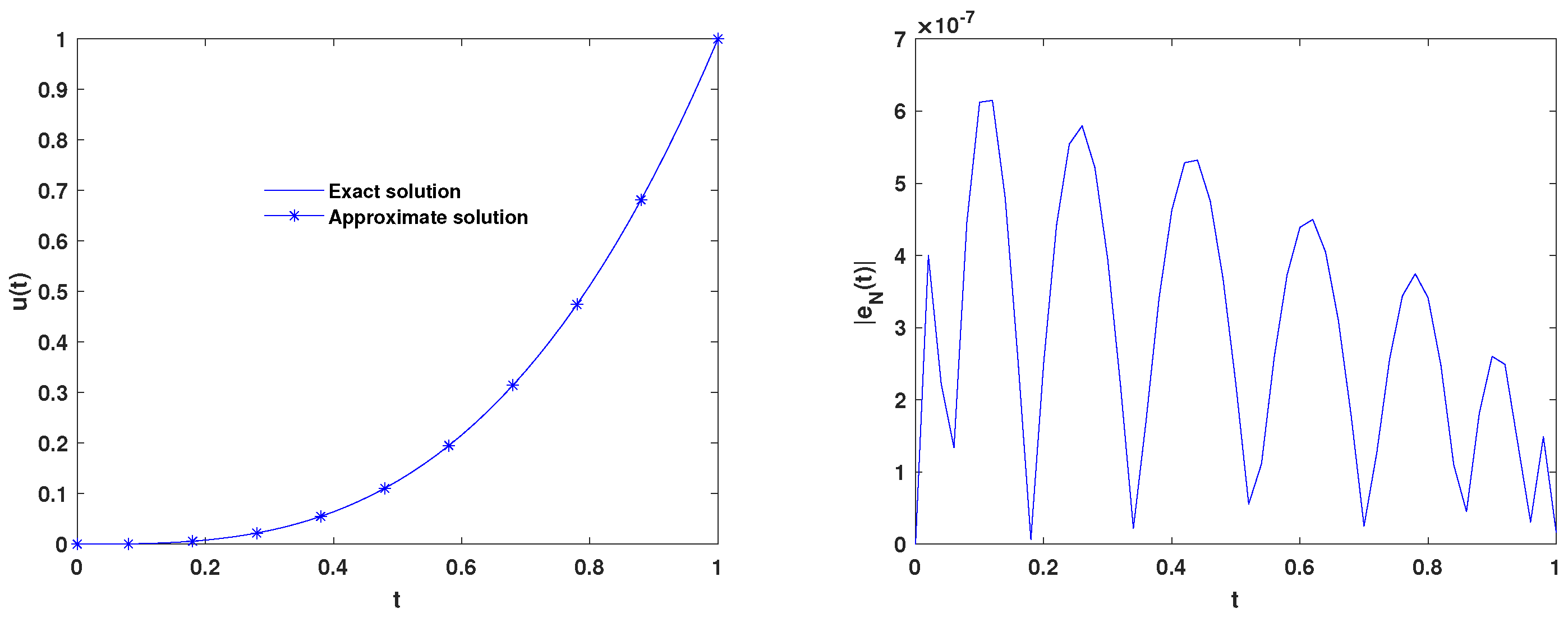
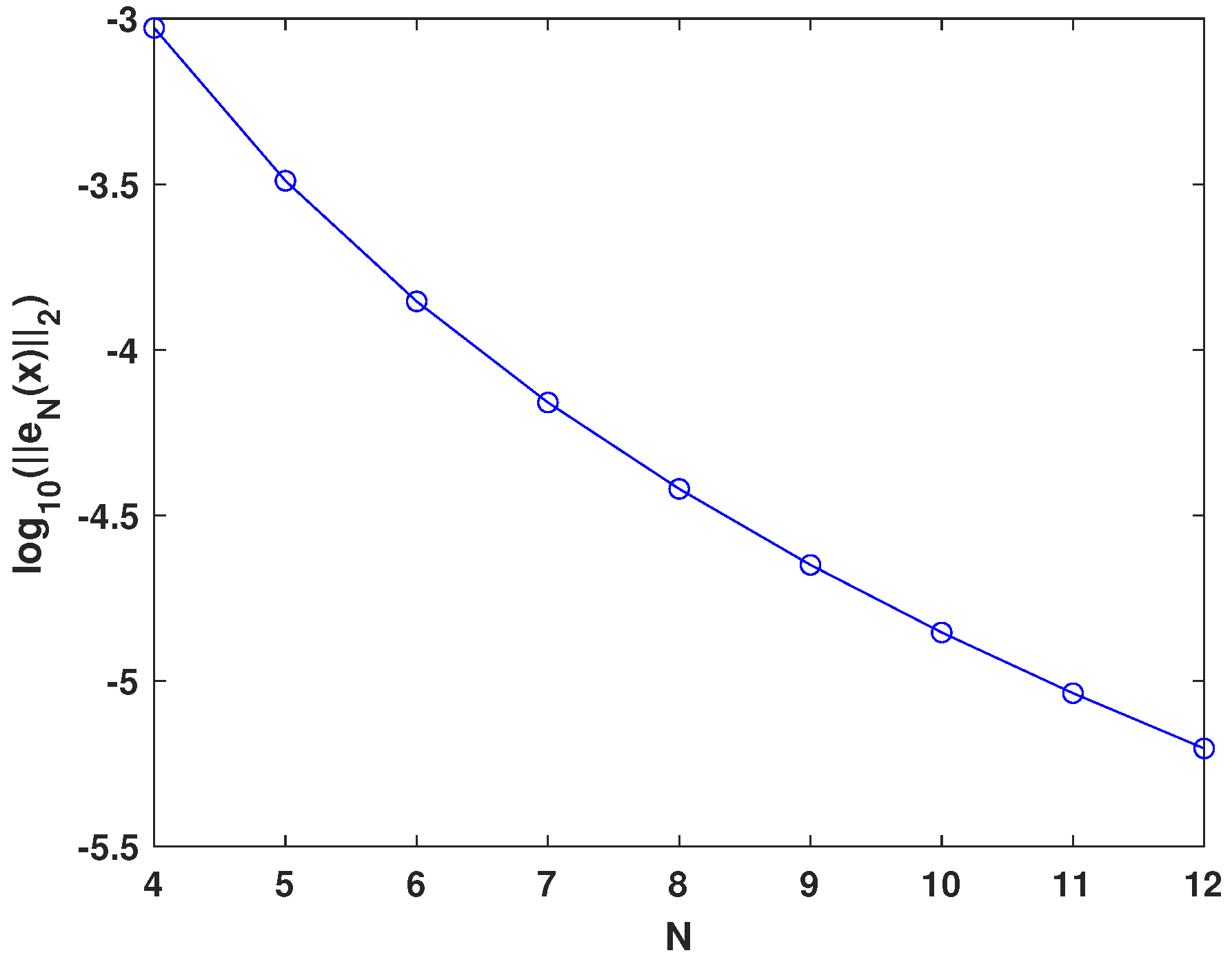
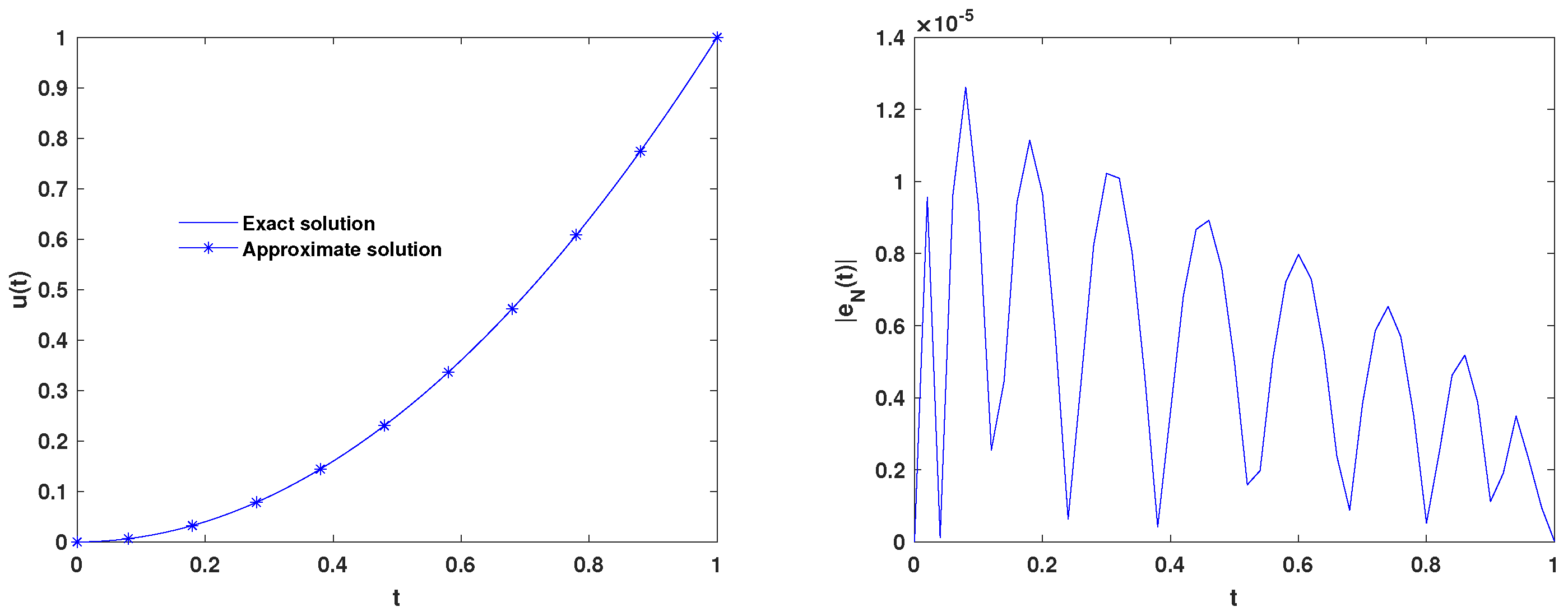
| N | Presented Method | N | Results of [40] | N | Results of [41] |
|---|---|---|---|---|---|
| 4 | 4 | 10 | |||
| 6 | 8 | 20 | |||
| 8 | 16 | 40 | |||
| 10 | 32 | 80 |
| N | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|---|---|---|---|---|---|---|---|
| -error | |||||||
| Order | − |
| N | Presented Method | N | Results of [40] | N | Results of [41] |
|---|---|---|---|---|---|
| 6 | 4 | 10 | |||
| 8 | 8 | 20 | |||
| 10 | 16 | 40 | |||
| 12 | 32 | 80 |
| N | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|
| -error | ||||||
| Order | − |
| N | 4 | 8 | 16 | 32 | 64 | 128 | 25 |
|---|---|---|---|---|---|---|---|
| -error | |||||||
| Order | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jebreen, H.B.; Dassios, I. The Collocation Method Based on the New Chebyshev Cardinal Functions for Solving Fractional Delay Differential Equations. Mathematics 2024, 12, 3388. https://doi.org/10.3390/math12213388
Jebreen HB, Dassios I. The Collocation Method Based on the New Chebyshev Cardinal Functions for Solving Fractional Delay Differential Equations. Mathematics. 2024; 12(21):3388. https://doi.org/10.3390/math12213388
Chicago/Turabian StyleJebreen, Haifa Bin, and Ioannis Dassios. 2024. "The Collocation Method Based on the New Chebyshev Cardinal Functions for Solving Fractional Delay Differential Equations" Mathematics 12, no. 21: 3388. https://doi.org/10.3390/math12213388
APA StyleJebreen, H. B., & Dassios, I. (2024). The Collocation Method Based on the New Chebyshev Cardinal Functions for Solving Fractional Delay Differential Equations. Mathematics, 12(21), 3388. https://doi.org/10.3390/math12213388








