Approaches for the On-Line Three-Dimensional Knapsack Problem with Buffering and Repacking

Abstract

The rapid growth of the e-commerce sector, particularly in Latin America, has highlighted the need for more efficient automated packing and distribution systems. This study presents heuristic algorithms to solve the online three-dimensional knapsack problem (OSKP), incorporating buffering and repacking strategies to optimize space utilization in automated packing environments. These strategies enable the system to handle the stochastic nature of item arrivals and improve container utilization by temporarily storing boxes (buffering) and rearranging already packed boxes (repacking) to enhance packing efficiency. Computational experiments conducted on specialized datasets from the existing literature demonstrate that the proposed heuristics perform comparably to state-of-the-art methodologies. Moreover, physical experiments were conducted on a robotic packing cell to determine the time that buffering and repacking implicate. The contributions of this paper lie in the integration of buffering and repacking into the OSKP, the development of tailored heuristics, and the validation of these heuristics in both simulated and real-world environments. The findings indicate that including buffering and repacking strategies significantly improves space utilization in automated packing systems. However, they significantly increase the time spent packing.

1. Introduction

E-commerce, the process of buying and selling goods and services online, has fundamentally transformed the way people shop, establishing itself as a dominant force in the retail industry. Over time, the rapid growth of this field has led to a significant rise in demand for automated distribution centers, which are essential for managing the high volume of orders and the speed of delivery that online shoppers expect [1,2,3]. These automated centers enhance efficiency and productivity by employing conveyor belts and robotic solutions to pick and pack various orders [4,5].

A key challenge in these automated distribution centers is efficiently packing assorted boxes that arrive randomly via conveyor belts onto pallets for distribution. The stochastic nature of demand adds complexity to this task. The literature highlights various optimization challenges associated with container packing, especially in retail scenarios where vehicles or pallets are dispatched as soon as they are complete, and new ones are immediately introduced to continue the process. This scenario requires precise space optimization to maximize the number of boxes per vehicle or pallet. Such challenges are typically classified as the Online Single Container Loading Problem in academic studies. Depending on the range of box sizes, this may also be referred to as the Online Single Knapsack Problem (OSKP) or the Online Single Large Object Placement Problem (OSLOPP) [6]. In this study, the OSKP is the primary focus.

Traditional packing methods often overlook key strategies that can significantly improve space utilization, such as buffering and repacking. Buffering involves temporarily holding boxes before they are packed, allowing for greater flexibility in handling variations in size and arrival time. On the other hand, repacking entails rearranging already packed boxes to improve space utilization by finding better-fitting placements. This study focuses on integrating these two strategies into the OSKP, addressing a critical gap in the literature where few studies have explored their combined effect in automated environments.

The primary contributions of this paper are threefold:

• Developing heuristic algorithms tailored to incorporate buffering and repacking, improving packing efficiency.
• Demonstrating the competitiveness of these algorithms compared to state-of-the-art approaches through computational evaluations using standard OSKP datasets.
• Physically validating the proposed strategies, offering insights into their real-world applicability by executing experiments on a robotic packing system (Figure 1) composed of a conveyor belt, an industrial manipulator (UR10), a vision/perception system (Oak-D Lite) located at the end effector, and a vacuum gripper system (VG10).

By addressing these challenges, this study aims to enhance the flexibility and efficiency of automated packing systems, which is critical for meeting the growing demands of modern e-commerce logistics.

The remaining content is structured as follows: Section 2 defines the problem. Section 3 provides a review of the latest online packing methodologies. Section 4 describes the approach and methodology employed in the study. Section 5 discusses the results. Finally, Section 6 summarizes the key conclusions and suggests future research directions.

2. Problem Definition

The three-dimensional online knapsack problem (OKP) involves packing a set of heterogeneous boxes into a container with fixed dimensions, considering that not all necessary information is available from the start [6]. The necessary information for the packing process is gradually revealed, leading to uncertainty [7]. In this study, the information revealed in parts is the dimensions of the boxes to be packed. Each box’s dimensions are disclosed one at a time, without any lookahead feature that might simultaneously reveal the details of multiple boxes. This setup is typical in production lines where boxes are conveyed on a belt. The packing process in this study adheres to the following constraints:

• Containment: All boxes must fit within the container’s boundaries.
• Non-overlapping: Packed boxes must not overlap each other.
• Vertical stability: The packing configuration must remain stable during construction. This constraint is handled by implementing the full support constraint, i.e., each box must have its entire base supported by either the container floor or other boxes.
• Valid Orientations: This study considers two valid orientations for each box, following the “this side up” directive. The valid orientations are orthogonal, with 90° rotations along the vertical axis, maintaining content integrity and meeting robotic handling requirements [8]. Each instance can be executed with either one or two valid orientations. In the single orientation case, boxes are packed as received, with the box’s length parallel to the container’s. In the two-orientation case, the height remains fixed while length and width may interchange.

Additionally, this study considers buffering and repacking strategies. Buffering involves temporarily storing up to $k$ boxes, which can be accessed in any order, providing flexibility in the packing process [9]. Boxes from the conveyor can be directed to the packing pattern or the buffer slots. Repacking enhances space utilization by repositioning up to $r$ already packed boxes [10]. In this study, the packed boxes that are valid for repacking operations do not support other boxes. This condition ensures that repacking does not require additional movements, which would increase processing time.

The values of $k$ and $r$ vary depending on the packing application; in this study, several values are taken to assess their impact on container utilization. It is worth noting that when buffering and repacking are combined, the packing process becomes even more flexible, as packed boxes can be temporarily held in the buffer until a better placement position or orientation is identified.

3. Related Work

Packing problems have been extensively studied in the literature. They can be categorized into two main types based on the availability of information about the elements involved [8,11]. The first type, offline packing problems, involves scenarios where all relevant information is available before the packing process begins. In contrast, online packing problems are characterized by the gradual revelation of information during the packing process, such as the dimensions of the next item to be packed into the container.

Due to their combinatorial complexity, packing problems are often classified as NP-Hard [12]. Consequently, heuristic methods are frequently employed to tackle these problems, especially when dealing with large instances [11].

Table 1. Packing related research.

Ref.	Problem Type	Buffer	Rearrange	Methodology	Other Constraints
[13]	Online Bin Packing			Heuristics + Machine Learning	Full look-ahead
[14]	Online Knapsack		Deletion	Heuristic
[15]	Online Bin Packing			Deep Reinforcement Learning + Heuristics
[16]	Online Bin Packing	k		Deep Reinforcement Learning
[2]	Online Bin Packing			Simulation-Based Greedy Look-Ahead Algorithm	Robot collisions
[4]	Bin Packing			Deep Reinforcement Learning
[1]	Online Bin Packing			Heuristic
[5]	Online Bin Packing	k	r	Deep Reinforcement Learning + Heuristics
[3]	Online Bin Packing			Deep Reinforcement Learning + Heuristics
[17]	Online Knapsack	k		Reinforcement Learning	Irregular items
[18]	Bin Packing			Mathematical model
[19]	Online Bin Packing			Heuristic
[20]	Online Knapsack			Machine learning	Physical stability
[10]	Residual Bin Packing		r	Linear Programming + two auxiliary algorithms	Weight limit
[21]	Single Large Object Placement			Matheuristic	Stacking, weight, loading priorities, load balance
[22]	Bin Packing			Mathematical Model	Multidrop
[23]	Online Knapsack	k		Heuristic algorithm	Capacity constraint
[8]	Single Bin-Size Packing			Gradient Boosting + Integer Linear Programming	Collisions
[24]	Knapsack-block Packing			Mathematical model	Two-dimensional
[25]	Knapsack			Genetic Algorithm + heuristic algorithm	Weight limit, loading priorities
[26]	Residual Bin packing			Machine learning + Algorithm to minimize memory usage	Weight limit, allocation
[9]	Residual Bin Packing	2–3	2–3	Next-Fit Algorithm + rearrange algorithm	Allocation
[27]	Knapsack			Mathematical model for small instances, heuristic algorithm	Balance in packing center mass
[28]	Knapsack			Heuristic algorithm
[29]	Online Bin Packing		r	Resource Augmentation	Bounded space
[30]	Online Bin Packing	k		Heuristic	Weight limit
[31]	Single Bin-Size Packing		3	Heuristic algorithm	Stacking
[32]	Cutting Stock		1	Heuristic algorithm	Toxicity, crushability, stability

presents a summary of studies related to online packing problems, detailing the problem types according to the classification by [6], the methodologies used to solve them, and any special constraints considered. The table also indicates whether buffering and repacking were included in these studies, specifying the buffer capacity and the number of items subjected to repacking.

The Bin Packing Problem (BPP) is one of this field’s most widely studied problems. It is an input minimization problem, where the objective is to minimize the number of containers or resources needed to pack all items efficiently. Various algorithms have been proposed to address online packing, with notable contributions from researchers who introduced three algorithms for the Online Bin Packing Problem (OBPP): Best fit, first Fit, and next fit [19]. The best-fit algorithm places items in the most filled bin available, opening a new bin if necessary; the first fit uses a sequential approach, packing items into the first available bin; and the next fit packs items into the most recently opened bin, also opening a new bin if needed. Results indicate that the best-fit algorithm performs significantly better with larger items.

In addition to the basic online and offline classifications, the literature also addresses semi-online packing problems, which involve gathering additional information to improve packing decisions. For example, ref. [30] was one of the first to explore a semi-online packing problem by incorporating a finite look-ahead buffer, which allowed for more informed packing decisions. This study demonstrated that this approach reduced the total number of bins required compared to the unrelaxed online approach. Similarly, ref. [9] proposed a solution involving a small buffer relaxation for an OBPP with a heterogeneous assortment of items.

Ref. [29] tackled the OBPP using a resource augmentation technique and limited repacking, which allowed for a finite number of repacking operations and additional bin space. Their study showed that these relaxations significantly improved the asymptotic competitive ratio (ACR). Ref. [10] further enhanced OBPP solutions by incorporating rearrangement and partial deletion strategies, significantly improving ACR through a combination of linear programming and heuristic algorithms.

Output maximization problems involve packing items with associated profits or weights; thus, the objective is to maximize the profit of the packed items. These problems are classified differently according to the assortment of items. Weakly heterogeneous assortments are known as the Single Large Object Placement Problem (SLOPP), while strongly heterogeneous assortments are referred to as the Single Knapsack Problem (SKP). Ref. [28] formulated a mixed integer programming (MIP) model for these problems but found it challenging to solve, with linear programming (LP) relaxation providing solutions that are far from the optimal ones. Ref. [27] addressed this by including balancing constraints in the MIP model and implementing a heuristic that outperformed the MIP in larger instances.

The latest research highlights the growing interest in combining AI techniques, particularly reinforcement learning, with traditional packing heuristics. For instance, ref. [20] formulated the Online 3D Bin Packing Problem (3D-BPP) as a Markov Decision Process (MDP) and addressed it using deep reinforcement learning (DRL), significantly improving performance. However, the results of DRL methods still trail behind human packers in real-world logistics, as highlighted by [5], who proposed a packing-and-unpacking mechanism to simulate human adjustments in packing tasks.

Ref. [4] further advanced this by demonstrating that DRL, combined with virtual simulation environments, can significantly optimize real-time decision-making in dynamic logistics systems. However, they noted challenges with generalizing the models across different logistical setups. While the potential of DRL is apparent, it remains hindered by its scalability to larger, more complex problems—especially when incorporating unpacking or rearranging strategies to optimize space usage [5].

Ref. [23] explored the online knapsack problem with buffering, showing that increasing the buffer size improved the objective function but made the problem harder to solve. Ref. [14] introduced a deletion decision in a knapsack problem but did not yield significant improvements.

Table 1 shows considerable interest in developing methodologies for the online packing problem, with research focusing on heuristic approaches, machine learning techniques, and even their hybridizing. However, few studies have considered strategies to make online packing problems more flexible, such as incorporating buffering and repacking. While much progress has been made in heuristic and AI-driven methods, their applicability to real-world, dynamic environments remains a significant area for improvement. This study aims to address this gap by exploring the incorporation of buffering and repacking strategies within various heuristic schemes to achieve better solutions for the packing problem and further validate the practical applicability of the proposed methods through real-world robotic trials.

4. Methodology

This section outlines the foundational strategies employed to solve the OKP. Section 4.1 explains the encoding of problem elements and how this encoding ensures that the relevant constraints are met. Section 4.2 delves into the core principles of the packing process, which serve as the basis for all the heuristics discussed in Section 4.3. Lastly, Section 4.4 presents the methodology for validating the algorithms using a robotic packing cell.

4.1. Encoding

This study employs the concept of maximal spaces, which are empty spaces within the container where boxes can be placed [33,34]. Figure 2 illustrates the creation of maximal spaces after a box is packed into a corner of the container, resulting in three distinct maximal spaces that may overlap.

4.1.1. Update of Maximal Spaces

At the beginning of the packing process, when no boxes have been placed in the container, there is a single maximal space equal to the container’s dimensions. As the packing process progresses, the number of maximal spaces changes dynamically. The procedure for updating the list of maximal spaces is outlined in Algorithm 1. This algorithm takes the current list of maximal spaces and the most recently packed box as inputs. It returns the updated list of maximal spaces.

Algorithm 1. Maximal Spaces Update.

Input: List MaximalSpaces: list of current maximal spaces, Box: last packed box Output: MaximalSpaces

1.  List InitialMaximalSpaces $\leftarrow$ MaximalSpaces 2.  for each Space in MaximalSpaces do 3.    if Space Overlaps with Box then 4.      MaximalSpaces $\leftarrow$ Remove(Space) 5.      MaximalSpaces $\leftarrow$ GenerateNewMaximalSpaces(Space, Box) 6.  while MaximalSpaces != InitialMaximalSpaces do 7.    InitialMaximalSpaces $\leftarrow$ MaximalSpaces 8.    for each Space in MaximalSpaces do 9.      for each Space’ in MaximalSpaces do 10.       if Space != Space’ then 11.         if Contained(Space, Space’) then 12.          MaximalSpaces $\leftarrow$ RemoveContained(Space, Space’) 13.         else if CanJoin(Space, Space’) then 14.          MaximalSpaces $\leftarrow$ Join(Space, Space’) 15.         else if CanExpand(Space, Space’) then 16.          MaximalSpaces $\leftarrow$ Expand(Space, Space’) 17. return MaximalSpaces

Algorithm 1 begins by copying the current list of maximal spaces (line 1). This copy allows for comparison to detect any changes. The algorithm then iterates over all spaces in the input list (line 2). If a space overlaps with the newly packed box (line 3), it is removed from the list (line 4), and new maximal spaces are generated and added to the list (line 5). The process for generating new maximal spaces is thoroughly described in [34].

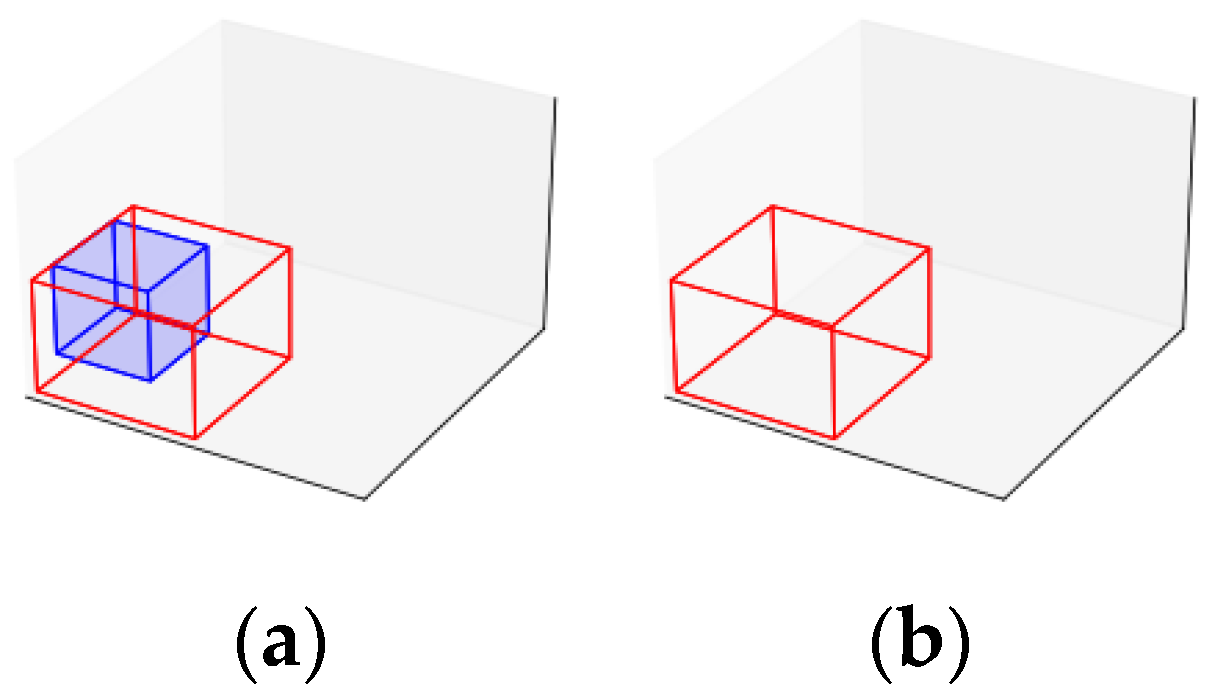
After generating new maximal spaces, an iterative procedure is executed until no differences remain between the modified maximal spaces list and the reference list (line 6). The first step in this iterative procedure is to update the reference list with the modified list (line 7) to track any changes during the iteration. Possible modifications involve evaluating each pair of different maximal spaces (lines 8 to 10). Suppose one maximal space is entirely contained within another (line 11). In that case, the contained space is removed from the list (line 12), as illustrated in Figure 3. If the spaces are not contained but can be merged (line 13), both spaces are removed and replaced with a larger combined space (line 14), as shown in Figure 4. Finally, suppose the maximal spaces cannot be merged but can be expanded (line 15). In that case, they are expanded, as illustrated in Figure 5 (line 16).

4.1.2. Constraint Handling

Using maximal spaces effectively addresses several constraints in the packing process. The containment constraint is naturally satisfied, as the entire container initially represents a single maximal space. As the packing process progresses, boxes are placed only within these maximal spaces, which are continually generated and updated based on the existing configuration within the container. The non-overlapping constraint is enforced because the list of maximal spaces is updated after a box is packed, ensuring that any spaces overlapping with the newly placed box are adjusted to form new non-overlapping spaces. Finally, the full support constraint is maintained, as the generation of maximal spaces is constrained by the upper surfaces of the packed boxes, as shown in Figure 3.

The only constraint not directly managed by maximal spaces is the valid orientation of boxes. This constraint is handled by generating two versions of each box, one for each valid orientation as dictated by the ‘this side up’ directive. Once one of these versions is packed into the container, the other is discarded.

4.2. General Packing Procedure

This section details the general packing strategy when buffering and repacking are considered. Algorithm 2 illustrates a packing iteration for all heuristics presented in Section 4.3. It takes a box and a packing pattern as input. The packing pattern includes lists of current maximal spaces, packed boxes, and boxes. The algorithm returns an updated packing pattern, placing the new box in the packed or buffered boxes. Five parameters control the execution of the algorithm:

• k: The maximum number of boxes in the buffer.
• r: The maximum number of boxes that can be unpacked for repacking.
• s: the number of packing scenarios executed.
• h: The packing heuristic used.
• Container: The container dimensions.

Algorithm 2. Packing Iteration.

Inputs: PackingPattern: {List MaximalSpaces: list of maximal spaces of the current packing pattern, List PackedBoxes: list of the packed boxes within the container, List Buffer: list of boxes located in the buffer}, Box: next box to be packed Parameters: k: number of buffer slots, r: number of repacking operations, s: number of packing scenarios, h: packing heuristic, Container: container dimensions Output: PackingPattern: {MaximalSpaces, PackedBoxes, Buffer}

1.  if GetSize(Buffer) < k then 2.    Buffer $\leftarrow$ Add(Box) 3.  else 4.    PackingPatternBest $\leftarrow$ PackingPattern 5.    for i = 1 to s do 6.      PackingPatterni $\leftarrow$ PackingPattern 7.      List TopBoxes $\leftarrow$ SelecRandomTopBoxes(PackedBoxesi, r) 8.      List Candidates $\leftarrow$ {Box, Bufferi, TopBoxes} 9.      PackedBoxesi $\leftarrow$ Remove(TopBoxes) 10.     MaximalSpacesi $\leftarrow$ Initiallize(Container) 11.     for each b in PackedBoxes do 12.       MaximalSpaces $\leftarrow$ MaximalSpaceUpdate(MaximalSpaces, b) 13.     while GetSize(Candidates) > 0 and all MaximalSpacesi are not visited do 14.       Space $\leftarrow$ SelectMaximalSpace(MaximalSpacesi, h) 15.       SelectedBox $\leftarrow$ SelectBox(Candidates, Space, h) 16.       if SelectedBox is null then 17.          MarkAsVisited(Space) 18.       Else 19.         Candidates $\leftarrow$ Remove(SelectedBox) 20.         NewPackedBox $\leftarrow$ Pack(Space, SelectedBox) 21.         PackedBoxesi $\leftarrow$ Add(NewPackedBox) 22.         MaximalSpacesi $\leftarrow$ MaximalSpaceUpdate(MaximalSpacesi, NewPackedBox) 23.     Bufferi $\leftarrow$ Candidates 24.     if GetUtilization(PackedBoxesi) > GetUtilization(PackedBoxesBest) and GetSize(Bufferi) ≤ k then 25.       PackingPatternBest $\leftarrow$ PackcingPatterni 26.   PackingPattern $\leftarrow$ PackingPatternBest 27. return PackingPattern

The general strategy in Algorithm 2 converts the online packing problem into a semi-online one, making packing decisions with as much information as possible. The algorithm begins by checking buffer availability; if a slot is available (line 1), the box is added to the buffer (line 2). Otherwise, the packing procedure begins if the buffer is full (line 3) by copying the current packing pattern (line 4), and several scenarios are executed according to the parameter s (line 5).

In each scenario, a copy of the packing pattern is made (line 6), and r top boxes are selected (line 7) for potential repacking. Along with the box on the conveyor belt, the boxes in the buffer and the top boxes form the candidate list (line 8). The top boxes are removed from the packed boxes list (line 9). Then, the maximal spaces list is initialized with the container’s dimensions (line 10) and updated with the packed elements (line 11) using Algorithm 1 (line 12).

Next, the algorithm iterates until all candidate boxes are packed or all maximal spaces are visited (line 13). Each iteration selects a maximal space (line 14) and a box that fits it (line 15) [35,36]. These selections follow the criteria within the heuristic used. If no box fits (line 16), the space is marked as visited (line 17). Otherwise (line 18), the selected box is removed from the candidate list (line 19) and packed within the selected maximal space (line 20). The new packed box is added to the packed boxes list (line 21), and the maximal spaces list is updated using Algorithm 1 (line 22).

After the scenario’s packing process, the buffer is updated with the unpacked boxes (line 23). Then, it is verified whether the best packing pattern must be updated with the scenario’s pattern. This occurs if the utilization of the scenario’s pattern is better than the utilization of the best pattern and the buffered boxes are less than k (line 24). In that case, the best packing pattern is updated with the packing pattern of the current scenario (line 25). Finally, the packing pattern is updated with the best pattern found across all scenarios (line 26) and returned by the algorithm (line 27).

4.3. Packing Heuristics

This section outlines the packing heuristics in lines 14 and 15 of Algorithm 2. The selection of heuristics in this study was guided by the need to balance computational efficiency and container utilization in online packing scenarios, where real-time decisions are required with limited information. Classical heuristics, such as stacking and best fit (discussed in Section 4.3.1 and Section 4.3.2, respectively), were selected for their simplicity and speed in determining box placement. Stacking prioritizes vertical space utilization by packing items in columns, although it can lead to underutilization of horizontal space. best fit, on the other hand, seeks to fill smaller gaps by placing boxes in the tightest possible locations, making it particularly effective in dense packing situations. These classical heuristics serve as a baseline for comparison with more complex or combined heuristics. By establishing this baseline, we can evaluate whether more sophisticated heuristics, combining classical methods or introducing more complex decision-making processes, outperform or underperform relative to the simpler, well-established approaches.

This study considers more complex heuristics like semi-perfect fit (described in Section 4.3.3). This approach reduces wasted space by fitting boxes as optimally as possible in one, two, or three dimensions, effectively minimizing gaps. However, this method is computationally more intensive, requiring a higher level of evaluation across dimensions.

Random fit (discussed in Section 4.3.4) is also considered due to its adaptability in dynamically adjusting the packing strategy based on the current container utilization. This heuristic increases the likelihood of selecting more sophisticated strategies (such as semi-perfect fit) as the container fills up while defaulting to simpler heuristics (like stacking) in the early stages when space is more abundant. This adaptability ensures that the method remains computationally efficient while also maximizing space usage as container occupancy increases.

Finally, complex fit (explained in Section 4.3.5) is an innovative approach entirely different from classical heuristics. It does not combine previous methods but proposes a novel way of optimizing space by planning for future placements based on expected box characteristics. This heuristic is particularly valuable in cases where future box arrivals follow predictable patterns, allowing for forward-looking optimization. By considering potential future boxes, complex fit enables a more holistic utilization of container space, making it suitable for environments where uniformity or predictability is expected in the arriving items.

These heuristics were chosen based on their proven effectiveness in maximizing container utilization while maintaining computational feasibility in online packing environments. The proposed methodology strategically combines classical, dynamic, and innovative approaches to tackle the challenges of the 3D knapsack problem.

4.3.1. Stacking

This heuristic builds vertical columns within the container, selecting the highest possible maximal space corresponding to the one with the smallest height since the top face of all maximal spaces coincides with the top face of the container. The heuristic then identifies the largest box (by volume) that fits within the selected space, aiming to maximize space utilization. Figure 6 shows an example of the packing sequence that may be generated with the stacking heuristic.

4.3.2. Best Fit

The best fit heuristic seeks to fill spaces by selecting the smallest maximal space available. The best-fitting box is chosen based on the difference between the box’s dimensions and those of the maximal space, as indicated in [36]. Figure 7 shows an example of the packing sequence that may be generated with the best fit heuristic.

4.3.3. Semi-Perfect Fit

This heuristic simultaneously selects a maximal space and a box to minimize wasted space across as many dimensions as possible. It considers scenarios where the box perfectly fits in three, two, or one dimension(s). The best fit heuristic is applied if none of these conditions are met. Figure 8 shows an example of the packing sequence that may be generated with the semi-perfect fit heuristic.

4.3.4. Random Fit

Combining the advantages of stacking and semi-perfect fit, this heuristic dynamically assigns probabilities to each method based on container utilization. As utilization increases, the probability of selecting each heuristic changes.

4.3.5. Complex Fit

This heuristic strives for maximal space utilization by assuming subsequent boxes will be identical (see Figure 9). It begins by evaluating perfect fits in three, two, or one dimension(s). If these are impossible, it selects the smallest maximal space and applies an extended best fit to a 100% utilization block formed by replicating the selected box in the same orientation.

4.4. Robotic Validation

Including buffering and repacking operations potentially increases container utilization but introduces additional movements, thereby consuming more time in practice. This study proposes a robotic validation to determine the time spent considering buffering and repacking operations. This determination is performed by measuring the time taken during the packing process.

Following the structure and classifications found in [8], the robotic packing cell used in this study consists of a UR10 robotic arm, which allows a maximum load of 10 kg. The cell is equipped with a VG10 suction-type gripper to handle the boxes, which grasps boxes from their top surface. Due to this gripper design, the limitation in this study is that only two orientations are allowed for each box, with rotations restricted to the vertical axis.

In this system, the boxes arrive via a conveyor belt (with no obstacles such as walls to overcome), and the robot can pick only one box at a time. The picked boxes are moved to the packing area, which consists of a pallet in this case (with no container walls present). The packing cell uses a single sensor, an RGB-D camera (Oak-D Lite), for perception. This sensor is attached to the robot’s end effector. It is fixed to the last joint of the robotic arm to avoid collisions between the camera and the gripper during box handling.

Three key modules work synergistically within this robotic packing cell: the vision module, the packing module, and the robotic trajectory module. The system initiates by positioning the robot over the conveyor belt while the belt is in motion. When the perception system detects a box, the belt stops, allowing the perception system to identify the dimensions, position, and orientation. The position and orientation data are then sent to the trajectory module, which determines the picking position for the robot. Simultaneously, the dimension data are sent to the packing module, which calculates the packing position for the box and returns this information to the trajectory module for the robot to execute the packing operation.

Once the robot places the box in the designated packing position, it returns to its initial position over the conveyor belt, and the belt resumes motion, starting a new iteration of the process. It is worth noting that, as highlighted in [8], buffering and repacking—the focus of this study—are considered critical constraints in automated environments. By integrating these operations into the robotic packing system, this study explores the trade-off between increased container utilization and the time required for these additional movements.

5. Computational Experiments and Results Analysis

The heuristics were implemented in Python (3.9.13), and experiments were conducted on a MacBook Pro running macOS Big Sur, equipped with a 2.9 GHz Dual-Core Intel Core i5 processor (5th generation) and 8 GB RAM manufactured in Shangai, China by Tech Chom (Shangai) Computer Co.

The datasets used include RS, Cut-1, and Cut-2 from [20], each containing 2100 instances designed to test the algorithms. These datasets are among the few publicly available for the online knapsack problem (OKP), making them particularly valuable for benchmarking. Additionally, other authors have widely used these datasets to compare the performance of methodologies addressing online problems. Cut-1 and Cut-2 allow for perfect packing, while RS consists of randomly generated sequences of boxes to be packed into a 10 × 10 × 10 container. It is worth noting that these instances are specific to the OKP, not the Online Bin Packing Problem (OBPP). Instances for OBPP were not used because they are designed for multiple containers. In contrast, the OKP focuses on a single container.

5.1. Calibration of the Random Fit Heuristic

The random fit heuristic requires assigning probabilities for selecting between stacking and semi-perfect fit heuristics. Two probability levels (33.33% and 66.67%) were used. Initially, 66.67% was allocated to the stacking heuristic and 33.33% to the semi-perfect fit heuristic because building columns (stacking) is a solid early strategy. As packing progresses and the complexity of maximal space distribution increases, the semi-perfect fit heuristic, which fills gaps between columns, is favored. Hence, by the end of the packing process, the stacking heuristic’s probability reduces to 33.33%, while the semi-perfect fit heuristic rises to 66.67%.

The point at which this probability shift occurs is the tuning parameter of this heuristic. This study suggests that the shift depends on container utilization. Therefore, all three datasets were tested without buffering or rearrangement and with one valid orientation for the boxes, shifting every 10% of volume utilization.

Table 2. Best shifting points of the probabilities to select the stacking and the semi-perfect fit heuristics.

Dataset	Threshold (%)	Utilization (%)
Cut-1	10	57.67
Cut-2	0	57.78
RS	10	45.10

shows the best shifting points for each dataset.

The best shifting point for Cut-1 and RS is 10%, while for Cut-2, it is 0%. Taking the value that works best for most instances, the random fit heuristic’s chosen shifting point is 10%, meaning the probabilities behave as shown in Figure 10.

5.2. Comparisons with Methodologies from the Literature

Unfortunately, online packing problems lack a common repository of instances, limiting the comparisons with the literature [8]. However, the instances from [20] are available online, allowing comparisons between the proposed heuristic and the method from [20]. It is worth noting that direct comparison is challenging because of the methodological differences. Heuristics cannot be directly compared with machine learning approaches, like those proposed in [20], because machine learning requires a training phase. In contrast, heuristics rely on fast decision-making rules. Moreover, machine learning models may be overfitted to specific instance types. Therefore, the comparisons provided here are for reference purposes only.

Table 3. Comparison of container utilization (percentage) with literature studies. Values in bold indicate the best value for the instance.

	Dataset	[20]	This Study
			Stacking	Best Fit	Semi-Perfect Fit	Random Fit	Complex Fit
Fixed Orientation	CUT-1	73.4	51.48	55.77	54.32	57.25	55.77
	CUT-2	66.9	52.27	56.30	55.72	57.73	56.30
	RS	50.5	49.40	45.84	44.39	45.05	45.84
This Side Up	CUT-1	76.2	55.38	61.38	60.19	62.37	61.81
	CUT-2	70.2	55.91	61.95	61.14	63.38	62.07
	RS	62.1	49.40	55.77	53.81	55.24	56.00

compares the container utilization achieved by the machine learning approach in [20] and the proposed heuristics. Results indicate that including two valid orientations (“this side up”) yields better container utilization than using just one fixed orientation. This is because more valid orientations increase the search space, allowing for better solutions. The results show that machine learning approaches currently outperform classical heuristics for online packing problems, suggesting the need for more advanced heuristics to address this issue effectively.

In comparing the heuristic algorithms developed in this study with a deep learning-based approach from the literature, several computational trade-offs become evident. Heuristic methods are computationally efficient, particularly in online settings where real-time decision-making is crucial. These methods provide a predictable and relatively low computational cost, making them suitable for scenarios where quick packing decisions are needed without heavy reliance on computational resources.

On the other hand, deep learning approaches provide the advantage of adaptability by training on historical data. DRL, for instance, can learn intricate packing patterns and optimize container utilization over time. However, these approaches have significant computational trade-offs: the training phase is highly resource-intensive, demanding considerable time and powerful hardware. Additionally, they are affected by the curse of dimensionality, which limits their scalability and applicability to larger, more complex problems [4].

Additionally, while deep learning-based approaches can outperform heuristics in scenarios with extensive historical data, they face limitations related to overfitting and generalizability. The performance of such models may degrade when dealing with items or scenarios that significantly deviate from the training data, making them less reliable in unpredictable environments. In contrast, heuristic methods maintain consistent performance across different scenarios, albeit with less capacity to learn from past experiences [15].

Considering these trade-offs, a hybrid approach incorporating machine learning elements into heuristic frameworks might balance adaptability and computational efficiency. Future research could explore combining the adaptability of deep learning with the simplicity and efficiency of heuristics to create a robust packing strategy that addresses the weaknesses of each method.

5.3. Results with Buffering and Repacking

This section explores the impact of buffering and rearrangement on container utilization within the random fit and complex fit heuristics. Each heuristic was tested with varying numbers of buffer slots and boxes eligible for rearrangement, ranging from 0 to 5. The selection of buffer sizes and repacking values in this study was guided by the principle that, in general, the more buffer slots and repacking operations are allowed, the better the expected results regarding container utilization. However, there is a point of diminishing returns where increasing these operations no longer leads to significant improvements. This point is a natural limit for evaluating results. However, the physical limitations of the packing environment have to be considered.

In this context, the buffer sizes range from 0 to 5, allowing the system to have limited but flexible options for temporary storage and rearrangement options. This range reflects the balance between the expected performance improvements from buffering and the physical limitations of the packing environment, such as space and time constraints. Larger buffer sizes could lead to better outcomes. However, they would require more space, and managing large buffers would increase the system’s complexity.

Similarly, the number of repacking operations was capped at 5 to maintain the focus on the problem’s online framework, where decisions must be made as items arrive. Allowing unlimited repacking would shift the problem closer to an offline setting, where all boxes are available for optimization before placement, defeating the purpose of real-time decision-making.

Experiments were conducted on the three datasets using one and two valid box orientations. Results presented in

Table 4. Results of the complex fit and random fit heuristics when considering buffering and rearrangement with a single valid orientation for the boxes. Values in bold indicate the best value for the instance.

B	R	CUT-1					CUT-2					RS
		S	BF	SPF	RF	CF	S	BF	SPF	RF	CF	S	BF	SPF	RF	CF
0	0	51.48	55.77	54.32	57.25	55.77	52.27	56.30	55.72	57.73	56.30	49.40	45.84	44.39	45.05	45.84
0	1	53.23	58.75	56.98	58.85	58.22	53.12	58.58	57.47	58.95	58.16	51.78	48.79	47.15	48.08	48.06
0	2	53.63	60.27	59.09	60.86	59.65	53.88	60.05	59.66	61.69	59.76	52.90	51.10	49.42	51.13	49.84
0	3	54.87	61.70	61.10	62.82	61.14	54.82	61.42	60.99	62.95	60.98	54.22	52.67	50.61	52.95	51.37
0	4	55.33	62.36	62.06	64.28	61.77	55.59	62.67	62.12	64.80	61.72	55.22	53.75	51.90	54.58	52.30
0	5	55.63	63.32	62.72	65.59	62.14	55.79	63.32	63.05	65.40	62.49	55.52	54.64	52.61	55.47	52.67
1	0	58.43	62.84	62.09	63.47	62.37	58.92	62.95	62.49	63.56	62.92	58.80	55.17	54.33	55.02	54.84
1	1	58.94	65.01	64.25	65.22	64.28	59.29	64.77	64.13	65.23	64.55	60.27	57.25	55.53	56.40	56.26
1	2	58.95	66.27	65.68	67.24	65.99	59.17	66.43	65.68	66.72	65.75	59.65	58.73	57.24	58.90	56.98
1	3	59.21	67.84	66.68	68.22	66.33	59.37	66.90	66.62	68.26	66.52	59.87	60.21	58.45	59.70	58.27
1	4	59.18	68.20	67.44	69.47	66.96	59.17	67.96	67.33	69.50	67.23	59.71	60.80	59.24	61.28	59.11
1	5	59.36	68.55	67.96	70.20	67.56	59.34	68.57	68.07	70.50	68.01	59.78	61.58	59.48	62.34	59.03
2	0	63.61	67.89	67.52	67.98	68.13	64.02	67.81	67.34	67.96	68.01	64.83	62.08	61.07	62.00	61.75
2	1	63.97	69.56	69.15	69.92	69.49	63.89	69.63	69.32	70.03	69.65	65.32	64.03	62.77	63.59	62.94
2	2	62.96	70.91	70.35	70.89	70.14	63.22	70.71	69.91	70.72	70.17	64.47	64.68	63.55	64.58	63.82
2	3	62.62	71.52	70.86	72.03	70.54	62.59	71.37	70.60	71.75	71.19	63.91	65.37	63.80	65.61	64.36
2	4	62.23	72.09	71.41	72.79	71.43	61.96	71.66	71.54	72.62	71.26	62.54	66.03	64.39	66.50	64.04
2	5	61.98	72.28	71.78	73.05	71.43	61.74	72.30	71.36	73.01	71.53	62.46	66.49	64.56	66.24	64.61
3	0	65.96	70.33	70.31	70.16	70.49	66.15	70.32	70.33	70.46	70.26	68.22	65.78	65.13	65.85	66.09
3	1	66.77	72.30	72.06	72.39	72.16	67.15	71.95	72.33	72.19	72.02	69.19	67.96	67.47	67.98	67.43
3	2	66.47	73.42	73.16	73.29	72.88	66.60	73.10	72.79	73.17	72.97	68.18	69.14	68.67	69.36	68.94
3	3	65.30	73.86	73.68	73.96	73.65	65.28	73.78	73.35	74.16	73.45	66.98	69.80	69.05	69.95	69.29
3	4	63.89	74.15	73.71	74.87	73.42	64.24	74.14	73.39	74.80	73.67	65.54	70.24	68.88	70.26	69.82
3	5	62.91	74.15	73.48	74.90	73.40	63.35	74.30	73.74	75.10	73.59	64.44	70.26	68.38	70.29	69.45
4	0	67.87	71.96	71.73	71.74	72.18	68.06	71.85	71.73	71.71	72.00	70.77	68.50	68.24	68.69	68.79
4	1	68.72	73.77	73.67	73.69	73.69	68.65	73.28	73.65	73.65	73.73	71.88	70.72	70.79	71.03	71.31
4	2	67.86	74.51	74.59	74.59	73.87	68.31	74.35	74.79	74.62	74.56	71.17	72.18	71.91	72.29	72.11
4	3	66.75	75.12	74.90	75.19	74.66	66.92	74.97	74.75	75.25	74.59	70.02	72.79	72.34	73.06	72.57
4	4	65.68	75.36	75.09	75.40	74.88	66.07	75.13	75.13	75.51	74.82	67.39	73.37	72.78	73.49	73.06
4	5	64.83	75.57	74.97	75.74	74.51	64.76	75.56	75.31	75.83	75.05	66.20	73.49	72.23	73.47	73.19
5	0	68.94	72.97	72.75	72.72	73.01	68.86	72.84	72.95	72.84	72.98	72.62	70.79	70.34	70.94	71.19
5	1	69.77	74.22	74.57	74.46	74.33	69.94	74.48	74.45	74.65	74.63	73.91	72.82	72.82	73.47	73.10
5	2	69.02	74.74	74.85	75.00	74.58	69.40	75.16	75.14	75.37	75.13	73.58	74.15	74.45	74.72	74.32
5	3	67.61	75.26	75.24	75.30	74.77	68.00	75.16	75.45	75.53	75.14	72.21	74.94	75.27	75.63	75.01
5	4	65.97	75.42	75.49	75.94	74.43	66.51	75.63	75.59	76.19	75.23	70.56	75.24	75.49	75.72	75.70
5	5	64.74	75.73	75.28	75.92	74.65	65.57	75.86	75.37	76.15	75.21	68.38	75.94	75.22	75.88	75.85

and

Table 5. Results of the complex fit and random fit heuristics when considering buffering and rearrangement with two valid orientations for the boxes (this side up). Values in bold indicate the best value for the instance.

B	R	CUT-1					CUT-2					RS
		S	BF	SPF	RF	CF	S	BF	SPF	RF	CF	S	BF	SPF	RF	CF
0	0	55.38	61.38	60.19	62.37	61.81	55.91	61.95	61.14	63.38	62.07	49.40	55.77	53.81	55.24	56.00
0	1	56.72	64.09	62.80	70.58	64.10	57.17	64.18	62.49	70.29	69.43	51.78	58.48	56.46	65.47	65.24
0	2	57.49	65.75	65.00	74.25	65.19	58.22	65.69	65.03	74.39	74.37	52.90	60.49	58.61	70.84	70.84
0	3	58.49	67.06	66.67	76.28	66.39	58.57	66.93	66.86	76.26	76.47	54.22	61.91	59.87	73.88	74.50
0	4	59.07	67.79	68.01	77.27	67.67	59.14	68.03	68.02	77.30	77.95	55.22	62.91	61.25	75.93	76.37
0	5	59.39	68.99	69.11	77.88	68.18	59.77	68.73	68.46	77.96	78.43	55.52	63.61	62.02	77.40	78.17
1	0	63.10	69.65	69.15	64.41	69.74	63.53	69.20	69.02	64.97	64.48	58.80	65.29	64.67	57.37	58.25
1	1	63.60	71.26	70.82	71.71	71.18	63.88	70.73	70.42	71.58	70.89	60.27	66.81	66.11	66.67	66.56
1	2	63.68	72.29	72.00	75.65	71.91	63.98	71.89	72.03	75.82	75.58	59.65	68.00	66.99	72.34	72.35
1	3	64.01	73.16	73.14	77.82	72.66	63.77	72.91	72.70	77.74	77.94	59.87	69.01	68.01	75.99	76.00
1	4	63.64	73.67	73.68	78.45	73.48	63.94	73.61	73.58	78.79	78.69	59.71	69.49	68.65	77.69	78.38
1	5	64.00	74.40	74.16	78.68	73.37	63.74	73.81	73.96	78.78	79.11	59.78	70.14	69.19	79.64	80.03
2	0	68.21	73.78	74.03	65.96	74.25	68.47	73.71	73.89	67.05	65.51	64.83	70.61	70.59	60.04	59.94
2	1	68.16	75.17	75.53	72.98	75.31	68.10	75.57	75.32	72.76	71.75	65.32	72.20	72.04	68.55	67.31
2	2	67.53	75.78	76.41	76.17	76.42	68.09	76.14	76.01	76.50	76.56	64.47	73.43	72.98	73.56	73.06
2	3	67.16	76.62	77.02	78.28	76.76	67.04	76.81	76.28	78.37	78.25	63.91	74.08	73.34	76.84	77.12
2	4	66.79	76.66	76.96	78.98	76.90	66.53	76.79	76.98	79.50	79.30	62.54	73.99	74.03	79.02	79.44
2	5	66.37	77.12	76.99	79.01	77.05	66.43	77.24	77.18	79.30	79.24	62.46	74.49	73.51	80.53	81.10
3	0	70.82	76.17	76.54	68.07	76.54	70.73	75.99	76.00	68.39	66.78	68.22	73.92	74.11	62.23	61.42
3	1	71.11	77.24	77.51	74.21	78.13	71.50	77.45	77.84	73.89	72.45	69.19	75.74	75.65	69.23	68.64
3	2	70.43	78.04	78.48	77.31	78.56	70.07	78.01	78.28	77.24	76.69	68.18	76.71	76.98	74.44	73.40
3	3	69.59	78.43	78.79	78.90	78.63	68.92	78.38	78.80	78.96	78.98	66.98	77.13	77.04	77.61	77.75
3	4	68.27	78.71	78.63	79.18	78.47	68.32	78.64	78.59	79.77	79.48	65.54	77.80	77.33	79.94	80.05
3	5	67.27	78.89	78.87	79.28	78.27	67.63	78.64	79.18	79.76	79.10	64.44	77.74	77.22	81.21	82.01
4	0	72.40	77.31	77.56	69.45	77.55	72.44	76.98	77.49	69.68	67.73	70.77	75.70	76.11	63.67	62.03
4	1	72.56	78.23	78.84	75.04	78.71	72.64	78.12	79.08	74.69	73.48	71.88	77.34	78.26	70.49	68.41
4	2	71.37	78.51	79.26	77.60	78.82	71.88	78.90	79.47	77.85	77.16	71.17	78.70	79.49	74.87	73.64
4	3	70.50	78.85	79.37	79.14	79.16	70.83	79.13	79.46	79.12	78.77	70.02	79.16	80.11	77.91	77.83
4	4	69.17	79.15	79.49	79.55	79.14	69.53	79.30	79.66	80.04	79.35	67.39	79.63	79.74	79.98	80.36
4	5	67.97	3.97	79.43	79.40	78.85	68.80	79.29	79.98	79.75	79.14	66.20	79.77	79.79	81.76	82.43
5	0	73.24	77.51	78.35	70.67	78.27	73.45	77.88	78.45	70.69	68.37	72.62	77.47	77.87	65.09	62.64
5	1	73.23	78.32	78.94	75.40	78.66	73.43	78.64	79.14	75.89	73.51	73.91	78.93	80.23	71.11	68.93
5	2	72.00	78.47	78.97	77.93	78.82	72.43	78.74	79.58	78.03	77.64	73.58	79.93	81.36	74.96	73.86
5	3	70.53	78.75	79.24	79.79	78.60	71.14	79.21	79.56	79.56	78.32	72.21	80.49	82.02	77.78	77.68
5	4	69.23	79.18	79.29	79.33	78.09	69.62	79.15	79.43	80.07	79.42	70.56	80.92	82.25	80.33	80.49
5	5	68.70	78.91	79.07	79.65	78.12	69.06	79.42	79.50	79.96	79.24	68.38	81.28	82.23	81.98	82.32

reveal that the random fit heuristic generally outperforms the complex fit heuristic across most scenarios.

Table 4 shows that all heuristics benefit from increased buffering and rearrangement, with the random fit heuristic consistently yielding higher container utilization. Adding one more box to the rearrangement process for the random fit heuristic can increase container utilization by approximately 1%, and the other heuristics show slightly smaller gains. The RS dataset, in particular, exhibits more pronounced improvements due to its initially lower utilization rates without rearrangement.

Buffering has a more significant impact than rearrangement on container utilization. Increasing buffer slots by one results in over a 2% increase for the Cut-1 and Cut-2 datasets and nearly a 4% increase for the RS dataset. Additionally, the computational load of implementing buffering and rearrangement is minimal, with each execution taking less than 200 ms.

Table 5 demonstrates that container utilization improves further when two valid box orientations are considered, as the additional orthogonal positions allow for better placements. While all heuristics produce similar results, the random fit heuristic tends to deliver better outcomes. However, the gains in container utilization from buffering and rearrangement are slightly smaller than those in Table 4.

Overall, buffering and rearrangement in the heuristics significantly enhance performance, surpassing previous best-known solutions. Moreover, these relaxations enable the heuristics to achieve similar container utilization across all datasets, even in complex instances like RS, where no optimal solution is known.

5.4. Validation with a Robotic Packing Cell

This study uses a robotic packing cell to analyze the impact of buffering and repacking on packing time. The system comprises a conveyor belt, a UR10 industrial manipulator, an Oak-D Lite vision system on the end effector, and a VG10 vacuum gripper (Figure 1). The number of buffer slots and repacking boxes varies from zero to three. The buffer values were limited to three due to the available space in the laboratory for the packing cell, which constrained the physical setup. Additionally, the number of repacking operations was capped at three, as trends in performance could already be observed within this range. Extending beyond this would not significantly alter the results and would incur additional costs, particularly in terms of time, since conducting physical experiments is resource-intensive. The random fit heuristic was chosen based on its superior performance in previous results. Ten test cases were for the packing procedure; all of them used five box types (

Table 6. Dimensions of the box types used for validation in the robotic packing cell experiments.

Box Type	Length	Width	Height	Quantity
1	12	15	12	10
2	12	19	16	10
3	15	30	20	10
4	25	40	30	10
5	30	50	40	10

) and a container with dimensions 120 × 100 × 160. The container is significantly larger than the total volume of the boxes, allowing all of them to fit. The difference across test cases is the sequence of the boxes on the conveyor belt.

Table 7. Average packing times (in seconds) for the 10 test cases, incorporating buffering and repacking, evaluated at three different robotic arm accelerations.

		Acceleration [rad/s2]	Rearrangement
			0	1	2	3
Buffer Slots	0	0.5	722.24	1348.82	2052.95	2673.66
		1	555.54	1062.86	1631.11	2132.52
		2	437.01	873.74	1360.28	1790.28
	1	0.5	719.63	1341.54	1934.96	2378.75
		1	648.49	1125.68	1595.83	1950.18
		2	602.35	989.32	1383.46	1683.53
	2	0.5	719.63	1796.20	1901.18	2146.81
		1	648.49	1495.72	1579.99	1775.64
		2	602.35	1308.42	1379.88	1545.34
	3	0.5	719.94	1394.79	1805.54	2066.73
		1	646.75	1179.91	1507.76	1716.20
		2	599.06	1044.87	1322.29	1499.17

presents the results of physical experiments on packing time, in which the robot was tested at three accelerations. The first acceleration, 0.5 rad/s², corresponds to a standard one that ensures no damage to the robot. At one rad/s², the robot operates without affecting packing performance. At 2 rad/s², however, the acceleration disrupts the experiments by causing the robot’s base to shift, leading to misalignments and eventual collisions.

The results in Table 7 indicate that rearrangement operations take significantly longer than buffer operations, likely due to the frequent reprocessing required each time a box is added or adjusted within the packing pattern. Rearrangement involves complex movements, including unpacking and repacking, which significantly increases operational time, especially as the number of repacking operations grows. In contrast, buffering primarily serves as temporary storage, and the proximity of the buffer to the packing area or conveyor belt minimizes delays in transferring boxes. Consequently, increasing the number of buffer slots provides greater flexibility in packing decisions and does not significantly increase packing time. Therefore, these results suggest that it is recommended to prioritize buffering over repacking operations in time-sensitive scenarios, as buffering improves packing efficiency without significantly increasing the packing time. Repacking operations should be reserved for situations where space utilization is critical.

While buffering and repacking strategies have shown significant potential in improving container utilization, their application in fast-paced or larger-scale environments presents clear challenges. There is a notable impact when these strategies are implemented, as the additional time required for buffer management and repacking operations may become a bottleneck, especially when high throughput is essential. Buffering, in particular, requires more space than repacking due to the need for temporary storage areas, which can further constrain available resources in such environments. To fully capitalize on these strategies, there is a need for the development of advanced algorithms, possibly leveraging machine learning techniques, that can optimize their usage. These algorithms would be critical in minimizing the number of buffering and repacking operations applied at any given location, ensuring that the trade-offs between space utilization and packing time are favorable. In larger-scale or high-speed environments, selectively applying these strategies, supported by real-time decision-making algorithms, will be essential to prevent adverse impacts on overall system efficiency.

Considering the results from Table 5 and Table 7, it is evident that buffering has a greater impact on container utilization and takes significantly less time than rearrangement operations. Based on this, we suggest that an optimal strategy for designing an online packing system should prioritize the maximum number of buffering operations over rearrangement. Even though the results come from different instances, we can infer that, for example, if only three buffer operations are considered without any rearrangement, container utilization tends to increase by slightly more than 10%. At the same time, the packing time becomes approximately three times longer compared to a scenario with no buffering or rearrangement. For future research, it would be valuable to conduct robotic trials where the boxes to be packed have a total volume greater than the container to understand better the impact of packing time and container utilization percentage that strategies like buffering and repacking may have. However, based on the findings of this study, we recommend focusing more on evaluating the buffering strategy than on repacking.

6. Conclusions

The three-dimensional online knapsack packing problem was tackled using heuristic methods, proposing five approaches: stacking, best fit, semi-perfect fit, random fit, and complex fit. The results identified random fit and complex fit as the most effective heuristics. Incorporating buffering and rearrangement ranging from 0 to 5, showed that buffering had a more significant impact on improving container utilization than rearrangement. Buffering increased utilization by over 2% per slot, while rearrangement provided nearly a 1% improvement per box subjected to rearrangement operations.

Comparing the top heuristics with a machine learning approach revealed that the heuristics underperformed in container utilization. However, including buffering and rearrangement allowed the heuristic methods to achieve superior solutions for the given datasets.

The robotic validation shows that rearrangement operations significantly increase packing time compared to buffer operations. This increase is because rearrangement can happen each time a box is placed in the packing pattern, while buffer operations involve temporary storage that, if located near the conveyor belt or packing area, does not add much time.

Future research should explore the integration of hybrid heuristic-AI models, which combine the flexibility and adaptability of heuristic methods with the predictive capabilities of AI. Such approaches could further optimize the trade-offs between packing efficiency and computational time, particularly in complex, real-time scenarios. Additionally, research could focus on developing algorithms that better handle the dynamic nature of buffering and repacking, possibly by incorporating reinforcement learning to optimize these operations. Exploring these avenues could lead to more robust, adaptive solutions that maintain high container utilization while minimizing operational costs and time.