Abstract
The emergence of higher-dimensional evolution equations in dissimilar scientific arenas has been on the rise recently with a vast concentration in optical fiber communications, shallow water waves, plasma physics, and fluid dynamics. Therefore, the present study deploys certain improved analytical methods to perform a solitonic analysis of the newly introduced three-dimensional nonlinear dynamical equations (all within the current year, 2024), which comprise the new (3 + 1) Kairat-II nonlinear equation, the latest (3 + 1) Kairat-X nonlinear equation, the new (3 + 1) Boussinesq type nonlinear equation, and the new (3 + 1) generalized nonlinear Korteweg–de Vries equation. Certainly, a solitonic analysis, or rather, the admittance of diverse solitonic solutions by these new models of interest, will greatly augment the findings at hand, which mainly deliberate on the satisfaction of the Painleve integrability property and the existence of solitonic structures using the classical Hirota method. Lastly, this study is relevant to contemporary research in many nonlinear scientific fields, like hyper-elasticity, material science, optical fibers, optics, and propagation of waves in nonlinear media, thereby unearthing several concealed features.
Keywords:
higher-order evolution equations; Kairat equations; Boussinesq equation; KdV equation; Kudryashov method; solitonic analysis MSC:
76B05; 35B35; 35Q53
1. Introduction
Recently, the demand for higher-dimensional evolution equations has been on the rise due to their high precision in “perfectly describing a variety of nonlinear phenomena in science and technological domains” [1]. Dissimilar scientific arenas such as optical fiber communications, shallow water waves, plasma physics, fluid dynamics, and materials science and engineering, to mention but a few, heavily depend on nonlinear dynamical equations to model various scientific processes. “Certainly, the study of these models analytically, especially higher-order ones, means a lot to researchers working in various fields of relevance, as the underlying phenomena are entirely unearthed …” [1]. Application-wise, higher-dimensional equations model the propagation of light beams in a nonlinear medium, describe the dynamicity in photonic and optical devices, utilizing solitonic properties for effective pulsefication transmission, and also play a vital role in theoretical physics, where M- and string theorem are used in the understanding of wave dynamics and soliton solutions to mention but a few [2,3]. Moreover, reviewing the wide area of evolution equations is demanding, and requires additional efforts in line with the vast existing literature. However, one may encounter the early models, which include the classical Boussinesq equation [4] and the renowned Korteweg–de Vries (KdV) equation [5], which play vital parts in describing water waves among others. In addition, the classical Boussinesq equation was first initiated by Joseph Boussinesq in the year 1871, which then mathematically affirmed the findings of John Scott Russell [6], a Scottish civil engineer and architect on the concept of solitary waves that was primarily discovered in the 1830s.
Moreover, away from the mathematical modeling of physical processes using both the real and complex-valued (Schrodinger) nonlinear evolution equations, it is indeed pertinent to equally extend the discussion to nonlinear evolution equations to mathematical methods, mainly analytical, that exactly predict the evolution of fields in the underlying medium. Hence, several scientists have devised many promising analytical and semi-analytical methods, which squarely portray the resulting wave fields and many other underlying physical assumptions under consideration. In fact, we begin by calling the efficient Kudryashov method by Nikolay A. Kudryashov [7], which yields exact structures for nonlinear evolution equations in terms of exponential functions. In addition, this method solves many dynamical models and further enjoys various extensions to reveal several other exact solutions, including the modified Kudryashov method [8], and the enhanced Kudryashov method [9], to mention a few. Additionally, several other mathematical methods comprise the modified Riccati method [10], the exponential function method [11], the Lie symmetry approach [12], the sine-Gordon expansion analytical approach [13], and the tanh function expansion method [14] among others. In particular, the tanh function expansion method is a renowned analytical method that yields exact solutions in terms of and periodic functions. Later, this method underwent several modifications to accommodate several other exact solutions, including the hyperbolic and functions; we mention the modified extended tanh function method [15,16] in this regard. In the same vein, we equally extend the literature section to mention a few semi-analytical methods like the Adomian decomposition technique [17], variational semi-inverse principle [18], the collective variable technique [19], and the iteration variation method [20]; see also [21,22,23] for more studies on both the modeling and solution methods for tackling various physical scenarios.
However, motivated by the recent quest by many scientists to devise more higher-dimensional nonlinear evolution equations in favor of their high precision in “perfectly describing a variety of nonlinear phenomena in science and technological domains”, the present study thus aims to carry out a solitonic analysis of some of the recently introduced three-dimensional (3 + 1) nonlinear dynamical equations, thereby augmenting the findings at hand that mainly deliberate on the satisfaction of Painleve’s integrability property and the existence of solitonic structures using the classical Hirota method; that is, ensuring the models are integrable and further admit exponential function solutions. More precisely, the study analytically examines the following new three-dimensional equations: the new (3 + 1) Kairat-II and the new (3 + 1) Kairat-X nonlinear equations by Wazwaz [24] introduced in 2024, the new (3 + 1) Boussinesq type nonlinear equation by Wazwaz et al. [25] introduced in 2024, and the new (3 + 1) generalized nonlinear Korteweg–de Vries (KdV) equation by Ismaeel et al. [26] introduced in the year 2024 as well.
Certainly, the study of these new models, all introduced within the current year (2024), will pave the way to new revelations in the realm of higher-order nonlinear evolution equations, which play roles in the fields of fluid mechanics and hydrodynamic waves, among others. In addition, in analyzing these models, two of the considered methods, including the modified Kudryashov method [8], and the modified extended tanh method [15,16] are utilized for a solitonic analysis in line with their effectiveness, constructing several solutions for the governing nonlinear evolution equations. What is more, the solutions to be acquired are graphically analyzed, via the help of Mathematica software to further examine the variational effects of some of the parameters involved. Moreover, the study of these new equations, especially with regard to constructing assorted wave solutions, is set to widens the framework of the models to encompass more possibilities of unearthing untapped advantages of the models. Moreover, part of the significance of this analytical study is to create more grounds for both numerical and experimental analyses; in addition, various fluid flow phenomena are fully uncovered through an analytical examination of this nature. Furthermore, the paper is organized in the following way: Section 2 outlines the governing equations. Section 3 gives the outline of the considered analytical methods. Section 4 constructs exact solutions for the governing models using the considered methods. Section 5 gives the graphical illustrations and further discusses some of the obtained solutions, while Section 6 submits some concluding notes.
2. Governing Newly Extended Nonlinear Equations
This section gives the outline of examining newly extended nonlinear evolution equations. These equations are essential for several scientific applications, including mathematical physics, plasma physics, nonlinear optics, solitonic theory, and fluid dynamics, to mention but a few. In particular, the field of fluid dynamics enjoys much from higher-dimensional models as they effectively model various fluid phenomena, including the interaction of waves with obstacles, internal waves in turbulence, and oceans, in addition to their relevance in modeling stable waves in dissimilar fluid media. Moreover, we provide in what follows some of the newly extended Kairat equations of interest.
2.1. Newly Extended Kairat Equations
In 2024, Wazwaz [24] gave new extensions for the famous Kairat evolution equations that found various applications in many fields like wave propagation, solitons, integrable systems, and fluid dynamics among others. In fact, these equations help in the description of soliton solutions, which are localized, preserving wave packets that maintain their shapes; they also model the interaction of nonlinear waves in plasmas [2]. In addition, the equations offer insights into the propagation of waves in complex media, in addition to their relevance in the study of hydrodynamic waves in higher-dimensional fluid systems and multi-phase fluid processes, to mention a few [3]. What is more, the newly extended Kairat evolution equations of interest read as follows:
- (i).
- Extended Kairat-II equation
- (ii).
- Extended Kairat-X equationwhere in the above equations are the wave fields, with , and for as non-zero constants. Notably, the above extended Kairat equations differ in the first and the fifth terms, in addition to the difference in the constant coefficients in the third and fourth terms. In fact, the second-order temporal derivative in (2) together with the second-order spatial derivative in (1) are what sets the two models apart, thereby behaving differently and modeling different processes.
2.2. Newly Extended Boussinesq Type Equation
Th newly extended (3 + 1) Boussinesq type nonlinear equation by Wazwaz, Alhejaili, and El-Tantawy (2024) reads as follows [25]
where is the wave solution of the equation. This equation has various applications. In particular, we mention its application in modeling shallow water waves. In fact, the Boussinesq equation helps in the characterization and forecasting of wave transmission in shallow waters. In addition, the model is essential to various wave types, including the interaction of solitons, and cnoidal waves in various waters [27]. Moreover, one may look at the current equation to align with the considered extended Kairat Equations (1) and (2) and think that the extended Boussinesq type equation only has a less temporal derivative presence apart from the leading second-order temporal derivative. However, as can be shown in the subsequent section, all three equations mentioned in (1)–(3) virtually admits the same structural formation after deploying a relevant wave transformation, which recast the equations to the corresponding ordinary differential equations.
2.3. Newly Extended Generalized KdV Equation
The newly extended (3 + 1) generalized nonlinear KdV equation by Ismaeel, Wazwaz, and El-Tantawy (2024) has the following structure [26]
where is the wave field, while , and are constants. Moreover, this equation generalizes the evolution of waves in fluids like internal and shallow water waves in three-dimensional spaces. More so, it assists in the perfect description of stable wave interaction over time. In addition, the equation models acoustic waves in nonlinear magnetized media and has notable uses in the design and analysis of optical devices in telecommunication systems in higher dimension.
3. Analytical Methods Considered
The present part of the manuscript outlines the steps taken for the solitonic analysis of the examining dynamical models presented in the preceding section. In this regard, we make consideration of the following generalized nonlinear partial differential equation (PDE) to give a brief structure of the considered analytical methods
where P is a polynomial, featuring the solution together with its partial derivatives. Thus, we give the stepwise procedure to acquiring the resultant solutions of the latter equation in what follows:
Step I. First, a wave transformation expressed as
is considered, where is a new variable that takes over the three spatial variables and z and the temporal t variable, with k and as non-zero constants, which can be explicitly determined from the model’s parameters or prescribed as constants. Further, the above transformation in (6) recasts (5) into the following nonlinear ordinary differential equation (ODE)
and Q is a polynomial, featuring the solution together with its total derivatives, where
Step II. This step makes consideration of the considered analytical methods as follows:
- 1.
- Modified Kudryashov method [8]The solution of (7) via the use of the modified Kudryashov method is sought in the following predicted solution formwhere n is a natural number to be determined later on, for are arbitrary constants (not all equal to zero) to be computationally determined as well. In addition, the function satisfies the following ODEupon which the latter ODE admits the following exact solutionwhere is a non-zero arbitrary constant, known as the Kudryashov index, while is a non-zero constant.However, when in (9) is replaced by unity, that is, then, the solution to the corresponding equation becomeswhich is the basic solution kernel for the renowned classical Kudryashov method [7].
- 2.
- Modified extended tanh method [15,16]With the consideration of the modified extended tanh method, it is presumed that (7) admits a solution of the following formwhere n is a natural number, while and for are arbitrary constants (not all equal to zero) to be determined later. Further, the function in the latter equation satisfies an ODE, having the following expressionIn addition, Equation (13) admits the following solutions when the sign is consideredand the following solutions when the sign in (13) is consideredwhere is a non-zero arbitrary constant. Moreover, when nonlinear evolution equations admit and as solutions, these solutions are generally referred to as dark and singular solitons, respectively. In addition, in a situation where a combination of the and function happens, such solution is called the dark–singular combined soliton solution. Moreover, the concept of solitonic solutions is well explored when complex-valued nonlinear evolution (Schrodinger) equations are considered; see [9,18] and the references therewith. In addition, the solutions appearing in (14) are called periodic solutions. Thus, this study is limited to the consideration of the hyperbolic solutions only, in favor of their vast applications in nonlinear media.
Step III. The natural number n in (8) and (12) can be found via the use of the homogeneous balancing principle; where the degrees of both the highest linear and nonlinear terms in the ODE expressed in (7) are balanced using the following formalism [28]
Step IV. By substitution (8) together with (9) into (7) through the utilization of symbolic computation, and further setting all the coefficients of the resulting polynomial in for for to zero, one obtains a system of algebraic equations in for k and . Subsequently, a solution of (5) is acquired upon solving this resulting system of algebraic equation after tracing back the wave transformation procedure.
4. Solitonic Analysis
The current section makes use of the considered modified Kudryashov method to analytically analyze and further construct some assorted solitonic structures for the governing three-dimensional nonlinear dynamical equations in fluid media. Thus, to begin with, the wave transformation as enshrined in the methodology is first utilized, followed by the full implementation of the modified Kudryashov method in what follows.
4.1. Newly Extended Kairat Equations
- (i).
- Extended Kairat-II equationThus, with the utilization of the wave transformation earlier given in (6) in the governing Kairat-II equation expressed in (1), one obtains the following nonlinear ODEupon which the above equation is balanced to explicitly give the value of n as followsModified Kudryashov methodTherefore, with the determination of above, the assumed solution from (8) via the use of the modified Kudryashov method takes the following solution formwhere and are constants to be determined. Certainly, upon substituting the later predicted equation into (17), one obtains the over-determined system of algebraic equations after setting the coefficients of for to zero as followsHence, on solving the resulting algebraic system expressed in (20), one obtains the following solution sets:Set 1.which yields the following exact solutionwhere the constraint condition is such that Moreover, upon unbundling the constraint condition, one obtains the corresponding solution put forward by the classical Kudryashov method.Set 2.which yields the following exact solutionwhere the constraint condition is such that and Consequently, the above solution sets via the application of the classical Kudryashov method are then reduced to yield particular solution cases when In this regard, the acquired solutions using the modified Kudryashov method are more general, with the solutions put forward by the classical Kudryashov method only as particular cases. In fact, the classical Kudryashov method, upon replacing with in the above solution, yields the following particular solutionsandwith the condition that Moreover, “it is pertinent to mention the strong relationship, or rather similarity, between the classical Kudryashov method [7] and the tanh-coth method [15,16], which is an important analytical method primarily used to construct various periodic and dark solitonic solutions. In fact, these two methods work hand-in-hand when manipulating the constant coefficients of the associated Riccati equation. Certainly, we refer interested reader(s) to the work of Kudryashov and Shilnikov [29] that deeply analyzed all the possibilities of the involving Riccati equation to divulge various exact analytical solutions”; see Althobaiti [30].Modified extended tanh methodAccordingly, with the determination of above, the assumed solution from (12) via the use of the modified extended tanh method takes the following solution formwhere and are constants to be determined after obtaining the over-determined system of algebraic equations under the adopted method. In this regard, the resulting algebraic equations yield the following solution sets:Set 1.Set 2.Set 3.In addition, the above three solution sets yield the following classes of hyperbolic solitonic solutions from sets 1 and 2wherewhile set 3 gives the following solutionswhere
- (ii).
- Extended Kairat-X equationEqually, with the utilization of the wave transformation in (6) in Kairat-X Equation (2), one obtains the following nonlinear ODEwhere n is equally found to be as in the previous model.Modified Kudryashov methodTherefore, with the modified Kudryashov method gives the following solution formwhere and are constants, which further reveals the following algebraic equationswhich, when solved, yields the following solution setwhich subsequently yields the following exact solutionswhen Accordingly, the above solution set upon considering the classical Kudryashov method is reduced to yield a particular solution case when and further replacing with as followswhere the existence of valid solution requires thatModified extended tanh methodAccordingly, with the determination of above, the assumed solution from (12) via the use of the modified extended tanh method takes the following solution formwhere and are constants to be determined after obtaining the over-determined system of algebraic equations under the adopted method. In this regard, the resulting algebraic equations yield the following solution sets:Set 1.Set 2.Set 3.Additionally, the three solution sets above yield the following hyperbolic solitonic solutions:whereandwhere
4.2. Newly Extended Boussinesq Type Equation
The utilization of the wave transformation in (6) in the Boussinesq type Equation (3) gives the following nonlinear ODE
where n is determined by homogeneous balancing as
Modified Kudryashov method
In the same vein, the modified Kudryashov method gives the following solution for the latter nonlinear ODE as follows
where and are constants. Accordingly, upon substituting the latter solution in (51), one obtains the following algebraic system of equations
Moreover, solving the above systems in (53) yields the following solution set
which yields the following exact solution
In the same vein, the above solution, upon deploying the renown classical Kudryashov method when and further replacing with , becomes
Modified extended tanh method
As a result of , the presumed solution from (12) via the governing method yields the following predicted solution
where and are constants to be determined. Accordingly, the resulting system of algebraic equations is acquired and solved to give the following solution sets:
Set 1.
Set 2.
Set 3.
Moreover, the above solution sets reveal the following hyperbolic solitonic solutions:
where
and
where
Moreover, one may equally impose the related constraint conditions in the above solutions as earlier presented in the previous subsection without any loss of generality.
4.3. Newly Extended Generalized KdV Equation
Accordingly, the utilization of the wave transformation in (6) in the generalized nonlinear KdV Equation (4) gives the following nonlinear ODE
where n has been determined by homogeneous balancing as
Modified Kudryashov method
In the same vein, the modified Kudryashov method gives the following solution for the latter nonlinear ODE as follows
where and are constants. Accordingly, upon substituting the latter solution in (51), one obtains the following algebraic system of equations
after setting the value of n as Then, the modified Kudryashov method gives the following solution form
where and are constants. Accordingly, upon substituting the latter solution in (74), one obtains the following algebraic system of equations
Moreover, solving the above systems in (53) yields the following solution set
which yields the following exact solution
In the same vein, the above solution, upon deploying the renown classical Kudryashov method when and further replacing with , becomes
Modified extended tanh method
In the same fashion, with , the presumed solution from (12) via the governing method yields the following predicted solution
where and are constants to be determined. Accordingly, the resulting system of algebraic equations is acquired and solved to give the following solution sets:
Set 1.
Set 2.
Set 3.
In the same fashion, the above solution sets reveal the following hyperbolic solitonic solutions:
where
and
where
5. Graphical Illustrations and Analysis
This section gives graphical illustrations of some of the acquired exact analytical solutions of the present study via the help of the modified Kudryashov and modified extended tanh methods; for more on some of the trending efficient numerical counterparts, one may consult [31,32,33,34]. The section further analyses these solutions with respect to their relevance in fluid media. Mathematica software was used for the graphical illustrations, which are portrayed in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 using two-dimensional (2D), three-dimensional (3D), and contour depictions. Moreover, it is worth stating here that this section only limits both the graphical illustrations and analysis to the case of the newly extended (3 + 1) Kairat-II model for the remaining models, which include the newly extended (3 + 1) Kairat-X equation, the newly extended (3 + 1) Boussinesq-type equation, and the newly extended (3 + 1) generalized KdV equation, have the same solution structure; thus, there is no need for repetition.
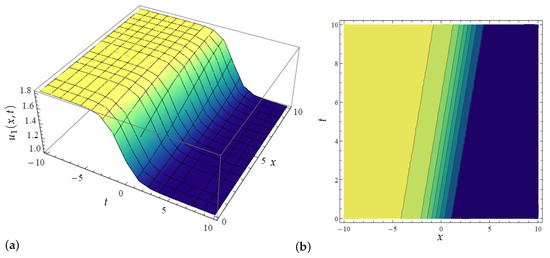
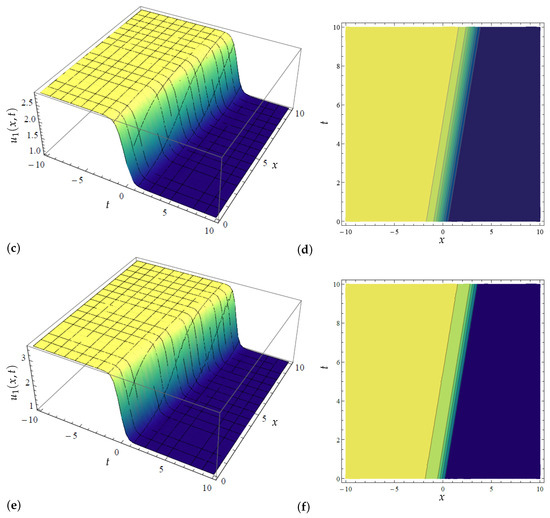
Figure 1.
Three-dimensional and contour plots for the modified Kudryashov method’s solution determined in (22) with variations in when and (a) Three-dimensional plot for in (22) when (b) Contour plot for in (22) when (c) Three-dimensional plot for in (22) when (d) Contour plot for in (22) when (e) Three-dimensional plot for in (22) when (f) Contour plot for in (22) when .
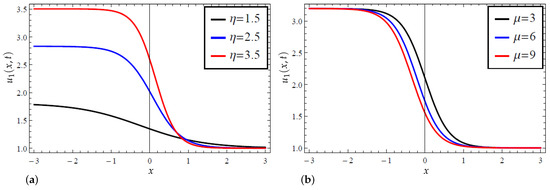
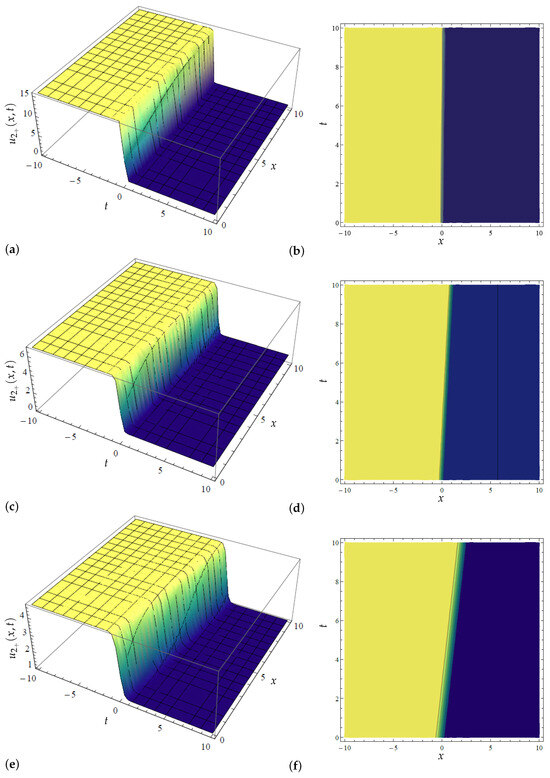
Figure 3.
Three-dimensional and contour plots for the modified Kudryashov method’s solution determined in (24) with variations in when and (a) Three-dimensional plot for in (24) when (b) Contour plot for in (24) when (c) Three-dimensional plot for in (24) when (d) Contour plot for in (24) when (e) Three-dimensional plot for in (24) when (f) Contour plot for in (24) when .
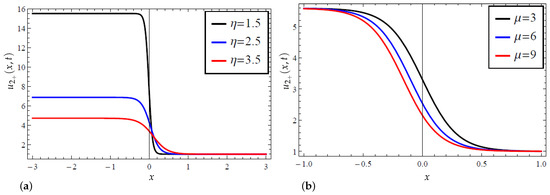
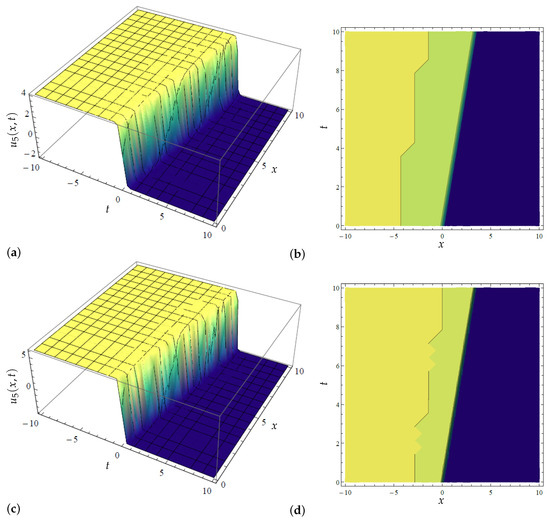
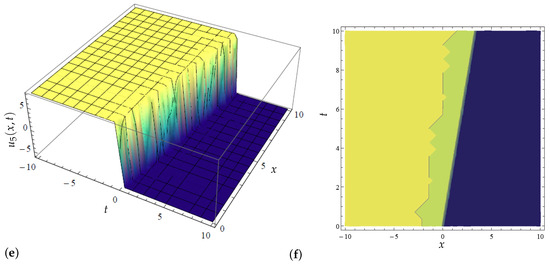
Figure 5.
Three-dimensional and contour plots for the modified extended tanh method’s solution determined in (31) with variations in when and (a) Three-dimensional plot for in (31) when (b) Contour plot for in (31) when (c) Three-dimensional plot for in (31) when (d) Contour plot for in (31) when (e) Three-dimensional plot for in (31) when (f) Contour plot for in (31) when .
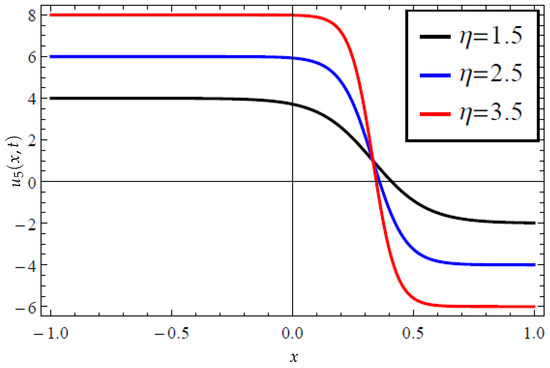
Figure 6.
Two-dimensional plot for the modified extended tanh method’s solution determined in (31) with variations in when and .
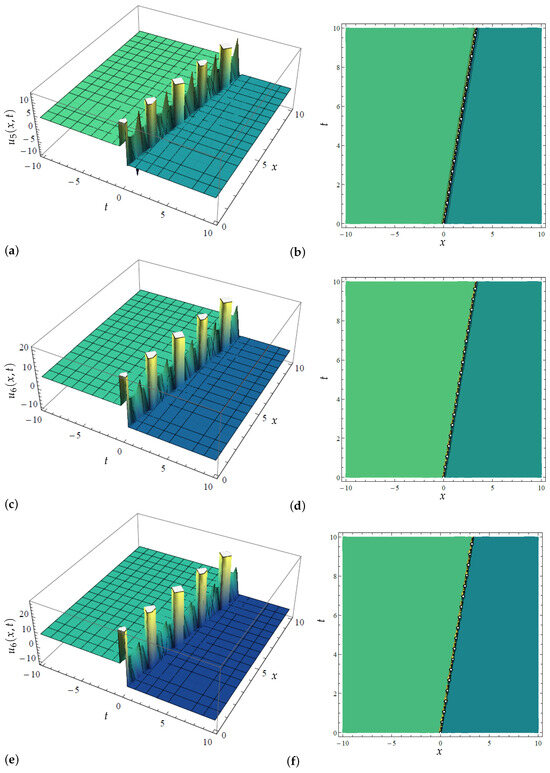
Figure 7.
Three-dimensional and contour plots for the modified extended tanh method’s solution determined in (32) with variations in when and (a) Three-dimensional plot for in (32) when (b) Contour plot for in (32) when (c) Three-dimensional plot for in (32) when (d) Contour plot for in (32) when (e) 3D plot for in (32) when (f) Contour plot for in (32) when .
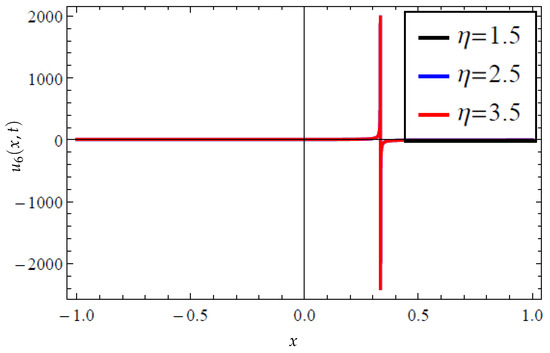
Figure 8.
Two-dimensional plot for the modified extended tanh method’s solution determined in (32) with variations in when and .
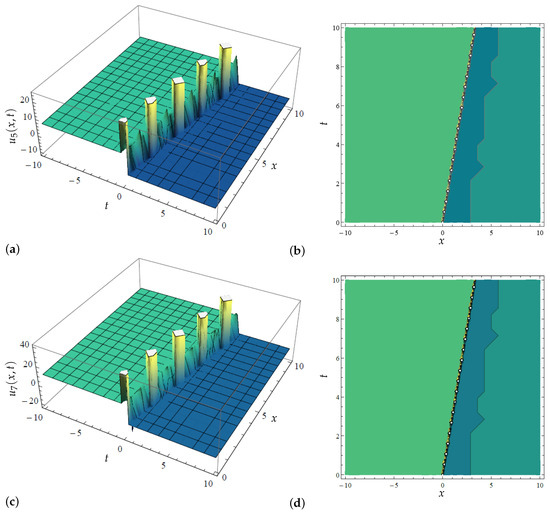
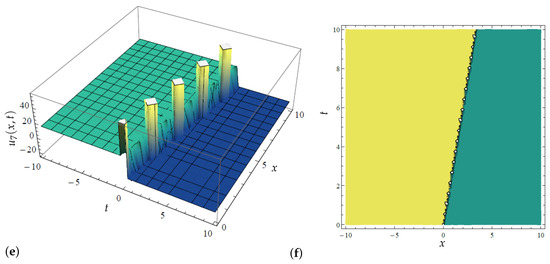
Figure 9.
Three-dimensional and contour plots for the modified extended tanh method’s solution determined in (34) with variations in when and (a) Three-dimensional plot for in (34) when (b) Contour plot for in (34) when (c) Three-dimensional plot for in (34) when (d) Contour plot for in (32) when (e) Three-dimensional plot for in (34) when (f) Contour plot for in (34) when .
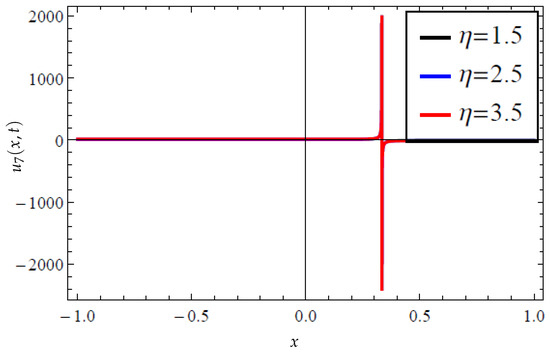
Figure 10.
Two-dimensional plot for the modified extended tanh method’s solution determined in (34) with variations in when and .
In addition, it is pertinent to state here that the reported solutions in this study provide generalized versions of those discovered in [24,25,26]; in fact, our study constructs various exponential, logarithmic, and hyperbolic solutions, generalizing the solutions in the aforesaid references that are of exponential functions put forward by Hirota’s method. What is more, the discovered solution with regard to the deployed Kudryashov based approaches are said to equally reveal various bright and singular solitonic expressions upon making some internal assumptions in the related Riccati ODEs; see [8] and the references therein.
To begin with, in Figure 1, Figure 2, Figure 3 and Figure 4, we graphically examined the acquired exact solutions for the newly extended (3 + 1) Kairat-II nonlinear model through the application of the modified Kudryashov method [8] in Equations (22) and (24) via 2D, 3D, and contour plots. More explicitly, Figure 1 displays the acquired exponential solution in (22) specifically concerning the influence of the second parameter in the modified Kudryashov method responsible for the existence of multiple solutions. Indeed, when this solution takes the form of the solution by the classical Kudryashov method [7]. Thus, the study of the variational influence of this parameter is important. Hence, as can be observed from the 3D plots in Figure 1a,c,e, an increase in accelerates the wave profile in the medium; see also the corresponding plots in Figure 1b,d,f, where the contour views further confirm the influence of an increase in the value of on shifting the wave’s profile forward, for the case of propelling the transmission in the media. In fact, one may examine the 2D plot in Figure 2a that equally depicts the influence of the variational effects of on solution (22), clearly showing an increase in the wave field with the increase in In the same vein, the 2D plot in Figure 2b examines the influence of the Kudryashov index on the solution (22), where an increase in the Kudryashov index opposes the propagation rate. Moreover, without much delay, the interpretation of Figure 1 and Figure 2, respectively, is applied to Figure 3 and Figure 4, respectively, for the solution determined in (24). Moreover, both solutions are exponential solutions that portray kink-shaped profiles.
In the same fashion, in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, we graphically examined the acquired exact solutions for the newly extended (3 + 1) Kairat-II nonlinear model through the application of the modified extended tanh method [15,16] in Equations (31), (32) and (34) via 2D, 3D, and contour plots. Thus, before proceeding with the discussion of these new structures, it is pertinent to mention here that this study presents only the hyperbolic solutions of the method in line with their vast uses in fluid media, optics, and nonlinear media, among others; the corresponding periodic solutions of the governing models can equally be acquired in the same way. Therefore, Figure 5 graphically portrays the acquired dark solitonic solution in (31). Moreover, “a dark soliton is a localized wave disturbance that is surrounded by regions of higher intensity in the waveform and frequently manifests as an aperture or depression. In nonlinear systems, dark soliton solutions and bright soliton solutions are both significant because they represent stable, confined wave solutions” [35]. Now, back to the 3D and contour plots given in Figure 5, the variational significance of on this dark solitonic solution is captured in Figure 5a–f, where it is observed that an increase in propels the wave transmission in the media. In addition, a precise snap of the variational influence of on the dark solution (31) is portrayed in Figure 6 via 2D plots, where one can vividly observe a positive impact of increasing the parameter on the wave profile by accelerating the propagation in the medium.
Equally, the solutions reported in (32) and (34) are singular and dark–singular solitonic solutions, respectively, which are further illustrated in Figure 7 and Figure 8, and Figure 9 and Figure 10, sequentially. Such kinds of solitonic solutions are characterized by singular points, as can be observed from these plots, and have found several applications in fluid media, among other applications. Thus, as can be observed from Figure 7, the variational significance of the parameter is captured on the governing singular solution. It is noted that an increase in increases the wave’s propagation in the medium; observe in the 3D plots in Figure 7a,c,e the variation in while Figure 7b,d,f portray the corresponding contour plots of the singular solution. Moreover, one may notice the singular holes in the contour plots, featuring white points. Additionally, Figure 8 shows a typical singular solution that extends to infinity on both sides of the wave field. However, the obtained dark–singular solitonic solution determined in (34) is depicted in Figure 9 (showing the 3D and contour plots) and Figure 10 (showing the 2D plot) of the solution, where the interpretation of these figures follows that of Figure 7 and Figure 8, sequentially.
6. Conclusions
In conclusion, the current study examined the newly introduced three-dimensional nonlinear dynamical equations that play vital roles in fluid media. Two proficient modified analytical approaches were considered for the solitonic analysis of new three-dimensional models, including the new (3 + 1) Kairat-II equation, the new (3 + 1) Kairat-X equation, the new (3 + 1) Boussinesq type equation, and the new (3 + 1) generalized KdV equation. The methods, comprising the modified Kudryashov method and the modified extended tanh methods are known for their high efficiency in tackling various real and complex evolution equations. Thus, several exponential and hyperbolic solutions were revealed by the methods, including dark, singular, and dark–singular combined solitonic solutions, among others. Moreover, several other solutions such as the periodic solutions were posed via the adopted modified extended tanh method; however, these solutions were omitted in the current study since hyperbolic solutions are more applicable in the context of optical communication. On the other hand, the acquired hyperbolic solutions are confined, stable wave structures that help in the understanding of the dynamicity of wave transmission in a variety of fluid types, including deep water, stratified fluids, and both natural and artificial fluids. In the end, the present study is set to benefit a wide range of researchers working in dissimilar branches of fluid dynamics, and other fields of relevant interest, such as hyper-elasticity, material science, optical fibers, optics, and propagation of waves in nonlinear media. In the same vein, it is highly recommended to look into the deployed methods with regard to improving the methods toward revealing more exact solutions; see the case of the recent enhancement of the classical Kudryashov method by Elsherbeny et al. [9], which gives assorted exact solitonic expressions, for instance. Thus, the governing infused ODEs in the respective methodologies will be generalized in the future to create more room for exact solutions.
Author Contributions
M.N.A., S.A., A.A., R.I.N., H.S.S. and A.F.A.: conceptualization, methodology, writing—original draft preparation, methodology, data curation, and supervision. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Acknowledgments
The authors are thankful to the Deanship of Graduate Studies and Scientific Research at Najran University for funding this work under the Easy Funding Program grant code (NU/EFP/SERC/13/40-1).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Althobaiti, S.; Nuruddeen, R.I.; Magaji, A.Y.; Gomez-Aguilar, J.F. New revelations and extensional study on the recent sixth-order 3D Kadomtsev-Petviashvili-Sawada-Kotera-Ramani equation. Opt. Quantum Electron. 2024, 56, 820. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, Z.; Wazwaz, A.M. Solitons, nonlinear wave transitions and characteristics of quasi-periodic waves for a (3 + 1)-dimensional generalized Calogero-Bogoyavlenskii-Schiff equation in fluid mechanics and plasma physics. Chin. J. Phys. 2024, 89, 896–929. [Google Scholar] [CrossRef]
- Shen, Y.; Tian, B.; Gao, X.T. Bilinear auto-Backlund transformation, soliton and periodic-wave solutions for a (2 + 1)-dimensional generalized Kadomtsev-Petviashvili system in fluid mechanics and plasma physics. Chin. J. Phys. 2022, 77, 2698–2706. [Google Scholar] [CrossRef]
- Boussinesq, J. Theorie de I’intumescence liquide, applelee onde solitaire ou de translation, se propageant dans un canal rectangulaire. CR Acad. Sci. 1871, 72, 755–759. [Google Scholar]
- Bakodah, H.O. Modified Adomain decomposition method for the generalized fifth order KdV equations. Am. J. Comput. Math. 2013, 3, 53–58. [Google Scholar] [CrossRef]
- Russell, J.S. Report on Waves: Made to the Meetings of the British Association in 1842-43; Harvard University: Cambridge, MA, USA, 1845. [Google Scholar]
- Kudryashov, N.A. One method for finnding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Althrwi, F.A.; Alshaery, A.A.; Bakodah, H.O.; Nuruddeen, R.I. Supplementary optical solitonic expressions for Gerdjikov-Ivanov equations with three Kudryashov-based methods. Comm. Theor Phys. 2024. [Google Scholar] [CrossRef]
- Elsherbeny, A.M.; Arnous, A.H.; Biswas, A.; González-Gaxiola, O.; Moraru, L.; Moldovanu, S.; Iticescu, C.; Alshehri, H.M. Highly dispersive optical solitons with four forms of self-phase modulation. Universe 2023, 9, 51. [Google Scholar] [CrossRef]
- Yomba, E. A generalized auxiliary equation method and its application to nonlinear Klein-Gordon and generalized nonlinear Camassa-Holm equations. Phys. Lett. A 2008, 372, 1048–1060. [Google Scholar] [CrossRef]
- Hosseini, K.; Bekir, A.; Ansari, R. Exact solutions of nonlinear conformable time-fractional Boussinesq equations using the exp(-θ(ξ))-expansion method. Opt Quantum Electron. 2017, 49, 131. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Kara, A.H.; Zaman, F.D. Exact solutions of some general nonlinear wave equations in elasticity. Nonlinear Dyn. 2007, 48, 49–54. [Google Scholar] [CrossRef]
- Bulut, H.; Sulaiman, T.A.; Demirdag, B. Dynamics of soliton solutions in the chiral nonlinear Schrodinger equations. Nonlinear Dyn. 2018, 1, 1985–1991. [Google Scholar] [CrossRef]
- Mubaraki, A.M.; Kim, H.; Nuruddeen, R.I.; Akram, U.; Akbar, Y. Wave solutions and numerical validation for the coupled reaction-advection-diffusion dynamical model in a porous medium. Commun. Theor. Phys. 2022, 74, 125002. [Google Scholar] [CrossRef]
- Raslan, K.R.; Khalid, K.A.; Shallal, M.A. The modified extended tanh method with the riccati equation for solving the space-time fractional EW and MEW equations. Chaos Solitons Fractals 2017, 103, 404–409. [Google Scholar] [CrossRef]
- Park, C.; Nuruddeen, R.I.; Ali, K.K.; Muhammad, L.; Osman, M.S.; Baleanu, D. Novel hyperbolic and exponential ansatz methods to the fractional fifth-order Korteweg-de Vries equations. Adv. Diff. Equ. 2020, 627, 1–12. [Google Scholar] [CrossRef]
- AlQarni, A.A.; Badaqah, A.M.; Mohammed, A.S.H.F.; Alshaery, A.A.; Bakodah, H.O.; Biswas, A. Cubic-quartic optical solitons for Lakshmanan-Porsezian-Daniel equation by the improved Adomian decomposition scheme. Ukr. J. Phys. Opt. 2022, 8, 2117–2136. [Google Scholar]
- Alzahrani, A.K. Cubic-quartic optical soliton perturbation with Lakshmanan–Porsezian–Daniel model by semi-inverse variational principle. Ukr. J. Phys. Opt. 2021, 22, 123. [Google Scholar]
- Asma, M.; Othman, W.; Wong, B.; Biswas, A. Chirped optical Gausson perturbation with quadratic-cubic nonlinearity by collective variables. Opt. Quant. Electron. 2019, 51, 200. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Babatin, M.M.; Biswas, A. Bright optical solitons for Lakshmanan-Porsezian-Daniel model by semi-inverse variational principle. Optik 2018, 154, 109–114. [Google Scholar] [CrossRef]
- Salih, R.I.; Jawad, S.; Dehingia, K.; Das, A. The effect of a psychological scare on the dynamics of the tumor-immune interaction with optimal control strategy. Int. J. Optim. Control Theor. Appl. 2024, 14, 276–293. [Google Scholar] [CrossRef]
- Ahmed, M.; Jawad, S. The role of antibiotics and probiotics supplements on the stability of gut flora bacteria interactions. Commun. Math. Biol. Neurosci. 2023, 2023, 33. [Google Scholar] [CrossRef]
- Ali, A.; Jawad, S.; Ali, A.H.; Winter, M. Stability analysis for the phytoplankton-zooplankton model with depletion of dissolved oxygen and strong Allee effects. Results Eng. 2024, 22, 102190. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Extended (3 + 1)-dimensional Kairat-II and Kairat-X equations: Painleve integrability, multiple soliton solutions, lump solutions, and breather wave solutions. Int. J. Numer. Meth. Heat Fluid Flow 2024, 34, 2177–2194. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Alhejaili, W.; El-Tantawy, S.A. On the Painleve integrability and nonlinear structures to a (3 + 1)-dimensional Boussinesq-type equation in fluid mediums: Lumps and multiple soliton/shock solutions. Phys. Fluids 2024, 36, 033116. [Google Scholar] [CrossRef]
- Ismaeel, S.M.E.; Wazwaz, A.M.; El-tantawy, S.A. New (3 + 1)-dimensional integrable generalized KdV equation: Painleve property, multiple soliton/shock solutions, and a class of lump solutions. Romanian Rep. Phys. 2024, 76, 102. [Google Scholar]
- Kumar, S.; Mohan, B. A study of multi-soliton solutions, breather, lumps, and their interactions for Kadomtsev-Petviashvili equation with variable time coefficient using Hirota method. Phys. Scr. 2021, 96, 125255. [Google Scholar] [CrossRef]
- Rehman, U.; Ahmed, S.; Mubaraki, A.M. Optical devices: Motion via breathers, rogue waves and rational solitons. Opt. Quantum Electr. 2024, 56, 851. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Shilnikov, K.E. A note on The tanh-coth method combined with the Riccati equation for solving nonlinear coupled equation in mathematical physics. J. King Saud Uni. Sci. 2012, 24, 379–381. [Google Scholar] [CrossRef]
- Althobaiti, A. Novel wave solutions for the sixth-order Boussinesq equation arising in nonlinear lattice dynamics. AIM Math. 2024; Under Review. [Google Scholar]
- Alsisi, A. Analytical and numerical solutions to the Klein-Gordon model with cubic nonlinearity. Alexandria Eng. J. 2024, 99, 31–37. [Google Scholar] [CrossRef]
- Alqudah, M.A.; Ashraf, R.; Rashid, S.; Singh, J.; Hammouch, Z.; Abdeljawad, T. Novel numerical investigations of fuzzy Cauchy reaction-diffusion models via generalized fuzzy fractional derivative operators. Fractal Fract. 2021, 5, 151. [Google Scholar] [CrossRef]
- Mohamed, K.; Alsisi, A. Numerical simulation of Suliciu relaxation model via an mR scheme. AIMS Math. 2024, 9, 6513–6527. [Google Scholar] [CrossRef]
- Biazar, J.; Aminikhah, H. Exact and numerical solutions for non-linear Burgers equation by VIM. Math. Comp. Model. 2009, 47, 1394–1400. [Google Scholar] [CrossRef]
- Afsar, H.; Alshamrani, G.; Aldandani, M.; Alam, M.M.; Aljohani, A.F. Dimensionless dynamics: Multipeak and envelope solitons in perturbed nonlinear Schrodinger equation with Kerr law nonlinearity. Phys. Fluids 2024, 36, 067126. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).