Riemannian Manifolds, Closed Geodesic Lines, Topology and Ramsey Theory
Abstract
1. Introduction
2. Results
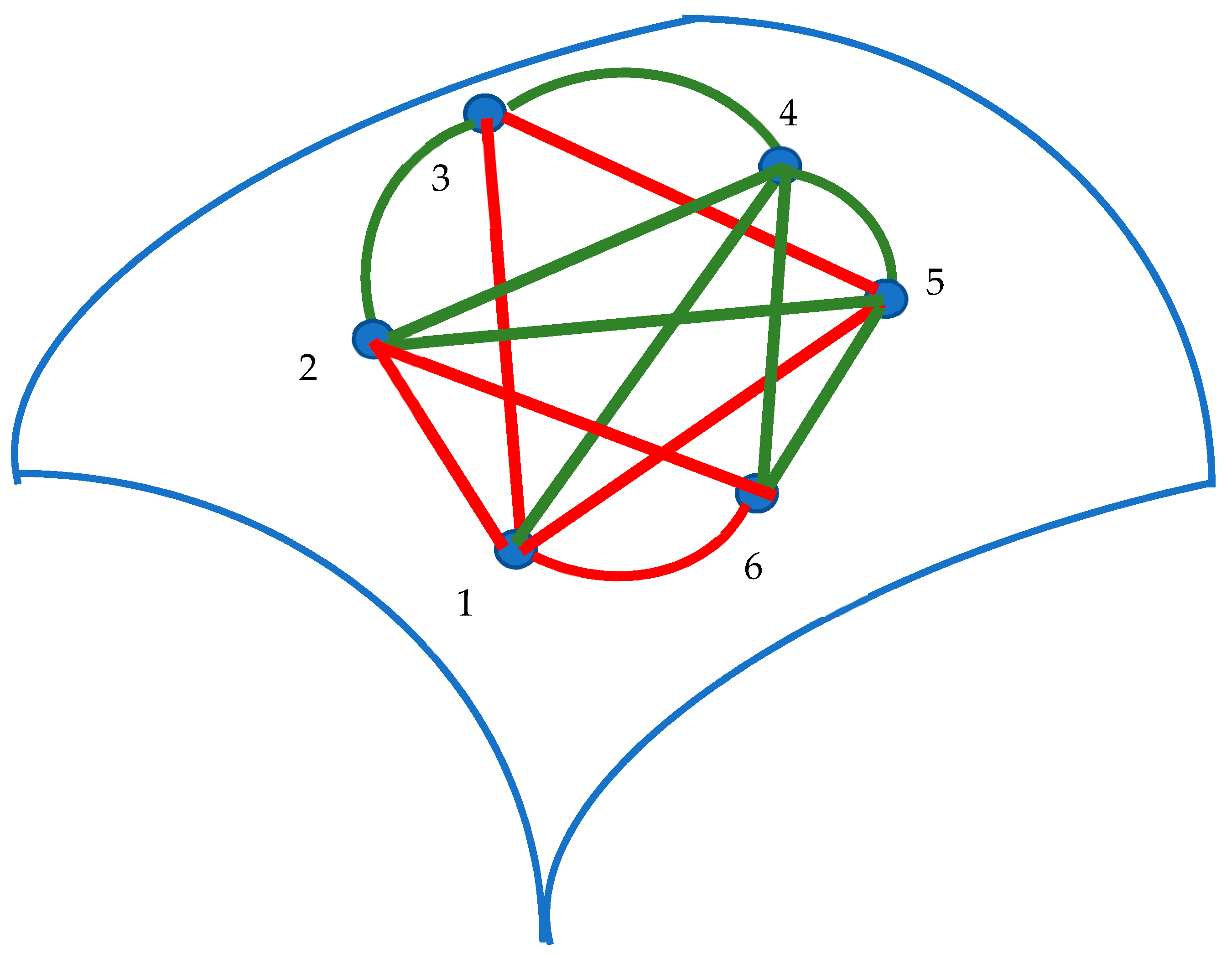
2.1. Geodesic and Non-Geodesic Lines Defined on a Riemannian Manifold Form a Complete Graph
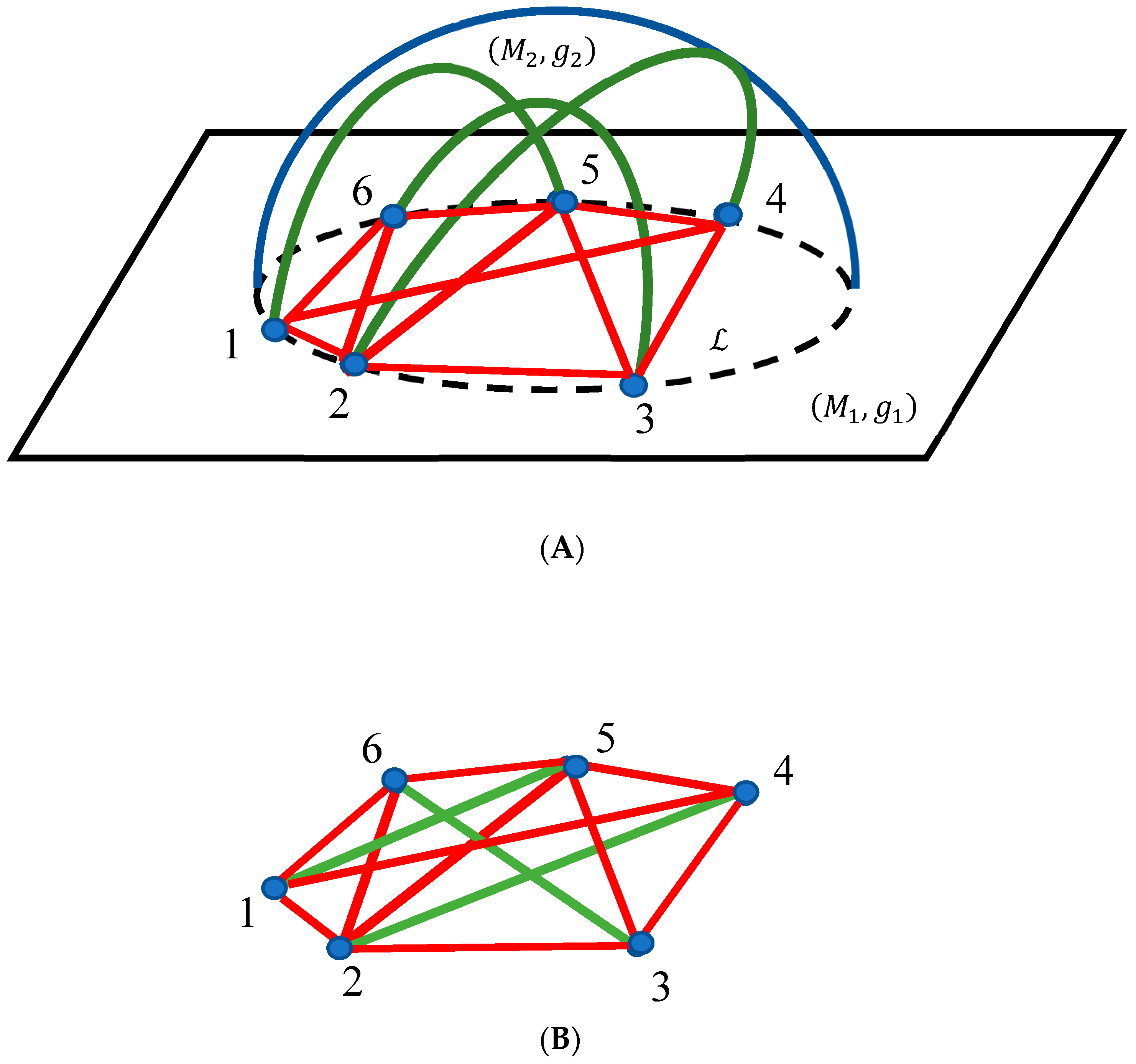
2.2. Bi-Colored, Complete Ramsey Graph Emerging from Intersection of Two Riemannian Manifolds
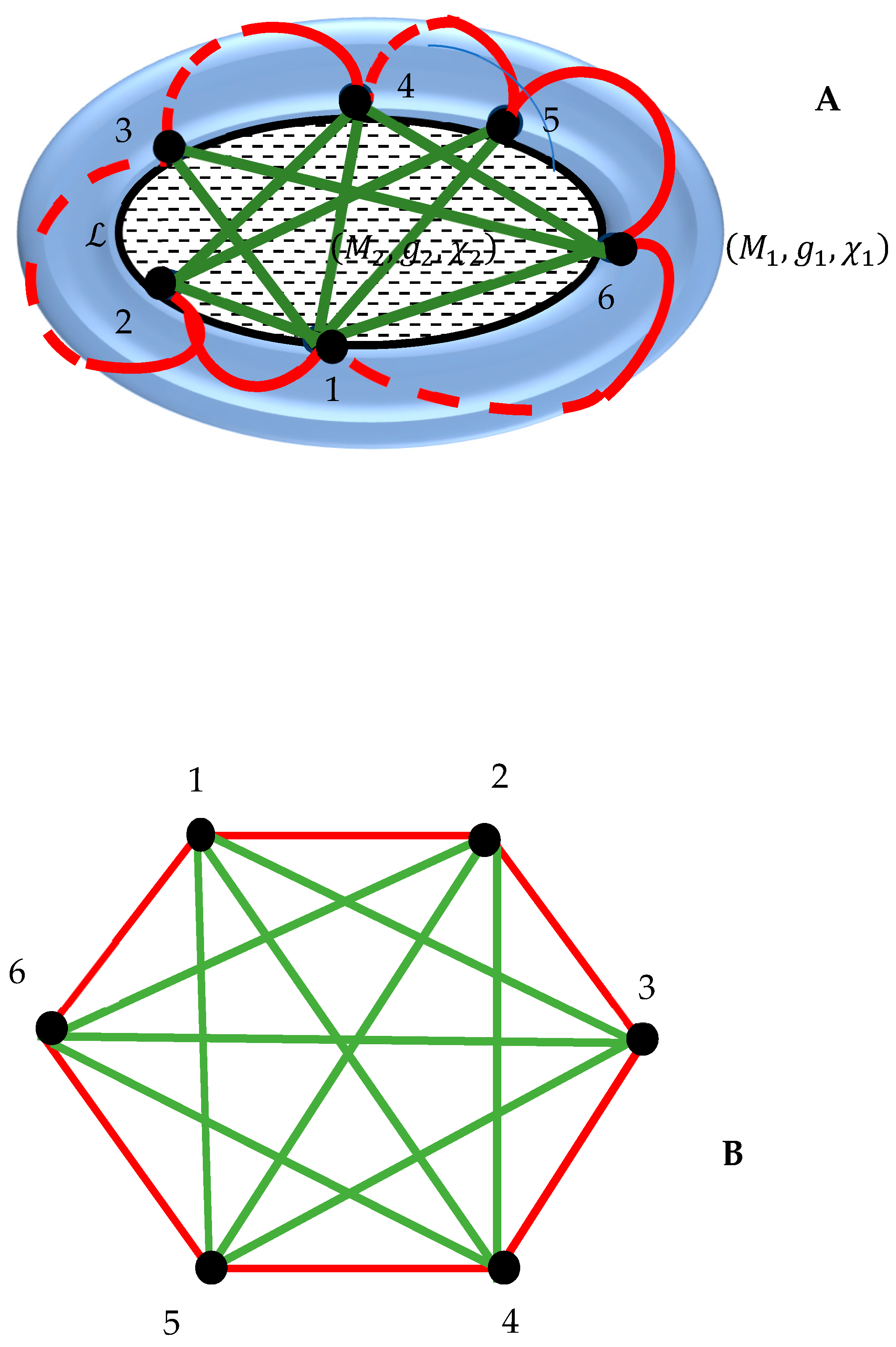
2.3. Bi-Colored, Complete Ramsey Graph Emerging from Intersection of Two Riemannian Manifolds Represented by the Surfaces Possessing Different Euler Characteristics
3. Corollary
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilbert, D.; Cohn-Vossen, S. Geometry and The Imagination; Chelsea Publishing Company: New York, NY, USA, 1990. [Google Scholar]
- Toponogov, V.A.; Rovenski, V. Differential Geometry of Curves and Surfaces: A Concise Guide; Birkhäuser Boston: New York, NY, USA, 2005. [Google Scholar]
- Polthier, K.; Schmies, M. Straightest geodesics on polyhedral surfaces. In ACM SIGGRAPH 2006 Courses on—SIGGRAPH ’06 30; ACM Press: New York, NY, USA, 2006. [Google Scholar]
- Spivak, M.A. Comprehensive Introduction to Differential Geometry; Publish or Perish: Houston, TX, USA, 1999; Volume 2, Chapter 9; pp. 301–341. [Google Scholar]
- Landau, L.; Lifshitz, E.M. The Classical Theory of Fields, 3rd ed.; Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1971; Volume 2, Chapter 10; pp. 225–254. [Google Scholar]
- Ramsey, F.P. On a Problem of Formal Logic. In Classic Papers in Combinatorics; Modern Birkhäuser Classics; Gessel, I., Rota, G.C., Eds.; Birkhäuser Boston: New York, NY, USA, 2009; pp. 264–286. [Google Scholar]
- Graham, R.L.; Rothschild, B.L.; Spencer, J.H. Ramsey Theory, 2nd ed.; Wiley-Interscience Series in Discrete Mathematics and Optimization; John Wiley & Sons, Inc.: New York, NY, USA, 1990; pp. 10–110. [Google Scholar]
- Di Nasso, M.; Goldbring, I.; Lupini, M. Nonstandard Methods in Combinatorial Number Theory; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2019; Volume 2239. [Google Scholar]
- Katz, M.; Reimann, J. Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics; Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2018; Volume 87, pp. 1–34. [Google Scholar]
- Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. A Note on the Geometry of Closed Loops. Mathematics 2023, 11, 1960. [Google Scholar] [CrossRef]
- Poincare, H. Surles lignes geodesiques des surfaces convexes. Trans. Am. Math. Soc. 1905, 6, 237–274. [Google Scholar]
- Lyusternik, L.A.; Fet, A.I. Variational problems on closed manifolds. Doklady Akad. Nauk SSSR 1951, 81, 17–18. (In Russian) [Google Scholar]
- Ahmed, F. Cylindrically symmetric pure radiation space-time and closed timelike geodesics. Prog. Theor. Exp. Phys. 2017, 2017, 043E02. [Google Scholar] [CrossRef][Green Version]
- Lee, J.M. Introduction to Riemannian Manifolds; Springer International Publishing: New York, NY, USA, 2018; Chapters 2–3; pp. 9–83. [Google Scholar]
- Busemann, H. On spaces in which two points determine a geodesic. Trans. Am. Math. Soc. 1943, 54, 171–184. [Google Scholar] [CrossRef]
- Pestov, L.; Uhlmann, G. Two dimensional compact simple Riemannian manifolds are boundary distance rigid. Ann. Math. 2005, 161, 1093–1110. [Google Scholar] [CrossRef]
- Klingenberg, W. Lectures on Closed Geodesics; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Lusternik, L.; Schnirelmann, L. Existence de trois lignes gêodêsiques fermées, sur la surface de genre 0, C.R. Acad. Sci. Paris 1929, 188, 269–271. [Google Scholar]
- Fet, A.I. Varational problems on closed manifolds. Mat. Sb. 1952, 30, 271–316, English transl. Am. Math. Soc. Transi. No. 90 Am. Math. Soc. Providence, R.I., 1953; reprinted in Am. Math. Soc. Transl. 1962, 6, 14. [Google Scholar]
- Borisenko, A.A.; Sukhorebska, D.D. Simple closed geodesics on regular tetrahedra in spherical space. arXiv 2021, arXiv:2101.07059. [Google Scholar] [CrossRef]
- Berestovskii, V.; Nikonorov, Y. Riemannian Manifolds and Homogeneous Geodesics; Springer: Cham, Switzerland, 2020. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E. Riemannian Manifolds, Closed Geodesic Lines, Topology and Ramsey Theory. Mathematics 2024, 12, 3206. https://doi.org/10.3390/math12203206
Bormashenko E. Riemannian Manifolds, Closed Geodesic Lines, Topology and Ramsey Theory. Mathematics. 2024; 12(20):3206. https://doi.org/10.3390/math12203206
Chicago/Turabian StyleBormashenko, Edward. 2024. "Riemannian Manifolds, Closed Geodesic Lines, Topology and Ramsey Theory" Mathematics 12, no. 20: 3206. https://doi.org/10.3390/math12203206
APA StyleBormashenko, E. (2024). Riemannian Manifolds, Closed Geodesic Lines, Topology and Ramsey Theory. Mathematics, 12(20), 3206. https://doi.org/10.3390/math12203206





