Abstract
In recent years, parcel volumes have reached record highs, prompting the logistics industry to explore innovative solutions to meet growing demand. In densely populated areas, delivery robots offer a promising alternative to traditional truck-based delivery systems. These autonomous electric robots operate on sidewalks and deliver time-sensitive goods, such as express parcels, medicine and meals. However, their limited cargo capacity and battery life require a return to a depot after each delivery. This challenge can be modeled as an electric vehicle-routing problem with soft time windows and single-unit capacity constraints. The objective is to serve all customers while minimizing the quadratic sum of delivery delays and ensuring each vehicle operates within its battery limitations. To address this problem, we propose a mixed-integer quadratic programming model and introduce an enhanced formulation using a layered graph structure. For this layered graph, we present two solution approaches based on relaxations that reduce the number of nodes and arcs compared to the expanded formulation. The first approach, Iterative Refinement, solves the current relaxation to optimality and refines the graph when the solution is infeasible for the expanded formulation. This process continues until a proven optimal solution is obtained. The second approach, Branch and Refine, integrates graph refinement into a branch-and-bound framework, eliminating the need for restarts. Computational experiments on modified Solomon instances demonstrate the effectiveness of our solution approaches, with Branch and Refine consistently outperforming Iterative Refinement across all tested parameter configurations.
Keywords:
integer programming; layered graph refinement; delivery robots; electric vehicle-routing problem; partial recharging MSC:
90B06; 90B20; 90C11; 90C20
1. Introduction
Over the past decade, e-commerce has transformed consumer markets globally. According to [1], global e-commerce revenue reached USD 2415 billion in 2020, representing a 25% increase from 2019. The rapid growth of e-commerce has significantly increased the volume of parcels requiring delivery. In 2019, it was estimated that over 100 billion parcels were shipped worldwide [2]. This surge exacerbates existing traffic-related challenges, including congestion, noise and air pollution.
In response, many Western European cities have implemented regulations to curb transportation emissions, with some areas introducing pedestrian-only, low-emission or zero-emission zones. These measures are reshaping how people move, order goods and how logistics companies operate. To comply with these regulations and to enhance their environmental credentials, logistics companies have launched initiatives to improve carbon efficiency and reduce local emissions. Some companies have even committed to achieving net-zero carbon emissions in the future. Consequently, there is growing interest in environmentally friendly solutions, particularly for last-mile deliveries, which present the greatest logistical and cost challenges. It is estimated that last-mile delivery accounts for 50% of total transportation costs [3].
One promising approach for urban goods distribution is a two-tier system. In this model, goods are first transported in bulk to decentralized micro-depots on the outskirts of cities via conventional trucks. From these depots, environmentally friendly vehicles are used for last-mile delivery. One such option is electrically assisted cargo bikes, which offer flexibility and can help reduce traffic, noise and air pollution [4]. However, this approach is weather-dependent, and the cargo capacity of these bikes remains limited.
Another promising concept for last-mile transportation involves the use of small autonomous parcel robots. These robots are equipped with technology similar to that found in autonomous vehicles, but differ primarily in size and speed. Over the past few years, several startups and established companies, including Starship Technologies, Amazon, Kiwibot and Teleretail, have developed delivery robots. These electric robots are designed to travel on sidewalks or within pedestrian zones at walking speed, with size constraints ensuring they do not obstruct pedestrians. The robots produced by these companies are typically limited to carrying a single delivery unit. This limited capacity necessitates a return to the depot after each delivery. Despite this, delivery robots offer a high level of service compared to conventional trucking, as they allow customers to schedule specific time slots for parcel delivery. They are especially well-suited for delivering small, time-sensitive goods, operating efficiently within urban environments where their capacity and range are sufficient for short trips. These robots are versatile in what they can transport, provided the items fit within their compartment. Some models even feature heating or refrigeration units, enabling the delivery of temperature-sensitive goods. Applications include the delivery of parcels, food, clothing, groceries and medicine.
To further illustrate how delivery robots can be integrated into logistics operations, we present an example scenario. Suppose a customer purchases a product online. This product is first transported from a warehouse to a nearby micro-depot, where a fleet of delivery robots is stationed. To provide a high level of service, the customer has the option to select a preferred delivery time slot. Shortly before the selected time slot, a robot is loaded with the product at the micro-depot and begins its journey to the customer’s location. Upon arrival, the robot is unlocked and the package is retrieved by the customer. The robot then returns to the micro-depot, where it either recharges or is prepared for the next delivery.
In this work, we investigate the optimal routing, scheduling and charging strategies for a fixed number of battery-powered vehicles with single-unit capacity. The objective is to minimize the sum of the squared differences between the actual service start times at customer locations and their desired delivery times—effectively minimizing delivery delays. Our problem formulation is based on the classical vehicle-routing problem (VRP), but we introduce additional variables and constraints to account for arrival times, states of charge (SoC) and delays. Given that the objective involves squared delays, the resulting formulation is a mixed-integer quadratic program (MIQP). We refer to this problem as the time- and battery-constrained delivery robot problem (TBDRP).
As we demonstrate in the computational experiments, using state-of-the-art MIQP solvers is only feasible for problems with a relatively small number of delivery robots and customers. To address larger instances, we derive an alternative formulation based on a layered graph, where nodes represent customers and are characterized by a combination of customer ID, arrival time and SoC upon arrival. However, constructing a suitable layered graph proved to be as challenging as solving the original problem, making this approach impractical for direct use. The advantage of this formulation, though, is that it allows for relaxations that yield solutions with small optimality gaps and are relatively easy to solve. Building on this, we develop an iterative method that progressively refines the relaxation until its solution can be transformed into a solution for the original problem with the same cost. In other words, the gap between the relaxation and the original problem becomes zero, resulting in a proven optimal solution. Leveraging these relaxations, we propose two algorithms: Iterative Refinement, in which relaxations are refined in an outer loop, and Branch and Refine, where relaxations are refined during the exploration phase of a branch-and-bound algorithm.
In summary, the contributions of this work are as follows:
- We present and model a real-world problem, the TBDRP, as a MIQP. This model accounts for battery consumption, soft time-window constraints and supports partial recharging.
- We propose an alternative formulation using two-dimensional layered graphs and demonstrate that aggregated layered graphs can be employed to find relaxations of the TBDRP.
- We develop two algorithms based on these relaxations and show through computational experiments that they outperform direct approaches to solving the MIQP formulation using state-of-the-art solvers.
The outline of this paper is as follows: In Section 2, we provide a review of the existing literature on last-mile logistics and refinement algorithms. Section 3 presents the mathematical formulation of the problem and various mixed-integer models, along with the concept of time- and battery-expanded graphs. In Section 4, we discuss relaxation techniques for a fully time- and battery-expanded graph. This theoretical background is used to define a refinement algorithm in Section 5. Section 6 presents the results of computational experiments. Finally, Section 7 concludes the paper and provides an outlook on future research directions.
2. Literature Review
The use of innovative delivery concepts, such as drones or autonomous delivery robots, for parcel delivery is a relatively recent topic. A comprehensive overview of current and future concepts is provided by [5,6], while [7] discusses broader trends in transportation.
The body of literature on optimizing last-mile delivery networks using delivery robots is still limited and can be divided into two main categories: (1) approaches involving mobile vans capable of transporting robots, and (2) approaches focused on stationary micro-depots.
In the first category, [8] consider the scheduling of a delivery truck carrying robots. The truck can load robots at micro-depots and launch them at predefined locations along its route. The objective is to minimize the weighted number of late deliveries. The authors formulate the problem as a mixed-integer linear program (MILP) and propose a multi-start local search heuristic to solve the scheduling problem. A related problem is studied by [9], who present a different objective function. Their model incorporates a multi-objective function aiming to minimize the total tour length of the truck, the distances traveled by the robots and the lateness of deliveries. The authors also provide a MILP formulation and a two-stage heuristic to solve this problem.
In the second category, where micro-depot locations are fixed, [10] present a simulation framework that models parcel deliveries in a city of one million inhabitants. In this model, up to 3% of parcels are delivered by robots in a two-tiered system, with the remainder delivered by conventional vehicles. In a follow-up study, [11] examine the number of delivery robots required to service a city center. Two delivery slot selection strategies are considered: in the first, customers pre-select delivery time slots, and delays are minimized using a simulated annealing approach; in the second, customers request deliveries on-demand, and available robots from nearby micro-depots are dispatched accordingly.
In another contribution, [12] address a location-routing problem for delivery robots. The goal is to minimize the delivery costs of urban shipments using parcel robots. The problem is modeled as a MILP and solved using optimization software. In a case study, the authors examine the impact of varying the number of compartments on delivery efficiency.
Recently, [13] studies last-mile distribution with delivery robots and public transportation lines. They used a heuristic destroy-and-repair mechanism embedded into a neighborhood search, and applied their method on test instances from drug distribution to pharmacies in Rome.
Optimizing unmanned aerial vehicles (UAVs) or drones is a more widely explored topic in the literature. Ref. [14] provide a comprehensive overview of routing problems involving UAVs. However, only a limited number of studies focus on battery management and recharging processes. In most publications where batteries are considered, they are treated merely as range constraints, with recharging assumed to occur instantaneously. This is typically modeled as a battery swap at a micro-depot, where an empty battery is exchanged for a fully charged one (see [15,16,17]).
A more closely related field of research is the Electric Vehicle Routing Problem (EVRP), which extends the standard VRP to include electric vehicles that require recharging at dedicated stations. A survey of the EVRP is provided by [18]. Ref. [19] extend the EVRP by incorporating time windows (EVRPTW) at customer locations. They formulate the problem as a MILP and propose a Variable Neighborhood Search and Tabu Search heuristic to solve it, though their model only considers full recharges.
Ref. [20] build upon this by allowing partial recharges in their extension of the EVRPTW. They present a MILP formulation and develop an adaptive large neighborhood search heuristic. Additionally, Ref. [21] propose an exact algorithm for the EVRPTW, discussing both full and partial recharging strategies. They introduce a branch-price-and-cut algorithm to solve this problem effectively.
The TBDRP is closely related to the EVRPTW but differs in two significant ways. First, we relax the time window constraints, allowing for late deliveries, which are penalized in the objective function. This choice of objective function is motivated by the autonomy of the delivery vehicles, where operational costs are not significantly influenced by operating time. As a result, the focus shifts towards maximizing customer satisfaction by minimizing delivery delays.
The second key difference lies in the limited cargo capacity of autonomous delivery vehicles. In our model, each vehicle has a single-unit capacity, necessitating a mandatory return to the depot or recharging station between each pair of customer deliveries. Consequently, each customer visit consists of a round trip from the depot to the customer and back, making it independent of the sequence of other customers. This implies that the order in which customers are visited has no direct impact on the total travel time of the vehicles in the TBDRP.
Despite this, the problem remains complex, as customers must still be assigned to vehicles and sequenced in a way that minimizes time-window violations. Additionally, the scheduling of vehicle recharging plays a crucial role in the overall optimization.
In contrast to studies on the EVRPTW, our modeling approach for the TBDRP is based on layered graphs. This concept has recently gained traction in the literature and has been applied to various optimization problems. The nodes in a layered graph are derived from the nodes of an underlying graph. For each original node, the layered graph contains a set of nodes, referred to as copies, with each copy representing a different state of one or more commodities at that node. Arcs between these copies represent feasible transitions between states, allowing constraints on the commodities to be naturally integrated into the graph structure.
Ref. [22] provide a survey on models based on layered graphs and the solution methods associated with them. Compared to traditional formulations that use additional variables to track commodities, layered graph formulations often exhibit much stronger linear relaxations, as noted by [23]. This characteristic is particularly advantageous for branch-and-bound algorithms, where the ability to prune nodes from the search tree is heavily influenced by the quality of the linear relaxation.
One of the most commonly used layered graphs is the well-known time-expanded graph, where nodes representing locations are expanded into sets of copies that represent different arrival times. Refinement algorithms have been proposed for a variety of problems modeled using time-expanded graphs. Ref. [23] offer an in-depth perspective on the potential of these algorithms for solving time-dependent problems. The general concept involves constructing partially expanded graphs, which contain fewer nodes and arcs than a fully expanded graph while still representing the problem. Depending on whether travel times are underestimated or overestimated, these graphs can provide either lower or upper bounds. They are then dynamically refined to improve the bounds and reduce the gap between them.
For example, Ref. [24] successfully apply this strategy to a delivery problem where shipments can be consolidated if they share the same route and departure time. Other examples include [25], who apply it to a time-dependent variant of the traveling salesman problem, and [26], who use it to solve the minimum duration shortest path problem. Additionally, Ref. [27] employ refinement steps based on the linear relaxation of a MILP formulation in their approach to solving the traveling salesman problem with time windows.
As an example of a layered graph where nodes do not represent arrival times, we reference [28], who apply refinement techniques in a graph where the node copies represent the number of arrivals at a location. Additionally, the works of [29,30] demonstrate that this technique is not limited to formulations derived from layered graphs but can be applied more broadly to problems where node contractions can be used to obtain relaxed formulations.
Our Branch and Refine approach is closely related to one of the methods presented by [29]. To the best of our knowledge, they were the first to incorporate graph refinement into a branch-and-bound algorithm, thus avoiding the need to repeatedly solve MILPs in a loop to progressively improve bounds.
3. Problem Description and Mathematical Formulation
In this section, we provide a detailed description of the TBDRP. Although the practical application involves delivery robots, we adopt a more theoretical perspective in the following sections and therefore use the more general term “vehicle.”
Let represent a set of locations, where locations 0 and are copies of the depot, and let represent the customer locations. We also define the following set of ordered location pairs:
There are m identical vehicles available at the depot, each with a single-unit capacity, and each customer has a single-unit demand. Consequently, a depot visit is required between any two consecutively visited customers.
Each location has a soft time window , where represents the lower bound, and represents the upper bound of the time window. For depot locations , we set , where T is the time horizon, chosen sufficiently large to avoid constraining potential routes. Additionally, we assume that servicing each customer requires a known duration .
An early arrival at a customer location is not permitted, and any tardy arrival incurs a penalty, which is the squared delay. Let denote the travel time between the depot and customer , both to and from the depot. Let represent the service time at customer i, plus the travel time between the arrival at customers i and . This includes the travel time from i back to the depot, followed by the travel time from the depot to j. For ease of notation, we define and for .
The depot functions not only as a storage facility for goods but also as a recharging station for the vehicles. We assume that the recharging capacity is sufficient to charge all vehicles simultaneously. Since the vehicles are battery-powered, let B denote the battery capacity. For simplicity, we assume that the state of charge (SoC) of the battery is expressed in terms of the number of time units the vehicle can still travel. This assumption allows for a direct conversion between the resources of time and energy.
Furthermore, we assume that the SoC increases linearly during charging and decreases linearly during driving, although in real-world applications, the charging rate typically decreases for the last 10% to 20% of the battery capacity (see [31]), research indicates that the linearity assumption holds well within the crucial 20% to 90% SoC range, which is the most relevant for our model. In addition, given that our test area is relatively flat, the vehicle motor operates under stable conditions, making the linearity assumption more reasonable.
We also assume that real-world factors such as traffic or pedestrian interference are minimal. Although the robot can slow down or wait for obstacles, such interference is considered negligible compared to overall daytime operations in the test scenarios. Finally, processes such as loading, unloading or waiting do not impact the SoC, as vehicles are assumed to enter a standby mode during these activities, consuming only negligible amounts of energy.
Let represent the travel time units gained by charging for one unit of time. Let denote the battery units consumed when traveling between customers i and . For consistency, we also define and for . Upon arrival at each customer , the SoC of the vehicle’s battery must lie within a battery window , where and .
The optimization problem involves determining m routes that minimize the sum of squared delays, subject to the following constraints: (i) each customer is visited exactly once by any of the vehicles, (ii) no customer is served earlier than their specified lower time window bound and (iii) the vehicles’ state of charge (SoC) must always remain within the bounds .
3.1. Exact Mixed-Integer Formulations
In this subsection, we present a mixed-integer quadratic programming (MIQP) formulation for modeling the TBDRP. Since each vehicle has a single-unit capacity, it must return to the depot after each delivery before proceeding to the next. In our formulation, we implicitly model these return trips by adjusting the travel times and battery consumption, which leads to the following definition. Given locations with , we define the tuple as a tour if the locations are pairwise disjoint, and if and .
We introduce binary decision variables for . For , these variables indicate whether customer i precedes customer j in the tour: if and only if a vehicle returns from i to the depot and then serves customer j next. The variables for indicate whether customer j is the first customer in a tour, while for indicate whether customer i is the last customer in a tour.
We also introduce continuous decision variables to represent the start time of service at location . Additionally, for each location , the state of charge (SoC) at the start of service is captured by the continuous variable , and any potential delay at the location is represented by the continuous variable .
An overview of all decision variables and parameters is provided in Table 1.

Table 1.
Decision variables and parameters.
Using these variables, the TBDRP can be modeled as the following mixed-integer quadratic program (MIQP):
In the objective function (1), delays are squared to penalize significant individual delays more heavily than multiple short delays. Constraint (2) ensures that no more than m vehicles are used. Constraints (3) and (4) guarantee that each customer is visited exactly once. For two consecutively visited locations i and j, constraints (5) ensure that the time difference between the arrival at these locations is sufficient. Similarly, constraints (6) ensure that the difference between the SoC levels reflects battery consumption and the time spent charging.
Additionally, constraints (5) implicitly impose an ordering of the customers within the same tour, preventing cycles in the solution. The domains of the variables are enforced by (7), (8) and (10). The time window for any location can only be violated if a positive value is assigned to , ensuring that the delay variables are correctly applied.
3.2. The Time- and Battery-Expanded Formulation
For fractional values of the x-variables, the right-hand side of (5) can become large, while the right-hand side of (6) can become small, making these constraints very weak in the linear relaxation of (10). This can result in a significant gap between the objective function value in the original problem (1)–(10) and its linear relaxation, which is known to hinder the performance of branch-and-bound algorithms used to solve the problem.
As an alternative to the MIQP formulation, we propose modeling the problem using a type of layered graph called a partially time- and battery-expanded graph (TBEG). Such formulations are known to provide much stronger linear relaxations (see, for example, Ref. [22]).
To define this approach, for a location , we introduce a tuple , which we refer to as a node representative of i, where . In this case, represents the arrival state of the node representative .
For any arc , we define a tuple as an arc representative of , where is a node representative of i, and is a node representative of j.
A TBEG is a graph , where the set of nodes consists of node representatives, and the set of arcs consists of arc representatives. Furthermore, for each location , there must be at least one node representative in , and for each node representative and each arc , there must be at least one arc representative of in , with as its tail. For a location , the subset of containing all node representatives of i is denoted by and for , the subset of containing all arc representatives of is denoted by .
Figure 1 illustrates the concept of TBEGs. For simplicity, in the example shown in Figure 1a, there are only three customers and one vehicle. Figure 1b illustrates the TBEG obtained by considering the six possible paths, where each customer is visited as early as possible. The different line styles of the circles in both figures indicate their correspondence. The nodes of this graph represent tuples consisting of the customer index, the arrival time and the battery level upon arrival. Arcs connect only those nodes where travel is feasible, i.e., the difference in arrival times is sufficiently large, and the battery consumption is accurately tracked.

Figure 1.
A minimalistic example.
The highlighted tour in the graph represents the sequence of customer visits that minimizes the objective function. The individual contribution of each arc to the objective function is indicated above the arcs of the highlighted tour. In this example, customers 1 and 2 can be visited without requiring a recharge. However, for the trip to customer 3 and the subsequent return to the depot, the vehicle needs to spend 6 units of time charging. Finally, the vehicle returns to the depot, using up the remainder of its battery.
For any TBEG , we can derive a model that, depending on , can serve as an exact formulation of the TBDRP. We use variables for all in the same way they are used in (1)–(10). However, instead of the continuous variables, we now use binary variables for each , which take the value 1 if and only if a vehicle transitions from the arrival state of the tail of a to the arrival state of the head of a.
Using these variables, we propose the following mixed-integer linear program (MILP) for any TBEG :
We refer to this MILP as , depending on the TBEG from which it is derived. The objective function (11) minimizes the squared delay of the arrival states indicated by the heads of the arcs in the TBEG. Constraint (12) limits the number of vehicles, while constraints (13) ensure that each customer is visited exactly once. The constraints (14) enforce consistency between the values assigned to the x- and y-variables.
Flow conservation is enforced by constraints (15), where denotes the set of outgoing arcs and denotes the set of incoming arcs for the node .
It is important to note that, at this stage, the solutions may contain cycles, which will need to be addressed in subsequent algorithmic steps.
Since the nodes in represent arrival states at locations, we can use Algorithm 1 with a solution of as its input and check if its output satisfies the constraints (2)–(10). For all nodes where the flow described by the y-variables in (11)–(17)is non-zero, the algorithm assigns t to the variable , b to the variable , and to the variable of (9). The objective function (11) then becomes the squared delay given by the -variables in (1).
| Algorithm 1: |
 |
Based on this, we can make the following observation:
Proposition 1.
Let be a TBEG, with a set of arcs that ensures that for any input to Algorithm 1, the output of Algorithm 1 satisfies the constraints (8) and (7). Then, the solution vectors of can be transformed by Algorithm 1 into vectors that satisfy all the constraints (2)–(10). Furthermore, if it is guaranteed that at least one optimal solution of (1)–(10) can be expressed as a tour in , the solution of can be transformed by Algorithm 1 into a feasible solution of (2)–(10).
In the remainder of this section, we derive a TBEG that satisfies the conditions of Proposition 1. We refer to this graph as the completely time- and battery-expanded graph.
We begin by introducing the matrix
Since , this transformation will be useful for considering arrival states in a different coordinate system.
For , we call a node representative of j reachable from a node representative of i, and an arc representative of an arc realizable if there exist such that
A possible interpretation of is the charging time, while non-zero values of cannot be realized in practice. can be interpreted as an instantaneous loss of charge or an overestimation of battery consumption. Although energy stored in the battery cannot simply disappear, this is allowed by constraint (7). This choice will be useful later, as it helps to expand the set of reachable arrival states as much as possible. Importantly, there is no downside to overestimating battery consumption when considering the feasibility of transitions.
We can deduce that if the arcs in are realizable, all tours in are guaranteed to satisfy both the time and battery constraints. Therefore, if we include node representatives with all possible arrival states for the locations, along with all realizable arc representatives, the conditions of Proposition 1 would be fulfilled by .
However, the set of node representatives is defined as a rectangle (for each customer index), meaning it is not possible to include all of them in a finite graph. To apply the described approach, we first need to demonstrate that it suffices to consider only a finite set of node representatives, i.e., for to contain a finite number of nodes. We achieve this by introducing the concept of domination, based on a specific partial order ⪯ of the states.
A closer examination of the definition of reachable arrival states reveals that they form part of a shifted convex cone. Moreover, this convex cone depends solely on the recharging rate . Thus, it is natural to define the partial order induced by this cone. The cone is given by
For two node representatives and of a location , we define if and only if . Similarly, for the arrival states, we write .
An easy way to verify whether two node representatives can be compared using this partial order is presented in the following lemma.
Lemma 1.
Given two node representatives and of a location , define and . Then, if and only if and .
Proof.
By the definition of and , any point can be expressed as for some . The result then follows directly from the definition of the partial order ⪯. □
With the previously outlined interpretation of and in mind, for two arrival states at the same location means that less time must be spent charging, and the battery consumption must be overestimated by a smaller amount to reach instead of . For this reason, we now use the partial order to state that a node representative dominates a node representative for some location if . This is further justified by the following observation.
Proposition 2.
Let and be node representatives of some location , such that , and let be a node representative of some other location , where . If is reachable from , then is also reachable from .
Proof.
This follows directly from the definition of arrival states. □
The following result demonstrates that our concept of domination is useful for reducing the number of node representatives that need to be included in .
Lemma 2.
Let be a node representative of some location , and let be another location such that . Then, there exists at most one node representative of j that is reachable from and is not dominated by another reachable node representative of j.
Proof.
Assume there are two distinct node representatives and of j that are reachable from and are not dominated by any other node representative that is also reachable from . Then, we can find such that
Since they are not dominated by any other node representative, they also cannot dominate each other. This implies and . For this to hold, either or must be true, but not both. Without loss of generality, assume and .
Now, consider the point given by
This point dominates both and . Moreover, since and , fulfills the conditions to be a node representative of j if and are node representatives. Furthermore, is also reachable from . Thus, we have found a node representative of j that is reachable from and dominates both and , contradicting the initial assumption. □
Lemma 2 demonstrates that we do not need to consider the entire set of node representatives. Instead, we only need to find the reachable node representative that dominates all others. While it is possible to use an LP formulation to identify this point, the geometry of the reachable node representatives is simple enough that it can be found by distinguishing a few special cases. The steps for this process are outlined in Algorithm 2.
| Algorithm 2: |
1 Input: A node representative of some location and another location j, such that ; 2 ; (forced charging time) 3 ; (forced wait time) 4 ; (time at depot) 5 ; (arrival time at j) 6 ; (SoC at j) 7 Output: A node representative of j; |
In this strategy, the time that must be spent at the depot is calculated first. It is the maximum of the following two values: (1) the waiting time required at the depot to ensure that the vehicle does not arrive too early at the next customer, and (2) the time needed to charge the battery sufficiently for the journey to the next customer and back. Based on this, the vehicle’s arrival time and state of charge (SoC) at the next customer can be determined.
Using this strategy ensures that the vehicles spend the minimum possible time at the depot. As a result, for any given tour assignment, there exists no recharging strategy that allows a customer to be reached earlier while still guaranteeing the feasibility of the transition. This, in turn, minimizes delays and ensures that the recharging strategy is optimal.
Let be an arc representative, and let be the output of the function recharge. This implies that , and provides a better estimation of the arrival time than . Thus, we can replace with in (11) to obtain a more accurate estimation of the delays.
More explicitly, by using for the arrival time calculated in this manner, we replace the objective (11) of the MILP with:
This modified objective function provides tighter bounds in our algorithms but does not affect the broader discussion, as the two objective functions are identical for the time- and battery-expanded graph .
The next step is to convert tours in G into tours of node representatives. We first extend the concept of representatives to tours by calling a tour in a TBEG a tour representative of a tour P in G if all the nodes in are node representatives of the corresponding nodes in P.
Given two tours and in some TBEG that are tour representatives of the same tour P in G, we write if the relation ⪯ holds for all node representatives in and .
With this notation, we can now prove the following result for Algorithm 2.
Lemma 3.
Given a tour P of length k in G, Algorithm 3 returns a tour representative of P, where the arcs between subsequent nodes are realizable. Furthermore, it holds that for all other tour representatives of P.
| Algorithm 3: expand |
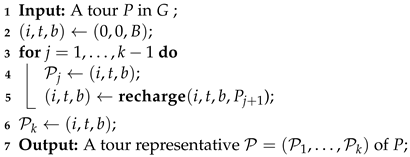 |
Proof.
Since the subsequent nodes in the output of Algorithm 3 are computed using Algorithm 2, the transitions between them must be realizable. By Lemma 2, the second node is the unique non-dominated node representative of that is reachable from . In particular, this also holds for of any other tour representative of P. Inductively, this property holds for all nodes in , which completes the proof. □
Now, interpreting the tours as graphs with nodes and arcs between subsequent nodes, by Lemma 3, Algorithm 3 can be used to convert tours in G into their tour representatives, which contain only realizable arc representatives. Moreover, no other tour representative with realizable arc representatives has nodes that are non-dominated by the nodes in the output of Algorithm 3.
Based on this, we define and , where denotes the set of all tours in G. By construction, any tour (including those in a solution of the TBDRP) has a tour representative in the graph . Furthermore, since all arc representatives in this graph are realizable, each tour representative in can be transformed into vectors that satisfy all time and battery constraints.
Therefore, fulfills the conditions outlined in Proposition 1, and thus is an exact formulation of the TBDRP. For this reason, it is justified to refer to as the time- and battery-expanded formulation of the TBDRP.
It is important to note that, based on the derivation of , this formulation is not practical for solving the TBDRP in real-world scenarios. Listing all possible tours in G, whose number grows exponentially with the size of the graph, would be computationally infeasible. However, as we will demonstrate in the following section, it is possible to use other TBEGs , for which serves as a relaxation of the time- and battery-expanded formulation of the TBDRP.
For any TBEG , it is straightforward to check whether a solution of is also contained in . This can be done by applying Algorithm 3 to the tours in G described by the x-variables and comparing the resulting tour to the one described by the y-variables. If they match, we have found an optimal solution to . If they differ, the output of Algorithm 3 can still be used to generate solution candidates.
4. Relaxations of the Time- and Battery-Expanded Formulation
As outlined earlier, the first step in developing an algorithm that leverages the time- and battery-expanded formulation is to find TBEGs for which serves as a good relaxation of . We begin by introducing the TBEG , where
This represents the TBEG with the smallest possible number of nodes and arcs.
We define arc representatives of an arc as underestimating if . Additionally, we say an arc is minimally underestimating in a TBEG if there exists no other node representative , with , such that and .
Let us illustrate this definition with a simplified example. Consider a situation where the set of node representatives in for some customer is represented by the black dots in Figure 2a, and we want to include an arc from a node to a node representative of j. Even if the node representative given by the output of Algorithm 2 is not an element of , it is guaranteed to be located within one of the colored areas.
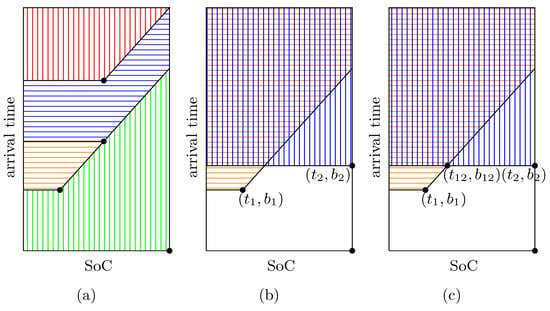
Figure 2.
Arrival states at some customer j.
Since all points in any of these areas are dominated by the bottom right corner (the apex of a shifted ), connecting to the node representative with an arrival state equal to the bottom right corner of this area results in a graph that underestimates the arrival states. Arc representatives chosen in this manner are minimally underestimating.
Constructing the entire set of arcs in this way leads to a graph where the nodes do not represent a single arrival state but rather an entire section of the rectangle of arrival states. Note that the graph can be interpreted similarly, but it is designed such that the outputs of Algorithm 2 used in the definition of underestimating arcs are already present in .
Another reason for using TBEGs in which the arc representatives are minimally underestimating is demonstrated by the following result.
Proposition 3.
Let , where all arcs are minimally underestimating, P a tour, a tour representative of P in , and a tour representative of P in . Then, holds for .
Proof.
Assume the assertion does not hold. Then, there exists a minimal index such that . It must therefore hold that . Since the output of recharge is always reachable from its input, by Proposition 2, this implies
However, since the arcs in are underestimating and by the construction of , it follows that
which contradicts the initial assumption. □
Since our concept of domination implies that the arrival times are underestimated, a direct consequence of Proposition 3 is that for any chosen tour, the objective value of the MILP is always less than or equal to the objective value of . This means that we can use as a relaxation of if all the arcs in the TBEG are minimally underestimating. Consequently, we will now only consider TBEGs in which all arcs are minimally underestimating.
The situation in Figure 2a, where all nodes can be strictly ordered with respect to the partial order ⪯, is a special case, as it implies that there is always only one minimally underestimating arc for a given node and a fixed destination. A more complex scenario is illustrated in Figure 2b, where there are two nodes and , and neither dominates the other. If the output of for a node falls within the vertically and horizontally striped area, there are two possible choices for minimally underestimating arcs.
In this situation, two issues can arise, which we will illustrate with a simple example. The TBEGs and , shown in Figure 3, were derived for an instance of the TBDRP given by the parameters in Table 2 (with a service time of 0 min for all locations) and include all minimally underestimating arcs. The numbers next to the arcs represent the delays that occur when an arc is used.
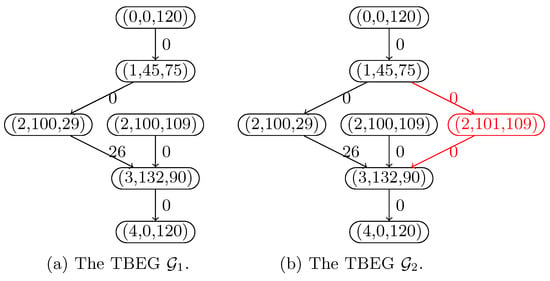
Figure 3.
Illustrations of two TBEGs.

Table 2.
Parameters of a VRPTB instance.
Starting at the node , the output of is . Therefore, in , the node is only connected to and not to , because . Now, consider , which contains the nodes of and an additional node (highlighted in red). Since and , both are successors of .
In this case, the arc to significantly underestimates the correct battery consumption, allowing customer 3 to be reached without any delay. Both TBEGs could be used to create relaxations of the time- and battery-expanded formulation, but the problem arises because, although can be obtained from by adding a node, the MILP has a smaller objective value than . In this case, the graph with fewer nodes provides a better relaxation than the one with more nodes.
In an algorithm that dynamically expands the set of nodes, however, the quality of the relaxation should only improve in order to provide tighter bounds.
In addition to this, there is another issue we will address shortly. In , there are two different tour representatives for the tour . However, in and , there is a one-to-one correspondence between tours and their representatives. One of the goals in designing our refinement strategy is to maintain this one-to-one correspondence between tours in G and their tour representatives in , as it simplifies checking whether a certain tour in the graph underestimates delays or if its arrival states are accurately represented.
Our approach to prevent both of the previously mentioned problems is to expand the set of nodes more carefully, ensuring that there is always only one minimally underestimating arc to choose. The idea we will use is illustrated in Figure 2c. We add the bottom-right corner of the intersecting areas as nodes. As depicted, the node representatives with arrival states in the blue and orange striped areas can be connected to , and this is now the only minimally underestimating arc.
To formalize this approach, we start by providing an algorithm to find the bottom-right corner of the intersecting areas, which is denoted as in the illustration. Algorithm 4 formalizes this idea.
| Algorithm 4: |
1 Input: Node representatives and of some location ; 2 ; 3 ; 4 ; 5 ; 6 Output: A node representative of j; |
In this approach, a location j and two node representatives and of j are used as input. The matrix is then employed to transform their arrival states into a different coordinate system, which is defined using the same vectors that describe . In this transformed coordinate system, the coordinates of the new point can be easily calculated using the maximum function. Finally, we convert back to the original coordinate system and return the calculated point.
Using this algorithm, we define a TBEG as intersection complete if, for any node representatives of some location , the node representative is also an element of .
The following two results demonstrate that intersection-complete TBEGs avoid the problem of multiple minimally underestimating arcs, as previously illustrated.
Lemma 4.
Let be an intersection-complete TBEG, and let be a node representative of a location . If there are two node representatives and such that and , then there exists a node representative such that , , and .
Proof.
Let , and define
By Lemma 1, it follows that and . Furthermore, by the same lemma, we have and , so and .
Since , it follows again by Lemma 1 that , which completes the proof. □
Proposition 4.
Given a tour P in G and an intersection-complete TBEG , where all arc representatives are minimally underestimating, there exists a unique tour representative of P in .
Proof.
Assume there are two different tour representatives and of P in . Then, there must exist a minimal index k with for which .
Let , , and . It also holds that . Furthermore, we have and , which must both be underestimating arcs.
This implies , placing us in the situation described in Lemma 4. The existence of the state from Lemma 4 now yields a contradiction to the arcs and being minimally underestimating, unless , which contradicts our initial assumption.
Therefore, there is a unique tour representative of P in . □
In the remainder of this section, we demonstrate how intersection-complete TBEGs can be constructed in practice. Note that is an intersection-complete TBEG, as each location has only one node representative, and it holds that for any .
Before going into the details, we provide an example showing how refinements can be used to correct the objective of a tour. The graph for the instance considered earlier in Figure 1 is depicted in Figure 4a. We have highlighted the tour and its associated delays, which we aim to correct. The refined graph is shown in Figure 4b. To obtain this graph, two nodes were added, which represent the correct arrival times and SoCs for the tour . After the refinement, the representative of this tour has the correct delays. As a side effect, the representatives of other tours, such as , now contain different node representatives.

Figure 4.
Illustrations of two TBEGs.
As a first step towards our refinement routine, we present an algorithm that incorporates a new node representative. Algorithm 5 takes a TBEG and a node representative of a location as its input. The output is a larger TBEG in which and some additional nodes are included in its set of nodes.
| Algorithm 5: |
 |
For the returned TBEG, we can prove the following result.
Lemma 5.
Given an intersection-complete TBEG , a location and a node representative of i, the output is an intersection-complete TBEG.
Proof.
Assume that the output is not intersection-complete. Then, there exists a location and two node representatives , such that . We set
Note that must hold, because otherwise is not intersection-complete. For the same reason, at least one of or is not an element of . Without loss of generality, let . Now, both and lead to a contradiction.
Without loss of generality, assume that . This implies and . Since was added during the execution of Algorithm 5, there must be a node representative such that and , where . Similarly, we can find a node representative such that and , where . If , we can choose .
Since is intersection-complete, it must hold that . Since and , we have . This implies , which is a contradiction.
Thus, is intersection-complete. □
Finally, we present Algorithm 6, which takes a TBEG and a tour P as input, and returns a TBEG where the tour representative of P is unique and is also contained in .
| Algorithm 6: |
 |
The input consists of a tour P in G. If some of the transitions in the tour representative of P in underestimate the arrival states, the following result shows that this algorithm guarantees that the tour representative in the output models the arrival states correctly.
Proposition 5.
Given an intersection-complete TBEG and a tour P in G, the output of Algorithm 6 is an intersection-complete TBEG. Furthermore, there is a unique tour representative of the tour P in , and this tour representative is the same as the tour representative of P in .
Proof.
The first statement is a direct consequence of Lemma 5, as the output is created by iteratively applying Algorithm 5 to an intersection-complete graph. The uniqueness of the tour representative follows from Proposition 4, and the final assertion comes from the fact that we use Algorithm 3 both for deriving and in Algorithm 5 to determine the added nodes. □
Now, we have a strategy to construct practically useful TBEGs. We start with as the initial TBEG and iteratively correct the tour representatives of tours in G, until the solution of the MILP from the current TBEG matches that of . In the following section, we convert this strategy into two different algorithms that solve the TBDRP.
5. Refinement Algorithms
Based on the results from the previous section, we can derive refinement algorithms to solve the TBDRP. For ease of notation, we denote the linear relaxation of a MILP M by . We further use for the optimal value of a MILP and for the set of feasible points of a MILP. Additionally, for a subtour S in G, we refer to the constraint
as the subtour elimination constraint (SEC) for S.
We begin with Iterative Refinement, as outlined in Algorithm 7.
| Algorithm 7: Iterative Refinement Algorithm |
 |
In theory, the initial TBEG for this algorithm could be any intersection-complete TBEG, but for simplicity, we choose to start with . This graph is then iteratively refined until its solution is feasible for the time- and battery-expanded formulation. Additionally, if the solution contains subtours, we address this by adding subtour elimination constraints (SECs) rather than refining the graph.
Since, upon termination, the solution of the relaxation is found to be feasible, the returned values are proven to be optimal solutions of the TBDRP. After each iteration, either one more tour is represented correctly (as guaranteed by Proposition 5) or a subtour is excluded. Therefore, the algorithm must terminate after a finite number of iterations.
An alternative approach, called Branch and Refine, is presented in Algorithm 8. In line 23, the function performs the usual branching step of a branch-and-bound algorithm. Since the integer variables are binary, it returns two MILPs: one in which a variable that had a fractional value in the solution is set to 0, and one in which it is set to 1. Furthermore, in line 20, the function takes the list of open problems, the old graph and the new graph as input, and returns an updated list of open problems where the constraints and objective derived from the old graph are replaced by those from the new graph.
| Algorithm 8: Branch and Refine |
 |
This algorithm is similar to the usual branch-and-bound algorithms applied to solve MILPs, with the main difference being that graph refinement is integrated into the exploration of the branch-and-bound search tree. Branch-and-bound algorithms divide the problem into subproblems and use relaxations to find valid bounds that reduce the number of subproblems to consider. Typically, the linear relaxation of the MILP is used, but this is not the only option. In Branch and Refine, we use the linear relaxation of another MILP and adjust this MILP during execution. Since any of the MILPs used are relaxations of , Branch and Refine fits within the branch-and-bound paradigm for solving and thus returns a solution.
Note that this algorithm is very similar to Iterative Refinement. However, in Iterative Refinement, the exploration of the branch-and-bound search tree is implicit, as we directly use the solutions of the MILPs. Therefore, the search tree is explored in every iteration, whereas in Branch and Refine, it is explored only once. This does not guarantee an advantage, as early branching decisions during search tree exploration can significantly affect the runtime of branch-and-bound algorithms. To evaluate the performance of these approaches, we conducted a computational study implementing both algorithms.
6. Computational Experiments and Implementation Details
In this section, we compare the two refinement algorithms presented in this work, not only to each other but also to a direct approach for solving the MIQP (1)–(10) using a state-of-the-art solver. To ensure the comparison is as objective as possible, our goal was to create a framework where all three approaches could be implemented without favoring one over the others. The challenge, however, is that not all state-of-the-art solvers are suitable for implementing Branch and Refine.
To implement Branch and Refine efficiently, the solver must not only allow for adding constraints and variables (i.e., rows and columns) to the MILP representation but also for changing the coefficients of some variables in certain constraints. This is necessary because, after adding nodes, some of the previously used arcs may no longer be minimally underestimating. Instead of adding a cutting plane that sets the associated variables to zero, an efficient implementation would remove the variable from the flow constraint of its old head and add it to the new head. However, none of the state-of-the-art solvers we tested allowed for this type of modification during the solution process, as removing a variable from a constraint can invalidate previously computed bounds.
As a result, we dropped this requirement and adopted a workaround where we added cutting planes to set the old variables to zero and introduced new variables. With this approach, we successfully implemented Branch and Refine in the SCIP Optimization Suite, maintained by the Zuse Institute Berlin. For a fair comparison, we also used SCIP Optimization Suite 6.0.1 to solve the MIQP formulation in (1)–(10) and the MILPs that must be solved during Iterative Refinement. Within SCIP, the SoPlex 4.0.1 solver was used to solve the linear relaxations at the nodes of the search tree.
All experiments were executed on a single core of a computer with a 3.30 GHz CPU running Windows 10 as the operating system.
To test the performance of the implementations, we conducted an extensive computational study on a variety of instances. All instances are based on the benchmark set introduced by [32]. This set contains instances for the capacitated VRP and is divided into six classes, featuring problems with either short or long scheduling horizons, randomly distributed customers, clustered customers and a mixed version of both. An important detail is that within each class, the customer locations are fixed, with only the time windows being varied.
In the TBDRP, since vehicles always return to the depot, the distances between customers are irrelevant—only the distance to the depot matters. Therefore, the distinction between clustered and non-clustered customers is not applicable in our case. In preliminary tests, we also observed minimal variation in the solutions within each instance class. As a result, we derived new instances by selecting unique customer locations and time window combinations from the benchmark set. For each instance, we randomly selected 50 of these combinations to create a new test case. These instances are available via DOI 10.26127/BTUOpen-5493. The time limit for all instances was set to 1 h.
The goal of the computational experiments was to evaluate the effectiveness of the three solution methods presented in this paper.
In the first experiment, we examine the impact of an increasing number of customers on computation time while keeping the number of vehicles fixed. We ran two sets of experiments: one with vehicles and one with vehicles. In both cases, the battery capacity was set to , and the recharging rate was set to 2.5. For the experiments with 3 vehicles, we started with the first 10 to 27 customers of 20 different instances.
The results of these experiments are shown in Figure 5, where we use the abbreviations IR for Iterative Refinement and BaR for Branch and Refine. For the experiments with 10 vehicles, we followed a similar procedure, but the number of customers ranged from 30 to 50. The results are shown in Figure 6. Each solution method’s run is represented by a marker in the plot, with a transparency of 40%, and the marker’s color and shape indicate the method used. The x-axis of the graphs shows the number of customers, while the y-axis is split into two parts: a lower section for instances solved within 3600 s, and an upper section displaying the gap for instances that timed out.
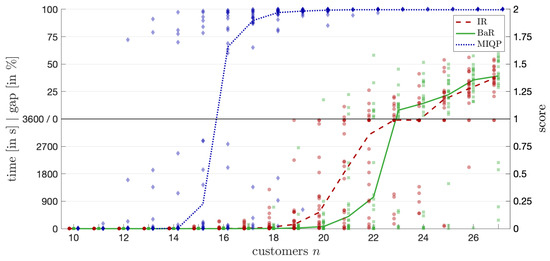
Figure 5.
Computation times for different customer numbers and 3 vehicles.
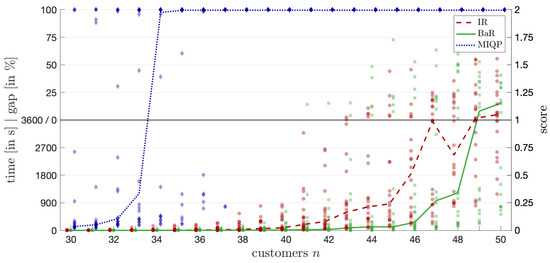
Figure 6.
Computation times for different customer numbers and 10 vehicles.
To facilitate a comprehensive comparison of the algorithms’ performance across different instances, we introduce a scoring function that combines computation time and optimality gap into a single metric. This scoring function allows us to compute a median performance measure even when some instances are not solved to optimality within the time limit. The scoring function is defined as follows:
- Computation Time Score (): For instances solved to proven optimality within the time limit s, we compute a normalized computation time score:where t is the computation time in seconds. This maps the computation time linearly onto the interval , with lower values indicating better performance.
- Optimality Gap Score (): For instances not solved to proven optimality within the time limit, we record the optimality gap at termination:where and are the best upper and lower bounds found by the algorithm, respectively. We normalize the gap to a score between 0 and 1:with higher values indicating a larger gap and thus poorer performance.
- Total Score (): The total score for each instance is the sum of the computation time score and the optimality gap score:This results in a total score s ranging from 0 (best possible performance) to 2 (worst possible performance), effectively combining both time and solution quality into a single metric.
Using this scoring function, we rank the instances for each fixed parameter setting (e.g., number of customers) based on their total scores. The median is then computed with respect to these total scores, allowing us to plot a representative performance measure for each group of instances.
In all figures (Figure 5, Figure 6, Figure 7 and Figure 8), the y-axis is divided into two sections: The lower section displays the computation times (in seconds) for instances solved within the time limit, and the upper section displays the optimality gaps (in percentages) for instances where the time limit was reached. Each algorithm’s performance on an individual instance is represented by a marker. The markers are semi-transparent to illustrate the distribution of results across multiple instances. The line connecting the median points represents the general trend of the algorithms’ performance as problem size or other parameters vary, based on the total score s. This approach allows us to present both computation time and solution quality in a single figure, providing a comprehensive comparison of the algorithms under various conditions.
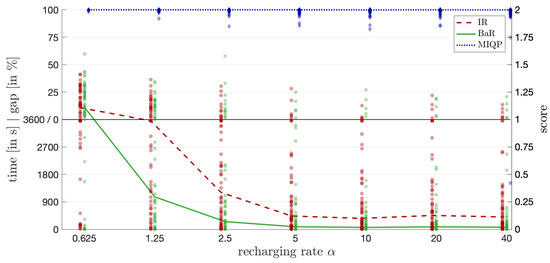
Figure 7.
Computation times for different recharging rates.
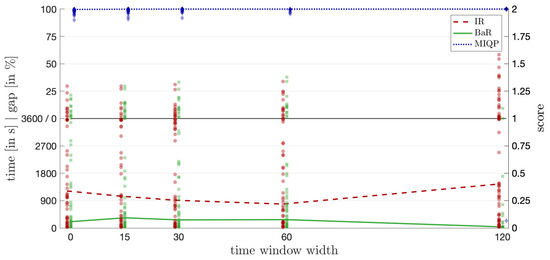
Figure 8.
Computation times for different time window widths.
In Figure 5 and Figure 6 it is clear that directly solving the MIQP formulation is not competitive with the approaches presented in this work. For example, in the 3-vehicle setting, the MIQP timed out on more than half of the instances with 15 customers, whereas both refinement approaches solved all instances with up to 19 customers to optimality.
When comparing Iterative Refinement and Branch and Refine for 19 to 22 customers, Branch and Refine outperforms Iterative Refinement. However, for larger instances, the two methods perform similarly, and the median trends suggest that Iterative Refinement may perform better as the number of customers increases. Notably, few instances with more than 23 customers were solved to global optimality by any method. It is also important to note that the smaller gaps found by Iterative Refinement within 3600 s do not necessarily imply that an optimal solution would be found faster compared to Branch and Refine.
The results for the 10-vehicle experiments show similar behavior. For instances with more than 33 customers, most were unsolved within the time limit using the MIQP formulation, while both refinement methods solved instances for all customer amounts. Between 40 and 48 customers, Branch and Refine clearly outperforms Iterative Refinement, suggesting that Branch and Refine is more effective in this range. However, for 49 and 50 customers, when more than half the instances remain unsolved, it becomes less clear which algorithm performs better.
In another computational experiment, we investigated the impact of the recharging rate on the difficulty of the instances. The recharging rate influences how much the battery constraints affect the problem. For very small values of , nearly all the time is spent charging at the depot, while large values of make charging almost instantaneous, meaning the battery constraints impose minimal restrictions on the routes. The results for instances with 3 vehicles and between 20 and 22 customers are shown in Figure 7. The plot layout is similar to the previous one, but the x-axis now represents different values of , and a logarithmic scale is used.
The results show that as increases, the instances become easier to solve for both Iterative Refinement and Branch and Refine. We do not expect computation times to decrease significantly for values of larger than 40, as routing decisions seem to have the greatest impact on delays at this point. It is also clear that Branch and Refine outperformed Iterative Refinement in most cases, even for instances where recharging was nearly instantaneous.
The final set of computational tests studied the effect of the time window width on computation times. We used instances with 20 to 22 customers, a recharging rate of and vehicles. The lower bounds of the time windows were kept constant, and the due dates were set to the lower bounds plus a varying constant that determined the time window width. The results, shown in Figure 8, follow the same plot structure as before, with the time window width displayed on the x-axis.
As expected, given the number of customers in the instances, the MIQP formulation could only be solved for a few cases, and most had an optimality gap of 100% after one hour. Once again, Branch and Refine performed better than Iterative Refinement. Interestingly, while Branch and Refine benefited from wider time windows, Iterative Refinement and the direct MIQP approach performed worst on instances with the largest time window widths.
7. Conclusions and Future Work
We introduced a variant of the Vehicle Routing Problem (VRP), the Time- and Battery-Constrained Delivery Robot Problem (TBDRP), which incorporates soft time windows alongside vehicle battery consumption constraints. To address this problem, we proposed two formulations: a Mixed-Integer Quadratic Programming (MIQP) formulation that can be solved directly using state-of-the-art solvers, and a formulation based on a two-dimensional layered graph. While the latter is not suitable for direct solution approaches, it allows for relaxations that not only provide lower bounds but can also be solved efficiently. These relaxations were employed in two structurally similar algorithms: Branch and Refine and Iterative Refinement. Both algorithms start with a coarse layered graph where travel times are underestimated and battery consumption is overestimated. The graph is dynamically refined based on the solutions provided by the relaxations.
The results of our computational study indicate that both algorithms significantly outperform the direct MIQP approach. Additionally, Branch and Refine, which integrates graph refinement into a branch-and-bound framework, consistently outperforms Iterative Refinement in most cases.
There are several limiting assumptions underlying our study, which could be addressed in future research. One key limitation is the assumption of linear battery consumption and charging behavior, which, while simplifying the model, does not fully capture the non-linearities found in real-world battery systems. Factors such as the vehicle’s speed, load and terrain can affect battery discharge, while charging times typically increase as the battery approaches full capacity. Another important limitation is that our model operates in static environments, where all delivery locations, traffic patterns and vehicle statuses are known in advance. Real-world conditions are far more dynamic, and incorporating factors like fluctuating traffic or real-time battery deterioration would be essential for more practical applications. Furthermore, while our methods perform well on modified Solomon instances, the scalability of the approach for larger datasets involving many customers or robots could present computational challenges. Lastly, our focus on minimizing delivery delays is a single-objective approach, which does not consider other important factors such as total energy consumption or the number of deliveries per day. Future work could explore these additional performance metrics and investigate alternative objective functions to achieve a more comprehensive optimization.
Additionally for future work, we plan to explore whether similar techniques can be applied in more general settings. A natural extension would be to consider multiple depots. If each vehicle is strictly assigned to one depot and can only recharge and pick up parcels there, it is feasible to use a layered graph for each depot. A more challenging, yet realistic, scenario would involve a setting where the assignment of parcels to depots is not predefined. In this case, vehicles would need to choose a depot for picking up parcels and decide whether recharging is necessary.
In this more complex scenario, even if the next customer is known, the closest depot might not always be the best option. The vehicle’s current state of charge (SoC) could be insufficient to reach the nearest depot, while another depot might still be within range. Additionally, a more distant depot might allow for a higher SoC before visiting the next customer, optimizing the overall route. An even more complex situation arises when these factors occur simultaneously, and visiting two depots could be the optimal solution. In such cases, a layered graph approach would need to incorporate all these possibilities into its topology.
Besides single-compartment delivery robots, multi-compartment delivery robots are also used. In this scenario, the robots are not required to return to the depot after each delivery. Consequently, our charging strategy cannot be applied, as spending extra time charging earlier might be necessary to consolidate multiple deliveries into one trip. In future work, we aim to investigate how this impacts the charging strategy and to explore suitable layered graph structures that could adapt our algorithm to this more general setting.
Another promising direction for future research is to explore whether layered graph approaches are effective for the Electric Vehicle Routing Problem with Time Windows (EVRPTW). In this VRP variant, much like in a multi-depot version of the TBDRP, the routes between customers are not predetermined, which requires more sophisticated modeling techniques to construct the appropriate layered graph.
We also see potential for improving our current methodology, particularly Branch and Refine. Thus far, we have utilized SCIP’s pre-implemented node selection strategy, which was designed for branch-and-cut or branch-and-price algorithms. Since our implementation uses SCIP functions in a non-standard way, it would be interesting to explore whether a customized node selection strategy could enhance the performance of Branch and Refine. Moreover, we have consistently enforced graph refinement for all nodes in the search tree, although the theoretical framework we presented does not require this. A local refinement strategy is sufficient, and whether such local refinements could offer practical benefits remains an open question worthy of deeper analysis.
Author Contributions
Conceptualization, F.G., S.S., U.C. and A.F.; methodology, F.G. and S.S.; software, F.G. and S.S.; validation, F.G., S.S., U.C. and A.F.; formal analysis, F.G. and S.S.; investigation, F.G., S.S.; resources, U.C. and A.F.; data curation, F.G. and S.S.; writing—original draft preparation, F.G. and S.S.; writing—review and editing, F.G., S.S., U.C. and A.F.; visualization, F.G. and S.S.; supervision, U.C. and A.F.; project administration, U.C. and A.F.; funding acquisition, U.C. and A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeinschaft (DFG), grant numbers FU 860/1-1 and CL 318/26-1.
Data Availability Statement
Acknowledgments
The authors Fabian Gnegel and Armin Fügenschuh acknowledge the funding by the German Research Association (DFG) grant number FU 860/1-1. The authors Stefan Schaudt and Uwe Clausen acknowledge the funding by the German Research Association (DFG) grant number CL 318/26-1.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Statista Digital Market Outlook. Ecommerce Report 2022. 2022. Available online: https://www.statista.com/study/42335/ecommerce-report/ (accessed on 7 October 2024).
- Pitney Bowes Inc. Pitney Bowes Parcel Shipping Index Reports Continued Growth as Global Parcel Volume Exceeds 100 Billion for First Time Ever. 2020. Available online: https://www.businesswire.com/news/home/20180828005237/en/ (accessed on 7 October 2024).
- Heinemann, G. Der Neue Online-Handel; Springer Fachmedien: Wiesbaden, Germany, 2018. [Google Scholar]
- Kreuz, F.; Clausen, U. Einsatzfelder von eLastenrädern im Städtischen Wirtschaftsverkehr; Springer Fachmedien: Wiesbaden, Germany, 2017; pp. 323–333. [Google Scholar]
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-mile delivery concepts: A survey from an operational research perspective. OR Spectr. 2020, 43, 1–58. [Google Scholar] [CrossRef]
- Engesser, V.; Rombaut, E.; Vanhaverbeke, L.; Lebeau, P. Autonomous Delivery Solutions for Last-Mile Logistics Operations: A Literature Review and Research Agenda. Sustainability 2023, 15, 2774. [Google Scholar] [CrossRef]
- Speranza, M.G. Trends in transportation and logistics. Eur. J. Oper. Res. 2018, 264, 830–836. [Google Scholar] [CrossRef]
- Boysen, N.; Schwerdfeger, S.; Weidinger, F. Scheduling last-mile deliveries with truck-based autonomous robots. Eur. J. Oper. Res. 2018, 271, 1085–1099. [Google Scholar] [CrossRef]
- Ostermeier, M.; Heimfarth, A.; Hübner, A. Cost-optimal truck-and-robot routing for last-mile delivery. Networks 2022, 79, 364–389. [Google Scholar] [CrossRef]
- Poeting, M.; Schaudt, S.; Clausen, U. Simulation of an Optimized Last-Mile Parcel Delivery Network Involving Delivery Robots. In Advances in Production, Logistics, and Traffic—Proceedings of the 4th Interdisciplinary Conference on Production Logistics and Traffic 2019; Clausen, U., Langkau, S., Kreuz, F., Eds.; Lecture Notes in Logistics; Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 1–19. [Google Scholar]
- Poeting, M.; Schaudt, S.; Clausen, U. A comprehensive case study in last-mile delivery concepts for parcel robots. In Proceedings of the 2019 Winter Simulation Conference (WSC), National Harbor, MD, USA, 8–11 December 2019. [Google Scholar]
- Sonneberg, M.-O.; Leyerer, M.; Kleinschmidt, A.; Knigge, F.; Breitner, M.H. Autonomous unmanned ground vehicles for urban logistics: Optimization of last mile delivery operations. In Proceedings of the 52nd Hawaii International Conference on System Sciences, Hawaii International Conference on System Sciences, Hawaii, HI, USA, 8–11 January 2019. [Google Scholar]
- Maio, A.D.; Ghiani, G.; Laganá, D.; Manni, E. Sustainable last-mile distribution with autonomous delivery robots and public transportation. Transp. Res. Part C Emerg. Technol. 2024, 163, 104615. [Google Scholar] [CrossRef]
- Viloria, D.R.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned aerial vehicles/drones in vehicle routing problems: A literature review. Int. Trans. Oper. Res. 2021, 28, 1626–1657. [Google Scholar] [CrossRef]
- Boysen, N.; Briskorn, D.; Fedtke, S.; Schwerdfeger, S. Drone delivery from trucks: Drone scheduling for given truck routes. Networks 2018, 72, 506–527. [Google Scholar] [CrossRef]
- Poikonen, S.; Wang, X.; Golden, B. The vehicle routing problem with drones: Extended models and connections. Networks 2017, 70, 34–43. [Google Scholar] [CrossRef]
- Wang, Z.; Sheu, J.-B. Vehicle routing problem with drones. Transp. Res. Part B Methodol. 2019, 122, 350–364. [Google Scholar] [CrossRef]
- Erdelić, T.; Carić, T. A survey on the electric vehicle routing problem: Variants and solution approaches. J. Adv. Transp. 2019, 2019, 5075671. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The electric vehicle-routing problem with time windows and recharging stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. Partial recharge strategies for the electric vehicle routing problem with time windows. Transp. Res. Part C Emerg. Technol. 2016, 65, 111–127. [Google Scholar] [CrossRef]
- Desaulniers, G.; Errico, F.; Irnich, S.; Schneider, M. Exact algorithms for electric vehicle-routing problems with time windows. Oper. Res. 2016, 64, 1388–1405. [Google Scholar] [CrossRef]
- Gouveia, L.; Leitner, M.; Ruthmair, M. Layered graph approaches for combinatorial optimization problems. Comput. Oper. Res. 2019, 102, 22–38. [Google Scholar] [CrossRef]
- Boland, N.L.; Savelsbergh, M.W. Perspectives on integer programming for time-dependent models. Top 2019, 27, 147–173. [Google Scholar] [CrossRef]
- Boland, N.; Hewitt, M.; Marshall, L.; Savelsbergh, M. The continuous-time service network design problem. Oper. Res. 2017, 65, 1303–1321. [Google Scholar] [CrossRef]
- Vu, D.M.; Hewitt, M.; Boland, N.; Savelsbergh, M. Dynamic discretization discovery for solving the time-dependent traveling salesman problem with time windows. Transp. Sci. 2020, 54, 703–720. [Google Scholar] [CrossRef]
- He, E.; Boland, N.; Nemhauser, G.; Savelsbergh, M. A dynamic discretization discovery algorithm for the minimum duration time-dependent shortest path problem. In International Conference on the Integration of Constraint Programming, Artificial Intelligence, and Operations Research; Springer: Berlin/Heidelberg, Germany, 2018; pp. 289–297. [Google Scholar]
- Riedler, M.; Ruthmair, M.; Raidl, G.R. Strategies for iteratively refining layered graph models. In International Workshop on Hybrid Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 46–62. [Google Scholar]
- Gnegel, F.; Fügenschuh, A. An iterative graph expansion approach for the scheduling and routing of airplanes. Comput. Oper. Res. 2020, 114, 104832. [Google Scholar] [CrossRef]
- Bärmann, A.; Liers, F.; Martin, A.; Merkert, M.; Thurner, C.; Weninger, D. Solving network design problems via iterative aggregation. Math. Program. Comput. 2015, 7, 189–217. [Google Scholar] [CrossRef]
- Clautiaux, F.; Hanafi, S.; Macedo, R.; Voge, M.-E.; Alves, C. Iterative aggregation and disaggregation algorithm for pseudo-polynomial network flow models with side constraints. Eur. J. Oper. Res. 2017, 258, 467–477. [Google Scholar] [CrossRef]
- Marra, F.; Yang, G.Y.; Træholt, C.; Larsen, E.; Rasmussen, C.N.; You, S. Demand profile study of battery electric vehicle under different charging options. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).