A Novel Approach to Enhance DIRECT-Type Algorithms for Hyper-Rectangle Identification
Abstract
1. Introduction
- Dedicated Vertex Database Integration: This work introduces a new approach by incorporating a dedicated vertex database. The purpose of this strategic embedding is to constrain sampling points within descent sub-regions, effectively mitigating the risk of oversampling. By implementing this vertex database, the algorithm provides more efficient computations, improving both the accuracy and speed of the optimization process.
- Innovative Grouping Strategy for Hyper-Rectangle Identification: A groundbreaking grouping strategy is introduced, specifically designed for the efficient identification of hyper-rectangles in DIRECT-type algorithms. This innovation addresses the challenge of managing and organizing data points in the search space. By taking advantage of this advanced clustering strategy, the algorithm optimizes the hyper-rectangle identification process, resulting in a more rational and powerful exploration of the solution space.
- Performance Enhancement in the BIRECTv Algorithm: This paper outlines the significant improvements made to the BIRECTv algorithm. These developments have a positive and noticeable impact on the overall efficiency of the algorithm. By refining the BIRECTv approach, this research contributes to a more robust and efficient optimization algorithm, with advances in convergence rates and solution quality. The refined BIRECTv algorithm illustrates the practical implications of the suggested contributions in the design of the underlying optimization process.
2. Overview of Existing Methods for Selecting (POHs) in Various DIRECT-Type Approaches
3. From BIRECT to BIRECTv(impr.)
3.1. The Original BIRECT
3.1.1. Selection Criterion
- At each iteration (kth iteration), starting from the current partitionwhere is the index set identifying the current partition, a new partition is created by bisecting a set of POHs from the previous partition.
- The identification of a potentially optimal hyper-rectangle (POH) is based on lower bound estimates of the objective function over each hyper-rectangle, with a fixed rate of change (analogous to a Lipschitz constant).
- A hyper-rectangle , is considered potentially optimal if specific inequalities involving (a positive constant) and the current best-known function value are satisfied.where the measure (distance, size) of the hyper-rectangle is given by
| Algorithm 1 Main steps of the BIRECT algorithm |
|
3.1.2. Division and Sampling Criterion
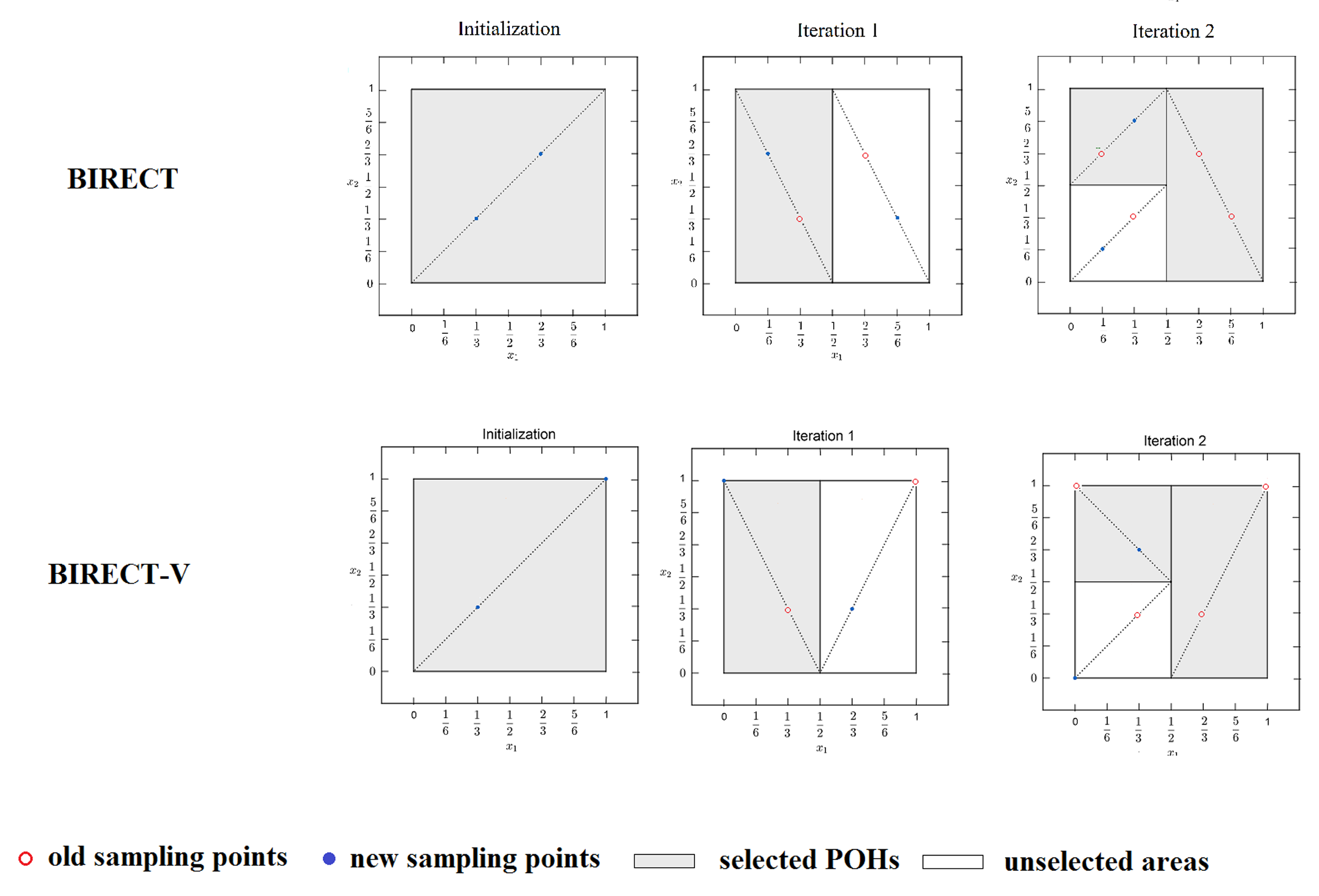
- After the initial partitioning, BIRECT proceeds to future iterations by partitioning POHs and evaluating the objective function at new sampling points.
- New sampling points are generated by adding and subtracting a distance equal to half the side length of the branching coordinate from the previous points. This approach allows for the reuse of old sampled points in descendant subregions.
- An important aspect of the algorithm is how the selected hyper-rectangles are divided. For each POH, the set of maximum coordinates (edges) is computed, and the hyper-rectangle is bisected along the coordinate (branching variable ) with the largest side length (). Starting from the coordinates associated with the smallest index j (in case multiple coordinates are eligible):
3.2. Description of the BIRECTv Algorithm
3.3. Integration Scheme for Identification of Potentially Optimal Hyper-Rectangles in DIRECT-Based Frameworks
- Tolerance :
- A tolerance of (0.01) means that the algorithm will consider hyper-rectangles whose and values are within 0.01 of each other.
- This allows for a relatively larger difference between and , meaning the algorithm will be more lenient in selecting POHs.
- This might result in a larger set of POHs, including some with relatively larger differences in their norm values.
- Tolerance :
- A tolerance of (0.0000001) means that the algorithm will consider hyper-rectangles whose and values are within of each other.
- This uses a much smaller tolerance, making the algorithm much stricter in selecting POHs.
- This will result in a smaller set of POHs, only including those with extremely close norm values.
Convergence
4. Results and Discussion
4.1. Implementation
| Algorithm 2 Find first index within tolerance |
|
4.2. Discussion
- The improved versions of BIRECTv appear to be reliable choices for optimization tasks, as they consistently outperformed the previously published versions and demonstrated competitive performances in terms of both objective value and computational effort.
- The new algorithms, BIRECT-l (new) and BIRECT (new), show promise and are particularly efficient in terms of the number of function evaluations. However, their objective function values may vary depending on the problem.
- The choice of algorithm should be problem-dependent. Some algorithms may be more suitable for specific problem characteristics, such as unimodal or multimodal objective functions, and global or local optimization.
- These sets of information provide a comprehensive assessment of the algorithms’ performance across various aspects, including solution quality and computational efficiency.
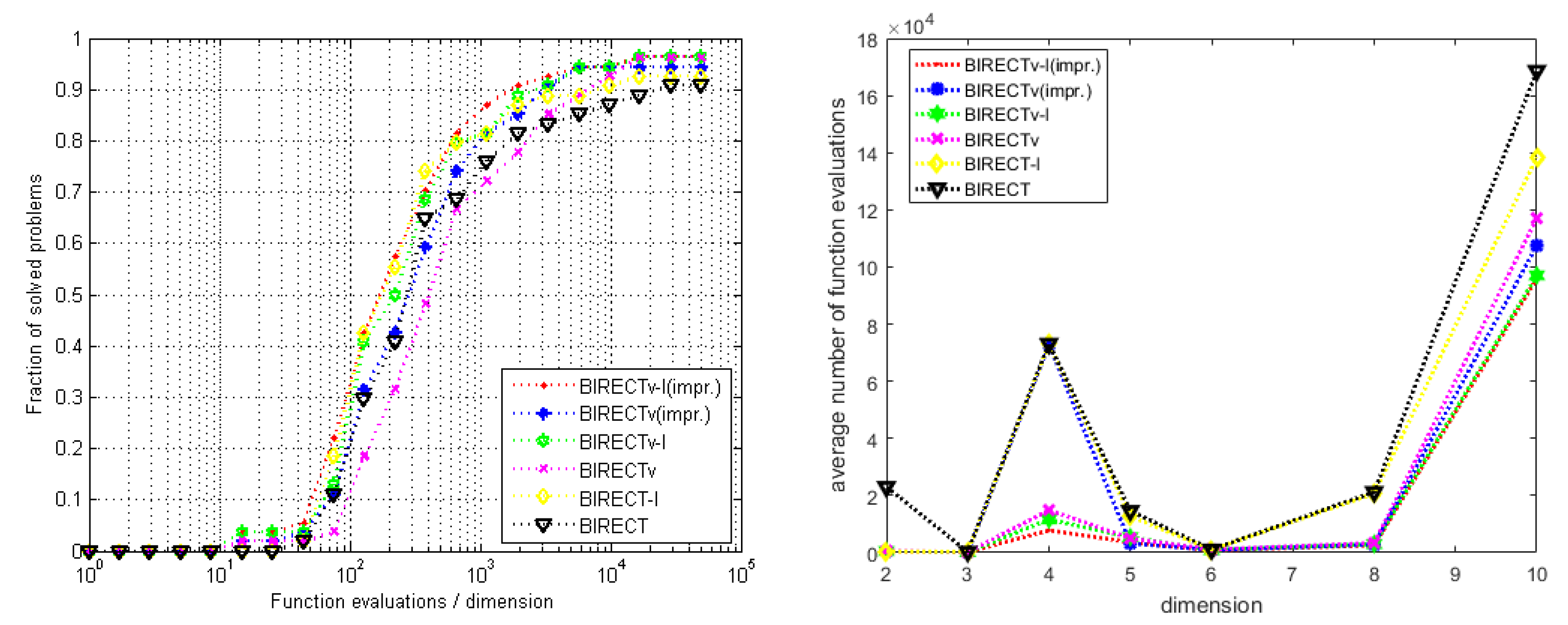
4.3. Examining the Success Rate of Algorithms and Function Evaluation Metrics
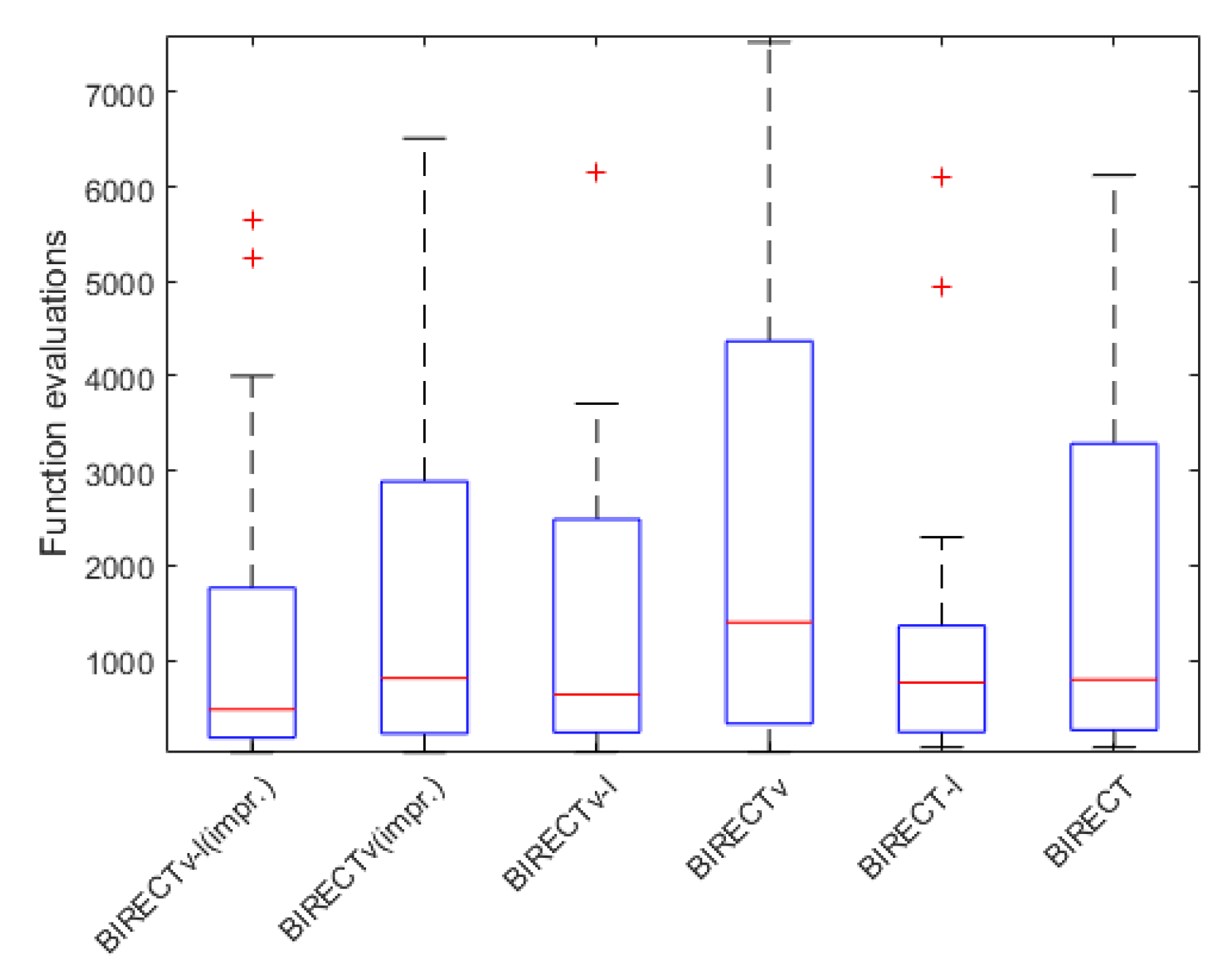
4.4. Statistical Analysis of the Results
5. Conclusions and Future Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Elements of the vector | |
| D | Search domain: an n-dimensional hyper-rectangle |
| Normalized search space (unit hyper-cube) | |
| Hyper-rectangle in normalized search space at iteration k | |
| Measure (size) of hyper-rectangle | |
| Objective function | |
| Known optimal value: | |
| Number of function evaluations | |
| The best-found function value | |
| Hyper-rectangles representing the current partitioning at iteration k | |
| L | Lipschitz constant |
| Index set identifying the current partition | |
| Potentially optimal hyper-rectangle | |
| Percent error | |
| Tolerance threshold: | |
| Current optimal solution vector | |
| Current best-known function value: |
Appendix A
| Problem No. | Problem Name | Dimension n | Feasible Region | No. of Local Minima | Optimum |
|---|---|---|---|---|---|
| Ackley | 2, 5, 10 | multimodal | 0.0 | ||
| 4 | Beale | 2 | multimodal | 0.0 | |
| Bohachevsky 1 | 2 | multimodal | 0.0 | ||
| Bohachevsky 2 | 2 | multimodal | 0.0 | ||
| Bohachevsky 3 | 2 | multimodal | 0.0 | ||
| 8 | Booth | 2 | unimodal | 0.0 | |
| 9 | Branin | 2 | 3 | ||
| 10 | Colville | 4 | multimodal | 0.0 | |
| Dixon & Price | 2, 5, 10 | unimodal | 0.0 | ||
| 14 | Easom | 2 | multimodal | ||
| 15 | Goldstein & Price | 2 | 4 | 3.0 | |
| Griewank | 2 | multimodal | 0.0 | ||
| 17 | Hartman | 3 | 4 | ||
| 18 | Hartman | 6 | 4 | ||
| 19 | Hump | 2 | 6 | ||
| Levy | 2, 5, 10 | multimodal | 0.0 | ||
| Matyas | 2 | unimodal | 0.0 | ||
| 24 | Michalewics | 2 | 2! | ||
| 25 | Michalewics | 5 | 5! | ||
| 26 | Michalewics | 10 | 10! | ||
| 27 | Perm | 4 | multimodal | ||
| Powell | 4, 8 | multimodal | |||
| 30 | Power Sum | 4 | multimodal | ||
| Rastrigin | 2, 5, 10 | multimodal | |||
| Rosenbrock | 2, 5, 10 | unimodal | |||
| Schwefel | 2, 5, 10 | unimodal | |||
| 40 | Shekel, | 4 | 5 | ||
| 41 | Shekel, | 4 | 7 | ||
| 42 | Shekel, | 4 | 10 | ||
| 43 | Shubert | 2 | 760 | ||
| Sphere | 2, 5, 10 | multimodal | |||
| Sum squares | 2, 5, 10 | unimodal | |||
| 50 | Trid | 6 | multimodal | ||
| 51 | Trid | 10 | multimodal | ||
| Zakharov | 2, 5, 10 | multimodal |
| Problem No. | BIRECT-(New) | BIRECT | DIRECT-l | DIRECT | ||||
|---|---|---|---|---|---|---|---|---|
| f.eval. | f.eval. | f.eval. | f.eval. | |||||
| 1 | 202 | 202 | 255 | |||||
| 2 | 1268 | 1777 | 8845 | |||||
| 3 | ||||||||
| 4 | 436 | 436 | 655 | |||||
| 5 | 468 | 476 | 327 | |||||
| 6 | 472 | 478 | 233 | 345 | ||||
| 7 | 480 | 573 | 693 | |||||
| 8 | 194 | 215 | 295 | |||||
| 9 | 242 | 242 | 195 | |||||
| 10 | 794 | 3379 | 6585 | |||||
| 11 | 722 | 722 | 513 | |||||
| 12 | ||||||||
| 13 | ||||||||
| 14 | 6851 | |||||||
| 15 | 274 | 274 | 191 | |||||
| 16 | 5106 | 8379 | 9215 | |||||
| 17 | 352 | 352 | 199 | |||||
| 18 | 764 | 764 | 571 | |||||
| 19 | 196 | 334 | 321 | |||||
| 20 | 152 | 152 | 105 | |||||
| 21 | 968 | 1024 | 705 | |||||
| 22 | 6402 | 7904 | 5589 | |||||
| 23 | 90 | 94 | 107 | |||||
| 24 | 126 | 126 | 69 | |||||
| 25 | ||||||||
| 26 | ||||||||
| 27 | ||||||||
| 28 | ||||||||
| 29 | ||||||||
| 30 | ||||||||
| 31 | 180 | 1727 | 987 | |||||
| 32 | 1394 | |||||||
| 33 | ||||||||
| 34 | 285 | 1621 | ||||||
| 35 | 1690 | 1700 | 2703 | |||||
| 36 | ||||||||
| 37 | 341 | 255 | ||||||
| 38 | 7210 | |||||||
| 39 | ||||||||
| 40 | 1272 | 1200 | 155 | |||||
| 41 | 1204 | 1180 | 145 | |||||
| 42 | 1140 | 1140 | 145 | |||||
| 43 | 2043 | 2967 | ||||||
| 44 | 118 | 118 | 209 | |||||
| 45 | 602 | 712 | 4653 | |||||
| 46 | 8742 | |||||||
| 47 | 226 | 244 | 107 | |||||
| 48 | 1000 | 1034 | 833 | |||||
| 49 | 5538 | 7688 | 8133 | |||||
| 50 | 1506 | 8731 | 5693 | |||||
| 51 | ||||||||
| 52 | 338 | 502 | 237 | |||||
| 53 | ||||||||
| 54 | ||||||||
| Average | ||||||||
| Median | ||||||||
References
- Ma, K.; Rios, L.M.; Bhosekar, A.; Sahinidis, N.V.; Rajagopalan, S. Branch-and-Model: A derivative-free global optimization algorithm. Comput. Optim. Appl. 2023, 85, 337–367. [Google Scholar]
- Liuzzi, G.; Lucidi, S.; Piccialli, V. Exploiting derivative-free local searches in DIRECT-type algorithms for global optimization. Comput. Optim. Appl. 2016, 65, 449–475. [Google Scholar]
- Stripinis, L.; Paulavičius, R. Gendirect: A generalized direct-type algorithmic framework for derivative-free global optimization. arXiv 2023, arXiv:2309.00835. [Google Scholar]
- Stripinis, L.; Paulavičius, R. Lipschitz-inspired HALRECT algorithm for derivative-free global optimization. J. Glob. Opt. 2023, 88, 139–169. [Google Scholar]
- Stripinis, L.; Paulavičius, R. An extensive numerical benchmark study of deterministic vs. stochastic derivative-free global optimization algorithms. arXiv 2022, arXiv:2209.05759. [Google Scholar]
- Stripinis, L.; Paulavičius, R. Derivative-Free DIRECT-Type Global Optimization: Applications and Software; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Floudas, C.A. Deterministic Global Optimization: Theory, Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 37. [Google Scholar]
- Horst, R.; Pardalos, P.M.; Thoai, N.V. Introduction to Global Optimization; Nonconvex Optimization and Its Application; Kluwer Academic Publishers: Berlin, Germany, 1995. [Google Scholar]
- Horst, R.; Tuy, H. Global Optimization: Deterministic Approaches; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Sergeyev, Y.D.; Kvasov, D.E. On deterministic diagonal methods for solving global optimization problems with Lipschitz gradients. In Optimization, Control, and Applications in the Information Age: In Honor of Panos M. Pardalos’s 60th Birthday; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 315–334. [Google Scholar]
- Sergeyev, Y.D.; Kvasov, D.E. Deterministic Global Optimization: An Introduction to the Diagonal Approach; SpringerBriefs in Optimization; Springer: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Liberti, L.; Kucherenko, S. Comparison of deterministic and stochastic approaches to global optimization. Int. Oper. Res. 2005, 12, 263–285. [Google Scholar]
- Zhigljavsky, A.; Žilinskas, A. Stochastic Global Optimization; Springer: New York, NY, USA, 2008. [Google Scholar]
- Paulavičius, R.; Sergeyev, Y.D.; Kvasov, D.E.; Zilinskas, J. Globally-biased DISIMPL algorithm for expensive global optimization. J. Glob. Optim. 2014, 59, 545–567. [Google Scholar]
- Paulavičius, R.; Zilinskas, J. Simplicial Lipschitz optimization without Lipschitz constant. J. Glob. Optim. 2014, 59, 23–40. [Google Scholar]
- Paulavičius, R.; Žilinskas, J.; Grothey, A. Parallel branch and bound for global optimization with combination of Lipschitz bounds. Optim. Methods Softw. 2011, 26, 487–498. [Google Scholar]
- Paulavičius, R.; Žilinskas, J. Simplicial Global Optimization; Springer: New York, NY, USA, 2014. [Google Scholar]
- Sergeyev, Y.D. Efficient strategy for adaptive partition of N-dimensional intervals in the framework of diagonal algorithms. J. Optim. Theory Appl. 2000, 107, 145–168. [Google Scholar]
- Sergeyev, Y.D. Efficient partition of N-dimensional intervals in the framework of one-point-based algorithms. J. Optim. Appl. 2005, 124, 503–510. [Google Scholar]
- Sergeyev, Y.D.; Kvasov, D.E. Global search based on efficient diagonal partitions and a set of Lipschitz constants. SIAM J. Optim. 2006, 16, 910–937. [Google Scholar]
- Jones, D.R.; Perttunen, C.D.; Stuckman, B.E. Lipschitzian optimization without the Lipschitz constant. J. Optim. Appl. 1993, 79, 157–181. [Google Scholar]
- Jones, D.R. The DIRECT global optimization algorithm. In The Encyclopedia of Optimization; Floudas, C.A., Pardalos, P.M., Eds.; Kluwer Academic Publishers: Dordrect, The Netherlands, 2001; pp. 431–440. [Google Scholar]
- Stripinis, L.; Paulavičius, R.; Žilinskas, J. Improved scheme for selection of potentially optimal hyper-rectangles in DIRECT. Optim. Lett. 2018, 12, 1699–1712. [Google Scholar]
- Stripinis, L.; Paulavičius, R. An empirical study of various candidate selection and partitioning techniques in the DIRECT framework. J. Glob. Optim. 2022, 1–31. [Google Scholar]
- Jones, D.R.; Martins, J.R.R.A. The DIRECT algorithm: 25 years Later. J. Glob. Optim. 2021, 79, 521–566. [Google Scholar]
- Paulavičius, R.; Sergeyev, Y.D. Globally-biased BIRECT algorithm with local accelerators for expensive global optimization. Expert Syst. Appl. 2020, 144, 113052. [Google Scholar]
- Guessoum, N.; Chiter, L. Diagonal Partitioning Strategy Using Bisection of Rectangles and a Novel Sampling Scheme. MENDEL 2023, 29, 131–146. [Google Scholar]
- Liu, H.; Xu, S.; Wang, X.; Wu, J.; Song, Y. A global optimization algorithm for simulation-based problems via the extended DIRECT scheme. Eng. Optim. 2015, 47, 1441–1458. [Google Scholar]
- Stripinis, L.; Paulavičius, R. Novel algorithm for linearly constrained derivative free global optimization of lipschitz functions. Mathematics 2023, 11, 2920. [Google Scholar]
- Chiter, L. Experimental Data for the Preprint “Diagonal Partitioning Strategy Using Bisection of Rectangles and a Novel Sampling Scheme”. Mendeley Data, V2. 2023. Available online: https://data.mendeley.com/datasets/x9fpc9w7wh/2 (accessed on 16 June 2023).
- Friedman, M. The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar]
- Hollander, M.; Wolfe, D. Nonparametric Statistical Methods, Solutions Manual; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Phan, D.T.; Liu, H.; Nguyen, L.M. StepDIRECT-A Derivative-Free Optimization Method for Stepwise Functions. In Proceedings of the 2022 SIAM International Conference on Data Mining (SDM), Society for Industrial and Applied Mathematics, Alexandria, VA, USA, 28–30 April 2022; pp. 477–485. [Google Scholar]
- Stripinis, L.; Paulavičius, R. Experimental Study of Excessive Local Refinement Reduction Techniques for Global Optimization DIRECT-Type Algorithms. Mathematics 2022, 10, 3760. [Google Scholar] [CrossRef]
- Gablonsky, J.M.; Kelley, C.T. A locally-biased form of the DIRECT algorithm. J. Glob. Optim. 2001, 21, 27–37. [Google Scholar]
- Baker, C.A.; Watson, L.T.; Grossman, B.M.; Mason, W.H.; Haftka, R.T. Parallel Global Aircraft Configuration Design Space Exploration; High Performance Computing Symposium 2000; Tentner, A., Ed.; Soc. for Computer Simulation Internat: Blacksburg, VA, USA, 2000; pp. 54–66. [Google Scholar]
- Mockus, J.; Paulavičius, R.; Rusakevixcxius, D.; Sešok, D.; Žilinskas, J. Application of Reduced-set Pareto-Lipschitzian Optimization to truss optimization. J. Glob. Optim. 2017, 67, 425–450. [Google Scholar]
- Liu, Q.; Zeng, J.; Yang, G. MrDIRECT: A multilevel robust DIRECT algorithm for global optimization problems. J. Glob. Opt. 2015, 62, 205–227. [Google Scholar]
- Stripinis, L.; Kůdela, J.; Paulavičius, R. DIRECTGOLib—Direct Global Optimization Test Problems Library. 2023. Available online: https://github.com/blockchain-group/DIRECTGOLib (accessed on 16 June 2023).
- Stripinis, L.; Paulavičius, R. DIRECTGO: A new DIRECT-type MATLAB toolbox for derivative-free global optimization. ACM Trans. Math. Softw. 2022, 48, 1–46. [Google Scholar]
- Paulavičius, R.; Chiter, L.; Žilinskas, J. Global optimization based on bisection of rectangles, function values at diagonals, and a set of Lipschitz constants. J. Glob. Optim. 2018, 71, 5–20. [Google Scholar]
- Tuy, H. Convex Analysis and Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tsvetkov, E.A.; Krymov, R.A. Pure Random Search with Virtual Extension of Feasible Region. J. Optim. Theory Appl. 2022, 195, 575–595. [Google Scholar]
- Hedar, A. Test Functions for Unconstrained Global Optimization; System Optimization Laboratory, Kyoto University: Kyoto, Japan, 2013; Available online: http://www-optima.amp.i.kyotou.ac.jp/member/student/hedar/Hedar_files/TestGO.htm (accessed on 26 February 2021).


| Problem No. | BIRECTv-l (impr.) | BIRECTv (impr.) | BIRECTv-l [27] | BIRECTv [27] | BIRECT-l (New) | BIRECT (New) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f.eval. | f.eval. | f.eval. | f.eval. | f.eval. | f.eval. | |||||||
| 1 | 153 | 156 | 192 | 134 | 158 | |||||||
| 2 | 387 | 1135 | 422 | 1578 | 358 | 1062 | ||||||
| 3 | 1000 | 1000 | ||||||||||
| 4 | 474 | 742 | 638 | 1034 | ||||||||
| 5 | 209 | 254 | 284 | 496 | 496 | |||||||
| 6 | 211 | 252 | 284 | 682 | 682 | |||||||
| 7 | 209 | 248 | 282 | 852 | 849 | |||||||
| 8 | 249 | 300 | 334 | 330 | 330 | |||||||
| 9 | 480 | 370 | 652 | 490 | 242 | |||||||
| 10 | 1614 | 1337 | 2318 | 1868 | 794 | |||||||
| 11 | 263 | 431 | 346 | 578 | 234 | |||||||
| 12 | 2087 | 2652 | 2912 | 6103 | 6125 | |||||||
| 13 | 8202 | 8282 | ||||||||||
| 14 | 138 | 716 | 180 | 1082 | 558 | |||||||
| 15 | 28 | 28 | 274 | 274 | ||||||||
| 16 | 3440 | 4700 | 5192 | 5756 | ||||||||
| 17 | 169 | 200 | 208 | 352 | 352 | |||||||
| 18 | 490 | 542 | 542 | 764 | 764 | |||||||
| 19 | 254 | 202 | 334 | 190 | 196 | |||||||
| 20 | 103 | 116 | 136 | 154 | ||||||||
| 21 | 388 | 459 | 454 | 558 | 354 | |||||||
| 22 | 1133 | 6246 | 1182 | 7440 | 2302 | |||||||
| 23 | 119 | 163 | 148 | 208 | 90 | |||||||
| 24 | 142 | 231 | 184 | 314 | 136 | 126 | ||||||
| 25 | 5654 | 8484 | 7526 | |||||||||
| 26 | ||||||||||||
| 27 | ||||||||||||
| 28 | 1837 | 2518 | 1624 | 1814 | 2108 | |||||||
| 29 | 2867 | 3058 | 3400 | |||||||||
| 30 | 204 | 4932 | 5623 | |||||||||
| 31 | 523 | 809 | 688 | 820 | 178 | |||||||
| 32 | 6511 | 8512 | ||||||||||
| 33 | 1439 | 1454 | 1240 | |||||||||
| 34 | 540 | 544 | 700 | 716 | ||||||||
| 35 | 1950 | 2231 | 2528 | 3058 | 1692 | |||||||
| 36 | ||||||||||||
| 37 | 384 | 413 | 486 | 564 | 214 | 268 | ||||||
| 38 | 17,061 | 3780 | ||||||||||
| 39 | 1366 | 2248 | ||||||||||
| 40 | 4002 | 3665 | 6146 | 5604 | 1254 | |||||||
| 41 | 1536 | 1655 | 2256 | 2456 | 1186 | |||||||
| 42 | 1740 | 2238 | 2476 | 3332 | 1138 | |||||||
| 43 | 432 | 570 | 226 | 766 | 642 | |||||||
| 44 | 143 | 112 | 190 | 106 | 118 | |||||||
| 45 | 364 | 987 | 392 | 1400 | 602 | |||||||
| 46 | 1043 | 1054 | 8742 | |||||||||
| 47 | 348 | 328 | 494 | 460 | 226 | |||||||
| 48 | 1141 | 1102 | 1484 | 1006 | 1134 | |||||||
| 49 | 5331 | 2452 | 6066 | |||||||||
| 50 | 1414 | 1312 | 1662 | 1322 | 1462 | |||||||
| 51 | 2965 | 10,470 | 3114 | 3122 | ||||||||
| 52 | 122 | 125 | 156 | 162 | 118 | |||||||
| 53 | 2805 | 2948 | 3710 | 3958 | 1858 | |||||||
| 54 | ||||||||||||
| Average | ||||||||||||
| Median | ||||||||||||
| Problem No. | BIRECT-(New) | BIRECT [26,41] | BIRECT-l-(New) | BIRECT-l [26] | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 202 | 202 | 176 | 176 | ||||
| 2 | 1268 | 454 | 454 | |||||
| 3 | 874 | 874 | ||||||
| 4 | 436 | 436 | 436 | 436 | ||||
| 5 | 476 | 468 | 468 | |||||
| 6 | 472 | 478 | 472 | 472 | ||||
| 7 | 480 | 474 | 474 | |||||
| 8 | 194 | 188 | 188 | |||||
| 9 | 242 | 242 | 242 | 242 | ||||
| 10 | 794 | 794 | 794 | 794 | ||||
| 11 | 722 | 722 | 722 | 722 | ||||
| 12 | 4060 | 4060 | 4060 | 4060 | ||||
| 13 | ||||||||
| 14 | 16,420 | 480 | ||||||
| 15 | 274 | 274 | 274 | 274 | ||||
| 16 | 5106 | 5106 | ||||||
| 17 | 352 | 352 | 352 | 352 | ||||
| 18 | 764 | 764 | 764 | 764 | ||||
| 19 | 334 | 190 | 190 | |||||
| 20 | 152 | 152 | 152 | 152 | ||||
| 21 | 1024 | 660 | ||||||
| 22 | 7904 | 1698 | 1698 | |||||
| 23 | 94 | 90 | 90 | |||||
| 24 | 126 | 126 | 126 | 126 | ||||
| 25 | ||||||||
| 26 | ||||||||
| 27 | ||||||||
| 28 | 2114 | 2114 | 1832 | |||||
| 29 | ||||||||
| 30 | 4994 | |||||||
| 31 | 180 | 180 | 156 | |||||
| 32 | 1394 | 474 | ||||||
| 33 | 1250 | 1250 | ||||||
| 34 | 242 | 242 | 242 | 242 | ||||
| 35 | 1690 | 1700 | 1496 | |||||
| 36 | 4620 | |||||||
| 37 | 236 | 236 | 214 | |||||
| 38 | 7210 | 1422 | ||||||
| 39 | ||||||||
| 40 | 1272 | 1286 | ||||||
| 41 | 1204 | 1224 | 1224 | |||||
| 42 | 1140 | 1140 | 1162 | |||||
| 43 | 1780 | 1780 | 2114 | 2114 | ||||
| 44 | 118 | 118 | 108 | |||||
| 45 | 712 | 294 | ||||||
| 46 | 784 | 784 | ||||||
| 47 | 244 | 226 | 226 | |||||
| 48 | 1034 | 836 | 836 | |||||
| 49 | 7688 | 3366 | 3366 | |||||
| 50 | 1506 | 1138 | ||||||
| 51 | ||||||||
| 52 | 502 | 338 | 338 | |||||
| 53 | ||||||||
| 54 | ||||||||
| Average | ||||||||
| Median | ||||||||
| Problem No./Δ | BIRECT-l | |||||
|---|---|---|---|---|---|---|
| 10−2 | 10−3 | 10−4 | 10−5 | 10−6 | 10−7 | |
| 1 | 168 | 182 | 178 | 174 | 176 | |
| 2 | 530 | 448 | 484 | 448 | 454 | 454 |
| 3 | 840 | 842 | 852 | 874 | 872 | 874 |
| 4 | 370 | 424 | 434 | 436 | 436 | 436 |
| 5 | 328 | 424 | 456 | 468 | 468 | 468 |
| 6 | 328 | 432 | 462 | 472 | 472 | 472 |
| 7 | 942 | 474 | 474 | 474 | ||
| 8 | 172 | 188 | 188 | 188 | 188 | 188 |
| 9 | 256 | 242 | 242 | 242 | 242 | |
| 10 | 722 | 790 | 794 | 790 | 794 | 794 |
| 11 | 732 | 718 | 722 | 722 | 722 | |
| 12 | 5352 | 4038 | 4060 | 4060 | 4060 | |
| 13 | ||||||
| 14 | 110 | 110 | 110 | 110 | 110 | 110 |
| 15 | 236 | 272 | 274 | 274 | 274 | 274 |
| 16 | 3236 | 3452 | 4148 | 4982 | ||
| 17 | 346 | 354 | 352 | 352 | 352 | 352 |
| 18 | 752 | 764 | 764 | 764 | 764 | 764 |
| 19 | 188 | 190 | 190 | 190 | 190 | 190 |
| 20 | 136 | 152 | 152 | 152 | 152 | 152 |
| 21 | 608 | 644 | 656 | 656 | 656 | 656 |
| 22 | 1590 | 1698 | 1698 | 1698 | 1698 | 1698 |
| 23 | 88 | 90 | 90 | 90 | 90 | 90 |
| 24 | 110 | 126 | 126 | 126 | 126 | 126 |
| 25 | ||||||
| 26 | ||||||
| 27 | ||||||
| 28 | 2440 | 2102 | 1814 | 1820 | 1820 | 1820 |
| 29 | ||||||
| 30 | 4810 | 5024 | 5014 | 5002 | 4994 | |
| 31 | 146 | 152 | 154 | 156 | 156 | 156 |
| 32 | 338 | 436 | 474 | 474 | 474 | 474 |
| 33 | 940 | 1166 | 1240 | 1250 | 1250 | 1250 |
| 34 | 236 | 242 | 242 | 242 | 242 | 242 |
| 35 | 1390 | 1470 | 1498 | 1496 | 1496 | 1496 |
| 36 | 4196 | 4510 | 4612 | 4620 | 4620 | 4620 |
| 37 | 172 | 204 | 214 | 214 | 214 | 214 |
| 38 | 1148 | 1280 | 1400 | 1434 | 1434 | 1074 |
| 39 | ||||||
| 40 | 666 | 810 | 1254 | 1248 | 1248 | 1248 |
| 41 | 636 | 818 | 1186 | 1224 | 1224 | 1224 |
| 42 | 632 | 766 | 1138 | 1162 | 1162 | 1162 |
| 43 | 1748 | 1880 | 2044 | 2086 | 2114 | 2114 |
| 44 | 104 | 106 | 106 | 106 | 106 | 106 |
| 45 | 286 | 294 | 294 | 294 | 294 | 294 |
| 46 | 786 | 784 | 784 | 784 | 784 | 784 |
| 47 | 202 | 226 | 226 | 226 | 226 | 226 |
| 48 | 728 | 826 | 836 | 836 | 836 | 836 |
| 49 | 2712 | 3162 | 3332 | 3366 | 3366 | 3366 |
| 50 | 1152 | 988 | 992 | 992 | 992 | 992 |
| 51 | ||||||
| 52 | 260 | 320 | 338 | 338 | 338 | 338 |
| 53 | ||||||
| 54 | ||||||
| Average | ||||||
| Median | ||||||
| Algorithm | BIRECTv-l(impr.) | BIRECTv(impr.) | BIRECTv-l | BIRECTv | BIRECT-l | BIRECT |
|---|---|---|---|---|---|---|
| Success | ||||||
| Fails | ||||||
| max f.eval. | ||||||
| min f.eval. | 28 | 28 | 80 | 80 | ||
| average f.eval. | ||||||
| Standard Deviation (std) | ||||||
| median f.eval. |
| Algorithm | |||||
|---|---|---|---|---|---|
| BIRECTv-l(impr.) | 2.313 | 2.321 | 2.398 | 2.344 | 2.327 |
| BIRECTv(impr.) | 3.594 | 3.641 | 3.636 | 3.531 | 3.541 |
| BIRECTv-l | 4.031 | 3.987 | 4.011 | 3.938 | 3.888 |
| BIRECTv | 5.250 | 5.282 | 5.273 | 5.229 | 5.224 |
| BIRECT-l | 2.594 | 2.513 | 2.432 | 2.563 | 2.571 |
| BIRECT | 3.219 | 3.256 | 3.250 | 3.396 | 3.449 |
| p-value |
| Algorithm | |||||
|---|---|---|---|---|---|
| BIRECTv(impr.) | |||||
| BIRECTv-l | |||||
| BIRECTv | |||||
| BIRECT-l | |||||
| BIRECT |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belkacem, N.-E.; Chiter, L.; Louaked, M. A Novel Approach to Enhance DIRECT-Type Algorithms for Hyper-Rectangle Identification. Mathematics 2024, 12, 283. https://doi.org/10.3390/math12020283
Belkacem N-E, Chiter L, Louaked M. A Novel Approach to Enhance DIRECT-Type Algorithms for Hyper-Rectangle Identification. Mathematics. 2024; 12(2):283. https://doi.org/10.3390/math12020283
Chicago/Turabian StyleBelkacem, Nazih-Eddine, Lakhdar Chiter, and Mohammed Louaked. 2024. "A Novel Approach to Enhance DIRECT-Type Algorithms for Hyper-Rectangle Identification" Mathematics 12, no. 2: 283. https://doi.org/10.3390/math12020283
APA StyleBelkacem, N.-E., Chiter, L., & Louaked, M. (2024). A Novel Approach to Enhance DIRECT-Type Algorithms for Hyper-Rectangle Identification. Mathematics, 12(2), 283. https://doi.org/10.3390/math12020283






