A Probability Proportional to Size Estimation of a Rare Sensitive Attribute Using a Partial Randomized Response Model with Poisson Distribution

Abstract

In this paper, we suggest using a partial randomized response model using Poisson distribution to efficiently estimate a rare sensitive attribute by applying the probability proportional to size (PPS) sampling method when the population is composed of several different and sensitive clusters. We have obtained estimators for a rare and sensitive attribute and their variances and variance estimates by applying PPS sampling and two-stage equal probability sampling. We compare the efficiency between the estimators of the rare sensitive attribute, one obtained via PPS sampling with replacement and the other obtained using the two-stage equal probability sampling with replacement. As a result, it is confirmed that the estimate obtained via the PPS sampling with replacement is more efficient than the estimate provided by the two-stage equal probability sampling with replacement when the cluster sizes are different.

1. Introduction

In a socially and personally very sensitive survey, if you directly ask a question to the respondents, they tend to refuse to answer or give a false answer. To solve this problem, ref. [1] proposed a randomized response model (RRM) that could obtain sensitive information while protecting the identity or confidentiality of the respondent through an indirect response using a randomization device. Since then, many researchers have suggested various randomized response models to improve the quality of estimation.

Subsequently, refs. [2,3,4] organized, summarized and systematized the randomized response models, ref. [5] applied two-stage cluster sampling to a randomized response model, and ref. [6] researched improving the practicality of randomized response model by suggesting a randomized response model using PPS sampling. Meanwhile, the authors of [7] suggested a unrelated question randomized response method to estimate the mean number of participants with a rare sensitive attribute using Poisson distribution. Examples of rare sensitive attributes include the proportion of people with AIDS who have persistent relationships with strangers, the proportion of people who witnessed murders, and the number of girls raped by their own fathers, etc. and examples of rare unrelated attributes include the proportion of people born correctly at 12 o’clock, the proportion of babies born blind, and the proportion of triplets delivered by women [8,9] suggested a stratified two-stage randomized response models for estimating a rare sensitive attribute under Poisson distribution.

Furthermore, ref. [10] proposed a partial randomized response model using Poisson distribution, providing an alternative approach to estimating rare sensitive attributes through simple random estimation and stratified estimation. Their model demonstrated higher efficiency compared to Suman and Singh’s model. However, this research also faces limitations when applied to actual surveys if the population is clustered. Therefore, when the population is clustered, it is expected that applying Narjis and Shabbir’s model, which is more efficient than Suman and Singh’s model, could offer a practical solution for estimating rare sensitive attributes in real surveys.

In this study, we proposed a method for estimating rare sensitive attributes when the survey question is highly sensitive, and the population is composed of clusters with varying sizes. We applied the probability proportional to the size sampling method, which assigns sampling probabilities in proportion to the size of the clusters, to the partial randomized response model of [10]. In Section 2, we first introduced the partial randomized response model and proposed estimation methods using Probability Proportional to Size (PPS) with replacement, PPS without replacement, and two-stage equal probability sampling. In Section 3, we compared the efficiency of the estimation methods, and finally, in Section 4, we presented conclusions and implications of the study.

2. PPS Estimation for a Rare Sensitive Attribute by Partial Randomized Response Model

In Section 2, when the survey questions are very sensitive and the population is composed of N clusters that each contains $M_i(i=1,2,\cdots ,N)$ sub-units, a two-stage selection method is used, in which n clusters are selected with PPS or with equal probability from the population, and then $m_i(i=1,2,\cdots ,n)$ survey units are selected through simple random sampling in each selected cluster, which is applied to the partial randomized response model using the Poisson distribution proposed by [10] to deal with the method of estimating a rare sensitive attribute.

In Section 2.1, we reviewed Narjis and Shabbir’s Partial randomized response model and then we considered the sampling method for the clusters via PPS sampling with replacements in Section 2.2. Clusters by PPS sampling without replacement are considered in Section 2.3, and clusters by equal probability sampling are examined in Section 2.4.

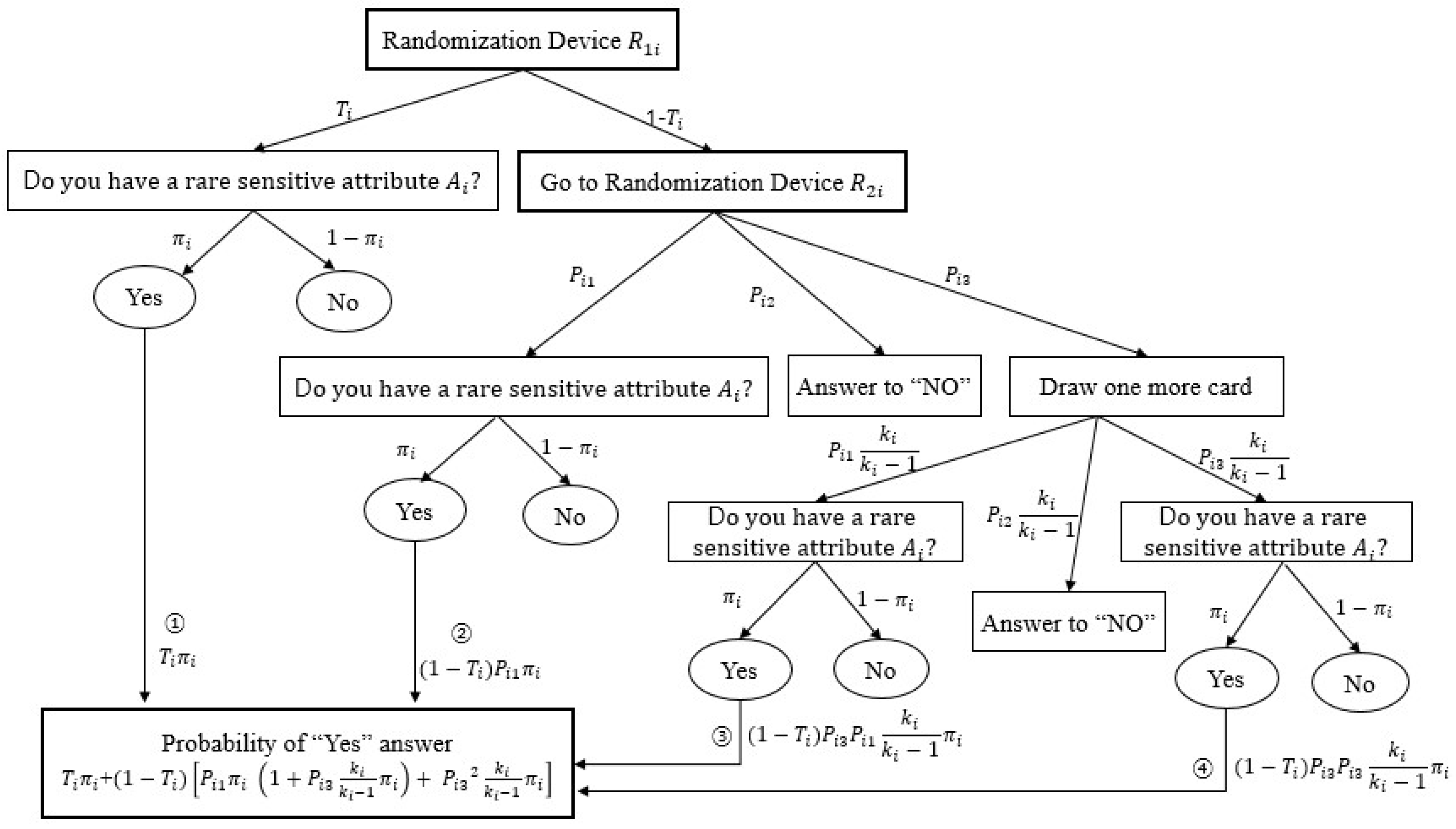
2.1. Narjis, Shabbir’s Partial Randomized Response Model

In the partial randomized response model, a sample of size n is selected via simple random sampling with replacement from the population. An individual is selected from the sample using two randomization devices $(R_1,R_2)$ and is requested to report his/her response as per following outcomes of the devices.

The first-stage randomization device $R_1$ consists of the following statements:

(1)

I have the sensitive attribute A with probability T.

(2)

Go to the randomization device $R_2$ with probability T.

The second-stage randomization device $R_2$ consists of the following statements:

(1)

I have the sensitive attribute A.

(2)

Forced to say No.

(3)

Draw one more card.

With probabilities $P_1$, $P_2$ and $P_3$ respectively, ${\sum }_{i=1}^3{P}_i=1$.

If the statement (3) appears on the card of the respondent, then it is necessary to carry out the process without replacing the card. In the second draw, if statement (3) reappears, then the respondent is suggested to report his/her actual status. The respondent should answer the question with s “Yes” (or “No”), if his/her actual status matches (un-matches) with the statement on the card.

The probability of getting a “Yes” from the respondent is given by:

$$l_0=T\pi +(1-T)\left[P_1\pi \left(1+P_3\frac{k}{k-1}\right)+P_3^2\frac{k}{k-1}\pi \right]$$

(1)

where k is the total number of cards in the randomization device $R_2$.

As before, assuming that $n\to \infty$ and ${\theta }_0\to 0$, then $n{\theta }_0={\lambda }_0$ (finite). Equation (1) can be rewritten as

$${\lambda }_0=T\lambda +(1-T)\left[P_1\lambda \left(1+P_3\frac{k}{k-1}\right)+P_3^2\frac{k}{k-1}\lambda \right]$$

(2)

Let $y_1,y_2,\cdots ,y_n$ be a random sample of n observations from the Poisson distribution with parameter ${\lambda }_0$.

The maximum-likelihood estimator of ${\lambda }_0$ is given by:

$${\widehat{\lambda }}_p=\frac{\frac{1}{n}{\sum }_{j=1}^n{y}_i}{T+(1-T)\left[P_1+P_3\left(\frac{k}{k-1}\right)(P_1+P_3)\right]}$$

(3)

The variance of the estimator ${\widehat{\lambda }}_p$ is given by:

$$V\left({\widehat{\lambda }}_p\right)=\frac{\lambda }{n\left[T+(1-T)\left\{P_1+P_3\left(\frac{k}{k-1}\right)(P_1+P_3)\right\}\right]}$$

(4)

2.2. Estimation by PPS When PSUs Are Selected with Replacement

Suppose n primary sampling units (PSUs) of size $M_i(i=1,2,\cdots ,n)$ have been selected from the population of N clusters with selection probability ${\phi }_i$ with replacement and the secondary sampling units (SSUs) of $m_i(i=1,2,\cdots ,n)$ size are selected from each chosen primary unit using SRSWR. We apply the two-stage sampling procedure to Narjis and Shabbir’s partial randomized response model to estimate a rare sensitive attribute. Each person selected via the two-stage sampling procedure is requested to answer “Yes” or “No” using Narjis and Shabbir’s randomization device such as

Table 1. First stage randomization device $R_{1i}$.

	Question	Selection Probability
Question 1	Do you have a rare sensitive attribute $A_i$?	$T_i$
Question 2	Go to randomization device $R_{2i}$.	$1-T_i$

and

Table 2. Second stage randomization device $R_{2i}$.

	Question	Selection Probability
Question 1	Do you have a rare sensitive attribute $A_i$?	$P_{i1}$
Question 2	Answer to “No”.	$P_{i2}$
Question 3	Draw one more card	$P_{i3}$

for each First and Second randomization device in ith cluster.

If Question 3 in randomization device $R_{2i}$ appears on the card of the respondent, then it is necessary to select a card repeatedly in $R_{2i}$ without replacing the card. In the second draw, if Question 3 reappears, then the respondent is suggested to report his/her “Yes” or “No”, according to his/her true response to the sensitive question.

From First and Second randomization devices, $T_i$ is the selection probability of a rare sensitive question in randomization device $R_{1i}$ for the ith cluster, ${\pi }_i$ is the population proportion of a rare sensitive attribute for the ith cluster, and $P_{i1}$ is the selection probability of a rare sensitive question in randomization device $R_{2i}$ for the ith cluster. And $P_{i2}$ is the selection probability of the forced answer “No” in randomization device $R_{2i}$, $P_{i3}$ is the selection probability of the statement “Draw one more cards” in randomization device $R_{2i}$ for the ith cluster, and $k_i$ is the number of cards in the card deck of randomization device $R_{2i}$ for the ith cluster.

The probability of answering “Yes” from the respondent in cluster i is given by

$$l_{i0}=T_i{\pi }_i+(1-T_i)\left[P_{i1}{\pi }_i\left(1+P_{i3}\frac{k_i}{k_i-1}\right)+P_{i3}^2\frac{k_i}{k_i-1}{\pi }_i\right]$$

(5)

To clarify the response process, we presented a flow chart for the probability of answering “Yes” for ith cluster in Figure 1.

Since the attribute $A_i$ in cluster i is very rare in the population, if we assume $m_i\to \infty$ and $l_{i0}\to 0$, then $m_i{l}_{i0}={\lambda }_{i0}$(finite).

Let $y_{i1},y_{i2},\cdots ,y_{i{m}_i}$ be a random sample of $m_i$ observations from the Poisson distribution with parameter ${\lambda }_{i0}$ in cluster i, then the estimator ${\widehat{\lambda }}_i$ of ${\lambda }_i$, the parameter of a rare sensitive attribute of cluster i, is given by

$${\widehat{\lambda }}_i=\frac{\frac{1}{m_i}{\sum }_{j=1}^{m_i}{y}_{ij}}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}$$

(6)

When respondents are selected via simple random sampling with replacement from the ith cluster, which was selected with replacement using sampling probability ${\phi }_i$ for the estimator ${\widehat{\lambda }}_{ppzwr}$ of $\lambda$, the parameter of a rare sensitive attribute is given by:

$${\widehat{\lambda }}_{ppzwr}=\frac{1}{n{M}_0}\sum _{i=1}^n\frac{M_i{\widehat{\lambda }}_i}{{\phi }_i}$$

(7)

where $M_0={\sum }_{i=1}^N{M}_i$.

Theorem 1.

The estimator ${\widehat{\lambda }}_{ppzwr}$ is an unbiased estimator of the parameter λ.

Proof. 

Since $y_{ij}\sim iidPo\left({\lambda }_{i0}\right)$ for each cluster and

$${\lambda }_{i0}=T_i{\lambda }_i+(1-T_i)\left[P_{i1}{\lambda }_i\left(1+P_{i3}\frac{k_i}{k_i-1}\right)+P_{i3}^2\frac{k_i}{k_i-1}{\lambda }_i\right].$$

We have

$$\begin{array}{cc}{E}_1{E}_2\left({\widehat{\lambda }}_{ppzwr}\right)\hfill & =E_1{E}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n}\frac{M_i{\widehat{\lambda }}_i}{{\phi }_i}\right]\hfill \\ \hfill & =E_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n}\frac{M_i{E}_2\left({\widehat{\lambda }}_i\right)}{{\phi }_i}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}{E}_2\left({\widehat{\lambda }}_i\right)\hfill & =E_2\left[\frac{\frac{1}{m_i}{\displaystyle \sum _{j=1}^{m_i}}{y}_{ij}}{T_i+(1-T_i)\left(P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right)}\right]\hfill \\ \hfill & =\frac{{\lambda }_{i0}}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}\hfill \\ \hfill & ={\lambda }_i,\hfill \end{array}$$

we can obtain

$$\begin{array}{cc}{E}_1{E}_2\left({\widehat{\lambda }}_{ppzwr}\right)\hfill & =E_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n}\frac{M_i{\lambda }_i}{{\phi }_i}\right]\hfill \\ \hfill & =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^N}{\phi }_i\frac{M_i{\lambda }_i}{{\phi }_i}\hfill \\ \hfill & =\lambda .\hfill \end{array}$$

□

Theorem 2.

The variance of ${\widehat{\lambda }}_{ppzwr}$ is given by

$$\begin{array}{cc}V\left({\widehat{\lambda }}_{ppzwr}\right)\hfill & =\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N}{{\phi }_i\left[\frac{M_i{\lambda }_i}{{\phi }_i}-M_0\lambda \right]}^2\hfill \\ \hfill & +\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N}\frac{M_i^2}{m_i{\phi }_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}\hfill \end{array}$$

(8)

Proof. 

By [11], we have

$$V\left({\widehat{\lambda }}_{ppzwr}\right)=V_1{E}_2\left({\widehat{\lambda }}_{ppzwr}\right)+E_1{V}_2\left({\widehat{\lambda }}_{ppzwr}\right),$$

where

$$\begin{array}{cc}{V}_1{E}_2\left({\widehat{\lambda }}_{ppzwr}\right)\hfill & =V_1{E}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n}\frac{M_i{\widehat{\lambda }}_i}{{\phi }_i}\right]\hfill \\ \hfill & =V_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n}\frac{M_i{\lambda }_i}{{\phi }_i}\right]\hfill \\ \hfill & =\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N}{\phi }_i{\left[\frac{M_i{\lambda }_i}{{\phi }_i}-M_0\lambda \right]}^2\hfill \end{array}$$

and

$$\begin{array}{cc}{E}_1{V}_2\left({\widehat{\lambda }}_{ppzwr}\right)\hfill & =E_1{V}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n}\frac{M_i{\widehat{\lambda }}_i}{{\phi }_i}\right]\hfill \\ \hfill & =E_1\left[\frac{1}{{\left(n{M}_0\right)}^2}{\displaystyle \sum _{i=1}^n}\frac{M_i^2}{{\phi }_i^2}{V}_2\left(\frac{\frac{1}{m_i}{\displaystyle \sum _{j=1}^{m_i}}{y}_{ij}}{T_i+(1-T_i)\left\{P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right\}}\right)\right]\hfill \\ \hfill & =E_1\left[\frac{1}{{\left(n{M}_0\right)}^2}{\displaystyle \sum _{i=1}^n}\frac{M_i^2}{{\phi }_i^2}\frac{\frac{1}{m_i^2}{\displaystyle \sum _{j=1}^{m_i}}{V}_2\left(y_{ij}\right)}{{\left\{T_i+(1-T_i)\left(P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right)\right\}}^2}\right].\hfill \end{array}$$

Because $y_{ij}\sim iidPo\left({\lambda }_{i0}\right)$, we have

$$\begin{array}{cc}{E}_1{V}_2\left({\widehat{\lambda }}_{ppzwr}\right)\hfill & =E_1\left[\frac{1}{{\left(n{M}_0\right)}^2}{\displaystyle \sum _{i=1}^n}\frac{M_i^2}{{\phi }_i^2}\frac{\frac{1}{m_i^2}{\displaystyle \sum _{j=1}^{m_i}}{\lambda }_{i0}}{{\left\{T_i+(1-T_i)\left(P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right)\right\}}^2}\right]\hfill \\ \hfill & =E_1\left[\frac{1}{{\left(n{M}_0\right)}^2}{\displaystyle \sum _{i=1}^n}\frac{M_i^2}{{\phi }_i^2{m}_i}\frac{{\lambda }_{i0}}{{\left\{T_i+(1-T_i)\left(P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right)\right\}}^2}\right]\hfill \\ \hfill & =E_1\left[\frac{1}{{\left(n{M}_0\right)}^2}{\displaystyle \sum _{i=1}^n}\frac{M_i^2}{{\phi }_i^2{m}_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}\right]\hfill \\ \hfill & =\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N}\frac{M_i^2}{{\phi }_i}\frac{1}{m_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}.\hfill \end{array}$$

Thus, we determine the variance of ${\widehat{\lambda }}_{ppzwr}$ as shown in (8). □

Also, the estimator of $V\left({\widehat{\lambda }}_{ppzwr}\right)$ is given by

$$\widehat{V}\left({\widehat{\lambda }}_{ppzwr}\right)=\frac{1}{n(n-1)M_0^2}\sum _{i=1}^n{\left(\frac{M_i{\widehat{\lambda }}_i}{{\phi }_i}-{\widehat{\lambda }}_{ppzwr}\right)}^2.$$

(9)

On the other hand, when the sampling probabilities of n PSUs are proportional to each cluster size $M_i$, then ${\phi }_i=M_i/M_0$, which is called PPS sampling. When a sample of n PSUs are selected via PPS sampling with replacement and $m_i$ SSUs are selected using simple random sampling with replacement from each PSU, the estimator ${\widehat{\lambda }}_{ppzwr}$ of $\lambda$ is as follows

$${\widehat{\lambda }}_{ppswr}=\frac{1}{n}\sum _{i=1}^n{\widehat{\lambda }}_i.$$

(10)

And the variance of ${\widehat{\lambda }}_{ppswr}$ and its estimator are, respectively,

$$\begin{array}{cc}V\left({\widehat{\lambda }}_{ppswr}\right)\hfill & =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^N}{M}_i{\left({\lambda }_i-\lambda \right)}^2\hfill \\ \hfill & +\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^N}\frac{M_i}{m_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]},\hfill \end{array}$$

(11)

and

$$\widehat{V}\left({\widehat{\lambda }}_{ppswr}\right)=\frac{1}{n(n-1)}\sum _{i=1}^n{\left({\widehat{\lambda }}_i-\frac{{\widehat{\lambda }}_{ppswr}}{M_0}\right)}^2.$$

(12)

2.3. Estimation by PPS When PSUs Are Selected without Replacement

Suppose n PSUs of size $M_i(i=1,2,\cdots ,n)$ have been selected from the population of N clusters with selection probability ${\varphi }_i$ without replacement and the SSUs of size $m_i$ are selected from each chosen primary unit via SRSWR. We apply the two-stage sampling procedure to Narjis and Shabbir’s RRT to estimate a rare sensitive attribute.

The estimator ${\widehat{\lambda }}_{ppswor}$ of $\lambda$, the parameter of a rare sensitive attribute obtained using the above sampling procedure is given by

$${\widehat{\lambda }}_{ppswor}=\frac{1}{M_0}\sum _{i=1}^n\frac{M_i{\widehat{\lambda }}_i}{{\varphi }_i}.$$

(13)

where ${\varphi }_i$ is the inclusion probability of survey unit i.

And the variance of ${\widehat{\lambda }}_{ppswor}$ is given by:

$$\begin{array}{cc}V\left({\widehat{\lambda }}_{ppswor}\right)\hfill & =\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j>i}^N}({\varphi }_i{\varphi }_j-{\varphi }_{ij}){\left[\frac{M_i{\lambda }_i}{{\varphi }_i}-\frac{M_j{\lambda }_j}{{\varphi }_j}\right]}^2\hfill \\ \hfill & +\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^N}\frac{M_i^2}{m_i{\varphi }_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]},\hfill \end{array}$$

(14)

where ${\varphi }_{ij}$ is the joint inclusion probability of survey units i and j.

Also, the estimator of $V\left({\widehat{\lambda }}_{ppswor}\right)$ is given by

$$\begin{array}{cc}\widehat{V}\left({\widehat{\lambda }}_{ppswor}\right)\hfill & =\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j>i}^n}\left(\frac{{\varphi }_i{\varphi }_j-{\varphi }_{ij}}{{\varphi }_{ij}}\right){\left(\frac{M_i{\widehat{\lambda }}_i}{{\varphi }_i}-\frac{M_j{\widehat{\lambda }}_j}{{\varphi }_j}\right)}^2\hfill \\ \hfill & +\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^n}\frac{M_0^2}{{\varphi }_i(m_i-1)}\frac{{\widehat{\lambda }}_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}\hfill \end{array}$$

(15)

2.4. Estimation via Two-Stage Equal Probability Sampling

Suppose n PSUs of size $M_i(i=1,2,\cdots ,n)$ have been selected from the population of N clusters by SRSWR and the SSUs of size $m_i$ are selected again from each chosen PSU via SRSWR. We consider the two-stage equal probability sampling procedure for Narjis and Shabbir’s RRT for estimating a rare sensitive attribute. The estimator ${\widehat{\lambda }}_{wr}$ of $\lambda$, the parameter of a rare sensitive attribute, obtained using the above procedure is given by

$${\widehat{\lambda }}_{wr}=\frac{1}{n\overline{M}}\sum _{i=1}^n{M}_i{\widehat{\lambda }}_i,$$

(16)

where $\overline{M}=M_0/N$.

$$\begin{array}{cc}V\left({\widehat{\lambda }}_{wr}\right)\hfill & =\frac{1}{n{\overline{M}}^2}\frac{1}{(N-1)}{\displaystyle \sum _{i=1}^N}{(M_i{\lambda }_i-\overline{M}\lambda )}^2\hfill \\ \hfill & +\frac{1}{n{\overline{M}}^2}{\displaystyle \sum _{i=1}^N}\frac{M_i^2}{m_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]},\hfill \end{array}$$

(17)

and

$$\widehat{V}\left({\widehat{\lambda }}_{wr}\right)=\frac{1}{n(n-1)}\sum _{i=1}^n{(N{M}_i{\widehat{\lambda }}_i-{\widehat{\lambda }}_{wr})}^2,$$

(18)

where $\overline{M}=M_0/N$.

3. Efficiency Comparisons for the PPS vs. Equal Probability Sampling

Narjis and Shabbir’s RRT model was developed under the assumption of simple random sampling and stratified random sampling, and the efficiency thereof was compared with that of the estimators [9]. Therefore, it is reasonable to compare the existing estimator with the estimator proposed in this paper using Narjis and Shabbir’s model. However, in the case of cluster sampling, the increase in variance compared to that obtained using simple random sampling or stratified sampling has already been dealt with in the typical sampling textbooks, so in this paper, as described above, when the population consists of N clusters, we consider the case the PPS with replacement estimator and two-stage equal probability estimator.

Now, the difference between the variance (17) of two-stage equal probability sampling and the variance (11) of PPS with replacement sampling is given as follows under $N-1\fallingdotseq N$

$$\begin{array}{cc}V\left({\widehat{\lambda }}_{wr}\right)-V\left({\widehat{\lambda }}_{ppswr}\right)\hfill & =\frac{1}{nN{\overline{M}}^2}\left[{\displaystyle \sum _{i=1}^N}{(M_i-\overline{M})}^2{\lambda }_i^2+\overline{M}\left\{{\displaystyle \sum _{i=1}^N}(M_i-\overline{M})({\lambda }_i^2-{\lambda }^2)\right\}\right.\hfill \\ \hfill & +{\displaystyle \sum _{i=1}^N}\frac{{(M_i-\overline{M})}^2}{m_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}\hfill \\ \hfill & +\left.\overline{M}{\displaystyle \sum _{i=1}^N}\frac{(M_i-\overline{M})}{m_i}\frac{{\lambda }_i}{T_i+(1-T_i)\left[P_{i1}+P_{i3}\left(\frac{k_i}{k_i-1}\right)(P_{i1}+P_{i3})\right]}\right].\hfill \end{array}$$

(19)

In (19), if $M_i=\overline{M}=M_0/N$ then $V\left({\widehat{\lambda }}_{wr}\right)=V\left({\widehat{\lambda }}_{ppswr}\right)$. In other words, if the cluster sizes are equal, the selection probability of PPS sampling with replacement becomes $1/N$ and is equal to that of two-stage equal probability sampling with replacement. Hence, they have the same efficiency.

If each cluster size $M_i$ is unequal, the values ${\sum }_{i=1}^N{(M_i-\overline{M})}^2{\lambda }_i^2$ of first term of the right-hand side in (19) are much increased, and the values ${\sum }_{i=1}^N(M_i-\overline{M})({\lambda }_i^2-{\lambda }^2)$ of the second term of the right-hand side in (19) have relatively small ones. Hence, the estimation using PPS sampling with replacement is more efficient than that of two-stage equal probability sampling with replacement.

We tabulate to summarize the relationship for each estimator in a cluster sampling design as follows.

Now, we compare the efficiency by calculating relative efficiencies (RE) between different sampling methods, such as simple random sampling with replacement (:ppzwr), PPS sampling with replacement (:ppswr) and two-stage equal probability sampling with replacement (:wr) according to varying parameter combinations by numerical example.

$$R{E}_1=\frac{V\left({\widehat{\lambda }}_{wr}\right)}{V\left({\widehat{\lambda }}_{ppzwr}\right)},R{E}_2=\frac{V\left({\widehat{\lambda }}_{ppzwr}\right)}{V\left({\widehat{\lambda }}_{ppswr}\right)},R{E}_3=\frac{V\left({\widehat{\lambda }}_{wr}\right)}{V\left({\widehat{\lambda }}_{ppswr}\right)}.$$

(20)

The values of $R{E}_1$ greater than one means that unequal probability sampling with replacement (:ppzwr) is more efficient than two-stage equal probability sampling with replacement (:wr), $R{E}_2$ greater than one means that PPS sampling with replacement (:ppswr) is more efficient than unequal probability sampling with replacement(:ppzwr), and $R{E}_3$ greater than one means that PPS sampling with replacement (:ppswr) is more efficient than two-stage equal probability sampling with replacement(:wr).

In calculating REs, we set parameters for ith cluster $(i=1,2,3,4)$ as follows.

• $M_0=$ 10,000; $M_1=1000$; $M_2=2000$; $M_3=3000$; $M_4=4000$,
• $m_0=1000$; $m_1=100$; $m_2=200$; $m_3=300$; $m_4=400$,
• $\lambda =1.25,1.5,2.0,2.25$;
• ${\lambda }_1=0.5$, ${\lambda }_2=1.0$, ${\lambda }_3=1.5$, ${\lambda }_4=2.0$;
• $k_1=k_2=k_3=k_4=15,75$;
• $P_{i1}$, $P_{i2}=\frac{1-P_{i1}}{3}$, $P_{i3}=1-P_{i1}-P_{i2}$.

We also assume the selection probabilities for ith cluster as follows.

• $T_1=T_2=T_3=T_4$;
• $P_{11}=P_{12}=P_{13}=P_{21}=P_{22}=P_{23}=P_{31}=P_{32}=P_{33}=P_{41}=P_{42}=P_{43}$,

varying from 0.2 to 0.8 by 0.2.

In order to compare the efficiency of the proposed estimators from numerical examples, we summarized the relative efficiencies according to various parameter values with their mean values.

From

Table 3. The relationship between different estimators for cluster sampling.

	${\mathit{P}}_{\mathit{i}}={\mathit{M}}_{\mathit{i}}/{\mathit{M}}_0$	${\mathit{M}}_{\mathit{i}}=\overline{\mathit{M}}={\mathit{M}}_0/\mathit{N}$
${\widehat{\lambda }}_{ppzwr}$	${\widehat{\lambda }}_{ppzwr}$ = ${\widehat{\lambda }}_{ppswr}$
${\widehat{\lambda }}_{ppswr}$		${\widehat{\lambda }}_{ppswr}$ = ${\widehat{\lambda }}_{wr}$
${\widehat{\lambda }}_{ppswor}$
${\widehat{\lambda }}_{wr}$

, it can be seen that for all the parametric combinations, the mean values of $R{E}_1$ are greater than one, which indicates that the unequal probability sampling with replacement estimator ${\widehat{\lambda }}_{ppzwr}$ is more efficient than the two-stage estimator, ${\widehat{\lambda }}_{wr}$, as the sensitive attribute value $\lambda$ decreases, and in contrast, if sensitive attribute $\lambda$ increases, then the efficiency of ${\widehat{\lambda }}_{ppzwr}$ decreases. In addition, the variation in $R{E}_1$ with respect to $k_i$ indicates that the $R{E}_1$ increases as the values of selection probability $T_i$ increase.

As shown in

Table 4. The mean values of $R{E}_1$ for ${\lambda }_{ppzwr}$ vs. ${\lambda }_{wr}$.

			${\mathit{k}}_{\mathit{i}}=15$				${\mathit{k}}_{\mathit{i}}=75$
			${\mathit{T}}_{\mathit{i}}$				${\mathit{T}}_{\mathit{i}}$
$\mathit{\lambda }$	${\mathit{\lambda }}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
1.25	0.5	0.2	5.1216	5.1218	5.1219	5.122	5.1216	5.1217	5.1219	5.122
	1	0.4	5.1218	5.1219	5.1219	5.122	5.1218	5.1218	5.1219	5.122
	1.5	0.6	5.1219	5.1219	5.122	5.122	5.1219	5.1219	5.122	5.122
	2	0.8	5.122	5.122	5.122	5.122	5.122	5.122	5.122	5.122
1.5	0.5	0.2	2.5931	2.5931	2.5931	2.5931	2.5931	2.5932	2.5932	2.5932
	1	0.4	2.5931	2.5931	2.5931	2.5931	2.5932	2.5932	2.5932	2.5932
	1.5	0.6	2.5931	2.5931	2.5931	2.5931	2.5932	2.5932	2.5932	2.5932
	2	0.8	2.5931	2.5931	2.5931	2.5931	2.5932	2.5932	2.5932	2.5932
2	0.5	0.2	1.2366	1.2366	1.2366	1.2366	1.2367	1.2367	1.2367	1.2367
	1	0.4	1.2366	1.2366	1.2366	1.2366	1.2367	1.2367	1.2367	1.2367
	1.5	0.6	1.2366	1.2366	1.2366	1.2366	1.2367	1.2367	1.2367	1.2367
	2	0.8	1.2366	1.2366	1.2366	1.2366	1.2367	1.2367	1.2367	1.2367
2.25	0.5	0.2	1.0524	1.0524	1.0524	1.0524	1.0525	1.0525	1.0524	1.0524
	1	0.4	1.0524	1.0524	1.0524	1.0524	1.0525	1.0524	1.0524	1.0524
	1.5	0.6	1.0524	1.0524	1.0524	1.0524	1.0524	1.0524	1.0524	1.0524
	2	0.8	1.0524	1.0524	1.0524	1.0524	1.0524	1.0524	1.0524	1.0524

, the probability proportional to size estimator, ${\widehat{\lambda }}_{ppswr}$, is more efficient than the unequal probability sampling with replacement estimator, ${\widehat{\lambda }}_{ppzwr}$. As the sensitive attribute value $\lambda$ increases, and in contrast, as $\lambda$ decreases, the probability proportional estimator decreases in efficiency.

As shown in

Table 5. The mean values of $R{E}_2$ for ${\lambda }_{ppswr}$ vs. ${\lambda }_{ppzwr}$.

			${\mathit{k}}_{\mathit{i}}=15$				${\mathit{k}}_{\mathit{i}}=75$
			${\mathit{T}}_{\mathit{i}}$				${\mathit{T}}_{\mathit{i}}$
$\mathit{\lambda }$	${\mathit{\lambda }}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
1.25	0.5	0.2	1.1104	1.1106	1.1107	1.1109	1.1102	1.1104	1.1106	1.1107
	1	0.4	1.1106	1.1107	1.1108	1.1109	1.1105	1.1106	1.1107	1.1108
	1.5	0.6	1.1108	1.1109	1.1109	1.111	1.1106	1.1107	1.1108	1.1108
	2	0.8	1.1109	1.1109	1.111	1.111	1.1108	1.1108	1.1108	1.1108
1.5	0.5	0.2	2.6033	2.604	2.6045	2.605	2.6027	2.6034	2.604	2.6045
	1	0.4	2.6041	2.6045	2.6048	2.6051	2.6036	2.604	2.6043	2.6046
	1.5	0.6	2.6047	2.6049	2.6051	2.6052	2.6042	2.6044	2.6046	2.6047
	2	0.8	2.6051	2.6052	2.6052	2.6053	2.6046	2.6047	2.6047	2.6048
2	0.5	0.2	3.2936	3.2941	3.2944	3.2947	3.2932	3.2937	3.2941	3.2944
	1	0.4	3.2942	3.2944	3.2946	3.2948	3.2938	3.2941	3.2943	3.2945
	1.5	0.6	3.2946	3.2947	3.2948	3.2949	3.2942	3.2943	3.2945	3.2946
	2	0.8	3.2948	3.2948	3.2949	3.2949	3.2945	3.2945	3.2946	3.2946
2.25	0.5	0.2	2.876	2.8762	2.8764	2.8766	2.8758	2.876	2.8762	2.8764
	1	0.4	2.8763	2.8764	2.8765	2.8766	2.8761	2.8762	2.8763	2.8764
	1.5	0.6	2.8765	2.8765	2.8766	2.8767	2.8763	2.8764	2.8764	2.8765
	2	0.8	2.8766	2.8766	2.8767	2.8767	2.8764	2.8765	2.8765	2.8765

, the probability proportional to size estimator, ${\widehat{\lambda }}_{ppswr}$, is more efficient than the two-stage sampling with replacement estimator, ${\widehat{\lambda }}_{wr}$. As the sensitive attribute value $\lambda$ decreases, and in contrast, as $\lambda$ decreases, the probability proportional estimator decreases in efficiency.

In summary, an examination of the efficiency of a partial randomized response model for rare sensitive attributes based on a cluster sampling design with numerical examples shows the following trends:

(1)

Between $ppzwr$ and $wr$, efficiency decreases as a rare sensitive attribute $\lambda$ increases (refer to Table 4).

(2)

Between $ppswr$ and $ppzwr$, efficiency increases as $\lambda$ increases, and efficiency is relatively low at specific values of $\lambda$ (refer to Table 5).

(3)

Between $ppswr$ and $wr$, efficiency increases as $\lambda$ decreases, similar to the relation between $ppswr$ and $ppzwr$, where efficiency sharply increases at specific values of $\lambda$ (refer to

Table 6. The mean values of $R{E}_3$ for ${\lambda }_{ppswr}$ vs. ${\lambda }_{wr}$.

			${\mathit{k}}_{\mathit{i}}=15$				${\mathit{k}}_{\mathit{i}}=75$
			${\mathit{T}}_{\mathit{i}}$				${\mathit{T}}_{\mathit{i}}$
$\mathit{\lambda }$	${\mathit{\lambda }}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
1.25	0.5	0.2	5.6869	5.6881	5.6891	5.6899	5.6859	5.6872	5.6883	5.6891
	1	0.4	5.6884	5.6891	5.6896	5.6901	5.6875	5.6882	5.6888	5.6894
	1.5	0.6	5.6894	5.6897	5.69	5.6903	5.6886	5.689	5.6893	5.6896
	2	0.8	5.6901	5.6902	5.6903	5.6905	5.6893	5.6895	5.6896	5.6897
1.5	0.5	0.2	6.7506	6.7524	6.7538	6.7551	6.7491	6.751	6.7526	6.7539
	1	0.4	6.7529	6.7538	6.7547	6.7554	6.7515	6.7525	6.7535	6.7543
	1.5	0.6	6.7544	6.7548	6.7553	6.7557	6.7531	6.7536	6.7541	6.7546
	2	0.8	6.7554	6.7556	6.7557	6.7559	6.7542	6.7544	6.7546	6.7548
2	0.5	0.2	4.0731	4.0736	4.074	4.0744	4.0726	4.0732	4.0737	4.0741
	1	0.4	4.0737	4.074	4.0742	4.0745	4.0733	4.0737	4.0739	4.0742
	1.5	0.6	4.0742	4.0743	4.0744	4.0745	4.0738	4.074	4.0741	4.0743
	2	0.8	4.0745	4.0745	4.0746	4.0746	4.0741	4.0742	4.0743	4.0743
2.25	0.5	0.2	3.0268	3.027	3.0272	3.0274	3.0266	3.0269	3.0271	3.0273
	1	0.4	3.0271	3.0272	3.0273	3.0274	3.0269	3.0271	3.0272	3.0273
	1.5	0.6	3.0273	3.0273	3.0274	3.0275	3.0271	3.0272	3.0273	3.0273
	2	0.8	3.0274	3.0274	3.0275	3.0275	3.0273	3.0273	3.0273	3.0274

).

(4)

The number of cards $k_i$ does not significantly impact efficiency.

4. Conclusions

In this paper, when the population is composed of several different and sensitive clusters, we suggest a randomized method for efficiently estimating a rare sensitive attribute by applying the PPS sampling method to the partial randomized response model of [10]. And by applying PPS sampling and two-stage equal probability sampling, estimators for a rare and sensitive attribute and its variance and variance estimates are obtained. We compare the efficiency between the estimators of the rare sensitive attribute, one obtained using the PPS with replacement sampling method and the other obtained using the two-stage equal probability sampling with replacement method when the cluster sizes are different. As a result, it was confirmed that the estimation obtained using the PPS sampling with replacement is more efficient than the estimation obtained based on the two-stage equal probability sampling with replacement when the cluster sizes are different from each other.