Lyapunov-Based Control via Atmospheric Drag for Tetrahedral Satellite Formation
Abstract
1. Introduction
2. Preliminaries
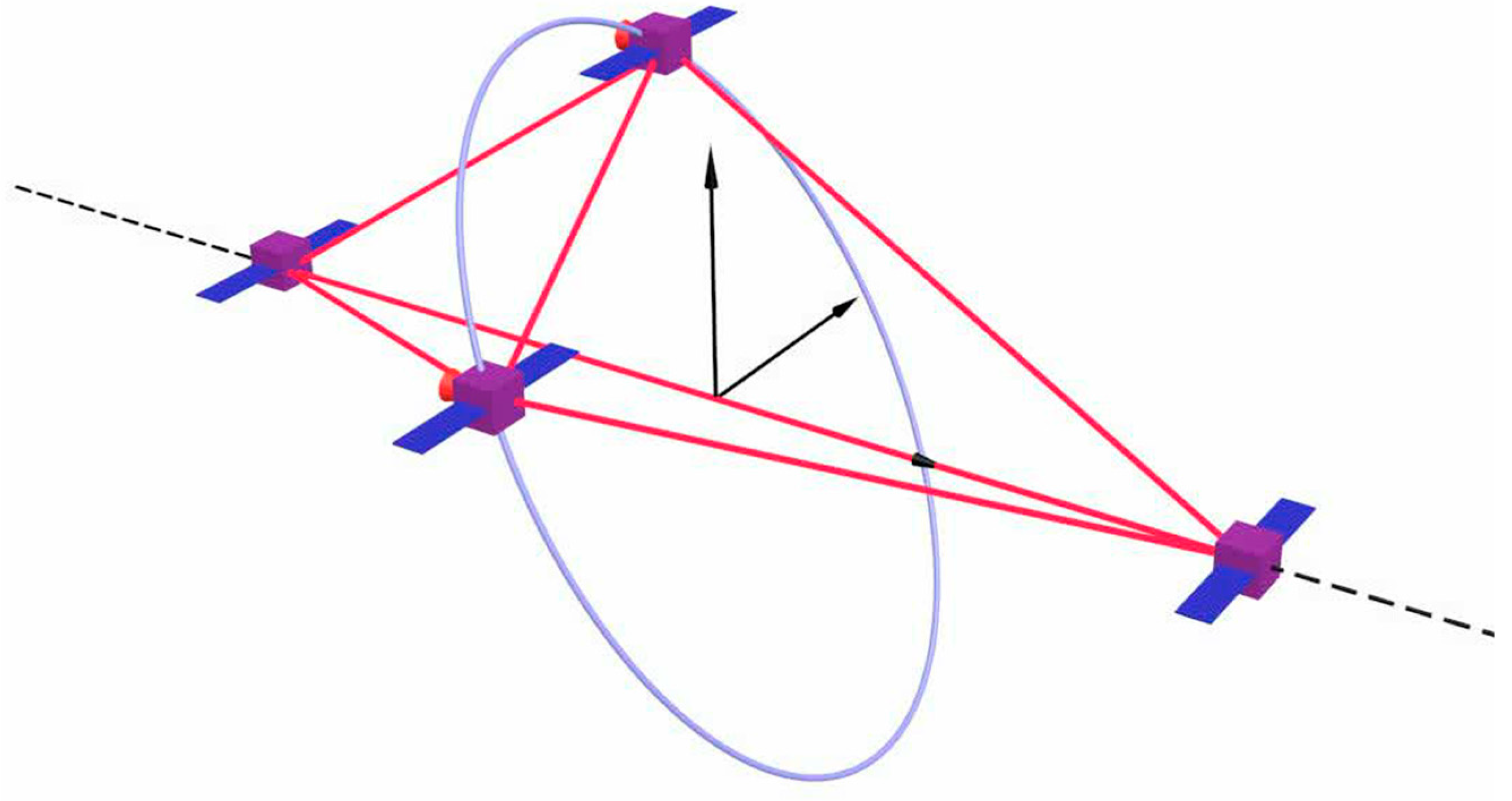
- Four satellites move passively in near-circular orbits, forming a tetrahedron.
- The quality of the tetrahedron at any particular moment in time is defined as
- in the CW motion model, the tetrahedron preserves quality and volume;
- the constant quality is maximal;
- one of the three satellites moves along the same orbit (in inertial space) as the reference satellite, i.e., there is a phase shift between them;
- two remaining satellites move in LVLH somehow;
3. Controlled Motion Model
3.1. Curvilinear Coordinates
- the oscillation amplitudes in and out of the orbital plane;
- the shift of each satellite along the orbit;
- drift (which must be equal to zero);
- the relative motion plane orientation;
- phase difference of oscillations between the pair of satellites that move outside the orbital plane.
- for the satellite shifted along the reference orbit,
- for the two remaining satellites,
3.2. Actuator Model Choice
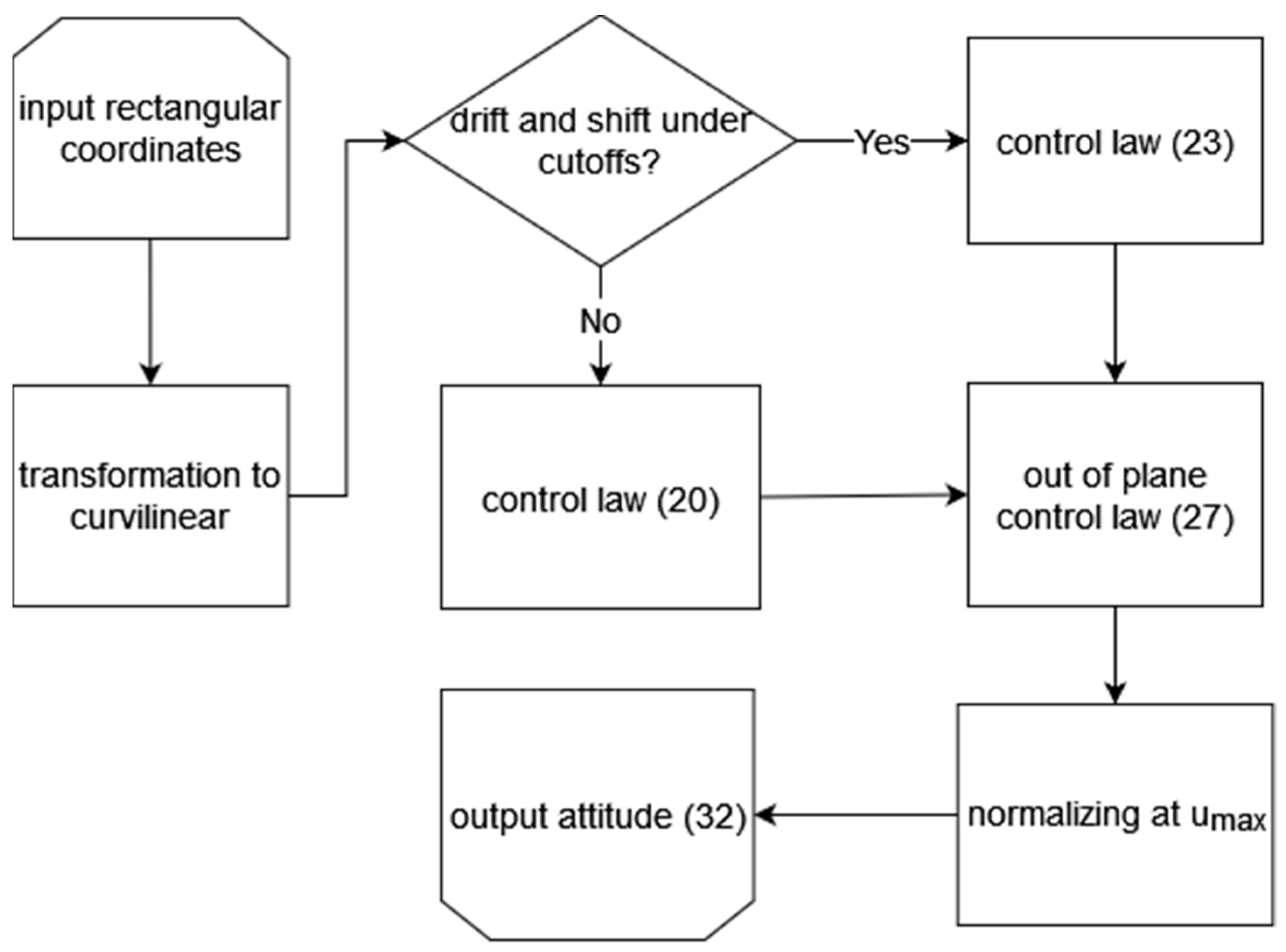
4. Lyapunov Direct Method
4.1. Shift and Drift Control
4.2. In-Plane Motion Control
4.3. Out-of-Plane Motion Control
4.4. The Choice of Control Law
- if the current relative drift is nonzero, ensuring the amplitudes and/or phases of satellite oscillations is meaningless because the relative motion is unbounded, so the tetrahedron degrades in a couple of revolutions;
- on the other hand, if the shift of the satellites in the group is close to the required one and the drift is close to zero, control law (23) can be used to maintain the amplitudes and phases of the oscillations.
4.5. Atmospheric Drag Implementation
5. Numerical Simulation
- Initial values are as in (4), (5), where , and the value is specified below.
- The altitude of the circular reference orbit is 400 km. The inclination is equal to .
- The motion of each satellite is integrated independently via the RK4 method in IRF.
- Initial values contain normally distributed noise.
- The Earth’s gravitational field is modelled up to terms of order (10, 10).
- The atmosphere is considered to rotate with the Earth; its density is calculated according to the Russian GOST model (it takes into account solar activity, day/night, and summer/winter variations).
- The satellite is a 5 kg square plate with an area of 0.1 m2. Its interaction with the atmosphere is in accordance with (13), where .
- The position and velocity in inertial space are known precisely.
- It is assumed that the necessary attitude is always achievable. Attitude change occurs instantly.
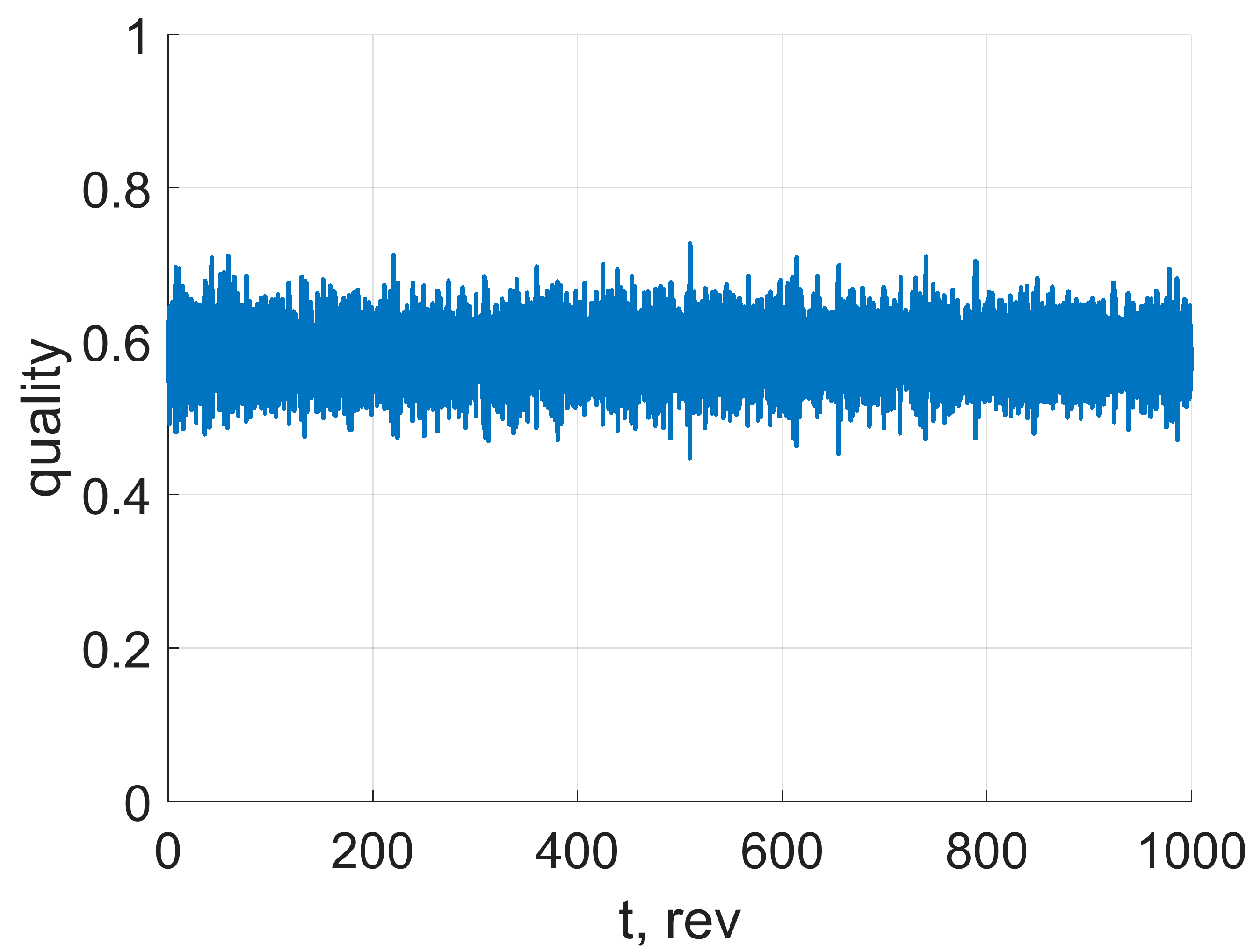
5.1. Small Formation
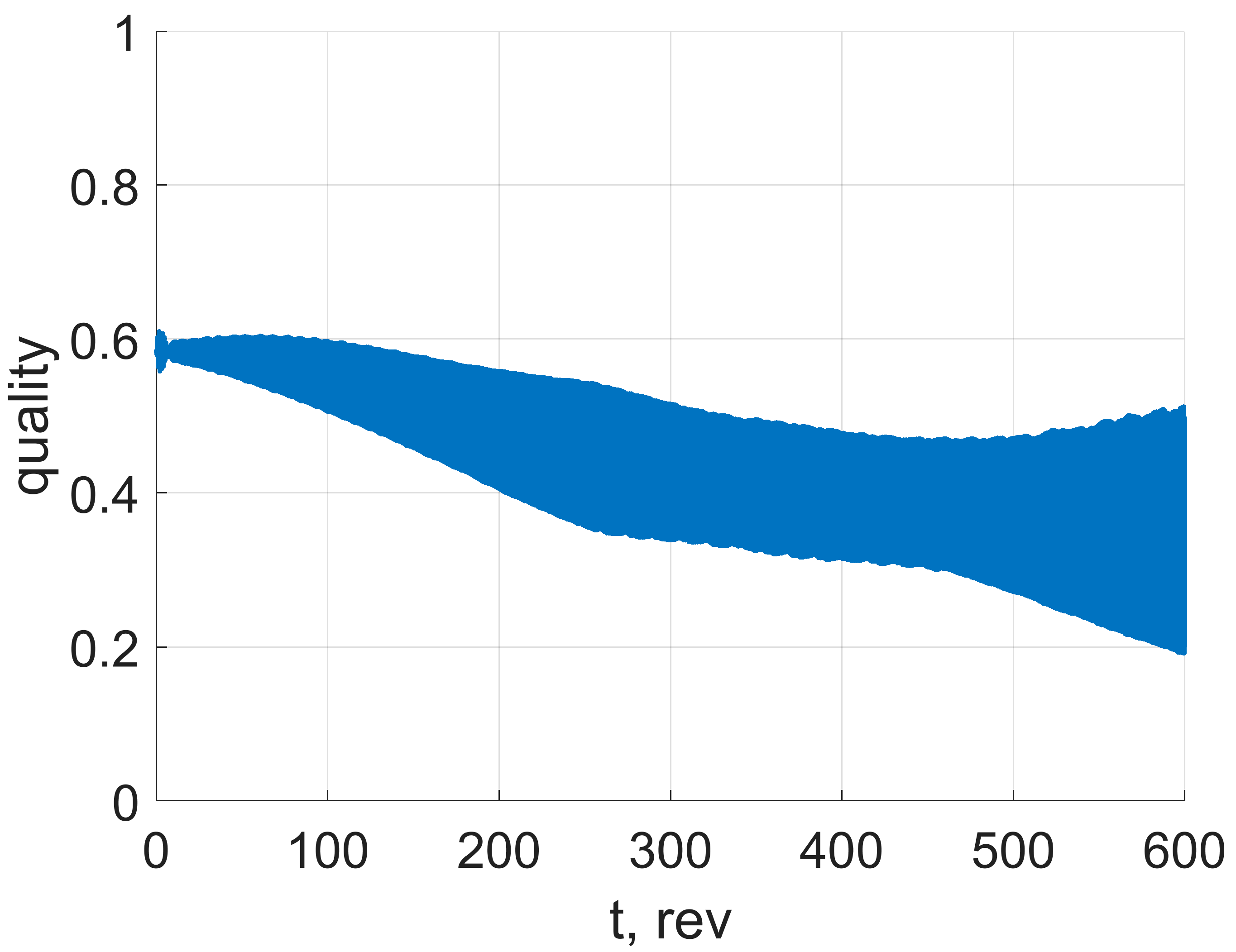
5.2. Possible Insufficiency of Control
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karlsson, T.; Marklund, G.T.; Figueiredo, S.; Johansson, T.; Buchert, S. Separating spatial and temporal variations in auroral electric and magnetic fields by Cluster multipoint measurements. Ann. Geophys. 2004, 22, 2463–2472. [Google Scholar] [CrossRef]
- Haerendel, G.; Roux, A.; Blanc, M.; Paschmann, G.; Bryant, D.; Korth, A.; Hultqvist, B. Cluster, study in three dimensions of plasma turbulence and small-scale structure. Mission Propos. 1982. [Google Scholar]
- Escoubet, C.; Schmidt, R. Cluster II: Plasma measurements in three dimensions. Adv. Space Res. 2000, 25, 1305–1314. [Google Scholar] [CrossRef]
- Paschmann, G.; Schwartz, S.J.; Escoubet, C.P.; Haaland, S. Outer Magnetospheric Boundaries: Cluster Results; Paschmann, G., Schwartz, S.J., Escoubet, C.P., Haaland, S., Eds.; Space Sciences Series of ISSI; Springer: Dordrecht, The Netherlands, 2005; Volume 20, ISBN 978-1-4020-3488-6. [Google Scholar]
- Balogh, A.; Dunlop, M.W.; Cowley, S.W.H.; Southwood, D.J.; Thomlinson, J.G.; Glassmeier, K.H.; Musmann, G.; Lühr, H.; Buchert, S.; Acuña, M.H.; et al. The Cluster Magnetic Field Investigation. In The Cluster and Phoenix Missions; Springer: Dordrecht, The Netherlands, 1997; pp. 65–91. [Google Scholar]
- Taylor, M.G.G.T.; Escoubet, C.P.; Laakso, H.; Masson, A.; Hapgood, M.; Dimbylow, T.; Volpp, J.; Sangiorgi, S.; Goldstein, M.L. The Science of the Cluster Mission. In Magnetospheric Plasma Physics: The Impact of Jim Dungey’s Research; Cowley Frs, S.W.H., Southwood, D., Mitton, S., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 159–179. [Google Scholar]
- Paschmann, G.; Daly, P.W. Analysis Methods for Multi-Spacecraft Data, 1st ed.; International Space Science Institute: Bern, Switzerland, 1998; ISBN 9290927968. [Google Scholar]
- Mauk, B.H.; McEntire, R.W.; Heelis, R.A.; Pfaff, R.F. Magnetospheric multiscale and global electrodynamics missions. Geophys. Monogr. 1999, 109, 225–235. [Google Scholar]
- Burch, J.L.; Moore, T.E.; Torbert, R.B.; Giles, B.L. Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 2016, 199, 5–21. [Google Scholar] [CrossRef]
- Guzman, J.J.; Edery, A. Mission design for the MMS tetrahedron formation. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No.04TH8720), Big Sky, MT, USA, 6–13 March 2004; Volume 1, pp. 533–540. [Google Scholar]
- Clemente, D.C.; Atkins, E.M. Optimization of a Tetrahedral Satellite Formation. J. Spacecr. Rockets 2005, 42, 699–710. [Google Scholar] [CrossRef]
- Hughes, S.P. Formation Tetrahedron Design for Phase I of the Magnetospheric Multiscale Mission. In Proceedings of the Flight Mechanics Symposium, Greenbelt, MD, USA, 28–30 October 2003. [Google Scholar]
- Roscoe, C.W.T.; Vadali, S.R.; Alfriend, K.T. Design of Satellite Formations in Orbits of High Eccentricity withPerformance Constraints Specified over a Region of Interest. J. Astronaut. Sci. 2012, 59, 141–160. [Google Scholar] [CrossRef]
- Draim, J.E. A common-period four-satellite continuous global coverage constellation. J. Guid. Control Dyn. 1987, 10, 492–499. [Google Scholar] [CrossRef]
- Hsu, D.Y. Relations between dilutions of precision and volume of the tetrahedron formed by four satellites. In Proceedings of the 1994 IEEE Position, Location and Navigation Symposium—PLANS’94, Las Vegas, NV, USA, 11–15 April 1994; Volume 1, pp. 669–676. [Google Scholar]
- Parsay, K.; Schaub, H. Designing solar sail formations in sun-synchronous orbits for geomagnetic tail exploration. Acta Astronaut. 2015, 107, 218–233. [Google Scholar] [CrossRef]
- Parsay, K.; Schaub, H.; Schiff, C.; Williams, T. Improving magnetosphere in situ observations using solar sails. Adv. Space Res. 2018, 61, 74–88. [Google Scholar] [CrossRef]
- Koptev, M.D.; Trofimov, S.P.; Ovchinnikov, M.Y. Design and deployment of a tetrahedral formation with passive deputy nanosatellites for magnetospheric studies. Adv. Space Res. 2019, 63, 3953–3964. [Google Scholar] [CrossRef]
- Hametz, M.E.; Conway, D.J.; Richon, K. Design of a Formation of Earth-Orbiting Satellites: The Auroral Lites Mission. In Proceedings of the 1999 NASA GSFC Flight Mechanics Estimation Conference, Greenbelt, MD, USA, 18–20 May 1999; pp. 295–308. [Google Scholar]
- Gluitz, K.J. The German Aeronomy Satellite AEROS. In Astronautical Research 1971; Springer: Dordrecht, The Netherlands, 1973; Volume 40, pp. 421–441. [Google Scholar]
- Reigber, C.; Lühr, H.; Schwintzer, P. CHAMP mission status. Adv. Space Res. 2002, 30, 129–134. [Google Scholar] [CrossRef]
- Hulot, G.; Eymin, C.; Langlais, B.; Mandea, M.; Olsen, N. Small-scale structure of the geodynamo inferred from Oersted and Magsat satellite data. Nature 2002, 416, 620–623. [Google Scholar] [CrossRef] [PubMed]
- Friis-Christensen, E.; Lühr, H.; Knudsen, D.; Haagmans, R. Swarm—An Earth Observation Mission investigating Geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
- Ovchinnikov, M.Y.; Ivanov, D.S.; Ivlev, N.A.; Karpenko, S.O.; Roldugin, D.S.; Tkachev, S.S. Development, integrated investigation, laboratory and in-flight testing of Chibis-M microsatellite ADCS. Acta Astronaut. 2014, 93, 23–33. [Google Scholar] [CrossRef]
- Cussac, T.; Buisson, F.; Parrot, M. The DEMETER Program: Mission and Satellite Description—Early in Orbit Performances. In Proceedings of the 55th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law, Vancouver, BC, Canada, 4–8 October 2004; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004; Volume 5, pp. 3371–3383. [Google Scholar]
- Immel, T.J.; England, S.L.; Mende, S.B.; Heelis, R.A.; Englert, C.R.; Edelstein, J.; Frey, H.U.; Korpela, E.J.; Taylor, E.R.; Craig, W.W.; et al. The Ionospheric Connection Explorer Mission: Mission Goals and Design. Space Sci. Rev. 2018, 214, 13. [Google Scholar] [CrossRef] [PubMed]
- Fish, C.; Swenson, C.; Neilsen, T.; Bingham, B.; Gunther, J.; Stromberg, E.; Burr, S.; Burt, R.; Whitely, M.; Petersen, J. DICE Mission Design, Development, and Implementation: Success and Challenges. In Proceedings of the 26th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 13–16 August 2012. [Google Scholar]
- Sadeghi, S.; Emami, M.R. Multi-spacecraft studies of the auroral acceleration region: From cluster to nanosatellites. Adv. Space Res. 2017, 59, 1173–1188. [Google Scholar] [CrossRef]
- Klimenko, M.V.; Klimenko, V.V.; Karpachev, A.T.; Ratovsky, K.G.; Stepanov, A.E. Spatial features of Weddell Sea and Yakutsk Anomalies in foF2 diurnal variations during high solar activity periods: Interkosmos-19 satellite and ground-based ionosonde observations, IRI reproduction and GSM TIP model simulation. Adv. Space Res. 2015, 55, 2020–2032. [Google Scholar] [CrossRef]
- Smith, A.M.; Mitchell, C.N.; Watson, R.J.; Meggs, R.W.; Kintner, P.M.; Kauristie, K.; Honary, F. GPS scintillation in the high arctic associated with an auroral arc. Space Weather 2008, 6. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Zhang, Y.; Mertens, C.; Truhlik, V.; Richards, P.; McKinnell, L.-A.; Reinisch, B. The International Reference Ionosphere 2012—A model of international collaboration. J. Space Weather Space Clim. 2014, 4, A07. [Google Scholar] [CrossRef]
- Shestakov, S.; Ovchinnikov, M.; Mashtakov, Y. Analytical Approach to Construction of Tetrahedral Satellite Formation. J. Guid. Control Dyn. 2019, 42, 2600–2614. [Google Scholar] [CrossRef]
- Smirnov, G.V.; Mashtakov, Y.; Ovchinnikov, M.; Shestakov, S.; Prado, A.F.B.A. Tetrahedron formation of nanosatellites with single-input control. Astrophys. Space Sci. 2018, 363, 180. [Google Scholar] [CrossRef]
- Prasad, A.; Sharma, B.; Vanualailai, J.; Kumar, S. Motion control of an articulated mobile manipulator in 3D using the Lyapunov-based control scheme. Int. J. Control 2022, 95, 2581–2595. [Google Scholar] [CrossRef]
- Hu, Q.; Chi, B.; Akella, M.R. Anti-Unwinding Attitude Control of Spacecraft with Forbidden Pointing Constraints. J. Guid. Control Dyn. 2019, 42, 822–835. [Google Scholar] [CrossRef]
- Clohessy, W.H.; Wiltshire, R.S. Terminal Guidance System for Satellite Rendezvous. J. Aerosp. Sci. 1960, 27, 653–658. [Google Scholar] [CrossRef]
- deBruijn, F.; Gill, E.; How, J. Comparative analysis of Cartesian and curvilinear Clohessy-Wiltshire equations. J. Aerosp. Eng. Sci. Appl. 2011, 3, 1–15. [Google Scholar] [CrossRef]
- Mashtakov, Y.; Ovchinnikov, M.; Petrova, T.; Tkachev, S. Two-satellite formation flying control by cell-structured solar sail. Acta Astronaut. 2020, 170, 592–600. [Google Scholar] [CrossRef]
- Beletsky, V.V.; Yanshin, A.M. Influence of Aerodynamic Forces on Satellites Attitude Motion; Naukova Dumka: Kiev, Ukraine, 1984. [Google Scholar]
- Teschl, G. Ordinary Differential Equations and Dynamical Systems; American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
| 1 m | 5 m | 10 m | 20 m | |
|---|---|---|---|---|
| 0.5 cm/s | 97% | 92% | 82% | 41% |
| 1 cm/s | 91% | 86% | 73% | 32% |
| 2 cm/s | 76% | 62% | 48% | 23% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ovchinnikov, M.; Mashtakov, Y.; Shestakov, S. Lyapunov-Based Control via Atmospheric Drag for Tetrahedral Satellite Formation. Mathematics 2024, 12, 189. https://doi.org/10.3390/math12020189
Ovchinnikov M, Mashtakov Y, Shestakov S. Lyapunov-Based Control via Atmospheric Drag for Tetrahedral Satellite Formation. Mathematics. 2024; 12(2):189. https://doi.org/10.3390/math12020189
Chicago/Turabian StyleOvchinnikov, Mikhail, Yaroslav Mashtakov, and Sergey Shestakov. 2024. "Lyapunov-Based Control via Atmospheric Drag for Tetrahedral Satellite Formation" Mathematics 12, no. 2: 189. https://doi.org/10.3390/math12020189
APA StyleOvchinnikov, M., Mashtakov, Y., & Shestakov, S. (2024). Lyapunov-Based Control via Atmospheric Drag for Tetrahedral Satellite Formation. Mathematics, 12(2), 189. https://doi.org/10.3390/math12020189







