Double Tseng’s Algorithm with Inertial Terms for Inclusion Problems and Applications in Image Deblurring
Abstract
1. Introduction
- firmly nonexpansive ifor equivalently, if;
- Lipschitz or Lipschitz continuous if there exists a constant , such that. In the specific case where , C is referred to as a nonexpansive operator.
- monotone if(It is equivalent toif D is single-value.);
- co-coercive (or inverse strongly monotone) if there is , such that(It is equivalent toif D is a single value.);
- maximally monotone if D is monotone and is not properly contained in any graph of any other multi-valued monotone operator, that is, if is a multi-valued monotone operator, such that , then .
2. Preliminaries
- 1.
- ,
- 2.
- and .
- 1.
- , where ,
- 2.
- there is such that .
- 1.
- for every , exists,
- 2.
- any weak sequential cluster point of is in C; that is, .
- Then, weakly converges to a point in C.
3. Main Results
Weak Convergence
| Algorithm 1 Double Tseng’s Algorithm. |
Initialization: Given . Let be arbitrary. Iterative Steps: Given the current iterates , calculate the next iterate as follows: Compute Update |
4. Applications to Image Deblurring Problems and Their Numerical Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lions, P.L.; Mercier, B. Splitting Algorithms for the Sum of Two Nonlinear Operators. SIAM J. Numer. Anal. 1979, 16, 964–979. [Google Scholar] [CrossRef]
- Passty, G.B. Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math Anal Appl. 1979, 72, 383–390. [Google Scholar] [CrossRef]
- Tseng, P. A Modified Forward-Backward Splitting Method for Maximal Monotone Mappings. SIAM J. Control. Optim. 2000, 38, 431–446. [Google Scholar] [CrossRef]
- Alvarez, F.; Attouch, H. An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set Valued Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Polyak, B.T. Some methods of speeding up the convergence of iterative methods. Zh. Vychisl. Mat. Mat. Fiz. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Lorenz, D.A.; Pock, T. An Inertial Forward-Backward Algorithm for Monotone Inclusions. J. Math. Imaging Vis. 2015, 51, 311–325. [Google Scholar] [CrossRef]
- Moudafi, A.; Oliny, M. Convergence of a splitting inertial proximal method for monotone operators. J. Comput. Appl. Math. 2003, 155, 447–454. [Google Scholar] [CrossRef]
- Padcharoen, A.; Kitkuan, D.; Kumam, W.; Kumam, P. Tseng methods with inertial for solving inclusion problems and application to image deblurring and image recovery problems. Comput. Math. Methods 2020, 3, e1088. [Google Scholar] [CrossRef]
- Berinde, V. Approximating Fixed Points of Lipschitzian Pseudocontractions. In Proceedings of the Mathematics & Mathematics Education, Bethlehem, Palestine, 9–12 August 2000; World Scientific Publishing: River Edge, NJ, USA, 2002. [Google Scholar]
- Berinde, V. Iterative Approximation of Fixed Points, 2nd ed.; Lecture Notes in Mathematics, 1912; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Takahashi, W. Nonlinear Functional Analysis; Yokohama Publishers: Yokohama, Japan, 2000. [Google Scholar]
- Takahashi, W. Introduction to Nonlinear and Convex Analysis; Yokohama Publishers: Yokohama, Japan, 2009. [Google Scholar]
- Ungchittrakool, K. Existence and convergence of fixed points for a strict pseudo-contraction via an iterative shrinking projection technique. J. Nonlinear Convex Anal. 2014, 15, 693–710. [Google Scholar] [CrossRef]
- Inchan, I. Convergence theorem of a new iterative method for mixed equilibrium problems and variational inclusions: Approach to variational inequalities. Appl. Math. Sci. 2012, 6, 747–763. [Google Scholar]
- Adamu, A.; Kumam, P.; Kitkuan, D.; Padcharoen, A. Relaxed modified Tseng algorithm for solving variational inclusion problems in real Banach spaces with applications. Carpathian J. Math. 2023, 39, 1–26. [Google Scholar] [CrossRef]
- Ungchittrakool, K.; Plubtieng, S.; Artsawang, N.; Thammasiri, P. Modified Mann-type algorithm for two countable families of nonexpansive mappings and application to monotone inclusion and image restoration problems. Mathematics 2023, 11, 2927. [Google Scholar] [CrossRef]
- Artsawang, N.; Plubtieng, S.; Bagdasar, O.; Ungchittrakool, K.; Baiya, S.; Thammasiri, P. Inertial Krasnosel’skiĭ-Mann iterative algorithm with step-size parameters involving nonexpansive mappings with applications to solve image restoration problems. Carpathian J. Math. 2024, 40, 243–261. [Google Scholar] [CrossRef]
- Alvarez, F. Weak convergence of a relaxed and inertial hybrid projection-proximal point algorithm for maximal monotone operators in Hilbert space. SIAM J. Optim. 2004, 14, 773–782. [Google Scholar] [CrossRef]
- Artsawang, N.; Ungchittrakool, K. Inertial Mann-type algorithm for a nonexpansive mapping to solve monotone inclusion and image restoration problems. Symmetry 2020, 12, 750. [Google Scholar] [CrossRef]
- Attouch, H.; Bolte, J.; Svaiter, B.F. Convergence of descent methods for semi-algebraic and tame problems: Proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Math. Program. 2009, 137, 91–129. [Google Scholar] [CrossRef]
- Baiya, S.; Plubtieng, S.; Ungchittrakool, K. An inertial shrinking projection algorithm for split equilibrium and fixed point problems in Hilbert spaces. J. Nonlinear Convex Anal. 2021, 22, 2679–2695. [Google Scholar]
- Baiya, S.; Ungchittrakool, K. Accelerated hybrid algorithms for nonexpansive mappings in Hilbert spaces. Nonlinear Funct. Anal. Appl. 2022, 27, 553–568. [Google Scholar] [CrossRef]
- Baiya, S.; Ungchittrakool, K. Modified inertial Mann’s algorithm and inertial hybrid algorithm for k-strict pseudo-contractive mappings. Carpathian J. Math. 2023, 39, 27–43. [Google Scholar] [CrossRef]
- Dong, Q.L.; Yuan, H.B.; Cho, Y.J.; Rassias, T.M. Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim. Lett. 2018, 12, 87–102. [Google Scholar] [CrossRef]
- Munkong, J.; Dinh, B.V.; Ungchittrakool, K. An inertial extragradient method for solving bilevel equilibrium problems. Carpathian J. Math. 2020, 36, 91–107. [Google Scholar] [CrossRef]
- Munkong, J.; Dinh, B.V.; Ungchittrakool, K. An inertial multi-step algorithm for solving equilibrium problems. J. Nonlinear Convex Anal. 2020, 21, 1981–1993. [Google Scholar]
- Nesterov, Y. A method for solving a convex programming problem with convergence rate O(1/K2). Dokl. Math. 1983, 27, 367–372. [Google Scholar]
- Yuying, T.; Plubtieng, S.; Inchan, I. Inertial hybrid and shrinking projection methods for sums of three monotone operators. J. Comput. Anal. Appl. 2024, 32, 85–94. [Google Scholar]
- Byrne, C. A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 2004, 20, 103–120. [Google Scholar] [CrossRef]
- Combettes, P.L. Constrained image recovery in a product space. In Proceedings of the IEEE International Conference on Image Processing, Washington, DC, USA, 23–26 October 1995; IEEE Computer Society Press: Los Alamitos, CA, USA, 1995; pp. 2025–2028. [Google Scholar]
- Kitkuan, D.; Kumam, P.; Martínez-Moreno, J.; Sitthithakerngkiet, K. Inertial viscosity forward–backward splitting algorithm for monotone inclusions and its application to image restoration problems. Int. J. Comput. Math. 2019, 97, 482–497. [Google Scholar] [CrossRef]
- Podilchuk, C.I.; Mammone, R.J. Image recovery by convex projections using a least-squares constraint. J. Opt. Soc. Am. 1990, 7, 517–521. [Google Scholar] [CrossRef]
- Artsawang, N. Accelerated preconditioning Krasnosel’skiĭ-Mann method for efficiently solving monotone inclusion problems. AIMS Math. 2023, 8, 28398–28412. [Google Scholar] [CrossRef]
- Brézis, H.; Chapitre, I.I. Operateurs maximaux monotones. North Holl. Math Stud. 1973, 5, 19–51. [Google Scholar]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; CMS Books in Mathematics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 1967, 73, 591–597. [Google Scholar] [CrossRef]
- Thammasiri, P.; Wangkeeree, R.; Ungchittrakool, K. A modified inertial Tseng’s algorithm with adaptive parameters for solving monotone inclusion problems with efficient applications to image deblurring problems. J. Comput. Anal. Appl. 2024; in press. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]

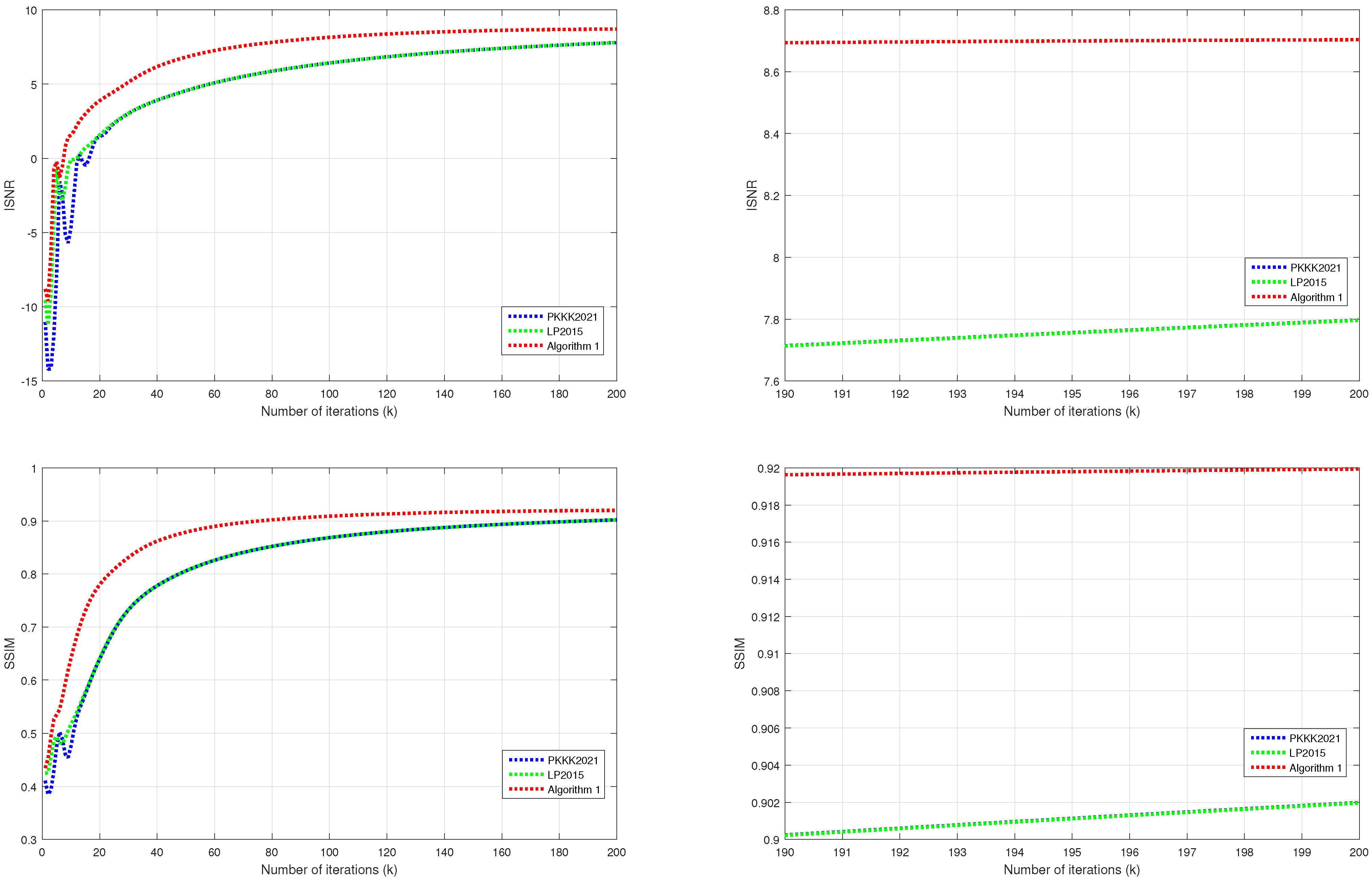

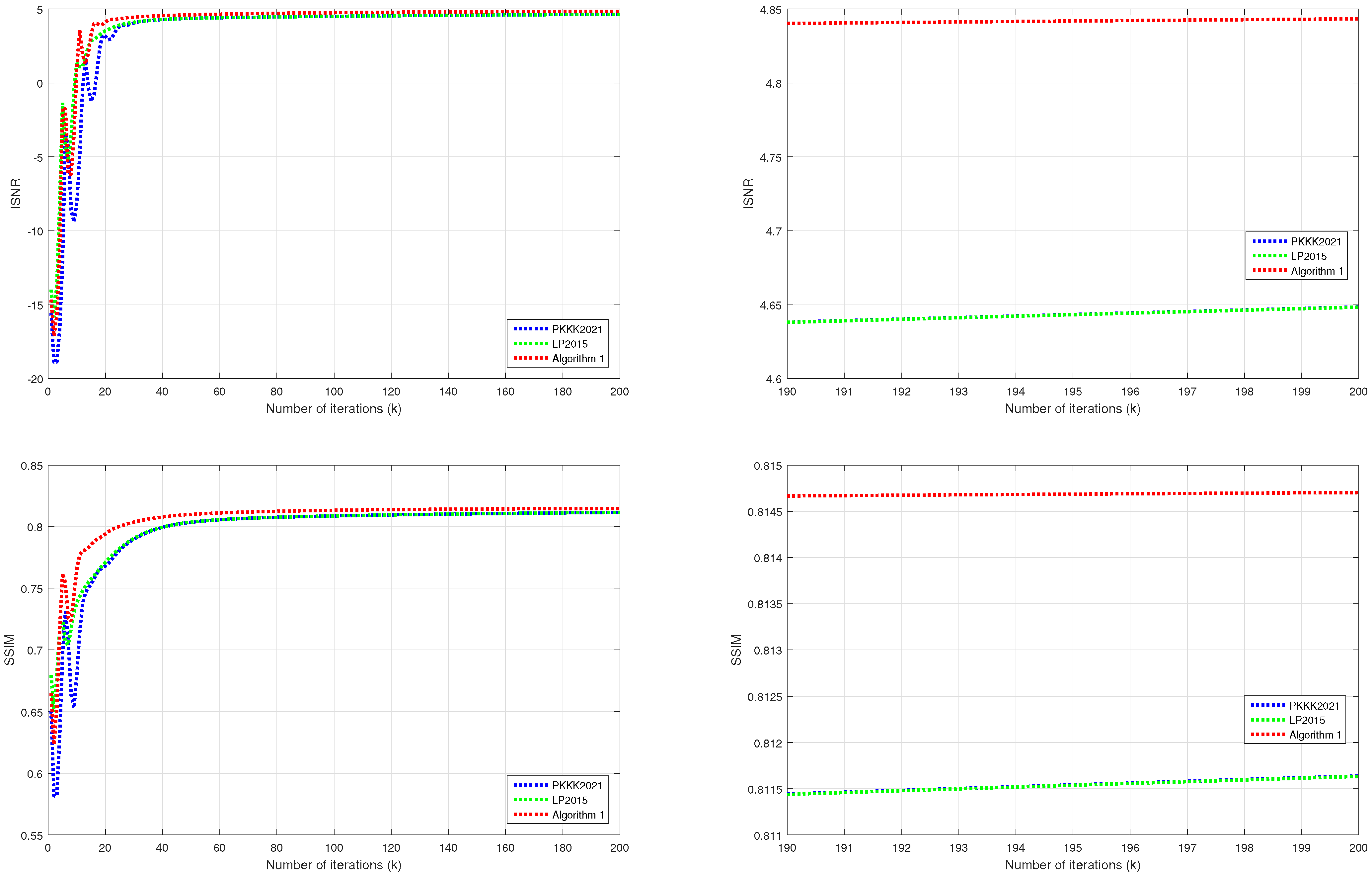
| (n) | ISNR | SSIM | ||||
|---|---|---|---|---|---|---|
| Algorithm 1 | PKKK2021 | LP2015 | Algorithm 1 | PKKK2021 | LP2015 | |
| 1 | −8.8946 | −11.0381 | −9.5612 | 0.4344 | 0.4107 | 0.4249 |
| 10 | 1.6975 | −4.6297 | −0.0611 | 0.6499 | 0.4763 | 0.5172 |
| 50 | 6.9335 | 4.5525 | 4.5535 | 0.8817 | 0.8057 | 0.8058 |
| 100 | 8.2197 | 6.4223 | 6.4226 | 0.9102 | 0.8685 | 0.8685 |
| 200 | 8.7097 | 7.7967 | 7.7961 | 0.9201 | 0.9019 | 0.9019 |
| (n) | ISNR | SSIM | ||||
|---|---|---|---|---|---|---|
| Algorithm 1 | PKKK2021 | LP2015 | Algorithm 1 | PKKK2021 | LP2015 | |
| 1 | −14.6677 | −15.5479 | −13.9892 | 0.6649 | 0.6509 | 0.6796 |
| 10 | 1.0734 | −8.0866 | 1.3429 | 0.7658 | 0.6796 | 0.7384 |
| 50 | 4.6121 | 4.3719 | 4.3731 | 0.8100 | 0.8036 | 0.8037 |
| 100 | 4.7562 | 4.5113 | 4.5115 | 0.8133 | 0.8087 | 0.8088 |
| 200 | 4.8434 | 4.6484 | 4.6483 | 0.8147 | 0.8116 | 0.8116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thammasiri, P.; Berinde, V.; Petrot, N.; Ungchittrakool, K. Double Tseng’s Algorithm with Inertial Terms for Inclusion Problems and Applications in Image Deblurring. Mathematics 2024, 12, 3138. https://doi.org/10.3390/math12193138
Thammasiri P, Berinde V, Petrot N, Ungchittrakool K. Double Tseng’s Algorithm with Inertial Terms for Inclusion Problems and Applications in Image Deblurring. Mathematics. 2024; 12(19):3138. https://doi.org/10.3390/math12193138
Chicago/Turabian StyleThammasiri, Purit, Vasile Berinde, Narin Petrot, and Kasamsuk Ungchittrakool. 2024. "Double Tseng’s Algorithm with Inertial Terms for Inclusion Problems and Applications in Image Deblurring" Mathematics 12, no. 19: 3138. https://doi.org/10.3390/math12193138
APA StyleThammasiri, P., Berinde, V., Petrot, N., & Ungchittrakool, K. (2024). Double Tseng’s Algorithm with Inertial Terms for Inclusion Problems and Applications in Image Deblurring. Mathematics, 12(19), 3138. https://doi.org/10.3390/math12193138






