A New Class of Braided Block Codes Constructed by Convolutional Interleavers
Abstract
1. Introduction
- To achieve the abovementioned goal, a new scheme of the braided block code is accomplished, whose component codes (FG and EG LDPC codes) are decoded using the Min-Sum Algorithm (MSA).
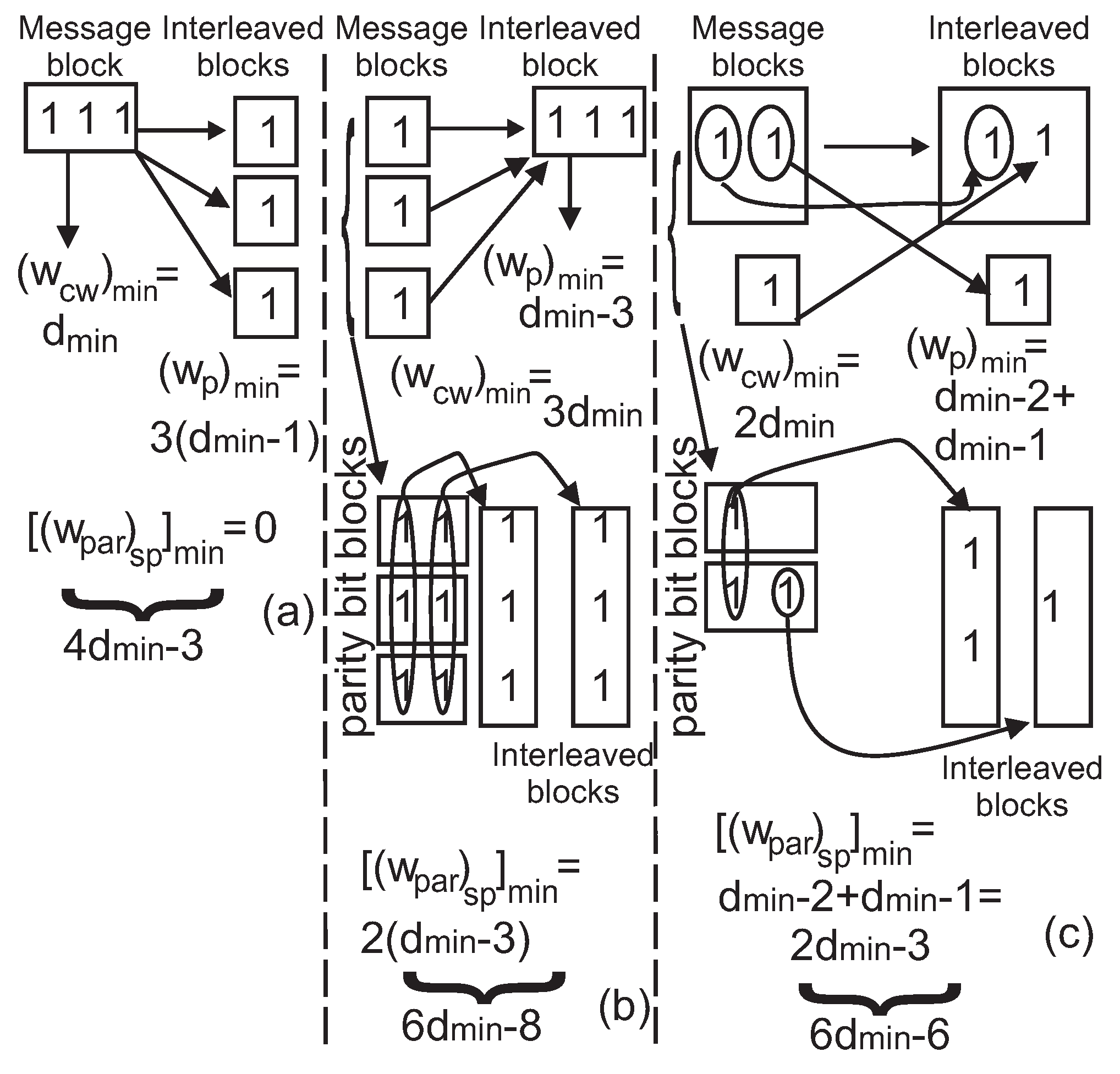
- Instead of re-encoding all codeword bits, the first encoder concentrates on the most important parity bits; those contribute to the generation of low-weight codewords. This is achievable by determining the low weight distribution of the constituent code when messages with weights 1 and 2 are encoded. Then, some parity bits contributed to those weights of codewords are interleaved and encoded by the second constituent encoder.
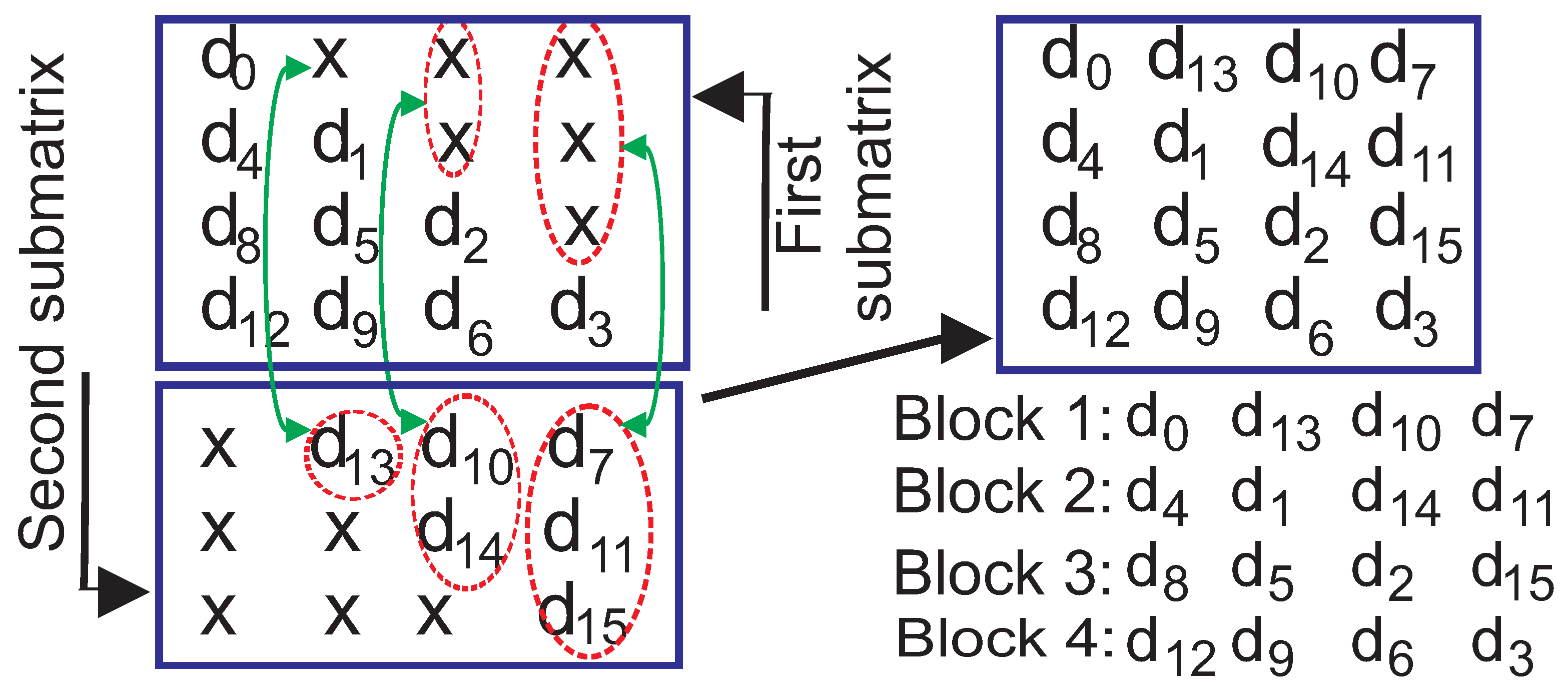
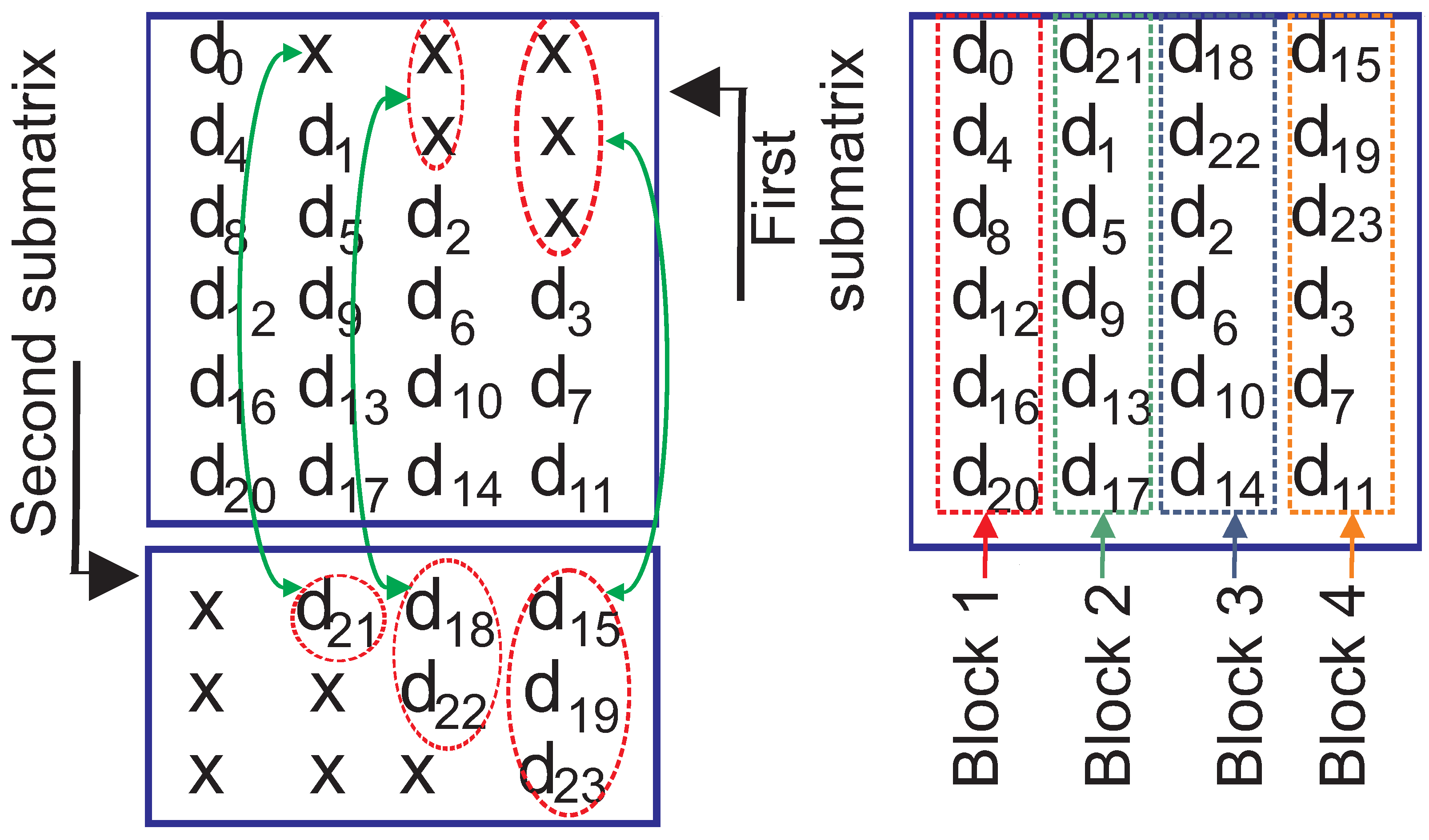
- The paper applies a non-stuff bit-based convolutional interleaver. Similar to the messages, the permutation of the selected parity bits is conducted by the convolutional interleaver. As a convolutional interleaver is flexible to permute data with different lengths, one interleaver for the permutation of both messages and selected parity bits is applied. Despite the method proposed in [2], the convolutional interleaver used for the braided code does not add any stuff bits to the interleaved data. However, it still guarantees that only one bit of a message block is placed in an interleaved data block.
- Based on the interleaver specifications, the minimum weight of braided code is presented. It is proven that the obtained minimum weight is much greater than the minimum weight of PCB code.
- A comprehensive analysis is provided to extract the advantage of the braided code. It is shown that codes have outstanding performance, while they require similar or lower computation on their iterative decoding compared to other well-known codes.
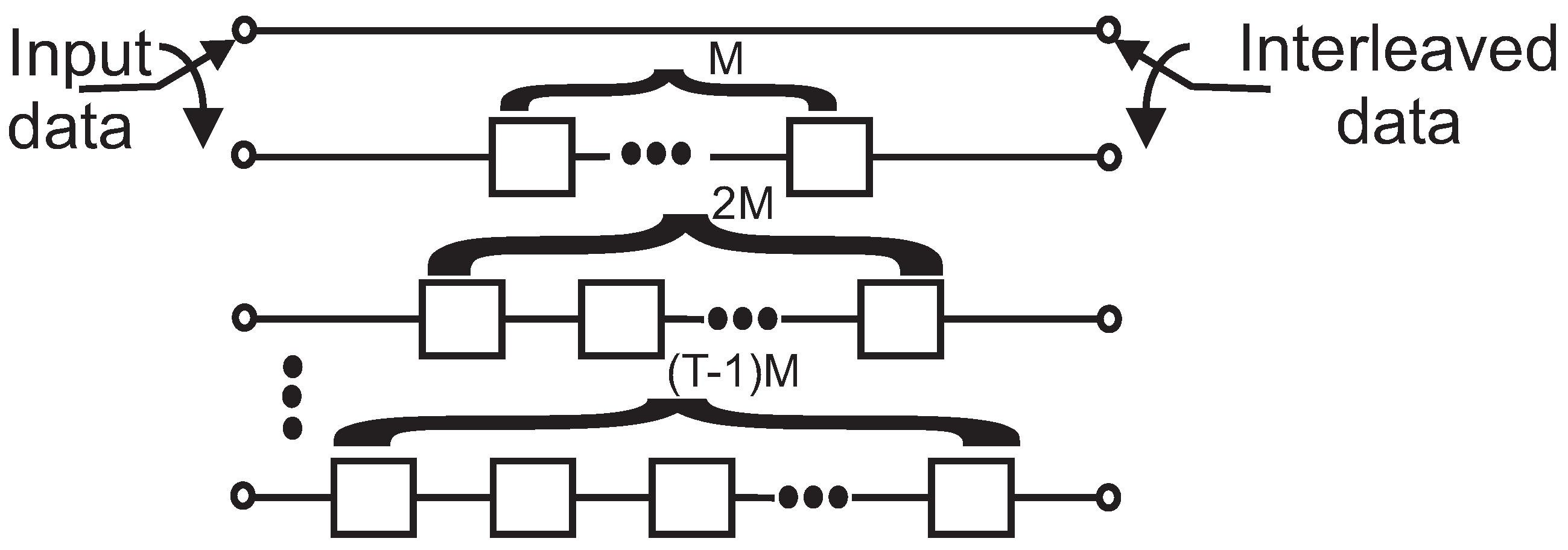
2. Non-Stuff-Based Convolutional Interleaver for PCB Codes
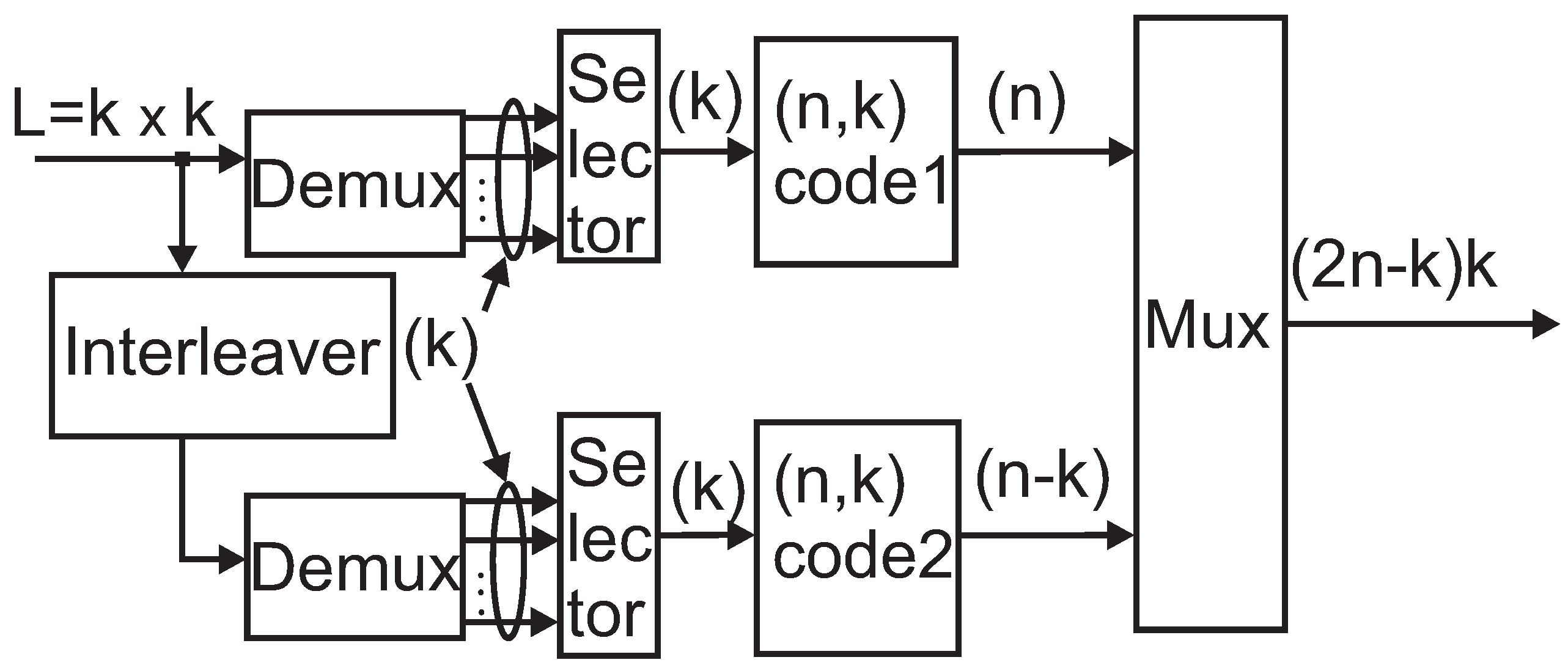
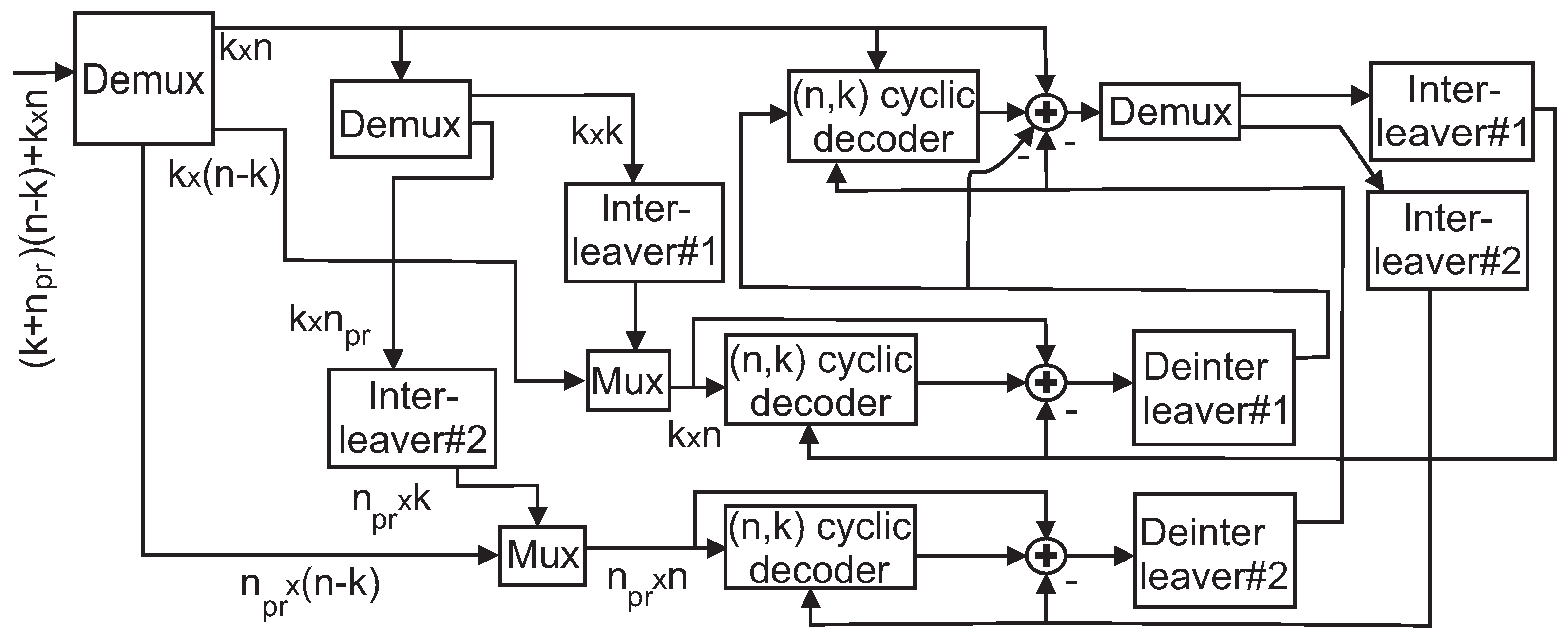
3. A New Scheme of PCB Codes
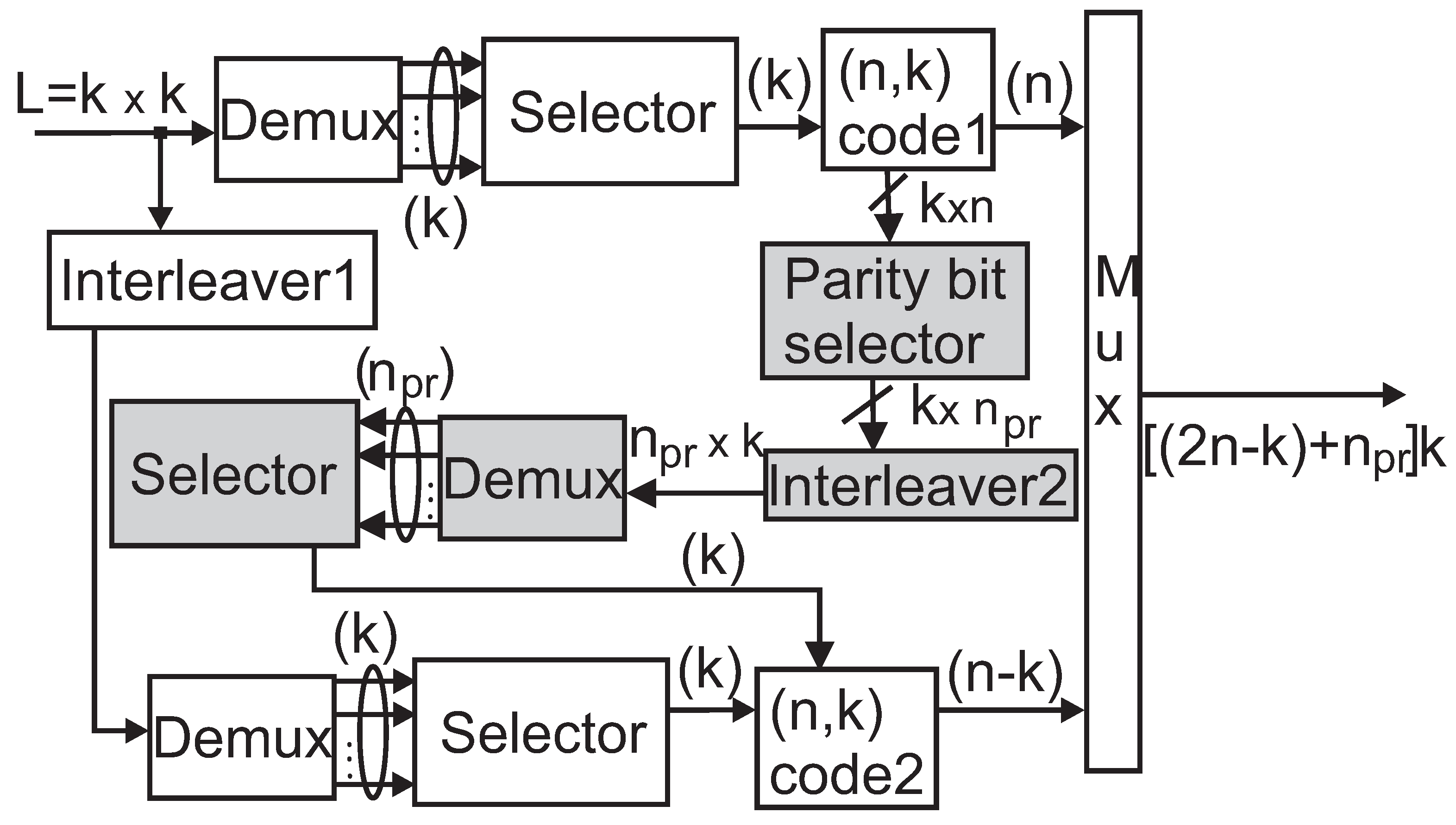
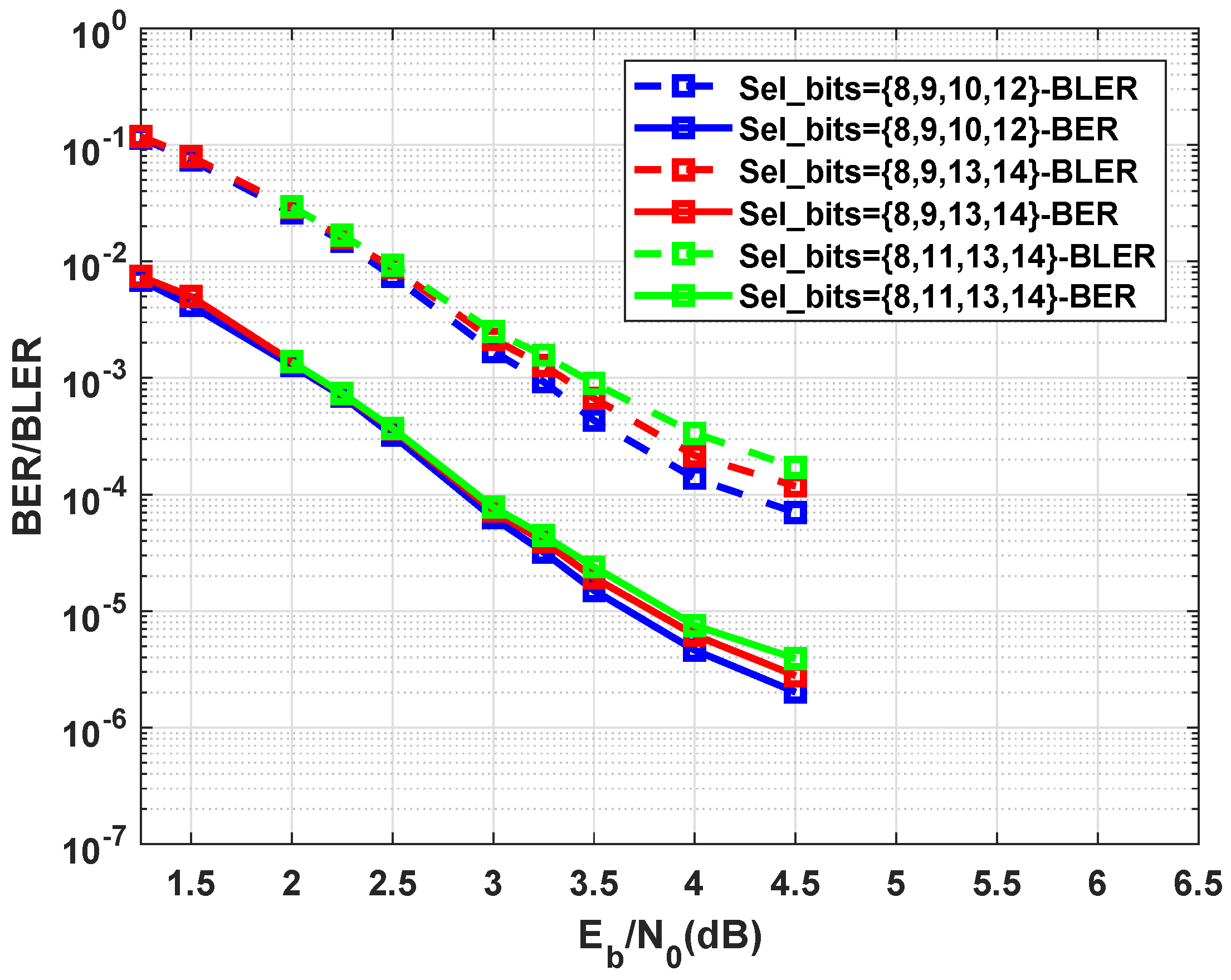
3.1. Selection of Important Parity Bits of the Cyclic Code
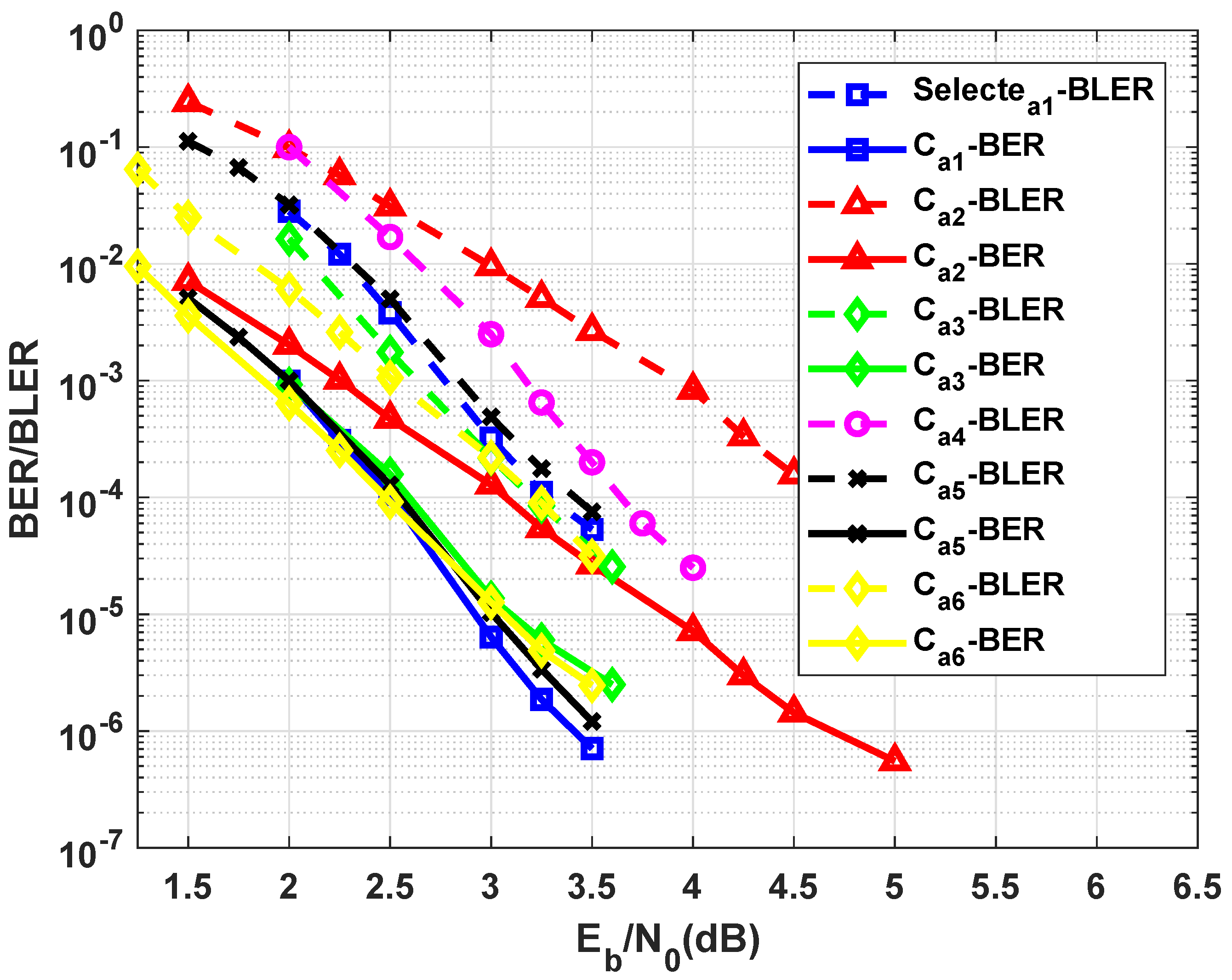
3.2. Structure of the Braided Code
4. Convergence Behavior of the Iterative Decoding of the Braided Code
5. Latency of the Designed Braided Code
6. Upper Bound of Probability of Error for Braided Codes Constructed by the Proposed Interleaver
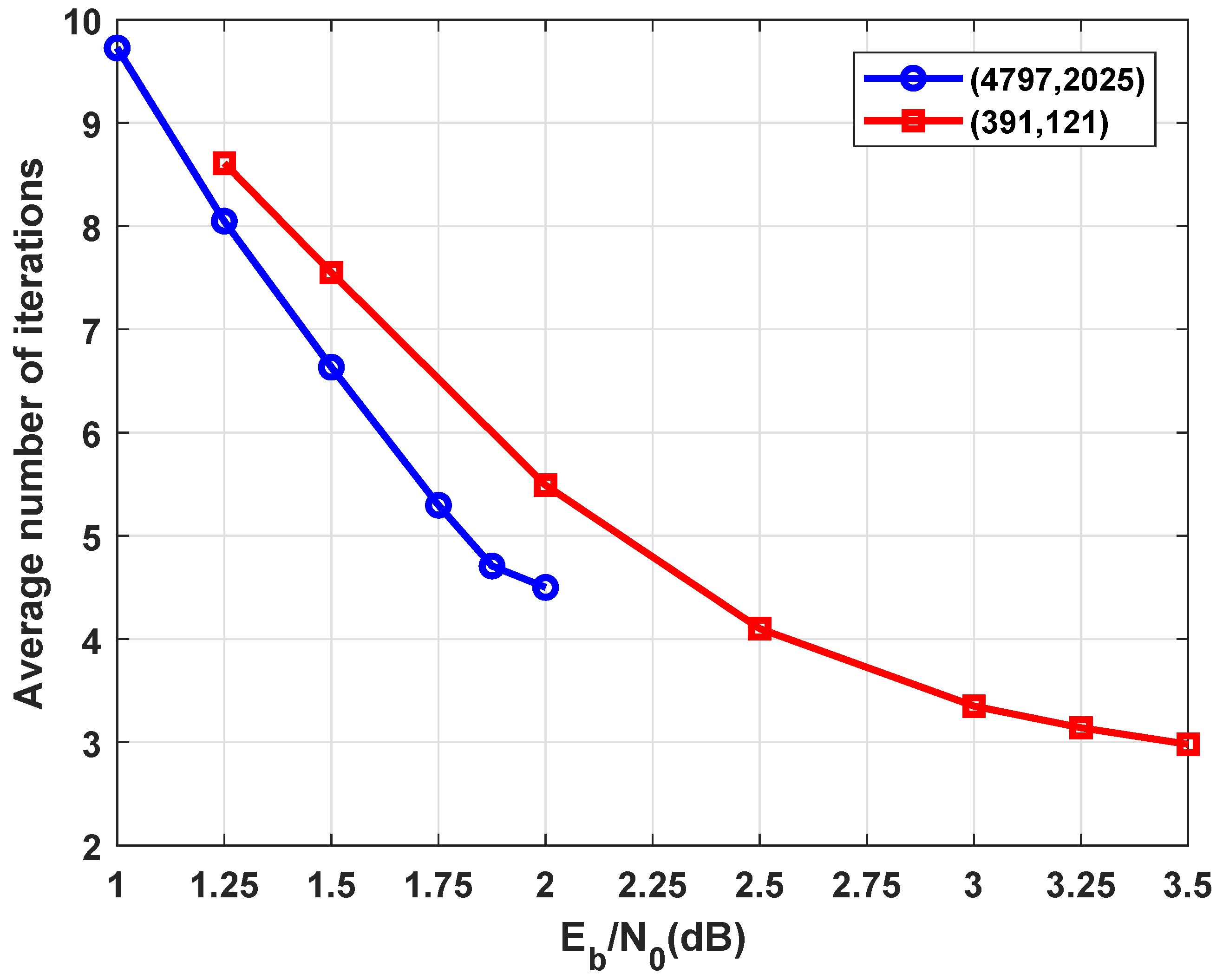
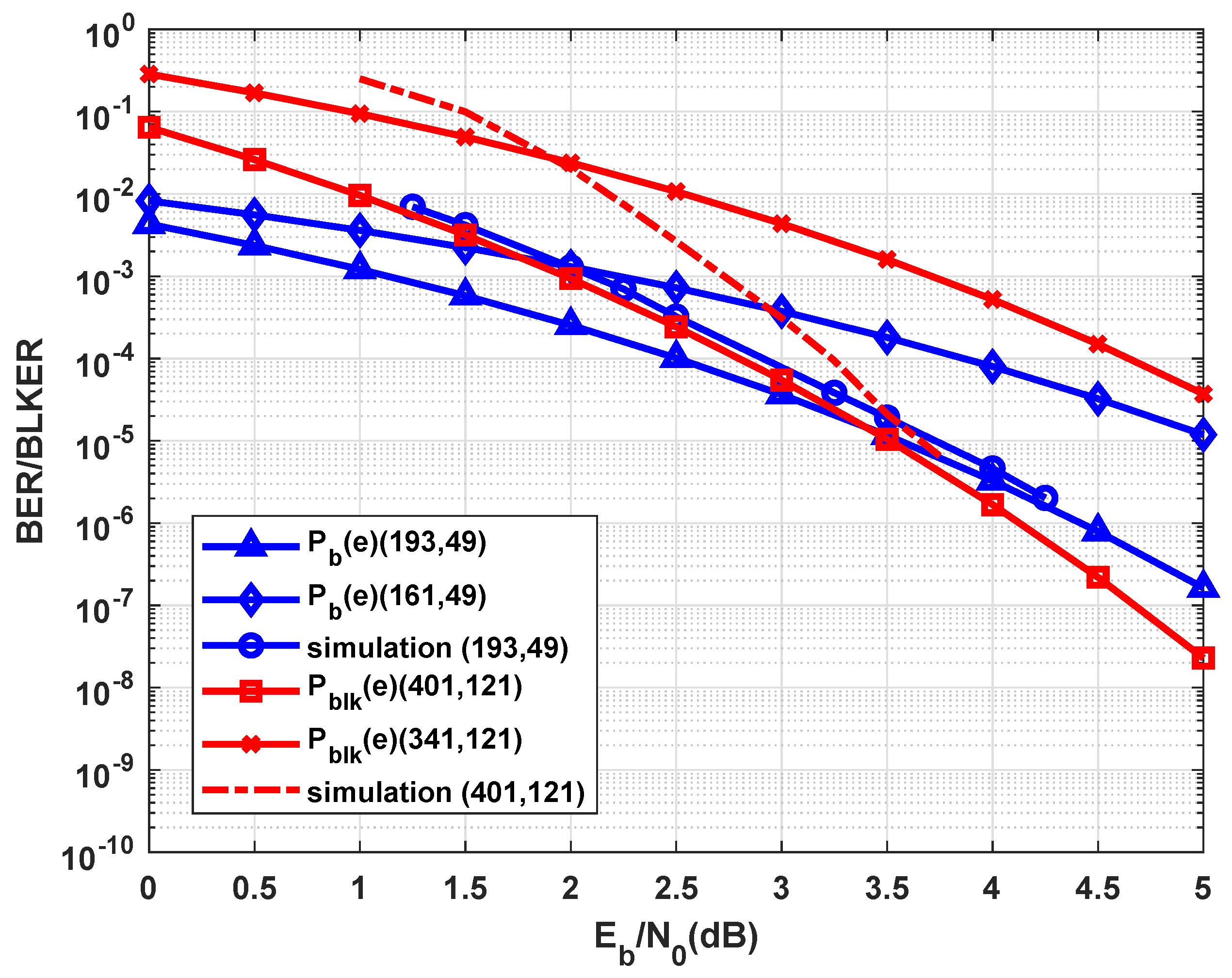
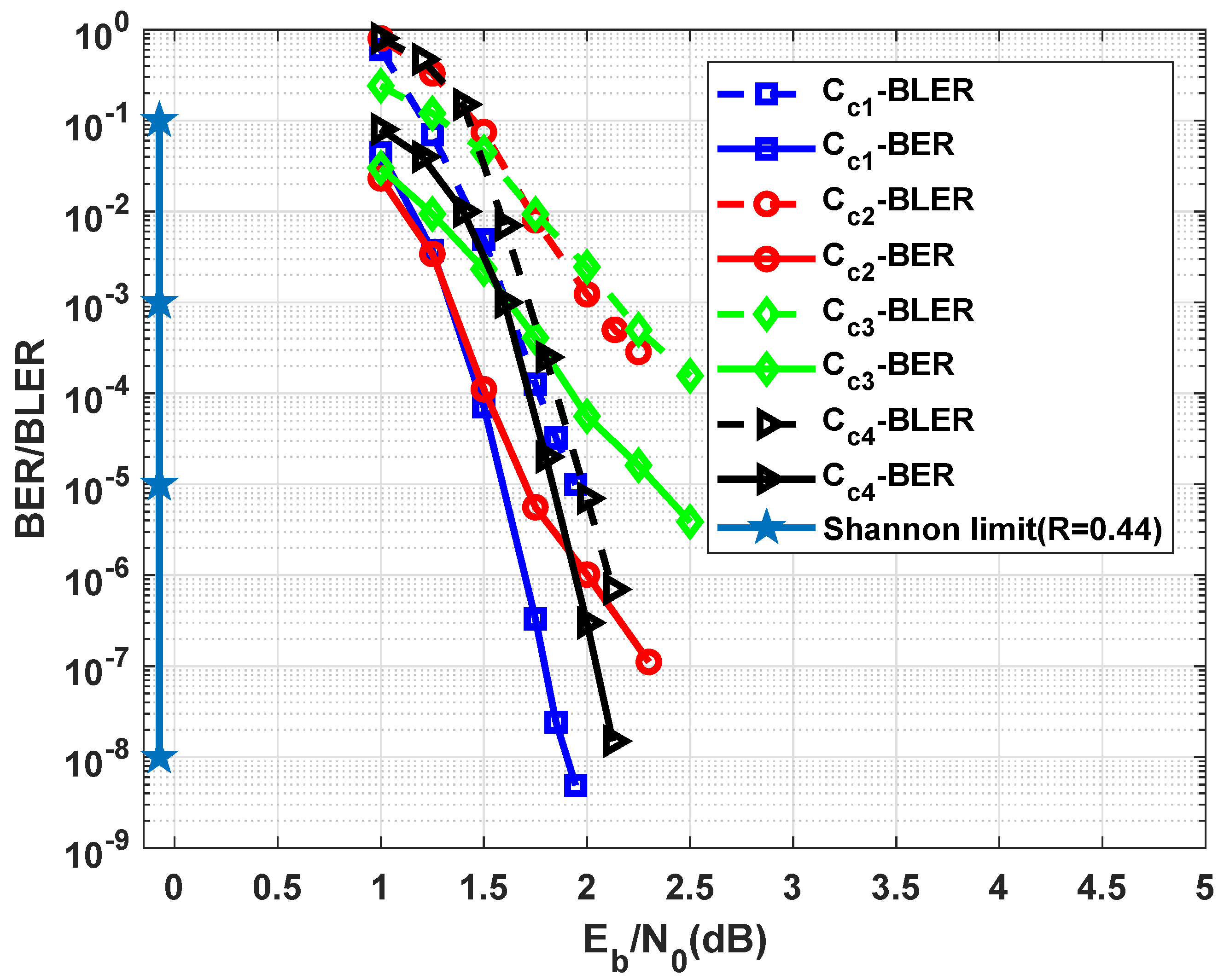
7. Simulation Results
Decoding Complexity of Braided Codes
8. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Description |
|---|---|
| L | Message length |
| k | Message length of cyclic codes |
| n | Codeword length of cyclic codes |
| T | Period of convolutional interleavers |
| Interleaver length | |
| M | Space value of the convolutional interleavers |
| Minimum weight of cyclic codes | |
| Number of message and interleaved blocks | |
| Multiplicity of from encoding of messages | |
| Multiplicity of from encoding of interleaved messages | |
| Weight of the message block | |
| Codeword weight of code obatined from encoding of k message blocks | |
| Weight of parity bits of code obtained from encoding of k interleaved message blocks | |
| Number of selected parity bits | |
| Multiplicity of | |
| Minimum weight of selected parity bits per block | |
| Multiplicity of | |
| Minimum weight of parity bits obtained from encoding of the selected parity bits | |
| Minimum weight of the braided code | |
| Weight of the message | |
| Number of iterations applied for the interactive iterative decoding | |
| soft output extrinsic information relevant to the ith message | |
| soft output extrinsic information relevant to the ith interleaved message | |
| Successive cancellation list size |
References
- Vafi, S. Parallel concatenated block codes constructed by convolutional interleavers. IEEE Access 2021, 9, 41218–41226. [Google Scholar] [CrossRef]
- Vafi, S. Modified convolutional interleavers for parallel concatenated block codes. IEEE Commun. Lett. 2022, 6, 1469–1473. [Google Scholar] [CrossRef]
- Lin, S.; Costello, D. Error Control Coding: Fundamentals and Applications, 2nd ed.; Printice Hall: Upper Saddle River, NJ, USA, 2004; Chapter 17; pp. 858–870. [Google Scholar]
- Diao, Q.; Tai, Y.T.; Lin, S.; Abdel-Ghaffar, K. Trapping set structure of LDPC codes on finite geometries. In Proceedings of the Information Theory and Applications Workshop, San Diego, CA, USA, 10–15 February 2013; pp. 3088–3092. [Google Scholar]
- Feltstrom, A.J.; Truhachev, D.; Lentmaier, M.; Zigangirov, K.S. Braided block codes. IEEE Trans. Inf. Theory 2009, 55, 2640–2658. [Google Scholar] [CrossRef]
- Justesen, J. Performance of product codes and related structures with iterated decoding. IEEE Trans. Commun. 2011, 59, 407–415. [Google Scholar] [CrossRef]
- Smith, B.P.; Farhood, A.; Hunt, A.; Kschischang, F.R.; Lodge, J. Staircase codes: FEC for 100 Gb/s OTN. IEEE J. Light. Technol. 2012, 30, 110–117. [Google Scholar] [CrossRef]
- Jian, Y.Y.; Pfister, H.D.; Narayan, K.; Rao, R.; Mazahreh, R. Iterative hard decision decoding of braided BCH codes for high speed optical communication. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 2376–2381. [Google Scholar]
- Galligan, K.; Solomon, A.; Riaz, A.; MÃľdard, M.; Yazicigil, R.; Duffy, K. IGRAND: Decode any product code. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Sukmadji, A.; M-PeÌČnas, U.; Kschischang, F.R. Zipper codes. J. Light. Technol. 2022, 40, 6397–6407. [Google Scholar] [CrossRef]
- Barakatain, M.; Kschischang, F.R. Low-complexity rate- and channel configurable concatenated codes. J. Light. Technol. 2021, 37, 1976–1983. [Google Scholar] [CrossRef]
- Moloudi, S.; Lentmaier, M.; Amat, A.G.I. Spatially coupled turbo like codes. IEEE Trans. Inf. Theory 2017, 63, 6199–6215. [Google Scholar] [CrossRef]
- Wang, Q.; Cai, S.; Lin, W.; Zhao, S.; Chen, L.; Ma, X. Spatially coupled LDPC codes via partial superposition and their application to HARQ. IEEE Trans. Veh. Technol. 2021, 70, 3493–3504. [Google Scholar] [CrossRef]
- Yang, C.; Zhao, S. Spatially Coupled Serially Concatenated Codes: Analysis and Extension; Elsevier: Amsterdam, The Netherlands, 2022; Volume 126, pp. 1–9. [Google Scholar]
- Mahdavi, M.; Weithoffer, S.; Herrmann, M.; Liu, L.; Edfors, O.; Wehn, N.; Lentmaier, M. Spatially coupled serially concatenated codes: Performance evaluation and VLSI design tradeoffs. IEEE Trans. Circ. Syst. Regul. Pap. 2022, 69, 1962–1975. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, C.; Wen, J. Spatially coupled serially concatenated codes via parity re-encoding. IET Electron. Lett. 2021, 57, 129–131. [Google Scholar] [CrossRef]
- Ali, I.; Ha, J. Partial spatial coupling of LDPC codes: Reducing the gap to capacity by improving the rate. IEEE Trans. Commun. 2023, 71, 6898–6912. [Google Scholar] [CrossRef]
- Wang, Q.; Cai, S.; Ma, X. Free-Ride coding for constructions of coupled LDPC codes. IEEE Trans. Commun. 2023, 71, 1259–1270. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Q.; Cai, S.; Xie, X. Implicit partial product-LDPC codes using free-ride coding. In Proceedings of the ICC 2022—IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 2471–2476. [Google Scholar]
- Wang, Y.; Wang, Q.; Ma, X. Design of implicit partial product-LDPC codes and low complexity decoding algorithm. IEEE Commun. Lett. 2023, 27, 419–423. [Google Scholar] [CrossRef]
- Benedetto, S.; Montorsi, G. Unveiling turbo codes:some results on parallel concatenated coding schemes. IEEE Trans. Inf. Theory 1996, 42, 409–428. [Google Scholar] [CrossRef]
- Clark, G.; Cain, J. Error-Correction Coding for Digital Communications; Plunum Press: Jundiaí, Brasil, 1981. [Google Scholar]
- Shao, R.Y.; Lin, S.; Fossorier, M.P.C. Two simple stopping criteria for turbo decoding. IEEE Trans. Commun. 1999, 47, 1117–1120. [Google Scholar] [CrossRef]
- Niu, K.; Chen, K.; Lin, J.; Zhang, Q.T. Polar codes: Primary concepts and practical decoding algorithms. IEEE Commun. Mag. 2014, 52, 192–203. [Google Scholar] [CrossRef]
- Kim, I.; Kojima, G.T.; Song, H.Y. Some short-length girth-8 QC-LDPC codes from primes of the form t2 + 1. IEEE Commun. Lett. 2022, 26, 1211–1215. [Google Scholar] [CrossRef]
- Li, J.; Liu, K.; Lin, S.; Abdel-Ghaffar, K. Algebraic Quasi-Cyclic LDPC codes: Construction, low error-floor, large girth and a reduced-complexity decoding scheme. IEEE Trans. Commun. 2014, 62, 2626–2637. [Google Scholar] [CrossRef]
- Abu-Surra, S.; Liva, G.; Ryan, W.E. Low-floor Tanner codes via Hamming node or RSCC-node doping. In Proceedings of the 16th International Symposium on Applied Algebra, Algebraic Algorithms and Error, Las Vegas, NV, USA, 20–24 February 2006; pp. 245–254. [Google Scholar]

| Cyclic Code | Input Weight | ||||
|---|---|---|---|---|---|
| (21,11) | 1(1) | 110 | 110 | 110 | |
| (63,37) | 1 | 1(1) | 740 | 740 | 740 |
| (73,45) | 1(1) | 900 | 900 | 900 | |
| (21,11) | 1(2) | 5500 | 495 | 253 | |
| (21,11) | 2(1) | 385 | 385 | 286 | |
| (63,37) | 2 | 1(2) | 26,640 | 7030 | 0 |
| (63,37) | 2(1) | 888 | 888 | 0 | |
| (73,45) | 1(2) | 396,000 | 8550 | 1665 | |
| (73,45) | 2(1) | 1080 | 1080 | 0 |
| Positions of Bit 1 | |
|---|---|
| 1(5) | (0,7,8,9,11), (1,8,9,10,12), |
| (2,9,10,11,13), (3,10,11,12,14), | |
| (6,7,8,10,14) | |
| 1(6) | (4,7,8,9,12,13), (5,8,9,10,13,14) |
| 2(5) | (0,4,11,12,13), (1,4,7,10,13), |
| (1,5,12,13,14), (2,5,8,11,14), | |
| (5,6,7,9,13) | |
| 2(6) | (0,1,7,10,11,12), (0,2,7,8,10,13), |
| (0,6,9,10,11,14), (1,2,8,11,12,13), | |
| (1,3,8,9,11,14), (1,6,7,9,12,14) | |
| (2,3,9,12,13,14), (3,6,7,8,11,12), | |
| (4,5,7,10,12,14) | |
| 2(7) | (0,5,7,10,11,13,14), (4,6,9,10,12,13,14) |
| (2,4,7,8,10,11,12), (3,5,8,9,11,12,13) | |
| 2(8) | (0,3,7,8,9,10,12,14), (2,6,7,8,9,11,13,14) |
| 2(9) | (3,4,7,8,9,10,11,13,14) |
| + | () | |||
|---|---|---|---|---|
| 2(2) | 44 | 2(1) | 56 | |
| 1(4) | 54 | 4(2) | 712 | |
| 1(2) | 2(1) | |||
| 2(1) | 54 | 3(1) | 79 | |
| 1(1) | 1(2) | |||
| 3(1) | 54 | 0(0) | 76 | |
| 4(1) | 54 | 0(0) | 0 |
| Code | Applied EG/PG Code | |
|---|---|---|
| (4797,2025) | (73,45) | |
| (3579,1369) | (63,37) | |
| (401,121) | (21,11) | |
| (193,49) | (15,7) | |
| Description | Code |
|---|---|
| (391,121) (, with convolutional interleaver) | |
| (391,121) (, with row-column interleaver) | |
| Braided codes | (3579,1369) ( with ) |
| (3579,1369) ( with ) | |
| (4797,2025) () | |
| (361,121) () | |
| PCB codes | (3345,1369) () |
| (4601,2025) () | |
| (401,121) ( with ) | |
| (391,121) ( with ) | |
| Polar codes | (3579,1369) (with ) |
| (3579,1369) (with ) | |
| (4601,2025) () | |
| LDPC codes | (500,125) () |
| (4608,2304) ( |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vafi, S. A New Class of Braided Block Codes Constructed by Convolutional Interleavers. Mathematics 2024, 12, 3127. https://doi.org/10.3390/math12193127
Vafi S. A New Class of Braided Block Codes Constructed by Convolutional Interleavers. Mathematics. 2024; 12(19):3127. https://doi.org/10.3390/math12193127
Chicago/Turabian StyleVafi, Sina. 2024. "A New Class of Braided Block Codes Constructed by Convolutional Interleavers" Mathematics 12, no. 19: 3127. https://doi.org/10.3390/math12193127
APA StyleVafi, S. (2024). A New Class of Braided Block Codes Constructed by Convolutional Interleavers. Mathematics, 12(19), 3127. https://doi.org/10.3390/math12193127





