A New Hybrid Descent Algorithm for Large-Scale Nonconvex Optimization and Application to Some Image Restoration Problems

Abstract

Conjugate gradient methods are widely used and attractive for large-scale unconstrained smooth optimization problems, with simple computation, low memory requirements, and interesting theoretical information on the features of curvature. Based on the strongly convergent property of the Dai–Yuan method and attractive numerical performance of the Hestenes–Stiefel method, a new hybrid descent conjugate gradient method is proposed in this paper. The proposed method satisfies the sufficient descent property independent of the accuracy of the line search strategies. Under the standard conditions, the trust region property and the global convergence are established, respectively. Numerical results of 61 problems with 9 large-scale dimensions and 46 ill-conditioned matrix problems reveal that the proposed method is more effective, robust, and reliable than the other methods. Additionally, the hybrid method also demonstrates reliable results for some image restoration problems.

1. Introduction

In this paper, we consider the following unconstrained problem:

$$\underset{x\in {\mathbb{R}}^n}{min}f\left(x\right),$$

(1)

where $f:{\mathbb{R}}^n\to \mathbb{R}$ is continuously differentiable, bound below, and its gradient is available. There are many effective methods for problem (1), such as Newton-type methods, quasi-Newton-type methods, spectral gradient methods, and conjugate gradient (CG for abbreviation) methods [1,2,3,4,5,6,7,8,9,10,11], etc. Meanwhile, there are also various free gradient optimization tools such as Nelder–Mead, generalized simulated annealing, and genetic algorithm [12,13,14], etc., for problem (1). In this part, we focus on CG methods and propose a new hybrid CG method for a large-scale problem (1). Actually, CG methods are one of the most effective methods for unconstrained problems, especially for large-scale cases, due to their low storage and globally convergent properties [3], in which the iterative point is usually generated by

$$x_{k+1}=x_k+{\alpha }_k{d}_k,k=0,1,\dots ,$$

(2)

where $x_k$ is the current iteration; the scalar ${\alpha }_k>0$ is the step length, determined by some line search strategy; and $d_k$ is the search direction, defined by

$$\begin{array}{c}\hfill d_k=\left\{\begin{array}{cc}-g_k,\hfill & \mathrm{if}k=0,\hfill \\ -g_k+{\beta }_k{d}_{k-1},\hfill & \mathrm{if}k\ge 1,\hfill \end{array}\right.\end{array}$$

(3)

where $g_k:=g\left(x_k\right)=\nabla f\left(x_k\right)$ and ${\beta }_k$ is called the conjugate parameter. A number of CG methods have been proposed by various modifications of the direction $d_k$ and the parameter ${\beta }_k$; see [4,5,6,7,8,9,10,11,15,16,17,18,19,20], etc. Some CG methods have strong convergence properties, but their numerical performances may not be good in practice due to the jamming phenomenon [4]. These methods include Fletcher–Reeves (FR) [5], Dai–Yuan (DY) [6], and Fletcher (CD) [7], with the following conjugate parameters:

$${\beta }_{k+1}^{FR}={\displaystyle \frac{\parallel g_{k+1}{\parallel }^2}{\parallel g_k{\parallel }^2}},{\beta }_{k+1}^{DY}={\displaystyle \frac{\parallel g_{k+1}{\parallel }^2}{y_k^T{d}_k}},{\beta }_{k+1}^{CD}=-{\displaystyle \frac{\parallel g_{k+1}{\parallel }^2}{g_k^T{d}_k}},$$

where $g_{k+1}=\nabla f\left(x_{k+1}\right)$, $y_k=g_{k+1}-g_k$, and $\parallel ·\parallel$ stands for the Euclidean norm. On the other hand, some other CG methods may perform well in practice, but their convergence may be not guaranteed, especially for nonconvex functions. These methods include Hestenes–Stiefel (HS) [8], Polak–Ribière–Polyak (PRP) [9,10], and Liu–Storey (LS) [11], with the following conjugate parameters:

$${\beta }_{k+1}^{HS}={\displaystyle \frac{g_{k+1}^T{y}_k}{y_k^T{d}_k}},{\beta }_{k+1}^{PRP}={\displaystyle \frac{g_{k+1}^T{y}_k}{\parallel g_k{\parallel }^2}},{\beta }_{k+1}^{LS}=-{\displaystyle \frac{g_{k+1}^T{y}_k}{g_k^T{d}_k}}.$$

In fact, these methods possess an automatically approximate restart feature which can avoid the jamming phenomenon, that is, when the step $s_k$ is small, the factor $y_k$ tends to zero, resulting in the conjugate parameter ${\beta }_{k+1}$ becoming small and the new direction $d_{k+1}$ approximating to the steepest descent direction $-g_{k+1}$.

To attain good computational performance and maintain the attractive feature of strong global convergence, many scholars have paid special attention to hybridizing these CG methods. Specifically, the authors in [21] proposed a hybrid PRP-FR CG method (H1 method in [22]) and the corresponding conjugate parameter was defined as ${\beta }_{k+1}^{H1}=max\left\{0,min\{{\beta }_{k+1}^{FR},{\beta }_{k+1}^{PRP}\}\right\}$. Moreover, based on the above hybrid conjugate parameter, a new form was proposed in [23], where the parameter was defined by ${\beta }_{k+1}=max\{-{\beta }_{k+1}^{FR},min\{{\beta }_{k+1}^{FR},{\beta }_{k+1}^{PRP}\}\}$, and the global convergence property was established for the general function without the convexity assumption. In [24], a hybrid of the HS method and DY method was proposed in which the conjugate parameter was defined by ${\beta }_{k+1}^{H2}=max\left\{0,min\{{\beta }_{k+1}^{HS},{\beta }_{k+1}^{DY}\}\right\}.$ The numerical results indicated that the above hybrid method was more effective than the PRP algorithm. In the above hybrid CG methods, the search direction was in the form of (3). Moreover, the authors in [25] proposed a new hybrid three-term method in which the conjugate parameter is ${\beta }_{k+1}^{H2}$ and the direction is $d_{k+1}=-g_{k+1}+(1-{\lambda }_{k+1}){\beta }_{k+1}^{H2}{d}_k+{\lambda }_{k+1}{\theta }_{k+1}{g}_k,$ where ${\lambda }_{k+1}$ is the convex parameter. The above hybrid method demonstrates attractive numerical performance. Furthermore, in [22], the authors proposed two new hybrid methods based on the above conjugate parameters with different search directions. Concretely, the directions have the following common form:

$$d_{k+1}=-\left(1+{\beta }_{k+1}{\displaystyle \frac{g_{k+1}^T{d}_k}{\parallel g_{k+1}{\parallel }^2}}\right)g_{k+1}+{\beta }_{k+1}{d}_k,$$

(4)

where ${\beta }_{k+1}={\beta }_{k+1}^{H1}$ or ${\beta }_{k+1}={\beta }_{k+1}^{H2}$. A remarkable feature of the above directions is that the sufficient descent property is automatically satisfied, independent of the accuracy of the line search strategy.

Motivated by the above discussions, in this paper, we propose a new hybrid descent CG method for large-scale nonconvex problems. The proposed hybrid method automatically enjoys the sufficient descent property independent of the accuracy of the line search technique. Furthermore, the global convergence for the general functions without convexity is established under the standard conditions. Numerical results of 549 large-scale problems and 46 ill-conditioned matrix problems indicate the proposed method is attractive and promising. Finally, we also apply the proposed method to some image restoration problems, which also verifies its reliability and effectiveness.

The rest of the paper is organized as follows. In Section 2, we propose a descent hybrid CG method which is based on the MHS method and DY method. Moreover, the sufficient descent property is satisfied independent of the accuracy of the line search techniques. Global convergence is established for the general function in Section 3. Numerical results are given in Section 4 to indicate the effectiveness and reliability of the proposed algorithm. Finally, some conclusions are presented.

2. Motivation, Algorithm, and Sufficient Descent Property

As mentioned in the above section, the HS method is generally regarded as one of the most effective CG methods, but its global convergence for general nonlinear functions is still erratic. Additionally, the HS method does not guarantee the descent property during the iterative process, that is, the condition $g_k^T{d}_k<0$ may not be satisfied for $\forall k\ge 1$. Therefore, many researchers have been devoted to designing some descent HS conjugate gradient methods [4,24,26,27,28,29,30], etc. Specifically, to obtain an intuitively modified conjugate parameter, the authors in [26] approximated the direction $d_{k+1}^{THS}$ by the two-term direction (3), where $d_{k+1}^{THS}$ was defined by (4) with ${\beta }_{k+1}={\beta }_{k+1}^{HS}$. Concretely, the least squares problem ${min}_{\beta }{\parallel -g_{k+1}+{\beta }_{k+1}{d}_k-d_{k+1}^{THS}\parallel }^2$ was solved. After some algebraic manipulations, the unique solution was

$${\beta }_{k+1}^{MHS}={\displaystyle \frac{g_{k+1}^T{y}_k}{y_k^T{d}_k}}\left(1-{\displaystyle \frac{{\left(g_{k+1}^T{d}_k\right)}^2}{\parallel g_{k+1}{\parallel }^2{\parallel d_k\parallel }^2}}\right)={\beta }_{k+1}^{HS}{\vartheta }_k,$$

(5)

where

$${\vartheta }_k=1-{\displaystyle \frac{{\left(g_{k+1}^T{d}_k\right)}^2}{\parallel g_{k+1}{\parallel }^2{\parallel d_k\parallel }^2}}.$$

(6)

The above parameter and its modifications have some nice theoretical properties [26] and the method with (5) and (3) performs well. Meanwhile, it is clear that if the exact line search is adopted (i.e., $g_{k+1}^T{d}_k=0$), it holds that ${\beta }_{k+1}^{MHS}={\beta }_{k+1}^{HS}={\beta }_{k+1}^{PRP}$.

To attain attractive computational performance and good theoretical properties, many researchers have proposed hybrid CG methods. Among these methods, hybridizations of the HS method and the DY method have shown promising numerical performance [31,32,33,34], etc. The HS method has a nice property of automatically satisfying the conjugate condition $d_{k+1}^T{y}_k=0$ for $\forall k\ge 0$ independent of the accuracy of the line search strategies and the convexity of the objective function and performs well in practice. On the other hand, the DY method has remarkable convergence properties. These characteristics motivate us to propose new hybridizations of the HS method and the DY method which not only have attractive theoretical properties but also better numerical performance for large-scale nonconvex problems.

In the following, we focus on the conjugate parameter ${\beta }_{k+1}^{MHS}$ and propose a new hybrid conjugate parameter of ${\beta }_{k+1}^{DY}$ and ${\beta }_{k+1}^{MHS}$:

$${\beta }_{k+1}^N=max\left\{0,min\left\{{\beta }_{k+1}^{DY},{\beta }_{k+1}^{MHS}\right\}\right\}.$$

(7)

Now, based on the new hybrid conjugate parameter ${\beta }_{k+1}^N$ and the modified descent direction (8), we propose our hybrid algorithm (NMHSDY) in detail.

It should be noted that the line search technique in Algorithm 1 is not fixed: It can be selected by the users. Next, we show that the search direction $d_k$ generated by Algorithm 1 automatically has a sufficient descent property independent of any line search strategy.

Algorithm 1 New descent hybrid algorithm of MHS and DY methods (NMHSDY) for nonconvex functions.

Step 0. Input and Initialization. Select an initial point $x_0\in {\mathbb{R}}^n$, parameter $\epsilon \ge 0$ and compute $f_0=f\left(x_0\right)$ and $g_0=g\left(x_0\right)$. Set $d_0=-g_0$ and $k=0$; Step 1. If $\parallel g_k\parallel \le \epsilon$, then stop; Step 2. Compute step length ${\alpha }_k$ along direction $d_k$ by some line search strategy; Step 3. Let $x_{k+1}=x_k+{\alpha }_k{d}_k$; Step 4. Compute the conjugate parameter ${\beta }_{k+1}^N$ by (7) and the search direction $d_{k+1}$ by $$d_{k+1}=-\left(1+{\beta }_{k+1}^N{\displaystyle \frac{g_{k+1}^T{d}_k}{\parallel g_{k+1}{\parallel }^2}}\right)g_{k+1}+{\beta }_{k+1}^N{d}_k,$$ (8) Step 5. Set $k:=k+1$ and go to Step 2.

Theorem 1.

Let the search direction $d_k$ be defined by (8) in Algorithm 1. Then, for any line search strategy, the sufficient descent property holds for nonconvex function $f\left(x\right)$, that is,

$$g_k^T{d}_k=-{\parallel g_k\parallel }^2,\forall k\ge 0.$$

(9)

Proof. 

By the definition of $d_{k+1}$ in (8), we have

$$g_{k+1}^T{d}_{k+1}=-\parallel g_{k+1}{\parallel }^2-{\beta }_{k+1}{g}_{k+1}^T{d}_k+{\beta }_{k+1}{g}_{k+1}^T{d}_k=-{\parallel g_{k+1}\parallel }^2.$$

Since $d_0=-g_0$, then $d_0^T{g}_0=-{\parallel g_0\parallel }^2$. All in all, (9) holds. This completes the proof. □

3. Convergence for General Nonlinear Functions

In this section, the global convergence of the NMHSDY method is presented. Before that, some common assumptions are listed.

Assumption 1.

The level set $\mathbb{L}=\{x\in {\mathbb{R}}^n:f\left(x\right)\le f\left(x_0\right)\}$ is bounded, where $x_0$ is the initial point, i.e., there exists a positive constant $D>0$ such that

$$\parallel x\parallel \le D,\forall x\in \mathbb{L}.$$

(10)

Assumption 2.

In some neighborhood $\mathbb{N}$ of $\mathbb{L}$, the gradient $g\left(x\right)=\nabla f\left(x\right)$ is Lipschitz continuous, i.e., there exists a constant $L_1>0$ such that

$$\parallel g\left(x\right)-g\left(y\right)\parallel \le L_1\parallel x-y\parallel ,\forall x,y\in \mathbb{N}.$$

(11)

Based on the above assumptions, we further obtain that there exists a constant $M>0$ such that

$$\parallel g\left(x\right)\parallel \le M,\forall x\in \mathbb{L}.$$

(12)

In fact, it holds that $\parallel g\left(x\right)\parallel =\parallel g\left(x\right)-g\left(x_0\right)+g\left(x_0\right)\parallel \le \parallel g\left(x\right)-g\left(x_0\right)\parallel +\parallel g\left(x_0\right)\parallel \le L_1\parallel x-x_0\parallel +\parallel g\left(x_0\right)\parallel \le 2L_{1}D+\parallel g\left(x_0\right)\parallel$; hence, M can be $2L_{1}E+\parallel g\left(x_0\right)\parallel$ or larger than that.

The line search strategy is another important element in iterative methods. In this part, we take the standard Wolfe line search strategy:

$$f(x_k+{\alpha }_k{d}_k)\le f_k+{\sigma }_1{\alpha }_k{g}_k^T{d}_k,g{(x_k+{\alpha }_k{d}_k)}^T{d}_k\ge {\sigma }_2{g}_k^T{d}_k,$$

(13)

where $0<{\sigma }_1<{\sigma }_2<1$. By property (9) and line search (13), it is satisfied that

$$f_{k+1}\le f_k-{\sigma }_1{\alpha }_k{\parallel g_k\parallel }^2\le f_k,$$

that is, the sequence $\left\{f_k\right\}$ is non-increasing and the sequence $\left\{x_k\right\}$ generated by Algorithm 1 is contained in the level set $\mathbb{L}$. Since f is continuously differentiable and the set $\mathbb{L}$ is bounded, then there exists a constant $f^{*}$ such that

$$\underset{k\to \infty }{lim}f\left(x_k\right)=f^{*}.$$

The Zoutendijk condition [35] plays an essential role in the global convergence of nonlinear CG methods. For completeness, we here state the lemma but omit its proof.

Lemma 1.

Suppose that Assumptions 1 and 2 hold. Consider any nonlinear CG method, in which ${\alpha }_k$ is obtained by the standard Wolfe line search (13) and $d_k$ is a descent direction ($g_k^T{d}_k<0$). Then, we have

$$\sum _{k=1}^{\infty }{\displaystyle \frac{{\left(g_k^T{d}_k\right)}^2}{\parallel d_k{\parallel }^2}}<\infty .$$

(14)

Thereafter, the convergence property is presented in the following theorem for the general functions without convexity assumption.

Theorem 2.

Let Assumptions 1 and 2 hold and the sequence $\left\{x_k\right\}$ be generated by the NMHSDY algorithm. Set $l_{k+1}={\displaystyle \frac{{\beta }_{k+1}^N}{{\beta }_{k+1}^{DY}}}$, and if $l_{k+1}\in [-{\displaystyle \frac{1-{\sigma }_2}{1+{\sigma }_2}},1-{\sigma }_2]$ holds, then we have

$$\underset{k\to \infty }{lim\; inf}\parallel g_k\parallel =0.$$

(15)

Proof. 

We now prove (15) by contradiction and assume that there exists a constant $\mu >0$ such that

$$\parallel g_k\parallel \ge \mu ,\forall k\ge 0.$$

(16)

Let ${\gamma }_{k+1}$ be $1+{\beta }_{k+1}^N{\displaystyle \frac{g_{k+1}^T{d}_k}{\parallel g_{k+1}{\parallel }^2}}$, then the direction (8) can be rewritten as

$$d_{k+1}=-{\gamma }_{k+1}{g}_{k+1}+{\beta }_{k+1}^N{d}_k.$$

After some algebraic manipulation, we have

$$\parallel d_{k+1}{\parallel }^2={\left({\beta }_{k+1}^N\right)}^2\parallel d_k{\parallel }^2-2{\gamma }_{k+1}{g}_{k+1}^T{d}_{k+1}-{\gamma }_{k+1}^2{\parallel g_{k+1}\parallel }^2.$$

Dividing both sides of the above equality by ${\left(g_{k+1}^T{d}_{k+1}\right)}^2$, from (9), we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\parallel d_{k+1}{\parallel }^2}{\parallel g_{k+1}{\parallel }^4}}& =& {\left({\beta }_{k+1}^N\right)}^2{\displaystyle \frac{\parallel d_k{\parallel }^2}{\parallel g_{k+1}{\parallel }^4}}+{\displaystyle \frac{2{\gamma }_{k+1}}{\parallel g_{k+1}{\parallel }^2}}-{\displaystyle \frac{{\gamma }_{k+1}^2}{\parallel g_{k+1}{\parallel }^2}}\hfill \\ & =& {\left({\beta }_{k+1}^N\right)}^2{\displaystyle \frac{\parallel d_k{\parallel }^2}{\parallel g_{k+1}{\parallel }^4}}+{\displaystyle \frac{1}{\parallel g_{k+1}{\parallel }^2}}-{\displaystyle \frac{{({\gamma }_{k+1}-1)}^2}{\parallel g_{k+1}{\parallel }^2}},\hfill \\ & =& l_{k+1}^2{\displaystyle \frac{\parallel d_k{\parallel }^2}{{\left(d_k^T{y}_k\right)}^2}}+{\displaystyle \frac{1}{\parallel g_{k+1}{\parallel }^2}}-{\displaystyle \frac{{({\gamma }_{k+1}-1)}^2}{\parallel g_{k+1}{\parallel }^2}},\hfill \\ & \le & {\displaystyle \frac{l_{k+1}^2}{{(1-{\sigma }_2)}^2}}{\displaystyle \frac{\parallel d_k{\parallel }^2}{\parallel g_k{\parallel }^4}}+{\displaystyle \frac{1}{\parallel g_{k+1}{\parallel }^2}}\le {\displaystyle \frac{\parallel d_k{\parallel }^2}{\parallel g_k{\parallel }^4}}+{\displaystyle \frac{1}{\parallel g_{k+1}{\parallel }^2}},\hfill \end{array}$$

(17)

where the first inequality holds by $d_k^T{y}_k\ge ({\sigma }_2-1)g_k^T{d}_k=(1-{\sigma }_2){\parallel g_k\parallel }^2$ and the last inequality holds by the bound for the scale $l_{k+1}$. By (17) and $\parallel d_0{\parallel }^2={\parallel g_0\parallel }^2$, it holds that

$${\displaystyle \frac{\parallel d_k{\parallel }^2}{\parallel g_k{\parallel }^4}}\le \sum _{i=0}^k{\displaystyle \frac{1}{\parallel g_i{\parallel }^2}}.$$

Then, by the above inequality and (16), it follows that

$${\displaystyle \frac{\parallel g_k{\parallel }^4}{\parallel d_k{\parallel }^2}}\ge {\displaystyle \frac{{\mu }^2}{k+1}},$$

which indicates that

$$\sum _{k=1}^{\infty }{\displaystyle \frac{\parallel g_k{\parallel }^4}{\parallel d_k{\parallel }^2}}=\sum _{k=1}^{\infty }{\displaystyle \frac{{\left(g_k^T{d}_k\right)}^2}{\parallel d_k{\parallel }^2}}=\infty ,$$

which contradicts the Zoutendijk condition (14). So, (15) holds. □

Remark 1.

In [24], the authors presented a class of hybrid conjugate parameters, one of which is ${\beta }_{k+1}=max\{0,min\{{\beta }_{k+1}^{DY},{\beta }_{k+1}^{HS}\}\}$, with the corresponding interval for $l_{k+1}$ being $[-(1-{\sigma }_2)/(1+{\sigma }_2),1]$. It is reasonable that the interval in our paper is smaller since we take ${\beta }_{k+1}^{MHS}$ instead of ${\beta }_{k+1}^{HS}$ and $0<{\vartheta }_k\le 1$.

In the following, we discuss the global convergence of Algorithm 1 for general nonlinear functions in the case of $l_{k+1}\notin [-{\displaystyle \frac{1-{\sigma }_2}{1+{\sigma }_2}},1-{\sigma }_2]$. Motivated by the modified secant conditions in [36,37], in this part, based on the Wolfe line search strategy (13), we consider the following settings:

$${\overline{y}}_k=y_k+m{s}_k,$$

(18)

where $m>0$ is a constant. With the above setting, the modified conjugate parameter becomes

$${\beta }_{k+1}^{NN}=max\left\{0,min\left\{{\beta }_{k+1}^{NDY},{\beta }_{k+1}^{NMHS}\right\}\right\},$$

(19)

where ${\beta }_{k+1}^{NDY}$ and ${\beta }_{k+1}^{NMHS}$ are, respectively,

$${\beta }_{k+1}^{NDY}={\displaystyle \frac{\parallel g_{k+1}{\parallel }^2}{{\overline{y}}_k^T{s}_k}},{\beta }_{k+1}^{NMHS}={\displaystyle \frac{g_{k+1}^T{\overline{y}}_k}{{\overline{y}}_k^T{s}_k}}\left(1-{\displaystyle \frac{{\left(g_{k+1}^T{s}_k\right)}^2}{\parallel g_{k+1}{\parallel }^2{\parallel s_k\parallel }^2}}\right).$$

Meanwhile, the corresponding direction turns to

$$d_{k+1}^N=-\left(1+{\beta }_{k+1}^{NN}{\displaystyle \frac{g_{k+1}^T{s}_k}{\parallel g_{k+1}{\parallel }^2}}\right)g_{k+1}+{\beta }_{k+1}^{NN}{s}_k,$$

(20)

The following lemma indicates the property of the scalar ${\overline{y}}_k^T{s}_k{s}_k$ and $\parallel {\overline{y}}_k\parallel$.

Lemma 2.

Let ${\overline{y}}_k$ be defined by (18); then, adopting the Wolfe line search strategy (13), we obtain

$${\overline{y}}_k^T{s}_k\ge m{\parallel s_k\parallel }^2,$$

(21)

and

$$\parallel {\overline{y}}_k\parallel \le \left(L_1+m\right)\parallel s_k\parallel .$$

(22)

Proof. 

By the Wolfe line search strategy (13), we have

$$y_k^T{s}_k={\left(g_{k+1}-g_k\right)}^T{s}_k\ge ({\sigma }_2-1)g_k^T{s}_k\ge (1-{\sigma }_2){\alpha }_k{\parallel g_k\parallel }^2\ge 0,$$

which indicates $y_k^T{s}_k\ge 0$. Therefore, it holds that

$${\overline{y}}_k^T{s}_k=y_k^T{s}_k+m\parallel s_k{\parallel }^2\ge m{\parallel s_k\parallel }^2.$$

Hence, (21) holds. Meanwhile, we also have

$$\parallel {\overline{y}}_k\parallel =\parallel y_k+m{s}_k\parallel \le \parallel y_k\parallel +m\parallel s_k\parallel \le \left(L_1+m\right)\parallel s_k\parallel ,$$

where the second inequality holds by Assumption 2. Hence, (22) holds. This completes the proof. □

In the following, we assume that Algorithm 1 never stops and there exists a constant $\mu >0$ such that for all k, (16) holds.

Lemma 3.

Suppose that Assumptions 1 and 2 and (16) hold. The sequences $\left\{x_k\right\}$ and $\left\{d_k^N\right\}$ are generated by Algorithm 1 with the conjugate parameter ${\beta }_k^{NN}$ and adopting the Wolfe line search technique (13). Then, there exists a positive constant Γ such that

$$\parallel g_k\parallel \le \parallel d_k^N\parallel \le (1+2\mathrm{\Gamma })\parallel g_k\parallel .$$

(23)

Proof. 

Based on the Wolfe line search technique (13), it holds that

$${\overline{y}}_k^T{d}_k^N=y_k^T{d}_k^N+m{\alpha }_k\parallel d_k^N{\parallel }^2\ge y_k^T{d}_k^N=-(1-{\sigma }_2)g_k^T{d}_k^N=(1-{\sigma }_2){\parallel g_k\parallel }^2,$$

(24)

where the first inequality holds by the non-negativity of ${\alpha }_k$ and the last inequality holds by the sufficient descent property (9). Meanwhile, by (9) and the Cauchy–Schwartz inequality, it holds that, for $\forall k\ge 0$,

$$\parallel g_k\parallel \parallel d_k^N\parallel \ge -g_k^T{d}_k^N={\parallel g_k\parallel }^2,$$

which implies that from condition (16),

$$\parallel d_k^N\parallel \ge \parallel g_k\parallel \ge \mu ,\forall k\ge 0.$$

(25)

By the definition of ${\beta }_{k+1}^{NN}$, we obtain that

$$\begin{array}{ccc}\hfill |{\beta }_{k+1}^{NN}|& \le & max\left\{{\displaystyle \frac{\parallel g_{k+1}{\parallel }^2}{|{\overline{y}}_k^T{s}_k|}},{\displaystyle \frac{|g_{k+1}^T{\overline{y}}_k|}{|{\overline{y}}_k^T{s}_k|}}\right\}\le max\left\{{\displaystyle \frac{\parallel g_{k+1}{\parallel }^2}{m\parallel s_k{\parallel }^2}},{\displaystyle \frac{\parallel g_{k+1}\parallel \parallel {\overline{y}}_k\parallel }{m\parallel s_k{\parallel }^2}}\right\}\hfill \\ & \le & {\displaystyle \frac{\parallel g_{k+1}\parallel }{\parallel s_k\parallel }}max\left\{{\displaystyle \frac{\parallel g_{k+1}\parallel }{m\parallel s_k\parallel }},{\displaystyle \frac{L_1+m}{m}}\right\}\le {\displaystyle \frac{\parallel g_{k+1}\parallel }{\parallel s_k\parallel }}max\left\{{\displaystyle \frac{M}{m\overline{\alpha }\parallel d_k^N\parallel }},{\displaystyle \frac{L_1+m}{m}}\right\}\hfill \\ & \le & {\displaystyle \frac{\parallel g_{k+1}\parallel }{\parallel s_k\parallel }}max\left\{{\displaystyle \frac{M}{m\overline{\alpha }\parallel g_k\parallel }},{\displaystyle \frac{L_1+m}{m}}\right\}\hfill \\ & \le & {\displaystyle \frac{\parallel g_{k+1}\parallel }{\parallel s_k\parallel }}max\left\{{\displaystyle \frac{M}{m\overline{\alpha }\mu }},{\displaystyle \frac{L_1+m}{m}}\right\}:=\mathrm{\Gamma }{\displaystyle \frac{\parallel g_{k+1}\parallel }{\parallel s_k\parallel }},\hfill \end{array}$$

where the second inequality holds by (21), the third inequality holds by (22), the fourth inequality holds by the condition ${\alpha }_k\ge \alpha >0$ for all $k\ge 0$, the fifth inequality holds by (25), and the last inequality holds by the condition (16). Furthermore, we have

$$\left|{\beta }_{k+1}^{NN}{\displaystyle \frac{g_{k+1}^T{s}_k}{\parallel g_{k+1}{\parallel }^2}}\right|\le \left|{\beta }_{k+1}^{NN}\right|{\displaystyle \frac{\parallel g_{k+1}\parallel \parallel s_k\parallel }{\parallel g_{k+1}{\parallel }^2}}\le \mathrm{\Gamma }{\displaystyle \frac{\parallel g_{k+1}\parallel }{\parallel s_k\parallel }}{\displaystyle \frac{\parallel s_k\parallel }{\parallel g_{k+1}\parallel }}=\mathrm{\Gamma }.$$

By the definition of $d_k^N$ in (20) and the above discussions, it holds that

$$\begin{array}{ccc}\hfill \parallel d_{k+1}^N\parallel & \le & \parallel g_{k+1}\parallel +\left|{\beta }_{k+1}^{NN}{\displaystyle \frac{g_{k+1}^T{s}_k}{\parallel g_{k+1}{\parallel }^2}}\right|\parallel g_{k+1}\parallel +|{\parallel }_{k+1}^{NN}|\parallel s_k\parallel \hfill \\ & \le & \parallel g_{k+1}\parallel +\mathrm{\Gamma }\parallel g_{k+1}\parallel +\mathrm{\Gamma }{\displaystyle \frac{\parallel g_{k+1}\parallel }{\parallel s_k\parallel }}\parallel s_k\parallel \hfill \\ & =& (1+2\mathrm{\Gamma })\parallel g_{k+1}\parallel .\hfill \end{array}$$

With the help of (25), we conclude that

$$\parallel g_{k+1}\parallel \le \parallel d_{k+1}^N\parallel \le (1+2\mathrm{\Gamma })\parallel g_{k+1}\parallel .$$

Hence, (23) holds. This completes the proof. □

Theorem 3.

Suppose that Assumptions 1 and 2 hold. The sequences $\left\{x_k\right\}$ and $\left\{d_k^N\right\}$ are generated by Algorithm 1 with the conjugate parameter ${\beta }_k^{NN}$ and the Wolfe line search technique (13) is adopted. Then, Algorithm 1 converges in the sense of (15).

Proof. 

We prove the conclusion by contradiction and assume that there exists a positive constant $\mu$ such that (16) holds. Otherwise, Algorithm 1 converges in the sense of (15). From (9), we conclude that the new direction enjoys the sufficient descent property. Therefore, Lemma 1 holds, which implies that

$$+\infty =\sum _{k=1}^{+\infty }{\displaystyle \frac{{\mu }^2}{{(1+2\mathrm{\Gamma })}^2}}\le \sum _{k=1}^{+\infty }{\displaystyle \frac{\parallel g_k{\parallel }^2}{{(1+2\mathrm{\Gamma })}^2}}=\sum _{k=1}^{+\infty }{\displaystyle \frac{\parallel g_k{\parallel }^4}{{(1+2\mathrm{\Gamma })}^2{\parallel g_k\parallel }^2}}\le \sum _{k=1}^{+\infty }{\displaystyle \frac{{\left(g_k^T{d}_k^N\right)}^2}{\parallel d_k^N{\parallel }^2}}<+\infty ,$$

where the first inequality holds by (16), the second inequality holds by (9) and (23), and the last inequality holds by Lemma 1. However, that is a contradiction and the assumption does not hold. So, the ${lim\; inf}_{k\to +\infty }\parallel g_k\parallel =0$ holds. This completes the proof. □

4. Numerical Performance

In this section, we focus on the numerical performance of Algorithm 1 and compare it with several effective CG methods. In the experiment, we code these algorithms in Matlab 2016b and perform them on a PC computer, whose processor has AMD 2.10 GHz, RAM of 16.00 GB and the Windows 10 operating system.

4.1. Performance on Benchmark Problems

In this subsection, we check the performance of the NMHSDY method and compare it with two effective modified HS methods in [26,28] and the hybrid method in [24]. In [26], the authors proposed an effective modified HS method (MHSCG method for abbreviation) in which the conjugate parameter is

$${\beta }_{k+1}=max\{0,{\overline{\beta }}_{k+1}^{MHS}\},{\overline{\beta }}_{k+1}^{MHS}={\beta }_{k+1}^{MHS}-\lambda {\left({\displaystyle \frac{\parallel y_k\parallel {\vartheta }_k}{y_k^T{d}_k}}\right)}^2{g}_{k+1}^T{d}_k,$$

where $\lambda >1/4$ is a parameter. The direction in [26] is in the form of (3) and the corresponding method has attractive numerical performance. Dai and Kou in [28] introduced another effective class of CG schemes (DK+ method for abbreviation) depending on the parameter ${\tau }_k$, where the corresponding conjugate parameter ${\beta }_{k+1}$ is defined by

$${\beta }_{k+1}^{DK}\left({\tau }_k\right)={\beta }_{k+1}^{HS}-\left({\tau }_k+{\displaystyle \frac{\parallel y_k{\parallel }^2}{y_k^T{s}_k}}-{\displaystyle \frac{y_k^T{s}_k}{\parallel s_k{\parallel }^2}}\right){\displaystyle \frac{g_{k+1}^T{s}_k}{y_k^T{d}_k}},s_k=x_{k+1}-x_k.$$

The direction in [28] is also in the form of (3). To establish global convergence for general nonlinear functions, a truncated strategy is used, that is,

$${\beta }_{k+1}^{DK+}\left({\tau }_k\right)=max\left\{{\beta }_{k+1}^{DK}\left({\tau }_k\right),\eta {\displaystyle \frac{g_{k+1}^T{d}_k}{\parallel d_k{\parallel }^2}}\right\},$$

where $\eta \in [0,1)$ is a parameter. The numerical results indicated the DK+ method has good and reliable numerical performance. Dai and Yuan, in [24], proposed an effective hybrid CG method (HSDY method for abbreviation) in which the conjugate parameter is

$${\beta }_{k+1}=max\{0,min\{{\beta }_{k+1}^{DY},{\beta }_{k+1}^{HS}\}\}.$$

The hybrid method also has global convergence and attractive numerical performance.

In the following, we focus on the numerical performance and the large-scale unconstrained problems in Table 1 (see [38] for details). In order to improve numerical performance, Andrei, in [39], proposed an accelerated strategy which modified the step in a multiplicative manner. In this part, we also utilize this strategy and regard Algorithm 1 with the accelerated strategy as Algorithm 1. To compare the conjugate parameters and the search directions fairly, here we adopt the Wolfe line search technique (13) for all methods.

Table 1. The test problems.

No.	Problem	No.	Problem
1	Extended Freudenstein and Roth Function	32	ARWHEAD (CUTE)
2	Extended Trigonometric Function	33	NONDIA (Shanno-78) (CUTE)
3	Extended Rosenbrock Function	34	DQDRTIC (CUTE)
4	Extended Beale Function	35	EG2 (CUTE)
5	Extended Penalty Function	36	DIXMAANA (CUTE)
6	Perturbed Quadratic Function	37	DIXMAANB (CUTE)
7	Raydan 1 Function	38	DIXMAANC (CUTE)
8	Raydan 2 Function	39	DIXMAANE (CUTE)
9	Diagonal 3 Function	40	Broyden Tridiagonal
10	Generalized Tridiagonal-1 Function	41	Almost Perturbed Quadratic
11	Extended Tridiagonal-1 Function	42	Tridiagonal Perturbed Quadratic
12	Extended Three Exponential Terms	43	EDENSCH Function (CUTE)
13	Generalized Tridiagonal-2	44	VARDIM Function (CUTE)
14	Diagonal 4 Function	45	LIARWHD (CUTE)
15	Diagonal 5 Function	46	DIAGONAL 6
16	Extended Himmelblau Function	47	DIXMAANF (CUTE)
17	Generalized PSC1 Function	48	DIXMAANG (CUTE)
18	Extended PSC1 Function	49	DIXMAANH (CUTE)
19	Extended Powell Function	50	DIXMAANI (CUTE)
20	Extended Cliff Function	51	DIXMAANJ (CUTE)
21	Quadratic Diagonal Perturbed Function	52	DIXMAANK (CUTE)
22	Extended Wood Function	53	DIXMAANL (CUTE)
23	Extended Hiebert Function	54	DIXMAAND (CUTE)
24	Quadratic Function QF1	55	ENGVAL1 (CUTE)
25	Extended Quadratic Penalty QP1 Function	56	COSINE (CUTE)
26	Extended Quadratic Penalty QP2 Function	57	Extended DENSCHNB (CUTE)
27	A Quadratic Function QF2 Function	58	Extended DENSCHNF (CUTE)
28	Extended EP1 Function	59	SINQUAD (CUTE)
29	Extended Tridiagonal-2 Function	60	Scaled Quadratic SQ1
30	BDQRTIC (CUTE)	61	Scaled Quadratic SQ2
31	TRIDIA (CUTE)

In the experiment, for each problem we consider nine large-scale dimensions with 300, 600, 900, 3000, 6000, 9000, 30,000, 60,000 and 90,000 variables. The parameters used in the Wolfe line search are ${\sigma }_1=0.20$ and ${\sigma }_2=0.85$. The other parameters for the MHSCG method and the DK+ method are as default.

During the progress, the Himmeblau stopping rule is adopted: if $|f\left(x_k\right)|>{\epsilon }_1$, let $stop1={\displaystyle \frac{|f\left(x_k\right)-f\left(x_{k+1}\right)|}{\left|f\right(x_k\left)\right|}}$, otherwise, $stop1=|f\left(x_k\right)-f\left(x_{k-1}\right)|$. If the conditions $\parallel g_k\parallel \le \epsilon$ or $stop1\le {\epsilon }_2$ are satisfied, then the progress is stopped, where the values of parameters $\epsilon$, ${\epsilon }_1$, and ${\epsilon }_2$ are $\epsilon ={10}^{-6}$, and ${\epsilon }_1={\epsilon }_2={10}^{-5}$. Meanwhile, we also stop the algorithm when the number of iterations is greater than 5000.

In order to present the performances of methods more intuitively, the tool in [40] is adopted to analyze the profiles of these methods. Robustness and efficiency rates are readable on the right and left vertical axes of the corresponding performance profiles, respectively. To present a detailed numerical comparison, two different scales have been considered for the $\tau$-axis. One is $\tau \in [1,1.5]$, which shows what happens for the values of $\tau$ near to 1. The other is used to present the trend for large values of $\tau$. In Figure 1, Figure 2 and Figure 3, we, respectively, show the performance of these methods relative to the number of iterations ($NI$), the number of function-gradient valuations ($NFG$; which is the sum of the number of function valuations and gradient valuations), and the CPU time consumed in seconds.

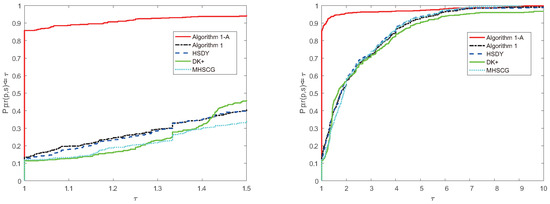
Figure 1. Performance profiles of the methods in the number of iterations case.

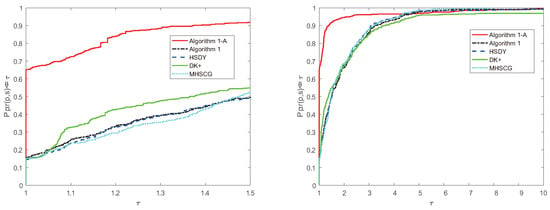
Figure 2. Performance profiles of the methods in the function and gradient case.

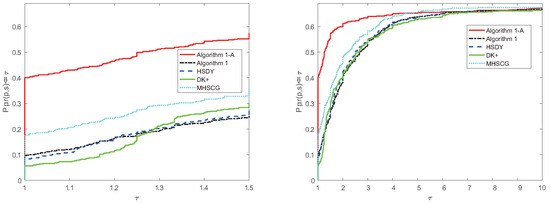
Figure 3. Performance profiles of the methods in the CPU time consumed case.

From Figure 1, Figure 2 and Figure 3, we have that Algorithm 1 is comparable and a little more effective than the HSDY method, the DK+ method, and the MHSCG method for the above problems. Meanwhile, Algorithm 1, with the accelerated strategy, is much effective and performs best in the experiment, which indicates that the accelerated technique indeed works and reduces the number of iterations and the number of function and gradient evaluations.

4.2. Comparison for Stability

In this subsection, we consider the numerical stability of Algorithm 1 for the ill-conditioned matrix problems and compare it with the MHSCG method in [26]. In fact, the quadratic objective function $f\left(x\right)=x^T\mathcal{I}x$ of (1) is ill-conditioned if matrix $\mathcal{I}\in {\mathbb{R}}^{n\times n}$ is in the form

$${\mathcal{I}}_{i,j}={\displaystyle \frac{1}{i+j-1}},i,j=1,2,\dots ,n.$$

It is clear that the matrix $\mathcal{I}$ is ill-conditioned and positive definite [41], with different dimensions $n=5,6,\dots ,50$. Furthermore, the authors in [42] show that the ${\ell }_{\infty }$ norm condition number of the Hessian matrix $\mathcal{I}$ gradually increases from $9.4366\times {10}^5$ for $n=5$ to $6.9007\times {10}^{20}$ for $n=50$. In the following, we explore the numerical performance. The experimental environment, the parameter values, and the stop rule remain the same as in the above subsection. Meanwhile, the initial point is selected as $x_0=(10,10,\cdots ,10)$. The corresponding numerical results are presented in Table 2 and Table 3, in which $Dim$ is the dimension of x, $NI$ means the number of iterations, $NFG$ is the sum of the number of function and gradient evaluations, $Time$ means the CPU time consumed in seconds, and $f^{*}$ denotes the optimal function obtained by the methods.

Table 2. Numerical results of the MHSCG method and Algorithm 1 in 5–40 dimensions.

	MHSCG Method				Algorithm 1
Dim	NI	NFG	Time	${\mathit{f}}^{*}$	NI	NFG	Time	${\mathit{f}}^{*}$
5	5	22	0.000000	0.000000	5	22	0.000000	0.000000
6	13	48	0.031250	0.000000	13	48	0.000000	0.000000
7	21	72	0.000000	0.000000	21	72	0.000000	0.000000
8	21	72	0.000000	0.000000	21	72	0.015625	0.000000
9	27	92	0.000000	0.000006	24	82	0.000000	0.000000
10	41	143	0.000000	0.000007	29	97	0.000000	0.000000
11	75	246	0.000000	0.000009	55	192	0.000000	0.000000
12	58	203	0.000000	0.000003	70	249	0.000000	0.000008
13	57	190	0.000000	0.000004	70	246	0.000000	0.000000
14	86	276	0.031250	0.000008	123	429	0.000000	0.000000
15	75	264	0.031250	0.000009	89	314	0.000000	0.000009
16	98	330	0.000000	0.000008	52	177	0.000000	0.000001
17	24	82	0.000000	0.000002	66	232	0.000000	0.000002
18	65	215	0.031250	0.000009	28	97	0.000000	0.000000
19	31	105	0.000000	0.000007	27	94	0.000000	0.000000
20	111	373	0.031250	0.000009	131	452	0.000000	0.000010
21	117	379	0.031250	0.000008	31	108	0.000000	0.000000
22	96	333	0.000000	0.000010	66	236	0.000000	0.000000
23	68	233	0.000000	0.000009	85	303	0.031250	0.000000
24	50	175	0.031250	0.000000	43	151	0.000000	0.000000
25	96	318	0.000000	0.000009	103	377	0.000000	0.000000
26	113	370	0.000000	0.000009	112	410	0.000000	0.000004
27	22	78	0.000000	0.000000	129	473	0.031250	0.000001
28	104	372	0.000000	0.000009	24	87	0.000000	0.000000
29	156	513	0.000000	0.000010	130	449	0.000000	0.000001
30	54	185	0.000000	0.000001	121	446	0.000000	0.000007
31	39	144	0.000000	0.000003	97	341	0.000000	0.000008
32	26	97	0.000000	0.000001	79	292	0.031250	0.000001
33	87	309	0.000000	0.000010	66	234	0.031250	0.000002
34	58	213	0.000000	0.000006	60	217	0.031250	0.000000
35	97	327	0.000000	0.000009	25	95	0.000000	0.000002
36	24	86	0.000000	0.000000	132	481	0.000000	0.000003
37	23	84	0.000000	0.000004	55	192	0.000000	0.000001
38	93	312	0.046875	0.000010	40	142	0.000000	0.000003
39	148	487	0.046875	0.000005	124	442	0.140625	0.000010
40	66	231	0.000000	0.000007	136	496	0.031250	0.000007

Table 3. Numerical results of the MHSCG method and Algorithm 1 in 41–50 dimensions.

	MHSCG Method				Algorithm 1
Dim	NI	NFG	Time	${\mathit{f}}^{*}$	NI	NFG	Time	${\mathit{f}}^{*}$
41	76	267	0.031250	0.000005	65	239	0.000000	0.000005
42	130	438	0.046875	0.000008	85	302	0.000000	0.000010
43	164	546	0.031250	0.000009	136	488	0.000000	0.000009
44	184	594	0.031250	0.000007	29	103	0.000000	0.000006
45	17	64	0.000000	0.000000	17	64	0.000000	0.000000
46	155	519	0.031250	0.000010	62	222	0.000000	0.000000
47	123	421	0.031250	0.000010	107	379	0.031250	0.000010
48	20	74	0.000000	0.000000	68	250	0.015625	0.000010
49	135	473	0.031250	0.000010	102	375	0.031250	0.000010
50	178	594	0.062500	0.000010	151	542	0.031250	0.000009

From Table 2 and Table 3, it can be found that for the dimensions from 5 to 50, Algorithm 1 and the MHSCG method successfully solve all of them and obtain reasonable optimal function values, which are all not greater than ${10}^{-5}$. For most problems, Algorithm 1 needed fewer iterations and function and gradient evaluations and obtained better optimal values. In order to show numerical performance intuitively, here we also adopt the performance profiles in [40] for the NI and NFG cases. The corresponding performance profiles are given in Figure 4 and Figure 5.

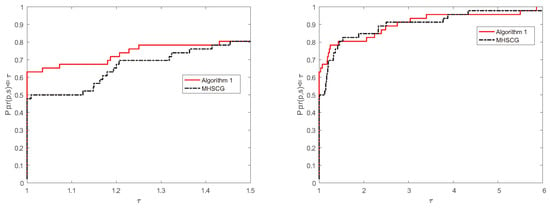
Figure 4. Performance profiles of Algorithm 1 and the MHSCG method in NI case.

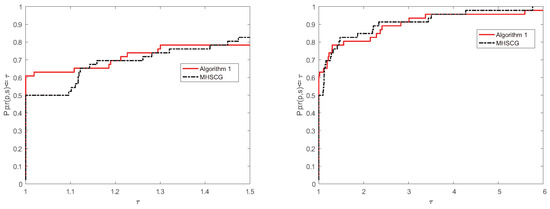
Figure 5. Performance profiles of Algorithm 1 and the MHSCG method in NFG case.

Figure 4 shows that Algorithm 1 and the MHSCG method solve these testing problems with the least total number of iterations in 63% and 48% of cases, respectively. Figure 5 indicates that Algorithm 1 and the MHSCG method solve these testing problems with the least total number of function and gradient evaluations in 61% and 50% of cases, respectively. All in all, the numerical results show that Algorithm 1 is more effective and stable than the MHSCG method for these ill-conditioned matrix problems.

4.3. Application to Image Restoration

In this subsection, we apply Algorithm 1 to some image restoration problems [43,44,45]. During the process, the normal Wolfe line search technique is adopted, the corresponding parameters remain unchanged, and two noise level cases for the Barbara.png ($512\times 512$) and Baboon.bmp ($512\times 512$) images are considered. In this part, we stop the process when the following criteria are both satisfied:

$${\displaystyle \frac{|f\left(x_{k+1}\right)-f\left(x_k\right)|}{\left|f\right(x_k\left)\right|}}<{10}^{-3},\parallel g\left(x_k\right)\parallel <{10}^{-3}(1+|f\left(x_k\right)\left|\right).$$

Meanwhile, to assess the restoration performance qualitatively, we also utilize the peak signal to noise ratio [45] (PSNR), which is defined by $PSNR=10{log}_{10}{\displaystyle \frac{{255}^2}{\frac{1}{M\times N}{\sum }_{i,j}{(u_{i,j}^r-u_{i,j}^{*})}^2}},$ where M and N are the true image pixels, and $u_{i,j}^r$ and $u_{i,j}^{*}$ denote the pixel values of the restored image and the original image, respectively. For the noise level, we consider two cases: $20\%$ (a low-level case) and $60\%$ (a high-level case). The consumed CPU time and the corresponding PSNR values are given in Table 4. Meanwhile, the detailed performances are presented in Figure 6 and Figure 7, respectively.

Table 4. Test results for Algorithm 1 and the MHSCG method.

		Algorithm 1		MHSCG Method
Image	Noise Level	PSNR	CPU Time	PSNR	CPU Time
Barbara	$20\%$	29.6638	2.265625	29.5831	2.578125
Baboon	$20\%$	27.9223	2.609375	27.8455	3.250000
Barbara	$60\%$	23.1256	3.593750	23.1103	3.765625
Baboon	$60\%$	21.1836	3.484375	21.1582	3.671875

Figure 6. The noisy Barbara image, corrupted by salt-and pepper noise (the first column); the images restored via Algorithm 1 (the second column), and via the MHSCG method (the third column).

Figure 7. The noisy Baboon image, corrupted by salt-and pepper noise (the first column); the images restored via Algorithm 1 (the second column), and via the MHSCG method (the third column).

From Table 4 and Figure 6 and Figure 7, we have that Algorithm 1 and the MHSCG method can all solve the image restoration problems successfully within a suitable time, and Algorithm 1 seems to perform a little better than the MHSCG method.

5. Conclusions

Conjugate gradient methods are attractive and effective for large-scale unconstrained optimization smooth problems due to their simple computation and low memory requirements. The Dai–Yuan conjugate gradient method has good theoretical properties and generates a descent direction in each iteration. Whereas, the Hestenes–Stiefel conjugate gradient method automatically satisfies the conjugate condition $y_k^T{d}_{k+1}=0$ without any line search technique and performs well in practice. By the above discussions, we propose a new descent hybrid conjugate gradient method. The proposed method has a sufficient descent property independent of any line search technique. Under some mild conditions, the proposed method is globally convergent. In the experiments, we first consider 61 unconstrained problems with 9 different dimensions up to $90,000$. Thereafter, 46 ill-conditioned matrix problems are also tested. The primary numerical results show that the proposed method is more effective and stable. Finally, we apply the hybrid method to some image restoration problems. The results indicate our method is attractive and reliable.