Hierarchical Learning-Enhanced Chaotic Crayfish Optimization Algorithm: Improving Extreme Learning Machine Diagnostics in Breast Cancer

Abstract

Extreme learning machines (ELMs), single hidden-layer feedforward neural networks, are renowned for their speed and efficiency in classification and regression tasks. However, their generalization ability is often undermined by the random generation of hidden layer weights and biases. To address this issue, this paper introduces a Hierarchical Learning-based Chaotic Crayfish Optimization Algorithm (HLCCOA) aimed at enhancing the generalization ability of ELMs. Initially, to resolve the problems of slow search speed and premature convergence typical of traditional crayfish optimization algorithms (COAs), the HLCCOA utilizes chaotic sequences for population position initialization. The ergodicity of chaos is leveraged to boost population diversity, laying the groundwork for effective global search efforts. Additionally, a hierarchical learning mechanism encourages under-performing individuals to engage in extensive cross-layer learning for enhanced global exploration, while top performers directly learn from elite individuals at the highest layer to improve their local exploitation abilities. Rigorous testing with CEC2019 and CEC2022 suites shows the HLCCOA’s superiority over both the original COA and nine renowned heuristic algorithms. Ultimately, the HLCCOA-optimized extreme learning machine model, the HLCCOA-ELM, exhibits superior performance over reported benchmark models in terms of accuracy, sensitivity, and specificity for UCI breast cancer diagnosis, underscoring the HLCCOA’s practicality and robustness, as well as the HLCCOA-ELM’s commendable generalization performance.

1. Introduction

In recent years, owing to the escalating complexity in problem-solving and the increasing uncertainties in final outcomes, there has been a marked rise in the demand for efficient optimization algorithms. These algorithms can be broadly categorized into two groups, i.e., deterministic algorithms and stochastic intelligent algorithms [1]. Deterministic algorithms are suitable for problems with a clear and unchanging pathway to the solution, whereas stochastic intelligent algorithms are better equipped for highly complex and ambiguous problems, iteratively approaching or attaining optimal solutions [2]. Among them, one type of stochastic intelligent algorithm, known as the meta-heuristic algorithm, has seen widespread application across numerous scientific fields, such as engineering [3,4], economics [5], computer science [6], and so on [7].

Their nature- and society-inspired mechanisms aim to avoid local optima, demonstrating the broad application potential of meta-heuristic algorithms when combined with neural networks. For instance, ref. [8] utilizes artificial neural networks to predict the heat transfer performance and pressure drop in a horizontal tube with twisted-tape inserts and employs a multi-objective genetic algorithm to find the Pareto optimal front for heat transfer efficiency and friction factors, thereby optimizing design parameters. Ref. [9] describes the adjustment of hyperparameters in long short-term memory (LSTM) networks using an improved reptile search algorithm (RSA) to enhance the efficiency of wind power generation forecasting. Ref. [10] discusses the application of the seagull optimization and particle swarm algorithm in optimizing the structural framework of convolutional neural networks (CNNs) for accurate cancer region detection in oral images. Ref. [11] uses an evolutionary crow search algorithm with adaptive flight length and interactive memory mechanisms to effectively overcome the local minima problem in multilayer perceptrons, successfully applying it to feature detection in diseases such as COVID-19, diabetes, breast cancer, and cardiovascular diseases.

Furthermore, based on the objects and methods they emulate [7,12,13], meta-heuristic algorithms can be roughly divided into four categories, as illustrated in Figure 1, i.e., evolution-based, physics-based, human-based, and swarm-based algorithms.

Evolution-based algorithms draw inspiration from Darwin’s and Mendel’s theories of natural evolution by simulating the selection and reproduction processes of biological entities within their environment. Some of the most popular algorithms include the genetic algorithm (GA) [14], differential evolution (DE) [15,16], evolutionary mating algorithm (EMA) [17], arithmetic optimization algorithm (AOA) [18], and genetic programming (GP) [19]. Physics-based optimization algorithms mimic rules and phenomena observed within physical systems. Some of the most widely accepted algorithms include the electrostatic discharge algorithm (ESDA) [20], multi-verse optimizer (MVO) [21], Henry gas solubility optimization (HGSO) [22], and nuclear reaction optimization (NRO) [23]. Human-based algorithms attempt to construct global optimization mechanisms by utilizing characteristics of human social and cognitive activities. Some of the most typical algorithms include teaching–learning-based optimization (TLBO) [24], student psychology-based optimization (SPBO) [25], league championship algorithm (LCA) [26], and imperialist competitive algorithm (ICA) [27]. Additionally, swarm-based algorithms aim to emulate the foraging behaviors and movement characteristics of biological swarms. The most popular algorithms are particle swarm optimization (PSO) [28], whale optimization algorithm (WOA) [12], gray wolf optimizer (GWO) [29], cheetah optimization algorithm (CO) [30], grasshopper optimization algorithm (GOA) [31], salp swarm algorithm (SSA) [32], gorilla troops optimizer (GTO) [33], artificial hummingbird algorithm (AHA) [34], prairie dog optimization (PDO) [35], sparrow search algorithm combining sine–cosine and Cauchy mutation (SCSSA) [36], and the recently developed crayfish optimization algorithm (COA) [37].

The COA introduces a creative approach by simulating the survival strategies of crayfish in nature, including foraging, summer resort, and competition [37]. This algorithm modulates crayfish behavior patterns by adjusting environmental temperature parameters and quantifies foraging effectiveness through the amount of food consumed. In high-temperature environments, crayfish tend to engage in competitive or summer resort behaviors, corresponding to the exploration phase. Conversely, in suitable temperate conditions, crayfish become active and enter a foraging mode, denoting the exploitation phase. Therefore, due to these biomimetic characteristics, the COA is effective in solving constrained engineering design problems. However, the COA does exhibit limitations, notably its lack of learning mechanisms for individuals other than the optimal exemplar, leading to reduced population diversity. This limitation leads to poor convergence and inadequate exploratory capabilities when dealing with high-dimensional and complex non-convex problems, resulting in premature convergence issues.

In designing meta-heuristic algorithms, balancing exploration and exploitation is crucial [38,39]. Effective exploration is essential to cover the search space and identify potential optimal regions. Thorough exploitation of these regions is necessary to facilitate rapid convergence to the global optimum. However, insufficient exploration can reduce search diversity, leading to entrapment in local optima, while inadequate exploitation may prevent accurate localization of the optimal solution. Additionally, the integration of special chaotic sequences has been shown to enhance global search performance beyond what is achievable with purely random methods, as reported in refs. [11,14]. Chaotic motion facilitates the traversal of every state around the attractors, allowing meta-heuristic algorithms to explore more extensively and avoid local optima. For example, the niching chaotic optimization algorithm (NCOA) [15] and concepts of chaotic evolution (CE) [16,17] utilize the rapid mixing properties of chaos to spread more effectively across the search spaces, facilitating faster convergence to optimal solutions. Relying solely on pseudo-random sequences from chaos maps for initializing population positions can enhance optimization performance, as demonstrated by the particle swarm optimization with chaos-based initialization [40] and the multi-strategy boosted hybrid artificial hummingbird algorithm (LCAHA), which combines Lévy flight and a sinusoidal chaotic map [41].

Moreover, although the COA exhibits innovative biomimetic features, its over-reliance on foraging in elite individuals, while also lacking inter-group learning and competitive behavior, reduces its population diversity. Furthermore, the “No Free Lunch” theorem [42,43] posits that no single algorithm can effectively solve all types of optimization problem, which underscores the necessity for continual innovation. Indeed, the complexity and difficulty of modern engineering optimization are increasing, with problems often being non-separable, non-convex, highly parameter-dependent, and having extensive search domains [41]. When faced with such engineering optimization challenges, most meta-heuristic algorithms may encounter performance degradation or insufficient convergence, underscoring the need for ongoing development of tailored improvement strategies for different engineering requirements [44]. Motivated by the four factors mentioned above, this paper seeks to employ a novel population update strategy aimed at enhancing the effectiveness of the COA in solving complex and practical optimization problems.

This paper proposes a novel Hierarchical Learning-based Chaotic Crayfish Optimization Algorithm (HLCCOA). Initially, to maintain population diversity and avoid premature convergence, the Tent and Chebyshev mapping initialization strategy is presented. It utilizes the ergodicity and pseudo-random characteristics of chaos to expand the initial solutions across the entire solution space, thereby enhancing the early global search ability through a higher-quality initial population. Additionally, to balance the exploration and exploitation abilities of the algorithm, a hierarchical learning mechanism is integrated into COA, which not only enhances population diversity but also assists in escaping local optima. The novelties and primary contributions of the HLCCOA are as follows:

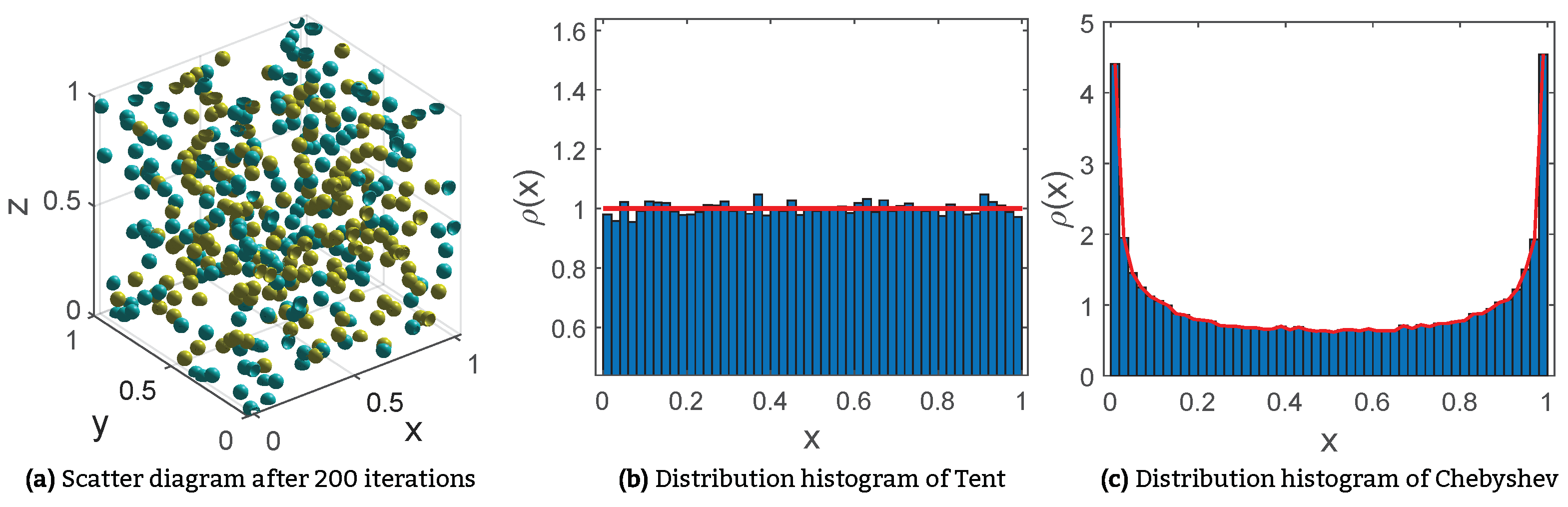
• Tent and Chebyshev maps are integrated into the HLCCOA for initializing the population, laying the foundation for subsequent global exploration by obtaining a high-quality initial population.
• A hierarchical learning mechanism is incorporated into the HLCCOA, which accelerates the convergence rate and improves the precision of optimization by strengthening the learning from exemplary individuals in each layer of the population.
• Comprehensive numerical experiments are designed. The HLCCOA is compared and analyzed against nine popular existing meta-heuristic optimization algorithms using the CEC2019 and CEC2022 suites, yielding favorable experimental results.
• An HLCCOA-ELM model for breast cancer diagnosis improves training by optimizing parameters to overcome local optima and raises accuracy, demonstrating the HLCCOA-ELM’s strong generalization performance.

The structure of this paper is outlined as follows. Section 2 briefly reviews COA’s theoretical aspects. Section 3 elaborates on the algorithmic design and structure of the HLCCOA. Section 4 presents and analyzes experimental results. Section 5 focuses on the HLCCOA-ELM model for breast cancer diagnosis, including experimental analysis and discussion. Finally, Section 6 points out conclusions and potential directions for future research.

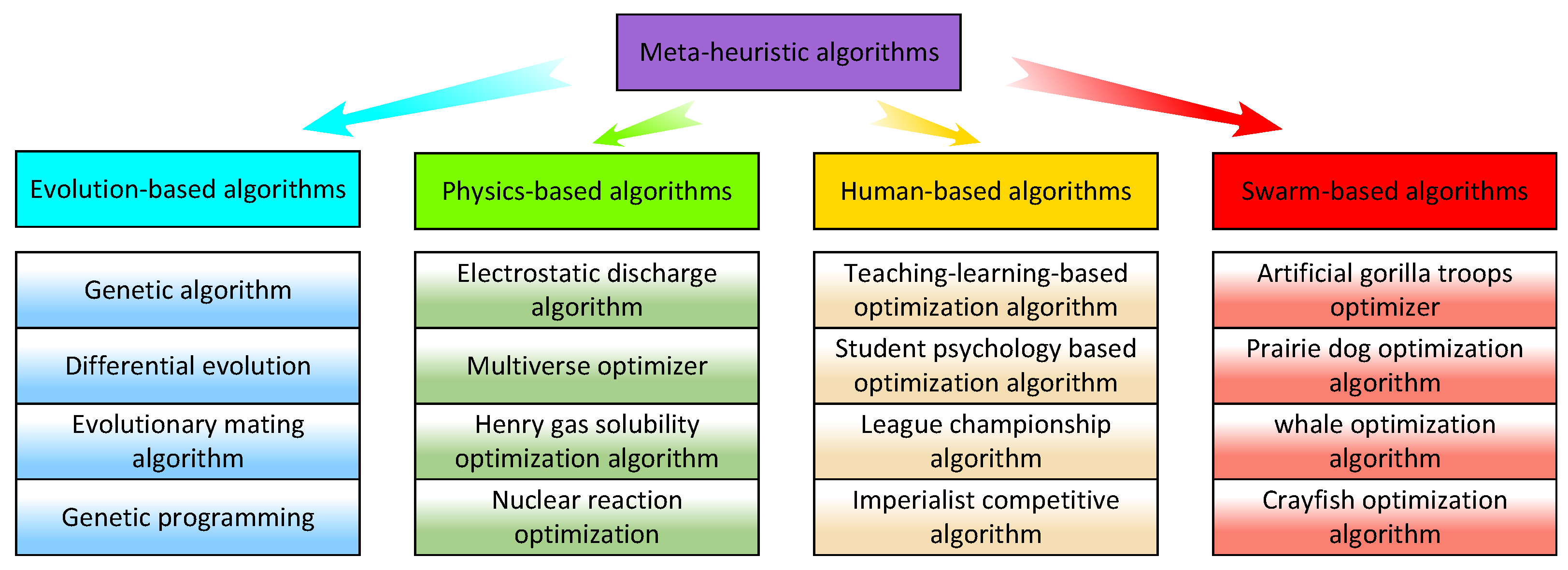
2. Crayfish Optimization Algorithm

The crayfish optimization algorithm is inspired by the foraging, summer resort, and competitive behaviors of crayfish [37,45]. The growth rate of crayfish is influenced by changes in environmental temperature, indicating that temperature plays a significant role in their survival and behavioral patterns [46].

The definition of temperature is as shown in Equation (1), where $temp$ represents the temperature of the crayfish’s environment. When the $temp$ exceeds 30 °C, crayfish seek cooler places for shelter. When the $temp <$ 30 °C, crayfish engage in foraging behavior. Additionally, the food intake of crayfish approximates a normal distribution in response to changes in environmental temperature, as modeled in Equation (2). Notably, crayfish exhibit strong foraging behavior in temperatures ranging from 20 °C to 30 °C. A schematic representation of crayfish food intake is illustrated in Figure 2.

$$temp=rand\times 15+20$$

(1)

$$p=C_1·\left({\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}·\exp \left(-{\displaystyle \frac{{(temp-\mu )}^2}{2{\sigma }^2}}\right)\right),$$

(2)

where $\mu$ denotes the optimal temperature for crayfish growth, and $\sigma$ and $C_1$ are used to regulate the crayfish’s food intake at different temperatures.

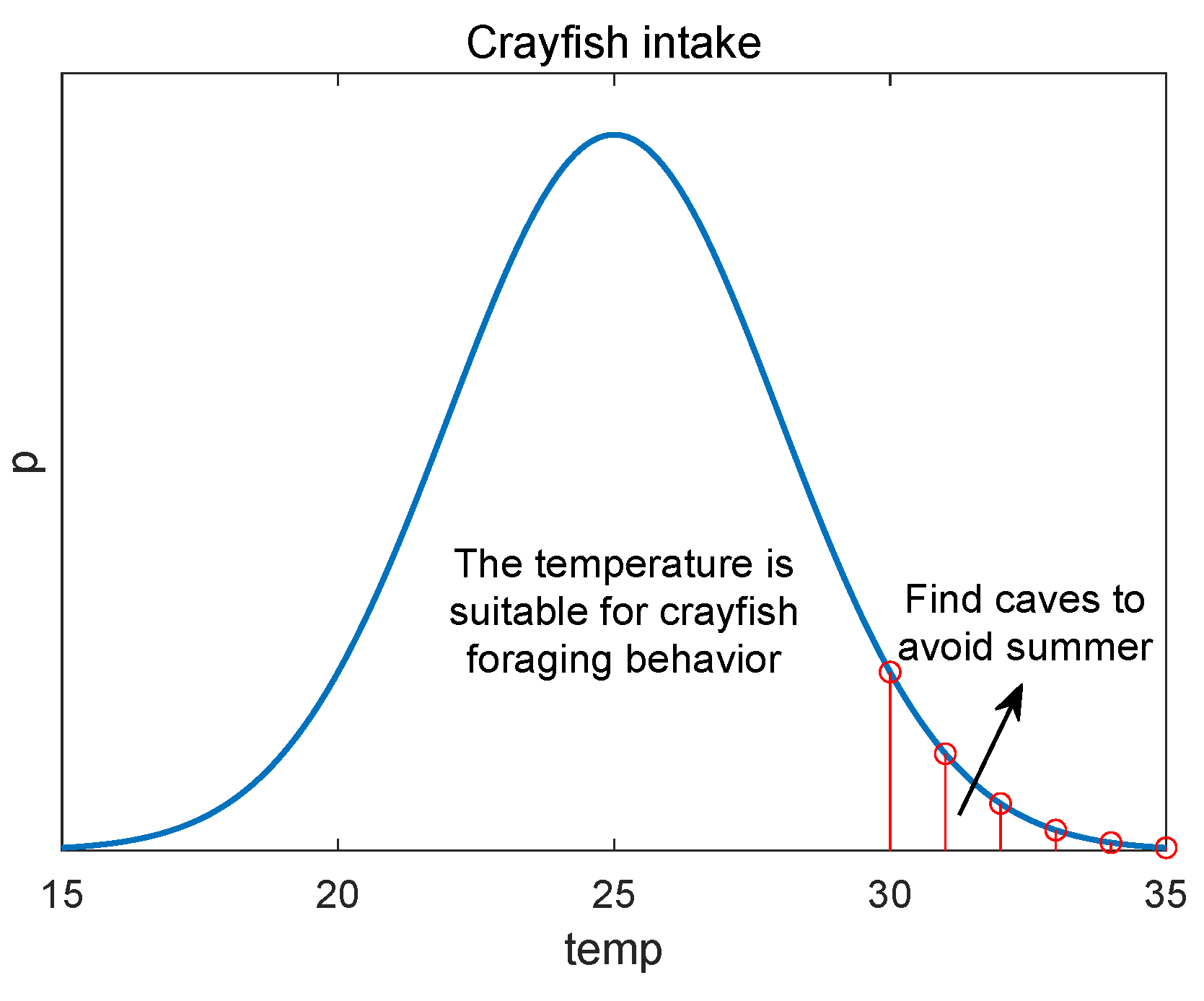
2.1. Summer Resort Pattern of Crayfish

When $temp>30$, it indicates that temperature is too high, and crayfish enter the summer resort pattern. The updated formula for the target shelter cave $X_{shade}$ is defined as in Equation (3):

$$X_{shade}=(X_{G1}+X_{G2})/\phantom{(X_{G1}+X_{G2})2}2,$$

(3)

where $X_{G1}$ represents the best position achieved so far, and $X_{G2}$ signifies the optimal position generated under the present motion state of the population. If $rand<0.5$, it suggests an absence of shelter competition, enabling direct shelter entry for crayfish to evade summer, utilizing Equation (4) for this process:

$$X_i^{It+1}=X_i^{It}+C_2·rand·(X_{shade}-X_i^{It}),$$

(4)

where $X_i^{It}$ represents the position of the i-th crayfish at the current iteration number, and $X_i^{It+1}$ denotes the position of the ($i+1$)-th crayfish at the next generation’s iteration number. Additionally, $C_2$ is a decreasing coefficient, as shown in Equation (5):

$$C_2=2-(It/Ma\mathit{x\_I}teration),$$

(5)

where $Ma\mathit{x\_I}teration$ represents the maximum number of iterations.

2.2. Competition Pattern of Crayfish

When $temp<$ 30 °C and $rand\ge 0.5$, it implies that multiple crayfish are interested in the same shelter. At this point, they compete for shelter according to Equation (6):

$$X_i^{It+1}=X_i^{It}-X_z^{It}+X_{shade},$$

(6)

where z represents a random individual crayfish, as shown in Equation (7):

$$z=round(rand·(N-1\left)\right)+1.$$

(7)

During the competition pattern, crayfish vie with each other, where crayfish $X_i$ adjusts its position according to the position of another crayfish $X_z$. Through the competition process among crayfish, the search range of COA is expanded.

2.3. Foraging Pattern of Crayfish

When $temp<$ 30 °C, it is suitable for crayfish to forage. Upon foraging, crayfish assess the size of the food. If the food is too large, crayfish use their claws to tear it apart, alternating feeding with their second and third legs. In this case, the position of the target food is defined as:

$$X_{food}=X_{G1}.$$

(8)

The size of food is defined as in Equation (9):

$$Q=C_3·rand·\left(fitnes{s}_i/\phantom{fitnes{s}_{i}fitnes{s}_{food}}fitnes{s}_{food}\right),$$

(9)

where $C_3$ is the food factor representing the maximum size of the food, typically set at 3; $fitnes{s}_i$ denotes the fitness value of the ith crayfish; and $fitnes{s}_{food}$ represents the fitness value of the target food position. When $Q>(C_3+1)/2$, it signifies that the food is too large, and the crayfish use their claws to tear the food. The corresponding mathematical equation is defined as in Equation (10):

$$X_{food}=\exp (-{\displaystyle \frac{1}{Q}})\times X_{food}.$$

(10)

After shredding the food into smaller pieces, crayfish alternately use their second and third legs to eat food. The simulation of this process uses a combination of sine and cosine functions. The captured food quantity also depends on the food intake of crayfish p, as described by Equation (11):

$$X_i^{It+1}=X_i^{It}+X_{food}·p·(\cos (2\pi ·rand)-\sin (2\pi ·rand)).$$

(11)

When $Q\le (C_3+1)/2$, it indicates that the food is not too big, allowing the crayfish to move directly towards the food. This process is expressed as in Equation (12):

$$X_i^{It+1}=(X_i^{It}-X_{food})·p+p·rand·X_i^{It}.$$

(12)

During the foraging pattern, crayfish adopt appropriate forging strategies based on the size of the encountered food Q.

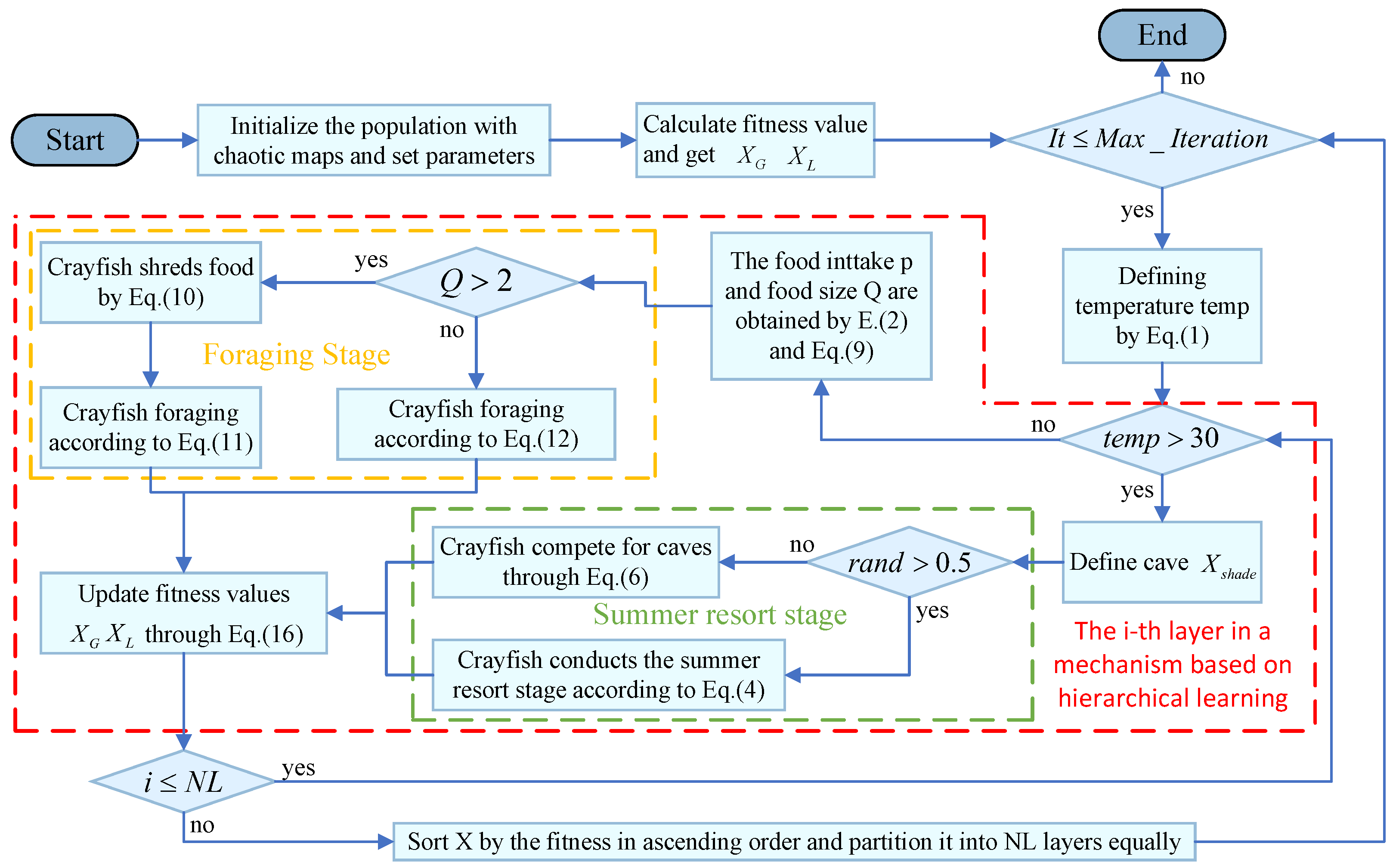
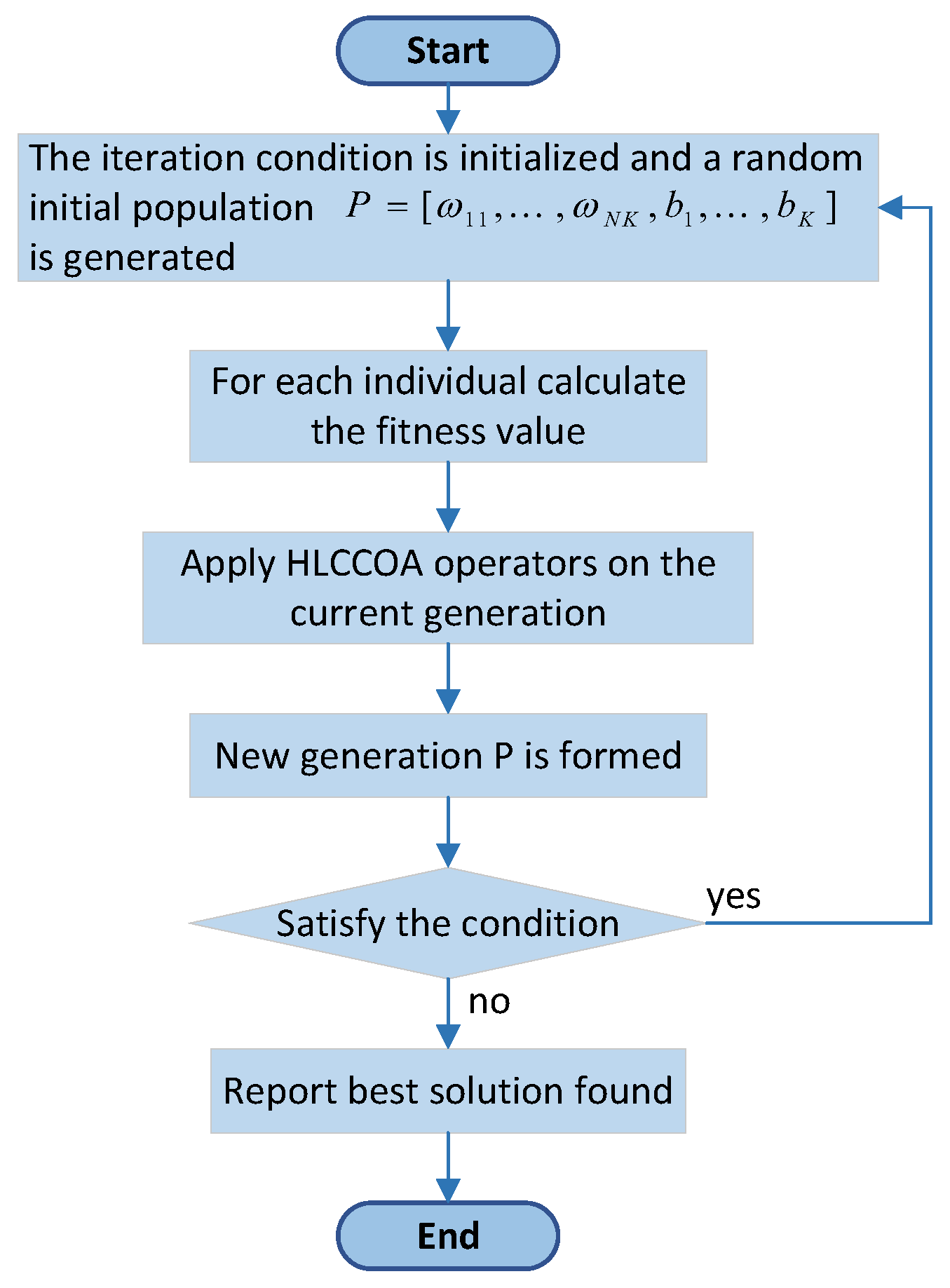
3. Hierarchical Learning-Based Chaotic Crayfish Optimization Algorithm

3.1. Chaotic Map

Chaos is a kind of nonlinear deterministic system, characterized by its extreme sensitivity to initial conditions, ergodicity, and pseudo-randomness, making it impractical for long-term predictions [47,48]. Recent studies have shown that certain chaotic systems with strong spatial ergodicity can exhibit relatively rapid search performance in exploring global optima [49,50]. Search strategies based on chaotic motion, as opposed to primarily probability-based random searches, can execute a more effective comprehensive search of the solution space [41,51]. This study introduces two types of chaotic maps with excellent ergodic properties, i.e., the Tent and Chebyshev maps, defined as follows.

The equation for the Tent map is given as follows in Equation (13):

$$y(t+1)=\left\{\begin{array}{cc}y\left(t\right)/\gamma & 0<y\left(t\right)<\gamma \\ (1-y(t\left)\right)/(1-\gamma )& \gamma <y\left(t\right)<1.\end{array}\right.$$

(13)

The equation for the Chebyshev map is as shown in Equation (14):

$$y(t+1)=\cos \left(k{\cos }^{-1}y\left(t\right)\right),$$

(14)

where t denotes the iteration number in chaotic map; $y\left(t\right)$ represents the chaotic value at the t-th iteration; $\gamma$ is the control parameter for the Tent map, ranging from 0 to 1; and k serves as the control parameter for the Chebyshev map, with its value range being $(0,+\infty )$. When $\gamma =0.4$ and $k=5$, the Lyapunov exponents of these two dynamic systems are 3.6247 and 1.6101, respectively, both of which are positive, indicating their entry into a chaotic state. Figure 3a presents a three-dimensional scatter diagram of chaotic sequences generated after 200 iterations of the Tent map (indicated by yellow points) and the Chebyshev map (indicated by cyan points). Figure 3b and Figure 3c respectively display the distribution histograms for the sequence points of the Tent and Chebyshev maps. Observations of the scatter diagram reveal that both chaotic maps exhibit outstanding spatial-filling characteristics, with their generated points nearly covering the entire spatial region. Moreover, the distributions in the histograms also illustrate the ability of the Tent and Chebyshev maps to effectively sample the space with varying degrees of probabilistic randomness during their exploration.

In the HLCCOA, the crayfish population is bifurcated into two distinct groups. The first leverages the Tent map for a uniform distribution across the search space, bolstering global exploration. The second utilizes the Chebyshev map for strategic boundary positioning, enhancing extreme value detection. This dual-strategy initialization ensures efficient boundary exploration of the solution space at the beginning and subsequent concentration on deep potential optima within the core area.

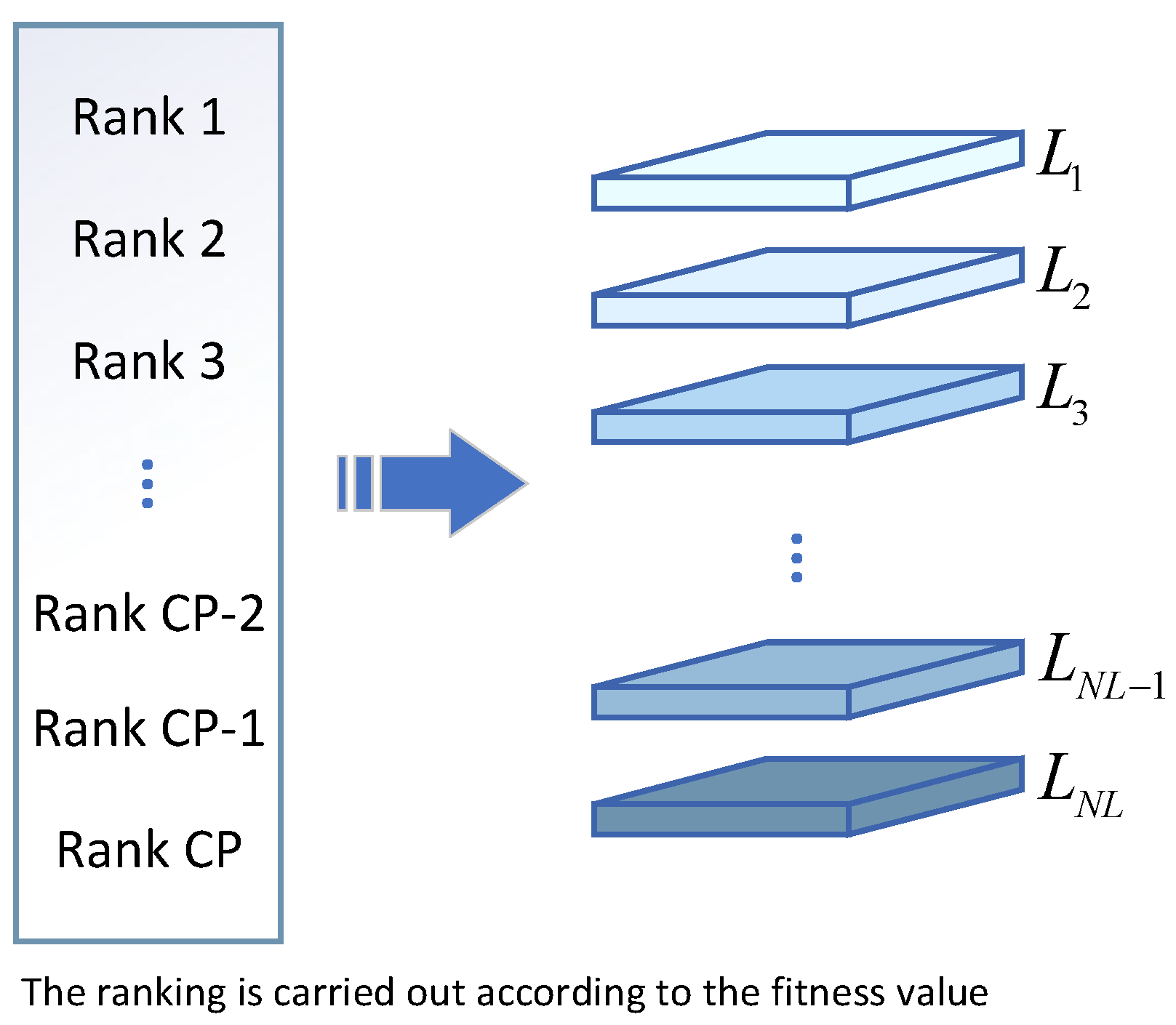
3.2. Hierarchical Learning Mechanism

To enhance the learning behavior among populations and diversity within the COA, this paper proposes a hierarchical learning mechanism. Figure 4 illustrates the division of the entire crayfish population ($CP$) into multiple hierarchies. Firstly, the population is sorted by fitness from best to worst. The ranking of the best individual is 1, while the worst is $CP$. The population is divided into $NL$ (an integer) number of hierarchies. If $CP$ is divisible by $NL$, each hierarchy will have an equal number of individuals; if not, the remainder $NP\mathrm{mod}NL$ is added to the last hierarchy, i.e., the $NL$-th layer. Concurrently, the crayfish population number in each hierarchy is defined as $LP$. The hierarchy with the best individuals is designated as the first hierarchy, i.e., $L_1$. Conversely, the layer containing the worst individuals is marked as the last hierarchy, i.e., $L_{NL}$. Let $X_{L,M}$ (where $L=1,2\dots ,NL$; $M=1,2,\dots ,LP$) denote the M-th crayfish individual in the L-th hierarchy. The aim of the HLCCOA is to allocate suitable learning exemplars to each hierarchy. Further, $p=(p_1,p_2,\dots ,p_{NL})$ governs the number of learning exemplars for crayfish populations in different hierarchies, with the number of exemplars for the L-th layer being defined as in Equation (15):

$$p_L={\displaystyle \frac{(i-1)·LP}{CP}}·100\%.$$

(15)

Building on Equation (15), individuals can choose to learn from better individuals in any hierarchy. Lower-ranking individuals enhance group diversity by doing more extensive learning from the majority of the whole group. Specifically, for $X_{1,M}$, learning is restricted to a few top individuals in the $L_1$ layer, where $p_1=0.2$, which means $X_{1,M}$ allows for learning only from the top $20\%$ of individuals in the $L_1$ layer. For $X_{L,M}$, they select from the top ${\displaystyle \sum _{l=1}^L}LP·p_l$ (where $l=1,\dots ,L$) elite of the entire population, thus continuously learning from elite individuals and effectively exploring and exploiting the surrounding space during behaviors like summer resort, competition, and foraging. As a result, the updating methods for individuals $X_{G1}$ and $X_{G2}$ in the population are as follows:

$$X_{G1}=X_{best}^{p_1};X_{G2}=X_{best}^r,$$

(16)

where $X_{best}^{p_1}$ represents the learning exemplars in the first layer, and $X_{best}^r$ denotes that the M-th individual $X_{L,M}$ in the L-th layer randomly selects a learning exemplar from the elite group. The expression for r is shown as follows:

$$r=round(rand·(\sum _{h=1}^{L}LP·p_h-1))+1.$$

(17)

This mechanism enables the crayfish elites to exhibit diversity and a certain degree of randomness in cave and food selection, aiding in escaping local optima and increasing the probability of discovering global optima. Additionally, the mechanism effectively retains information of potential solutions from the previous layer and integrates it thoroughly with the elite individuals of the current layer, thereby achieving a balance between search diversity and the convergence rate of the algorithm to some extent. The pseudo-code for the HLCCOA is presented in Algorithm 1, and its algorithmic workflow diagram is depicted in Figure 5.

Algorithm 1 Pseudo-Code of the HLCCOA Algorithm

Require:  N, $Dim$, $f\left(x\right)$, $X_i$, $Low$, $Up$, $NL$, $LP$, $Ma\mathit{x\_I}teration$ ($Ma\mathit{x\_I}teration$ is set to 500 in this paper). Ensure:  Output optimal solution and its fitness $f\left(X\right)$.   1: Initialize positions X of N crayfish with Tent map and Chebyshev map, calculate the fitness of value of population to obtain $X_G$, $X_L$.   2: Set parameters $C_1$, $C_2$, $C_3$.   3: while$It\le Ma\mathit{x\_I}teration$do   4:     Define temperature temp. And sort X by the fitness in ascending order and partition it into NL layers equally.   5:     for i-th layer from 1 to $NL$ do   6:         for j-th layer from 1 to $LP$ do   7:            if $temp>30$ °C then   8:                Define temperature $temp$   9:                Define cave $X_{shade}$ according to Equation (3). 10:                if $rand<0.5$ then 11:                    Crayfish conduct the summer resort stage according to Equation (4). 12:                else 13:                    Crayfish compete for caves through Equation (6). 14:                end if 15:            else 16:                The food intake p and food size Q are obtained by Equations (2) and (9). 17:                if $Q>2$ then 18:                    Crayfish shreds food by Equation (10) and crayfish forage according to Equation (11). 19:                else 20:                    Crayfish foraging according to Equation (12). 21:                end if 22:            end if 23:            Update $X_G$ and $X_L$ according to Equations (16) and (17). 24:            if $f\left(V_{i,j}\right)\le f\left(X_{i,j}\right)$ then 25:                $X_{i,j}\leftarrow V_{i,j}$ 26:            end if 27:         end for 28:     end for 29: end while

4. Experimental Results and Discussion of the HLCCOA

To rigorously assess the performance of the HLCCOA, this paper configures two sets of benchmark test suites, i.e., CEC2019 [52] and CEC2022 [53]. The CEC2019 test suite comprises 10 single-objective functions, each benchmarked against a theoretical optimum of 1. The CEC2022 suite features 12 test functions with boundary constraints, which are divided into four categories: unimodal (F1), multimodal (F2–F5), hybrid (F6–F8), and composition functions (F9–F12). The evaluations mainly consider two dimensions: 10D and 20D.

Additionally, nine current popular meta-heuristic optimization algorithms are selected for comparative analysis. Experimental results demonstrate that the HLCCOA proposed in this research shows significant promise in solving complex non-convex problems. For detailed information on the control parameters for the original COA and these nine competitors, refer to

Table 1. The currently popular meta-heuristic optimization algorithms.

Algorithms	Parameters	Values
HLCCOA	Number of population division layers $NL$	$NL=4$
	Sample selection probability ($p_1$) for $L_1$ layer	$p_1=0.2$
COA [37]	Decreasing coefficient $C_1$	$C_1=2$
	Ambient temperature $temp$	$(15,35)$
	Coefficient of food size $C_2$	$C_2=3$
	Coefficient of food intake $C_3$	$C_3=0.2$
AOA [18]	Minimum acceleration	0.2
	Maximum acceleration	0.2
	Control parameter	0.499
	Sensitive parameter	5
GOA [31]	Adaptive parameter c	$(c_{\min },c_{\max })$
	Intensity of attraction f	0.5
	Attractive length scale l	1.5
EMA [17]	Crossover probability $C_r$	$C_r=0.8$
	Probability of encountering the predator r	$r=0.2$
SSA [32]	Control parameters $r_1$, $r_2$, $r_3$	$r_1=2e^{-{\left({\displaystyle \frac{4l}{L}}\right)}^2}$
		$r_2\in [0,1]$
		$r_3\in [0,1]$
WOA [12]	$\overrightarrow{A}=2\overrightarrow{a}·\overrightarrow{r}-\overrightarrow{a}$	$\overrightarrow{a}\in [0,2]$
	$\overrightarrow{C}=2·\overrightarrow{r}$	$\overrightarrow{r}\in [0,1]$
SPBO [25]	Number of student subjects M	$M=5$
PDO [35]	Account for individual PD difference $\rho$	$\rho =0.005$
	Food source alarm $\epsilon$	$\epsilon =0.1$
	Old fitness values $GBest$	$GBest=\Phi$
	New fitness values $CBest$	$CBest=\Phi$
PSOGSA [54]	Gravitational constant $G_0$	$G_0=1$
	Velocity inertia weight $C_1$	$C_1=0.5$
	Velocity inertia weight $C_2$	$C_2=1.5$
SCSSA [36]	Proportion of finders $PD$	$PD=0.3$
	Proportion of investigators $SD$	$SD=0.1$
	Alert threshold $R_2$	$R_2=0.8$

. All experiments in this section set the population size of the algorithms at 50, with 500 generations of evolution, and they are independently repeated for 30 runs. This setup is designed to facilitate comparative analysis of the optimization performance and stability differences among different algorithms.

The hardware configuration of the computer used in this study is an AMD Ryzen 7-5800H CPU with Radeon Graphics @ 3.20 GHz, and the simulation platform used for implementing all the algorithms and comparative experiments mentioned in this paper is MATLAB R2021b. Detailed experimental procedures and analysis are elaborated in the following sections.

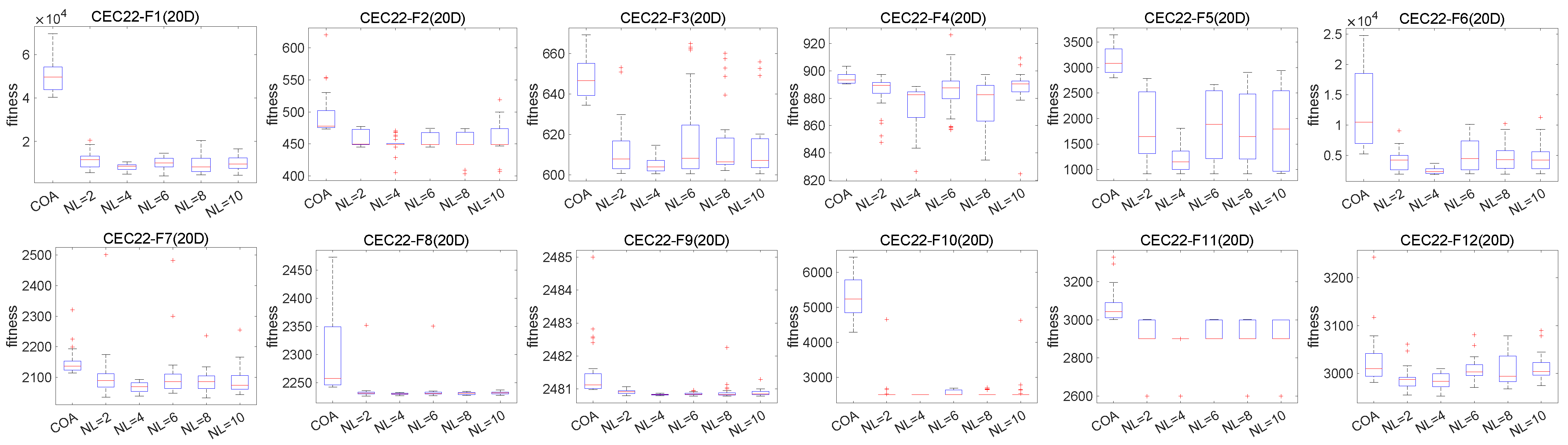
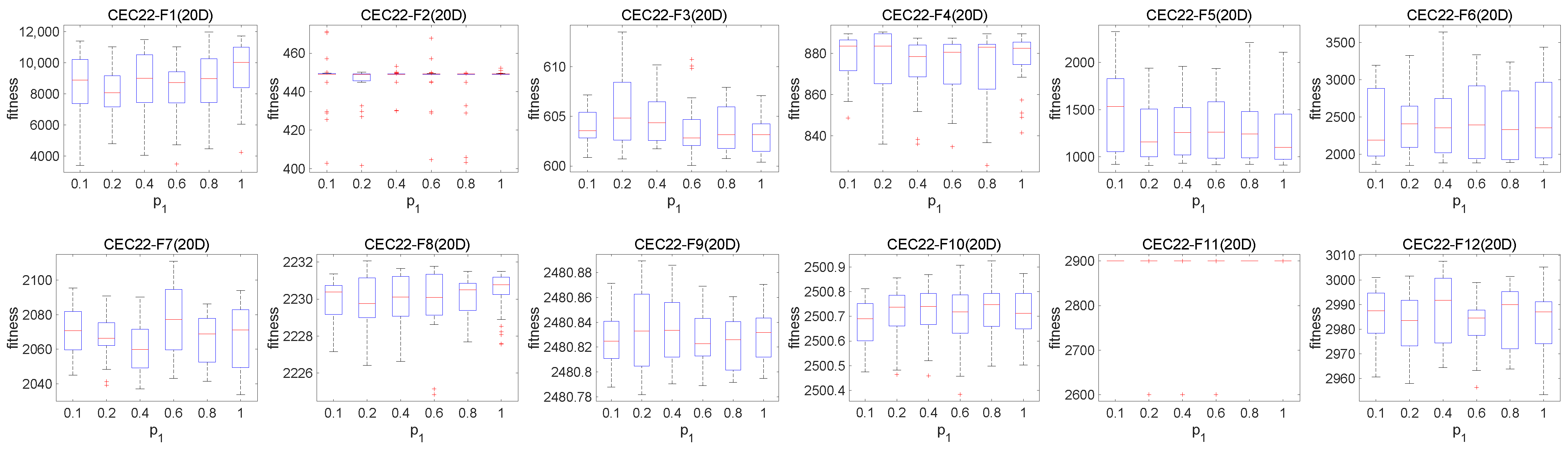
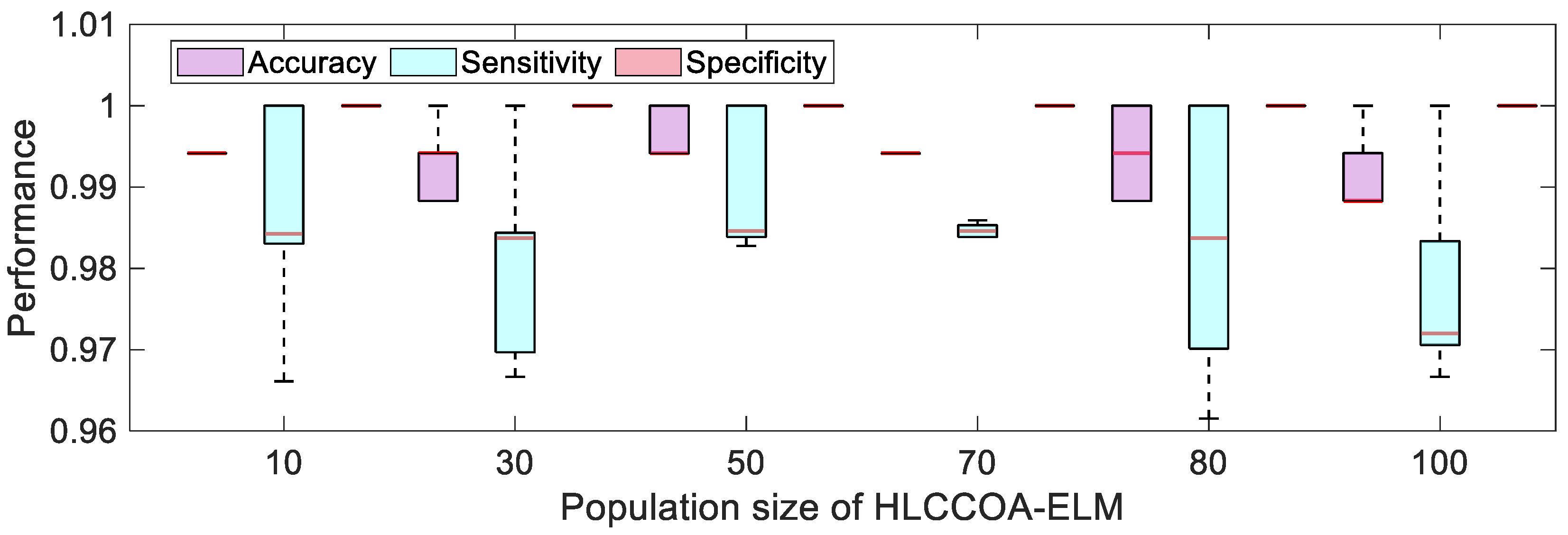
4.1. Parameter Analysis of the HLCCOA

The HLCCOA, compared to COA, incorporates two critical control parameters: the population division layers (NL) and the sample selection probability ($p_1$) for layer $L_1$, both of which significantly influence the evolutionary trends of the population. Therefore, conducting a sensitivity analysis on these parameters and determining the optimal configuration are essential.

Firstly, the impact of the number of the NL is examined. A smaller NL leads individuals to learn from a few optimal examples, while a larger NL decreases the likelihood of selecting top performers. Comparative experiments are conducted with five NL values (i.e., 2, 4, 6, 8, and 10). As shown in Figure 6, the box plots of the HLCCOA at various NL values for CEC2022-20D demonstrate performance improvements over COA. Notably, NL = 4 produces the most compact box plot distribution and the lowest median across most test functions, indicating higher stability and optimization efficiency. Rankings from the Friedman test, presented in

Table 2. Friedman’s mean rank among the HLCCOA with different NL and $p_1$.

NL Changes	Rank	${\mathit{p}}_1$ Changes	Rank
COA	5.6667	HLCCOA ($p_1=0.1$)	4.3000
HLCCOA (NL = 2)	1.6000	HLCCOA ($p_1=0.2$)	2.0667
HLCCOA (NL = 4)	1.4000	HLCCOA ($p_1=0.4$)	4.9667
HLCCOA (NL = 6)	3.7667	HLCCOA ($p_1=0.6$)	2.3667
HLCCOA (NL = 8)	3.7000	HLCCOA ($p_1=0.8$)	3.6667
HLCCOA (NL = 10)	4.8667	HLCCOA ($p_1=1$)	3.6333

, reveal that the HLCCOA with NL = 4 achieves the highest ranking, making it the optimal choice.

Secondly, the influence of $p_1$ is explored. A very small $p_1$ results in the selection of overly specific optimal individuals, whereas a very large $p_1$ leads to the selection of overly generalized optimal individuals. Comparative experiments are conducted with six $p_1$ values (i.e., 0.1, 0.2, 0.4, 0.6, 0.8, and 1). Figure 7 displays the box plots of the HLCCOA for various $p_1$ in CEC2022-20D. For unimodal problems, $p_1=0.1$ and $p_1=0.2$ demonstrate superior performance, whereas for multimodal problems, $p_1=0.2$, $p_1=0.4$, and $p_1=0.6$ exhibit even better performance. Rankings from the Friedman test, presented in Table 2, demonstrate that the HLCCOA with $p_1=0.2$ achieves the highest ranking, confirming it as the optimal choice.

4.2. Wilcoxon Signed-Rank Sum Test Results and Analysis

For an effective comparative analysis of algorithm performance differences on identical problems, the Wilcoxon signed-rank test [55] is applied. The significance level is set at $5\%$. In the statistical results, “≈” indicates no significant difference, “+” denotes superiority of the corresponding HLCCOA, and “- ” signifies the opposite.

In this experiment, all considered algorithms are compared using the mean ($Mean$) and standard deviation ($Std$) of the best solutions obtained so far as two evaluation criteria. The formulas are as follows:

$$Mean={\displaystyle \frac{1}{T}}\sum _{i=1}^T{P}_i^{*},$$

(18)

$$Std=\sqrt{{\displaystyle \frac{1}{T}}{(P_i^{*}-Mean)}^2},$$

(19)

where $P_i^{*}$ represents the best solution obtained so far in the i-th independent experimental run, and T denotes the number of independent runs. The smaller the mean, the closer the feasible solution obtained by the algorithm is to the standard solution (true value), indicating that the algorithm possesses superior average performance. Moreover, the smaller the standard deviation, the more stable and reliable the feasible solution provided by the algorithm.

Table 3. Statistical results of the HLCCOA compared with other optimization algorithms on CEC2019.

Fun	Index	HLCCOA	COA	AOA	GOA	EMA	SSA	WOA	SPBO	PDO	PSOGSA	SCSSA
F1	Mean	$1.00\times {10}^0$	$1.00\times {10}^0$≈	$2.94\times {10}^4$+	$2.05\times {10}^6$+	$1.79\times {10}^5$+	$1.58\times {10}^6$+	$1.10\times {10}^7$+	$8.49\times {10}^1$≈	$1.00\times {10}^0$≈	$2.29\times {10}^7$+	$1.00\times {10}^0$≈
	Std	0	0	$9.74\times {10}^4$	$2.45\times {10}^6$	$3.41\times {10}^5$	$1.53\times {10}^6$	$1.23\times {10}^7$	$4.60\times {10}^2$	0	$5.30\times {10}^7$	0
F2	Mean	$4.88\times {10}^0$	$4.80\times {10}^0$≈	$1.02\times {10}^4$+	$9.98\times {10}^2$+	$1.23\times {10}^3$+	$8.46\times {10}^2$+	$7.51\times {10}^3$+	$6.94\times {10}^1$+	$5.00\times {10}^0$≈	$3.07\times {10}^3$+	$5.00\times {10}^0$≈
	Std	$2.29\times {10}^{-1}$	$3.24\times {10}^{-1}$	$3.25\times {10}^3$	$5.70\times {10}^2$	$9.58\times {10}^2$	$7.06\times {10}^2$	$2.97\times {10}^3$	$1.94\times {10}^2$	$2.12\times {10}^{-6}$	$3.10\times {10}^3$	0
F3	Mean	$3.64\times {10}^0$	$6.45\times {10}^0$+	$9.65\times {10}^0$+	$8.44\times {10}^0$+	$3.63\times {10}^0$≈	$3.39\times {10}^0$≈	$5.60\times {10}^0$+	$5.32\times {10}^0$+	$7.47\times {10}^0$+	$6.61\times {10}^0$+	$3.16\times {10}^0$≈
	Std	$1.69\times {10}^0$	$2.60\times {10}^0$	$1.10\times {10}^0$	$2.16\times {10}^0$	$2.16\times {10}^0$	$1.92\times {10}^0$	$2.10\times {10}^0$	$1.43\times {10}^0$	$1.83\times {10}^0$	$2.87\times {10}^0$	$2.05\times {10}^0$
F4	Mean	$3.13\times {10}^1$	$3.64\times {10}^1$+	$4.87\times {10}^1$+	$2.17\times {10}^1$≈	$1.80\times {10}^1$≈	$2.52\times {10}^1$≈	$4.89\times {10}^1$+	$3.82\times {10}^1$+	$7.47\times {10}^1$+	$3.73\times {10}^1$+	$4.49\times {10}^1$+
	Std	$2.83\times {10}^1$	$2.06\times {10}^1$	$1.38\times {10}^1$	$1.02\times {10}^1$	$7.47\times {10}^0$	$1.09\times {10}^1$	$1.89\times {10}^1$	$9.44\times {10}^0$	$1.39\times {10}^1$	$1.46\times {10}^1$	$2.34\times {10}^1$
F5	Mean	$1.10\times {10}^0$	$1.20\times {10}^0$+	$6.52\times {10}^1$+	$1.27\times {10}^0$+	$1.09\times {10}^0$≈	$1.24\times {10}^0$+	$2.07\times {10}^0$+	$2.49\times {10}^0$+	$5.52\times {10}^1$+	$7.48\times {10}^0$+	$1.19\times {10}^0$+
	Std	$1.12\times {10}^{-1}$	$1.03\times {10}^{-1}$	$2.11\times {10}^1$	$1.68\times {10}^{-1}$	$4.90\times {10}^{-2}$	$1.50\times {10}^{-1}$	$3.91\times {10}^{-1}$	$4.24\times {10}^{-1}$	$2.07\times {10}^1$	$1.67\times {10}^1$	$1.13\times {10}^{-1}$
F6	Mean	$3.03\times {10}^0$	$3.90\times {10}^0$+	$1.04\times {10}^1$+	$4.63\times {10}^0$+	$2.87\times {10}^0$≈	$4.23\times {10}^0$+	$8.59\times {10}^0$+	$7.04\times {10}^0$+	$1.06\times {10}^1$+	$5.28\times {10}^0$+	$4.08\times {10}^0$+
	Std	$1.65\times {10}^0$	$1.74\times {10}^0$	$1.54\times {10}^0$	$1.98\times {10}^0$	$1.46\times {10}^0$	$2.34\times {10}^0$	$1.68\times {10}^0$	$1.18\times {10}^0$	$1.17\times {10}^0$	$1.88\times {10}^0$	$1.65\times {10}^0$
F7	Mean	$8.36\times {10}^2$	$1.19\times {10}^3$+	$1.29\times {10}^3$+	$1.00\times {10}^3$+	$5.85\times {10}^2$−	$1.04\times {10}^3$+	$1.25\times {10}^3$+	$1.20\times {10}^3$+	$1.70\times {10}^3$+	$1.26\times {10}^3$+	$1.25\times {10}^3$+
	Std	$1.99\times {10}^2$	$3.19\times {10}^2$	$2.74\times {10}^2$	$2.21\times {10}^2$	$2.42\times {10}^2$	$3.11\times {10}^2$	$3.07\times {10}^2$	$2.17\times {10}^2$	$3.08\times {10}^2$	$2.93\times {10}^2$	$3.61\times {10}^2$
F8	Mean	$3.59\times {10}^0$	$3.90\times {10}^0$+	$4.69\times {10}^0$+	$4.11\times {10}^0$+	$3.68\times {10}^0$≈	$4.18\times {10}^0$+	$4.63\times {10}^0$+	$4.32\times {10}^0$+	$4.87\times {10}^0$+	$4.63\times {10}^0$+	$4.10\times {10}^0$+
	Std	$4.95\times {10}^{-1}$	$3.16\times {10}^{-1}$	$3.91\times {10}^{-1}$	$4.37\times {10}^{-1}$	$4.42\times {10}^{-1}$	$3.03\times {10}^{-1}$	$3.61\times {10}^{-1}$	$2.80\times {10}^{-1}$	$2.23\times {10}^{-1}$	$4.10\times {10}^{-1}$	$3.95\times {10}^{-1}$
F9	Mean	$1.20\times {10}^0$	$1.34\times {10}^0$+	$2.32\times {10}^0$+	$1.28\times {10}^0$+	$1.25\times {10}^0$+	$1.37\times {10}^0$+	$1.34\times {10}^0$+	$1.40\times {10}^0$+	$3.00\times {10}^0$+	$1.46\times {10}^0$+	$1.32\times {10}^0$+
	Std	$6.23\times {10}^{-2}$	$9.58\times {10}^{-2}$	$8.02\times {10}^{-1}$	$1.13\times {10}^{-1}$	$8.16\times {10}^{-2}$	$1.68\times {10}^{-1}$	$1.65\times {10}^{-1}$	$1.49\times {10}^{-1}$	$8.70\times {10}^{-1}$	$2.24\times {10}^{-1}$	$1.33\times {10}^{-1}$
F10	Mean	$1.93\times {10}^1$	$1.91\times {10}^1$−	$2.11\times {10}^1$≈	$2.11\times {10}^1$+	$2.12\times {10}^1$≈	$2.03\times {10}^1$+	$2.13\times {10}^1$+	$2.12\times {10}^1$+	$2.13\times {10}^1$+	$2.11\times {10}^1$+	$2.07\times {10}^1$+
	Std	$5.66\times {10}^0$	$5.41\times {10}^0$	$3.85\times {10}^{-2}$	$7.50\times {10}^{-2}$	$1.00\times {10}^{-1}$	$3.65\times {10}^0$	$1.36\times {10}^{-1}$	$8.70\times {10}^{-2}$	$1.49\times {10}^{-1}$	$9.57\times {10}^{-2}$	$3.29\times {10}^0$
Chaos wins		+	7	9	9	3	8	10	9	8	10	7
Similar		≈	2	1	1	6	2	0	1	2	0	3
Competitor wins		-	1	0	0	1	0	0	0	0	0	0

presents the Wilcoxon signed-rank test results for various algorithms on the CEC2019 benchmark functions. It can be seen that, in dealing with most problems, the HLCCOA exhibits superior performance compared to other competitors, particularly AOA, GOA, SSA, WOA, PDO, and PSOGSA. Notably, the HLCCOA surpasses the original COA in 7 out of 10 test functions. Additionally,

Table 4. Statistical results of the HLCCOA compared with other optimization algorithms on CEC2022-10D.

Fun	Index	HLCCOA	COA	AOA	GOA	EMA	SSA	WOA	SPBO	PDO	PSOGSA	SCSSA
F1	Mean	$3.46\times {10}^2$	$1.84\times {10}^3$+	$1.16\times {10}^4$+	$3.00\times {10}^2$−	$1.65\times {10}^3$+	$3.00\times {10}^2$−	$2.50\times {10}^4$+	$5.51\times {10}^2$+	$1.20\times {10}^4$+	$5.17\times {10}^3$≈	$5.74\times {10}^2$+
	Std	$5.98\times {10}^1$	$1.08\times {10}^3$	$4.59\times {10}^3$	$3.96\times {10}^{-1}$	$1.08\times {10}^3$	$7.75\times {10}^{-1}$	$1.17\times {10}^4$	$2.55\times {10}^2$	$4.93\times {10}^3$	$7.91\times {10}^3$	$2.61\times {10}^2$
F2	Mean	$4.06\times {10}^2$	$4.10\times {10}^2$+	$1.19\times {10}^3$+	$4.06\times {10}^2$+	$4.09\times {10}^2$+	$4.07\times {10}^2$+	$4.56\times {10}^2$+	$4.32\times {10}^2$+	$9.92\times {10}^2$+	$4.47\times {10}^2$+	$4.11\times {10}^2$+
	Std	$1.62\times {10}^1$	$1.67\times {10}^1$	$4.99\times {10}^2$	$3.33\times {10}^0$	$4.73\times {10}^0$	$7.80\times {10}^0$	$7.41\times {10}^1$	$3.11\times {10}^1$	$3.47\times {10}^2$	$7.23\times {10}^1$	$1.75\times {10}^1$
F3	Mean	$6.02\times {10}^2$	$6.06\times {10}^2$+	$6.37\times {10}^2$+	$6.04\times {10}^2$+	$6.00\times {10}^2$−	$6.12\times {10}^2$+	$6.35\times {10}^2$+	$6.21\times {10}^2$+	$6.50\times {10}^2$+	$6.20\times {10}^2$+	$6.06\times {10}^2$+
	Std	$8.58\times {10}^0$	$9.58\times {10}^0$	$7.61\times {10}^0$	$5.22\times {10}^0$	$1.80\times {10}^{-1}$	$9.41\times {10}^0$	$1.18\times {10}^1$	$7.06\times {10}^0$	$8.72\times {10}^0$	$1.61\times {10}^1$	$1.17\times {10}^1$
F4	Mean	$8.23\times {10}^2$	$8.31\times {10}^2$+	$8.31\times {10}^2$+	$8.21\times {10}^2$≈	$8.20\times {10}^2$≈	$8.21\times {10}^2$≈	$8.40\times {10}^2$+	$8.28\times {10}^2$≈	$8.48\times {10}^2$+	$8.40\times {10}^2$+	$8.30\times {10}^2$≈
	Std	$9.93\times {10}^0$	$5.47\times {10}^0$	$8.17\times {10}^0$	$9.17\times {10}^0$	$1.21\times {10}^1$	$8.37\times {10}^0$	$1.48\times {10}^1$	$8.81\times {10}^0$	$9.46\times {10}^0$	$1.44\times {10}^1$	$7.46\times {10}^0$
F5	Mean	$9.15\times {10}^2$	$1.01\times {10}^3$+	$1.39\times {10}^3$+	$9.02\times {10}^2$≈	$9.01\times {10}^2$≈	$9.64\times {10}^2$+	$1.44\times {10}^3$+	$1.07\times {10}^3$+	$1.48\times {10}^3$+	$1.51\times {10}^3$+	$1.35\times {10}^3$+
	Std	$7.06\times {10}^1$	$1.96\times {10}^2$	$1.87\times {10}^2$	$3.29\times {10}^0$	$1.98\times {10}^0$	$1.47\times {10}^2$	$3.30\times {10}^2$	$1.13\times {10}^2$	$1.82\times {10}^2$	$4.46\times {10}^2$	$2.30\times {10}^2$
F6	Mean	$2.36\times {10}^3$	$4.13\times {10}^3$+	$8.58\times {10}^3$+	$3.76\times {10}^3$+	$4.66\times {10}^3$+	$4.27\times {10}^3$+	$5.13\times {10}^3$+	$3.54\times {10}^3$+	$8.61\times {10}^7$+	$5.65\times {10}^3$+	$3.28\times {10}^3$+
	Std	$5.65\times {10}^2$	$2.00\times {10}^3$	$2.41\times {10}^4$	$1.82\times {10}^3$	$2.16\times {10}^3$	$2.15\times {10}^3$	$2.57\times {10}^3$	$1.92\times {10}^3$	$1.84\times {10}^8$	$1.99\times {10}^3$	$1.56\times {10}^3$
F7	Mean	$2.02\times {10}^3$	$2.02\times {10}^3$≈	$2.11\times {10}^3$+	$2.06\times {10}^3$+	$2.03\times {10}^3$+	$2.05\times {10}^3$+	$2.07\times {10}^3$+	$2.05\times {10}^3$+	$2.11\times {10}^3$+	$2.05\times {10}^3$+	$2.04\times {10}^3$+
	Std	$1.02\times {10}^1$	$7.95\times {10}^0$	$4.09\times {10}^1$	$3.85\times {10}^1$	$1.19\times {10}^1$	$2.21\times {10}^1$	$2.89\times {10}^1$	$1.07\times {10}^1$	$3.84\times {10}^1$	$3.31\times {10}^1$	$3.22\times {10}^1$
F8	Mean	$2.22\times {10}^3$	$2.22\times {10}^3$+	$2.26\times {10}^3$+	$2.26\times {10}^3$+	$2.22\times {10}^3$−	$2.23\times {10}^3$+	$2.24\times {10}^3$+	$2.23\times {10}^3$+	$2.25\times {10}^3$+	$2.25\times {10}^3$+	$2.22\times {10}^3$−
	Std	$4.43\times {10}^0$	$6.78\times {10}^0$	$6.39\times {10}^1$	$5.66\times {10}^1$	$4.94\times {10}^0$	$3.03\times {10}^0$	$1.24\times {10}^1$	$2.62\times {10}^0$	$2.47\times {10}^1$	$4.74\times {10}^1$	$9.13\times {10}^0$
F9	Mean	$2.53\times {10}^3$	$2.53\times {10}^3$+	$2.73\times {10}^3$+	$2.55\times {10}^3$+	$2.53\times {10}^3$−	$2.55\times {10}^3$+	$2.59\times {10}^3$+	$2.54\times {10}^3$+	$2.74\times {10}^3$+	$2.56\times {10}^3$≈	$2.53\times {10}^3$+
	Std	$1.79\times {10}^{-5}$	$2.05\times {10}^{-4}$	$5.59\times {10}^1$	$4.78\times {10}^1$	$6.40\times {10}^{-12}$	$3.67\times {10}^1$	$4.94\times {10}^1$	$1.11\times {10}^1$	$6.68\times {10}^1$	$5.10\times {10}^1$	$2.68\times {10}^1$
F10	Mean	$2.53\times {10}^3$	$2.54\times {10}^3$≈	$2.65\times {10}^3$+	$2.62\times {10}^3$+	$2.55\times {10}^3$+	$2.51\times {10}^3$≈	$2.60\times {10}^3$+	$2.50\times {10}^3$−	$2.59\times {10}^3$+	$2.69\times {10}^3$+	$2.56\times {10}^3$+
	Std	$5.00\times {10}^1$	$6.03\times {10}^1$	$1.79\times {10}^2$	$2.01\times {10}^2$	$5.71\times {10}^1$	$3.80\times {10}^1$	$1.90\times {10}^2$	$3.96\times {10}^{-1}$	$8.12\times {10}^1$	$3.03\times {10}^2$	$6.28\times {10}^1$
F11	Mean	$2.68\times {10}^3$	$2.72\times {10}^3$+	$3.39\times {10}^3$+	$2.73\times {10}^3$+	$2.66\times {10}^3$≈	$2.65\times {10}^3$≈	$2.82\times {10}^3$+	$2.71\times {10}^3$+	$3.22\times {10}^3$+	$2.91\times {10}^3$+	$2.74\times {10}^3$+
	Std	$1.12\times {10}^2$	$1.34\times {10}^2$	$4.01\times {10}^2$	$1.73\times {10}^2$	$7.32\times {10}^1$	$1.13\times {10}^2$	$1.51\times {10}^2$	$4.24\times {10}^1$	$3.42\times {10}^2$	$2.15\times {10}^2$	$2.18\times {10}^2$
F12	Mean	$2.87\times {10}^3$	$2.87\times {10}^3$−	$3.02\times {10}^3$+	$2.86\times {10}^3$−	$2.86\times {10}^3$−	$2.86\times {10}^3$−	$2.89\times {10}^3$+	$2.88\times {10}^3$+	$2.89\times {10}^3$+	$2.88\times {10}^3$≈	$2.86\times {10}^3$−
	Std	$3.83\times {10}^0$	$1.79\times {10}^0$	$6.20\times {10}^1$	$1.93\times {10}^0$	$1.99\times {10}^0$	$1.68\times {10}^0$	$3.62\times {10}^1$	$1.46\times {10}^1$	$1.14\times {10}^1$	$2.44\times {10}^1$	$4.38\times {10}^0$
Chaos wins		+	9	12	8	5	7	12	10	12	9	9
Similar		≈	2	0	2	3	3	0	1	0	3	1
Competitor wins		-	1	0	2	4	2	0	1	0	0	2

and

Table 5. Statistical results of the HLCCOA compared with other optimization algorithms on CEC2022-20D.

Fun	Index	HLCCOA	COA	AOA	GOA	EMA	SSA	WOA	SPBO	PDO	PSOGSA	SCSSA
F1	Mean	$1.01\times {10}^4$	$4.13\times {10}^4$+	$3.50\times {10}^4$+	$1.05\times {10}^3$−	$4.73\times {10}^4$+	$4.19\times {10}^3$−	$2.64\times {10}^4$+	$1.48\times {10}^3$−	$7.63\times {10}^4$+	$2.12\times {10}^4$+	$4.52\times {10}^4$+
	Std	$3.69\times {10}^3$	$1.43\times {10}^4$	$1.23\times {10}^4$	$1.15\times {10}^3$	$1.08\times {10}^4$	$2.45\times {10}^3$	$7.00\times {10}^3$	$6.37\times {10}^2$	$1.85\times {10}^4$	$1.29\times {10}^4$	$1.52\times {10}^4$
F2	Mean	$4.52\times {10}^2$	$4.70\times {10}^2$+	$2.39\times {10}^3$+	$4.52\times {10}^2$≈	$4.54\times {10}^2$≈	$4.60\times {10}^2$≈	$5.82\times {10}^2$+	$5.48\times {10}^2$+	$2.18\times {10}^3$+	$4.96\times {10}^2$+	$4.66\times {10}^2$+
	Std	$1.19\times {10}^1$	$2.44\times {10}^1$	$7.13\times {10}^2$	$2.10\times {10}^1$	$1.25\times {10}^1$	$1.42\times {10}^1$	$7.10\times {10}^1$	$4.30\times {10}^1$	$5.69\times {10}^2$	$6.71\times {10}^1$	$3.64\times {10}^1$
F3	Mean	$6.12\times {10}^2$	$6.27\times {10}^2$+	$6.62\times {10}^2$+	$6.24\times {10}^2$+	$6.00\times {10}^2$−	$6.40\times {10}^2$+	$6.67\times {10}^2$+	$6.52\times {10}^2$+	$6.76\times {10}^2$+	$6.50\times {10}^2$+	$6.24\times {10}^2$+
	Std	$1.33\times {10}^1$	$1.73\times {10}^1$	$7.56\times {10}^0$	$1.10\times {10}^1$	$6.32\times {10}^{-1}$	$1.49\times {10}^1$	$1.25\times {10}^1$	$9.32\times {10}^0$	$8.06\times {10}^0$	$1.27\times {10}^1$	$1.47\times {10}^1$
F4	Mean	$8.81\times {10}^2$	$8.84\times {10}^2$≈	$9.49\times {10}^2$+	$8.71\times {10}^2$−	$9.25\times {10}^2$+	$8.78\times {10}^2$≈	$9.28\times {10}^2$+	$9.17\times {10}^2$+	$9.55\times {10}^2$+	$9.19\times {10}^2$+	$8.95\times {10}^2$+
	Std	$1.46\times {10}^1$	$1.77\times {10}^1$	$1.54\times {10}^1$	$2.25\times {10}^1$	$2.72\times {10}^1$	$2.36\times {10}^1$	$3.25\times {10}^1$	$1.60\times {10}^1$	$2.65\times {10}^1$	$3.71\times {10}^1$	$1.80\times {10}^1$
F5	Mean	$1.84\times {10}^3$	$2.61\times {10}^3$+	$2.94\times {10}^3$+	$1.77\times {10}^3$≈	$9.54\times {10}^2$−	$2.10\times {10}^3$≈	$4.15\times {10}^3$+	$3.05\times {10}^3$+	$3.10\times {10}^3$+	$3.71\times {10}^3$+	$2.39\times {10}^3$+
	Std	$6.77\times {10}^2$	$4.68\times {10}^2$	$4.43\times {10}^2$	$8.96\times {10}^2$	$9.31\times {10}^1$	$5.91\times {10}^2$	$1.34\times {10}^3$	$4.82\times {10}^2$	$6.29\times {10}^2$	$1.24\times {10}^3$	$2.61\times {10}^2$
F6	Mean	$4.38\times {10}^3$	$4.59\times {10}^3$≈	$8.61\times {10}^8$+	$1.15\times {10}^4$+	$5.03\times {10}^3$≈	$9.43\times {10}^3$≈	$1.28\times {10}^6$+	$8.28\times {10}^5$+	$9.57\times {10}^8$+	$1.91\times {10}^6$+	$7.44\times {10}^3$≈
	Std	$2.39\times {10}^3$	$4.14\times {10}^3$	$7.09\times {10}^8$	$1.37\times {10}^4$	$3.86\times {10}^3$	$8.52\times {10}^3$	$1.97\times {10}^6$	$5.44\times {10}^5$	$9.17\times {10}^8$	$7.01\times {10}^6$	$7.51\times {10}^3$
F7	Mean	$2.11\times {10}^3$	$2.12\times {10}^3$≈	$2.19\times {10}^3$+	$2.19\times {10}^3$+	$2.07\times {10}^3$−	$2.12\times {10}^3$+	$2.24\times {10}^3$+	$2.12\times {10}^3$+	$2.22\times {10}^3$+	$2.23\times {10}^3$+	$2.12\times {10}^3$+
	Std	$9.96\times {10}^1$	$8.44\times {10}^1$	$4.67\times {10}^1$	$7.76\times {10}^1$	$3.19\times {10}^1$	$3.62\times {10}^1$	$5.65\times {10}^1$	$2.67\times {10}^1$	$5.89\times {10}^1$	$7.59\times {10}^1$	$4.23\times {10}^1$
F8	Mean	$2.23\times {10}^3$	$2.28\times {10}^3$+	$2.47\times {10}^3$+	$2.30\times {10}^3$+	$2.23\times {10}^3$+	$2.29\times {10}^3$+	$2.30\times {10}^3$+	$2.25\times {10}^3$+	$2.78\times {10}^3$+	$2.36\times {10}^3$+	$2.25\times {10}^3$≈
	Std	$2.11\times {10}^0$	$6.35\times {10}^1$	$2.03\times {10}^2$	$6.53\times {10}^1$	$2.25\times {10}^1$	$7.47\times {10}^1$	$6.86\times {10}^1$	$2.25\times {10}^1$	$5.97\times {10}^2$	$1.22\times {10}^2$	$4.22\times {10}^1$
F9	Mean	$2.48\times {10}^3$	$2.48\times {10}^3$≈	$3.07\times {10}^3$+	$2.52\times {10}^3$+	$2.48\times {10}^3$+	$2.51\times {10}^3$+	$2.58\times {10}^3$+	$2.55\times {10}^3$+	$2.92\times {10}^3$+	$2.52\times {10}^3$+	$2.48\times {10}^3$−
	Std	$1.16\times {10}^{-1}$	$1.33\times {10}^{-1}$	$2.04\times {10}^2$	$4.84\times {10}^1$	$6.94\times {10}^0$	$3.25\times {10}^1$	$5.17\times {10}^1$	$3.96\times {10}^1$	$1.37\times {10}^2$	$4.62\times {10}^1$	$6.55\times {10}^{-2}$
F10	Mean	$2.60\times {10}^3$	$3.82\times {10}^3$+	$5.47\times {10}^3$+	$4.47\times {10}^3$+	$2.96\times {10}^3$+	$3.36\times {10}^3$+	$4.40\times {10}^3$+	$2.51\times {10}^3$−	$5.77\times {10}^3$+	$3.88\times {10}^3$+	$3.85\times {10}^3$+
	Std	$4.16\times {10}^2$	$1.26\times {10}^3$	$1.19\times {10}^3$	$7.88\times {10}^2$	$4.19\times {10}^2$	$1.07\times {10}^3$	$1.46\times {10}^3$	$5.28\times {10}^1$	$1.32\times {10}^3$	$1.08\times {10}^3$	$1.03\times {10}^3$
F11	Mean	$2.93\times {10}^3$	$3.00\times {10}^3$+	$8.30\times {10}^3$+	$3.12\times {10}^3$+	$3.01\times {10}^3$+	$2.95\times {10}^3$≈	$3.40\times {10}^3$+	$4.23\times {10}^3$+	$7.89\times {10}^3$+	$4.11\times {10}^3$+	$2.94\times {10}^3$+
	Std	$7.85\times {10}^1$	$1.20\times {10}^2$	$9.36\times {10}^2$	$4.06\times {10}^2$	$2.62\times {10}^2$	$1.45\times {10}^2$	$1.04\times {10}^2$	$3.67\times {10}^2$	$9.03\times {10}^2$	$1.27\times {10}^3$	$9.54\times {10}^1$
F12	Mean	$2.99\times {10}^3$	$2.99\times {10}^3$≈	$3.77\times {10}^3$+	$2.98\times {10}^3$≈	$2.95\times {10}^3$−	$2.97\times {10}^3$−	$3.10\times {10}^3$+	$3.15\times {10}^3$+	$3.18\times {10}^3$+	$3.01\times {10}^3$≈	$3.01\times {10}^3$≈
	Std	$3.15\times {10}^1$	$2.98\times {10}^1$	$2.04\times {10}^2$	$3.48\times {10}^1$	$1.11\times {10}^1$	$1.98\times {10}^1$	$1.21\times {10}^2$	$1.16\times {10}^2$	$8.04\times {10}^1$	$4.96\times {10}^1$	$5.03\times {10}^1$
Chaos wins		+	7	12	7	6	5	12	10	12	11	8
Similar		≈	4	0	3	2	5	0	0	0	1	3
Competitor wins		-	1	0	2	4	2	0	2	0	0	1

display the Wilcoxon signed-rank test results for algorithms on the 10-dimensional and 20-dimensional test problems of the CEC2022 suite, respectively. These statistical data indicate that the HLCCOA outperforms other competitors in solving the majority of these problems across both dimensions, particularly against AOA, WOA, PDO, and PSOGSA. It notably exceeds the performance of the original COA in more than $50\%$ of the test functions, demonstrating its strong competitiveness.

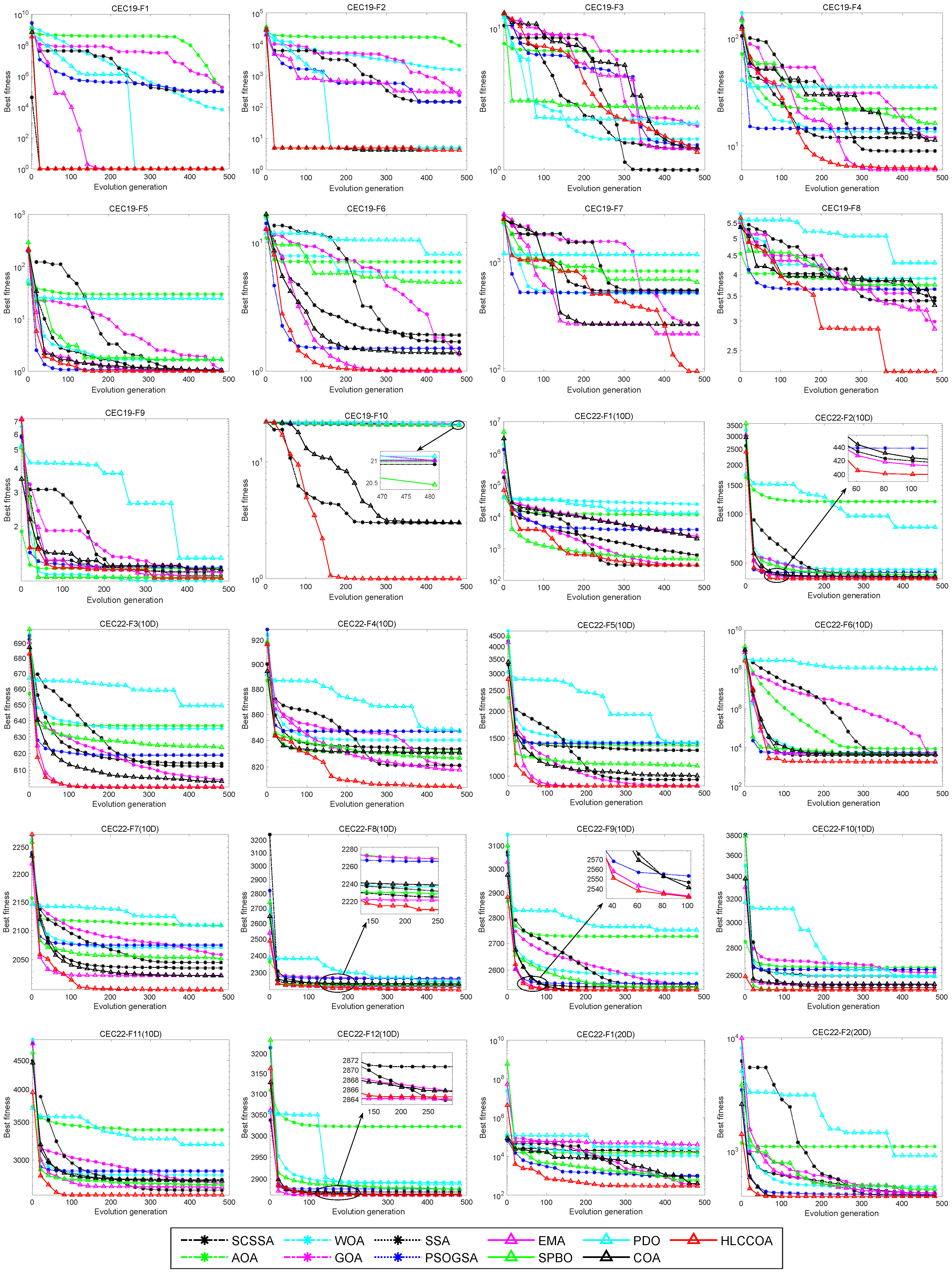
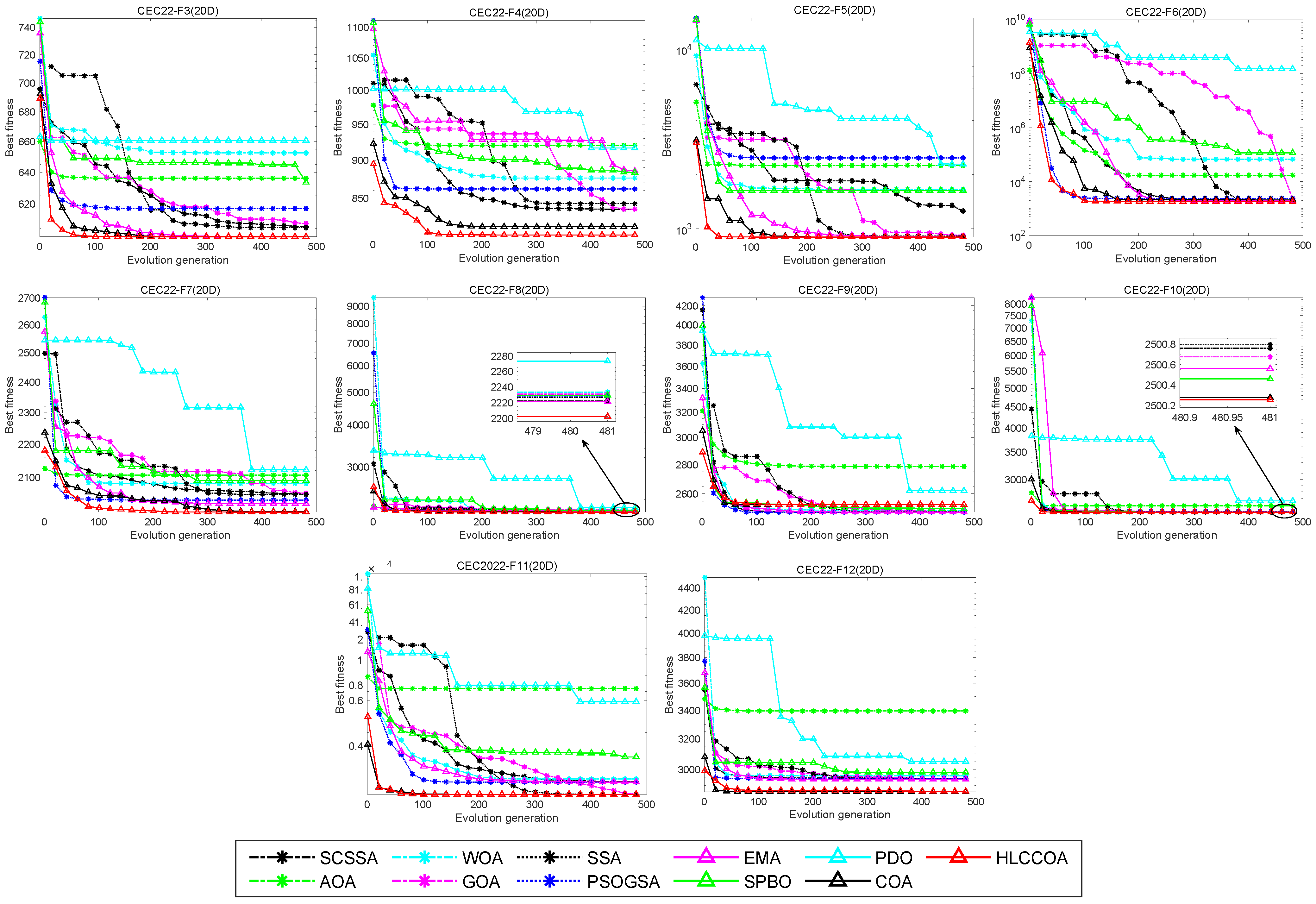
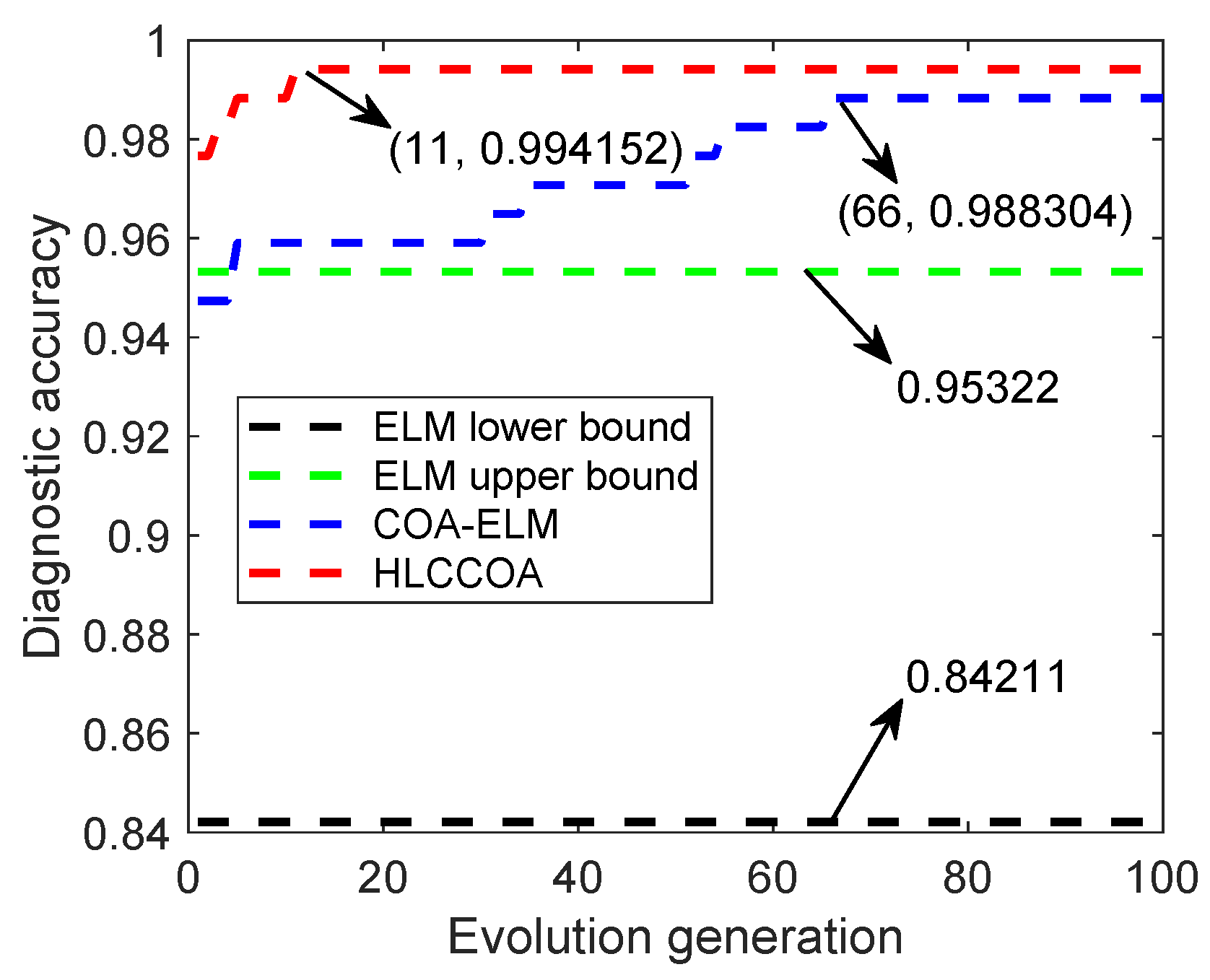
4.3. Convergence Curve Analysis

To comprehensively assess the convergence of the HLCCOA and other algorithms, the best fitness function curves based on the data from 30 independent runs are plotted and shown in Figure 8 and Figure 9. For CEC19-F1 and CEC19-F2, which are highly conditioned, non-separable, and fully parameter-dependent multimodal problems, the HLCCOA, SCSSA, and COA converged rapidly and performed admirably. For CEC19-F3, which is multimodal but not highly conditioned, SCSSA took the lead, with the HLCCOA also surpassing algorithms such as AOA, SPBO, and WOA. In functions CEC19-F4 to CEC19-F8, which have a large number of local optima, the HLCCOA stands out, especially in CEC19-F7, where it surpasses other algorithms in the later stages of iterations. In function CEC19-F8, the HLCCOA achieves better solutions during the middle and later stages. For multimodal, non-separable problems CEC19-F9 and CEC19-F10, the HLCCOA closely follows WOA and SPBO, showing its strong competitiveness. In CEC19-F10, the HLCCOA converges quickly and is significantly superior to the other competitors. For the unimodal function CEC22-F1, the HLCCOA approaches local optimality with the highest precision compared with 10 other competitive algorithms. In the case of multimodal functions CEC22-F2 to CEC22-F5, the HLCCOA demonstrates an effective ability to avoid the pitfalls of local optima. With regards to the composite functions CEC22-F6 to CEC22-F8, the HLCCOA exhibits rapid convergence in dealing with non-smooth optimization problems. As for the composite functions CEC22-F9 to CEC22-F12, the HLCCOA shows significant improvements in its ability to handle multiple interacting optimization issues.

The time complexity of optimization algorithms is primarily influenced by the complexity of the objective function, the size of the population, and the number of evolutionary iterations. Since the population size and target functions are consistent across different algorithms in this experiment, the number of evolutionary generations is used to assess the computational burden of the algorithms. Figure 8 and Figure 9 demonstrate that, in the tests for CEC2019, CEC2022-10D, and CEC2022-20D, the HLCCOA often finds better solutions within fewer iterations. Specifically, for CEC2019, functions F4, F6, F7, F8, and F10 reached optimal solutions in 200, 100, 410, 350, and 150 generations, respectively; for CEC2022-10D, functions F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, and F11 achieved optimal outcomes in 400, 60, 100, 200, 100, 100, 120, 220, 100, 20, and 80 generations, respectively; while for CEC2022-20D, functions F1, F2, F3, F4, F5, F6, F7, F8, F10, F11, and F12 achieved their best results in 260, 60, 100, 100, 40, 100, 200, 20, 20, 100, and 400 generations, respectively. Overall, the HLCCOA demonstrates a remarkable optimization advantage for these problems.

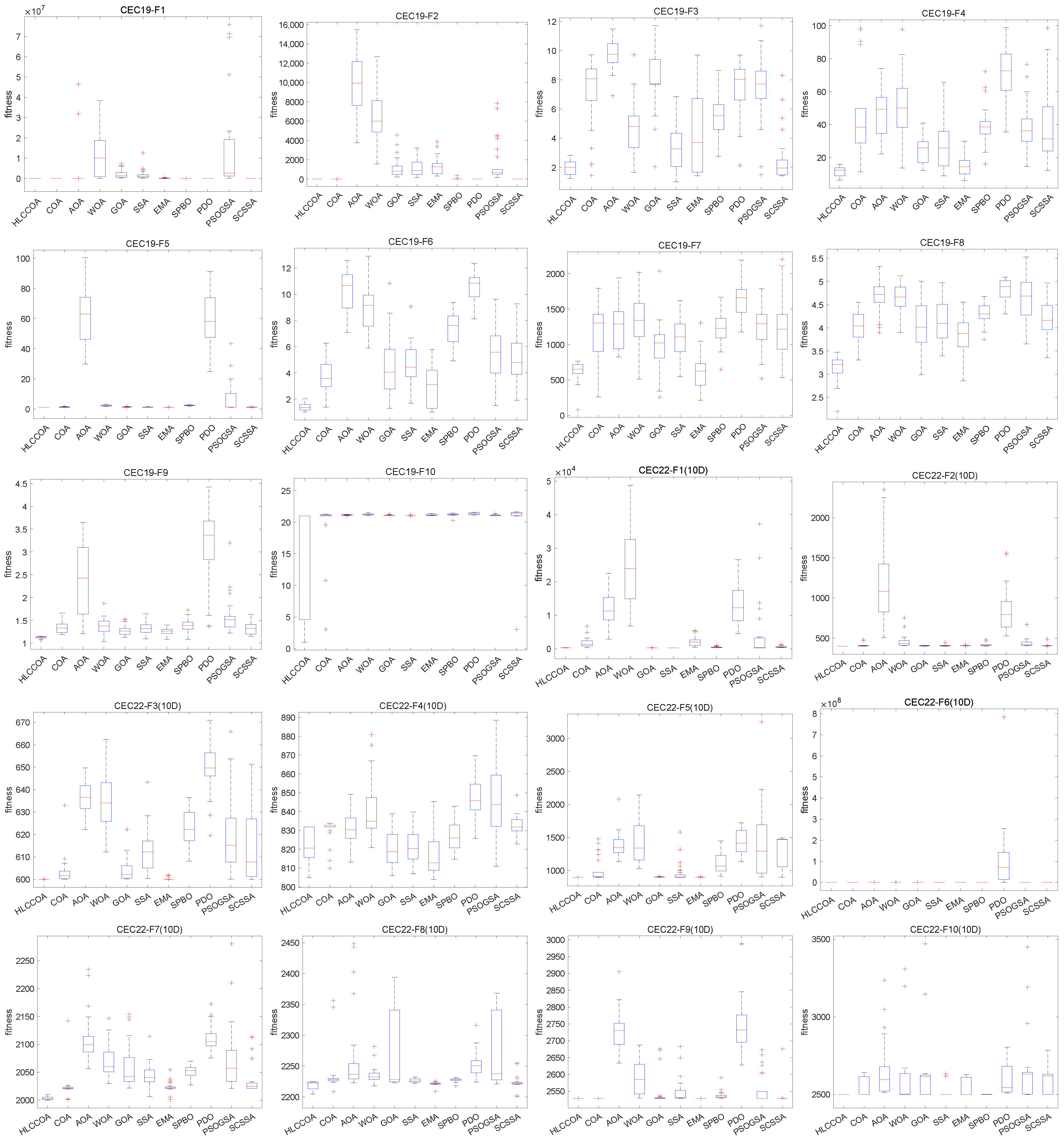
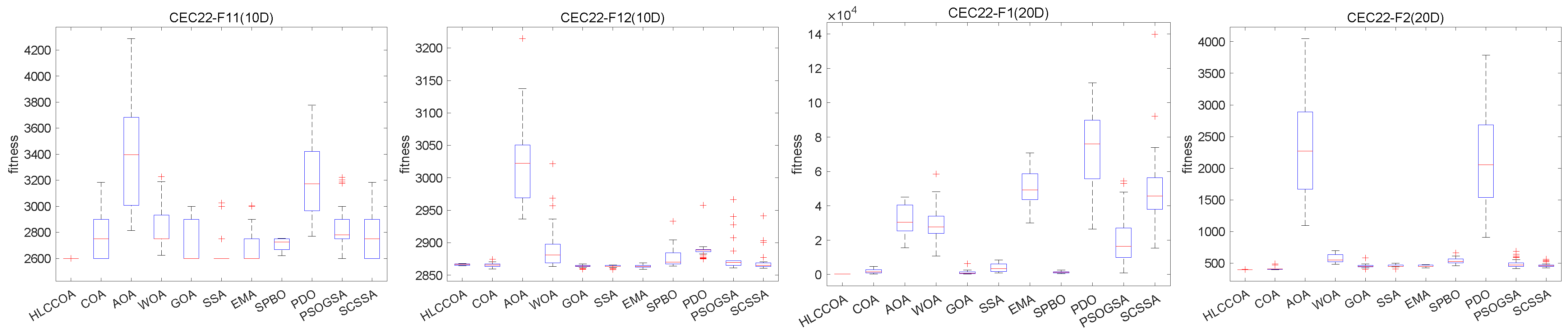
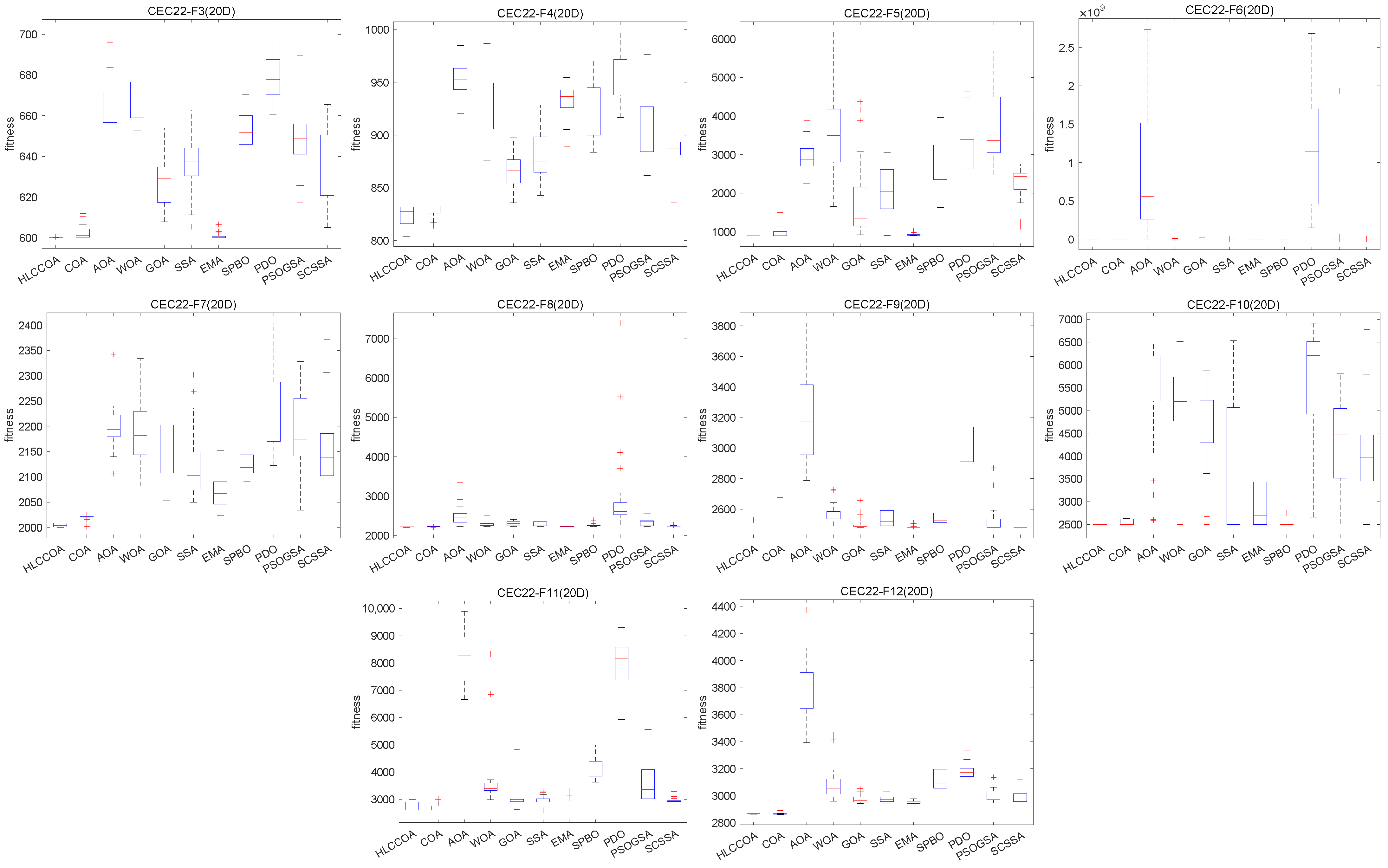
4.4. Analysis of Box Plot Results

To visually present the performance distribution of the algorithms, Figure 10 and Figure 11 display the box plots of the HLCCOA and its competing algorithms. The box plots illustrate the final outcome of 30 independent runs, including the median, quartiles, and extremes (marked with a red “+”). In the face of test functions CEC19-F1 and CEC19-F2, the HLCCOA, COA, PDO, and SCSSA all record obtaining the optimal solution in 30 runs. When dealing with the CEC19-F3 problem, although SSA has the chance to achieve the best result, its variability is higher than that of the HLCCOA. For the CEC19-F7 problem, excluding extremes, the lowest end of the EMA box plot is the lowest, indicating its potential to find the optimal solution; however, the box plot of the HLCCOA has a relatively narrow border, which indicates its good stability. For CEC22-F6, CEC22-F8, CEC22-F9, and CEC22-F12, the HLCCOA achieves similar statistical distribution results as COA, but the median of its statistics is better than the rest of the competitors. On other problems, the HLCCOA’s box plots are typically narrower, and the median is lower, indicating both good fitness and robust performance. Especially when dealing with the CEC19-F10 problem, the bottom of the HLCCOA’s box plot is the lowest, suggesting a greater likelihood of outperforming other competitors in searching for the optimal solution.

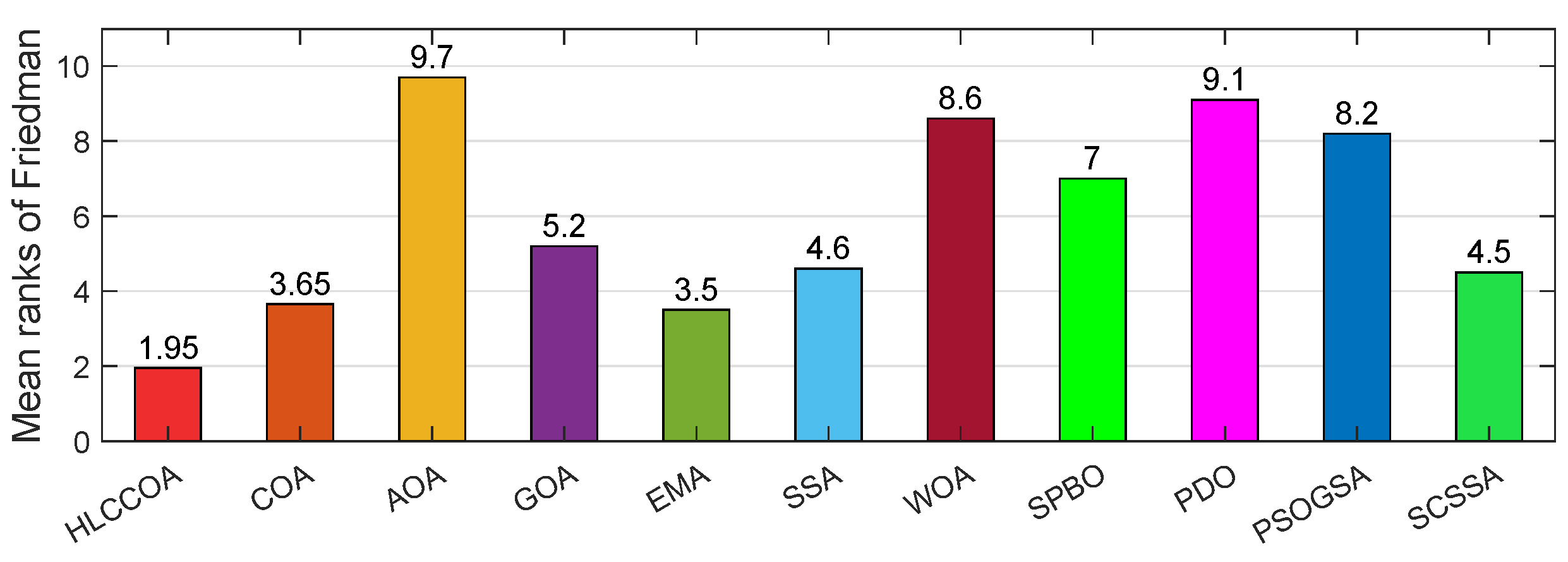
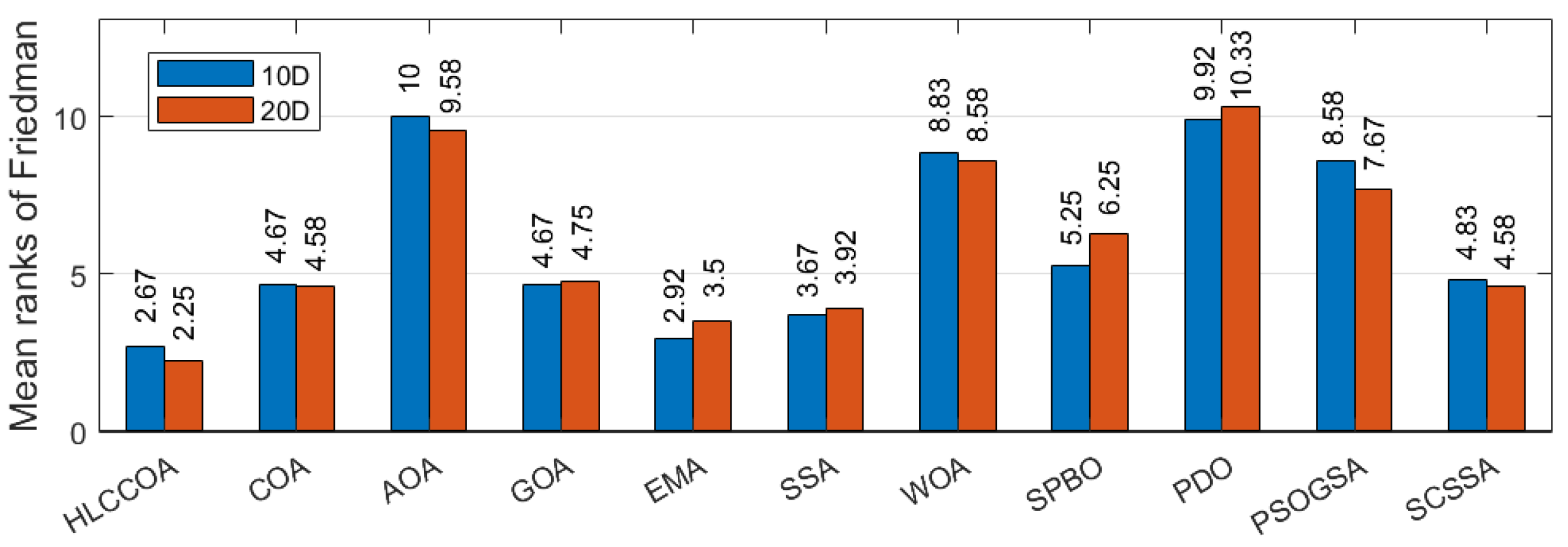
4.5. Friedman Test for the HLCCOA

In order to fairly and comprehensively compare the performance of different algorithms, the Friedman test [56] is utilized to calculate the average ranks of each algorithm on the CEC2019 and CEC2022 test sets. Figure 12 and Figure 13 respectively present bar charts of the Friedman average ranks of the HLCCOA and other competing algorithms on the two test sets. From Figure 12, it can be observed that the HLCCOA holds the top position with an average rank of 1.95, followed by EMA, COA, SCSSA, and SSA. Figure 13 demonstrates that, in 10-dimensional and 20-dimensional problems, the HLCCOA achieves average ranks of 1.42 and 1.33, respectively, surpassing EMA, SSA, COA, and GOA, and significantly outperforming the AOA, WOA, PDO, and PSOGSA algorithms. These results highlight the outstanding competitiveness and superiority of the HLCCOA algorithm in solving non-convex complex problems.

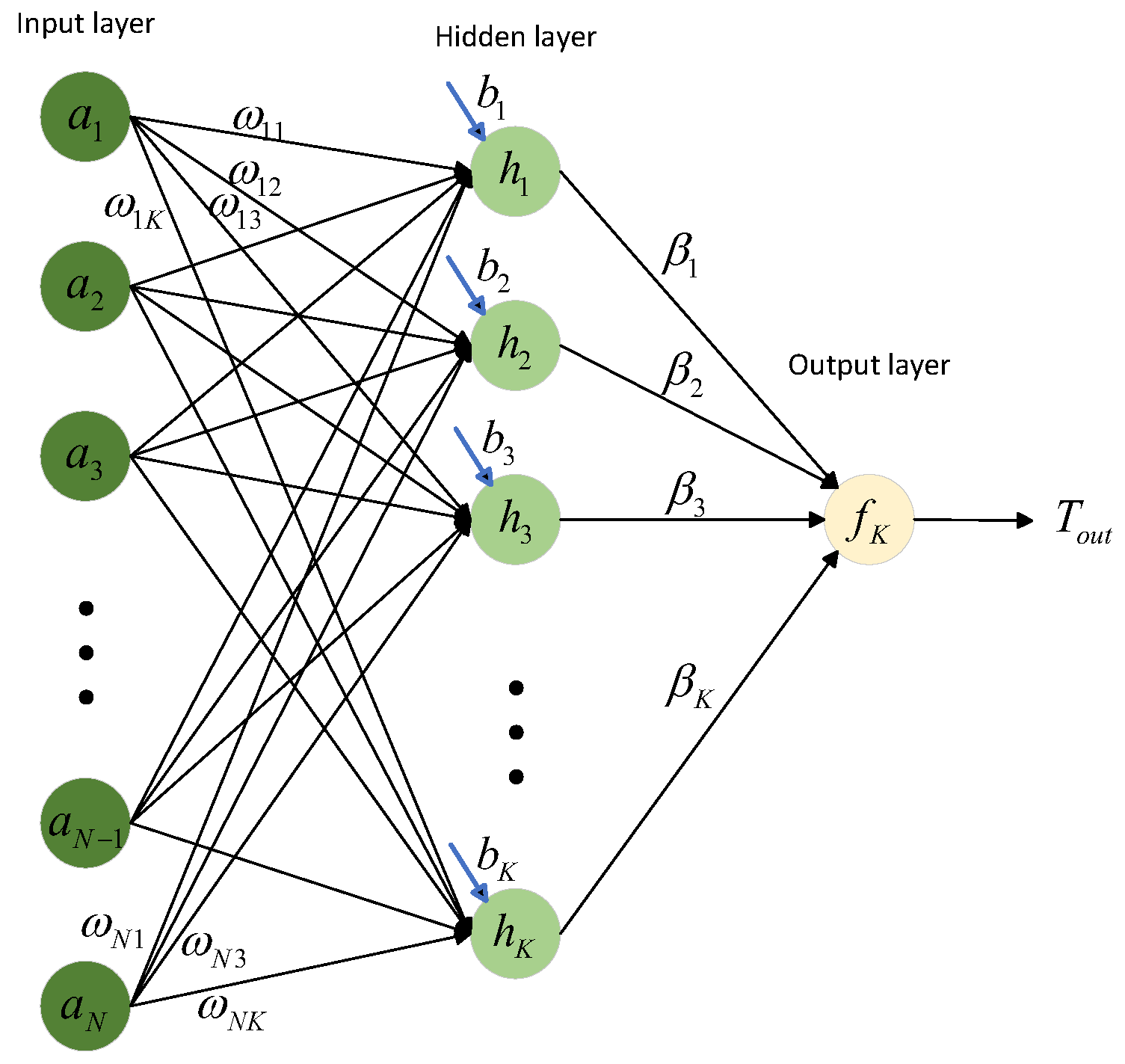
5. Breast Cancer Detection Based on the HLCCOA-ELM

Breast cancer (BC) is a common hereditary disease characterized by the uncontrolled proliferation and expansion of breast cells [57]. If breast cancer cells are not identified and differentiated early on, the diseased cells may invade adjacent vital organs, potentially posing a threat to life. Despite significant breakthroughs in research and treatment of breast cancer, it remains a major global public health issue, presenting ongoing challenges [58]. The extreme learning machine (ELM) [59], a type of single hidden-layer feedforward neural network, is widely used in classification and regression tasks due to its rapid and effective characteristics. Its theoretical framework is shown in Figure 14. The learning process of ELM primarily consists of two steps:

• Assume that the input of the ELM consists of N distinct samples $(a_i,t_i)$, with a hidden layer composed of K neurons. Further, $a_i={[a_{i1},a_{i2},\dots ,a_{in}]}^T$ is the n-dimensional input vector for the i-th sample, and $t_i={[t_{i1},t_{i2},\dots t_{il}]}^T$ is the l-dimensional output vector for the i-th sample. Random values are assigned to the connection weights ${\omega }_{i,j}$ ($i=1,2,\dots ,N$, $j=1,2,\dots K$) and to the biases $b_j$ ($j=1,2,\dots K$) between the input and hidden layers. Subsequently, the hidden layer output matrix H is generated. The expression for H is as follows:

  $$\begin{array}{c}H=\left[\begin{array}{ccc}{h}_1({\omega }_{1,1}·a_1+b_1)& \cdots & h_K({\omega }_{1,K}·a_1+b_K)\\ ⋮& \cdots & ⋮\\ h_1({\omega }_{N,1}·a_N+b_1)& \cdots & h_K({\omega }_{N,K}·a_N+b_K)\end{array}\right].\hfill \end{array}$$

  (20)
• The output function of the ELM can be expressed as follows:

  $$f_K=\sum _{j=1}^K{\beta }_j{h}_j(w_j,a,b_j)=H\beta ,$$

  (21)

  where ${\beta }_j$ represents the weight vector connecting the j-th hidden neuron to the output neurons, and $\beta =[{\beta }_1,{\beta }_2,\dots ,{\beta }_K]$ denotes the collective set of weight vectors between the hidden layer and the output layer. To achieve the minimum training error for the network, it is necessary to find the least squares solution $\widehat{\beta }$ for the linear system $H\beta =T$, where T is the real output of the ELM. This training process can be represented through Equations (22) and (23):

  $$\underset{\beta }{\arg \min }{∥T-H\beta ∥}_2,$$

  (22)

  $$\widehat{\beta }=H^{†}T,$$

  (23)

  where $H^{†}$ represents the Moore–Penrose generalized inverse matrix of H. The final output of the network can be obtained using Equation (24):

  $$T_{out}={\left(H\widehat{\beta }\right)}^T.$$

  (24)

In the field of BC research and diagnosis, the ELM is widely employed as a computer-aided diagnosis technique (CAD), primarily aimed at assisting physicians in making more accurate and prompt diagnostic decisions [60]. Despite the significant advantages demonstrated by the ELM, it does carry certain limitations [61]: the performance of the ELM is highly contingent upon the initial settings of the network structure. Due to the random generation of hidden-layer weights and biases, this may lead to instability in its generalization ability. In some instances, the ELM is capable of providing good generalization performance, but in other cases, particularly when dealing with extremely complex or noisy datasets, its performance might diminish.

To enhance the generalization ability, stability, and reliability of the ELM in processing nonlinear and complex data, this paper proposes an HLCCOA-optimized extreme learning machine model, i.e., HLCCOA-ELM, primarily applied in the classification diagnosis of breast cancer. The algorithmic flowchart of the model is shown in Figure 15. In this approach, the hidden layer weights and biases of the ELM are conceptualized as a solution set $P=[{\omega }_{11},\dots ,{\omega }_{NK},b_1,\dots ,b_K]$, which the optimization algorithm aims to refine. Initially, the positions of the individuals in the population are randomized in accordance with the dimensions of solution space P. These positions are dynamically updated as the HLCCOA algorithm progresses. Upon meeting the termination criteria, the algorithm yields the optimal initial parameters for the ELM’s network structure, as determined by the HLCCOA. To verify the efficacy of the HLCCOA-ELM model, this research selected the Wisconsin Diagnostic Breast Cancer (WDBC) data from the publicly available UCI dataset for classification experiments. In these experiments, the model uses the sine function as the activation function, has 30 input features and 8 neurons in the hidden layer, with the output being a binary classification indicating whether or not breast cancer is present. The population size of the HLCCOA algorithm is set to 30, and the number of iterations is set to 100. Further, $70\%$ of the dataset is used for training, and the remaining $30\%$ for testing, with classification accuracy as the main metric for assessing the iterative effects of the HLCCOA, conducted in 10 independent runs. For a fair assessment of the performance of the HLCCOA-ELM, the study also presents test results of the ELM model optimized by COA under the same experimental conditions. Figure 16 displays the confusion matrix diagrams corresponding to the highest accuracy rates of the standard ELM, COA-ELM, and HLCCOA-ELM, respectively, in 10 independent runs. The accuracy rate of the HLCCOA-ELM reached as high as $99.4152\%$, followed by COA-ELM at $98.8304\%$, and that of standard ELM only $95.3216\%$.

Table 6. Comparisons of the proposed model with benchmark models.

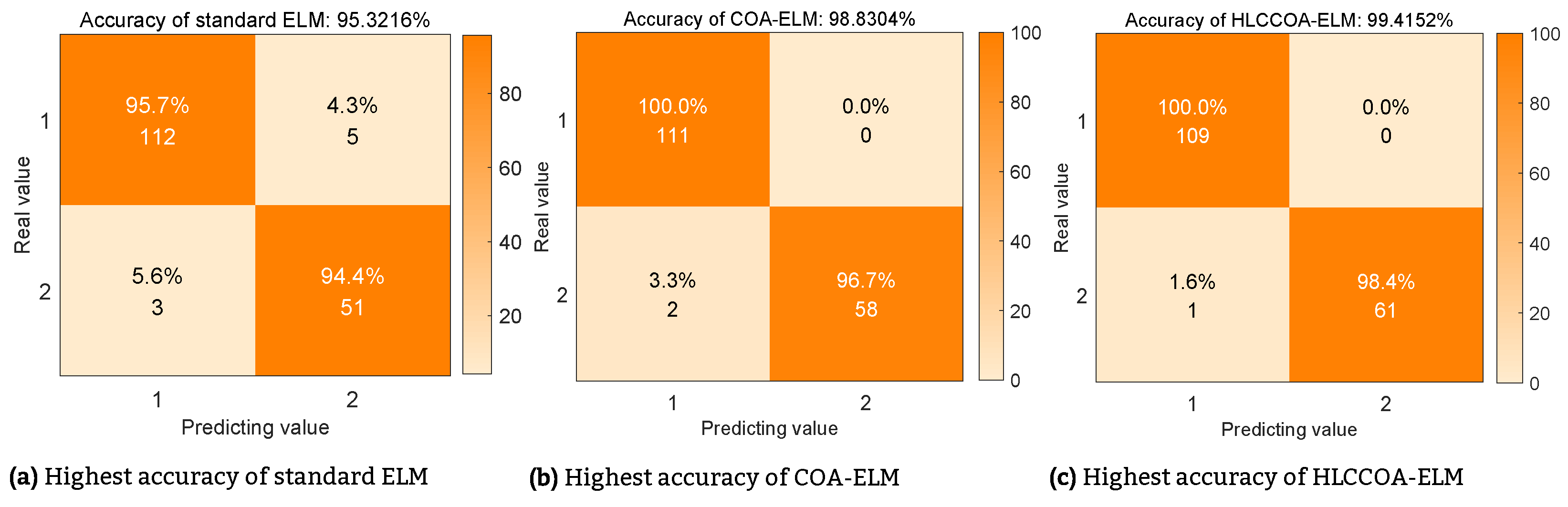
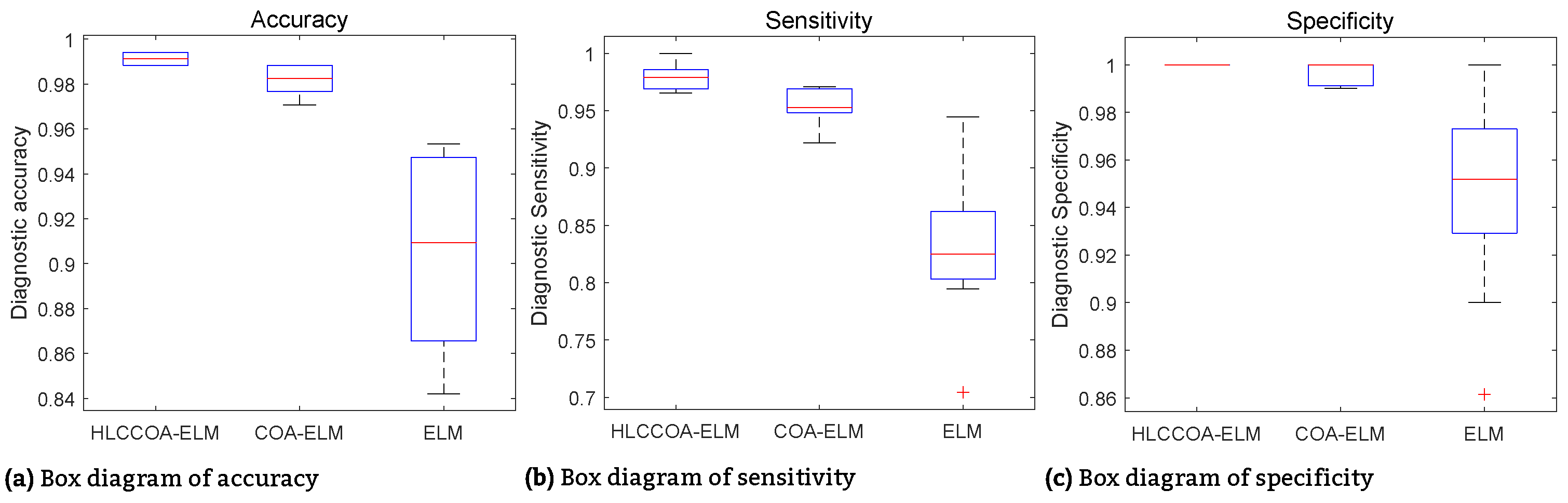
	Model	Lowest (%)	Highest (%)	Average (%)	Std (%)
Accuracy	BPNN	84.0237	94.0828	91.0651	3.0108
	GRNN	89.9408	89.9408	89.9408	0.0000
	ELM	84.2110	95.3220	90.3510	4.0539
	FW-ELM	94.0828	96.4497	95.0888	0.7026
	FW-HHO-ELM	97.0414	98.8166	97.7515	0.4428
	FW-WOA-ELM	96.4497	98.8166	97.8107	0.6509
	FW-AFSA-ELM	95.8580	98.2249	97.0414	0.7001
	FW-PHHO-ELM	98.2249	99.4083	98.7574	0.3187
	COA-ELM	97.0760	98.8300	98.1290	0.6639
	HLCCOA-ELM	98.8300	99.4150	99.1230	0.3082
Sensitivity	BPNN	70.4918	95.0820	82.9508	7.5196
	GRNN	86.8852	86.8852	86.8852	0.0000
	ELM	70.4230	94.4444	83.1400	6.4359
	FW-ELM	85.9649	91.2281	88.7719	1.4035
	FW-HHO-ELM	94.7368	98.2456	96.3158	1.4573
	FW-WOA-ELM	94.7368	96.4912	96.1404	0.7018
	FW-AFSA-ELM	92.9825	98.2456	95.9649	1.3702
	FW-PHHO-ELM	96.4912	98.2456	97.3684	0.8772
	COA-ELM	92.1880	97.1010	95.4630	1.5433
	HLCCOA-ELM	96.5520	100.0000	97.9970	1.3076
Specificity	BPNN	89.8148	99.0741	95.6481	3.0160
	GRNN	91.6667	91.6667	91.6667	0.0000
	ELM	86.1390	100.0000	94.7000	4.2570
	FW-ELM	96.4286	100.0000	98.3036	1.1607
	FW-HHO-ELM	97.3214	100.0000	98.4821	0.8036
	FW-WOA-ELM	96.4286	100.0000	98.6607	1.1469
	FW-AFSA-ELM	95.5357	99.1071	97.5893	1.2012
	FW-PHHO-ELM	99.1071	100.0000	99.4643	0.4374
	COA-ELM	99.0100	100.0000	99.7180	0.4545
	HLCCOA-ELM	100.0000	100.0000	100.0000	0.0000

and

Table 7. Comparisons of the proposed model with benchmark models.

Reference	Model	Acc (%)	Sens (%)	Spec (%)
Proposed model	HLCCOA-ELM	99.123	97.997	100
	COA-ELM	98.129	95.463	99.718
Feng et al. [60]	FW-PHHHO-ELM	98.76	97.37	99.46
Pratheep et al. [62]	FW-BOA-RDF	–	84	100
Singh et al. [63]	FW-ALO-BPNN	98.37	96.43	99.52
Wang et al. [64]	IRFRE	95.09	93.4	96.09
Abdel-Basset et al. [65]	FS-TMGWO-KNN	94.82	–	–
Naik et al. [66]	FS-BBA-OGCNN	93.54	90.76	95.24
Rao et al. [67]	FS-ABC-GBDT	92.8	–	–
Wang et al. [68]	SVM-Ensemble	97.68	94.75	99.49

summarize the test results of other ELM optimization models across 10 independent runs, including detailed assessments of accuracy, sensitivity, and specificity. These tables specifically present the lowest, highest, average, and standard deviation values for each of these evaluation criteria. The data for these models are derived from test results obtained under the same experimental conditions as those documented in other literature [60,62]. The comparative results clearly demonstrate the high accuracy, sensitivity, and specificity of the HLCCOA-ELM model, as well as the commendable generalization performance.

Furthermore, to investigate the impact of the number of hidden neurons and the HLCCOA population size on the ELM model, box plots from 10 independent experiments are drawn, as shown in Figure 17 and Figure 18. Figure 17 displays the diagnostic accuracy, sensitivity, and specificity of the model when the number of hidden layer neurons is 4, 8, 12, 16, 20, and 24. Although the specificity reaches the highest values, the HLCCOA-ELM model with 12 hidden neurons exhibits the highest median values for accuracy and sensitivity and the narrowest box plot, indicating the best model stability. Additionally, Figure 17 also indicates that increasing the number of hidden layer neurons does not necessarily enhance model performance. Figure 18 shows the diagnostic accuracy, sensitivity, and specificity for HLCCOA population sizes of 10, 30, 50, 70, 80, and 100. While all population sizes achieve the highest specificity, the HLCCOA-ELM model with a population size of 50 shows the highest median values for accuracy and sensitivity and the narrowest box plot, demonstrating optimal stability for this population size.

Figure 19 presents box plots for the HLCCOA-ELM, COA-ELM, and standard ELM models based on 10 independent trials conducted on the WDBC test set, illustrating the central tendency and dispersion for metrics such as accuracy, sensitivity, and specificity. It can be observed that the median value for the HLCCOA-ELM is the closest to 1 and exhibits the least dispersion among the data. This indicates that the HLCCOA-ELM not only maintains a high level of accuracy but also demonstrates strong robustness. Figure 20 depicts the fitness evaluation curves of the HLCCOA and COA during the ELM optimization process. The results indicate that the HLCCOA rapidly achieves an accuracy of $99.4152\%$ by the 11th generation, while COA only reaches an accuracy of $98.8304\%$ by the 66th generation. Additionally, the accuracy rates of both models are significantly higher than the optimum performance of the standard ELM model. Based on these results, it is apparent that the HLCCOA demonstrates higher applicability and effectiveness in such supervised learning optimization tasks.

6. Conclusions

This study presents the Hierarchical Learning-enhanced Chaotic Crayfish Optimization Algorithm (HLCCOA). Initially, the HLCCOA employs chaotic sequences from Tent and Chebyshev mappings for population initialization, enhancing diversity and improving global search effectiveness. The algorithm’s use of chaos’s excellent ergodicity increases the chances of identifying optimal solutions. To mitigate local optima challenges in complex non-convex problems, the HLCCOA incorporates a hierarchical learning mechanism. This approach prompts extensive cross-level learning for less efficient individuals to strengthen global exploration, while allowing high-performing individuals to learn directly from top-tier elites, refining their local exploitation skills. This strategy not only accelerates convergence but also balances exploration and exploitation. In comparative tests against 10 meta-heuristic algorithms using the CEC2019 and CEC2022 benchmarks, the HLCCOA shows superior effectiveness and robustness. Additionally, applying the HLCCOA to optimize the hidden layer weights and biases of extreme learning machines (ELMs) significantly enhances their generalization performance. The HLCCOA-ELM model, tested on the UCI breast cancer diagnostic dataset, validates the HLCCOA’s practicality and reliability, along with the strong generalization ability of the HLCCOA-ELM. Future work aims to apply HLCCOA to more complex real-world engineering challenges, including image segmentation, energy scheduling, and feature selection.