Sorting Permutations on an n − Broom
Abstract
1. Introduction
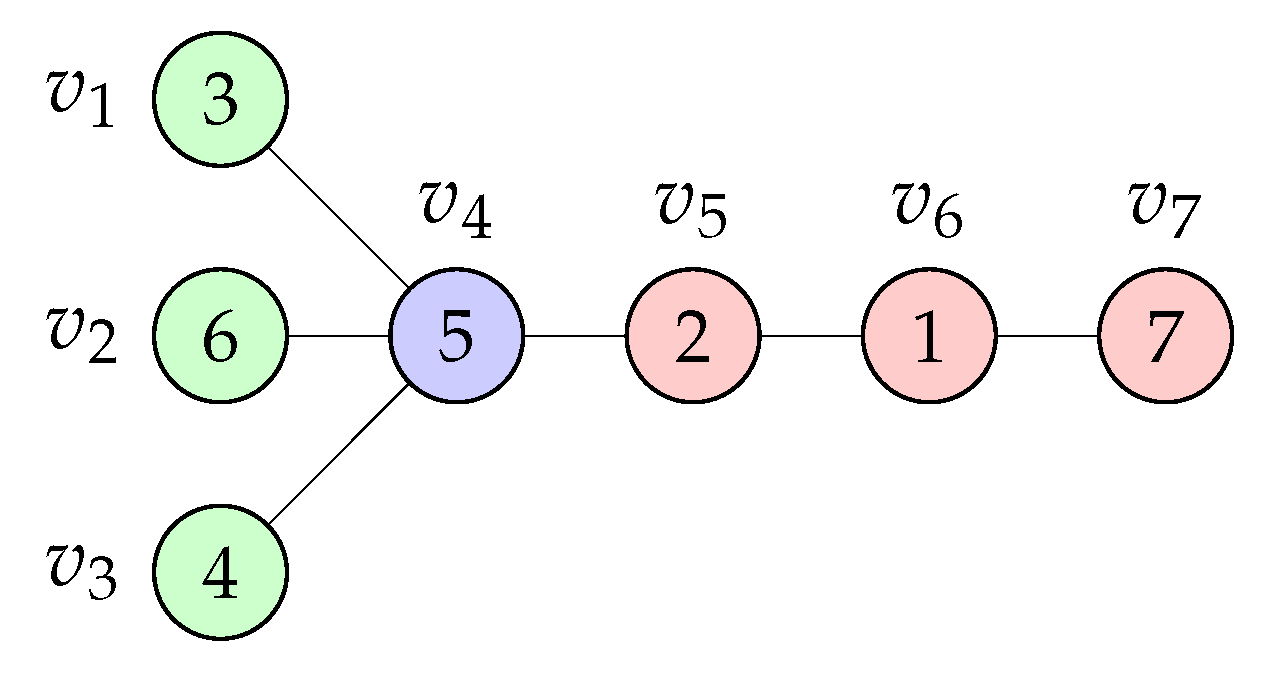
2. Preliminaries

3. Sorting Permutations with a Broom
3.1. Algorithm
- While there is a path token that is not home:
- (a)
- Let be the largest path token that is not home.
- (b)
- If is on a star leaf and there is a star leaf marker S on the center of the broom, home S.
- (c)
- Home .
- Solve the star.
- Assume that the marker t is homed prior to s. In this case, s will go to the center during the homing t process. Examine the markers’ arrangement on the broom immediately following t. s should be in the center in this case. We will now home s by swapping it with the marker on its home in accordance with the algorithm. Thus, in order to home the marker s, a total of two swaps were made in .
- Assume that before s, the marker t is not homed. Then, t should be in the home of s. Both of these markers will not be moved in the first step of our algorithm in this case. Only when solving the final star will s be moved. In this case, s and t should be a part of a chain in a star. The algorithm from [4] will be used to solve star in step 2. It is simple to observe that 2 is the number of swaps taken to home s.
3.2. Correctness of A*
- 1.
- No swap of two star markers occurs on a path edge.
- 2.
- For every swap on a path edge that involves a path marker, the larger of the two markers moves to the right.
- 3.
- No marker crosses the first path edge from left to right and later from right to left.
- 4.
- The path markers that cross the first path edge from left to right do so in order [14].
- Case 1: is on a non-center path vertex.
- Case 2: is in the center of the broom.
- Case 3: is on a star leaf vertex.
- If there is a star leaf marker in the center, then that marker will be homed first in .
- If there is a path marker in the center, then we will home first in .
- homing the markers in the center until there is a path marker in center.
- swapping the star leaf marker in the center with a path marker that is not in the home of .
- Swapping P with an un-homed star leaf marker, which is currently in a star leaf.
- Swapping P with a path marker currently residing in a star leaf.
- This swapping sequence will not be part of the optimal swap sequence
- The number of swaps is the same as that in the case where we are homing first.
4. Sorting Permutations with a
Algorithm
- Determine if the 2-broom is a union of two independent single brooms. If true, divide them and solve each broom using Algorithm A*.
- If a star leaf marker from the same star is present in the center of or , home it.
- (a)
- If there are star leaf markers ’s from in the center of and in the star leaves of , suppose a sequence of markers exists in consecutive vertices, from left to right, starting from the center of such that are star leaf markers of and t is another marker, then
- If t is not in the center of , swap with the marker on the right in that order.
- If t is in the center of , do the following:
- If t is a star leaf marker from , then, swap with the marker on the right in that order.
- Else, if there are any star leaf markers from in the star leaves of at this point.If the home of from is occupied by the star leaf markers , respectively, then if in the home of , there is a star leaf marker from , bring to the center such that the home of is occupied by a star leaf marker from . Otherwise, if there is a path marker in the home of , then move the smallest path marker out of these to the center. Else, move any one of the markers from to the center. Then, swap with the marker on the right in that order.Else, swap t with that star leaf marker whose home contains the largest marker out of all the markers in the home of the star leaf markers of in the star leaf of . Then, swap with the marker on the right in that order.
- Else, if there is a path vertex smaller than t in the star leaves of , swap t with the smallest of them first and then swap with the marker on the right in that order.
- Else, swap with the marker on the right in that order.
- (b)
- If the center of is occupied by a path marker P:
- If there are star leaf markers from in the star leaves of :If the home of from is occupied by the star leaf markers , respectively, then if in the home of , there is a star leaf marker from , bring to the center such that the home of is occupied by a star leaf marker from . Otherwise, if there is a path marker in the home of , then move the smallest path marker out of these to the center. Else, move any one of the markers from to the center.
- If there are path markers larger than P:Move the largest of them to the center by swapping with P.
- (c)
- Repeat Steps 1–3 until there are no more possible moves.
- (a)
- If there is a star leaf marker from in the center of and there is a star leaf marker from in the star leaves of , let us say there is a set of markers that are lined up from right to left, starting in the middle of . These markers are star leaf markers of , and t is another marker. We need to swap with the marker on the right, going in that order.
- (b)
- If the center of is occupied by a path marker P:
- If there exists a star leaf marker from in the star leaves of :Move the star leaf marker , whose home contains the largest marker out of all the markers in the home of star leaf markers of in the star leaf of , from to the center of by swapping it with P.
- If there are path markers larger than P:Move the largest of them to the center by swapping with P.
- (c)
- Repeat Steps 1, 2, and 4 until there are no more possible moves.
- (a)
- If there are any star leaf markers of in the path vertices, home the one closest to its home, and then repeat steps 1–4.
- (b)
- Else, if there are any star leaf markers of in the path vertices, home the one closest to its home, and then repeat steps 1–4.
- (c)
- Else, solve , , and the path independently.
5. Sorting Permutations with a for
5.1. Algorithm
- Determine if the contains a that contains all of its markers in itself. If true, remove the broom from and solve the using
- If a star leaf marker from the same star is present in the center of any of the star in , then home it.
- If there are star leaf markers from other stars in the center and the star leaves of a star , suppose that a sequence of markers exists in consecutive vertices, starting from the center of , in the direction of , such that are star leaf markers from other stars and t is some other marker. If t is not in , swap with the marker next to it in the direction of , in the given order.
- If there exists a path marker p in the center of , then
- (a)
- If there is a collection of star leaf markers from other stars in the star leaves of
- If there exists a single star leaf marker from a star other than , move it to the center of .
- Else, group the markers based on where their homes are and take a group. Out of all the markers in that group, find the markers whose home contains the markers that are farthest away from center and move one of them to the center.
- (b)
- Else, if there exist path markers s such that , then move one of the s with maximum value for to the center.
Repeat this process until there are no valid moves. - Perform steps 3 and 4 for all the stars in .
- Determine the clear path markers.
- (a)
- If there is a unique maximum clear path marker, home it.
- (b)
- Else, if there exists a chain of maximum clear path markers such that the path of to its home contains for and the path of to its home contains , then home in that order.
- (c)
- Else, if there are 2 maximum clear path markers, and such that is in the path of but is not in the path of , then home .
- (d)
- Item any one of the maximum clear path markers.
Repeat steps 1, 2, and 5 until there are no valid moves.
- Suppose s is in a path vertex and suppose that there exists a sequence of star leaf markers from other brooms in the adjacent vertices of s. It will then be swapped with all of these markers according to step 3 of . Keep in mind that these markers are moving closer to the center of the . This means that s is swapped closer to the star , which means it is moving closer to its home. At the end of this swap sequence, s will reach the center of the star and will become homed, as we discussed in Case 1.
- Imagine that it is not part of that swap sequence. Then, it will remain in the path until one of the following happens:
- (a)
- s becomes a maximum clear path marker.
- (b)
- A marker residing in , which is farther away from the center of the than s, becomes a maximum clear path marker before s.
In the first scenario, our result is obvious, since it will become homed directly at the moment, as per step 6 of . For that, it will take the shortest path from its position to its home and it will swap with the markers along that path until it gets home. In the second scenario, when the marker becomes homed, it will be swapped with s. It is very easy to note that s is moving closer to its home since is moving closer to the center of the at that instance. The above-mentioned swaps can happen until the s becomes a maximum clear path marker. Once it becomes a maximum clear path marker, as we mentioned in the first scenario, it will become homed directly, and during that, it will always move closer to its home.Case 3: If s is in the center of the , it will not be moved from there when we are executing steps 1 to 4. Now, if there exists a maximum clear path marker residing in whose home is in some other broom, then s will be part of the swap sequence to home according to step 5. Here, s will get moved to the broom , closer to its home. It is important to note that s will not be part of the swap sequence to home if it is a maximum clear path marker residing in some other brooms, because of the following reasons. If such a maximum clear path marker exists, then its home should be in the same broom. Otherwise, the path of this marker to its home will pass through the center of the , where s is, and as part of homing , the marker s will get moved away from its home, a contradiction to our assumption that is a clear path marker. Therefore, if such a marker exists, its home should be in the same broom. In that case, the path of to its home will not contain the center vertex and, as a consequence, the marker s will not become swapped when we are homing . The second possibility is when s is not part of any swap sequence until it becomes a maximum clear path marker. In this case, as we discussed earlier, it is easy to see that s will not be moved away from its home in any of the swaps it is part of.Case 4: Suppose s is residing in the path vertex of some other brooms. All the possible cases that we discussed in Case 3 are possible here, and we can show that s is not moving away from its home in any of these cases using similar arguments that we put forward in Case 3. A different possible scenario that can happen here is the following. Suppose that s is part of a sequence of star leaf markers in the path of the respective broom, as in step 3 of . In this case, as per algorithm , s will move closer to the center of the , i.e., closer to its home. Now, suppose that s is in the star leaf of some other broom. Then, by step 4 of algorithm , the following will happen: s will move to the center of the star by swapping the path marker in the center.If there is no other star leaf marker in the star leaves there, then s will stay there until it becomes a maximum clear path marker or until a star leaf marker from that star is homed. In the first scenario, the argument is the same as before. In the second one, s will first move to the path of the broom. Then, we can use the arguments given in the beginning of this case. If there is a star leaf marker from some other star in that star leaf, the same thing will happen: s will become moved to the first path vertex of that broom. Then, we can use the earlier arguments.
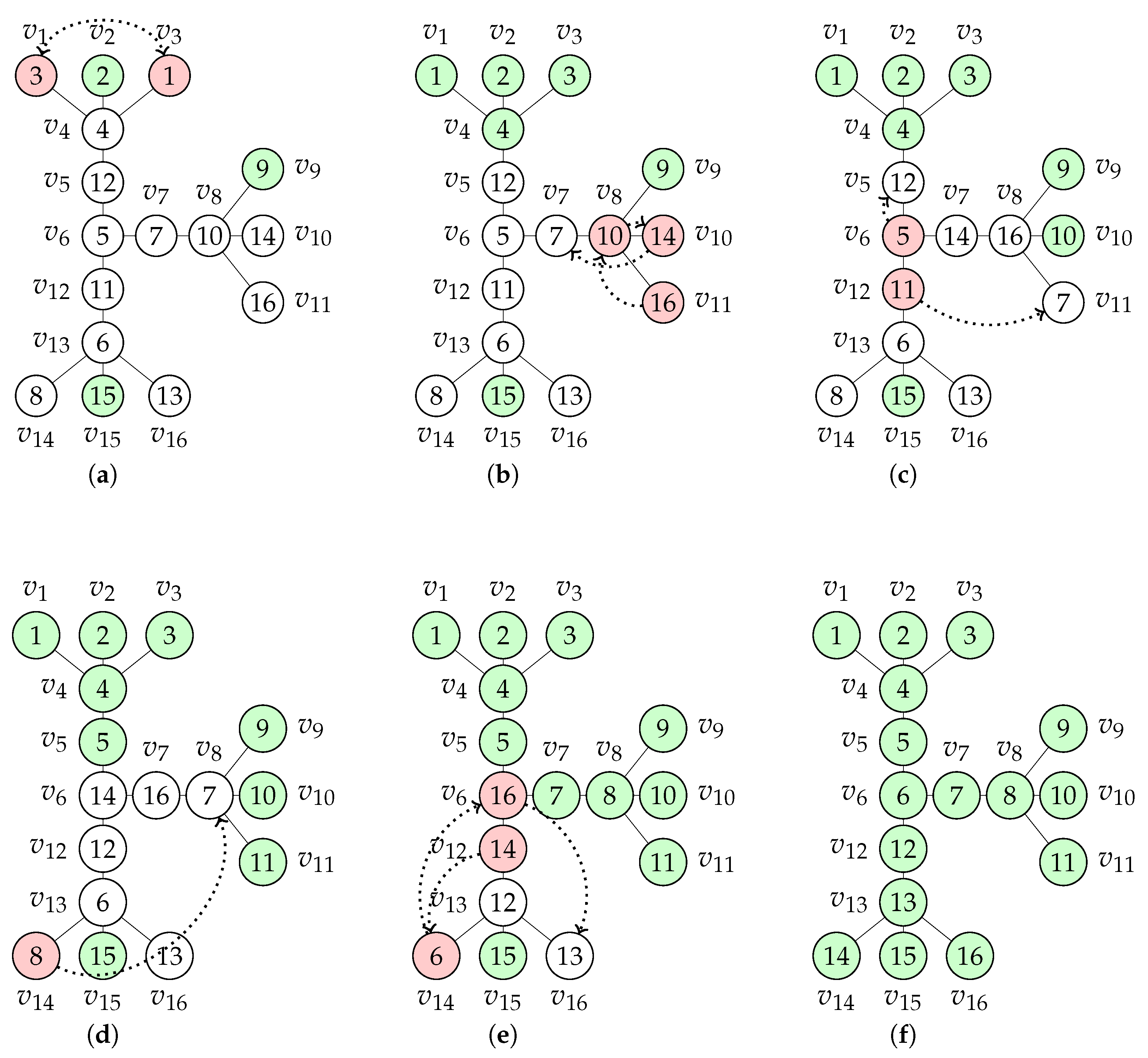
5.2. An Illustration of the Algorithm for Sorting
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Walter, M.E.M.; Curado, L.R.A.; Oliveira, A.G. Working on the problem of sorting by transpositions on genome rearrangements. In Combinatorial Pattern Matching: 14th Annual Symposium, CPM 2003 Morelia, Michoacán, Mexico, 25–27 June 2003; Proceedings 14; Springer: Berlin/Heidelberg, Germany, 2003; pp. 372–383. [Google Scholar]
- Christie, D.A. Genome Rearrangement Problems; University of Glasgow (United Kingdom): Glasgow, UK, 1998. [Google Scholar]
- Heydemann, M.-C. Cayley graphs and interconnection networks. In Graph Symmetry; Springer: Dordrecht, The Netherlands, 1997; pp. 167–224. [Google Scholar]
- Akers, S.B.; Krishnamurthy, B. A group-theoretic model for symmetric interconnection networks. IEEE Trans. Comput. 1989, 38, 555–566. [Google Scholar] [CrossRef]
- Lakshmivarahan, S.; Jwo, J.-S.; Dhall, S.K. Symmetry in interconnection networks based on Cayley graphs of permutation groups: A survey. Parallel Comput. 1993, 19, 361–407. [Google Scholar] [CrossRef]
- Xu, J. Topological Structure and Analysis of Interconnection Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 7. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming: Sorting and Searching, 2nd ed.; Pearson Education: London, UK, 1997; pp. 426–458. [Google Scholar]
- Mead, C.; Conway, S. Introduction to VLSI Systems; Addison-Wesley: Reading, MA, USA, 1980. [Google Scholar]
- Wang, M.; Guo, Y.; Wang, S. The 1-good-neighbour diagnosability of Cayley graphs generated by transposition trees under the PMC model and MM* model. Int. J. Comput. Math. 2017, 94, 620–631. [Google Scholar] [CrossRef]
- Wang, M.; Lin, Y.; Wang, S. The 2-good-neighbor diagnosability of Cayley graphs generated by transposition trees under the PMC model and MM* model. Theor. Comput. Sci. 2016, 628, 92–100. [Google Scholar] [CrossRef]
- Miltzow, T.; Narins, L.; Okamoto, Y.; Rote, G.; Thomas, A.; Uno, T. Approximation and hardness of token swapping. In Proceedings of the 24th Annual European Symposium on Algorithms (ESA 2016), Aarhus, Denmark, 22–24 August 2016; Volume 57. [Google Scholar]
- Bonnet, É.; Miltzow, T.; Rzazewski, P. Complexity of Token Swapping and Its Variants. Algorithmica 2017, 80, 2656–2682. [Google Scholar] [CrossRef]
- Portier, F.J.; Vaughan, T.P. Whitney Numbers of the Second Kind for the Star Poset. Eur. J. Comb. 1990, 11, 277–288. [Google Scholar] [CrossRef]
- Jain, B.A.; Lubiw, K.; Masárová, A.; Miltzow, Z.; Mondal, T.; Naredl, D.; Murty, A.; Josef, T.; Alexi, T. Token Swapping on Trees. arXiv 2019, arXiv:1903.06981. [Google Scholar]
- Sadanandan, I.T.; Chitturi, B. Optimal algorithms for sort- ing permutations with brooms. Algorithms 2022, 15, 220. [Google Scholar] [CrossRef]
- Vaughan, T.P. Factoring a permutation on a broom. J. Comb. Math. Comb. Comput. 1999, 30, 129–148. [Google Scholar]
- Kawahara, J.; Saitoh, T.; Yoshinaka, R. The Time Complexity of the Token Swapping Problem and Its Parallel Variants. Walcom Algorithms Comput. 2017, 10167, 448–459. [Google Scholar]
- Malavika, J.; Scaria, S.; Indulekha, T.S. On Token Swapping in Labeled Tree. In Proceedings of the 2021 Third International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 2–4 September 2021; pp. 940–945. [Google Scholar]
- Yamanaka, K.; Demaine, E.D.; Ito, T.; Kawahara, J.; Kiyomi, M.; Okamoto, Y.; Saitoh, T.; Suzuki, A.; Uchizawa, K.; Uno, T. Swapping labeled tokens on graphs. Theor. Comput. Sci. 2015, 586, 81–94. [Google Scholar] [CrossRef]
- Cayley, A. LXXVII. Note on the theory of permutations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1849, 34, 527–529. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajesh, R.; Sundaravaradhan, R.; Chitturi, B. Sorting Permutations on an n − Broom. Mathematics 2024, 12, 2620. https://doi.org/10.3390/math12172620
Rajesh R, Sundaravaradhan R, Chitturi B. Sorting Permutations on an n − Broom. Mathematics. 2024; 12(17):2620. https://doi.org/10.3390/math12172620
Chicago/Turabian StyleRajesh, Ranjith, Rajan Sundaravaradhan, and Bhadrachalam Chitturi. 2024. "Sorting Permutations on an n − Broom" Mathematics 12, no. 17: 2620. https://doi.org/10.3390/math12172620
APA StyleRajesh, R., Sundaravaradhan, R., & Chitturi, B. (2024). Sorting Permutations on an n − Broom. Mathematics, 12(17), 2620. https://doi.org/10.3390/math12172620





