Study on Ground Motion Amplification in Upper Arch Bridge Due to “W”-Type Deep Canyon Using Boundary-Integral and Peak Frequency Shift Methods
Abstract
1. Introduction
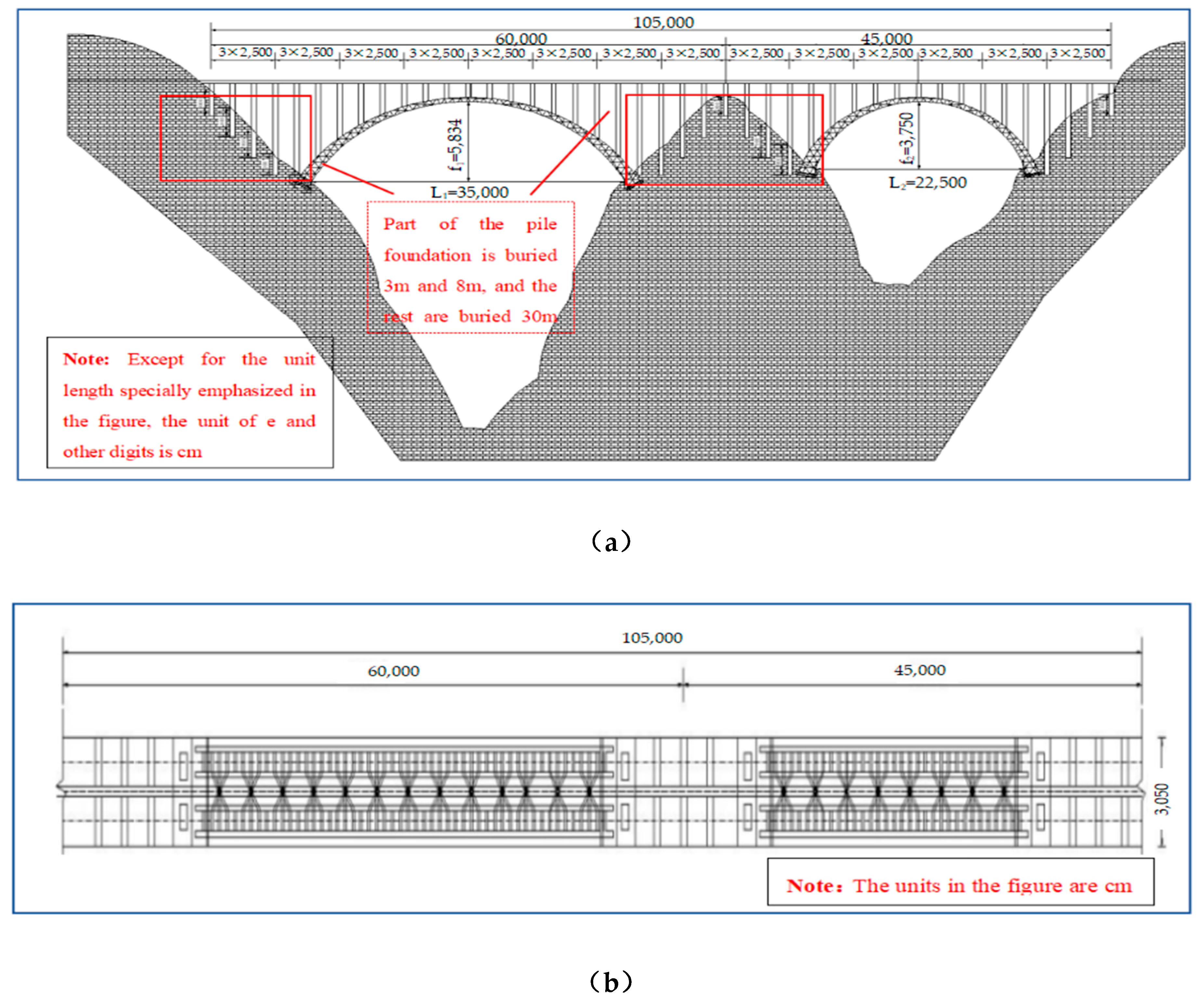
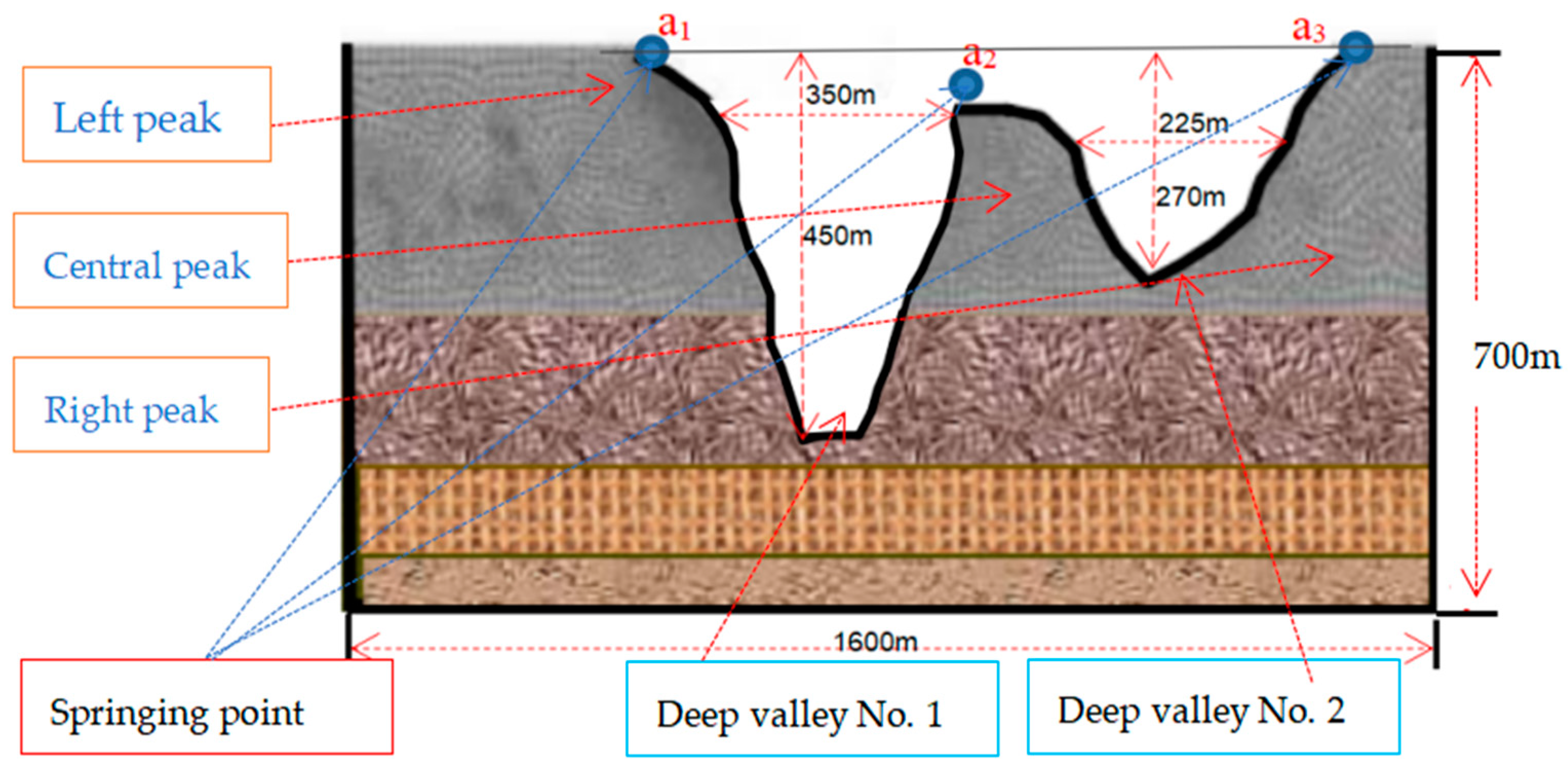
2. The Projects
Overview of Dependent Projects
3. Formula Calculation Principle
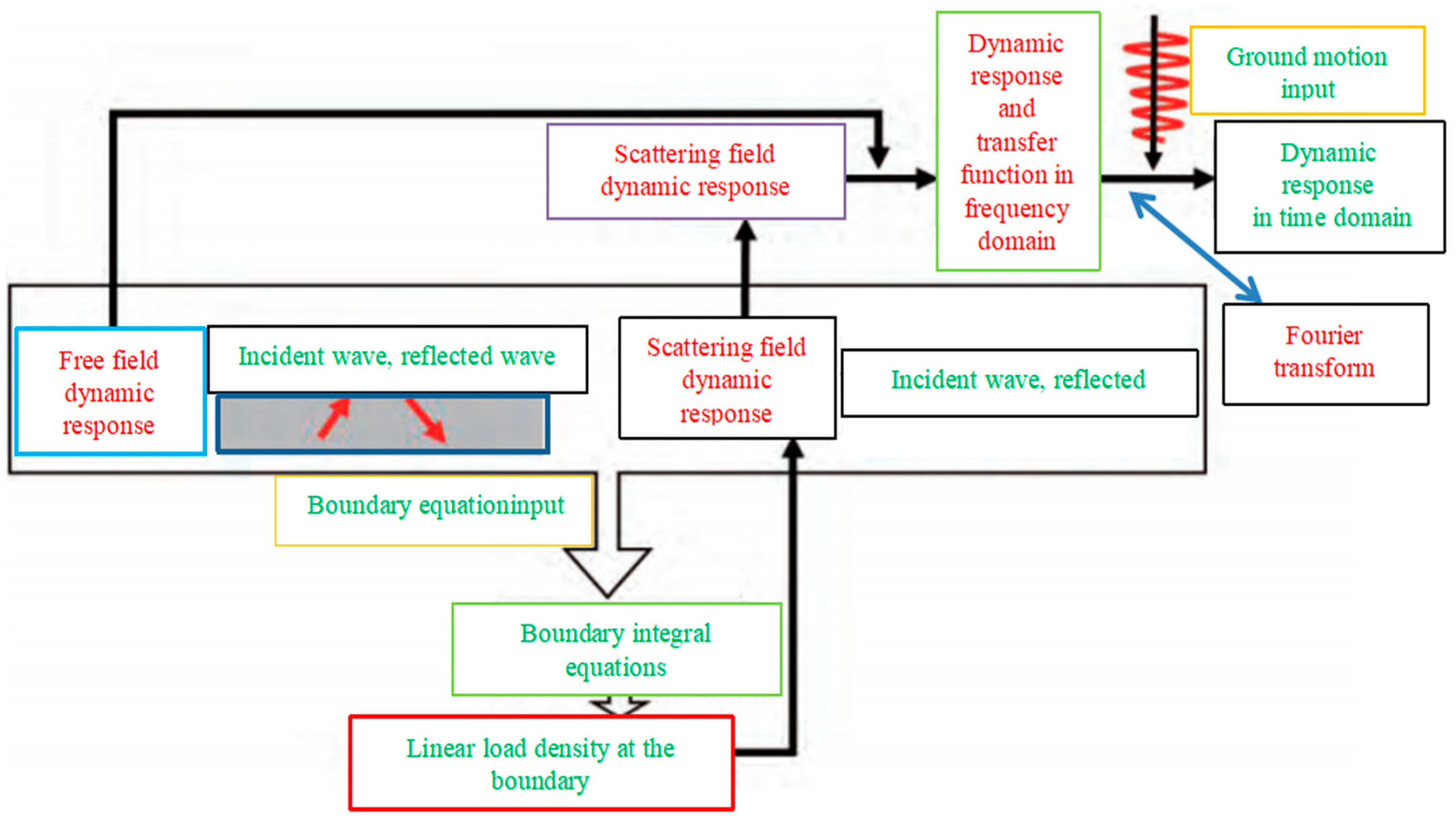
3.1. Boundary Integral Equation Method
3.2. Peak Frequency Shifting Method
4. Model Construction
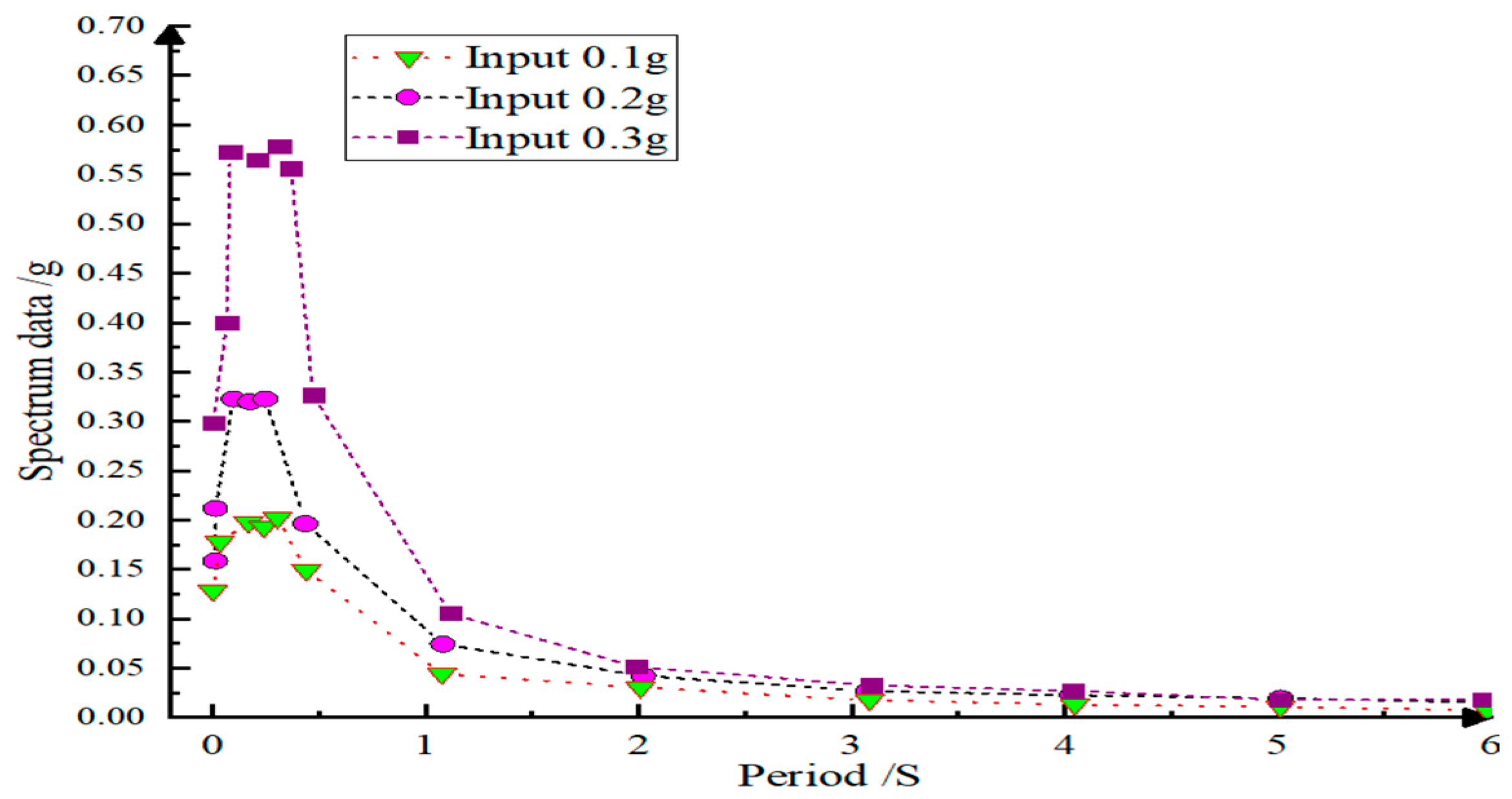
4.1. Loading Intensity and Corresponding Response Spectrum in the Model
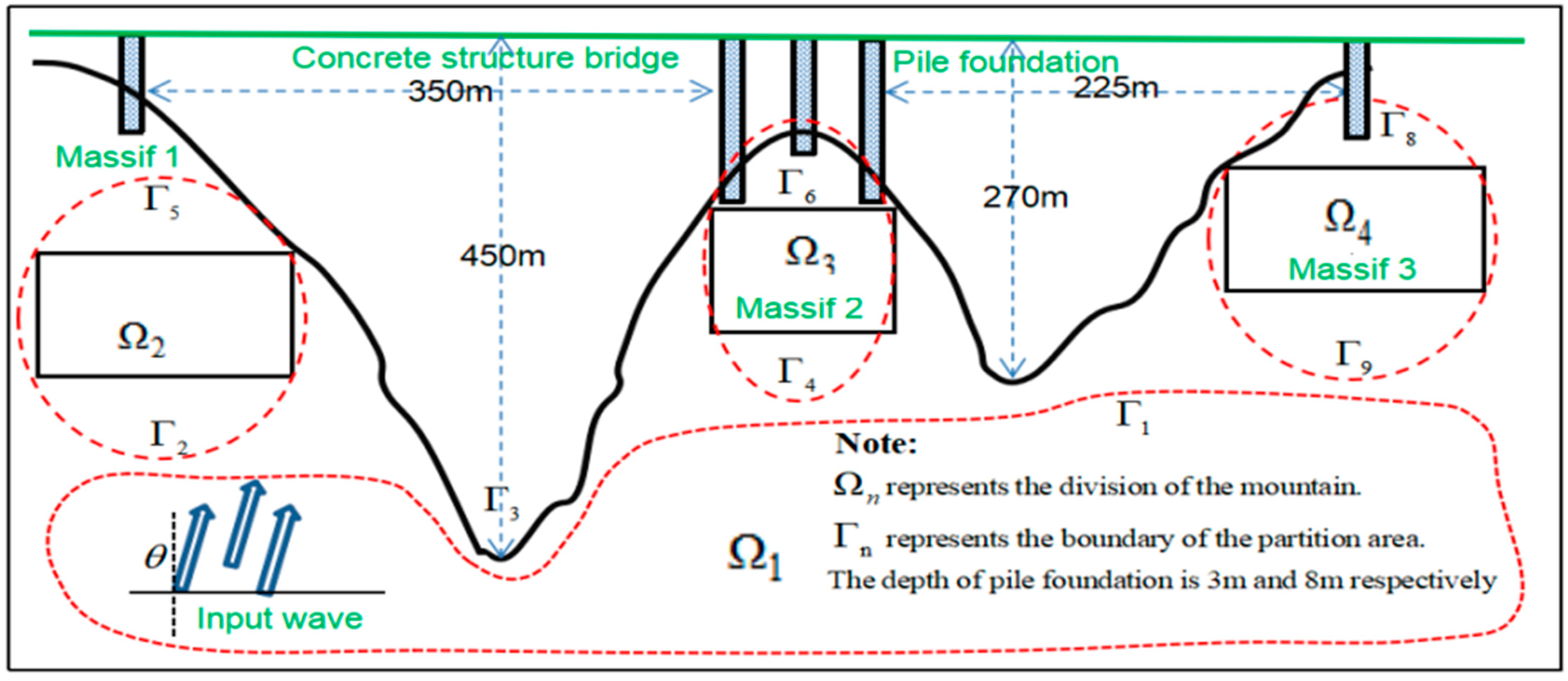
4.2. Establishment of Site Model
5. Test Results
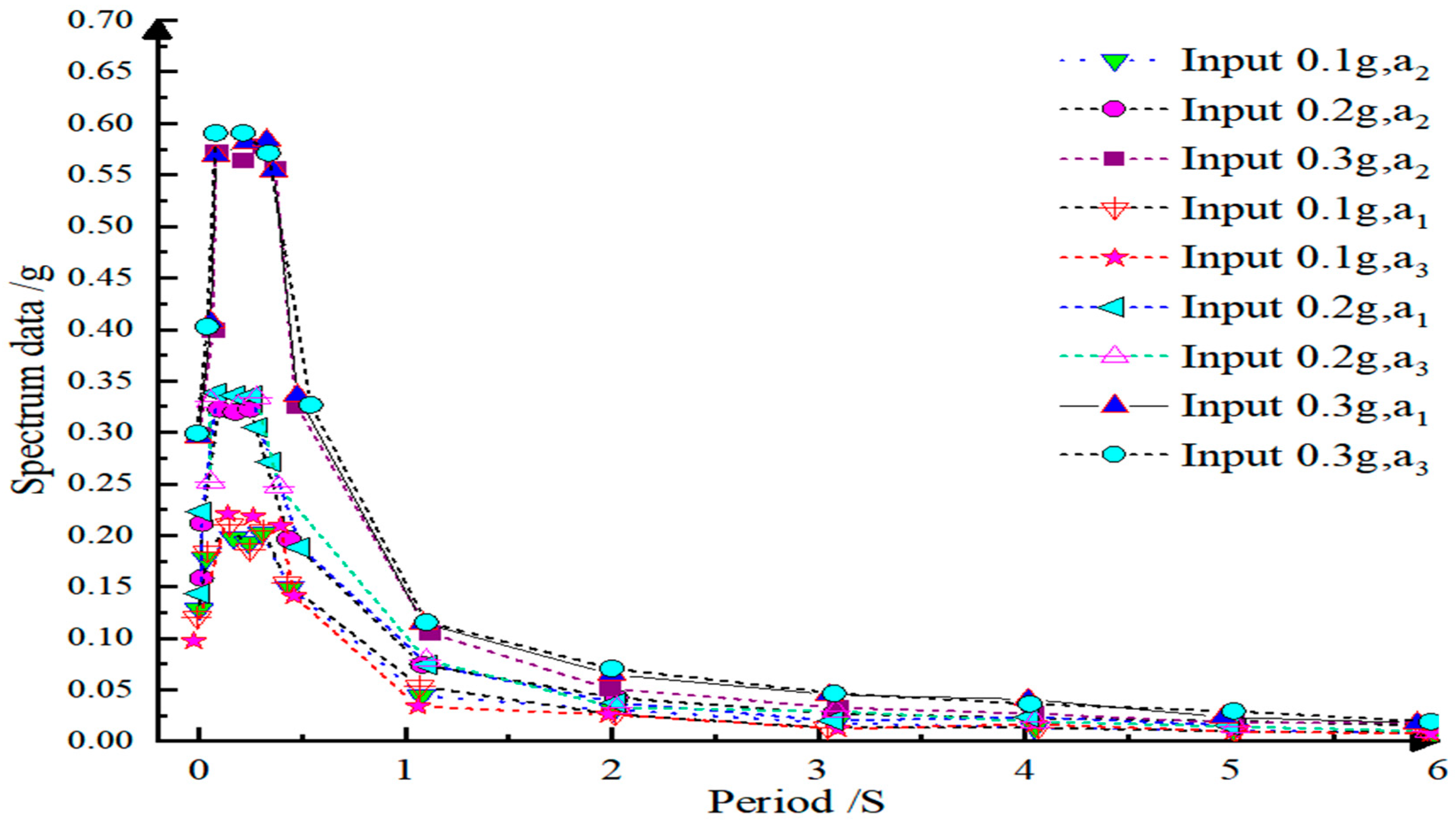
Analysis of Site Amplification Effect
6. Influence of Site Effect on Structural Seismic Response
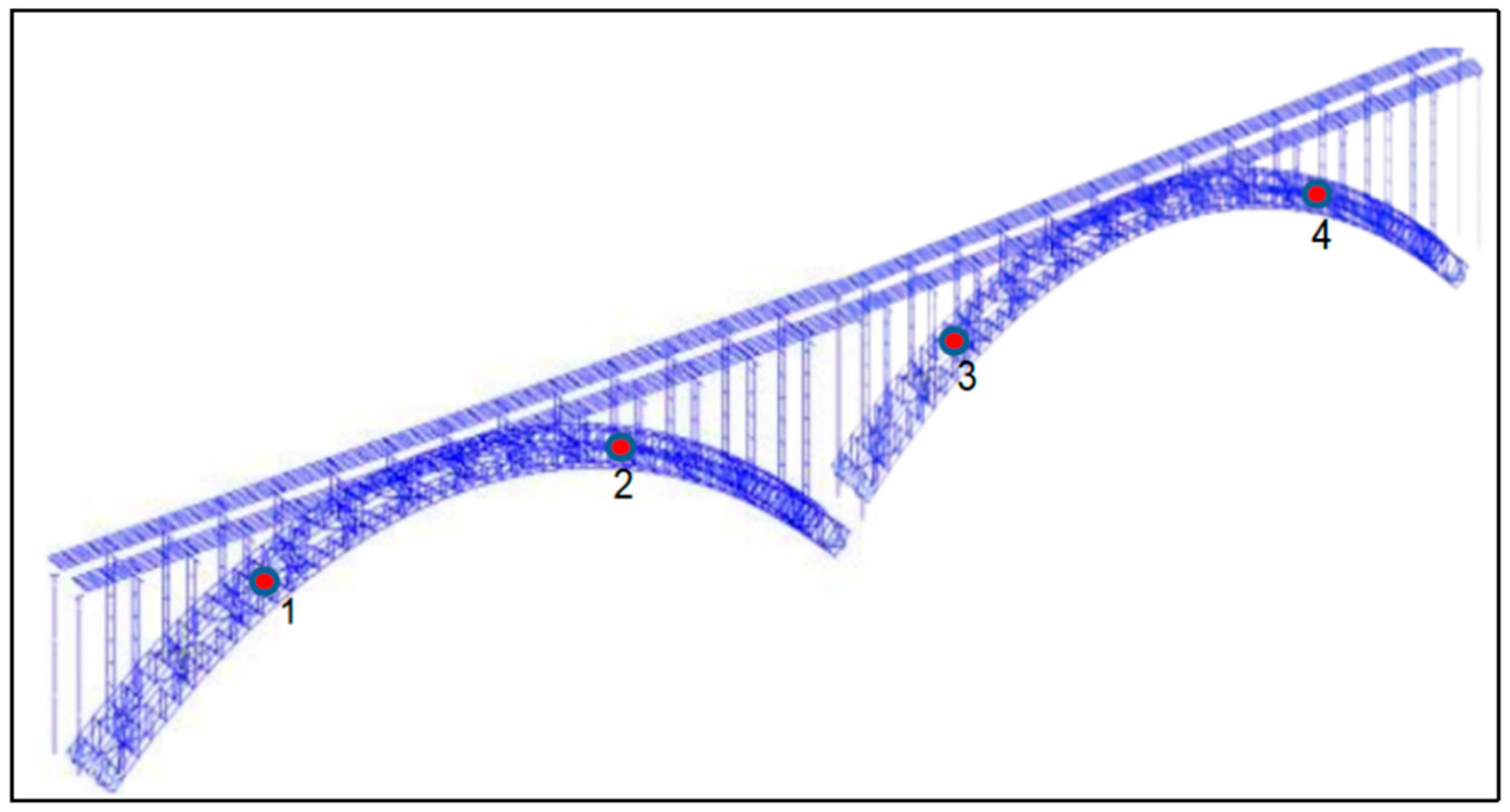
6.1. Dynamic Calculation Model
6.2. Analysis of Acceleration Response at the Top of the Structure under Different Loading Strengths
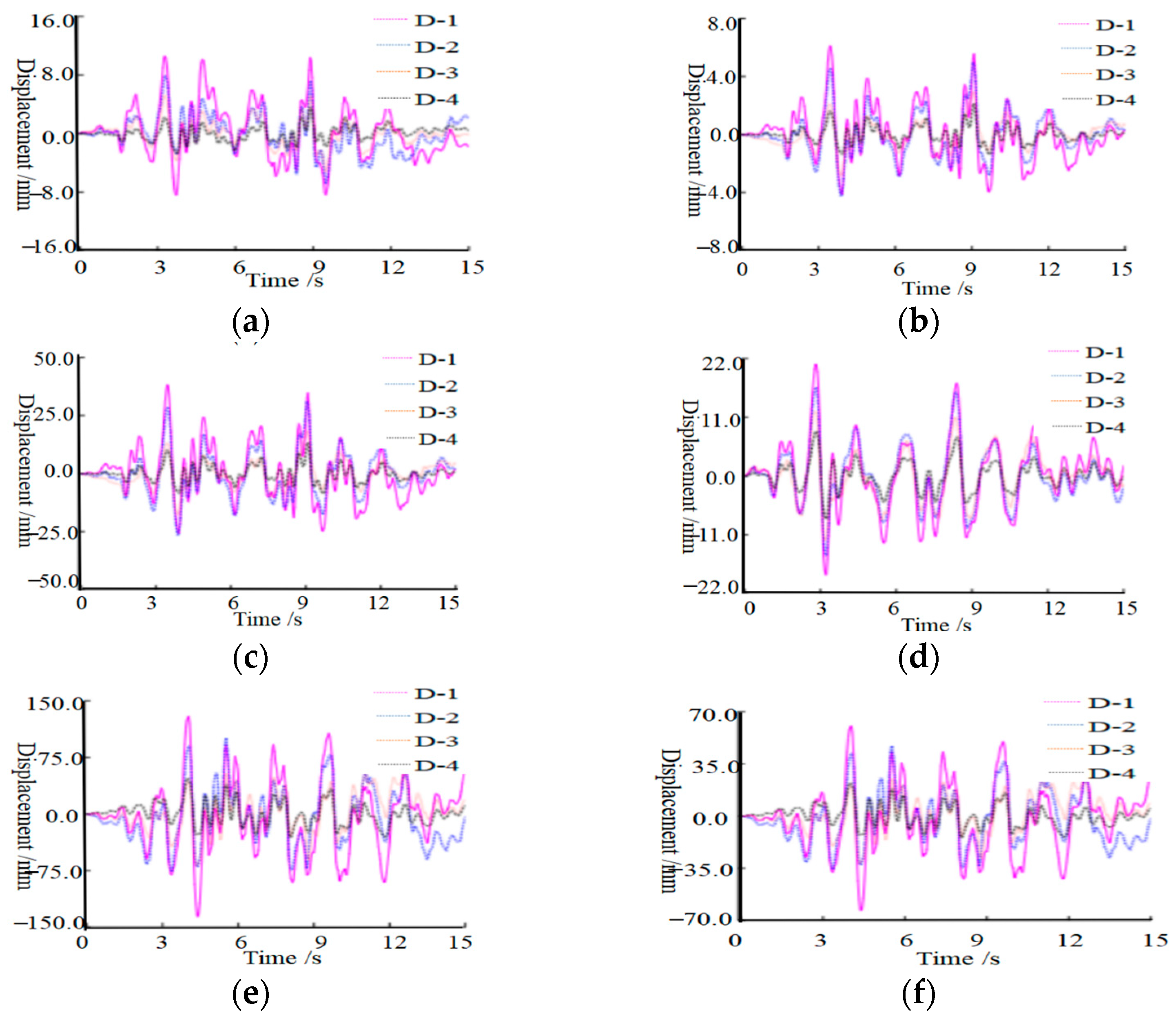
6.3. Displacement Analysis of the Top of the Structure under Different Loading Strengths
7. Conclusions
- (1)
- The site effect amplifies the peak value of acceleration and response spectrum, and changes the spectral characteristics of seismic waves. The amplification effect had a great influence on the seismic response of structures during a period of less than 2 s, but had no significant effect on the seismic response of structures during a period greater than 2 s. Moreover, the peak acceleration at the arch foot position of a1, a2, and a3 was larger than the original seismic data, and the amplification effect at the arch foot position of a3 was larger than that at the arch foot position of a1 and a2. The amplification effect was minimal at a2 near the input point.
- (2)
- When the input seismic wave intensity increased from 0.1 g to 0.3 g, the maximum acceleration increase at the top of the 3-m model was 102.63%, while the acceleration increase of the 8-m model was 79.16%. This suggests that shallower buried structures are more sensitive to seismic wave strength.
- (3)
- Under the influence of 0.1 g, 0.2 g, and 0.3 g EI-Centro seismic waves, the maximum displacement at the top of the model with a foundation buried depth of 3 m was measured at 8 mm, 32 mm, and 142 mm, respectively. Similarly, for the model with a foundation depth of 8 m, the maximum displacements were recorded as 6.2 mm, 21 mm, and 68 mm for the corresponding seismic wave intensities. These findings suggest that an increase in foundation burial depth effectively reduces displacement at the structure’s apex due to enhanced constraint between deeply buried foundations and surrounding soil, leading to improved overall structural stiffness.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, G.L.; Li, X.J.; Li, T.P.; Hou, C.L. Impact of canyon topography on seismic response of multi-supported long-span Bridges under SV wave incidence. Rock Soil Mech. 2012, 33, 1572–1578. [Google Scholar]
- Tan, Y.Q. Key Technology and Innovation of construction of steel pipe arch bridge connected by deep Canyon Bridge and tunnel. Railw. Constr. Technol. 2024, 5, 99–103. [Google Scholar]
- Zhang, X.X.; Zheng, S.X.; Tang, Y.; Zhang, L.Q.; Yuan, D.P. Numerical Simulation of Wind Parameters at long-span arch bridge site in Mountain Gorge. J. Railw. Sci. Eng. 2018, 15, 398–406. [Google Scholar]
- Wu, H.G.; Liang, Y.; Lai, T.W. Study on interaction mechanism between bridge and landslide under earthquake. J. Railw. Eng. 2023, 40, 54–61. [Google Scholar]
- Jia, Y.; Wang, Z.H.; Tian, H.; Liu, P.Z.; Song, H.B. Seismic response analysis of single-span asymmetric suspension bridge considering beam end impact. J. Shenyang Jianzhu Univ. (Nat. Sci. Ed.) 2023, 39, 1075–1083. [Google Scholar]
- Liao, Y.C.; Zhang, R.Y.; Lin, R.; Zong, Z.H.; Wu, G. Nonlinear seismic response prediction of Bridges based on cascading residual LSTM networks. Eng. Mech. 2024, 41, 47–58. [Google Scholar]
- Xu, L.Q.; Yuan, M.J.; Zuo, Y.; Shen, Z.X.; Xu, M.H. Nearly pulse type faults under the action of earthquake dynamic response analysis of long-span arch bridge. J. Vib. Shock 2024, 9, 94–104+148. [Google Scholar]
- Feng, J. Seismic response analysis of concrete-filled steel tube arch bridge in deep canyon. Highw. Traffic Technol. 2024, 1–11. [Google Scholar]
- Feng, Z.J.; Li, Y.T.; Zhao, R.X.; Cai, J.; Dong, J.S.; Meng, Y.Y. Research on dynamic response of pile group foundation with variable section in liquefiable site. Sci. Technol. Eng. 2023, 23, 7886–7894. [Google Scholar]
- Wang, J.H. Research on Seismic Response of Concrete-Filled Steel Tube Arch Bridge in Deep Canyon. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2023. [Google Scholar]
- Shi, C.Z.; Cheng, C.; Wang, Z.M.; Wu, H.G.; Hu, Y. Inverted siphon pipe bridge of large span structure seismic performance. J. Yangtze River Sci. Res. Inst. 2022, 33, 111–116. [Google Scholar]
- Chen, J.W.; Zheng, K.F.; Zuo, Z.C. Research on seismic response and damper parameter optimization of large-span railway steel truss flexible arch bridge. Sichuan Archit. 2023, 43, 94–104, 165. [Google Scholar]
- Li, X.Z.; Liu, M.; Yang, D.H.; Dai, S.Y.; Xiao, L. Earthquake damage evolution simulation of long-span top-bearing steel truss arch bridge. J. Southwest Jiaotong Univ. 2019, 55, 94–104, 1223. [Google Scholar]
- Shi, C.; Lin, P.Z.; Zhou, P.; He, Z.G. Spatial seismic response analysis of long-span continuous steel truss flexible arch bridge under multi-point excitation. J. Earthq. Eng. 2018, 40, 273–278. [Google Scholar]
- Xia, Z.H.; Zhang, X.Y.; Zong, Z.H. Analysis of Dynamic characteristics of reinforced concrete simply supported oblique wide beam bridge. J. Fuzhou Univ. (Nat. Sci. Ed.) 2008, 36, 278–283. [Google Scholar]
- Chen, B.; Zhao, L.; Chen, S.X.; Yue, Q. Analysis on dynamic characteristics of the second-line Niujiaoping Bridge added to Xiangyu Railway. Railw. Constr. 2007, 3, 1–4. [Google Scholar] [CrossRef]
- Huang, W.J.; Peng, G.H.; Chen, B.C.; Chen, Y.Y.; He, X.H.; Sun, C. Stress analysis of concrete-filled steel tube rigid frame tied arch bridge. J. Fuzhou Univ. (Nat. Sci. Ed.) 2004, 32, 190–194. [Google Scholar]
- Yun, D.; Liu, H.; Zhang, S.M. Half through bridge concrete filled steel tubular arch bridge seismic elastic-plastic time history analysis. J. Jilin Univ. (Eng. Sci.) 2014, 44, 1633–1638. [Google Scholar]
- Ye, D.; Zhou, J.T.; Wang, L.; Zhang, R.; Xu, L.; Jin, S. Seismic response analysis of long-span CFST arch bridge considering valley site effect. World Earthq. Eng. 2022, 38, 108–116. [Google Scholar]
- Luo, Y.H.; Wang, Y.S. Terrain amplification effect of mountain slope vibration induced by Wenchuan earthquake. J. Mt. Sci. 2013, 31, 200–210. [Google Scholar]
- Zhang, J.; Liang, J.W.; Ba, Z.N. When SH wave incident raised the site topography and soil amplification effect. Earthq. Eng. Eng. Vib. 2016, 4, 56–67. [Google Scholar]
- Fu, L.; Xie, J.J.; Chen, S.; Zhang, B.; Zhang, X.; Li, X.J. Characteristic analysis of site magnification factor and its application in simulation of strong ground motion in Sichuan area: A case study of the 2022 Lushan Ms6.1 earthquake. Geophys. J. 2023, 66, 2933–2950. [Google Scholar]
- JTG/T 2231-01-2020; Ministry of Transport of the People’s Republic of China. Code for Seismic Design of Highway Bridges. People’s Communications Press: Beijing, China, 2020.
- Luo, C.; Sheng, C.; Wan, J.Z.; Xu, C.R.; Guo, H.Q.; Wang, H. Influence of Rayleigh waves on seismic response of V-shaped valley arch bridge. Chin. J. Highw. Sci. 2023, 11, 1–17. [Google Scholar]
- Li, X.L.; Zou, Y.H.; Wang, D.S. Earthquake damage characteristics and aseismic research of bridge with arch system under strong earthquake. World Earthq. Eng. 2018, 34, 33–43. [Google Scholar]

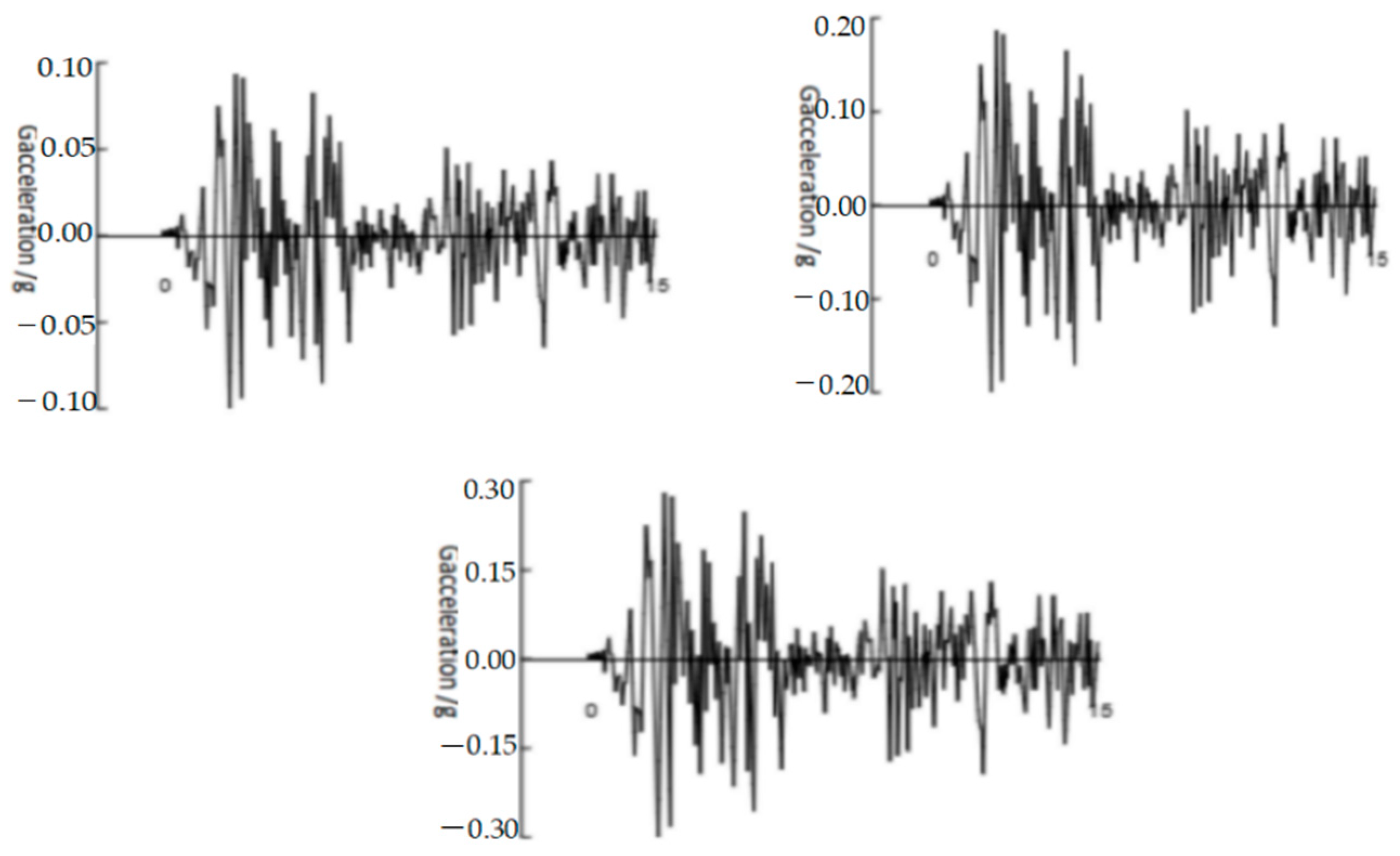
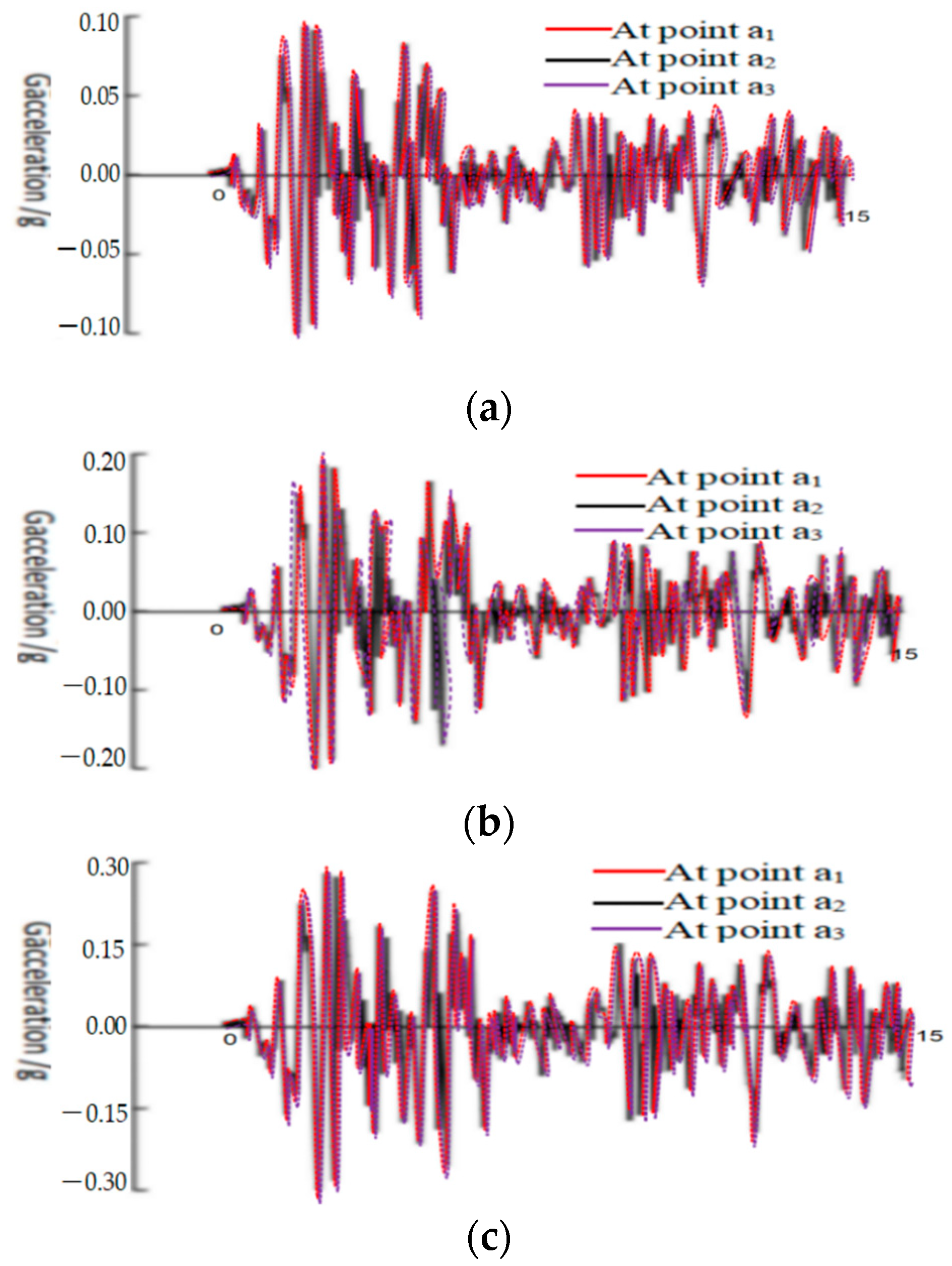

| Station Position | Input Strength 0.1 g | Input Strength 0.2 g | Input Strength 0.3 g | |||
|---|---|---|---|---|---|---|
| Peak Acceleration/g | Amplification Factor | Peak Acceleration/g | Amplification Factor | Peak Acceleration/g | Amplification Factor | |
| a1 | 0.112 | 1.12 | 0.212 | 1.06 | 0.311 | 1.04 |
| a2 | 0.103 | 1.03 | 0.201 | 1.01 | 0.304 | 1.01 |
| a3 | 0.117 | 1.17 | 0.217 | 1.09 | 0.322 | 1.07 |
| a1 (Formula method) | 0.130 | 1.30 | 0.248 | 1.24 | 0.350 | 1.12 |
| a2 (Formula method) | 0.124 | 1.24 | 0.231 | 1.16 | 0.325 | 1.08 |
| a3 (Formula method) | 0.137 | 1.37 | 0.272 | 1.36 | 0.343 | 1.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhou, C.; Huang, S. Study on Ground Motion Amplification in Upper Arch Bridge Due to “W”-Type Deep Canyon Using Boundary-Integral and Peak Frequency Shift Methods. Mathematics 2024, 12, 2622. https://doi.org/10.3390/math12172622
Liu Y, Zhou C, Huang S. Study on Ground Motion Amplification in Upper Arch Bridge Due to “W”-Type Deep Canyon Using Boundary-Integral and Peak Frequency Shift Methods. Mathematics. 2024; 12(17):2622. https://doi.org/10.3390/math12172622
Chicago/Turabian StyleLiu, Yi, Chenhao Zhou, and Sihong Huang. 2024. "Study on Ground Motion Amplification in Upper Arch Bridge Due to “W”-Type Deep Canyon Using Boundary-Integral and Peak Frequency Shift Methods" Mathematics 12, no. 17: 2622. https://doi.org/10.3390/math12172622
APA StyleLiu, Y., Zhou, C., & Huang, S. (2024). Study on Ground Motion Amplification in Upper Arch Bridge Due to “W”-Type Deep Canyon Using Boundary-Integral and Peak Frequency Shift Methods. Mathematics, 12(17), 2622. https://doi.org/10.3390/math12172622






