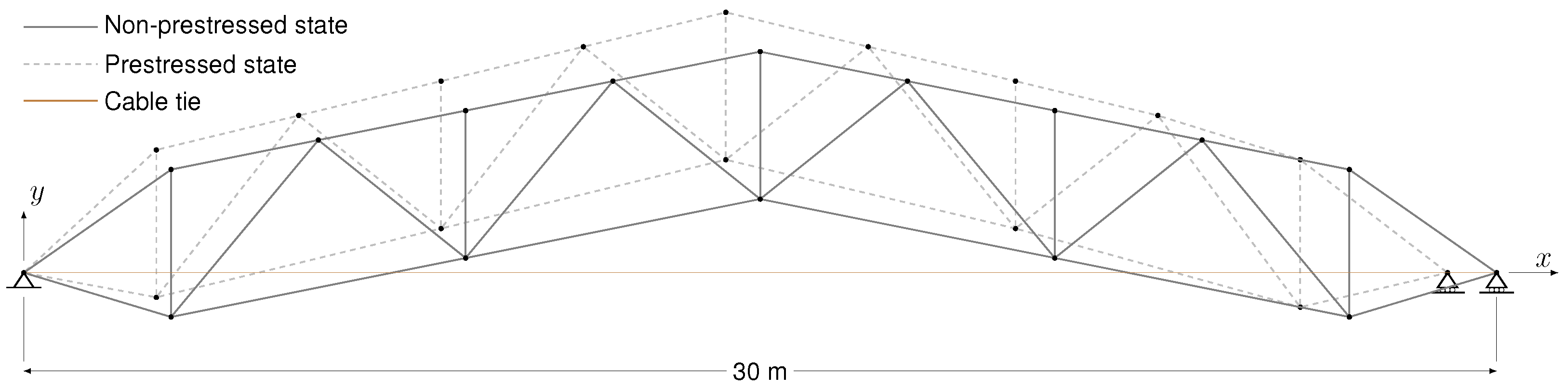
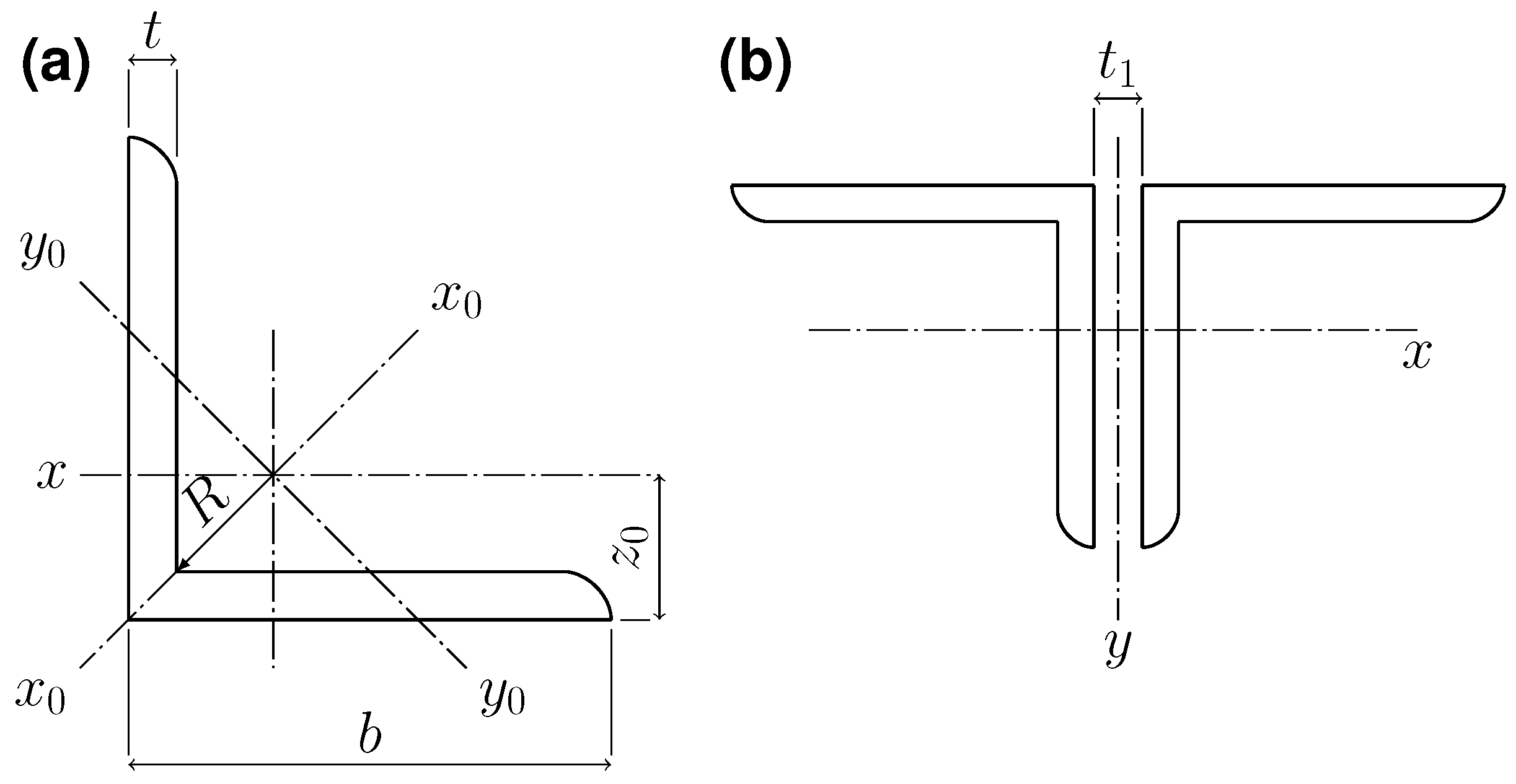
This section presents the results of the optimization using three algorithms: SMS-EMOA, NSGA-III, and CTAEA. In the subsection Algorithm Comparisons, the optimization values for four objective functions are detailed: structural capacity before tensioning, structural capacity after tensioning, structure weight, and constructability issues. Descriptive statistics are analyzed, and radar charts are presented, showing both individual solutions and the means and standard deviations for each algorithm.
3.1. Algorithm Comparisons
The CTAEA algorithm was utilized to define the probabilities for the crossover and mutation operators. The tuning process for the operators within the CTAEA algorithm was carried out systematically in two distinct phases, using the hypervolume metric as the main criterion for evaluation. In the first phase, the crossover probability was tested across various values—0.01, 0.1, 0.2, 0.3—to determine settings that could improve the optimization process. Similarly, the mutation probability was examined across a range of values—0.01, 0.02, 0.03, 0.04—to determine its impact on generating new solutions. During this exploratory phase, the crossover value was fixed at five to maintain consistency in the distribution tightness of solutions.
Advancing to the second phase, a more focused exploitation strategy was employed, narrowing down the crossover probability to finer values—0.08, 0.1, 0.12—to optimize the frequency of crossover events. Concurrently, the mutation probability was refined to values—0.015, 0.02, 0.025—to further enhance solution diversity. This phase was essential for identifying the exact parameter configurations that optimize the hypervolume metric, achieving an ideal balance between the convergence of the Pareto front and the maintenance of diversity within the solution set.
This section presents the optimization results of the three algorithms: CTAEA, NSGA-III, and SMS-EMOA.
Table 4 details the optimization values for each of the four objective functions: structural capacity before tensioning, structural capacity after tensioning, structure weight, and constructability issues. Subsequently, the descriptive statistics in
Table 5 provide a statistical analysis to help understand the results. In
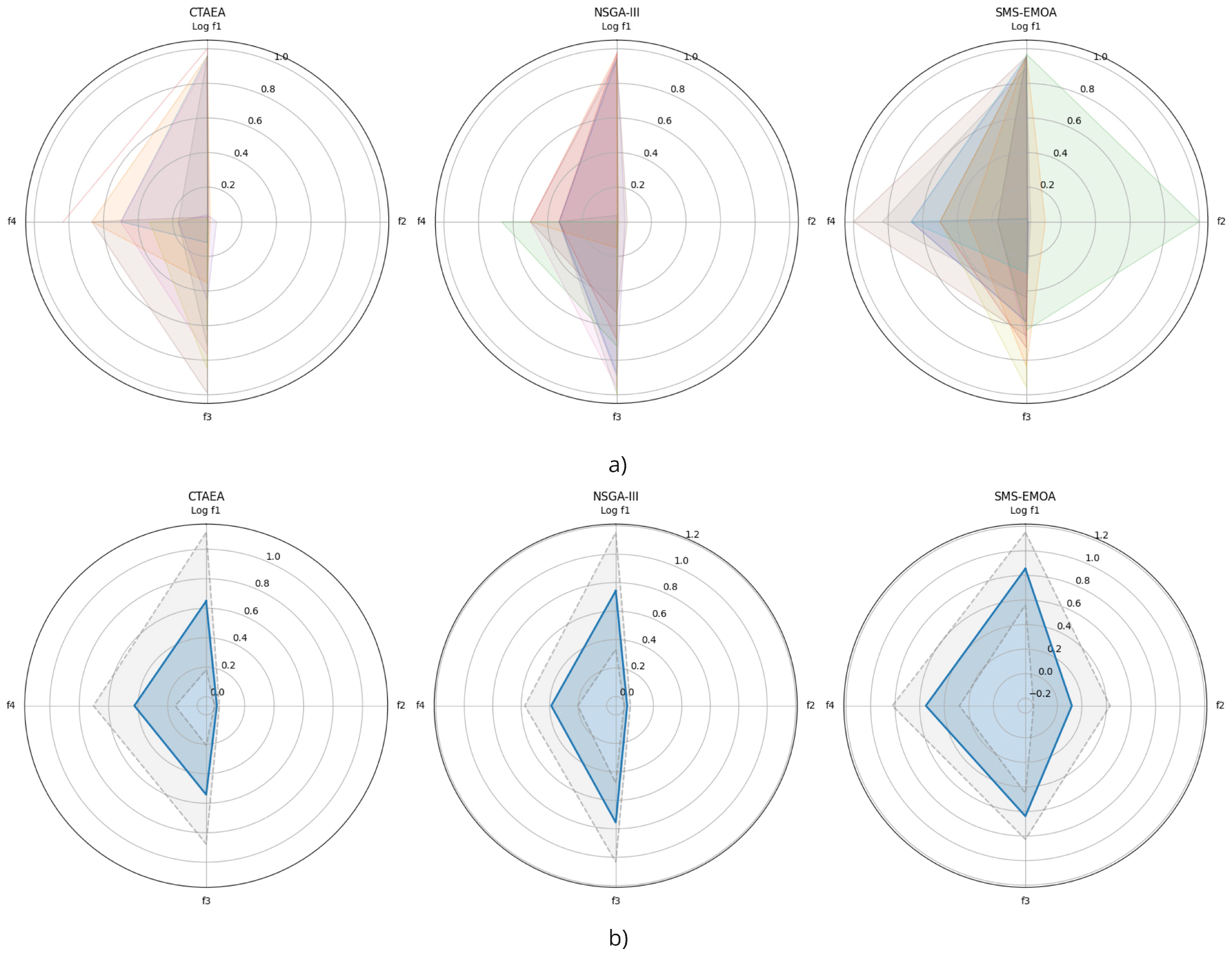
Figure 5, two types of visualizations are presented: radar charts displaying all individual solutions and radar charts showing the means and standard deviations for each algorithm. The metrics of the solutions were normalized using a MinMax scale based on all solutions. Specifically, the structural capacity before tensioning (
) was transformed to a logarithmic scale, and the structure weight (
) and constructability issues (
) were converted to one minus their normalized values to reflect their minimization objectives. The axes in the radar charts represent the four objective functions: structural capacity before tensioning (
), structural capacity after tensioning (
), structure weight (
), and constructability issues (
). The shaded areas in the individual solution charts indicate the variability in the solutions, while the solid lines and shaded areas in the mean charts represent the averages and the ranges of one standard deviation, respectively.
The CTAEA algorithm exhibits a high variability in structural capacity before tensioning, with a maximum value of and a significant standard deviation of . This suggests that CTAEA can generate solutions with a wide range of structural capacities. On the other hand, NSGA-III shows a lower mean () and a lower standard deviation (), indicating more consistent solutions. SMS-EMOA, while having a similar mean (), has a considerably high standard deviation (), suggesting high variability in its solutions.
CTAEA presents significant variability in structural capacity after tensioning, with a standard deviation of 13.74 and a maximum value of 44.76. This indicates that some CTAEA solutions are significantly better after tensioning. NSGA-III, with a more balanced structural capacity after tensioning, has a mean of 17.31 and a standard deviation of 15.75, showing less variability. SMS-EMOA displays an extremely high mean (91.60) and a very large standard deviation (225.22), suggesting high variability and some exceptionally good solutions after tensioning.
In terms of structure weight, CTAEA has a mean of 31.85 with a standard deviation of 6.16, indicating relatively consistent solutions. NSGA-III shows a lower mean (28.12) and a standard deviation of 7.77, suggesting good consistency. SMS-EMOA, with a mean of 29.48 and a low standard deviation (2.73), also produces fairly consistent solutions.
Regarding constructability issues, CTAEA has a mean of 17.33 and a standard deviation of 1.41, indicating good consistency. NSGA-III is similar, with a mean of 17.78 and a standard deviation of 1.41, demonstrating consistent solutions. SMS-EMOA, with a lower mean (16.50) and a standard deviation of 1.89, indicates slightly less consistent solutions.
In conclusion, CTAEA produces solutions with high variability in structural capacity but consistent results in terms of weight and constructability issues. NSGA-III generates balanced and consistent solutions across all aspects. SMS-EMOA shows high variability in structural capacity after tensioning but consistent results in weight and constructability issues, which could be advantageous in specific scenarios where variability in structural capacity is acceptable or desirable.
From the radar charts and the analysis of the normalized data,
Figure 5, it is observed that the CTAEA algorithm exhibits high variability in structural capacity before tensioning, suggesting it can generate solutions with a wide range of structural capacities. However, it shows consistency in terms of weight and constructability issues. The NSGA-III algorithm produces more balanced and consistent solutions across all metrics, which may be preferable for applications requiring stability. On the other hand, SMS-EMOA shows high variability in structural capacity after tensioning but generates consistent results in weight and constructability issues. Therefore, CTAEA is useful for exploring a wide range of structural capacities, NSGA-III offers balanced and consistent solutions, and SMS-EMOA could be beneficial in scenarios where variability in structural capacity is acceptable or desirable.
3.2. Performance Indicator Analysis
In this research, a systematic experimental setup was employed to assess the performance of three multi-objective optimization algorithms: CTAEA, NSGA-III, and SMS-EMOA. The experiment consisted of 30 independent runs, with each algorithm producing a varying number of points using a set of predefined parameters. This methodology enabled a direct comparison of the algorithms’ effectiveness under uniform parameter conditions. To maintain consistency across different objective functions, a min-max normalization was applied to each function individually. This involved standardizing the units of the variables across all data points, including those on the Pareto front. For every experiment, the points generated by each algorithm were normalized by scaling their values between the minimum and maximum observed within the dataset. This normalization ensured that the varied scales were converted into a common metric, allowing for consistent comparisons across different optimization scenarios.
To assess the effectiveness of the optimization algorithms more thoroughly, two performance metrics were introduced: generational distance (GD) and inverted generational distance (IGD). These metrics evaluated the quality of the solutions produced by the algorithms, focusing on their convergence and diversity relative to a known Pareto front.
The
generational distance (GD) measures the average Euclidean distance between each solution in a given set and the closest point on the Pareto front, providing an indication of how well the algorithm’s solutions converge. In our experiment, the size of set
A varied, representing the number of points obtained in each run. The GD is computed using the following equation:
where
represents the Euclidean distance between the
ith solution
in set
A and the closest point on the Pareto front
Z. The sets
A and
Z are defined as follows:
This metric is crucial for evaluating how close the generated solutions are to the ideal points on the Pareto front.
The
inverted generational distance (IGD) is a metric that reverses the concept of generational distance by measuring the distance from each point in
Z, the Pareto front, to the nearest point in
A. In our experiment, set
A included a variable number of points generated in each run. The IGD is computed using the following equation:
where
represents the Euclidean distance (using
) from a point
on the Pareto front to its closest reference point in set
A. The set
A is defined as
, which represents the solutions generated in each run. This metric is essential for assessing how well the generated solutions cover the Pareto front.
Advantages of each metric:
The GD is especially valuable for evaluating how closely the generated solutions approach the Pareto front. A smaller GD value implies that the solutions produced by the algorithm are nearer to the optimal set, indicating better convergence performance.
The IGD provides a comprehensive view of both the convergence and diversity of the solutions. It not only measures the proximity of the solutions to the Pareto front but also evaluates how evenly the solutions are spread across the front. A lower IGD value suggests that the solutions effectively cover the Pareto front with good distribution as well as proximity.
By utilizing both GD and IGD metrics, this study offers a thorough assessment of the algorithms’ capability to produce solutions that are not only close to but also well spread across the ideal set of solutions, highlighting the subtle performance distinctions among the algorithms in multi-objective optimization tasks.
To assess the performance of the optimization algorithms, descriptive statistics were calculated to provide basic insights into the distribution of results for each algorithm. These statistics included the mean, maximum, minimum, standard deviation, and median values, which were key for understanding the central tendency and spread of the data. Additionally, the non-parametric Kruskal–Wallis test was applied to determine whether there were statistically significant differences between the algorithms. This test was selected due to its strength in dealing with non-normally distributed data and its suitability for comparing more than two groups without assuming equal variances, making it an ideal choice for the ordinal data produced in this experiment.
The results of the Kruskal–Wallis test, presented in
Table 6, revealed statistically significant differences between the algorithms, with
p-values of
for the generational distance (GD) and
for the inverted generational distance (IGD). These highly significant
p-values indicate that the differences observed in the GD and IGD metrics were not due to random variation but reflected genuine performance discrepancies among the algorithms. Specifically, the GD results suggest that the proximity of solutions to the Pareto front varied significantly across the algorithms, while the IGD results highlight notable differences in how well the solutions covered the Pareto front. This statistical analysis underscores the distinct advantages and limitations of each algorithm in generating optimal solutions within the defined multi-objective optimization framework.
The combination of GD and IGD metrics provides a robust framework for evaluating multi-objective optimization algorithms. The statistical significance of the differences between the algorithms, as revealed by the Kruskal–Wallis test, confirms that these metrics effectively differentiate the performance of the algorithms. Specifically, NSGA-III demonstrated superior convergence with lower GD values, indicating its solutions were closer to the Pareto front. However, when considering the IGD metric, NSGA-III also showed a balanced performance in terms of both convergence and diversity, ensuring a good spread of solutions across the Pareto front. This comprehensive evaluation highlights NSGA-III’s strengths in generating well-converged and diverse solutions, making it a robust choice for multi-objective optimization tasks.
3.3. Multi-Criteria Decision Analysis for Structural Design Optimization
This paper examined the performance of the CTAEA, NSGA-III, and SMS-EMOA multi-objective algorithms.
Section 3.1 and
Section 3.2 thoroughly evaluate each algorithm’s capability to generate balanced solutions that achieve equilibrium among conflicting objectives within a complex solution space. This section focuses on the results concerning the main structural characteristics of the non-dominated optimal solutions resulting from the MOO and the scoring and ranking of these balanced solutions using several decision-making algorithms detailed in
Section 3.3.
Traditional and SOO design consider criteria either in isolation or sequentially. In contrast, the novel design approach in this study integrates multiple factors simultaneously within a framework integrating MOO and MCDM. Conventional prestressed arch truss design processes do not support this simultaneous consideration. The experimental results in this paper demonstrate the effectiveness of a multi-objective framework, enabling a more nuanced and comprehensive optimization of design parameters. This study seeks to move beyond the traditional and SOO approaches via a novel integrated methodology.
The cross-sectional area is a critical characteristic in structural analysis as it directly influences the load-bearing capacity and stability of the arched truss.
Table 7 presents the average cross-sectional values for the upper chord (elements 1–5 and 16–20), lower chord (elements 6–8 and 21–23), lattice elements (elements 9–15 and 24–29), and the tie member (element 30), along with the associated prestressing force for the non-dominated solutions.
Figure 6 illustrates the interdependencies in structural element sizing and the design implications by comparing the cross-sectional areas (in cm
2) of the upper and lower chords, lattice elements, and cable ties. Each dot in the scatter plots represents a specific design configuration obtained through MOO, with the trend line highlighting the overall relationship between the cross-sectional areas of the elements being compared. The shaded regions in the diagonal plots (the
positions) indicate the range and distribution of these configurations, enabling an assessment of how various sizing decisions influence the overall truss design.
The results indicated a slight positive correlation between the upper and lower chords, suggesting an interdependent element sizing to ensure balanced stiffness and strength. Lattice elements showed a positive correlation with the lower chord but a negative correlation with the upper chord, indicating that lattice elements were scaled more closely with the lower chord to maintain stability while allowing flexibility in the upper chord’s design. Cable tie elements exhibited a positive correlation with the upper chord but a slight negative correlation with the lower chord and lattice elements, highlighting their specialized role in accommodating prestressing requirements within the lower section of the prestressed arched truss.
Figure 7 presents the distribution of prestressing forces (in kN) for the non-dominated optimal solutions achieved by the CTAEA, NSGA-III, and SMS-EMOA algorithms. Each violin plot represents the distribution and emphasizes the mean and median values for each MOO algorithm. The results for the CTAEA algorithm showed a relatively narrow distribution around the median value, indicating a consistent generation of solutions with similar prestressing force selection. In contrast, the NSGA-III algorithm displayed a slightly higher mean and median, suggesting a tight clustering of solutions around these slightly greater forces.
The SMS-EMOA algorithm, however, exhibited a significantly higher mean prestressing force with a more dispersed distribution. This indicated that while SMS-EMOA could produce solutions with higher prestressing forces, there was more significant variability in the results, potentially offering a wider range of balanced solutions but with less predictability.
Figure 8 illustrates the effect of the prestressing force on the objective function results across all non-dominated solutions. Each subplot illustrates how an objective function varies with the prestressing force, with dots representing non-dominated solution data, lines indicating trends, and shaded areas representing variability through confidence intervals.
The prestressing force slightly enhanced the non-prestressed structural capacity , potentially due to higher sizing requirements for greater prestressing forces. It did not significantly affect the structure’s weight . However, it slightly increased constructability issues , presumably due to the need for larger sections in specific areas, such as the upper chord. Notably, a positive correlation existed between prestressing force and prestressed-state resistance, mainly concentrated around the mid-range of 600 kN. This behavior corresponded with the enlarged elastic range attained with greater prestressing. This was particularly evident in the A21 solution achieved by the SMS-EMOA algorithm.
Table 8 presents the results for the MCDM problem, including criteria weighting via an entropy theory-based approach, normalized objective functions, and the corresponding scoring and ranking results for the non-dominated solutions. The scoring and ranking were conducted using the SAW, FUCA, TOPSIS, PROMETHEE, and VIKOR techniques for the balanced designs attained by the CTAEA, NSGA-III, and SMS-EMOA algorithms.
The criteria weighting, calculated via entropy theory, objectively assesses the importance of each criterion in the multi-criteria decision-making process, minimizing subjective biases for a balanced evaluation. The results showed higher weights for the structural capacity objectives. The prestressed state structural capacity was identified as the primary source of information within the MCDM process, followed by the non-prestressed state . Constructability issues and structural self-weight received moderate and very similar weightings.
The scoring and ranking results using various MCDM techniques indicated a multifaceted scenario where no algorithm consistently outperformed the others, highlighting the complexity of balancing conflicting objectives.
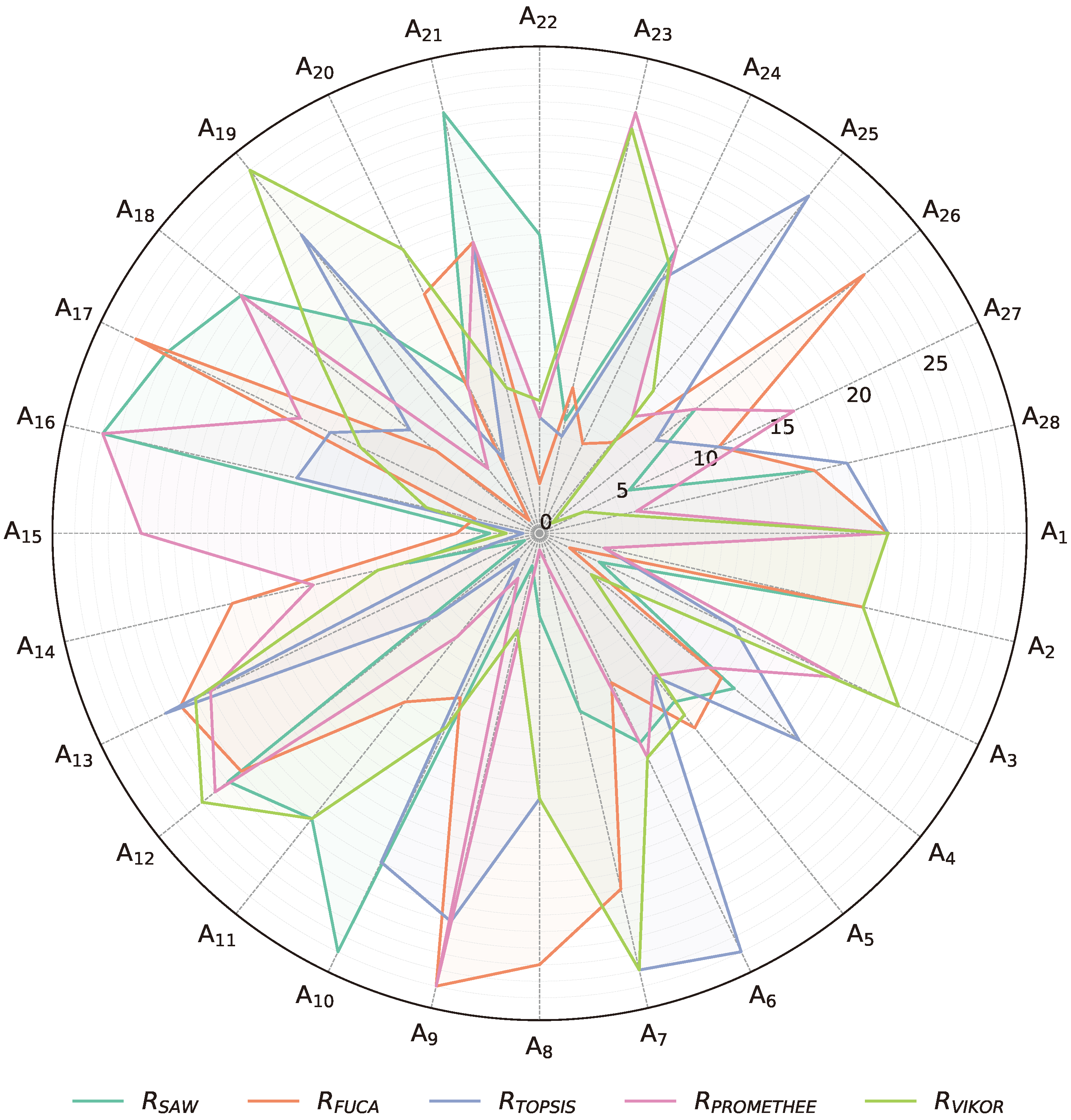
Figure 9 represents the alternative ranking for each technique, clearly illustrating how each algorithm shows strengths in specific non-dominated solutions but may lag in others. This reflects the trade-offs inherent in the MOO problem in this paper. The radar chart compares the performance of the design alternatives (A
1 to A
28) across the five decision-making techniques. Each axis represents one of the alternatives, and each line shows how a specific MCDM technique ranks across all non-dominated solutions.
Alternatives A7 and A8 from CTAEA stood out due to their performance in the PROMETHEE method, securing the top and second ranks, respectively. Additionally, A8 remained within the top five for the SAW technique but was poorly ranked by FUCA and exhibited mid-range performance in both TOPSIS and VIKOR. This variability indicated context-dependent alternatives with strengths for specific techniques and limitations when evaluated by other methods.
In contrast, some CTAEA alternatives, such as A1 and A5, displayed more consistent rankings across different techniques. A1 consistently appeared in the lower rankings, indicating a general lack of competitiveness across all criteria. On the other hand, A5 maintained mid-tier positions, reflecting balanced but non-exceptional performance across the board. This consistency could indicate non-dominated solutions with characteristics advantageous in decision contexts that value stability and predictability over specialization.
The NSGA-III algorithm demonstrated notable performance, particularly with alternative A15, which ranked in the top five across four out of five techniques, including securing the top rank for TOPSIS. This non-dominated solution exhibited significant robustness and versatility across all techniques, making it a strong candidate under diverse evaluation methodologies. However, FUCA ranked A15 lower, favoring other alternatives such as CTAEA’s designs. This discrepancy suggested that while the NSGA-III-generated solution excelled in most contexts, its suitability may be limited using FUCA’s algorithmic approach.
SMS-EMOA alternatives presented a diverse range of rankings. Alternative A19 was ranked highest by FUCA and performed well in PROMETHEE, yet it was poorly ranked by VIKOR, indicating a solid alignment with specific techniques but a lack of general transferability. Similarly, A26 showed strong performance with a top rank in VIKOR but mid and low rankings across other techniques, suggesting its strengths were evaluation-specific.
Across algorithms, NSGA-III and SMS-EMOA alternatives generally achieved higher ranks more consistently than CTAEA alternatives. NSGA-III’s and SMS-EMOA’s non-dominated alternatives frequently appeared in higher positions, indicating their robustness and adaptability. The stark contrast in rankings for some alternatives, such as CTAEA’s A8 and SMS-EMOA’s A19, underscores the importance of selecting and applying multiple MCDM techniques and evaluating top-ranked alternatives that better align with stakeholders’ specific decision criteria and objectives for the MOO problem posed in this paper.