Finite Element Method for a Fractional-Order Filtration Equation with a Transient Filtration Law

Abstract

In this article, a numerical method is proposed and investigated for an initial boundary value problem governed by a fractional differential generalization of the nonlinear transient filtration law which describes fluid motion in a porous medium. This type of equation is widely used to describe complex filtration processes such as fluid movement in horizontal wells in fractured geological formations. To construct the numerical method, a high-order approximation formula for the fractional derivative in the sense of Caputo is applied, and a combination of the finite difference method with the finite element method is used. The article proves the uniqueness and continuous dependence of the solution on the input data in differential form, as well as the stability and convergence of the proposed numerical scheme. The linearization of nonlinear terms is carried out by the Newton method, which allows for achieving high accuracy in solving complex problems. The research results are confirmed by a series of numerical tests that demonstrate the applicability of the developed method in real engineering problems. The practical significance of the presented approach lies in its ability to accurately and effectively model filtration processes in shale formations, which allows engineers and geologists to make more informed decisions when designing and operating oil fields.

1. Introduction

Fractional differential equations play a crucial role in modeling systems with memory effects that classical differential equations of integer-order cannot adequately describe. By introducing fractional derivatives, which extend the concept of integer-order derivatives, these equations can capture complex dynamics and memory phenomena, including hereditary properties and anomalous diffusion. The universality of fractional calculus has led to its widespread application across various fields [1]. An overview of the definitions of derivatives and integrals of fractional order as well as fractional differential equations that occur in mathematics, physics, and engineering are presented in [2,3,4,5]. The value of fractional derivatives lies in their ability to capture the non-local behavior inherent in many complex systems. In various real-world systems—such as those found in physics, biology, economics, and engineering—the behavior at a given time is shaped not only by recent events but also by older interactions and influences. Fractional derivatives provide a mathematical tool for quantifying and incorporating these non-local effects into the modeling process. The nonlocality provided by fractional derivatives expands our ability to describe and understand the behavior of complex systems in various fields of science and technology, which makes them invaluable tools for both researchers and practitioners [6].

The phenomenon of fluid motion in heterogeneous fractured porous media is one of many areas where the use of a fractional calculus is considered to be justified [7]. The motion equation in this model, Darcy’s linear law [8], describes the direct relationship between the pressure gradient and velocity. However, in many real-world applications, a violation of Darcy’s law may occur, and the fluid flow through a porous medium exhibits a so-called transient (non-stationary) mode [9,10,11], meaning that the filtration properties change over time. An example of this scenario is the flow in a horizontal well drilled in a dense and fractured shale formation. Another example is the change in the fluid flow rate as the reservoir pressure changes in the initial stages of oil production. Understanding filtration transients is important for predicting system response over time and optimizing operational decisions in resource extraction, environmental management, and engineering design.

There are a few papers devoted to the numerical study of the integer-order model of transient flow in porous media [9,10,12,13]. The need to apply fractional differential calculus to this problem is discussed in [12]. However, in these works, the construction of numerical methods is based on the use of low-order approximation formulas. In addition, a rigorous mathematical analysis of the developed methods has not been carried out for the fractional differential generalization of the problem.

Taking this aspect into account, this paper discusses a numerical approach to solving a new fractional differential generalization of the fluid flow model with the transient filtration law. This generalization is based on the replacement of time derivatives with Caputo fractional order derivatives to take into account the hereditary properties of the porous medium. To justify the choice of the fractional derivative type, recall that there are several definitions of fractional derivatives, including Riemann–Liouville, Caputo, Weyl, Marchaud, Riesz, and Caputo–Fabrizio, each of which has its own properties and applications. The Riemann–Liouville fractional derivative is the classical definition of a fractional derivative and is widely utilized in fractional integral and fractional differential equations, which are used to describe many phenomena, including diffusion, relaxation, and wave processes. However, difficulties arise in interpreting the initial conditions and mathematically describing processes with memory when employing it [14]. Unlike the fractional Riemann–Liouville derivative, the fractional time derivative in the sense of Caputo has advantages in terms of determining initial conditions and simpler physical interpretations within the context of dynamic processes in fractured fractal media. Weyl and Riesz fractional derivatives are mainly used in signal theory and quantum mechanics problems, respectively. The Caputo–Fabrizio fractional derivative [15], a variant of the Caputo fractional derivative, offers certain computational benefits. Nevertheless, some researchers question its validity in representing memory effects [16].

The use of numerical methods to solve fractional differential equations emphasizes their importance in solving complex problems where analytical solutions are not amenable to analysis [17,18]. Numerous research works have been aimed at developing numerical schemes that take into account the features of fractional derivatives of order $\alpha \in \left(0,1\right)$. These methods include a wide range of approaches, each with its own advantages and challenges. Finite difference methods are widely used [19,20,21,22,23,24,25], which have been extensively studied and applied to fractional differential equations with various variants of finite difference approximations of integer and fractional order derivatives. However, to accurately represent the behavior of fractional derivatives, a high resolution mesh may be required, which leads to increased computational costs. Along with the finite difference method, finite element methods are widely used [26,27,28,29,30,31,32], which are well-suited for processing complex geometric shapes and boundary conditions in fractional differential equations. Compact difference schemes [22,23,25], finite volume methods [33,34,35], mixed finite element schemes [31], collocation methods [36], and many others have also been adapted for effective numerical solutions to fractional differential problems.

The choice of a discretization formula for a fractional derivative is a crucial aspect in the construction of numerical schemes for solving fractional differential equations. These formulas play a fundamental role in approximating fractional derivatives, allowing numerical methods to accurately represent the behavior of fractional order systems. The choice of method depends on factors such as the nature of the problem, computational resources, and the desired level of accuracy. There are many approximating formulas for the fractional derivative of order $\alpha \in \left(0,1\right)$ in the sense of Caputo; for example, the L1 method [19,37,38,39]; the modified L1 method [40]; the inverse Euler method [41] of order $O\left({\tau }^{2-\alpha }\right)$, where $\tau$ denotes the time step; the L1-2 scheme [42]; the L2-1_σ [20] scheme; the Lagrange interpolation-type approximation [43]; the L2-type difference analog [44] of order $O\left({\tau }^{3-\alpha }\right)$; the L1-3 method of order $O\left({\tau }^{4-\alpha }\right)$ [45]; and many others [46]. Employing these formulas allows us to obtain higher-order numerical schemes for fractional differential equations in various fields [43,44].

The aim of this contribution is to study a numerical method for a fractional-order generalization of a nonlinear equation describing fluid flow in a porous medium with a transient (non-stationary) filtration law. An essential part of the proposed numerical scheme lies in the usage of a high-order approximation formula of order $O\left({\tau }^{4-\alpha }\right)$ for fractional time derivatives proposed by Cao et al. [45]. To the best of our knowledge, this formula had not previously been applied to solving practical problems in fluid dynamics. Being a higher-order method that produces more accurate results, it is known to increase the computational complexity. Having sufficient computing resources to solve complex problems, we intend to demonstrate the applicability of a high-order approximation formula to this problem. To achieve a global convergence order $O\left({\tau }^{4-\alpha }\right)$, a substep technique [47] is applied on the first two time intervals, $\left(0,\tau \right)$ and $\left(\tau ,2\tau \right)$, since the approximation order is known to be below $O\left({\tau }^{4-\alpha }\right)$ in $\left(0,2\tau \right)$ according to [45].

This work has several key differences from previous studies. First of all, we consider a fractional-order generalization of the fluid flow model with a transient (non-stationary) filtration law to take into account hereditary properties of the porous medium. We propose a numerical method to implement the proposed model and rigorously prove its stability and convergence. Secondly, unlike many works using the discretization of fractional derivatives of the order $O\left({\tau }^{2-\alpha }\right)$, the constructed numerical scheme is of convergence order $O\left({\tau }^{4-\alpha }\right)$ with respect to the time variable. Thirdly, the linearization of the nonlinear term was carried out by the Newton method, the convergence of the iterative process was proved, and sufficient conditions for its quadratic convergence were obtained.

The main contribution of this study is a numerical scheme of increased order for a nonlinear fractional differential filtration problem with a transient filtration law.

The paper’s structure unfolds as follows. Section 2.1 presents a concise derivation of the fractional-order model and delineates the problem statement. Section 2.2 discusses the uniqueness of the solution and its constant dependence on the input data. In Section 2.3, both semi-discrete and fully discrete problem formulations are introduced, while Section 2.4 delves into the stability analysis of the numerical scheme. The convergence theorems for the semi-discrete scheme, the fully discrete scheme, and an iterative process are discussed in Section 2.5. Section 3 presents the results of several numerical tests conducted to validate the theoretical analysis.

2. Materials and Methods

2.1. Formulation of the Problem

In the classical filtration theory, the motion of an incompressible fluid through a porous medium is represented by the following partial differential equations [9,10,11]:

$${\displaystyle \frac{\mu }{k}}\overrightarrow{u}+\nabla p=0,$$

(1)

$$S{\partial }_{t}p+\nabla ·\overrightarrow{u}=q\left(x,t,p\right),$$

(2)

where the first equation represents the linear Darcy law, the second equation is a continuity equation, k denotes the absolute permeability of the formation, $\mu$ represents the fluid viscosity, S is the coefficient of elastic capacity of the formation, p is pressure, and $\overrightarrow{u}$ is filtration rate. Suppose that the right-hand side of Equation (2) can be represented as

$$q\left(x,t,p\right)=\phi \left(p\right)+f\left(x,t\right),$$

where $\phi \left(p\right)$ takes into account possible nonlinear mass transfer from other continua.

Combining Equations (1) and (2) and formally replacing the time derivative with the fractional derivative of order $\alpha \in \left(0,1\right)$ in the sense of Caputo [4,48],

$${\partial }_{0,t}^{\alpha }p\left(x,t\right)={\displaystyle \frac{1}{\Gamma \left(1-\alpha \right)}}{\int }_0^t{\displaystyle \frac{{\partial }_{t}p\left(x,\theta \right)}{{\left(t-\theta \right)}^{\alpha }}}d\theta ,$$

(3)

we obtain the following fractional-order generalization of the filtration problem with a transition filtration law.

Problem 1.

In ${\overline{Q}}_T=\overline{\Omega }\times \overline{J}$, where $\Omega \subset {\mathbb{R}}^2$, $J=\left(0,T\right]$, find $p\left(x,t\right)$ that satisfies the conditions

$$\left\{\begin{array}{cc}{\partial }_{0,t}^{\alpha }p-\lambda {\nabla }^{2}p=\phi \left(p\right)+f\left(x,t\right),\hfill & x\in \Omega ,t\in J,\hfill \\ p\left(x,0\right)=p_0\left(x\right),\hfill & x\in \overline{\Omega },\hfill \\ p\left(0,t\right)=p\left(1,t\right)=0,\hfill & t\in J,\hfill \end{array}\right.$$

where $\alpha \in \left(0,1\right)$, and λ is a positive constant.

2.2. The Uniqueness of the Solution and Its Continuous Dependence on the Input Data

2.2.1. Weak Variational Formulation of the Problem

Let us formulate a weak variational formulation of Problem 1 under consideration.

Problem 2.

Find $p:J\to H_0^1\left(\Omega \right)$ such that, for any $v\in H_0^1\left(\Omega \right)$:

$$\left({\partial }_{0,t}^{\alpha }p,v\right)+\left(\lambda \nabla p,\nabla v\right)=\left(\phi \left(p\right),v\right)+\left(f,v\right),$$

(4)

where $\alpha \in \left(0,1\right)$.

Let us define the following assumptions.

Assumption A1.

There exists a sufficiently smooth solution to Problem 1.

Assumption A2.

The following conditions hold for the function $\phi \left(p\right)$:

(a) There is a constant $c_1>0$ such that $\left|\phi \left(p\right)\right|\le c_1\left|p\right|$.

(b) There is a constant $c_2>0$ such that $\left|\phi \left(p_1\right)-\phi \left(p_2\right)\right|\le c_2\left|p_1-p_2\right|$.

(c) There is a constant ${\phi }^{**}>0$ such that $\left|{\phi }^{\prime }\left(p\right)\right|\le {\phi }^{**}$.

(d) ${\phi }^{\prime }$ is Lipschitz continuous, i.e., there exists $L_{{\phi }^{\prime }}>0$ such that

$$\left|{\phi }^{\prime }\left(p_1\right)-{\phi }^{\prime }\left(p_2\right)\right|\le L_{{\phi }^{\prime }}\left|p_1-p_2\right|.$$

2.2.2. Uniqueness of the Solution and Its Continuous Dependence on the Input Data

We use the standard notation of Sobolev and Lebesgue spaces throughout the paper. In addition, we use the notation $\left(·,·\right)$ and $∥·∥$ to denote the inner product and norm in $L^2\left(\Omega \right)$. Let us introduce the following well-established lemma, which will be used while obtaining the main results.

Lemma 1

([49]). The following inequality holds for any absolutely continuous function $g\left(t\right)$ on $\overline{J}$:

$$\left({\partial }_{0,t}^{\nu }g,g\right)\ge {\displaystyle \frac{1}{2}}{\partial }_{0,t}^{\nu }{∥g∥}^2,\nu \in \left(0,1\right).$$

Let us first prove the following result.

Theorem 1.

The following inequality holds for the solution to Problem 1 under Assumptions 1 and 2:

$${∥p∥}^2+\lambda {\partial }_{0,t}^{-\alpha }{∥\nabla p∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\left({∥p_0∥}^2+{\partial }_{0,t}^{-\alpha }{∥f∥}^2\right),C>0,$$

(5)

which yields the uniqueness of the solution and its continuous dependence on the input data.

Proof. 

Take $v=p$ in (4) to obtain

$$\left({\partial }_{0,t}^{\alpha }p,p\right)+\left(\lambda \nabla p,\nabla p\right)=\left(\phi \left(p\right),p\right)+\left(f,p\right).$$

(6)

Estimating the terms in (6) by applying Cauchy’s inequality and Lemma 1, and considering Assumption 2, it is easy to see that

$${\partial }_{0,t}^{\alpha }{∥p∥}^2+\lambda {∥\nabla p∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\left({∥f∥}^2+{∥p∥}^2\right).$$

(7)

By virtue of the inequality ${\displaystyle {∥p∥}^2\le \frac{1}{2}{∥\nabla p∥}_{{\mathit{L}}^2\left(\Omega \right)}^2}$, we obtain

$${\partial }_{0,t}^{\alpha }{∥p∥}^2+{∥\nabla p∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{∥f∥}^2.$$

(8)

Applying the fractional integration operator [50,51]

$$I_{0,t}^{\alpha }p\left(x,t\right)=g\left(t\right)+{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t}p\left(x,\theta \right){\left(t-\theta \right)}^{\alpha -1}d\theta$$

(9)

to both parts of (7), we obtain the estimate (5), where $g\left(t\right)$ is the function defined in [50]. □

2.3. A Numerical Method

2.3.1. Construction of a Semi-Discrete Numerical Scheme

To devise a numerical approach, we introduce a homogeneous partition in the time span $\overline{J}$ into intervals defined by points $t_n=n\tau$, $\tau >0$, $n=0,1,\dots ,N$, where $N\tau =T$. Here, $p^n$ denotes the semi-discrete approximation of the function p at time $t=t_n$.

In contrast to the approximation formula of order $O\left({\tau }^{2-\alpha }\right)$ used in the construction of numerical methods in earlier works, we will use the following approximation formula for the fractional derivative in the sense of Caputo of increased order $O\left({\tau }^{4-\alpha }\right)$ from [45].

Lemma 2

([45]). If $p\in C^4\left(J\right)$, then the discrete analogue ${\Delta }_{0,t}^{\alpha }p\left(t_n\right)$ of the fractional derivative in the sense of Caputo ${\partial }_{0,t}^{\alpha }p\left(t_n\right)$ of order $0<\alpha <1$ can be represented as

$${\partial }_{0,t}^{\alpha }p\left(t_n\right)\approx {\Delta }_{0,t}^{\alpha }{p}^n:={\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}\sum _{s=0}^n{g}_{n,s}{p}^{n-s},$$

(10)

where the coefficients $g_{n,s}$ are defined as

$$\begin{array}{cccc}& \left\{\begin{array}{c}{g}_{n,0}=a_0,\hfill \\ g_{n,1}=-a_0,\hfill \end{array}\right.\hfill & \hfill & n=1,\hfill \\ & \left\{\begin{array}{c}{g}_{n,0}=a_0+b_0,\hfill \\ g_{n,1}=a_1-a_0-2b_0,\hfill \\ g_{n,2}=b_0-a_1,\hfill \end{array}\right.\hfill & & n=2,\hfill \\ & \left\{\begin{array}{c}{g}_{n,0}=w_{1,0},\hfill \\ g_{n,1}=w_{2,0}+a_1+b_1,\hfill \\ g_{n,2}=w_{3,0}+a_2-a_1-2b_1,\hfill \\ g_{n,3}=w_{4,0}-a_2+b_1,\hfill \end{array}\right.\hfill & & n=3,\hfill \\ & \left\{\begin{array}{c}{g}_{n,0}=w_{1,0},\hfill \\ g_{n,1}=w_{1,1}+w_{2,0},\hfill \\ g_{n,2}=w_{2,1}+w_{3,0}+a_2+b_2,\hfill \\ g_{n,3}=w_{3,1}+w_{4,0}+a_3-a_2-2b_2,\hfill \\ g_{n,4}=w_{4,1}-a_3+b_2,\hfill \end{array}\right.\hfill & & n=4,\hfill \\ & \left\{\begin{array}{c}{g}_{n,0}=w_{1,0},\hfill \\ g_{n,1}=w_{1,1}+w_{2,0},\hfill \\ g_{n,2}=w_{1,2}+w_{2,1}+w_{3,0},\hfill \\ g_{n,3}=w_{2,2}+w_{3,1}+w_{4,0}+a_3+b_3,\hfill \\ g_{n,4}=w_{3,2}+w_{4,1}+a_4-a_3-2b_3,\hfill \\ g_{n,5}=w_{4,2}-a_4+b_3,\hfill \end{array}\right.\hfill & & n=5,\hfill \\ & \left\{\begin{array}{c}{g}_{n,0}=w_{1,0},\hfill \\ g_{n,1}=w_{1,1}+w_{2,0},\hfill \\ g_{n,2}=w_{1,2}+w_{2,1}+w_{3,0},\hfill \\ g_{n,s}=w_{1,s}+w_{2,s-1}+w_{3,s-2}+w_{4,s-3}\left(3\le s\le n-3\right),\hfill \\ g_{n,n-2}=a_{n-2}+b_{n-2}+w_{2,n-3}+w_{3,n-4}+w_{4,n-5},\hfill \\ g_{n,n-1}=w_{3,n-3}+w_{4,n-4}+a_{n-1}-a_{n-2}-2b_{n-2},\hfill \\ g_{n,n}=w_{4,n-3}-a_{n-1}+b_{n-2},\hfill \end{array}\right.\hfill & & n\ge 6,\hfill \end{array}$$

in which the auxiliary quantities $a_k$, $b_k$, $w_{k,n-s}$ are determined by the relations

$$\begin{array}{cc}& a_n={\displaystyle {\left(n+1\right)}^{1-\alpha }-n^{1-\alpha },}\hfill \\ & b_n={\displaystyle \frac{{\displaystyle {\left(n+1\right)}^{2-\alpha }-n^{2-\alpha }}}{{\displaystyle 2-\alpha }}}-{\displaystyle \frac{{\displaystyle {\left(n+1\right)}^{1-\alpha }+n^{1-\alpha }}}{{\displaystyle 2}}},\hfill \\ & w_{1,n-s}={\displaystyle \frac{1}{6}}\left[2{\left(n-s+1\right)}^{1-\alpha }-11{\left(n-s\right)}^{1-\alpha }\right]-{\displaystyle \frac{1}{2-\alpha }}\left[2{\left(n-s\right)}^{2-\alpha }-{\left(n-s+1\right)}^{2-\alpha }\right]\hfill \\ & {\displaystyle -\frac{1}{\left(2-\alpha \right)\left(3-\alpha \right)}}\left[{\left(n-s\right)}^{3-\alpha }-{\left(n-s+1\right)}^{3-\alpha }\right],\hfill \\ & w_{2,n-s}={\displaystyle \frac{1}{2}}\left[6{\left(n-s\right)}^{1-\alpha }+{\left(n-s+1\right)}^{1-\alpha }\right]+{\displaystyle \frac{1}{2-\alpha }}\left[5{\left(n-s\right)}^{2-\alpha }-2{\left(n-s+1\right)}^{2-\alpha }\right]\hfill \\ & {\displaystyle +\frac{3}{\left(2-\alpha \right)\left(3-\alpha \right)}}\left[{\left(n-s\right)}^{3-\alpha }-{\left(n-s+1\right)}^{3-\alpha }\right],\hfill \\ & w_{3,n-s}=-{\displaystyle \frac{1}{2}}\left[3{\left(n-s\right)}^{1-\alpha }+2{\left(n-s+1\right)}^{1-\alpha }\right]-{\displaystyle \frac{1}{2-\alpha }}\left[4{\left(n-s\right)}^{2-\alpha }-{\left(n-s+1\right)}^{2-\alpha }\right]\hfill \\ & {\displaystyle -\frac{3}{\left(2-\alpha \right)\left(3-\alpha \right)}}\left[{\left(n-s\right)}^{3-\alpha }-{\left(n-s+1\right)}^{3-\alpha }\right],\hfill \\ & w_{4,n-s}={\displaystyle \frac{1}{6}}\left[2{\left(n-j\right)}^{1-\alpha }+2{\left(n-s+1\right)}^{1-\alpha }\right]+{\displaystyle \frac{1}{2-\alpha }}{\left(n-s\right)}^{2-\alpha }\hfill \\ & {\displaystyle +\frac{3}{\left(2-\alpha \right)\left(3-\alpha \right)}}\left[{\left(n-s\right)}^{3-\alpha }-{\left(n-s+1\right)}^{3-\alpha }\right],3\le s\le n,\hfill \end{array}$$

and in which the following estimates hold for $r_n^{\alpha }={\partial }_{0,t}^{\alpha }p\left(t_n\right)-{\Delta }_{0,t}^{\alpha }p\left(t_n\right)$:

$$\left|r_1^{\alpha }\right|\le c_1\underset{t_0\le t\le t_1}{max}\left|p^{\prime \prime }\right|{\tau }^{2-\alpha },c_1>0,$$

(11)

$$\left|r_2^{\alpha }\right|\le c_2\underset{t_0\le t\le t_2}{max}\left|p^{\prime \prime \prime }\right|{\tau }^{3-\alpha },c_2>0,$$

(12)

$$\left|r_n^{\alpha }\right|\le {\displaystyle \frac{1}{\Gamma \left(1-\alpha \right)}}\left[{\displaystyle \frac{2\alpha }{3}}\underset{t_0\le t\le t_2}{max}\left|p^{\prime \prime \prime }\left(t\right)\right|{\left(t_n-t_2\right)}^{-\alpha -1}{\tau }^4\right.$$

$$\left.+\left({\displaystyle \frac{1}{12}}+{\displaystyle \frac{3{\alpha }^2}{2\left(1-\alpha \right)\left(2-\alpha \right)}}\right)\underset{t_0\le t\le t_n}{max}\left|p^{\left(4\right)}\left(t\right)\right|{\tau }^{4-\alpha }\right],n\ge 3.$$

(13)

The coefficients $g_{n,s}$ have the following properties:

(a) $g_{n,0}>0$, $g_{n,2}>0$.

(b) $g_{n,s}<0$, $s\ge 1$, $s\ne 2$.

(c) ${\displaystyle \sum _{i=0}^n{g}_{n,i}=0}$.

Now let us define a semi-discrete formulation of the problem.

Problem 3.

Let ${\left\{p^i\right\}}_{i=0}^{n-1}$, $p^i\in H_0^1\left(\Omega \right)$ be known; in particular, $p^0=p_0\left(x\right)$. Find $p^n\in H_0^1\left(\Omega \right)$ such that, for all $v\in H_0^1\left(\Omega \right)$:

$$\left({\Delta }_{0,t}^{\alpha }{p}^n,v\right)+\left(\lambda \nabla p^n,\nabla v\right)=\left(\phi \left(p^n\right),v\right)+\left(f,v\right),$$

(14)

where $\alpha \in \left(0,1\right)$.

2.3.2. Construction of the Fully Discrete Scheme

Let ${\mathcal{K}}_h$ be a quasi-uniform triangulation on $\overline{\Omega }$. For $l\in \mathbb{N}$, we denote by $P_l\left(e\right)$ the space of polynomials of degree at most l on $e\in {\mathcal{K}}_h$. Let us define the discrete space $V_h\subset H_0^1\left(\Omega \right)$:

$$V_h=\left\{v_h\in H_0^1\left(\Omega \right)\cap C^0\left(\overline{\Omega }\right)|v_h{|}_e\in P_1\left(e\right),\forall e\in {\mathcal{K}}_h\right\}.$$

Then, the fully discrete scheme is defined as follows.

Problem 4.

Let ${\left\{p_h^i\right\}}_{i=0}^{n-1}$, $p_h^i\in V_h$ be known; in particular, let $p_h^0$ be the $L^2$-projection of $p_0$. Find $p_h^n\in V_h$, $n=1,2,\dots ,N$, satisfying the following identities for any $v_h\in V_h$:

$$\left({\Delta }_{0,t}^{\alpha }{p}_h^n,v_h\right)+\left(\lambda \nabla p_h^n,\nabla v_h\right)=\left(\phi \left(p_h^n\right),v_h\right)+\left(f,v_h\right),$$

(15)

where $\alpha \in \left(0,1\right)$.

The identity (15) is non-linear. Therefore, we use Newton’s method for its linearization. Specifically, the finite element procedure defined above in Problem 4 is repeated for the iteration parameter $i=1,2,\dots$ Let us denote the value of the function $p_h^n$ at the i-th iteration by $p_h^{n,i}$ and define the following iterative method.

Problem 5.

Let $p_h^j\in V_h$, $j=0,1,\dots ,n-1$ be known; in particular, $p_h^0$ is the $L^2$-projection of $p_0$. In addition, let $p_h^{n,k}\in V_h$, $k=0,1,\dots ,i-1$ be known; in particular, $p_h^{n,0}=p_h^{n-1}$. Find $p_h^{n,i}\in V_h$, $i=1,2,\dots$, satisfying the following identity for all $v_h\in V_h$:

$${\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}\left(g_{n,0}^{\alpha }\left(p_h^{n,i},v_h\right)+\sum _{s=1}^n{g}_{n,s}^{\alpha }\left(p_h^{n-s},v_h\right)\right)+\left(\lambda \nabla p_h^{n,i},\nabla v_h\right)$$

$$=\left(\phi \left(p_h^{n,i-1}\right)+{\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right)\left(p_h^{n,i}-p_h^{n,i-1}\right),v_h\right)+\left(f,v_h\right),$$

(16)

where $\alpha \in \left(0,1\right)$.

2.4. Stability of the Numerical Scheme

Let us formulate the following well-known lemma, which will be referenced several times throughout the manuscript.

Lemma 3.

Let the following inequalities be satisfied for non-negative sequences $\left\{y_n\right\}$, $\left\{f_n\right\}$, $\left\{g_n\right\}$:

$$y_n\le f_n+\sum _{k=0}^{n-1}{g}_k{y}_k.$$

Then,

$$y_n\le f_n+\sum _{k=0}^{n-1}{f}_k{g}_{k}exp\left(\sum _{j=k+1}^{n-1}{g}_j\right).$$

Let us prove the following stability result for the constructed method defined in Problem 4.

Theorem 2.

The numerical scheme defined in Problem 4 is stable with respect to the initial data and right-hand side for a sufficiently small $\tau >0$ under Assumption 2, and the following estimate is valid:

$${∥p_h^n∥}^2+{\displaystyle \frac{\Gamma \left(2-\alpha \right){\tau }^{\alpha }}{g_{n,0}^{\alpha }}}{∥\nabla p_h^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\left({∥p_h^0∥}^2+{∥f∥}^2\right).$$

(17)

Proof. 

Take $v_h=p_h^n$ in (15), separate the term corresponding to $s=0$, and multiply both sides of the resulting identity by ${\displaystyle \frac{\Gamma \left(2-\alpha \right){\tau }^{\alpha }}{g_{n,0}^{\alpha }}}$ to obtain

$$\left(p_h^n,p_h^n\right)+{\displaystyle \frac{\Gamma \left(2-\alpha \right){\tau }^{\alpha }}{g_{n,0}^{\alpha }}}\left(\lambda \nabla p_h^n,\nabla p_h^n\right)=-{\displaystyle \frac{1}{g_{n,0}^{\alpha }}}\sum _{s=1}^n{g}_{n,s}^{\alpha }\left(p_h^{n-s},p_h^n\right)$$

$$+{\displaystyle \frac{\Gamma \left(2-\alpha \right){\tau }^{\alpha }}{g_{n,0}^{\alpha }}}\left[\left(\phi \left(p_h^n\right),p_h^n\right)+\left(f,p_h^n\right)\right].$$

Apply the Cauchy inequality on the right-hand side, taking into account Assumption 2, to obtain

$${∥p_h^n∥}^2+{\displaystyle \frac{\Gamma \left(2-\alpha \right)\lambda {\tau }^{\alpha }}{g_{n,0}^{\alpha }}}{∥\nabla p_h^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le {\displaystyle \frac{1}{4\epsilon g_{n,0}^{\alpha }}}\sum _{s=1}^n\left|g_{n,s}^{\alpha }\right|{∥p_h^{n-s}∥}^2$$

$$+{\displaystyle \frac{\epsilon }{g_{n,0}^{\alpha }}}{∥p_h^n∥}^2\sum _{s=0}^n\left|g_{n,s}^{\alpha }\right|+C{\tau }^{\alpha }{∥p_h^n∥}^2+C{\tau }^{\alpha }\left({\displaystyle \frac{1}{4\epsilon }}{∥f∥}^2+\epsilon {∥p_h^n∥}^2\right).$$

(18)

Considering the properties of the coefficients $g_{n,s}$ presented in Lemma 2, it is easy to see that [27]

$$\sum _{s=0}^n\left|g_{n,s}^{\alpha }\right|=g_{n,0}^{\alpha }-g_{n,1}^{\alpha }+g_{n,2}^{\alpha }-g_{n,3}^{\alpha }-\dots -g_{n,n}^{\alpha }=-\sum _{s=0}^n{g}_{n,s}^{\alpha }+2\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right).$$

Thus, we obtain the following useful relation under Lemma 2:

$$\sum _{s=0}^n\left|g_{n,s}^{\alpha }\right|=2\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right).$$

(19)

Therefore, it follows from (18) that

$${∥p_h^n∥}^2+{\displaystyle \frac{\Gamma \left(2-\alpha \right)\lambda {\tau }^{\alpha }}{g_{n,0}^{\alpha }}}{∥\nabla p_h^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le {\displaystyle \frac{1}{4\epsilon g_{n,0}^{\alpha }}}\sum _{s=1}^n\left|g_{n,s}^{\alpha }\right|{∥p_h^{n-s}∥}^2$$

$$+{\displaystyle \frac{2\epsilon \left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)}{g_{n,0}^{\alpha }}}{∥p_h^n∥}^2+C{\tau }^{\alpha }{∥p_h^n∥}^2+C{\tau }^{\alpha }\left({\displaystyle \frac{1}{4\epsilon }}{∥f∥}^2+\epsilon {∥p_h^n∥}^2\right).$$

Let us choose ${\displaystyle \epsilon =\frac{g_{n,0}^{\alpha }}{4\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)}}$ and note that

$$\sum _{s=1}^n\left|g_{n,s}^{\alpha }\right|{∥p_h^{n-s}∥}^2=\sum _{k=0}^{n-1}\left|g_{n,n-k}^{\alpha }\right|{∥p_h^k∥}^2.$$

Then, we obtain, for a sufficiently small $\tau$, that

$${∥p_h^n∥}^2+{\displaystyle \frac{\Gamma \left(2-\alpha \right)\lambda {\tau }^{\alpha }}{g_{n,0}^{\alpha }}}{∥\nabla p_h^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le {\displaystyle \frac{g_{n,0}^{\alpha }+g_{n,2}^{\alpha }}{{\left(g_{n,0}^{\alpha }\right)}^2}}\sum _{k=0}^{n-1}\left|g_{n,n-k}^{\alpha }\right|{∥p_h^{n-s}∥}^2+C{\tau }^{\alpha }{∥f∥}^2.$$

Applying Lemma 3 to this inequality yields

$${∥p_h^n∥}^2+{\displaystyle \frac{\Gamma \left(2-\alpha \right)\lambda {\tau }^{\alpha }}{g_{n,0}^{\alpha }}}{∥\nabla p_h^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le {∥p_h^0∥}^2+C{\tau }^{\alpha }{∥f∥}^2$$

$$+\sum _{k=0}^{n-1}{∥p_h^0∥}^2·{\displaystyle \frac{g_{n,0}^{\alpha }+g_{n,2}^{\alpha }}{{\left(g_{n,0}^{\alpha }\right)}^2}}\left|g_{n,n-k}^{\alpha }\right|exp\left(\sum _{j=k+1}^{n-1}{\displaystyle \frac{\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)}{{\left(g_{n,0}^{\alpha }\right)}^2}}\left|g_{n,n-j}^{\alpha }\right|\right).$$

(20)

Note that

$$\sum _{j=k+1}^{n-1}{\displaystyle \frac{\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)}{{\left(g_{n,0}^{\alpha }\right)}^2}}\left|g_{n,n-j}^{\alpha }\right|={\displaystyle \frac{g_{n,0}^{\alpha }+g_{n,2}^{\alpha }}{{\left(g_{n,0}^{\alpha }\right)}^2}}\sum _{s=1}^{n-k-1}\left|g_{n,s}^{\alpha }\right|$$

$$\le {\displaystyle \frac{g_{n,0}^{\alpha }+g_{n,2}^{\alpha }}{{\left(g_{n,0}^{\alpha }\right)}^2}}\sum _{s=0}^n\left|g_{n,s}^{\alpha }\right|={\displaystyle \frac{g_{n,0}^{\alpha }+g_{n,2}^{\alpha }}{{\left(g_{n,0}^{\alpha }\right)}^2}}·2\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)=2{\left({\displaystyle \frac{g_{n,0}^{\alpha }+g_{n,2}^{\alpha }}{g_{n,0}^{\alpha }}}\right)}^2;$$

therefore, considering (20), we obtain the inequality (17). □

2.5. Convergence of the Numerical Method

2.5.1. Convergence of a Semi-Discrete Scheme

Let us introduce the projector $Q_h:H_0^1\left(\Omega \right)\to V_h$ such that

$$\left(\nabla \left(Q_{h}p-p\right),\nabla p_h\right)=0\forall p\in H_0^1\left(\Omega \right),p_h\in V_h,$$

(21)

which has the following property

$$∥p-Q_{h}p∥+h{∥p-Q_{h}p∥}_{H^1\left(\Omega \right)}\le C{h}^{k+1}{∥p∥}_{H^{k+1}\left(\Omega \right)}$$

(22)

for all $p\in H_0^1\left(\Omega \right)\cap H^{k+1}\left(\Omega \right)$. Let

$$p\left(t_n\right)-p_h^n=\left(p\left(t_n\right)-Q_h{p}^n\right)+\left(Q_h{p}^n-p_h^n\right):={\psi }^n+{\xi }^n.$$

(23)

To attain a global convergence order of $O\left({\tau }^{4-\alpha }+h^{k+1}\right)$, we implement the substep scheme technique [47] on the intervals $\left(0,t_1\right)$ and $\left(t_1,t_2\right)$. Let $l_1$ and $l_2$ represent the smallest integers satisfying ${\displaystyle l_1\ge \frac{1}{\tau }}$, ${\displaystyle {\displaystyle l_2\ge {\tau }^{-\frac{2-\alpha }{6-\alpha }}}}$. Let us introduce the corresponding lengths of the substeps:

$${\tau }_1={\displaystyle \frac{\tau }{l_1}},{\tau }_2={\displaystyle \frac{\tau }{l_2}}.$$

Lemma 4.

Let $p^n$ be the solution to Problem 3 and p be the solution to Problem 2. Then, there exists ${\tau }_0>0$ such that the following inequality holds under Assumptions 1 and 2 for all $\tau \le {\tau }_0$:

$${∥p\left(t_n\right)-p^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla \left(p\left(t_n\right)-p^n\right)∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\tau }^{8-2\alpha },$$

(24)

where C is a constant that depends on the norms of the solution but does not depend on the mesh parameters.

Proof. 

Consider the difference between the identities (4) and (14):

$$\left({\partial }_{0,t}^{\alpha }p\left(t_n\right)-{\Delta }_{0,t}^{\alpha }{p}^n,v\right)+\left(\lambda \left(\nabla p\left(t_n\right)-\nabla p^n\right),\nabla v\right)=\left(\phi \left(p\left(t_n\right)\right)-\phi \left(p^n\right),v\right).$$

(25)

Denote ${\pi }^n=p\left(t_n\right)-p^n$ and note that

$${\partial }_{0,t}^{\alpha }p\left(t_n\right)-{\Delta }_{0,t}^{\alpha }{p}^n={\Delta }_{0,t}^{\alpha }{\pi }^n+r_n^{\alpha },$$

where $r_n^{\alpha }={\partial }_{0,t}^{\alpha }p\left(t_n\right)-{\Delta }_{0,t}^{\alpha }p\left(t_n\right)$. Choosing $v={\pi }^n$ in (25), and taking into account Assumption 2, we obtain

$$\left({\Delta }_{0,t}^{\alpha }{\pi }^n,{\pi }^n\right)+\lambda {∥\nabla {\pi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le c_2{∥{\pi }^n∥}^2+\left(r_n^{\alpha },{\pi }^n\right).$$

Using the relation (10), rewrite this inequality in the form

$${\displaystyle \frac{g_{n,0}^{\alpha }{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}{∥{\pi }^n∥}^2+\lambda {∥\nabla {\pi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2$$

$$\le -{\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}\sum _{s=1}^n{g}_{n,s}^{\alpha }\left({\pi }^{n-s},{\pi }^n\right)+c_2{∥{\pi }^n∥}^2+\left(r_n^{\alpha },{\pi }^n\right).$$

Applying Cauchy’s inequality to the first and third terms on the right-hand side of this inequality, then using the relation (19) and multiplying the resulting inequality by ${\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}$, we conclude that

$${∥{\pi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)\lambda }{g_{n,0}^{\alpha }}}{∥\nabla {\pi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2$$

$$\le {\displaystyle \frac{1}{4{\epsilon }_1{g}_{n,0}^{\alpha }}}\sum _{s=1}^n\left|g_{n,s}^{\alpha }\right|{∥{\pi }^{n-s}∥}_0^2+{\displaystyle \frac{2{\epsilon }_1}{g_{n,0}^{\alpha }}}\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right){∥{\pi }^n∥}^2$$

$$+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{4g_{n,0}^{\alpha }{\epsilon }_2}}{∥r_n^{\alpha }∥}^2+{\displaystyle \frac{{\epsilon }_2{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥{\pi }^n∥}^2+{\displaystyle \frac{c_2{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥{\pi }^n∥}^2.$$

Taking

$${\epsilon }_1={\displaystyle \frac{g_{n,0}^{\alpha }}{8\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)}},{\epsilon }_2={\displaystyle \frac{g_{n,0}^{\alpha }}{4{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}},$$

we infer that, for a sufficiently small $\tau$:

$${∥{\pi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla {\pi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\sum _{s=1}^n\left|g_{n,s}^{\alpha }\right|{∥{\pi }^{n-s}∥}^2+C{\tau }^{2\alpha }{∥r_n^{\alpha }∥}^2.$$

(26)

Considering the identity (14) in the case of $n=1$ with the substep ${\tau }_1$, we arrive at an inequality similar to (26):

$${∥{\pi }^1∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{1,0}^{\alpha }}}{∥\nabla {\pi }^1∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\left|g_{1,1}^{\alpha }\right|{∥{\pi }^0∥}^2+C{\tau }_1^{2\alpha }{∥r_1^{\alpha }∥}^2,$$

(27)

where the first term on the right-hand side vanishes due to ${\pi }^0=0$. Considering that $r_1^{\alpha }=O\left({\tau }_1^{2-\alpha }\right)$ and ${\displaystyle {\tau }_1=\frac{\tau }{l_1}\le \frac{\tau }{\left({\tau }^{\frac{\alpha -2}{2}}\right)}={\tau }^{\frac{4-\alpha }{2}}}$, we obtain

$${∥{\pi }^1∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{1,0}^{\alpha }}}{∥\nabla {\pi }^1∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\left({\tau }^{{\displaystyle \frac{4-\alpha }{2}}}\right)}^{2\alpha }{\left({\tau }^{\left({\displaystyle \frac{4-\alpha }{2}}\right)\left(2-\alpha \right)}\right)}^2$$

$$\le C\left({\tau }^{4\alpha -{\alpha }^2}{\tau }^{8-4\alpha -2\alpha +{\alpha }^2}\right),$$

and thus,

$${∥{\pi }^1∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{1,0}^{\alpha }}}{∥\nabla {\pi }^1∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\tau }^{8-2\alpha }.$$

(28)

Similarly, considering the identity (14) in the case of $n=2$, we obtain

$${∥{\pi }^2∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{2,0}^{\alpha }}}{∥\nabla {\pi }^2∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\left(\left|g_{2,1}^{\alpha }\right|{∥{\pi }^1∥}^2+\left|g_{2,2}^{\alpha }\right|{∥{\pi }^0∥}^2\right)+C{\tau }_2^{2\alpha }{∥r_2^{\alpha }∥}^2,$$

and, given that $r_2^{\alpha }=O\left({\tau }_2^{3-\alpha }\right)$ and ${\displaystyle {\displaystyle {\tau }_2=\frac{\tau }{l_2}\le \frac{\tau }{\left({\tau }^{\frac{\alpha -1}{3}}\right)}={\tau }^{\frac{4-\alpha }{3}}}}$, and also taking into account the inequality (28), we obtain

$${∥{\pi }^2∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{2,0}^{\alpha }}}{∥\nabla {\pi }^2∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\tau }^{8-2\alpha }+C{\left({\tau }^{{\displaystyle \frac{4-\alpha }{3}}}\right)}^{2\alpha }{\left({\tau }^{{\displaystyle \frac{4-\alpha }{3}}}\right)}^{\left(3-\alpha \right)·2},$$

or

$${∥{\pi }^2∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{2,0}^{\alpha }}}{∥\nabla {\pi }^2∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\tau }^{8-2\alpha }.$$

(29)

Considering the identity (14) in the same way as in the case of $n=3$, we obtain

$${∥{\pi }^3∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{3,0}^{\alpha }}}{∥\nabla {\pi }^3∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\sum _{s=1}^3\left|g_{3,s}^{\alpha }\right|{∥{\pi }^{3-s}∥}^2+C{\tau }^{2\alpha }{∥r_3^{\alpha }∥}^2,$$

whence, taking into account the inequalities (28) and (29), we obtain

$${∥{\pi }^3∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{3,0}^{\alpha }}}{∥\nabla {\pi }^3∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\left({\tau }^{8-2\alpha }+{\tau }^{8-2\alpha }\right)+C{\tau }^{2\alpha }{\tau }^{8-2\alpha }$$

or

$${∥{\pi }^3∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{3,0}^{\alpha }}}{∥\nabla {\pi }^3∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\tau }^{8-2\alpha }.$$

(30)

By repeating this process for $n\ge 4$, we can conclude that

$${∥{\pi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla {\pi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\sum _{s=1}^{n-4}\left|g_{n,s}^{\alpha }\right|{∥{\pi }^{n-s}∥}^2$$

$$+C\left[\left|g_{n,n-3}^{\alpha }\right|{∥{\pi }^3∥}^2+\left|g_{n,n-2}^{\alpha }\right|{∥{\pi }^2∥}^2+\left|g_{n,n-1}^{\alpha }\right|{∥{\pi }^1∥}^2\right]+C{\tau }^{2\alpha }{∥r_n^{\alpha }∥}^2.$$

Thus, using the inequalities (28)–(30) gives

$${∥{\pi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla {\pi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C\sum _{s=1}^{n-4}{\tau }^{8-2\alpha }+C\left[{\tau }^{8-2\alpha }+{\tau }^{8-2\alpha }\right]+C{\tau }^{2\alpha }·{\tau }^{8-2\alpha },$$

which yields inequality (24). □

2.5.2. Convergence of a Fully Discrete Scheme

Lemma 5.

Let $p_h^n$ be the solution to Problem 4, and let $p^n$ be the solution to Problem 3. Then, the following inequality holds under Assumptions 1 and 2:

$${∥Q_h{p}^n-p_h^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla \left(Q_h{p}^n-p_h^n\right)∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{h}^{2k+2},$$

where C is a constant that depends on the norms of the solution to Problem 2 but does not depend on the mesh parameters.

Proof. 

Consider the difference between the identities (14) and (15):

$$\left({\Delta }_{0,t}^{\alpha }\left(p^n-p_h^n\right),v_h\right)+\left(\lambda \nabla \left(p^n-p_h^n\right),\nabla v_h\right)=\left(\phi \left(p^n\right)-\phi \left(p_h^n\right),v_h\right).$$

Using Assumption 2 and notation (23), and choosing $v_h={\xi }^n$, we arrive at the inequality

$$\left({\Delta }_{0,t}^{\alpha }{\xi }^n,{\xi }^n\right)+\lambda {∥\nabla {\xi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2+\left({\Delta }_{0,t}^{\alpha }{\psi }^n,{\xi }^n\right)+\left(\lambda \nabla {\psi }^n,\nabla {\xi }^n\right)\le C{∥{\xi }^n∥}^2+C\left({\psi }^n,{\xi }^n\right).$$

Using the expansion (10) and property (21) we obtain:

$${\displaystyle \frac{{\tau }^{-\alpha }{g}_{n,0}^{\alpha }}{\Gamma \left(2-\alpha \right)}}{∥{\xi }^n∥}^2+\lambda {∥\nabla {\xi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le -{\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}\sum _{s=1}^n{g}_{n,s}^{\alpha }\left({\xi }^{n-s},{\xi }^n\right)$$

$$-{\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}\sum _{s=0}^n{g}_{n,s}^{\alpha }\left({\psi }^{n-s},{\xi }^n\right)+C{∥{\xi }^n∥}^2+C\left({\psi }^n,{\xi }^n\right).$$

By estimating the right-hand side of this inequality using Cauchy’s inequality, using relation (19), and multiplying the resulting inequality by ${\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}$, we obtain

$${∥{\xi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\lambda \Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla {\xi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2$$

$$\le {\displaystyle \frac{1}{4{\epsilon }_1{g}_{n,0}^{\alpha }}}\sum _{s=1}^n\left|g_{n,s}^{\alpha }\right|{∥{\xi }^{n-s}∥}^2+{\displaystyle \frac{1}{4{\epsilon }_1{g}_{n,0}^{\alpha }}}\sum _{s=0}^n\left|g_{n,s}^{\alpha }\right|{∥{\psi }^{n-s}∥}^2+{\displaystyle \frac{4{\epsilon }_1\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)}{g_{n,0}^{\alpha }}}{∥{\xi }^n∥}^2$$

$$+{\displaystyle \frac{C{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥{\xi }^n∥}^2+C\left({\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{4{\epsilon }_2{g}_{n,0}^{\alpha }}}{∥{\psi }^n∥}^2+{\displaystyle \frac{{\epsilon }_2{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥{\xi }^n∥}^2\right).$$

Let ${\displaystyle {\epsilon }_1=\frac{g_{n,0}^{\alpha }}{16\left(g_{n,0}^{\alpha }+g_{n,2}^{\alpha }\right)}}$, ${\displaystyle {\epsilon }_2=\frac{g_{n,0}^{\alpha }}{4C{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}}$. Then, we obtain the following inequality for a sufficiently small $\tau$ considering inequality (22):

$${∥{\xi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\lambda \Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla {\xi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2$$

$$\le C\left(\sum _{s=1}^n{∥{\xi }^{n-s}∥}^2+\sum _{s=0}^n{h}^{2k+2}{∥p∥}_{H^{k+1}\left(\Omega \right)}^2\right)+C{h}^{2k+2}{∥p∥}_{H^{k+1}\left(\Omega \right)}^2.$$

(31)

Now, we prove the inequality

$${∥{\xi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla {\xi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{h}^{2k+2}$$

(32)

by the method of mathematical induction using inequality (31), similar to that in [52]. For $n=1$, inequality (31) takes the form

$${∥{\xi }^1∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{1,0}^{\alpha }}}{∥\nabla {\xi }^1∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{h}^{2k+2},$$

where we take into account that $∥{\xi }^0∥=0$.

Suppose that inequality (32) holds for all $i=2,3,\dots ,n-1$, and let us prove inequality (32) for $i=n$. In this case, it follows from (31) that

$${∥{\xi }^n∥}^2+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla {\xi }^n∥}_{{\mathit{L}}^2\left(\Omega \right)}^2$$

$$\le C\left(\sum _{s=1}^n{∥{\xi }^{n-s}∥}^2+\sum _{s=0}^n{h}^{2k+2}{∥p∥}_{H^{k+1}\left(\Omega \right)}^2\right)+C{h}^{2k+2}{∥p∥}_{H^{k+1}\left(\Omega \right)}^2\le C{h}^{2k+2},$$

which yields inequality (32). □

Now, we are ready to formulate the convergence theorem for the constructed numerical method defined in Problem 4.

Theorem 3.

Let $p_h^n$ be the solution to Problem 4, and let p be the solution to Problem 2. Then, there exists ${\tau }_0>0$ such that the following inequality holds for all $\tau \le {\tau }_0$ under Assumptions 1 and 2:

$$∥p\left(t_n\right)-p_h^n∥+{\displaystyle \frac{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}{g_{n,0}^{\alpha }}}{∥\nabla \left(p\left(t_n\right)-p_h^n\right)∥}_{{\mathit{L}}^2\left(\Omega \right)}\le C\left({\tau }^{4-\alpha }+h^{k+1}\right),$$

where C is a constant that depends on the norms of the solution to Problem 2 but does not depend on the mesh parameters.

Proof. 

The proof of the theorem follows from the inequality

$$∥p\left(t_n\right)-p_h^n∥\le ∥p\left(t_n\right)-p^n∥+∥p^n-Q_{h}p∥+∥Q_{h}p-p_h^n∥,$$

from Lemmas 4 and 5 and inequality (22). □

2.5.3. Convergence of the Iterative Process

Now, we discuss the convergence of Newton’s iterative process defined in Problem 5 and determine the sufficient conditions for its quadratic convergence. The proof of this result relies on the following well-known lemma.

Lemma 6

([53]). Let $f:\mathbb{R}\to \mathbb{R}$ be a differentiable function and $f^{\prime }$ be Lipschitz continuous. Then,

$$\left|f\left(x\right)-f\left(y\right)-f^{\prime }\left(y\right)\left(x-y\right)\right|\le {\displaystyle \frac{L_{f^{\prime }}}{2}}{\left|x-y\right|}^2,\forall x,y\in \mathbb{R},$$

where $L_{f^{\prime }}$ is the Lipschitz constant.

Theorem 4.

The following inequality holds under the condition $\tau <{\tau }_0,$${\tau }_0={\left({\displaystyle \frac{2g_{n,0}^{\alpha }}{{\phi }^{**}\Gamma \left(2-\alpha \right)}}\right)}^{1/\alpha }$:

$${∥p_h^n-p_h^{n,i}∥}^2+{\tau }^{\alpha }{∥\nabla \left(p_h^n-p_h^{n,i}\right)∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\tau }^{\alpha }{h}^{-d}{∥p_h^n-p_h^{n,i-1}∥}^4.$$

Proof. 

Let us introduce the notation ${\vartheta }^{n,i}=p_h^n-p_h^{n,i}$. Subtracting (16) from (15), we obtain:

$${\displaystyle \frac{g_{n,0}^{\alpha }{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}\left({\vartheta }^{n,i},v_h\right)+\left(\lambda \nabla {\vartheta }^{n,i},\nabla v_h\right)$$

$$-\left(\phi \left(p_h^n\right)-\phi \left(p_h^{n,i-1}\right)-{\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right)\left(p_h^{n,i}-p_h^{n,i-1}\right),v_h\right)=0.$$

(33)

Let us choose $v_h={\vartheta }^{n,i}$ and evaluate the terms in (33). Concerning the initial two terms on the left-hand side of Equation (33), we have

$$T_1\equiv {\displaystyle \frac{g_{n,0}^{\alpha }{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}\left({\vartheta }^{n,i},{\vartheta }^{n,i}\right)={\displaystyle \frac{g_{n,0}^{\alpha }{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}}{∥{\vartheta }^{n,i}∥}^2,$$

$$T_2\equiv \left(\lambda \nabla {\vartheta }^{n,i},\nabla {\vartheta }^{n,i}\right)=\lambda {∥\nabla {\vartheta }^{n,i}∥}_{{\mathit{L}}^2\left(\Omega \right)}^2.$$

Let us represent the third term as follows:

$$T_3\equiv \left(\phi \left(p_h^n\right)-\phi \left(p_h^{n,i-1}\right)-{\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right)\left(p_h^{n,i}-p_h^{n,i-1}\right),{\vartheta }^{n,i}\right)$$

$$=\left(\phi \left(p_h^n\right)-\phi \left(p_h^{n,i-1}\right)+{\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right)\left(p_h^n-p_h^{n,i}-p_h^n+p_h^{n,i-1}\right),{\vartheta }^{n,i}\right)$$

$$=\left({\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right){\vartheta }^{n,i},{\vartheta }^{n,i}\right)+\left(\phi \left(p_h^n\right)-\phi \left(p_h^{n,i-1}\right),{\vartheta }^{n,i}\right)$$

$$-\left({\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right)\left(p_h^n-p_h^{n,i-1}\right),{\vartheta }^{n,i}\right)=T_{31}+T_{32},$$

where

$$\left|T_{31}\right|=\left|\left({\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right){\vartheta }^{n,i},{\vartheta }^{n,i}\right)\right|\le {\phi }^{**}{∥{\vartheta }^{n,i}∥}^2,$$

$$\left|T_{32}\right|\equiv \left|\left(\phi \left(p_h^n\right)-\phi \left(p_h^{n,i-1}\right)-{\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right)\left(p_h^n-p_h^{n,i-1}\right),{\vartheta }^{n,i}\right)\right|$$

$$=\left|{\int }_{\Omega }\left[\phi \left(p_h^n\right)-\phi \left(p_h^{n,i-1}\right)-{\displaystyle \frac{d\phi }{dp}}\left(p_h^{n,i-1}\right)\left(p_h^n-p_h^{n,i-1}\right)\right]·{\vartheta }^{n,i}dx\right|$$

$$\le L_{{\phi }^{\prime }}{\int }_{\Omega }{\left|p_h^n-p_h^{n,i-1}\right|}^2\left|{\vartheta }^{n,i}\right|dx$$

$$\le {\displaystyle \frac{L_{F^{\prime }}^2}{4\epsilon }}{∥{\vartheta }^{n,i-1}∥}_{L^4\left(\Omega \right)}^4+\epsilon {∥{\vartheta }^{n,i}∥}^2.$$

Using the inverse inequality ${∥{\vartheta }^{n,i-1}∥}_{L^4\left(\Omega \right)}\le C{h}^{-d/4}∥{\vartheta }^{n,i-1}∥$, we obtain

$$\left|T_{32}\right|\le C{h}^{-d}{∥{\vartheta }^{n,i-1}∥}^4+\epsilon {∥{\vartheta }^{n,i}∥}^2.$$

Taking ${\displaystyle \epsilon =\frac{{\phi }^{**}}{2}}$, we obtain from (33) that

$${\displaystyle \frac{g_{n,0}^{\alpha }}{\Gamma \left(2-\alpha \right)}}{∥{\vartheta }^{n,i}∥}^2+{\tau }^{\alpha }\lambda {∥\nabla {\vartheta }^{n,i}∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le {\tau }^{\alpha }{\displaystyle \frac{{\phi }^{**}}{2}}{∥{\vartheta }^{n,i}∥}^2+{\tau }^{\alpha }C{h}^{-d}{∥{\vartheta }^{n,i-1}∥}^4.$$

Choosing $\tau \le {\tau }_0$, where ${\tau }_0$ is defined in the condition of the theorem, we obtain

$${∥{\vartheta }^{n,i}∥}^2+{\tau }^{\alpha }{∥\nabla {\vartheta }^{n,i}∥}_{{\mathit{L}}^2\left(\Omega \right)}^2\le C{\tau }^{\alpha }{h}^{-d}{∥{\vartheta }^{n,i-1}∥}^4,$$

which yields the statement of the theorem. □

It follows from the proven theorem that the sufficient condition for the quadratic convergence of Newton’s iterative method takes the form:

$$C{\tau }^{\alpha }{h}^{-d}{∥p_h^n-p_h^{n,i-1}∥}^2\le 1.$$

3. Results

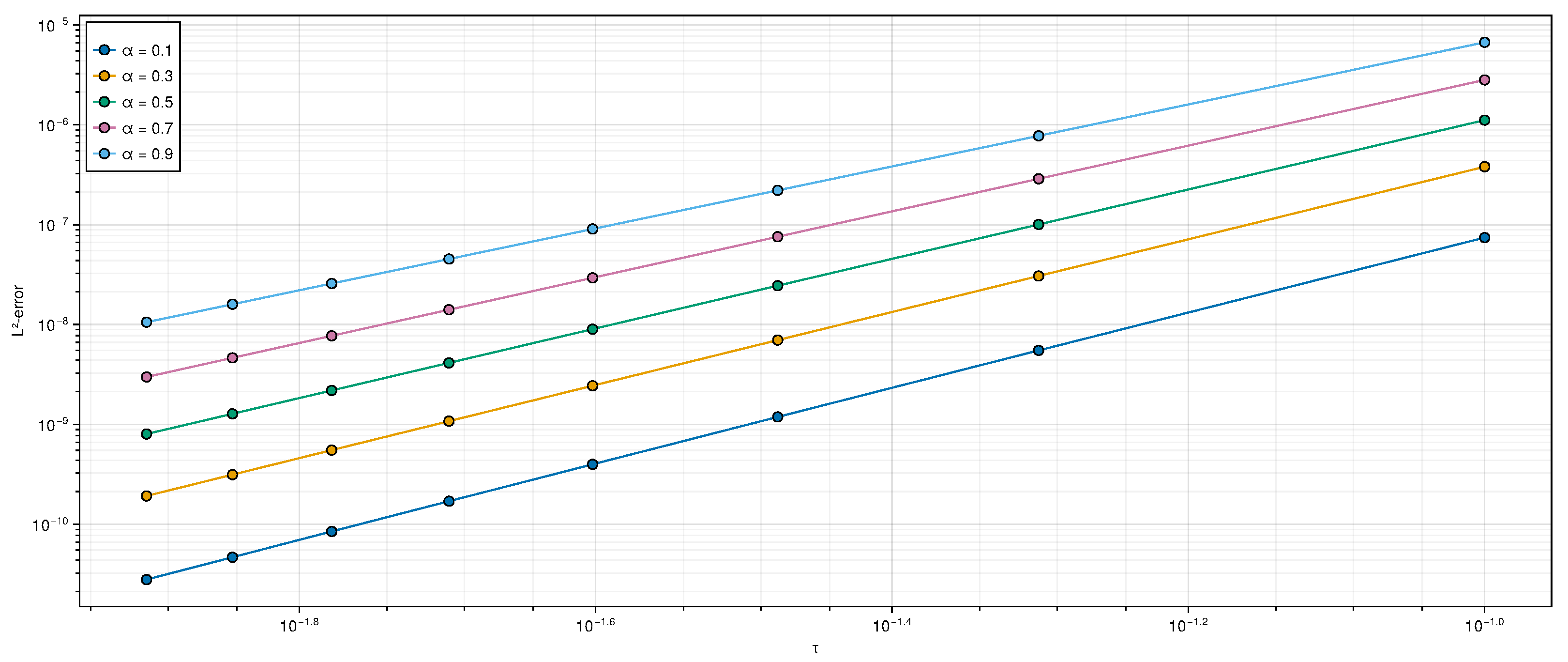
Verification of the Order of Convergence Based on Computational Experiments

To validate the theoretical convergence estimate derived in Theorem 3 for a fully discrete scheme, numerical tests have been conducted for a model problem with a known exact solution.

The objective of the numerical tests is to ascertain the relationship between the observed empirical convergence order and the orders of fractional derivatives, and to juxtapose them with the theoretical convergence orders derived in Theorem 3.

Example 1.

In $Q_T=\overline{\Omega }\times \overline{J}$, where $\Omega =\left(0,1\right)\times \left(0,1\right)$, $J=\left(0,1\right]$, consider the problem

$${\partial }_{0,t}^{\alpha }p-2{\nabla }^{2}p=p^2+f\left(x,t\right),\left(x,t\right)\in \Omega \times J,$$

$$f\left(x,t\right)={\displaystyle \frac{24t^{4-\alpha }{x}_1\left(1-x_1\right)x_2\left(1-x_2\right)}{\Gamma \left(5-\alpha \right)}}$$

$$+4t^4\left(x_1\left(1-x_1\right)+x_2\left(1-x_2\right)\right)-t^8{x}_1^2{\left(1-x_1\right)}^2{x}_2^2{\left(1-x_2\right)}^2,\left(x,t\right)\in \Omega \times J,$$

$$p\left(x,0\right)=0,x\in \overline{\Omega },$$

$$p\left(x,t\right)=0,\left(x,t\right)\in \partial \Omega \times J.$$

The exact solution to the problem is $p\left(x,t\right)=t^4{x}_1{x}_2\left(1-x_1\right)\left(1-x_2\right)$. By varying the time step value within the range from $\tau =1/10$ to $\tau =1/80$ for a fixed number of elements $M=2500$, we use the algorithm proposed in Problem 5 and compute the associated errors $E_{\tau }$ in the $L^2$-norm, then determine the empirical convergence order by the formula

$$r={\displaystyle \frac{ln\left(E_{2\tau }/E_{\tau }\right)}{ln2}}.$$

The iterative process defined in Problem 5 was performed until the condition

$∥p_h^{n,i}-p_h^{n,i-1}∥<{10}^{-9}$ was reached. In all numerical tests, this condition was achieved in 2–3 iterations.

The $L^2$-error values and empirical convergence orders corresponding to various values of the fractional derivative orders $\alpha \in \left\{0.1,0.2,\dots ,0.9\right\}$ are presented in

Table 1. $L^2$-errors and empirical convergence orders for Example 1 for different orders of the fractional derivative $\alpha$. The last row of the table shows the theoretical orders of convergence.

$\mathit{\tau }$	$\mathit{\alpha }=0.1$		$\mathit{\alpha }=0.2$		$\mathit{\alpha }=0.3$
	${\mathit{L}}^{\mathbf{2}}$-Error	Order	${\mathit{L}}^{\mathbf{2}}$-Error	Order	${\mathit{L}}^{\mathbf{2}}$-Error	Order
1/10	$7.4187\times {10}^{-8}$	-	$1.9246\times {10}^{-7}$	-	$3.7971\times {10}^{-7}$	-
1/20	$5.5046\times {10}^{-9}$	3.75	$1.4866\times {10}^{-8}$	3.69	$3.0620\times {10}^{-8}$	3.63
1/30	$1.1875\times {10}^{-9}$	3.78	$3.2904\times {10}^{-9}$	3.72	$6.9802\times {10}^{-9}$	3.65
1/40	$3.9815\times {10}^{-10}$	3.80	$1.1248\times {10}^{-9}$	3.73	$2.4386\times {10}^{-9}$	3.66
1/50	$1.7014\times {10}^{-10}$	3.81	$4.8846\times {10}^{-10}$	3.74	$1.0774\times {10}^{-9}$	3.66
1/60	$8.4683\times {10}^{-11}$	3.83	$2.4673\times {10}^{-10}$	3.75	$5.5230\times {10}^{-10}$	3.67
1/70	$4.6780\times {10}^{-11}$	3.85	$1.3830\times {10}^{-10}$	3.76	$3.1367\times {10}^{-10}$	3.67
1/80	$2.7939\times {10}^{-11}$	3.86	$8.3626\times {10}^{-11}$	3.77	$1.9200\times {10}^{-10}$	3.68
Predicted		3.9		3.8		3.7
$\mathbf{\tau }$	$\mathbf{\alpha }=\mathbf{0.4}$		$\mathbf{\alpha }=\mathbf{0.5}$		$\mathbf{\alpha }=\mathbf{0.6}$
	${\mathit{L}}^{\mathbf{2}}$-Error	Order	${\mathit{L}}^{\mathbf{2}}$-Error	Order	${\mathit{L}}^{\mathbf{2}}$-Error	Order
1/10	$6.6852\times {10}^{-7}$	-	$1.1124\times {10}^{-6}$	-	$1.7888\times {10}^{-6}$	-
1/20	$5.6895\times {10}^{-8}$	3.55	$1.0035\times {10}^{-7}$	3.47	$1.7163\times {10}^{-7}$	3.38
1/30	$1.3401\times {10}^{-8}$	3.57	$2.4485\times {10}^{-8}$	3.48	$4.3459\times {10}^{-8}$	3.39
1/40	$4.7955\times {10}^{-9}$	3.57	$8.9882\times {10}^{-9}$	3.48	$1.6386\times {10}^{-8}$	3.39
1/50	$2.1589\times {10}^{-9}$	3.58	$4.1288\times {10}^{-9}$	3.49	$7.6864\times {10}^{-9}$	3.39
1/60	$1.1242\times {10}^{-9}$	3.58	$2.1858\times {10}^{-9}$	3.49	$4.1402\times {10}^{-9}$	3.39
1/70	$6.4720\times {10}^{-10}$	3.58	$1.2764\times {10}^{-9}$	3.49	$2.4534\times {10}^{-9}$	3.39
1/80	$4.0101\times {10}^{-10}$	3.58	$8.0083\times {10}^{-10}$	3.49	$1.5591\times {10}^{-9}$	3.40
Predicted		3.6		3.5		3.4
$\mathbf{\tau }$	$\mathbf{\alpha }=\mathbf{0.7}$		$\mathbf{\alpha }=\mathbf{0.8}$		$\mathbf{\alpha }=\mathbf{0.9}$
	${\mathit{L}}^{\mathbf{2}}$-Error	Order	${\mathit{L}}^{\mathbf{2}}$-Error	Order	${\mathit{L}}^{\mathbf{2}}$-Error	Order
1/10	$2.8113\times {10}^{-6}$	-	$4.3448\times {10}^{-6}$	-	$6.6895\times {10}^{-6}$	-
1/20	$2.8761\times {10}^{-7}$	3.29	$4.7486\times {10}^{-7}$	3.19	$7.7435\times {10}^{-7}$	3.11
1/30	$7.5674\times {10}^{-8}$	3.29	$1.2991\times {10}^{-7}$	3.20	$2.2045\times {10}^{-7}$	3.10
1/40	$2.9329\times {10}^{-8}$	3.29	$5.1780\times {10}^{-8}$	3.20	$9.0395\times {10}^{-8}$	3.10
1/50	$1.4057\times {10}^{-8}$	3.30	$2.5366\times {10}^{-8}$	3.20	$4.5270\times {10}^{-8}$	3.10
1/60	$7.7066\times {10}^{-9}$	3.30	$1.4158\times {10}^{-8}$	3.20	$2.5728\times {10}^{-8}$	3.10
1/70	$4.6359\times {10}^{-9}$	3.30	$8.6472\times {10}^{-9}$	3.20	$1.5956\times {10}^{-8}$	3.10
1/80	$2.9847\times {10}^{-9}$	3.30	$5.6412\times {10}^{-9}$	3.20	$1.0548\times {10}^{-8}$	3.10
Predicted		3.3		3.2		3.1

. The last row of the table indicates the theoretical convergence orders predicted in Theorem 3. Corresponding error plots are depicted in Figure 1.

Table 1 indicates that the convergence order of the time step $\tau$ notably varies with the order of the fractional derivative $\alpha$. Notably, for $\alpha =0.1$, the observed empirical convergence order was approximately 3.9, decreasing notably as $\alpha$ increased. When $\alpha =0.9$, the convergence order was approximately equal to 3.1. These observations align well with the theoretical expectations regarding convergence order.

Let us briefly dwell on the software implementation details of the proposed algorithm. The algorithm was implemented in the Julia programming language (version 1.10.3) and run on MacBook Pro laptop equipped with a 12-core Apple M2 Max processor and 32 GB of unified memory. The Ferrite.jl package (version 0.3.14) was utilized to implement finite element analysis. We implemented the parallel stiffness matrix assembly, which is based on a graph coloring technique in which only non-adjacent local elements are computed at a time. In addition, the AppleAccelerate.jl package (version 0.4) was used to perform optimized mathematical computations. Then, the parallel linear algebraic equation solver from the SparseArrays library was used.

Table 2. Average CPU time required to solve Example 1 on various mesh configurations.

Mesh Parameters
Nodes	441	1681	10,201	40,401	160,801
Cells	100	400	2500	10,000	40,000
$\mathbf{\tau }$	CPU Time (s)
1/10	0.0322	0.1113	1.0653	3.6686	16.0136
1/20	0.0828	0.2362	1.2875	6.2702	30.8062
1/30	0.1233	0.3537	1.9482	9.3582	46.3597
1/40	0.1564	0.4630	2.5717	12.3262	61.7358
1/50	0.1866	0.5783	3.1718	15.0545	76.6795
1/60	0.2306	0.6953	3.8219	18.0586	91.8569
1/70	0.2624	0.8053	4.5044	21.4017	106.8736
1/80	0.2985	0.9102	5.1263	24.2711	122.1779

contains some benchmark results obtained for $\alpha =0.5$ and various mesh configurations. It follows from the table that the developed program makes it possible to obtain an approximate solution to Problem 1 in an acceptable time.

4. Conclusions

Thus, drawing from both theoretical analysis and the outcomes of computational experiments, the following conclusions can be inferred:

(1) It can be concluded based on Theorem 1 that the solution to Problem 1 is unique and that it continuously depends on the input data.

(2) The numerical method constructed in Section 2.3.2 allows us to obtain an approximate solution to the increased convergence order $O\left({\tau }^{4-\alpha }+h^{k+1}\right)$, $\alpha \in \left(0,1\right)$, and k depends on the chosen basis functions in the finite element implementation. The results of computational experiments conducted for different mesh configurations and different orders of fractional derivatives are in good agreement with the results of theoretical analysis.

(3) The results of this study have broader implications beyond the specific application of filtration equations. The finite element method presented in the work for modeling fractional differential equations with transitional filtration laws lays the foundation for a comprehensive analysis of various scientific and technological processes.

Firstly, the developed numerical method allows for more accurate and efficient modeling of complex fluid flow phenomena in porous media. Its integration into existing software packages, such as the ISAR-2 hydrodynamic simulator, provides expanded modeling capabilities and improves the quality of forecasts in field exploration.

Secondly, the developed methodology can be applied to study a wide range of phenomena other than filtration, such as diffusion processes, thermal conductivity, electromagnetic wave propagation, and the behavior of viscoelastic materials. These processes often exhibit fractional-order dynamics and transient behavior, which makes the developed approach relevant for various scientific fields.

In addition, the numerical methods and a priori analyses presented in this study provide valuable insights into the computational aspects of solving fractional differential equations. These ideas can be used to improve numerical simulations in fields ranging from fluid dynamics and materials science to signal processing and control theory.

Another important decision was the use of a high-order approximation formula, which underscores our commitment to pushing the boundaries of computational methods to solve complex problems. By demonstrating the applicability of this formula, we not only enrich our understanding of the problem but also make a significant contribution to the development of methodology for solving such problems.

In essence, the results of this study not only contribute to the understanding of filtration processes but also provide a versatile set of tools for the analysis and modeling of complex systems in science and engineering. This versatility highlights the broader relevance and impact of the developed methodology on the development of computer modeling and simulation capabilities.

In conclusion, despite the fact that this study has made significant progress in solving problems related to the application of a high-order approximation formula for the numerical implementation of a nonlinear filtration equation with transient filtration laws, it is important to recognize its limitations and identify potential directions for future research. One limitation is the simplifying assumptions made in the numerical simulation of fluid flow, such as homogeneous porous media or constant physical properties. In addition, this study mainly focuses on the numerical solution of filtration equations, ignoring experimental verification and application in real conditions. Also, in numerical tests, the order $O\left({\tau }^{4-\alpha }+h^{k+1}\right)$ is achieved due to smooth conditions and on a certain right-hand side; therefore, in future studies, a broader analysis can be carried out taking into account various boundary conditions and more complex geometries in order to improve the applicability and accuracy of the developed methods.