Universal Network for Image Registration and Generation Using Denoising Diffusion Probability Model

Abstract

Classical diffusion model-based image registration approaches require separate diffusion and deformation networks to learn the reverse Gaussian transitions and predict deformations between paired images, respectively. However, such cascaded architectures introduce noisy inputs in the registration, leading to excessive computational complexity and issues with low registration accuracy. To overcome these limitations, a diffusion model-based universal network for image registration and generation (UNIRG) is proposed. Specifically, the training process of the diffusion model is generalized as a process of matching the posterior mean of the forward process to the modified mean. Subsequently, the equivalence between the training process for image generation and that for image registration is verified by incorporating the deformation information of the paired images to obtain the modified mean. In this manner, UNIRG integrates image registration and generation within a unified network, achieving shared training parameters. Experimental results on 2D facial and 3D cardiac medical images demonstrate that the proposed approach integrates the capabilities of image registration and guided image generation. Meanwhile, UNIRG achieves registration performance with NMSE of 0.0049, SSIM of 0.859, and PSNR of 27.28 on the 2D facial dataset, along with Dice of 0.795 and PSNR of 12.05 on the 3D cardiac dataset.

1. Introduction

Image registration plays a fundamental role in various applications [1,2,3,4,5]. It achieves image alignment by establishing correspondence between corresponding points and mapping them to the same spatial coordinates. By registering images at different times, the trajectory or trend of the motion of the target can be analyzed, which has a wide range of applications in medical image registration [6]. The image registration task faces significant challenges as imaging technologies advance and image quality improves. However, traditional registration approaches [7,8] are hindered by issues such as poor robustness and high computational complexity, which constrain further advances in image registration.

To overcome these difficulties, innovative approaches [9,10,11] using deep learning techniques have been applied in image registration. The typical deep learning-based image registration approach involves feeding moving and fixed images into a network and training the network to estimate the deformation field between the paired images, which is used to transform and register the images. Prominent examples of such approaches include DIRNet [12], VoxelMorph (VM) [13], and VM-diff [14], which demonstrate fast and accurate image deformations during evaluation while ensuring high precision and robustness even on unseen images within the same dataset.

Deep learning-based image registration tasks have recently embraced the use of generative models such as GANs [15] and VAEs. These models are widely applied in image translation, generation [16,17], and super-resolution processing [18]. By leveraging the learned distribution from the training data, the generative model enables the network to generate realistic target samples, effectively capturing complex data distributions.

In a typical example, Mahapatra et al. [19] successfully applied a cyclic GAN to achieve accurate multimodal retinal and cardiac image registration by incorporating additional constraints. Fan et al. [20,21] employed a GAN in medical image registration, leveraging unsupervised autonomous learning loss to obtain precise results. Rezayi et al. [22] proposed an efficient approach for simultaneous super-resolution and image registration with a continuous generative model utilizing Gaussian kernels instead of conventional interpolation.

Among generative models, diffusion models have gained attention for their excellent performance in image generation, prompting researchers to explore their applications in various image processing tasks. By introducing noise and ensuring consistency between the noise distributions of the forward and reverse processes, the diffusion model achieves the requirements of the target task. Notable instances of such models include the denoising diffusion probability model in [23] based on Markov Chains, as well as conditional diffusion models [24,25] designed for generating images with target semantics.

It is worth mentioning the notable image registration method called DiffuseMorph (DM) proposed by Kim et al. [26], which utilized the denoising diffusion model in image registration for the first time. The DM method employs two separate networks to handle the generation and registration tasks. By incorporating latent variables, DM enables joint training of both tasks through data transfer.

In this paper, we propose an innovative approach to address the issues of computational cost and task balancing by sharing the training process of generating and registering tasks. Specifically, our approach utilizes a universal model based on the U-net [27] architecture. By feeding diffused fixed images and incorporating additional spatial conditions into the generative model during training, we achieve image registration and obtain deformed images and deformation fields. Then, we leverage the learned target distribution to perform sampling for generating synthetic deformed images. Furthermore, we employ a mean-shift strategy to guide the generation of images with desired semantics.

The proposed approach offers several advantages over classical diffusion model-based registration methods. Primarily, it performs both image registration and generation tasks using a unified network, avoiding the need to design separate network structures for different tasks. Such a strategy results in increased registration accuracy and reduced computational cost while avoiding the challenge of balancing energy functions based on different tasks. Additionally, unlike traditional deep learning-based registration methods, the proposed model maintains accurate registration performance even in the presence of perturbations in the input image. Moreover, the model allows for control over the quality and content of the generated images by attaching a shift factor as a generative constraint.

2. Background and Related Works

2.1. Deformable Image Registration Model

Image registration can be described as an optimization problem, that is, finding the optimal deformation field $d^{*}$ between a moving image J and fixed image I such that the dissimilarity between the deformed image $J\left(d\right)$ and I is minimized:

$$d^{*}=\underset{d}{argmin}{E}_D(I,J\left(d\right))+\lambda E_R\left(d\right)$$

(1)

where $E_D(I,J\left(d\right))$ is the dissimilarity function used to measure the similarity between $J\left(d\right)$ and I, the term $E_R\left(d\right)$ represents the regularization constraint responsible for preserving the smoothness of the predicted deformation field, and the hyperparameter $\lambda$ is usually introduced to adjust the contributions of $E_D(I,J\left(d\right))$ and $E_R\left(d\right)$.

2.2. Denoising Diffusion Probabilistic Model

A denoising diffusion probabilistic model (DDPM) [23] is a type of generative model that learns the Markov Chain from the simple Gaussian distribution to the data distribution. The forward diffusion process of DDPM involves gradually adding noise ${ϵ}_t\sim \mathcal{N}(\mathbf{0},\mathbf{I}),t\in [1,T]$ to the original data $x_0$ using a fixed Markov Chain. Here, each step in sampling the latent variables $x_t$ is defined as a Gaussian transition:

$$q\left(x_t\right|x_{t-1})=\mathcal{N}(x_t;x_{t-1}\sqrt{1-{\beta }_t},{\beta }_t\mathbf{I})$$

(2)

where the noise variance ${\beta }_t\in (0,1)$ follows the fixed variance schedule. Given data $x_0$, the resulting sampling of $x_t$ is then expressed as follows:

$$q\left(x_t\right|x_0)=\mathcal{N}(x_t;x_0\sqrt{{\overline{\alpha }}_t},(1-{\overline{\alpha }}_t)\mathbf{I})$$

(3)

where ${\overline{\alpha }}_t={\prod }_{i=1}^t(1-{\beta }_i)$. According to the reparameterization trick [28], given $x_0$ and $ϵ\sim \mathcal{N}(\mathbf{0},\mathbf{I})$, $x_t$ can be sampled by

$$x_t=x_0\sqrt{{\overline{\alpha }}_t}+ϵ\sqrt{1-{\overline{\alpha }}_t}.$$

(4)

The generative (or reverse) process in DDPM shares the same functional form as the forward process, and involves learning parameterized Gaussian transitions $p_{\theta }\left(x_{t-1}\right|x_t)$, expressed as follows:

$$p_{\theta }\left(x_{t-1}\right|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t)).$$

(5)

The training of the DDPM involves optimizing the usual variational bound on the negative log-likelihood. The training loss is approximated by aligning $p_{\theta }\left(x_{t-1}\right|x_t)$ with the forward process posteriors conditioned on $x_0$ for tractability:

$$q\left(x_{t-1}\right|x_t,x_0)=\mathcal{N}(x_{t-1};{\mu }_q(x_t,t),{\Sigma }_q(x_t,t))$$

(6)

where

$${\mu }_q(x_t,t)={\displaystyle \frac{{\beta }_t\sqrt{{\overline{\alpha }}_{t-1}}}{1-{\overline{\alpha }}_t}}{x}_0+{\displaystyle \frac{(1-{\overline{\alpha }}_{t-1})\sqrt{{\alpha }_t}}{1-{\overline{\alpha }}_t}}{x}_t$$

(7)

$${\Sigma }_q(x_t,t)={\displaystyle \frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}}{\beta }_t\mathbf{I}$$

(8)

Thereby, the generated ${\widehat{x}}_{t-1}$ can be obtained by sampling from the learned target distribution $p_{\theta }$ and represented as a linear combination of ${\mu }_{\theta }(x_t,t)$ and ${\Sigma }_{\theta }(x_t,t)$:

$${\widehat{x}}_{t-1}={\mu }_{\theta }(x_t,t)+ϵ\sqrt{{\Sigma }_{\theta }(x_t,t)}$$

(9)

where

$${\mu }_{\theta }(x_t,t)={\displaystyle \frac{{\beta }_t\sqrt{{\overline{\alpha }}_{t-1}}}{1-{\overline{\alpha }}_t}}{\tilde{x}}_0(\theta ,x_t,t)+{\displaystyle \frac{(1-{\overline{\alpha }}_{t-1})\sqrt{{\alpha }_t}}{1-{\overline{\alpha }}_t}}{x}_t$$

(10)

and ${\Sigma }_{\theta }={\Sigma }_q$. Here, ${\tilde{x}}_0$ is a parameterized model.

2.3. Conditional Diffusion Models

Recently, conditional diffusion models have been proposed to condition the generative process in well-performing unconditional DDPM, enabling the model to generate images with desired semantics similar to the reference image. Among the conditional diffusion models, the iterative latent variable refinement model (ILVR) [24] and classifier-guided diffusion model (CGD) [25] stand out as the most representative.

2.3.1. Iterative Latent Variable Refinement Model

Under the framework of DDPM, ILVR [24] controls the semantics of generated images ${\widehat{x}}_{t-1}$ by introducing a condition $c:{\varphi }_N\left(y_{t-1}\right)={\varphi }_N\left(x_{t-1}\right)$ into the unconditional generative process $x_{t-1}\sim p_{\theta }\left(x_{t-1}\right|x_t)$ of DDPM. Here, ${\varphi }_N(\ast )$ is the low-pass filtering operation (https://github.com/assafshocher/ResizeRight, accessed on 7 August 2024) with scale N, while $y\sim q\left(y_{t-1}\right|y_0)$ denotes the reference image containing the target semantics. Therefore, the generated ${\widehat{x}}_{t-1}$ can be expressed as

$${\widehat{x}}_{t-1}={\varphi }_N\left(y_{t-1}\right)-{\varphi }_N\left(x_{t-1}\right)+x_{t-1}.$$

(11)

2.3.2. Classifier-Guided Diffusion Model

Similar to ILVR, CGD [25] does not require additional changes to the training process of DDPM. Instead, it directly decomposes the distribution $p_{\theta ,\psi }\left(x_{t-1}\right|x_t,y)$ into an unconditional process $p_{\theta }\left(x_{t-1}\right|x_t)$ and conditional classifier-guided process $p_{\psi }\left(y\right|x_{t-1})$. Consequently, the generated target ${\widehat{x}}_{t-1}$ can be obtained from the sampling process:

$${\widehat{x}}_{t-1}={\mu }_{\theta }+s·{\Sigma }_{\theta }·grad+ϵ\sqrt{{\Sigma }_{\theta }}$$

(12)

where $grad={\nabla }_{x_{t-1}}log{p}_{\psi }\left(y\right|x_{t-1}){|}_{x_{t-1}=\mu }$ is the gradient of the classifier, the scaling s implies the intensity of the guidance of the classifier, and $\theta$ and $\psi$ represent the learned parameters of the generation and classification networks, respectively.

2.4. DiffuseMorph

To the best of our knowledge, DiffuseMorph (https://github.com/DiffuseMorph/DiffuseMorph, accessed on 7 August 2024) (DM) [26] is the first work to apply diffusion models to image registration, with the others mainly used in generation tasks. In DM, the conditional noise added in the forward process is predicted by the generative network. The predicted noise ${\widehat{ϵ}}_{\theta }(I_0,t,c=(I_0,J_0))$ is then utilized by the registration network to learn the optimal deformation field $d^{*}$ for image registration:

$$d^{*}=\underset{\theta ,\psi }{argmin}{E}_G(\theta ,I_0,t,c)+{\lambda }_1{E}_D\left(J\left(d_{\psi }\right),{\widehat{ϵ}}_{\theta }\right)+{\lambda }_2{E}_R\left(d_{\psi }\right)$$

(13)

where $E_G(\theta ,I_0,t,c)$ and $E_D\left(J\left(d_{\psi }\right),{\widehat{ϵ}}_{\theta }\right)$ denote the generation and registration loss functions, respectively, $\theta$ and $\psi$ represent the learned parameters of the generation and the registration networks, respectively, $E_R\left(d_{\psi }\right)$ describes the regularization constraint of the deformation field, and ${\lambda }_1$ and ${\lambda }_2$ are hyperparameters that balance the loss for different tasks. However, the requirement of two separate networks for registration in DM leads to a series of issues, including challenges in model optimization, difficulty in balancing losses from different networks, and low registration accuracy.

3. Proposed Method

Leveraging the capability of DDPM, we propose a universal network to perform image registration and image generation simultaneously. Specifically, the proposed method is illustrated in Figure 1. The network takes a moving image $J_0$, fixed image $I_0$, and the diffused fixed image $I_t$ (obtained by Equation (4) with $x_0=I_0$) as inputs, then computes the deformation field d. Subsequently, we warp the moving image $J_0$ to ${\tilde{I}}_0$, i.e., $J_0\left(d\right)={\tilde{I}}_0$, using the Spatial Transformer Layer (STL) [29], allowing the similarity between $I_0$ and ${\tilde{I}}_0$ to be evaluated. Furthermore, we use the predicted ${\tilde{I}}_0$ and the equations in Figure 1 to perform the reverse diffusion process for image generation.

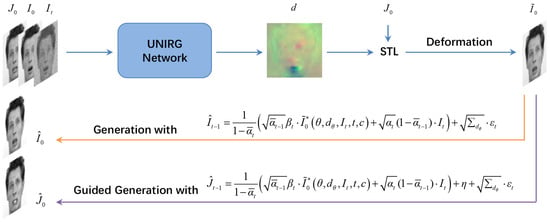
Figure 1. The graphical model. The blue arrows indicate the direction of feature propagation when training the network. The orange arrow depicts the basic generation task. The guided generation process is indicated by the purple arrow. Input: moving image $J_0$, fixed image $I_0$, and diffused fixed image $I_t$. Output: deformed image ${\tilde{I}}_0$, generated image ${\widehat{I}}_0$, and guided generated image ${\widehat{J}}_0$.

3.1. Universal Training Process of UNIRG

Referring to [23,24,25], diffusion model-based image generation can be achieved by solving a probabilistic matching problem between forward and reverse diffusion (or the matching problem between true noise and predicted noise). Because the distributions of the forward and reverse processes follow the Gaussian distribution, the matching problem can be transformed into a mean matching problem. Furthermore, the generated target in Equations (9), (11) and (12) can be reformulated as follows:

$${\widehat{x}}_{t-1}=M_{\theta }+ϵ\sqrt{{\Sigma }_{\theta }}$$

(14)

where $M_{\theta }$ denotes the modified mean. For example, in DDPM we have $M_{\theta }={\mu }_{\theta }$, while for ILVR and CGD we have

$$\begin{array}{cc}\hfill ILVR:& M_{\theta }={\varphi }_N\left(y_{t-1}\right)-{\varphi }_N\left(x_{t-1}\right)+{\mu }_{\theta },\hfill \\ \hfill CGD:& M_{\theta }=s·{\Sigma }_{\theta }·grad+{\mu }_{\theta }.\hfill \end{array}$$

(15)

Because these models share the same training process as DDPM, ${\tilde{x}}_0(\theta ,x_t,t)$ can be obtained by solving $\underset{\theta }{argmin}\left|\right|{\mu }_{\theta }-{\mu }_q{\left|\right|}^2$. Therefore, we can make the following modifications to incorporate the modified means into the training process:

$$\begin{array}{cc}\hfill ILVR:& \underset{\theta }{argmin}\left|\right|M_{\theta }-\left({\mu }_q+{\varphi }_N\left(y_{t-1}\right)-{\varphi }_N\left(x_{t-1}\right)\right){\left|\right|}^2,\hfill \\ \hfill CGD:& \underset{\theta }{argmin}\left|\right|M_{\theta }-\left({\mu }_q+s·{\Sigma }_{\theta }·grad\right){\left|\right|}^2.\hfill \end{array}$$

(16)

In general, we define $M_{\theta }=A·{\tilde{x}}_0^{\prime }(\theta ,x_t,t)+B·x_t$ following the form of Equation (10), where $A={\displaystyle \frac{{\beta }_t\sqrt{{\overline{\alpha }}_{t-1}}}{1-{\overline{\alpha }}_t}}$, $B={\displaystyle \frac{(1-{\overline{\alpha }}_{t-1})\sqrt{{\alpha }_t}}{1-{\overline{\alpha }}_t}}$ and ${\tilde{x}}_0^{\prime }(\theta ,x_t,t)$ is the modified parameterized model, which varies between different tasks. Subsequently, Equation (16) can be expressed as

$$\begin{array}{cc}\hfill ILVR:& \underset{\theta }{argmin}\left|\right|{\tilde{x}}_0^{\prime }-\left(x_0+{\displaystyle \frac{{\varphi }_N\left(y_{t-1}\right)-{\varphi }_N\left(x_{t-1}\right)}{A}}\right){\left|\right|}^2,\hfill \\ \hfill CGD:& \underset{\theta }{argmin}\left|\right|{\tilde{x}}_0^{\prime }-\left(x_0+{\displaystyle \frac{s·{\Sigma }_{\theta }·grad}{A}}\right){\left|\right|}^2.\hfill \end{array}$$

(17)

To summarize, the training objective of the generative model ${\tilde{x}}_0^{\prime }$ is to generate an image $x_0^{\prime }$ with the desired semantics. This training process shares similarities with dissimilarity loss optimization in image registration models. Therefore, by considering the fixed image $I_0$ as the desired target image, i.e., $x_0^{\prime }=I_0$, and incorporating condition $c=(I_0,J_0)$ with deformation information into the generative model ${\tilde{I}}_0(\theta ,d_{\theta },I_t,t,c)$, we can simultaneously achieve image registration. The deformation field is estimated by

$$d^{*}=\underset{\theta }{argmin}\left|\right|{\tilde{I}}_0(\theta ,d_{\theta },I_t,t,c)-I_0{\left|\right|}^2.$$

(18)

Furthermore, a regularization term is added to Equation (18) to preserve the smoothness of the predicted deformation field d. The overall training step of UNIRG is shown in Algorithm 1.

$$d^{*}=\underset{\theta }{argmin}\left|\right|{\tilde{I}}_0(\theta ,d_{\theta },I_t,t,c)-I_0{\left|\right|}^2+\lambda \sum \left|\right|{\nabla }_{d_{\theta }}{\left|\right|}^2$$

(19)

Algorithm 1: Training Process

3.2. Image Generation via Reverse Diffusion

3.2.1. Generation

Similar to DDPM, UNIRG can perform a reverse diffusion process to generate target images. Specifically, according to Equation (18), the mean of the generated distribution can be written as $M_{\theta }=A·{\tilde{I}}_0(\theta ,d_{\theta },I_t,t,c)+B·I_t$. Then, the specific form of the generated samples can be obtained:

$${\widehat{I}}_{t-1}=A·{\tilde{I}}_0^{*}(\theta ,d_{\theta },I_t,t,c)+B·I_t+ϵ\sqrt{{\Sigma }_{d_{\theta }}}$$

(20)

where $ϵ\sim \mathcal{N}(\mathbf{0},\mathbf{I})$ from $t=T$ to $t=1$, ${\tilde{I}}_0^{*}$ represents the deformed images with optimal deformation field $d_{{\theta }^{*}}$ after network training, and ${\Sigma }_{d_{\theta }}={\Sigma }_q$, which is the same as DDPM. The pseudocode for image generation is described in Algorithm 2.

Algorithm 2: Sampling Process

3.2.2. Guided Generation

In addition, UNIRG can achieve guided generation in the same way as ILVR or CGD by further modifying Equation (18) to the form of Equation (17):

$$\underset{\theta }{argmin}\left|\right|{\tilde{I}}_0^{\prime }(\theta ,d_{\theta },I_t,t,c)-\left(I_0+{\displaystyle \frac{\eta }{A}}\right){\left|\right|}^2$$

(21)

where ${\tilde{I}}_0^{\prime }$ is a latent model, $\eta$ is set as a shift factor to control the direction of the generation, and the guided generated samples are provided by

$${\widehat{I}}_{t-1}^{\prime }=A·{\tilde{I}}_0^{*}(\theta ,d_{\theta },I_t,t,c)+B·I_t+\eta +ϵ\sqrt{{\Sigma }_{d_{\theta }}}.$$

(22)

In particular, $\eta =0$ denotes the unconditional reverse process, while $\eta ={\varphi }_N\left(y_{t-1}\right)-$${\varphi }_N\left(x_{t-1}\right)$ and $\eta =s·{\Sigma }_d·grad$ represent the same conditional reverse process as ILVR and CGD, respectively. Here, we set $\eta =g(J_0-I_0)$ to perform the guided generation in this paper and generate an image with similar content as $J_0$, where $g(\ast )$ denotes the operation of image transformations.

3.3. Network Architecture

UNIRG utilizes a typical encoder–decoder network (U-net) as the backbone for estimating $\theta$. The encoding part consists of residual and downsampling layers, while the decoding structure uses residual and upsampling layers instead. Meanwhile, encoding and decoding features of the same dimension are matched and fused by some skip connections. To comprehensively improve registration and generation performance, we modify the architecture of U-net used in VM as follows:

• Adding a multihead attention module to enhance the model’s attention regarding the input features.
• Embedding time information to help the model determine the time step.
• Using the low-pass filtering operation in ILVR instead of the downsampling or pooling operation to retain more features and improve the accuracy of image registration.

The modified architecture ensures accurate capture of the deformation field between images even in the presence of considerable input noise, thereby improving the robustness of the model. After these modifications and the use of dense STL, the proposed model can achieve better registration and generation performance. The specific network structure is shown in Figure 2.

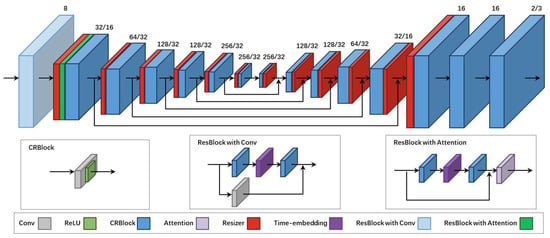
Figure 2. Architecture of the registration network. The number of output channels is denoted as $a/b$, where a corresponds to 2D tasks and b corresponds to 3D tasks. For 3D image registration, only two CRBlocks are used before the output. Among the various residual blocks, only the first CRBlock adjusts the channel size of the features, while the second CRBlock maintains the same channel size. The LeakyReLU activation function is used with a parameter of 0.2 for all CRBlocks in the experiment. Moreover, all CRBlocks preserve the feature size and only adjust the number of channels, that is, using convolution layers with a kernel size of 3, stride of 1, and padding of 1. In addition, time embedding is employed to project the time steps and embed temporal information. A scaling factor of 1/2 is chosen in the encoding phase for the low-pass filtering operation, and a 2× low-pass filtering operation is performed in the decoding phase. Moreover, linear interpolation is performed for all interpolation operations. Because the deepest feature size may be smaller than a pixel, we still assign it as a pixel. In the decoding path, following the idea of super-resolution, encoded and decoded features of the same scale are concatenated and then fed into the CRBlocks to enhance the image sharpness and retain more detailed features.

4. Experimental Results

We conducted experiments on various datasets to validate the effectiveness of the proposed method using the modified network architecture. The evaluation focused on the performance of the proposed method in both image registration and generation tasks. For comparison, we compared UNIRG to VM [13], VM-diff [14], and DM [26]. Specifically, our experiments used the 2D Radboud Faces Database (RaFD) [30] and the 3D Automated Cardiac Diagnosis Challenge Dataset (ACDC) [31]. Further details regarding the datasets, experiments, and analysis of the results are provided below.

4.1. Radboud Faces Database

4.1.1. Dataset and Preprocessing

The RaFD database comprises 67 subjects exhibiting eight emotional expressions: angry, disgusted, fearful, happy, sad, surprised, contemptuous, and neutral. Each emotion is displayed in three different gazes (left, frontal, and right) while maintaining a consistent head orientation. We divided the dataset into a training set (60 groups) and a test set (7 groups) to better adapt the image registration task. Additionally, we resized the images to 128 × 128 pixels for further processing.

4.1.2. Implementation Details

During the training process, we used the Adam optimizer with a learning rate of 5 × ${10}^{-6}$ for optimization. The training process was conducted on a single NVIDIA RTX 2080S GPU using 50 epochs and a batch size of 8, considering both time consumption and accuracy. The time step was set to $T=2000$, and linear noise scheduling was applied with levels ranging from ${10}^{-6}$ to ${10}^{-2}$. The number of attention heads was set to 4. Furthermore, to ensure that the regularization loss remained smaller than the dissimilarity loss and considering the randomness introduced by the initial noise and random sample selection, we found that setting the coefficient $\lambda$ to 2.5 × ${10}^{-2}$ yielded better results.

4.1.3. Image Registration

During the evaluation, we fixed the random seed to 0 for easier analysis. To ensure fairness, we conducted comparison experiments using the same size of VM and VM-diff models as well as the DM model with the same size of registration network. The registration performance of the proposed method was verified by comparing it with VM, VM-diff, and DM. Visual comparisons of the 2D facial grayscale image registration results can be seen in Figure 3. Additionally, by applying the trained deformation field to the image in each channel, we obtained the registration results for 2D facial RGB expressions, as illustrated in Figure 4.

Figure 3. Comparison results for 2D facial expression grayscale image registration. Original images (left two columns), deformed images (middle four columns), deformation fields (right four columns), and NMSE/SSIM values for grayscale image registration. Top: Fearful front gaze (moving) to surprised front gaze (fixed). Bottom: Disgusted left gaze (moving) to happy left gaze (fixed).

Figure 4. Comparison results for 2D facial expression RGB image registration. From top to bottom: surprised front gaze (moving) to fearful front gaze (fixed); sad left gaze (moving) to angry left gaze (fixed). The NMSE/SSIM values below correspond to grayscale image registration.

As part of the image evaluation, we carried out numerical comparisons for further analysis. We utilized NMSE, SSIM, PSNR, and the ratio of non-positive Jacobian determinants over the deformation field as metrics to enrich the experimental comparison. The first three metrics are used to assess the accuracy of image registration, while the last metric aim to compare the folding degree and smoothness of the deformation field. The results of these comparisons are presented in Table 1.

Table 1. Numerical results for grayscale facial image registration.

Method	NMSE × ${10}^{-1}$	SSIM	PSNR	|Ja(d)|≤ 0
Origin	0.301 (0.213)	0.668 (0.100)	19.692 (3.172)
DM	0.279 (0.100)	0.643 (0.065)	19.210 (1.347)	0.424 (0.047)
VM	0.098 (0.037)	0.828 (0.058)	23.770 (1.664)	0.506 (0.013)
VM-diff	0.103 (0.038)	0.823 (0.060)	23.567 (1.647)	0.510 (0.021)
UNIRG	0.049 (0.030)	0.859 (0.054)	27.280 (2.617)	0.500 (0.026)

The results shown in Figure 3 and Figure 4 demonstrate the accuracy of registration achieved by the proposed method, even on unseen images, moreover, in comparing our model with other models, our model achieves superior registration accuracy. The evaluation values in the figures indicate higher SSIM values and lower NMSE values for our model. Notably, our model exhibits a nearly two-fold performance improvement in NMSE compared to VM and VM-diff.

Table 1 further demonstrate the effectiveness of the proposed model in image registration. Compared to VM, our model reveals significant improvements in NMSE and PSNR along with a slight enhancement in SSIM. Compared to VM-diff, our model shows more noticeable improvement. These results indicate the better registration performance of the proposed model. Furthermore, our model aligns well with VM and VM-diff in terms of $\left|Ja\right(d\left)\right|$, validating its topological preservation ability during registration.

4.1.4. Guided Generation

Utilizing $\eta =g(J_0-I_0)$, we performed reverse diffusion starting from $t=200$ for generation. This process begins with a noisy fixed image $I_{200}=I_0\sqrt{{\overline{\alpha }}_{200}}+ϵ\sqrt{1-{\overline{\alpha }}_{200}}$, which serves as the initial point for generating an image resembling the moving image. Figure 5 displays the visualization of generation results on 2D facial grayscale images. Furthermore, the comparison results combined with registration are shown in Figure 6.

Figure 5. Visualization of 2D facial grayscale image generation results. Original image (left), guided generated images with $\eta =J_0-I_0$ (middle), and guided generated images with ${\eta }_1=0$ and ${\eta }_2=g(J_0-I_0)$ (right), where $g(\ast )$ in ${\eta }_2$ represents using a center mask with a width of 40 for smoothing operations. From top to bottom: sad front gaze (moving) to neutral right gaze (fixed), contemptuous front gaze (moving) to angry right gaze (fixed), and happy front gaze (moving) to disgusted left gaze (fixed).

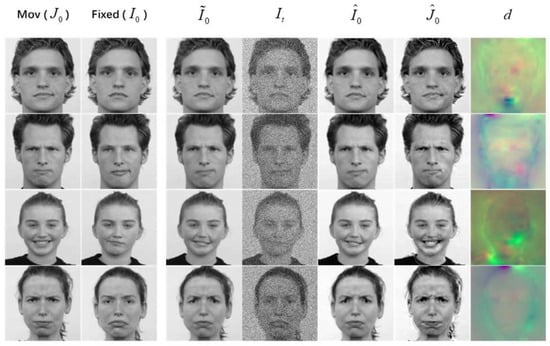
Figure 6. Comparison of 2D facial expression grayscale image registration and generation results, showing moving–fixed expressions. From top to bottom: contemptuous front gaze–neutral front gaze; angry left gaze–contemptuous left gaze; happy front gaze–contemptuous front gaze; angry front gaze–sad front gaze.

The experimental results presented in Figure 5 and Figure 6 show that the proposed method using the shift factor enables guidance in image generation, resulting in high-quality generated images when there are slight changes in expressions or poses. Despite ghosting in cases of significant image changes, the generated images preserve the desired semantics from the target image. Additionally, we find that the pixel value range impacts the quality of the generated results. In this paper, we normalize the pixel values to the range of $[-1,1]$, consistent with previous DDPM generation tasks.

4.2. Automated Cardiac Diagnosis Challenge Dataset

4.2.1. Dataset and Preprocessing

The ACDC dataset is a fully annotated public MRI cardiac dataset. It comprises 150 exams from different patients and includes additional information such as weight, height, and diastolic/systolic phase instants. The dataset is divided into five subgroups: normal subjects (NOR), patients with previous myocardial infarction (MINF), patients with dilated cardiomyopathy (DCM), patients with hypertrophic cardiomyopathy (HCM), and patients with abnormal right ventricle (RV). Each subgroup consists of 30 cases. For each case, 4D MRI images and corresponding segmentation images at the diastolic and systolic phases are provided. We resampled each case to a voxel spacing of 1.5 × 1.5 × 3.15 mm³ and then cropped them to a size of 128 × 128 × 32. Subsequently, we selected one sample out of every five to form a test set consisting of 30 cases, with the remaining 120 cases used as training samples.

4.2.2. Implementation Details

In contrast to the 2D facial image training process, we changed the learning rate to 2 × ${10}^{-4}$. We set the epoch number to 800 and the batch size to 1. The other parameters remained the same.

4.2.3. Continuous Image Registration

Considering the medical image registration task, continuous deformations can be taken into account to make the results more meaningful. In this paper, the continuous deformation from the end-diastolic phase (ED) to the end-systolic phase (ES) can be observed by treating the 4D MRI serial images at each phase as fixed images. Specifically, the parameter $Phas{e}_{\gamma }$ was set, where $\gamma =0$ is the ED phase and $\gamma =1$ is the ES phase. The 3D MRI image at the $\gamma \in [0,1]$ phase was chosen as the fixed image and the image at the $\gamma =0$ phase was used as the moving image for the registration experiment. By observing the deformation fields obtained in the cardiac registration experiment from ED to ES phases, the cardiac continuous deformations could be analyzed. The continuous deformations are displayed in Figure 7 and Figure 8 to illustrate the motion of the anatomical structures. A common observable and significant change from the ED to the ES state is the reduction of the diastolic volume. This reduction is a key focus of our observations, and highlights a consistent trend across different cases. Moreover, the performance of the various models was evaluated based on how closely the registration results resemble the fixed images. Figure 9 shows the registration results from the ED to ES phases for different groups with various pathological conditions, offering a comprehensive understanding of the registration performance in different cardiac states.

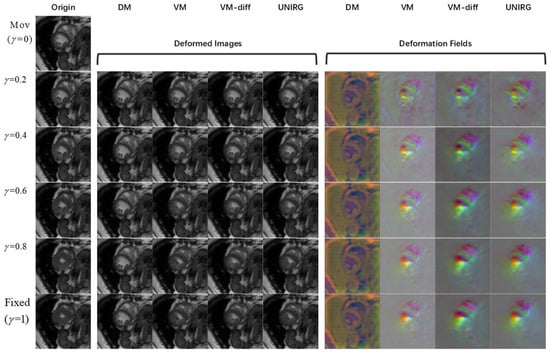
Figure 7. Continuous registration results for cardiac MRI images. Visualization of patient No. 35 with hypertrophic cardiomyopathy. Left column: original image in $Phas{e}_{\gamma }$. Middle columns: registration results obtained by deforming the moving image to the $Phas{e}_{\gamma }$ image. Right columns: corresponding deformation fields.

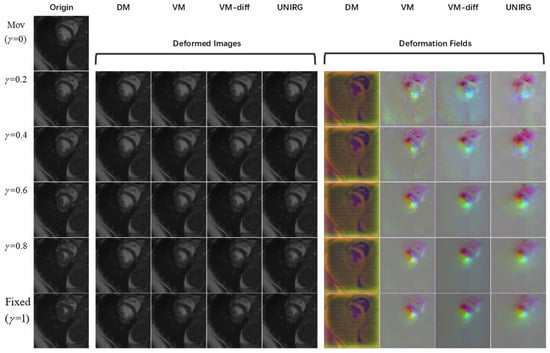
Figure 8. Continuous registration results for cardiac MRI images. Visualization of fixed images for registration from ED to ES phase of a normal subject (No. 110) on the left. The middle columns show the registration results and the right columns display the corresponding deformation fields.

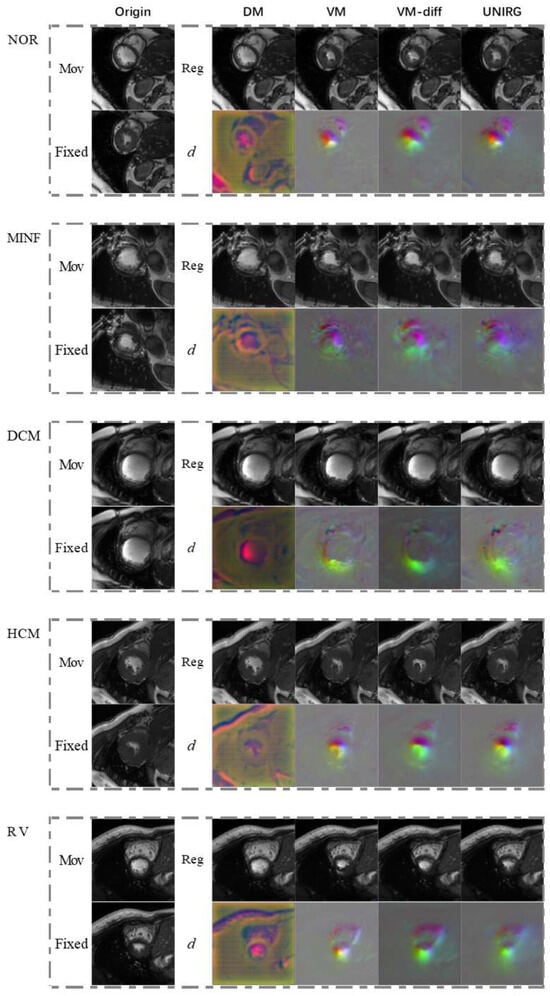
Figure 9. ED–ES registration results for different pathological cases. Cases 70, 120, 10, 40, and 85, respectively representing NOR, MINF, DCM, HCM, and RV, are selected for display.

In addition, the NMSE, PSNR, and Dice metrics were employed in an accuracy evaluation to quantify the registration performance, and $\left|Ja\right(d\left)\right|$ was selected to measure the quality of the deformation field. The registration results for phases $\gamma =0.4$ and $\gamma =1$ are presented in Table 2. Meanwhile, the mask images of the end-diastolic and end-systolic phases were also used for registration quality analysis, as shown in Table 3.

Table 2. Evaluation results of cardiac MRI image registration.

Phase	Method	NMSE	PSNR	|Ja(d)|≤ 0
$\gamma =0.4$	Origin	0.102 (0.168)	26.307 (6.149)
	DM	0.112 (0.162)	24.330 (4.775)	0.498  (0.001)
	VM	0.091 (0.178)	30.068 (6.863)	0.501 (0.005)
	VM-diff	0.095 (0.179)	28.947 (6.622)	0.501 (0.006)
	UNIRG	0.079 (0.159)	31.162  (6.690)	0.506 (0.009)
$\gamma =1$	Origin	0.135 (0.163)	22.644 (4.292)
	DM	0.144 (0.158)	21.915 (3.720)	0.498  (0.001)
	VM	0.092 (0.165)	27.540 (5.251)	0.498 (0.004)
	VM-diff	0.099 (0.166)	26.499 (4.938)	0.499 (0.006)
	UNIRG	0.079  (0.149)	28.914  (5.117)	0.502 (0.009)

Table 3. Evaluation results of cardiac MRI mask registration.

Method	Dice	PSNR	NMSE	Time
Origin	0.708 (0.184)	10.753 (1.745)	0.197  (0.091)
DM	0.708 (0.182)	10.691 (1.671)	0.202 (0.090)	0.533 (0.549)
VM	0.770 (0.145)	11.500 (1.981)	0.279 (0.311)	0.160  (0.441)
VM-diff	0.786 (0.139)	11.986 (1.855)	0.235 (0.233)	0.182 (0.233)
UNIRG	0.795  (0.124)	12.050  (2.126)	0.227 (0.160)	0.516 (0.536)

As can be seen from Figure 7 and Figure 8, the proposed model achieves continuous deformation in medical images. Compared to other models, our model exhibits better performance in anatomical structure registration. Furthermore, our model achieves accurate deformations while maintaining robustness for different pathological features. According to Figure 9, the model in this paper can effectively capture useful features and preserve essential image details to complete the registration task, even for complex anatomical structures. The results of UNIRG in Figure 9, showing that our model achieves higher similarity between registration results and fixed images, demonstrating improved registration performance.

Moreover, according to Table 2, our model achieves the minimum NMSE and the maximum PSNR at each stage of continuous deformations while maintaining similar Jacobian ratios as the other models. These results demonstrate that the proposed model maintains a topological structure and achieves higher registration accuracy. From Table 3, it can be seen that the proposed model is also advantageous for the mask image registration task, even when the mask images are not used for network training.

4.2.4. Ablation Study on Module Modifications

Based on our experiments on the 3D cardiac diagnosis dataset, we evaluated the impact of different model structures on end-diastolic and end-systolic mask image registration. The results in Table 4 demonstrate the positive influence of module modifications on registration; combining all three modules yields the most significant improvement. The number of modules used positively correlates with the PSNR metric evaluation results. The Resizer module has a stronger effect than the ResAtten module, which in turn outperforms the ResConv module. The Resizer module also plays a crucial role when considering the NMSE metric, resulting in a minor difference between deformed and fixed images and achieving higher registration accuracy. These results confirm the effectiveness of the proposed method in enhancing 3D cardiac mask image registration.

Table 4. Comparison among UNIRG variants.

ResConv	ResAtten	Resizer	Dice	PSNR	NMSE
			0.791 (0.132)	11.943 (2.191)	0.255 (0.245)
✓			0.783 (0.145)	11.949 (2.286)	0.275 (0.335)
	✓		0.789 (0.140)	11.953 (2.187)	0.284 (0.413)
		✓	0.790 (0.129)	11.975 (2.132)	0.241 (0.187)
✓	✓		0.789 (0.137)	11.962 (2.267)	0.254 (0.235)
✓		✓	0.794 (0.122)	11.983 (2.064)	0.230 (0.164)
	✓	✓	0.789 (0.139)	12.005 (2.254)	0.272 (0.348)
✓	✓	✓	0.795  (0.124)	12.050  (2.126)	0.227 (0.160)

5. Discussion and Conclusions

In this paper, we have presented an analysis of DDPM and applied it to image registration tasks. By leveraging a modified U-net architecture, we successfully implement both image generation and registration tasks within a unified network. In addition, we propose a shift factor to realize the guidance of the target generation. Specifically, regarding the improvement of the network architecture, the Resizer module is employed to replace the traditional pooling operation, thereby enabling noise filtering and reducing the impact of irrelevant information on the results. The ResAtten module is utilized to enhance the focus on the target features. Finally, the ResConv module is used to capture temporal features, which improves the predictive performance of the model. Each of the three modules serves a distinct purpose; according to ablation studies, the combined use of all three modules significantly enhances registration accuracy. Experimental results demonstrate the superior registration performance of our model compared to the VM, VM-diff, and DM models. Specifically, we achieve impressive results in the guided generation and registration for facial expression images as well as accurate continuous motion estimation for medical images. It is noteworthy that the NMSE and other similar metrics are determined by the difference in pixel intensity between the images being compared. UNIRG achieves higher similarity between the deformed image and the target image, demonstrating superior performance on these metrics. Although the proposed model is not explicitly designed for enhanced topological preservation, it does leverage convolution operations, similar to the VM and VM-diff models. Convolutional layers ensure that spatially local information is processed together, thereby preserving the spatial structure. Moreover, the use of the Resizer module, which also processes information based on local information, further guarantees topological preservation.

Nevertheless, some directions for further improvement are worth noting, such as reducing computational time, improving image preprocessing quality, and exploring the impact of the value range on generation. Moreover, the ResAtten module incorporating the attention mechanism requires careful control of the number of these modules in order to avoid introducing excessive parameters. Additionally, the Resizer module modifies the feature scale, requiring consideration regarding its placement. Future research can be consider these issues to enhance the performance of the proposed model and complete more complex registration tasks.