Self-Intersections of Cubic Bézier Curves Revisited

Abstract

Recently, Yu et al. derived a factorization procedure for detecting and computing the potential self-intersection of 3D integral Bézier cubics, claiming that their proposal distinctly outperforms existing methodologies. First, we recall that in the 2D case, explicit formulas already exist for the parameter values at the self-intersection (the singularity called crunode in algebraic geometry). Such values are the solutions of a quadratic equation, and affine invariants depend only on the curve hodograph. Also, the factorization procedure for cubics is well known. Second, we note that only planar Bézier cubics can display a self-intersection, so there is no need to address the problem in the more involved 3D setting. Finally, we elucidate the connections with the previous literature and provide a geometric interpretation, in terms of the affine classification of cubics, of the algebraic conditions necessary for the existence of a self-intersection. Cubics with a self-intersection are affine versions of the celebrated Tschirnhausen cubic.

1. Introduction

Integral (i.e., polynomial) cubics are the most popular Bézier curves in CAGD (Computer-Aided Geometric Design) [1,2] for their straightforward analysis and beautiful simplicity [3], especially compared to their rational or higher-order counterparts. Bézier cubics deserve our attention as they find numerous practical applications, including the following:

• Free-form design: They provide the tool to define freeform paths in vector-based design programs, such as Adobe Illustrator and Inkscape, the page-description language PostScript [4] and the Scalable Vector Graphics (SVG) format [5];
• Manufacturing: Bézier cubics are implemented as the G5 command in G-code, the standard programming language for CNC (Computer Numerical Control) and additive manufacturing [6];
• Geometry processing [7]: Cubics can be pieced together to define $C^2$ splines, which are employed in CAD systems to approximate geometry, such as offsets [8] or sections of sculptured surfaces.

Detecting the curve singularities is critical to these applications. In particular, a curve $\mathbf{b}\left(t\right)$ with a self-intersection $\mathbf{S}$ means a loop, which violates the assumptions required for CNC milling [9]. Also, it implies that $\mathbf{b}\left(t\right)$ has zero reach (shortest distance to the cut locus) at $\mathbf{S}$, so no smooth (trimmed) tube or offset can be constructed using $\mathbf{b}\left(t\right)$ as the generator [10]. To compute the potential self-intersection of an integral cubic, we could resort to numerical algorithms for Bézier curves of an arbitrary degree, such as those by Lasser [11] or Farouki [12], based on subdivision. However, for the specific cubic case, simple closed-form formulas are well known.

Yu et al. [13], in a recent article in this journal and unaware of these previous explicit formulas, present an alternative analytical method in a 3D setting, claiming that it overcomes the limitations of existing algorithms. Our article contesting this claim is arranged as follows. First, Section 2 briefly reviews the rich literature, mostly overlooked in [13], on explicit methods for finding the self-intersection of plane cubics. Section 3 shows that solving the 2D case with existing techniques suffices because all Bézier cubics with a self-intersection are planar. Next, Section 4 revisits the factorization procedure employed in [13] and checks the equivalence between existing formulas. Section 5 reinterprets geometrically the algebraic conditions for the existence of a self-intersection in terms of the affine classification of cubics, concluding that all Bézier cubics with a self-intersection can be regarded as affine segments of a Tschirnhausen cubic. Finally, Section 6 closes with practical conclusions.

2. Finding the Self-Intersection of a Cubic: Existing Explicit Procedures

Finding a self-intersection $\mathbf{S}$ [14,15] boils down to seeking a double point and, hence, pairs $u,v$ of distinct parameter values ($u\ne v$) such that

$$\mathbf{b}\left(u\right)=\mathbf{b}\left(v\right)=\mathbf{S}.$$

(1)

For integral plane cubics, a quadratic equation furnishes the values $u,v$ corresponding to the only double point. More than four decades ago, Wang [16] (Theorem 3) provided explicit formulas for $u,v$, albeit for cubics in the power basis. Later, and unaware of [16], Su and Liu [17] (p. 265) put forward the equivalent expression in the Bernstein basis, rewritten by Degen [18] (p. 261) in terms of a pair of affine invariants. These works [16,17,18] do not detail how equality (1) is solved for $u,v$, simply providing ready-to-use formulas. The methods reported by Thompson [19] or on the Mathematics Stack Exchange website [20] resort to the factorization procedure, also employed by Yu et al. [13].

The solution for integral cubics can be regarded as a particular instance of that by Patterson [21] (p. 151) for the superset of rational cubics. Unsurprisingly, $u,v$ also come as the roots of a quadratic polynomial, the so-called auxiliary quadratic form. Fiorot et al. [22] adapted this result to rational cubics given in the alternative BR-form controlled by a massic polygon via Bernstein polynomials.

Implicitization techniques provide another option to find $\mathbf{S}$. Loop and Blinn [23] obtain a simple implicit representation for rational Bézier curves based on classical algebraic geometry and derive an explicit formula for $u,v$ in the integral case. Chionh and Sederberg [24] extend this result to rational cubics after revealing the connection between singularities and the implicitization Bézout matrix. Barrowclough [25] also gives formulas for the rational case by devising a tailor-made basis for the implicitization of Bézier cubics. As expected, $u,v$ always come as the roots of a quadratic polynomial.

3. All Bézier Cubics with Self-Intersections Are Planar

In this Section, we recall that no twisted (i.e., non-planar) cubic with a self-intersection $\mathbf{S}$ exists, a fact overlooked in [13]. Indeed, consider the Bézier form $\mathbf{b}\left(t\right)$ of the loop segment bounded by $\mathbf{S}$ (Figure 1), whose control polygon ${\left\{{\mathbf{b}}_i\right\}}_{i=0}^3$ has coincident endpoints ${\mathbf{b}}_0={\mathbf{b}}_3=\mathbf{S}$ and, thus, defines a triangle on a certain plane $\Pi$ containing $\mathbf{b}\left(t\right)$. Any segment of the cubic also lies on $\Pi$, as its control points stem from barycentric combinations of those of $\mathbf{b}\left(t\right)$.

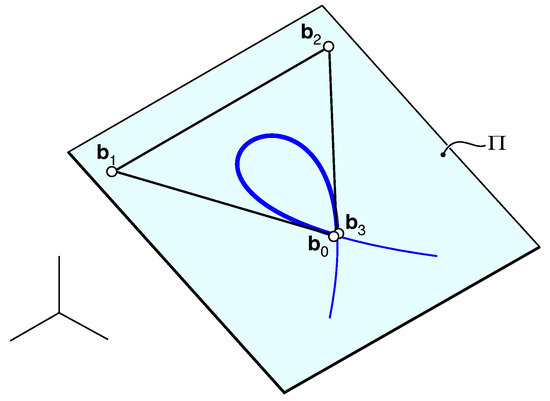
Figure 1. Any cubic with a self-intersection lies on the plane $\Pi$ containing the triangular Bézier polygon defining the loop.

We can easily check whether a given 3D cubic is planar by inspecting its derivative, called a hodograph [1]. This hodograph is expressible in quadratic Bézier form, with three control points, aside from a common dilation, generated by the forward difference operator $\Delta$ as follows:

$${\Delta \mathbf{b}}_k={\mathbf{b}}_{k+1}-{\mathbf{b}}_k,k=0,1,2.$$

(2)

Therefore, the planarity of $\mathbf{b}\left(t\right)$ is tantamount to a vanishing determinant as follows:

$$\left|\mathbf{D}\right|=0,\mathbf{D}=\left[{\Delta \mathbf{b}}_0,{\Delta \mathbf{b}}_1,{\Delta \mathbf{b}}_2\right],$$

(3)

where the differences (2) form the columns of the 3 × 3 matrix $\mathbf{D}$. Equivalently, rank $\mathbf{D}<3$. This condition is met by all the 3D cubics with self-intersection that Yu et al. [13] plot in their Figure 5d–f, whose control points are not generated at random as claimed but chosen to lie on a plane.

The condition rank $\mathbf{D}=1$ (for either a 2D or 3D curve) means that all points are aligned and $\mathbf{b}\left(t\right)$, hence, degenerates to a straight line, the only improperly parametrized cubic [26]. A non-overlapping parametrization of this line ([13], Theorem 1) amounts to the injectivity of a cubic function, a property easy to test [27]. From now on, we exclude the degenerate geometry of a straight line.

4. Finding the Parameter Values for the Double Point via Factorization

In the preceding section, we concluded that only plane cubics admit a self-intersection $\mathbf{S}$. Next, we focus on such curves, revisit the factorization algorithm [19,20] for finding the parameter values $u,v$ (1), and employ it to derive the formulas by Wang [16] (power basis) and Su and Liu [17] (the Bernstein basis), showing their equivalence.

Given a polynomial curve $\mathbf{b}\left(t\right)$ of arbitrary degree, both components of the bivariate difference $\mathbf{b}\left(u\right)-\mathbf{b}\left(v\right)$ contain the common factor $u-v$ [28]. We can, thus, remove the trivial solution $u=v$ to obtain what Farouki [12] calls reduced difference:

$$\mathbf{d}(u,v)={\displaystyle \frac{\mathbf{b}\left(u\right)-\mathbf{b}\left(v\right)}{u-v}}.$$

(4)

If $\mathbf{b}\left(t\right)$ is written in the power basis

$$\mathbf{b}\left(t\right)=\sum _{k=0}^3{\mathbf{a}}_k{t}^k,{\mathbf{a}}_k=\left[\begin{array}{c}{x}_k\\ y_k\end{array}\right],$$

(5)

then $\mathbf{d}(u,v)$ (4) admits a simple expression involving only the coefficients ${\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3$

$$\mathbf{d}(u,v)={\mathbf{a}}_1+\beta {\mathbf{a}}_2+\gamma {\mathbf{a}}_3,\begin{array}{c}\beta =u+v\hfill \\ \gamma ={(u+v)}^2-uv\hfill \end{array}.$$

(6)

If $\mathbf{b}\left(t\right),t\in [0,1]$ is given in Bernstein–Bézier form, we compute such coefficients as linear combinations of forward differences (2) as follows:

$$\left[\begin{array}{c}{\mathbf{a}}_1\\ {\mathbf{a}}_2\\ {\mathbf{a}}_3\end{array}\right]=\left[\begin{array}{ccc}3& 0& 0\\ -3& 3& 0\\ 1& -2& 1\end{array}\right]\left[\begin{array}{c}{\Delta \mathbf{b}}_0\\ {\Delta \mathbf{b}}_1\\ {\Delta \mathbf{b}}_2\end{array}\right].$$

(7)

Setting $\mathbf{d}(u,v)=0$, the values $\beta ,\gamma$ (6) come as solutions of a system of linear equations. In matrix form and writing the power coefficients ${\mathbf{a}}_k$ as column vectors (5), the following expression is obtained:

$${\mathbf{a}}_1+{\mathbf{A}}_1\left[\begin{array}{c}\beta \\ \gamma \end{array}\right]=0,{\mathbf{A}}_1=\left[{\mathbf{a}}_2,{\mathbf{a}}_3\right].$$

(8)

This system admits infinite solutions if rank $\mathbf{A}=1$, where $\mathbf{A}=\left[{\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3\right]$. However, using (7), rank $\mathbf{A}=\mathrm{rank}\mathbf{D}$, where $\mathbf{D}$ is the matrix (3). Therefore, rank $\mathbf{A}=1$ implies a straight line, a degenerate case ruled out in Section 2. If $\mathrm{rank}{\mathbf{A}}_1=2$, Cramer’s rule furnishes the unique solution as a quotient of determinants $A_i$ as follows:

$$\{\beta ,\gamma \}=\{-A_2,A_3\}/A_1,A_i=\left|{\mathbf{A}}_i\right|,$$

(9)

where the 2 × 2 square matrix ${\mathbf{A}}_i$ is obtained by dropping ${\mathbf{a}}_i$ in $\mathbf{A}$. Finally, using Viete’s formulas, the sought values $u,v$ are the roots of the quadratic polynomial $t^2-(u+v)t+uv$. In terms of $\beta ,\gamma$ (6), we reach the formula by Wang [16]

$$\{u,v\}=\frac{1}{2}\left(\beta \pm \sqrt{4\gamma -3{\beta }^2}\right),$$

or the particularized expressions for the special coordinate systems in [19,20]. Equivalently

$$\{u,v\}={\displaystyle \frac{-A_2\pm \sqrt{d}}{2A_1}},d=4A_3{A}_1-3A_2^2.$$

(10)

We can employ relationship (7) to rewrite the determinants $A_i$ (9) as follows:

$$\left[\begin{array}{c}{A}_1\\ A_2\\ A_3\end{array}\right]=3\left[\begin{array}{ccc}1& -1& 1\\ 0& 1& -2\\ 0& 0& 3\end{array}\right]\left[\begin{array}{c}{D}_0\\ D_1\\ D_2\end{array}\right],D_i=\left|{\mathbf{D}}_i\right|,$$

(11)

where ${\mathbf{D}}_i$ is similarly obtained by dropping ${\Delta \mathbf{b}}_i$ into $\mathbf{D}$. Substitution into (10) generates the alternative expression in Bernstein form derived by Su and Liu [17]:

$$\{u,v\}={\displaystyle \frac{2D_2-D_1\pm \sqrt{3\delta }}{2(D_0-D_1+D_2)}},\delta =4D_0{D}_2-D_1^2=d/27$$

(12)

Degen [18] rewrites this expression in terms of the pair $\{\rho ,\sigma \}=\{D_0,D_2\}/D_1$ of affine invariants such that ${\Delta \mathbf{b}}_1=\rho {\Delta \mathbf{b}}_0+\sigma {\Delta \mathbf{b}}_2$, which implies that $\{u,v\}$ are also affine invariants. It must be warned that this formula blows up when $D_1=0$, i.e., when the end control legs are parallel.

5. Conditions for the Existence of a Self-Intersection

The equivalent Formulas (10) and (12) for $\{u,v\}$ yield the self-intersection (1) only if the following three conditions are met:

(i)

$A_1=\left|{\mathbf{A}}_1\right|\ne 0$, tantamount to $D_0-D_1+D_2\ne 0$: The formulas are well defined;

(ii)

Discriminant $d>0$, tantamount to $\delta >0$: The values $\{u,v\}$ are distinct and real;

(iii)

$u,v\in [0,1]$, when considering the Bézier segments.

Su and Liu [17] spell out the above necessary and sufficient conditions as a set of inequalities in terms of the determinants $D_i$ (11). Condition (i) corresponds to that described in Remark 2 (2D case) by Yu et al. [13]. In previous works [16,20], although $A_1$ appears to be a denominator, the possibility that it vanished is not considered.

Next, we geometrically interpret what happens when algebraic conditios (i) or (ii) is not met. First, we must answer a fundamental question: how many essentially different planar cubics are there? Let us consider cubics $\mathbf{b}\left(t\right)$ in untrimmed form, with $t\in (-\infty ,\infty )$, and only true cubics, hence ruling out not only straight lines but also parabolas. Based on the previous work by Wang [16], Stone and DeRose [9] answer this question. Pottmann [29] and Koprowski [30] show how the results in [9] relate to the classical theories of line and algebraic geometry, respectively. Untrimmed cubics are classified into four affine types according to their respective shapes. Formally speaking, we define four equivalence classes (Figure 2), whereby two cubics are equivalent if related by an affine map:

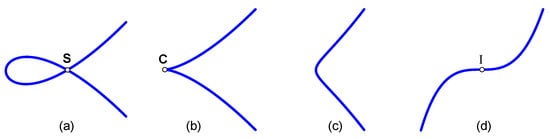
Figure 2. The four affine types of integral cubics are as follows: (a) crunodal; (b) cuspidal; (c) acnodal; (d) S-shaped.

(a)

Crunodal (loop-shaped): One self-intersection $\mathbf{S}$ (called crunode) and no inflections;

(b)

Cuspidal: One cusp $\mathbf{C}$ but neither inflection nor self-intersections;

(c)

Acnodal (hump-shaped): One acnode and two inflections but no self-intersections;

(d)

S-shaped: One inflection $\mathbf{I}$ but no self-intersections.

Each class is generated by its respective canonical representative [31]: (a) the Tschirnhausen cubic [32]; (b) semi-cubical parabola [32]; (c) acnodal cubic; (d) graph of the cubic function $y=x^3$. We conclude that cubics with self-intersections are simply crunodal cubics, i.e., affine versions of the Tschirnhausen cubic. When either condition (i) or (ii) is not fulfilled, we come across other curve classes. Indeed, depending on the circumstances, on of the following points is true:

(i)

If $A_1=0$, then the second derivative ${\mathbf{b}}^{″}\left(t\right)=2{\mathbf{a}}_2+6{\mathbf{a}}_{3}t$ is either a line through the origin, which implies the inflection $\mathbf{I}$ of type (d), or degenerates to point $2{\mathbf{a}}_2$, which means not a true cubic but a line or a parabola.

(ii)

A discriminant $d=0$ indicates a cusp (b), the limiting case $u=v$ of a self-intersection where two consecutive points coincide [33], whereas $d<0$ implies complex values $u,v\in \mathbb{C}$ and, hence, an acnodal cubic (c). In [9,19,21,22,25], a similar analysis characterizes the double point.

Finally, recall that the visual inspection of the Bézier polygon does not directly reveal the existence of a self-intersection $\mathbf{S}$. However, Vincent [34] identifies a necessary (but not sufficient) condition on the polygon. He categorizes cubic polygons according to the signed areas of the triangles formed by triples of control points, proving that the existence of $\mathbf{S}$ is possible only for the two types of polygons illustrated in Figure 3: self-intersecting or concave (but not zig-zag or convex). Yu et al. [13] call such polygons ill posed, adhering to the terminology introduced by Zhu and Zhao [35]. For rational Bézier cubics with positive weights, Chionh and Sederberg [24] derive the same configuration as a necessary condition for self-intersection. This geometry is more restrictive and, hence, encompasses the angle criterion by Lasser [11] for curves of arbitrary degree, stating that a self-intersection implies $\sum |{\alpha }_k|>\pi$, where ${\alpha }_k$ denotes the exterior angles of the Bézier polygon.

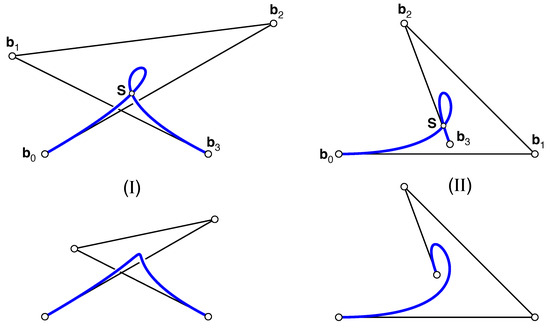
Figure 3. There are only two types of Bézier polygons associated with a cubic that may display a self-intersection $\mathbf{S}$: (I) self-intersecting; (II) concave.

6. Conclusions

Integral cubic curves admit a self-intersection $\mathbf{S}$ only in the planar case, so there is no need to address the problem in a 3D setting. Simple explicit formulas are well known for computing the parameter values at the potential self-intersection of a non-degenerate plane cubic (different from a straight line). Such values are affine invariants depending on the curve hodograph and come as the roots of a quadratic equation. If the cubic is given in power basis, employ expression (10) to obtain the parameter values $\{u,v\}$ for $\mathbf{S}$. In the Bernstein basis, firstly, compute the forward differences (2), from them compute the power coefficients (7), and finally $\{u,v\}$ (10), directly apply the equivalent Formula (12).

Formulas (10) and (12) yield a self-intersection only if three algebraic conditions, (i), (ii), and (iii), straightforward to check either in the power or Bernstein basis, are met. When (i) or (ii) are not fulfilled, we come across a cubic not of the crunodal type.