Numerical Solution of Linear Second-Kind Convolution Volterra Integral Equations Using the First-Order Recursive Filters Method
Abstract
1. Introduction
2. IIRFM and HPM-L Numerical Methods
2.1. First-Order IIR Filters Method (IIRFM)
2.1.1. Principle of the IIRFM Method
- It is possible to consider that each first-order partial transfer function corresponds to the Laplace transform of a first-order linear ODE with constant coefficients and zero initial condition, for :where . The partial solutions are obtained by applying the method of variation of constants, givingDepending on the expression of , the M convolutional integrals figuring in (13) will be calculated analytically or numerically.
- Noting that , the result (13) can be found directly by applying the convolution theorem.
- Finally, it is also possible to transform ordinary differential Equation (12) into partial recurrence relations by applying a bilinear transformation [12] to each partial transfer function . It follows that the partial solution verifies the following recurrence relation for , , and :where is the calculation step.
2.1.2. Application of the IIRFM to the Case of Second-Kind CVIEs
- Step 1.
- The Laplace transformation () is applied to Equation (1):with and . Using the convolution theorem, the Laplace transform of the previous integral can be written as follows:where and , of which the analytical expression is usually unknown.This gives the following expression for :Let us write and . Three of the following situations are possible:
- (a)
- and : this is the linear situation, for which the Volterra problem of the second kind can be described as a linear dynamics system with Laplace transfer function .With the exception of the special case of the unit kernel , note that the transfer function does not have the usual form of a quotient of polynomials in s, as it is usually the case for LTIS. Several examples of linear situations are presented in Section 3.
- (b)
- (c)
- and : this is a hybrid situation, in which the IIRFM numerical solution uses both the Laplace transfer function and the Adomian polynomials approach.We now explain the next steps of the IIRFM, but only in the case of the linear situation ( and ).
- Step 2.
- To solve the linear Volterra problem using the transfer function , it is first rewritten as a linear combination of first-order transfer functions (first-order partial fractions decomposition, noted FOD):with . This particular expression (other expressions are possible) of the transfer function is the founding point of the IIRFM applied to second-kind CVIEs. By introducing partial transfer functions , we can rewrite Equation (18) as with . With these notations, can still be written as:Depending on the convolution kernel considered, Equation (18) can be an exact form (see Section 3.1) or an approximation of (see Section 3.2, Section 3.3 and Section 4). In the latter case, coefficients and are determined by rational interpolation of the function . We will come back to this point later.The choice of (18) ensures that the approximate form tends to be 1 for , as does the exact form for the convolution kernels considered in this study, unit, generalized Abel, and logarithmic. This also reduces the interpolation interval to a set of s values close to 0, as will be shown later.The solution obtained by the IIRFM is now denoted by .
- Step 3.
- A bilinear transformation ([12]) is applied to the transfer function , where is a uniform time step (or sampling period) and z is the complex number introduced in the definition of the z-transform (noted here ) of a discrete-time signal : , with . After a few algebraic manipulations, we obtain the following z transfer function:with , , , and .The z-transform obtained by the IIRFM satisfies the following relations:where is the z-transform of the source function . The solution can be further decomposed into a sum of partial solutions, as follows: with .
- Step 4.
- The solution is calculated in the discrete time space using recurrence relations deduced from transfer function (20). In order not to unnecessarily complicate the theoretical developments in this paragraph, it is assumed here that the function is zero at the initial instant, which also imposes a zero initial condition for the solution: . The case of a non-zero initial condition will be considered later in this work (see Section “Exponential Source Term ”). The discrete-time solution at time is denoted by .Using time-shifting properties and linearity of the z-transform, the following partial recurrence relations are obtained:Note that the second recurrence relation of (22) leads to the following explicit expression for the partial solution :This is a particularly important result of this study. Depending on the expression of the source term , the expression of Equation (23) can be further simplified, as will be seen with some of the examples to be studied in Section 3.The complete solution provided at time by the IIRFM is therefore of the following general form:In the most general case, the calculation of involves two sums, with a total of terms. As a result, calculation times can become significant as k increases. However, these calculation times can be significantly reduced when an explicit expression of exists. In this case, the numerical solution can be written asand then the calculation only involves a single sum of M terms, which significantly reduces computation times.
2.2. Homotopic Peturbation Method with Laplace Transform (HPM-L)
- converges to a closed form, in which case the homotopic perturbation method leads to an analytic solution of Equation (2);
- There is no known closed form of , in which case the series is generally truncated at the first terms and the solution of the problem is written in the following approximate form:
3. Linear Convolutive Volterra Integral Equations of the Second Kind
3.1. Unit Kernel
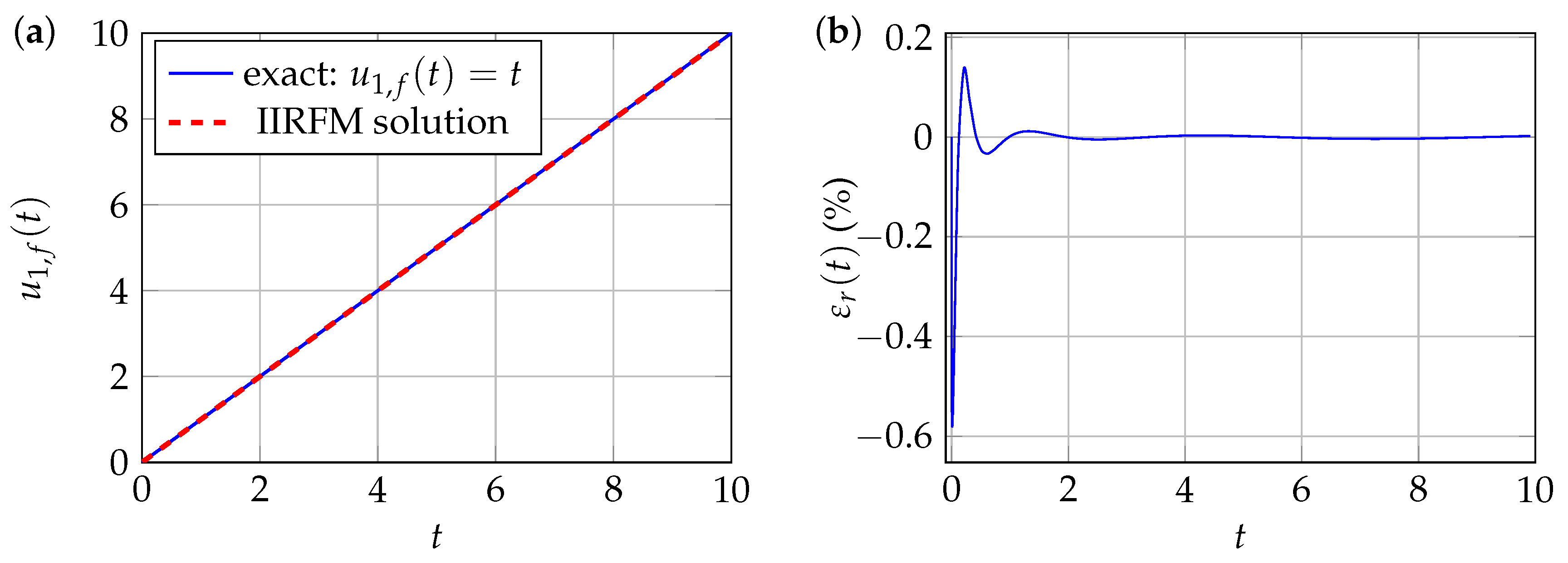
3.1.1. Monomial Source Term
Numerical Solution by the IIRFM
Exact Solution by Homotopic Perturbation Method with Laplace Transformation (HPM-L)
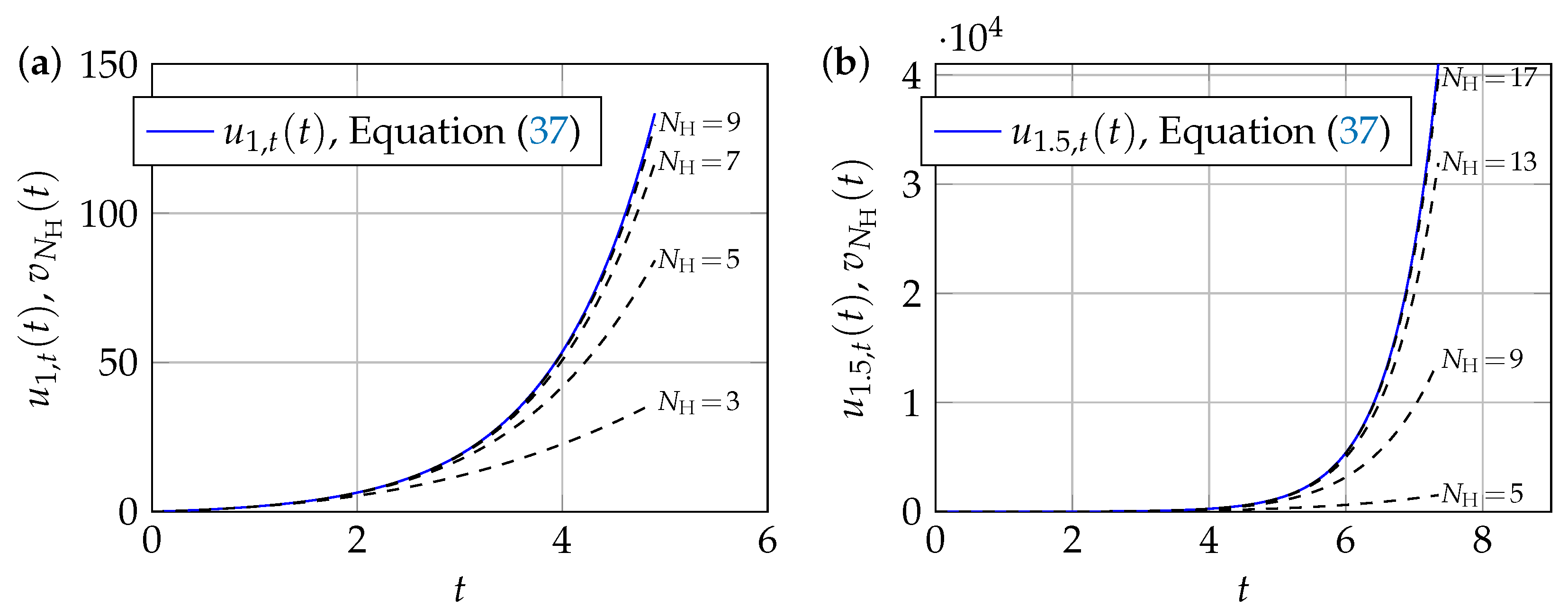
Approximate Numerical Solutions for
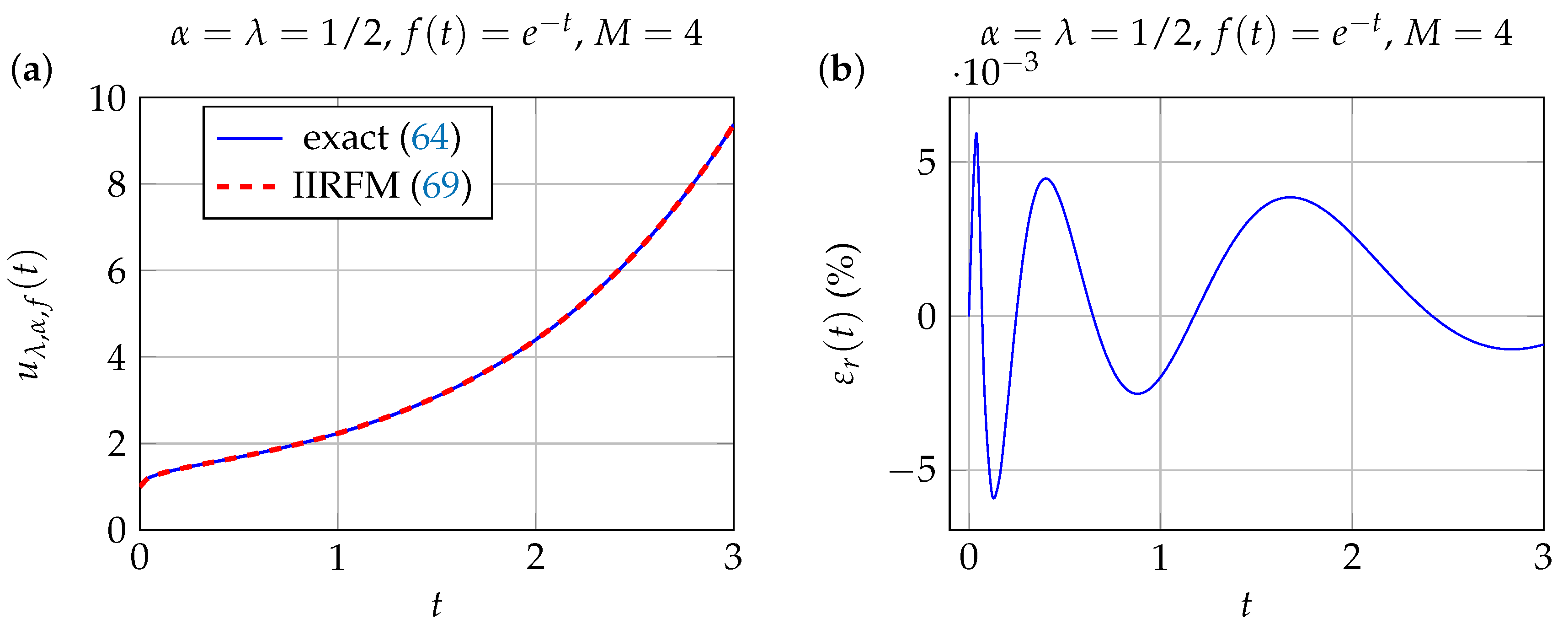
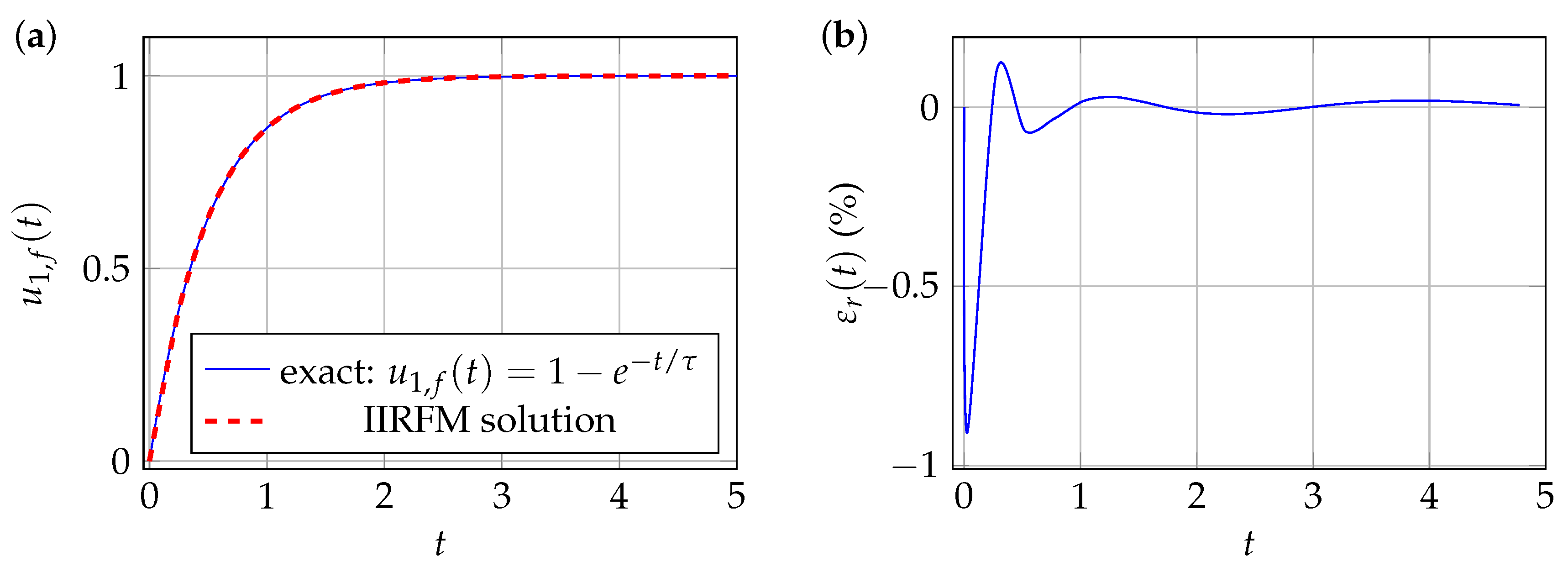
3.1.2. Exponential Source Term
Numerical Solution by the IIRFM
Solution by the HPM-L Method
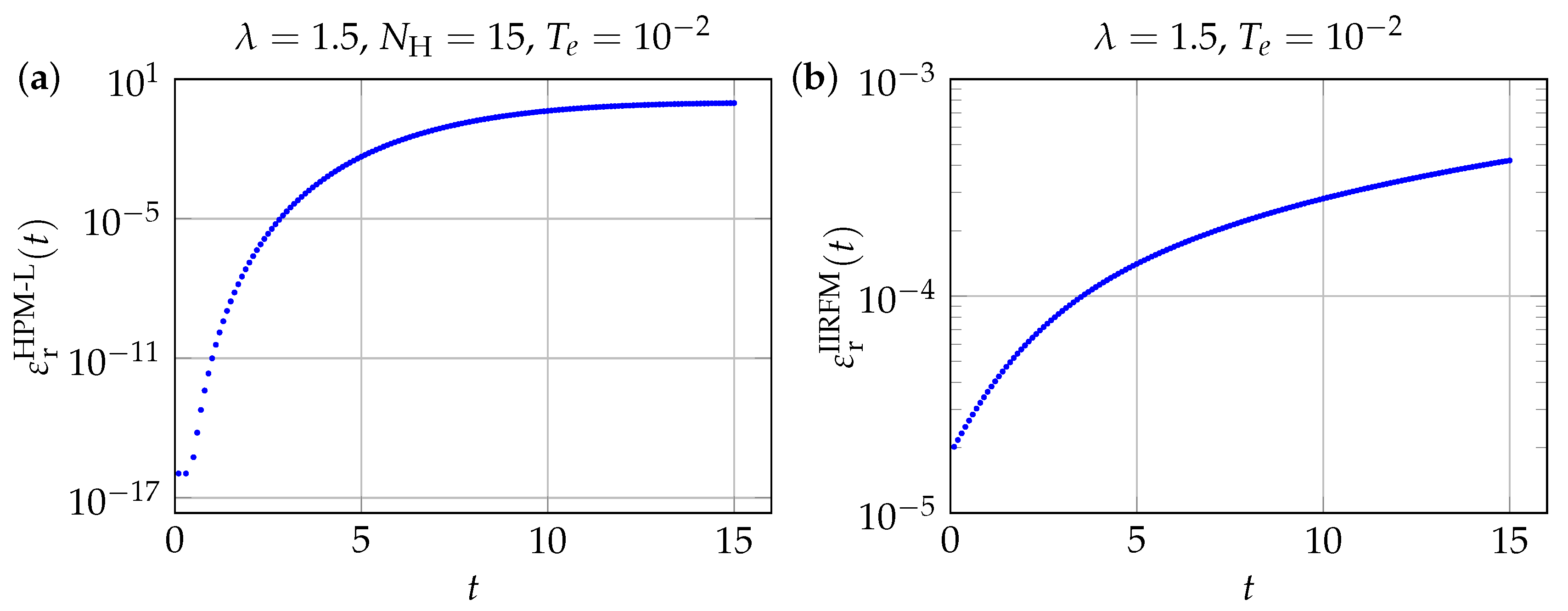
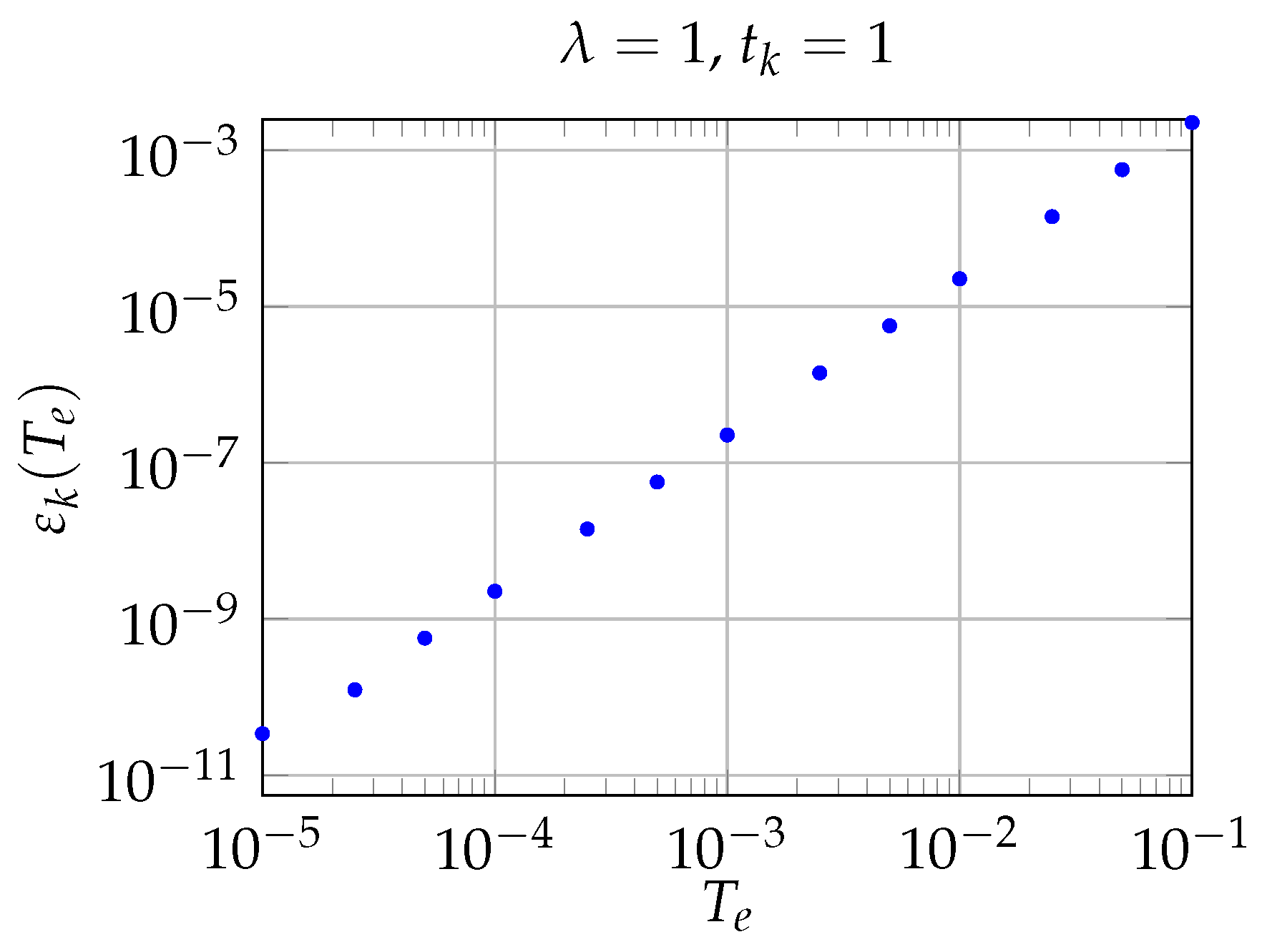
Numerical Results and Discussion
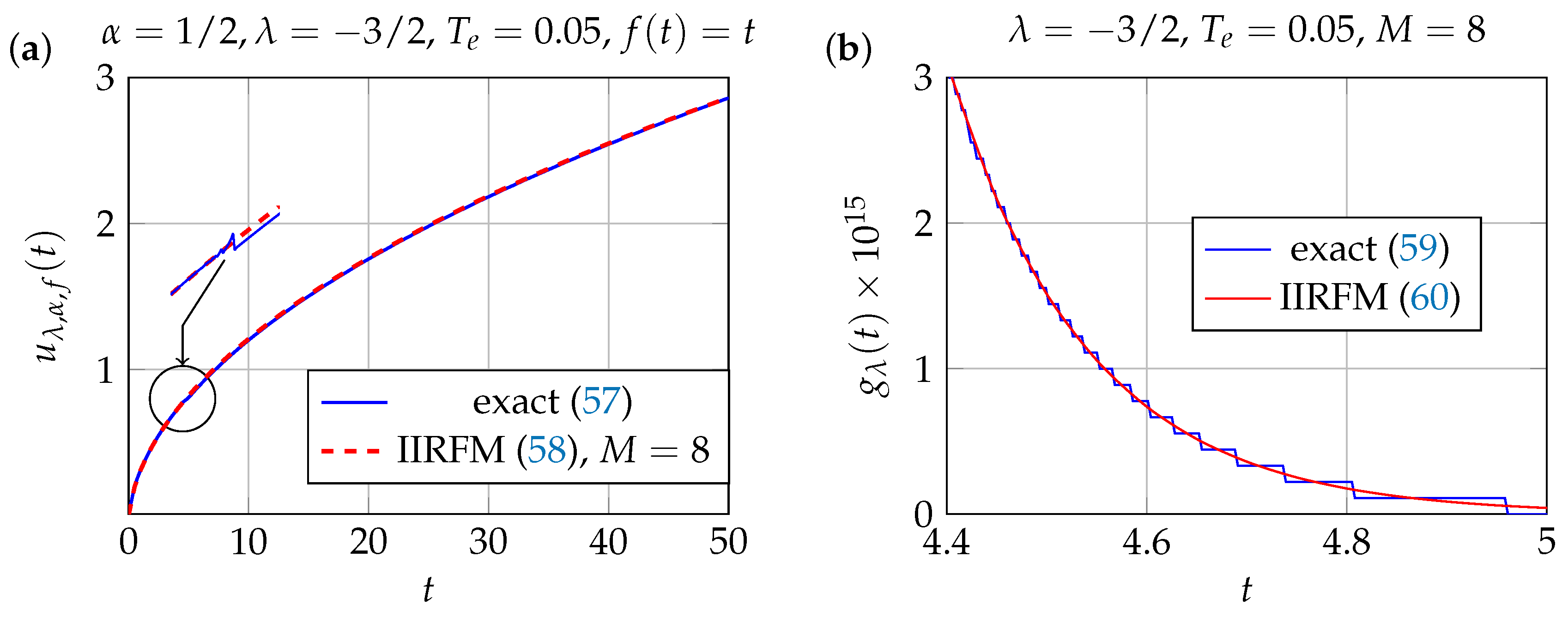
3.2. Abel’s Kernel (with )
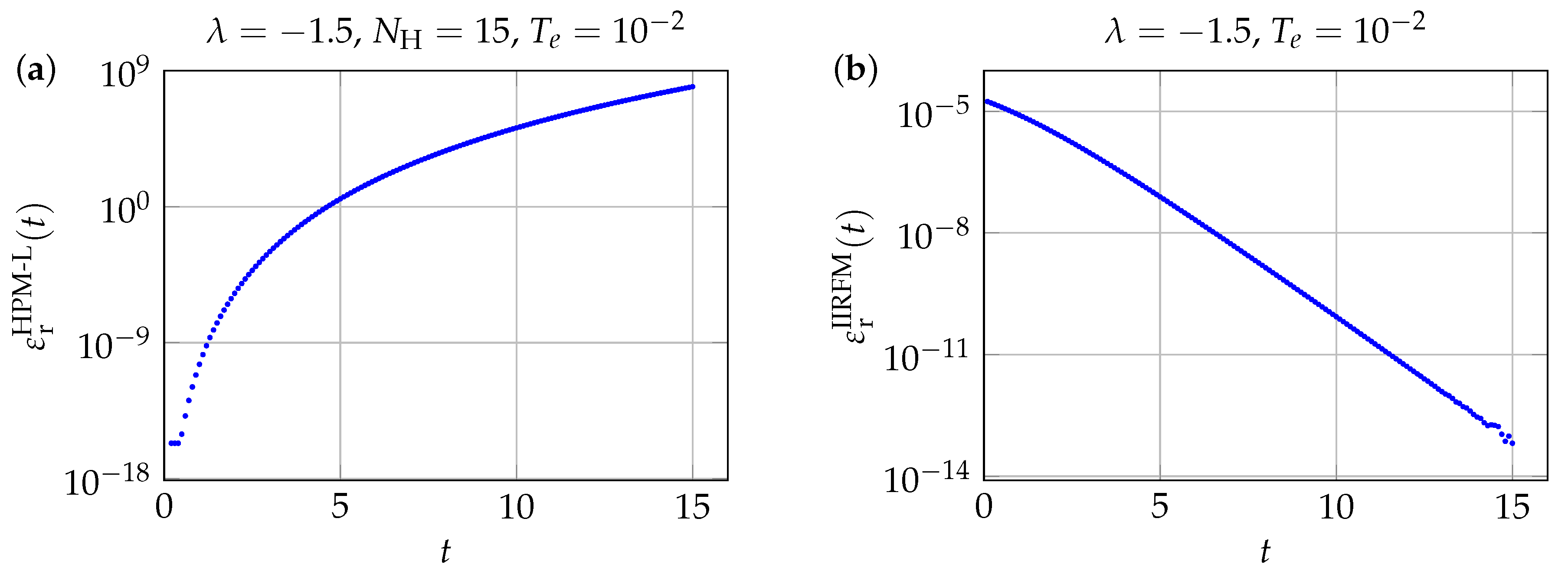
3.2.1. IIRFM Approach When and
Monomial Source Term
| Listing 1. Julia-1.10.4 code illustrating the pathological behavior of . |
| using SpecialFunctions, Plots function gL(t; La = -1.5) return 1 + erf(La*(pi*t)^0.5) end plot(t->gL(t, La = -1.5), 4.4, 5.5) |
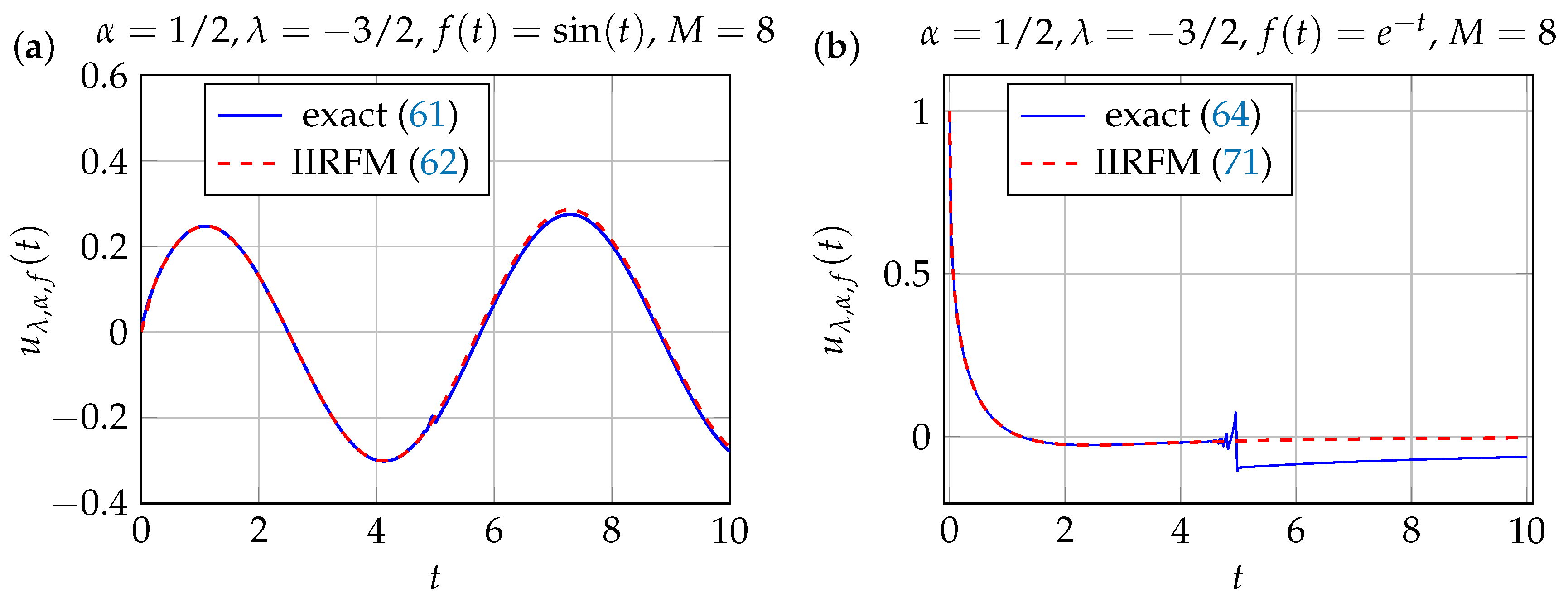
Sinusoidal Source Term
Exponential Source Term
Constant Term Source
3.2.2. IIRFM Approach When and
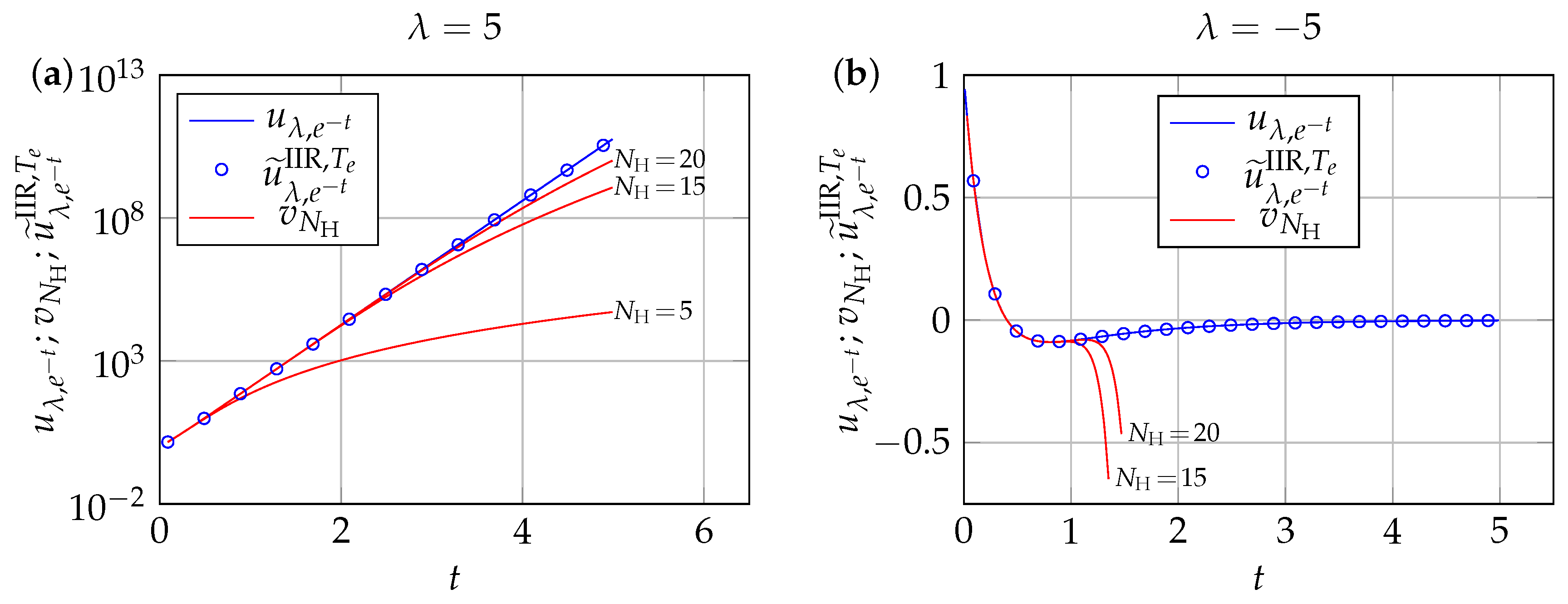
3.2.3. Comparison of the IIRFM with the Mouley et al. [13] Approach
First Example
Second Example
| 21,732 | 4370 | 1074 | 29 | 3 | 3 | ||
| 10,739 | 2774 | 683 | 28 | 3 | 1 | ||
| 8568 | 2091 | 515 | 15 | 1 | 1 | ||
| 6971 | 1695 | 417 | 32 | 1 | 1 | ||
| 5890 | 1433 | 353 | 9 | 2 | 1 | ||
| 5113 | 1244 | 307 | 27 | 1 | 1 | ||
| 4522 | 1101 | 271 | 54 | 1 | 0 | ||
3.2.4. Comparison of the IIRFM with the Singha et al. [14] Approach
First Example
Second Example
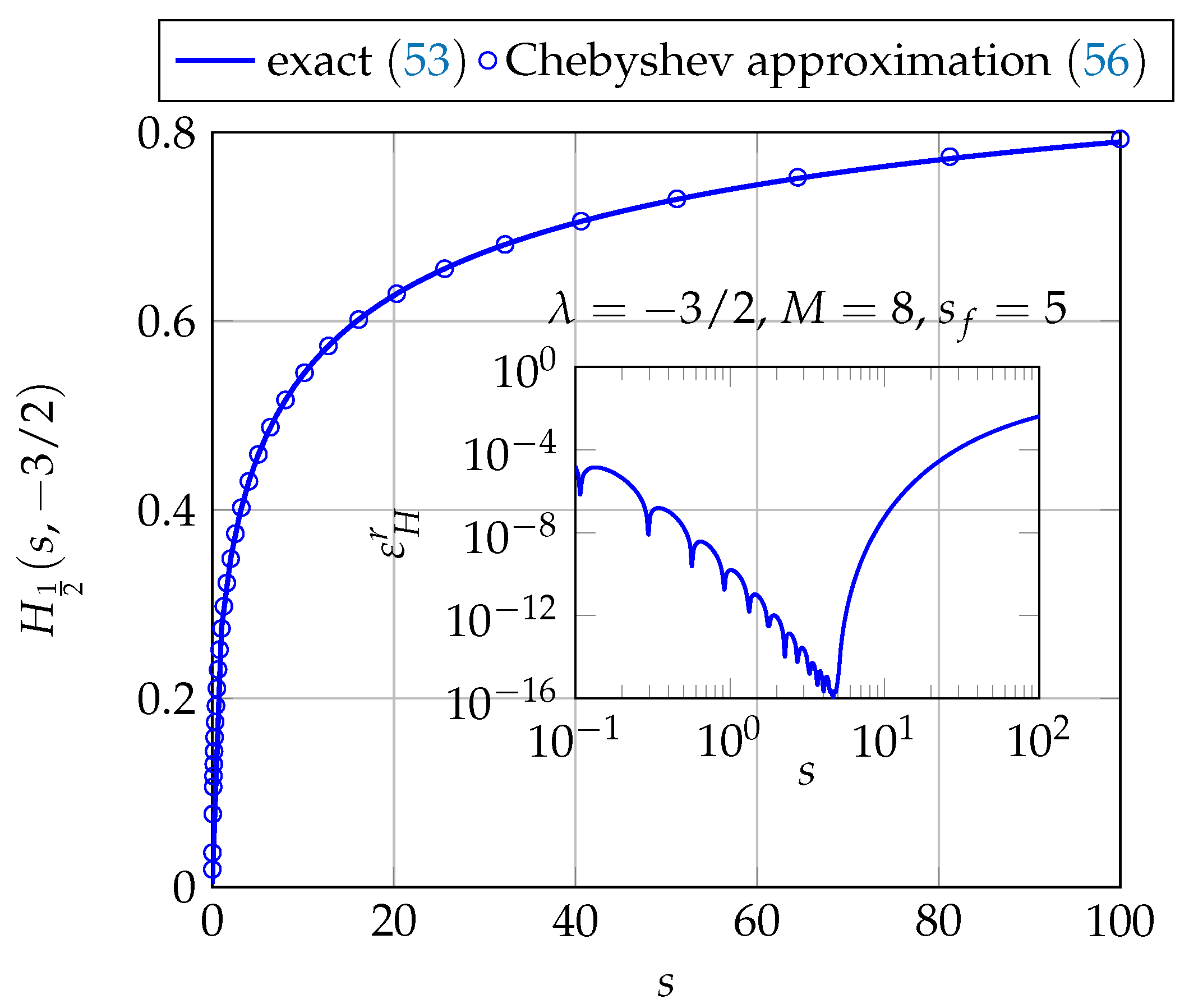
3.3. Logarithmic Kernel
3.3.1. First Example:
3.3.2. Second Example:
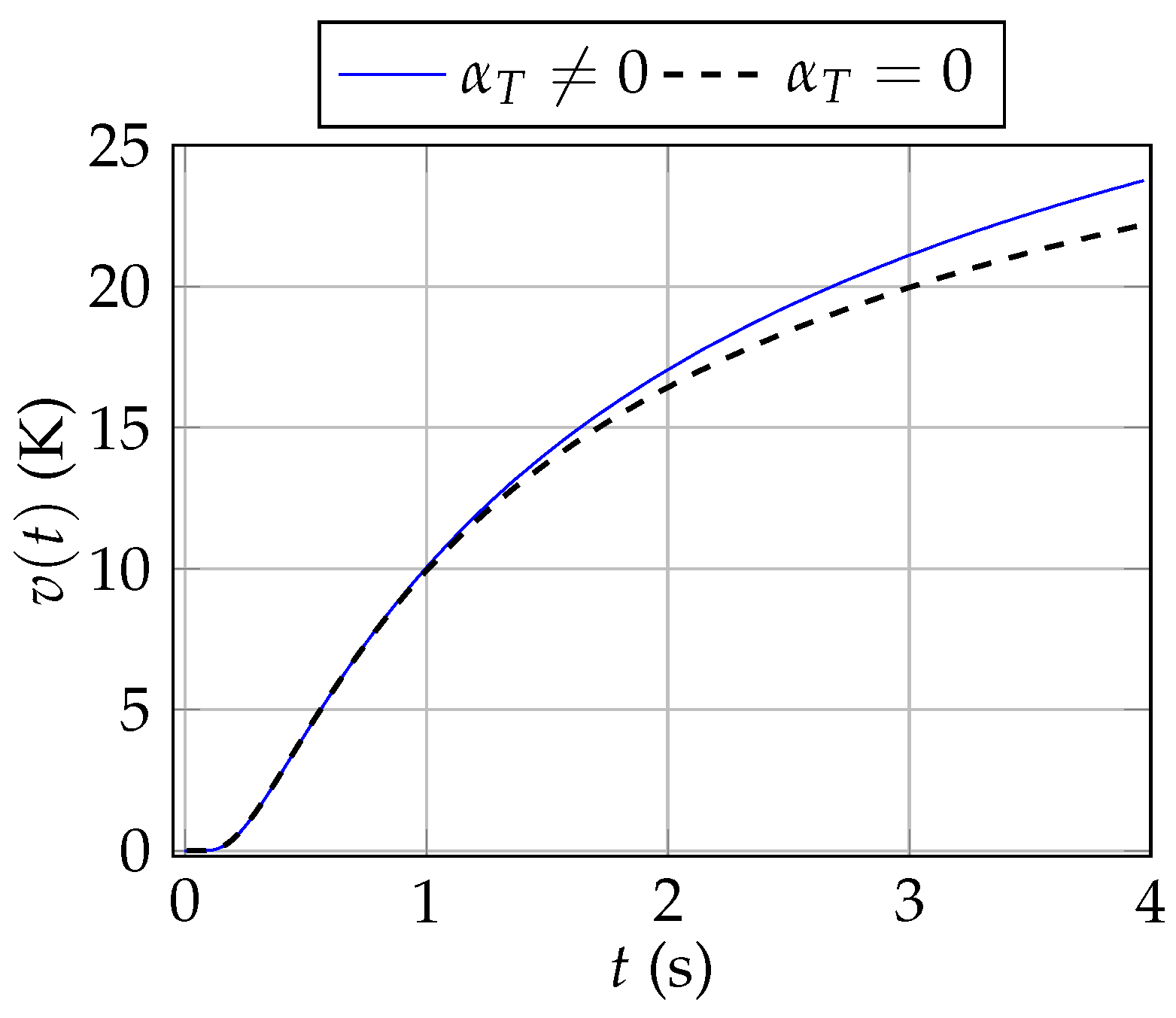
4. Basic Applications in Thermics
4.1. Heat Point Source
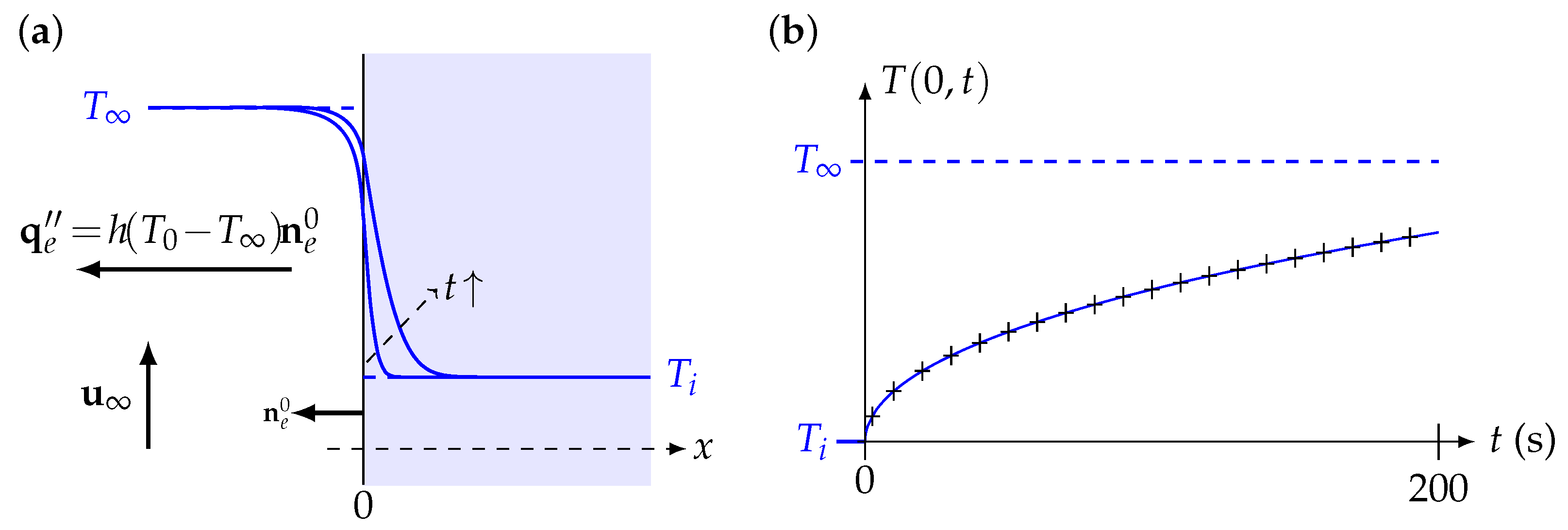
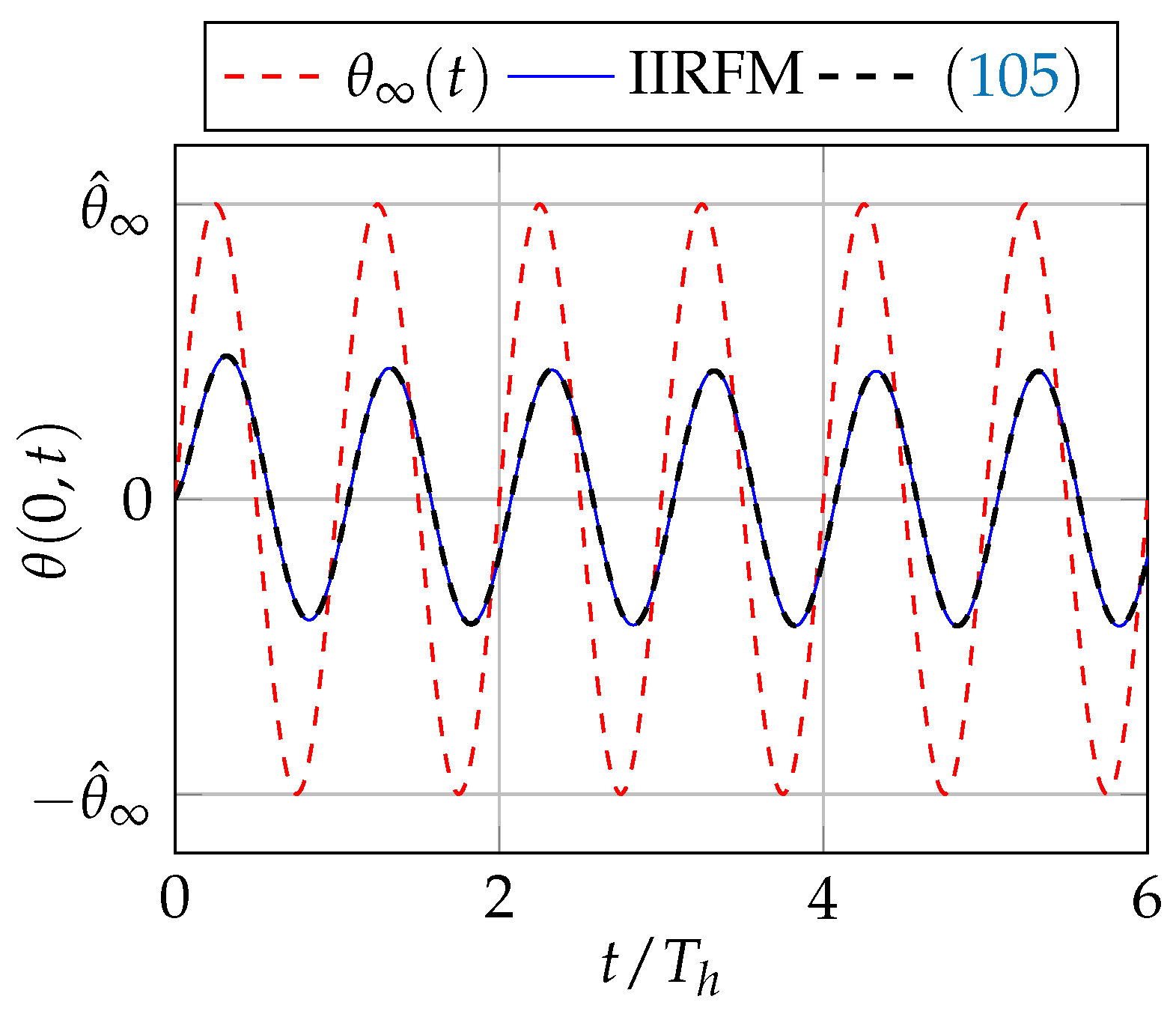
4.2. Surface Temperature of Semi-Infinite Solids
4.2.1. First Application:
4.2.2. Second Application:
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BLT | Bilinear Transformation |
| CAIE | Convolutive Abel Integral Equation |
| CIE | Convolutive Integral Equation |
| CVIE | Convolutive Volterra Integral Equation |
| FOD | First-Order Partial Fractions Decompositon |
| HPM | Homotopy Perturbation Method |
| HPM-L | Homotopy Perturbation Method with Laplace Transform |
| IIR | Infinite Impulse Response |
| IIRFM | Infinite Impulse Response First-Order Filters Method |
| ODE | Ordinary Differential Equation |
| OIDE | Ordinary Integro-Differential Equation |
| LT | Laplace Transformation |
| LTIS | Linear Time Invariant Systems |
| PDE | Partial Differential Equation |
References
- De, S.; Mandal, B.; Chakrabarti, A. Use of Abel integral equations in water wave scattering by two surface-piercing barriers. Wave Motion 2010, 47, 279–288. [Google Scholar] [CrossRef]
- Mirceski, V.; Tomovski, Z. Analytical solutions of integral equations for modelling of reversible electrode processes under voltammetric conditions. J. Electroanal. Chem. 2008, 619–620, 164–168. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Linear and Nonlinear Integral Equations—Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Integral Equations, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Kumar, S.; Kumar, A.; Kumar, D.; Singh, J.; Singh, A. Analytical solution of Abel integral equation arising in astrophysics via Laplace transform. J. Egypt. Math. Soc. 2015, 23, 102–107. [Google Scholar] [CrossRef]
- Thota, S. Solution of Generalized Abel’s Integral Equations by Homotopy Perturbation Method with Adaptation in Laplace Transformation. Sohag J. Math. 2022, 9, 29–35. [Google Scholar]
- Chowdhury, M.S.H.; Mohamed, M.S.; Gepreel, K.A.; Al-Malki, F.A.; Al-Humyani, M. Approximate Solutions of the Generalized Abel’s Integral Equations Using the Extension Khan’s Homotopy Analysis Transformation Method. J. Appl. Math. 2015, 2015, 357861. [Google Scholar]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S. Comparison between the homotopy analysis method and homotopy perturbation method. Appl. Math. Comput. 2005, 169, 1186–1194. [Google Scholar] [CrossRef]
- Bairwa, R.K.; Kumar, A.; Kumar, D. An Efficient Computation Approach for Abel’s Integral Equations of the Second Kind. Sci. Technol. Asia 2020, 25, 85–94. [Google Scholar]
- Heyd, R. Real-time heat conduction in a self-heated composite slab by Padé filters. Int. J. Heat Mass Transf. 2014, 71, 606–614. [Google Scholar] [CrossRef]
- Lahboub, D.; Heyd, R.; Bakak, A.; Lotfi, M.; Koumina, A. Solution of Basset integro-differential equations by IIR digital filters. Alex. Eng. J. 2022, 61, 11899–11911. [Google Scholar] [CrossRef]
- Mouley, J.; Panja, M.M.; Mandal, B.N. Approximate solution of Abel integral equation in Daubechies wavelet basis. CUBO A Math. J. 2021, 23, 245–264. [Google Scholar] [CrossRef]
- Singha, N.; Nahak, C. Solutions of the Generalized Abel’s Integral Equation using Laguerre Orthogonal Approximation. Appl. Appl. Math. Int. J. (AAM) 2019, 14, 1051–1066. [Google Scholar]
- Adomian, G.; Rach, R. Noise terms in decomposition series solution. Comput. Math. Appl. 1992, 24, 61–64. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer: Alphen aan den Rijn, The Netherlands, 1994. [Google Scholar]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Madani, M.; Fathizadeh, M. Homotopy Perturbation Algorithm using Laplace Transformation. Nonlinear Sci. Lett. A 2010, 1, 263–267. [Google Scholar]
- Khan, Y.; Wu, Q. Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 2011, 61, 1963–1967. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Rathore, S. Application of Homotopy Perturbation Transform Method for Solving Linear and Nonlinear Klein-Gordon Equations. J. Inf. Comput. Sci. 2012, 7, 131–139. [Google Scholar]
- Heyd, R.; Hadaoui, A.; Saboungi, M. 1D analog behavioral SPICE model for hot wire sensors in the continuum regime. Sens. Actuators A Phys. 2012, 174, 9–15. [Google Scholar] [CrossRef]
- Lotfi, M.; Mezrigui, L.; Heyd, R. Study of heat conduction through a self-heated composite cylinder by Laplace transfer functions. Appl. Math. Model. 2016, 40, 10360–10376. [Google Scholar] [CrossRef]
- Carslaw, H.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Zhao, K.; Liu, J.; Lv, X. A Unified Approach to Solvability and Stability of Multipoint BVPs for Langevin and Sturm–Liouville Equations with CH-Fractional Derivatives and Impulses via Coincidence Theory. Fractal Fract. 2024, 8, 111. [Google Scholar] [CrossRef]
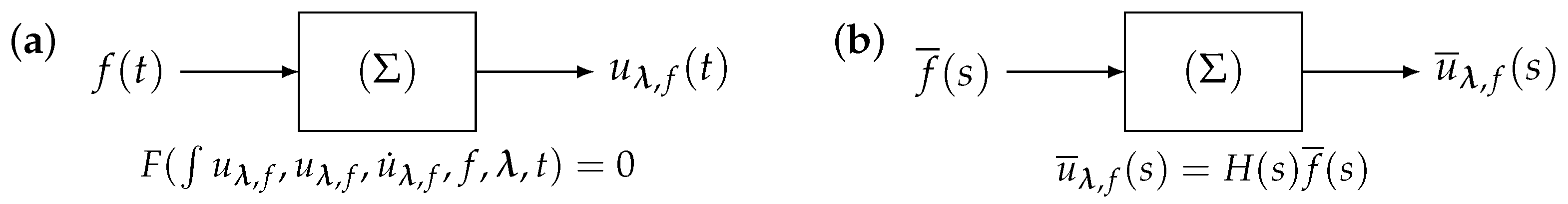
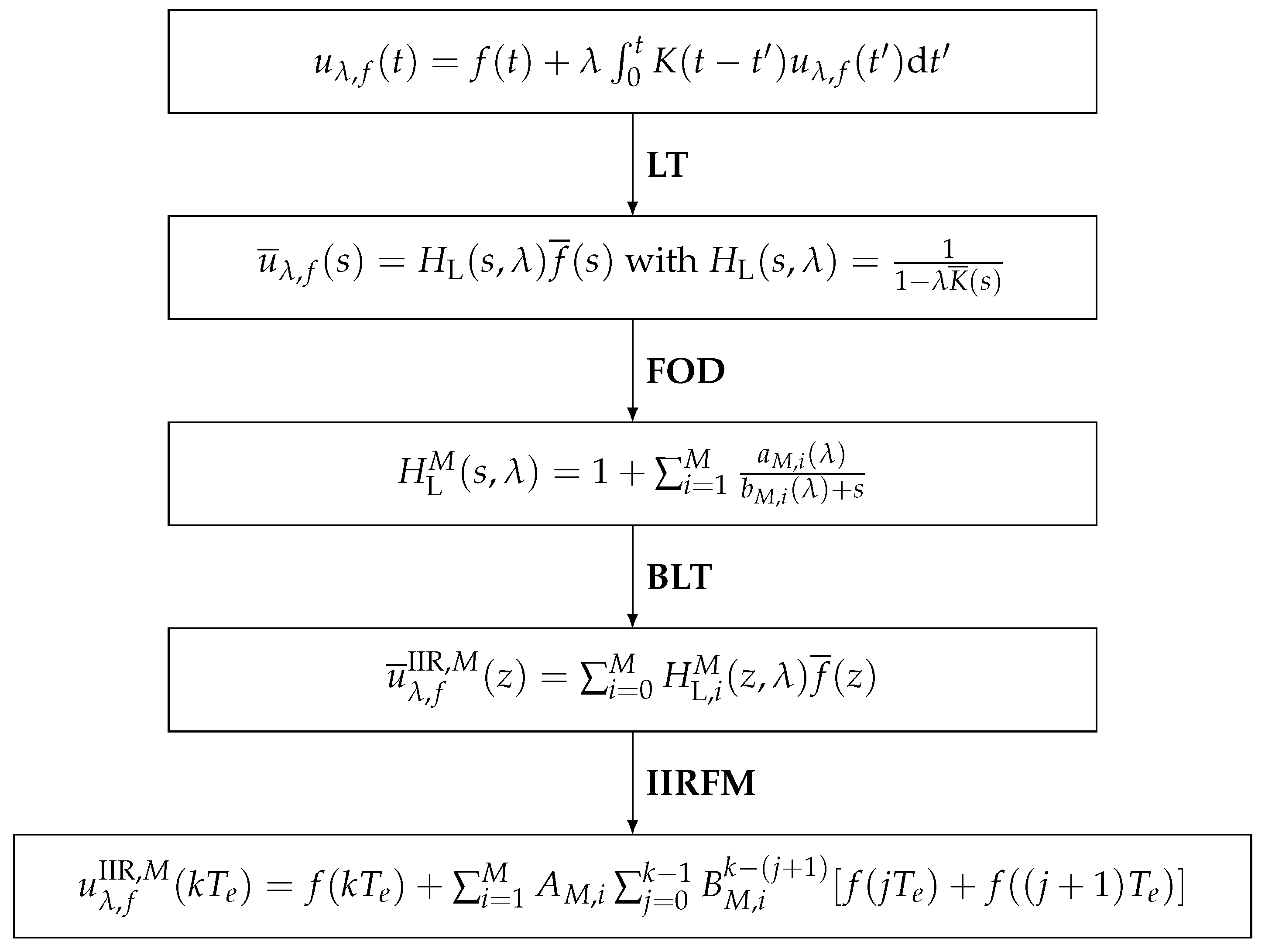
| = | 3 | 5 | 7 | 15 | 20 | 30 |
|---|---|---|---|---|---|---|
| - | ||||||
| = | = | ||||||
|---|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Approximated Solutions | Absolute Errors: | ||||
|---|---|---|---|---|---|
| Laguerre | IIRFM | Laguerre | IIRFM | ||
| 24,992 | 34 | ||||
| 31,841 | 17 | ||||
| 18,197 | 52 | ||||
| 1958 | 37 | ||||
| 11,487 | 91 | ||||
| 15,058 | 239 | ||||
| Approximated Solutions | Absolute Errors: | ||||
|---|---|---|---|---|---|
| Laguerre | IIRFM | Laguerre | IIRFM | ||
| 34,544 | 20 | ||||
| 38,653 | 6 | ||||
| 18,710 | 62 | ||||
| 353 | 101 | ||||
| 15,162 | 132 | ||||
| 15,191 | 194 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heyd, R. Numerical Solution of Linear Second-Kind Convolution Volterra Integral Equations Using the First-Order Recursive Filters Method. Mathematics 2024, 12, 2416. https://doi.org/10.3390/math12152416
Heyd R. Numerical Solution of Linear Second-Kind Convolution Volterra Integral Equations Using the First-Order Recursive Filters Method. Mathematics. 2024; 12(15):2416. https://doi.org/10.3390/math12152416
Chicago/Turabian StyleHeyd, Rodolphe. 2024. "Numerical Solution of Linear Second-Kind Convolution Volterra Integral Equations Using the First-Order Recursive Filters Method" Mathematics 12, no. 15: 2416. https://doi.org/10.3390/math12152416
APA StyleHeyd, R. (2024). Numerical Solution of Linear Second-Kind Convolution Volterra Integral Equations Using the First-Order Recursive Filters Method. Mathematics, 12(15), 2416. https://doi.org/10.3390/math12152416






