Abstract
Automatic International Classification of Disease (ICD) coding, a system for assigning proper codes to a given clinical text, has received increasing attention. Previous studies have focused on formulating the ICD coding task as a multi-label prediction approach, exploring the relationship between clinical texts and ICD codes, parent codes and child codes, and siblings. However, the large search space of ICD codes makes it difficult to localize target labels. Moreover, there exists a great unbalanced distribution of ICD codes at different levels. In this work, we propose LabGraph, which transfers ICD coding into a graph generation problem. Specifically, we present adversarial domain adaptation training algorithms, graph reinforcement algorithms, and adversarial perturbation regularization. Then, we present a discriminator for label graphs that calculates the reward for each ICD code in the generator label graph. LabGraph surpasses existing state-of-the-art approaches on core assessment measures such as micro-F1, micro-AUC, and P@K, leading to the formation of a new state-of-the-art study.
Keywords:
graph convolutional network; faster attention; transfer learning; ICD coding; adversarial domain adaptation MSC:
68T50
1. Introduction
Automatic ICD coding, which assigns the International Classification of Disease codes to patient visits, has attracted considerable research attention, as it can save valuable time and labor in billing. A clinical text includes admissions, clinical notes, medical history, and lab results, among other patient-related data [1]. Figure 1 depicts the hierarchical structure of the ICD codes, where siblings rarely appear concurrently in a single clinical text.
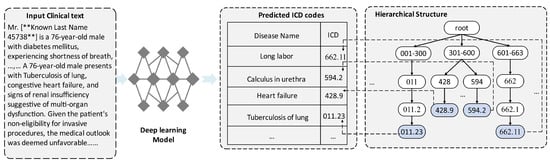
Figure 1.
Hierarchical diagram of ICD-9 codes and an example of an automatic ICD coding task. The input and output of the automatic ICD coding model are a clinical text and the predicted ICD codes, respectively.
The majority of neural network techniques treat automatic coding as a multi-label prediction method [2,3]. Regarding ICD codes, there are certain peculiarities. First, 122 of the 9219 codes match the most common top 50, indicating that the distribution of codes is severely imbalanced, and the majority of codes are inactive in clinical texts. Second, the relationships between ICD codes, such as parent–child relationships, sibling relationships, and mutually exclusive relationships, are neglected or undervalued by the majority of prior techniques [4]. For instance, “783.1” (ICD code for abnormal weight increase) and “783.2” are mutually incompatible (ICD code of abnormal loss of weight and being underweight). Thirdly, current approaches rely solely on a single training method to update their parameters [5,6,7], which may result in failure for some clinical texts covering uncommon disorders. We suggest reformulating automatic ICD coding as a labeled graph generation task along the ICD code graph to overcome the aforementioned difficulties. This novel formulation generates individual graph labels (nodes or codes). Intuitively, we first construct a global code graph using the ground labels of clinical training texts. Next, we build the first graph label with the root and insert the clinical text input. Then, we use the neighbors of the first produced label to forecast the second one, therefore reducing the ICD code candidate space. The third label is then predicted using the second and input embeddings. In this study, we propose a multi-algorithm label graph generation model called LabGraph to overcome the aforementioned concerns and obstacles. LabGraph uses four training methods to produce code graph labels, and the generation process ends when the generated labels can form a circle. LabGraph gives the labels in the last circle as codes to the specified clinical text. LabGraph comprises six primary elements: a label graph generator (LGG), a label graph discriminator (LGD), a message integration module (MIM), an MHR-CNN for LGG’s embedding, a Fat-RGCN for LGD’s embedding, and an adversarial adaptative training method. When provided with a clinical text, the text encoder can provide an input representation. MIM is then utilized to model the relationships between the clinical text and ICD codes. In particular, label graphs are intended to produce graph labels that are indistinguishable from original ICD labels, and the LGD differentiates between original and generated ICD labels.
The representation learning of knowledge graphs involves mapping many entities and relations into a dense low-dimensional vector representation in the same space. Existing knowledge bases include DBPedia [8], YAGC [9], and FreeBase [10], all of which have various building requirements and data sources. This study enhances the existing knowledge representation technique at the one-hop neighbor level and the multi-hop neighbor level based on the knowledge representation model using subgraph aggregation. First, when one-hop neighbor subgraphs are aggregated, both neighbor nodes and neighbor edges need to be taken into account at the same time. Furthermore, the influence on the central node’s representational importance must be considered. Second, using multi-hop neighbors as subgraphs for the adaptive representation of core nodes at the multi-hop neighbor level frees us from the limitations of one-hop neighbor subgraphs. Finally, a Fat-RGCN is created by fusing the two tiers of algorithms mentioned above. We designed ablation experiments to ensure the validity of the experimental findings and performed proper experimental validation of the improved knowledge representation algorithm to demonstrate the efficacy of each improved scheme. We also fused the two levels of the improved algorithms to demonstrate the efficacy of the fused model. We conducted numerous experiments on the MIMIC-III benchmark dataset [11] in order to provide empirical proof of LabGraph’s efficacy. Our experimental findings in Table 1 indicate that LabGraph outperforms state-of-the-art techniques by a wide margin. In conclusion, the main contributions of this paper can be summarized as follows:

Table 1.
Experiment results on MIMIC-III top 50 and MIMIC-III full. The results of LabGraph are shown in means ± standard deviations.
- •
- We first considered automatic electronic health record (EHR) coding as a labeled graph generation challenge and then developed a multi-algorithm model LabGraph for automatic ICD coding.
- •
- We proposed a message integration module (MIM) that simulates the parent–child, sibling, and mutually exclusive relationships.
- •
- We initially applied four training methods based on reinforcement learning in ICD coding.
- •
- We developed a label graph discriminator (LGD) with an adversarial reward to assess intermediate rewards as supervision signals for LabGraph.
- •
- We conducted comprehensive experiments on a frequently utilized dataset to validate and evaluate the efficacy of LabGraph.
2. Method and Theoretical Analysis
Given the clinical text X = {, , …, }, where represents the i-th token, our graph generation task is to generate labels Y = {, , …, }, where indicates the i-th label (code) in the generated graph. Note that all graphs start with the root node and end while a label circle is formed. As shown in Figure 2, the framework of LabGraph showcases the process of generating document embeddings from electronic health records (EHRs) and convolutional neural networks (CNNs), which are subsequently utilized to generate and discriminate label graphs. Additionally, it incorporates an information retrieval module, aiming to enhance the accuracy of information retrieval and classification. LabGraph contains two main parts: label graph generator and label graph discriminator . Next, we describe LabGraph in detail.
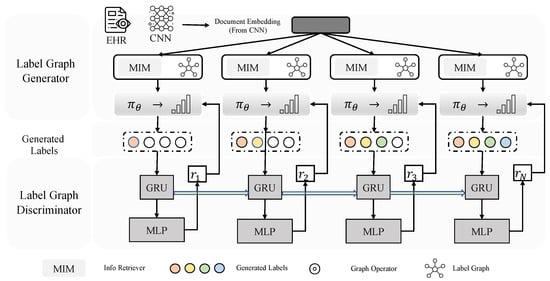
Figure 2.
The overall framework of LabGraph.
2.1. Meta-Parameter Learning
To encode EHRs, we present a multi-header residual embedding layer. Initially, words are embedded in the matrix using word2vec [12], which is a technique for generating word vectors, converting text words into low-dimensional vector representations in a higher-dimensional space, and making semantically similar words close to each other in the vector space. Given a phrase as input, we thus represent it as .
Multi-header convolutional filter (MCF): To record patterns with varying durations, we utilized MCF [13]. Suppose we have m and filters, and their kernel sizes are denoted by . Therefore, it is possible to apply m one-dimensional convolution layers to the input matrix X. The formalization of the convolutional technique is shown in Equations (1) and (2).
where specifies the left-to-right convolutional operations. and indicate the sub-matrices of X. and are the weight matrices of corresponding filters.
Multi-residual convolutional block (MCB): A residual convolutional layer with p residual blocks is placed on top of each filter in the multi-filter convolutional layer.
Three convolutional filters, namely , , and , constitute the residual block . The notation for the computing process is shown in Equation (3).
where represents convolutional operations. I represents the input matrix of this residual block, whereas represents its submatrices. The matrices and represent the weights of the three convolutional filters , and .
2.2. Label Graph Generator
The label graph generation process is a Markov decision process (MDP) [14] , where is the state space, and is the set of all possible actions. The subset of corresponding to a label, for instance, is its neighbors in the global graph. is the function that allows for transfer progression, and represents the reward function for each pair (state and action). To motivate to provide ground-truth-like labels, we suggest maximizing the anticipated rewards of the reinforcement algorithm [15]. For a trajectory ={} where a represents an action, the anticipated payoff can be calculated using Equation (4). yields the mean expected value of the rewards for the trajectories.
where represents the anticipated gain from one trajectory, is the anticipated overall gain from one episode, and denotes the trajectory. is the path generator, and is its hybrid policy network. is the label that is derived based on the present states and x; is the compensation for generating depending on and x. can be implemented in module . Equation (5) describes how the policy gradient could be used to modify : ( is irrelevant to ):
We determine using Equation (6).
where W is a matrix, and b is a bias; the sigmoid activation function is denoted by .
2.3. Label Graph Discriminator
Inspired by [5], we created a route discriminator module in order to obtain the reward for each code in the produced path (, , …,) till timestamp i. To be more specific, we modeled as the discrimination probability using Equation (7), which is as follows:
where ⊕ represents the concatenation operation, and represents the weight matrix; is the current produced route acquired by repeatedly applying an LSTM to the ICD code path. In addition, an adversarial-like domain adaptive training strategy is used, which entails utilizing produced pseudo labels as negative samples and the ground truth as positive samples.
We use a cross-entropy function as the loss function to determine and measure the correct value of , which is defined in Equation (8).
where and represent positive and negative samples, respectively; denotes the chance that sample (, x) is a positive sample.
Multi-Hop Model Integration (MHMI)
In this section, the revised algorithm model is first described in detail considering the one-hop and multi-hop neighbor levels. Next, MHMI is created for multi-relational deep graph representation by fusing multi-level enhancement approaches. In MHMI, handling the relationships between different entities and the directionality of these relationships is of paramount importance, and these relationships can be intuitively demonstrated in Figure 3. In order to allow the model to take into account both the influence of nodes and relationships between the representation and the weight of the influence, this paper introduces an improved attention mechanism into the multi-relational heterogeneous graph representation learning model (RGCN) at the one-hop neighbor level. The idea presented in this study is to take into account feature information in the multi-hop range during node aggregation at the level of multi-hop neighbors and proposes a gate mechanism to filter feature information.
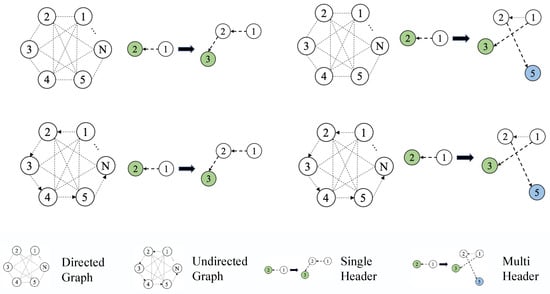
Figure 3.
Graph search engine.
The attention mechanism, multi-hop neighbors, and gate mechanism can be simply incorporated since the one-hop neighbor and multi-hop neighbor enhancement algorithms are both based directly on the RGCN method for modification. Utilizing the attention mechanism in one-hop and two-hop convergence while controlling node convergence through gates is a unique operation. The specific convergence process, incorporating the attention mechanism of the modified GAT through , is described in Equations (9)–(12).
With the introduction of an improved attention mechanism, it is clear that the formula above is based on the multi-hop , convergence scheme.
2.4. Adversarial Adaptative Training (AAT)
Countermeasure training involves adding a minor disruption to the original input to generate adversarial samples that could be utilized for training [16]. It is expressed using Equation (13).
In particular, given the model and k data points of the target task indicated by , where values signify the embedding of the input sentences derived from the first embedding layer of the language model, and values are the associated labels, with our technique, optimization is carried out for fine-tuning using Equation (14) as follows:
where is the loss function that changes based on the goal task, is a tuning parameter, and is the adversarial regularizer that promotes smoothness. We define using Equation (15).
where is an adjustment factor; note that produces a probability simplex for classification tasks, whereas is selected as the symmetrized KL divergence, as detailed in Equation (16).
where outputs a scalar for regression tasks, whereas is chosen as the squared loss. (M,N) = indicates that the computation of includes a problem involving maximization, which can be effectively accomplished via the projected gradient ascent.
3. Experimental Setup
Extensive experiments were undertaken to answer the following research questions:
- RQ1: How does LabGraph compare to existing automatic ICD coding systems in terms of ICD code prediction?
- RQ2: How can the label graph generation network be trained so that it has better generalization, robustness, and effectiveness?
- RQ3: What are the influences of different model configurations?
- RQ4: Is the improved graph representation learning algorithm effective on multi-relational medical graph data?
3.1. Dataset
- MIMIC-III [11]
LabGraph’s validation experiments are based on the well-known and publicly accessible MIMIC-III dataset. MIMIC-III has less than 50,000 recordings compiled during a twelve-year period beginning in 2000. The entire version of MIMIC-III is MIMIC-III full, while the top 50 version is MIMIC-III top 50.
- Cora [17]
The Cora graph dataset uses a 1433-dimensional vector to represent each node, with each dimension denoting a feature and each feature linking to a dictionary term. The edges of the Cora graph data represent the cross-citation relationships between papers. Each paper cites at least one other paper or is cited by other papers that constitute the edges of the Cora dataset. Most of the current training tasks based on the Cora dataset are node classification tasks, and considering the actual test graph data, they have a label sparsity problem.
- FB15k-237 [18]
FB15k-237 is a part of the considerable knowledge base Freebase [19], which contains 14,541 nodes and 237 types of edges. Freebase is an extensive knowledge base composed of metadata similar to Wikipedia [20]. The experiments based on the FB15k-237 dataset in this paper also adopted the same division as the existing Baselines.
3.2. Metrics
For a fair and impartial comparison with previous research, we employed macro-averaged and micro-averaged AUC as well as macro-averaged and micro-averaged F1 as the fundamental core metrics, calculating the performance score for each label and then averaging the score of macro-AUC or F1. AUC is used to measure the classifier’s ability to distinguish between positive and negative samples, while F1 provides a balanced measure of the classifier’s performance by combining precision and recall; both are dimensionless. In addition, we employed precision at K (P@K) as an evaluation metric, with precision at K (P@K) defined as the proportion of correctly predicted labels among the top K predicted labels. The LabGraph model evaluation metrics used in the experiments included accuracy, MR, MRR, Hit@1, Hit@3, and Hit@10 [21].
3.3. Baselines
To showcase the effectiveness of LabGraph, we evaluated its performance against various popular modeling frameworks, including the top-performing EHR coding model and its corresponding hierarchical text classification method. We assessed these models using several key metrics. The details of our baseline model and its associated summary are provided below.
- Hierarchy-SVM and Flat-SVM [22]
Compared with Hierarchy-SVM, Flat-SVM uses 10,000 tf-idf unigram features to train multiple binary SVMs for EHR coding. The authors of [22] proposed two coding approaches: one that treats each ICD9 code independently of each other (Flat-SVMs) and one that leverages the hierarchical nature of ICD9 codes into its modeling (Hierarchy-SVM).
- C-MemNN [23] and C-LSTM-Att [24]
C-MemNN is a novel model with iterative condensation of memory representations that preserves the hierarchy of features in the memory. C-LSTM-Att utilizes character-aware neural language models to generate hidden representations of written diagnosis descriptions and ICD codes and design an attention mechanism to address the mismatch between the numbers of descriptions and corresponding codes.
- BI-GRU [25] and HA-GRU [26]
BI-GRU employs a bidirectional gated recurrent unit to create a comprehensive embedded representation of EHRs, which is then used for the binary classification of ICD codes. HA-GRU is an advanced version of BI-GRU that incorporates BI-hierarchical attention mechanisms into the bidirectional gated recurrent unit. By enhancing BI-GRU’s focus on the gated recurrent unit, HA-GRU generates a more refined encoding output of EHRs, thereby improving disease classification accuracy.
- CAML and DR-CAML [2]
CAML employs convolutional attention networks to learn the embedding representations of each ICD code; DR-CAML is an enhanced version of CAML that incorporates a label-wise mechanism. By normalizing the descriptions of ICD codes through EHRs and adding regularization terms to the loss function’s classification weights, DR-CAML further optimizes CAML’s performance.
- LAAT and JointLAAT [6]
The label attention (LAAT) model introduces an approach to learning the attention distribution of ICD code encodings hidden within LSTM states, aiming to classify ICD encodings. Furthermore, JointLAAT enhances this by implementing a hierarchical joint learning algorithm, thereby boosting the efficiency and accuracy of ICD encoding classification.
- ISD [27], MSMN [28], and FUSION [29]
ISD employs an interactive network to tackle the long-tail issue and introduces a symbiotic model to link codes during the construction process. Additionally, MSMN, which relies on various synonym-matching techniques, is designed to enhance ICD code classification. It utilizes synonym-matching algorithms and data augmentation to bolster the model’s learning capacity for code embedding characterization. To solve the issue of redundant and sparse disease diagnosis vocabulary, FUSION is proposed, which models relationships between local features using an attention mechanism centered on a crucial query and completes the generation of global features.
4. Results and Analysis
The number of ICD codes at the fourth level accounts for 40.1% of the MIMIC-III top 50 dataset, but the number of codes in the first through third levels accounts for just 24.9% of the MIMIC-III full dataset. This indicates that the number of ICD codes at various levels varies significantly, with shallow levels having far fewer codes than deep ones. Consequently, searching for ICD code-generating pathways from low to high levels via the ICD tree hierarchy may effectively minimize the search space of ICD codes, accelerate inference and prediction time, and enhance the efficacy of LabGraph learning.
4.1. Comparison with Baselines (RQ1)
To address the inquiries raised by RQ1, we collated the experimental results from the MIMIC-III full dataset and the MIMIC-III top 50 dataset, concentrating on fundamental core assessment metrics and personalized metrics, as summarized in Table 1. The findings lead to the following conclusions:
First, the LabGraph model achieves the best results in both essential core assessments and individualized indicators, underscoring its validity and advancement. The minimal and consistent standard deviation observed in the assessment indices of the LabGraph model’s experimental findings attests to the framework’s stability. Furthermore, the performance variations shown by the same model across different datasets are as predicted. Overall, the model demonstrates better performance on the MIMIC-III full dataset compared to the MIMIC-III top 50 dataset, indicating that the LabGraph model has the capability to learn the underlying classification patterns of medical diagnosis texts at a deeper level as the data volume increases. Additionally, the MIMIC-III full dataset contains a smaller proportion of data on uncommon diseases compared to the top 50 dataset, implying that the model architecture presented in this study is effective in minimizing the long-tail influence of disease diagnostic texts.
Second, in comparison to LabGraph, the AUC and F1 values of CAML, DR-CAML, LAAT, and JointLAAT models are relatively lower, suggesting their limited coverage of rare codes. These models are prone to overlook a substantial volume of sparse ICD code data, which poses a significant challenge to their generalization abilities. Prompt and precise uncommon disease identification is crucial in medical diagnosis, and as the ICD code space continues to expand, accurate forecasting is increasingly challenging, emphasizing the need for high coverage of unique codes. LabGraph outperforms other baseline models due to its ability to reason through the ICD code generation process from the root to the leaf node. By identifying ICD code nodes one level at a time, from top to bottom, the proposed method narrows the search space and enhances inference efficiency, effectively addressing the aforementioned issues.
Third, upon analyzing and comparing the performance of recursive models belonging to the GRU class (BI-GRU, HA-GRU) listed in Table 1, it is evident that these models exhibit relatively poor performance in comparison to other models when tasked with the challenging assignment of classifying medical diagnoses. Long electronic health records (EHRs) frequently trigger the gradient disappearance issue in recursive models based on the GRU class. This leads to the model neglecting crucial information and the connection between preceding and succeeding data. We found that disease-related keywords or phrases yield crucial information, given the specific encoding requirements of EHRs, and models resembling CNN excel in capturing such vital data. Consequently, we developed the MHR-CNN embedding representation module specifically for LabGraph. This module provides a more comprehensive perspective of EHRs through the use of a multi-headed CNN. By incorporating a strategically designed CNN residual connection structure, the gradient disappearance problem can be mitigated. The effectiveness of LabGraph in addressing these issues was confirmed through a comparison of experimental outcomes with BI-GRU, HA-GRU, and other similar models.
4.2. LABGRAPH Ablation (RQ2)
We conducted several ablation experiments to explore the significance of various modules in LabGraph. The outcomes are listed in Table 2. The following LabGraph variations were examined: (1) No ARCL refers to LabGraph minus adversarial reinforcement casual learning (LGG & LGD). In this variant, we eliminated the adversarial reinforcement casual learning component and trained the model solely with teacher-forced and ground-truth paths. (2) No MIM signifies LabGraph without the MIM module, thereby eliminating the transfer of parent–child and sibling information. (3) No MHR-CNN represents LabGraph without the enhanced embedding representation, relying only on a standard CNN for extracting EHRs’ semantic information. (4) No AAT indicates LabGraph without the adversarial perturbation boost in the embedding layer.

Table 2.
Ablation experiment results on MIMIC-III top 50 and MIMIC-III full datasets. The standard deviation of LabGraph results is consistent with the previous table, so it is omitted in this table.
The results in Table 2 reveal the following: (1) No ARCL: The absence of ARCL significantly impacts LabGraph’s performance. Specifically, in the MIMIC-III full dataset, the model’s macro-AUC and micro-AUC metrics decreased by 15.61% and 12.62%, respectively. Additionally, the model’s macro-F1 and micro-F1 metrics decreased by 3.95% and 27.82%, with a 14.81% reduction in P@8. This downward trend is mirrored in the MIMIC-III top 50 dataset as well. The experimental ablation results highlight ARCL’s crucial role in generating ICD code paths and determining rewards for each ICD code within the generator label graph. (2) No MIM: In this instance, LabGraph exhibits a similarly disappointing performance, accompanied by a noticeable decrease in its overall functionality. In the MIMIC-III top 50 dataset, the model’s macro-AUC and micro-AUC metrics decreased by 15.01% and 11.33%, respectively. Furthermore, the model’s macro-F1 and micro-F1 metrics decreased by 12.41% and 13.73%, accompanied by a 15.70% decline in P@5. Simultaneously, the MIMIC-III full dataset demonstrates a considerable degree of deterioration. The investigations reveal that MIM involves an interaction between an EHR text, ICD code routes, and ICD codes through the message forwarding system. (3) No MHR-CNN: Using the MIMIC-III full dataset as an illustration, we found that removing the MHR-CNN module resulted in a significant decrease in performance. Specifically, the macro-AUC and micro-AUC measures decreased by an average of 12.42%. Additionally, the macro-F1 and micro-F1 metrics dropped by an average of 15.79%, respectively, and there was a 13.12% decrease in P@8. Similar results were observed in ablative tests on the MIMIC-III top 50 dataset. Through the analysis of these findings, it is apparent that the MHR-CNN module within the LabGraph model enhances the accuracy of text information definition. Utilizing a multi-head CNN architecture combined with the mechanical design of a residual CNN, the MHR-CNN serves as an embedding layer capable of integrating text information from diverse visual field domains while effectively reducing the impact of information loss caused by gradient vanishing, thereby minimizing the issue of information forgetting. (4) No AAT: We iteratively updated the LabGraph model parameters using a back-propagation algorithm, without employing AAT. Following ablative experiments, we analyzed the results, which are presented in Table 2. Using the MIMIC-III top 50 dataset as a reference, we found that the macro-AUC and micro-AUC metrics for the model proposed in this paper decreased by 5.40% and 9.61%, respectively. The model’s macro-F1 and micro-F1 indicators decreased by 3.53% and 15.89%, respectively, while the P@5 metric declined by 11.22%. Additionally, the comparative values of these indicators also diminished in experiments conducted on the MIMIC-III full dataset. After a careful comparison of the experiments, the effectiveness and necessity of integrating AAT into the LabGraph model were firmly established. Through the optimization of the back-propagation algorithm, AAT refines the characterization ability of the model’s embedding layer while resulting in a smoother model loss curve.
4.3. Graphical Representation Model Experiment (RQ3)
4.3.1. A Comparison of One-Hop Neighbor Attention Optimization Graph Representation
The enhancement of our algorithm at the one-hop neighbor level focuses on assessing the impact of neighbor nodes and their relationships on the central node’s representation within multi-relational knowledge graphs. We implemented an optimized attention mechanism at the point of convergence within the RGCN baseline model to enhance this assessment. Below, we detail a series of experiments designed to validate the efficacy of this optimized mechanism.
Experimental Setup and Results:
- Baseline RGCN Model: This initial experiment established our control setup with a learning rate of 0.005, batch size of 256, initial node feature dimension of 128, and a hidden layer dimension of 300 in the GCN convolutional layers. The model achieved optimal performance after 247 epochs.
- RGCN+NARC: This variant integrated the GAT model’s attention mechanism directly into the one-hop neighbor nodes upon model convergence. Parameters remained consistent with the baseline, achieving optimal performance after 281 epochs.
- RGCN+FAMC: Similar to the previous experiment, this experiment added an enhanced GAT attention mechanism to the one-hop neighbors at convergence. It mirrored the RGCN+NARC in terms of parameters, with convergence after 265 epochs.
- RGCN+FANR: This model extended the improved GAT attention to include both one-hop neighbor nodes and their relationships. It followed the same parameter setup as the previous experiments, converging after 239 epochs.
Figure 4 presents the comparative results of these experiments across various performance metrics.
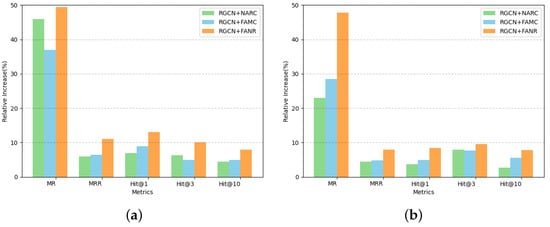
Figure 4.
Experimental results of attentional optimization mechanisms in one-hop neighborhood graph representation schemes on the homogeneous dataset FB15k-237 and the multi-relational heterogeneous dataset Cora. The vertical axis represents the percentage increase in the other models compared to the RGCN model for each metric, and the horizontal axis represents each metric: (a) FB15K-237; (b) CORA.
The experimental results showcased in Figure 4 indicate significant enhancements across the five core metrics (MRR, MR, Hit@1, Hit@3, and Hit@10) following the introduction of the optimized attention mechanisms. Notably, the RGCN+FANR model outperformed other variants, demonstrating superior improvements in all metrics. For instance, it achieved a 49.77% improvement in MR on the FB15K-237 dataset compared to the baseline. Given its stellar performance, the FANR attention mechanism was selected for integration into the final LabGraph configuration.
4.3.2. Experiments on Gate Mechanism for Multi-Hop Aggregation
The primary consideration for improvement at the multi-hop neighbor level is the need to consider the influence of multi-hop neighbors on the central node representation. Therefore, the improvement algorithm adds multi-hop neighbor aggregation based on the baseline model RGCN algorithm and uses a gate mechanism to filter valid and noisy information. In the first experiment, the RGCN baseline model was reproduced, and the performance of the RGCN model was verified on five core observables, such as MR, MRR, Hit@1, and Hit@3. The second experiment was the RGCN+Multi-Hop experiment, in which two-hop node information was added to the RGCN model convergence process. We stored the second-hop neighbor nodes of each node in the graph data before implementing the code and then optimized the algorithm based on the RGCN model code. The model parameters were kept consistent with the above RGCN replication experiments. Finally, the model converged to the best result after 279 epochs. The third experiment was the RGCN+Multi-Hop+Gate experiment. The gate mechanism was implemented using AliNet, as developed by [30], where the code was implemented by adding a gate mechanism on top of the RGCN+Multi-Hop experiment code. The model parameters were kept consistent with the RGCN replication experiment. Finally, the model converged to the best result after 357 epochs. Figure 5 shows the experimental results of the three model schemes, namely RGCN, RGCN+Multi-Hop, and RGCN+Multi-Hop+Gate.
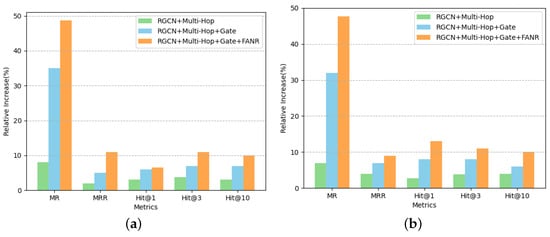
Figure 5.
Comparison of core metrics results of graph characterization methods based on multi-hop neighbor aggregation as well as gate mechanism on FB15k-237 and Cora datasets. The vertical axis represents the percentage increase in the other models compared to the RGCN model for each metric, and the horizontal axis represents each metric. (a) FB15K-237; (b) CORA.
In Figure 5, the metrics on the vertical axis are the percentage magnitude of improvement in the optimized model relative to the baseline model RGCN on each observed metric. Based on the analysis of the experimental results in Figure 5, it can be inferred that after adding the Multi-Hop mechanism to the RGCN, the new model improved the MR core metrics significantly, with a maximum increase of 31.83%, and slightly improved the four observed metrics of MRR, Hit@1, Hit@3, and Hit@10. After adding the Multi-Hop+Gate mechanism to the RGCN model, the new model showed significant improvements in all five core observables of MR, MRR, Hit@1, Hit@3, and Hit@10, and the average increase in each indicator could reach 12.35% on the FB15k-237 dataset. The above analysis demonstrates that the gate mechanism introduced in this paper can effectively filter out the noise information of neighbor nodes and retain the adequate feature information of key neighbor nodes. The one-hop and multi-hop level fusion model is a fusion of the attention mechanism, multi-hop information aggregation, and gate mechanism. LabGraph is implemented by treating one-hop and two-hop equally, using the FANR mechanism when converging towards the central node and then using the gate mechanism to filter the noisy nodes. The prediction results of the LabGraph model were obtained after fusing the improved one-hop neighbor-level algorithm and the improved multi-hop neighbor-level algorithm. It was found that LabGraph significantly improved MRR, MR, Hit@1, Hit@3, and Hit@10 core metrics, thus achieving the best results so far, which proves that the fusion of the two algorithms has a significant effect on optimization.
5. Conclusions and Future Work
In this study, we reconceived the encoding and classification of electronic health records (EHRs) as the construction of adversarial hierarchical label graphs. Our study proposes an adversarial migration-based labeled graph generation network (LabGraph) that includes not only MHR-CNN and Fat-RGCN modules to capture various medical text patterns but also a message integration module (MIM) to encode the connection between electronic health records (EHRs). Experimental findings on the MIMIC-III benchmark dataset demonstrate that LabGraph greatly outperforms numerous comparable baseline models and achieves the highest performance to date.
LabGraph provides the best classification results on the MIMIC-III dataset. However, LabGraph utilizes a restricted number of tuning methods, and the hyperparameters employed thus far may not exhibit the optimal performance on the MIMIC-III dataset. Solutions to knowledge graph pretraining models have been established one after another over the past several years, partly because of Bert’s study [31], revealing significant findings for natural language processing. For instance, the GCC [32] and GPT-GNN [33] have produced specific outcomes but are not as generalizable as the Bert model. If a graph pretraining model like the Bert model is suggested, generalizable graph representation will no longer be a problem. In conclusion, we plan to enhance the performance of the LabGraph model by researching the use of prior knowledge, automatic hyperparameter tweaking, an enhanced loss function, and an optimized graph representation strategy in the next phase.
Author Contributions
Conceptualization, P.N.; data curation, H.W.; funding acquisition, Z.C.; investigation, H.W.; methodology, P.N.; supervision, Z.C.; writing—original draft preparation, P.N.; writing—review and editing, P.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Development Fund of Macau under Grant 0052/2020/AFJ and Grant 0059/2020/A2, in part by Zhuhai Industry–University–Research Collaboration Program (ZH22017002210011PWC).
Data Availability Statement
The data are derived from public domain resources.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nadathur, S.G. Maximising the value of hospital administrative datasets. Aust. Health Rev. 2010, 34, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Mullenbach, J.; Wiegreffe, S.; Duke, J.; Sun, J.; Eisenstein, J. Explainable Prediction of Medical Codes from Clinical Text. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), New Orleans, LA, USA, 1–6 June 2018; pp. 1101–1111. [Google Scholar] [CrossRef]
- Cao, P.; Chen, Y.; Liu, K.; Zhao, J.; Liu, S.; Chong, W. HyperCore: Hyperbolic and Co-graph Representation for Automatic ICD Coding. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 3105–3114. [Google Scholar] [CrossRef]
- Xie, P.; Xing, E. A Neural Architecture for Automated ICD Coding. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Melbourne, Australia, 15–20 July 2018; pp. 1066–1076. [Google Scholar] [CrossRef]
- Wang, S.; Ren, P.; Chen, Z.; Ren, Z.; Nie, J.Y.; Ma, J.; de Rijke, M. Coding Electronic Health Records with Adversarial Reinforcement Path Generation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 July 2020; pp. 801–810. [Google Scholar]
- Vu, T.; Nguyen, D.Q.; Nguyen, A. A Label Attention Model for ICD Coding from Clinical Text. arXiv 2020, arXiv:2007.06351. [Google Scholar]
- Ji, S.; Cambria, E.; Marttinen, P. Dilated Convolutional Attention Network for Medical Code Assignment from Clinical Text. arXiv 2020, arXiv:2009.14578. [Google Scholar]
- Auer, S.; Bizer, C.; Kobilarov, G.; Lehmann, J.; Cyganiak, R.; Ives, Z. Dbpedia: A nucleus for a web of open data. In The Semantic Web; Springer: Berlin/Heidelberg, Germany, 2007; pp. 722–735. [Google Scholar]
- Song, Y.H.; Kwon, S.B.; Jung, M.K.; Park, W.K.; Yoo, J.H.; Lee, C.W.; Kang, B.K.; Yang, W.S.; Yoon, D.H. Fabrication design for a high-quality laser diode-based ceramic converter for a laser headlamp application. Ceram. Int. 2018, 44, 1182–1186. [Google Scholar] [CrossRef]
- Färber, M.; Bartscherer, F.; Menne, C.; Rettinger, A. Linked data quality of dbpedia, freebase, opencyc, wikidata, and yago. Semant. Web 2018, 9, 77–129. [Google Scholar] [CrossRef]
- Johnson, A.E.; Pollard, T.J.; Shen, L.; Li-Wei, H.L.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Celi, L.A.; Mark, R.G. MIMIC-III, a freely accessible critical care database. Sci. Data 2016, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. Syst. 2013, 26, 3111–3119. [Google Scholar]
- Kim, Y. Convolutional Neural Networks for Sentence Classification. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, EMNLP 2014, Doha, Qatar, 25–29 October 2014; Doha, Qatar, A meeting of SIGDAT, a Special Interest Group of the ACL. Moschitti, A., Pang, B., Daelemans, W., Eds.; ACL: Kerrville, TX, USA, 2014; pp. 1746–1751. [Google Scholar] [CrossRef]
- Bennett, C.C.; Hauser, K. Artificial intelligence framework for simulating clinical decision-making: A Markov decision process approach. Artif. Intell. Med. 2013, 57, 9–19. [Google Scholar] [CrossRef]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Zhao, T. Smart: Robust and efficient fine-tuning for pre-trained natural language models through principled regularized optimization. arXiv 2019, arXiv:1911.03437. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the European Semantic Web Conference, Crete, Greece, 3–7 June 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 593–607. [Google Scholar]
- Chah, N. Freebase-triples: A methodology for processing the freebase data dumps. arXiv 2017, arXiv:1712.08707. [Google Scholar]
- Stephany, F.; Braesemann, F. An exploration of wikipedia data as a measure of regional knowledge distribution. In Proceedings of the International Conference on Social Informatics, Oxford, UK, 13–15 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 31–40. [Google Scholar]
- Wang, Z.; Li, X. Hybrid-TE: Hybrid translation-based temporal knowledge graph embedding. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; IEEE: New York, NY, USA, 2019; pp. 1446–1451. [Google Scholar]
- Perotte, A.; Pivovarov, R.; Natarajan, K.; Weiskopf, N.; Wood, F.; Elhadad, N. Diagnosis code assignment: Models and evaluation metrics. J. Am. Med. Informatics Assoc. 2014, 21, 231–237. [Google Scholar] [CrossRef]
- Prakash, A.; Zhao, S.; Hasan, S.A.; Datla, V.; Lee, K.; Qadir, A.; Liu, J.; Farri, O. Condensed memory networks for clinical diagnostic inferencing. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Shi, H.; Xie, P.; Hu, Z.; Zhang, M.; Xing, E.P. Towards automated ICD coding using deep learning. arXiv 2017, arXiv:1711.04075. [Google Scholar]
- Zhou, P.; Shi, W.; Tian, J.; Qi, Z.; Li, B.; Hao, H.; Xu, B. Attention-based bidirectional long short-term memory networks for relation classification. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), Berlin, Germany, 7–12 August 2016; pp. 207–212. [Google Scholar]
- Baumel, T.; Nassour-Kassis, J.; Cohen, R.; Elhadad, M.; Elhadad, N. Multi-label classification of patient notes: Case study on ICD code assignment. In Proceedings of the Workshops at the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zhou, T.; Cao, P.; Chen, Y.; Liu, K.; Zhao, J.; Niu, K.; Chong, W.; Liu, S. Automatic icd coding via interactive shared representation networks with self-distillation mechanism. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Virtual, 1–6 August 2021; pp. 5948–5957. [Google Scholar]
- Yuan, Z.; Tan, C.; Huang, S. Code Synonyms Do Matter: Multiple Synonyms Matching Network for Automatic ICD Coding. arXiv 2022, arXiv:2203.01515. [Google Scholar]
- Luo, J.; Xiao, C.; Glass, L.; Sun, J.; Ma, F. Fusion: Towards Automated ICD Coding via Feature Compression. In Proceedings of the Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021, Virtual, 1–6 August 2021; pp. 2096–2101. [Google Scholar]
- Sun, Z.; Wang, C.; Hu, W.; Chen, M.; Dai, J.; Zhang, W.; Qu, Y. Knowledge graph alignment network with gated multi-hop neighborhood aggregation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 222–229. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Qiu, J.; Chen, Q.; Dong, Y.; Zhang, J.; Yang, H.; Ding, M.; Wang, K.; Tang, J. Gcc: Graph contrastive coding for graph neural network pre-training. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, San Diego, CA, USA, 23–27 August 2020; pp. 1150–1160. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Chang, K.W.; Sun, Y. Gpt-gnn: Generative pre-training of graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, San Diego, CA, USA, 23–27 August 2020; pp. 1857–1867. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).