Abstract
The design of chaotic systems with complex dynamic behaviors has always been a key aspect of chaos theory in engineering applications. This study introduces a novel fractional-order system characterized by hidden dynamics, hyperchaotic behavior, and multi-scroll attractors. By employing fractional calculus, the system’s order is extended beyond integer values, providing a richer dynamic behavior. The system’s hidden dynamics are revealed through detailed numerical simulations and theoretical analysis, demonstrating complex attractors and bifurcations. The hyperchaotic nature of the system is verified through Lyapunov exponents and phase portraits, showing multiple positive exponents that indicate a higher degree of unpredictability and complexity. Additionally, the system’s multi-scroll attractors are analyzed, showcasing their potential for secure communication and encryption applications. The fractional-order approach enhances the system’s flexibility and adaptability, making it suitable for a wide range of practical uses, including secure data transmission, image encryption, and complex signal processing. Finally, based on the proposed fractional-order system, we designed a simple and efficient medical image encryption scheme and analyzed its security performance. Experimental results validate the theoretical findings, confirming the system’s robustness and effectiveness in generating complex chaotic behaviors.
MSC:
34H10
1. Introduction
In recent years, with the rapid development of science and technology, chaos theory, as an important branch of nonlinear dynamic systems, has shown its unique value and broad application prospects in multiple fields. The complexity and randomness of chaotic systems make them demonstrate unparalleled advantages in simulating and predicting natural and social phenomena. Chaotic systems have been used in the past for neural networks [1,2,3,4,5,6,7,8,9], image encryption [10,11,12,13,14,15], secure communication [16,17], control synchronization [18,19,20], circuit systems [21,22,23,24], and pseudorandom number generator [25,26,27].
Memristors, as a fundamental nonlinear electronic component, have attracted widespread attention in the scientific community due to their unique characteristics in recent years. Memristors with memory resistance characteristics can change their resistance value based on the amount of charge passing through them, thus demonstrating enormous potential in fields such as circuit design, neural network simulation, and nonlinear dynamics research. Yu et al. extended the system dimension, added control parameters and memristors, and proposed a five dimensional (5D) memristive hyperchaotic system with hidden attractors [28]. Muthuswamy et al. proposed a memristor chaotic circuit, marking the beginning of the application of memristors in chaotic systems. This design demonstrates how memristors can increase dynamic complexity while maintaining low power consumption and scalability of the system [29]. Hu et al. proposed a 5D memristor chaotic system and introduced a quadratic nonlinear memristor model, opening up a new way to study the dynamic characteristics of memristor chaotic systems [30]. Wang et al. proposed a 4D four-wing memristor chaotic system, which achieved rich dynamic phenomena such as single-wing period and chaotic behavior by introducing memristors as feedback terms [31]. Gu et al. proposed a hyperbolic function memristor chaotic system, which demonstrates a new direction in the design of memristor chaotic systems, particularly in the study of conditional symmetry and attractor growth [32]. Wan et al. proposed a new five-dimensional memristive hyperchaotic system without equilibrium points by introducing an ideal flux-controlled memristor model and two constant terms into a 4D hyperchaotic system [33]. Reference [34] proposes a 4D chaotic system by introducing a memristor into a hybrid system, which exhibits rich dynamic behavior and five spectral equilibrium points with different stability. In summary, the memristors can make dynamical systems produce more complex dynamical behaviors.
Most physical phenomena in nature exist in the form of fractional-orders, and integer-order differential equations happen to be a special case of fractional-order differential equations. Compared with integer-order models, fractional-order models are closer to the real world and have more attractive development prospects. In recent years, they have received increased attention and are worth noting. Fractional-order chaotic system is a dynamic model based on fractional calculus, which describes a class of chaotic systems with non-integer order derivatives or integrals. Fractional calculus and memristors can introduce additional complexity and nonlinear characteristics into chaotic systems, which can make the system’s behavior more diverse and improve its stability and robustness, as well as expand its application scenarios. Ref. [35] proposed a fractional-order delayed memristive chaotic system and studied the rich dynamic characteristics of the designed fractional-order delayed memristive circuit through numerical simulation. It was found that although the fractional-order delayed memristive system does not have an equilibrium point, it can generate chaotic attractors. Ref. [36] introduces fractional calculus into a the simplest memristive circuit and constructs a new 4D fractional memristive chaotic system. The initial values of the system can better control the offset, amplitude, and frequency of the attractor, increasing the complexity and randomness of the chaotic sequence. Ref. [37] combines ideal flux-controlled memristors with fractional calculus theory and proposes a new fractional-order memristor model. In addition, a new fractional-order memristive hyperchaotic system was obtained by introducing a fractional-order memristor into a 4D chaotic system and solved using the Adomian decomposition method. In Refs. [38,39,40], the circuits implementation were completed based on the fractional-order chaotic systems. However, in the existing fractional-order chaotic systems, multi-scroll attractors are rarely studied.
A multi-scroll memristive chaotic system is a type of chaotic system with memory characteristics and multi-scroll structure, which has rich dynamic behavior and broad application prospects. In addition to multi-scroll attractors, researchers have also constructed other types of attractors, such as multi-wing attractors [41,42,43,44] and hidden attractors [45,46,47,48]. The interaction between nonlinear components and multi-scroll structures in the system forms complex nonlinear dynamic behaviors. These nonlinear characteristics lead to the chaotic nature of the system, resulting in unpredictable and complex behavior. Lin et al. proposed a universal design method called the Universal Variable Expansion Method (UVEM). This is a simple and effective method for generating one-dimensional and two-dimensional multi-scroll or multi-wing chaotic attractors [49]. Lai et al. established a new flow control memristor model using a hyperbolic function series. By using memristors as synapses in Hopfield neural networks (HNNs), three memristor HNNs were constructed. These memristive HNNs can generate multiple dual scroll chaotic attractors [50]. Wang et al. constructed a new noninductive Chua circuit using Chua diodes and second-order active Sallen Key high pass filters to generate multi-scroll chaotic attractors [51]. Yu et al. transformed the fourth-order memristor using piecewise nonlinear functions and introduced it into a ternary HNN with self-feedback, constructing a piecewise fourth-order memristor chaotic neural network model with multiple scroll [52]. In the fields of secure communication and image encryption, multi-scroll fractional-order chaotic systems have higher sequence complexity and larger key space, which improves system security performance. Therefore, discovering and constructing fractional-order chaotic systems with coexistence of multi-scroll chaotic attractors has greater value. However, fractional-order chaotic systems with multiple-scroll structure, hyperchaotic characteristics, and hidden dynamics have not yet been proposed.
Based on the above research background, a novel fractional-order system with hidden dynamics, hyperchaotic behavior, and multi-scroll attractors is designed in this paper. In the second section, the fractional-order system is proposed and its equilibrium characteristics is analyzed. In the third section, we mainly analyze the phase plots, bifurcation diagram, and Lyapunov exponents of the proposed fractional-order system. Furthermore, the existence of coexisting behavior is analyzed. In the fourth section, the hidden hyperchaotic multi-scroll fractional-order system is implemented on FPGA platform. In the fifth section, the application of the fractional-order system in chaotic medical image encryption is presented. Finally, some work in the paper is summarized.
2. Hidden Hyperchaotic Multi-Scroll Fractional-Order System
2.1. Design of System Model
In 2023, Yan et al. proposed a 4D multi-scroll hyperchaotic system [53]. The authors demonstrated that the system exhibits rich dynamic behavior by studying the stability of its equilibrium point, dissipative attractor, Lyapunov exponent spectrum, and bifurcation diagram. The system’s equations can be described as follows
This system exhibits rich dynamic characteristics, including multi-scroll chaotic attractors. We propose a 5D multi-scroll FOMHS with hidden attractors by introducing memristors and fractional-orders into the system and increasing the dimensionality of the system. The mathematical model is as follows
Among them, are the parameters of the chaotic system, and , and g are the control parameters of the system. As a positive parameter, k represents the strength of the memristor. is the memristor function, defined as
is a nonlinear function defined as
The sign function returns based on the input value. If the input is positive, it returns 1. If it is negative, it returns −1. If it is 0, it returns 0 directly. Figure 1 shows the relationship between function and x.
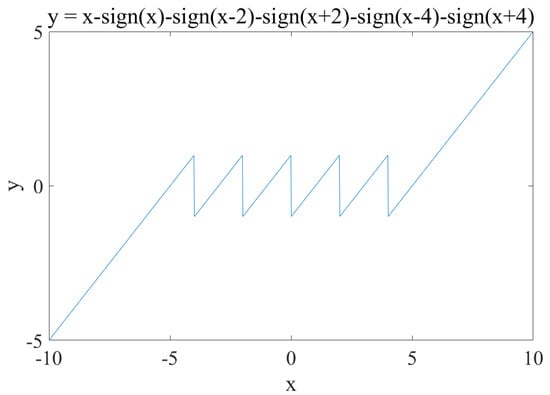
Figure 1.
The relationship between function and x.
The system exhibits rich dynamic characteristics, including phenomena such as multi-scroll attractors, coexistence of attractors, and bifurcation coexistence. When the control parameters of the system are set to , , , , , , , and , with initial conditions as and order , the phase diagram of the system about the plane, plane, plane, and plane is drawn on MATLAB R2019b, as shown in Figure 2, Figure 3, Figure 4 and Figure 5. Six-scrolls chaotic attractors appear in the plane.
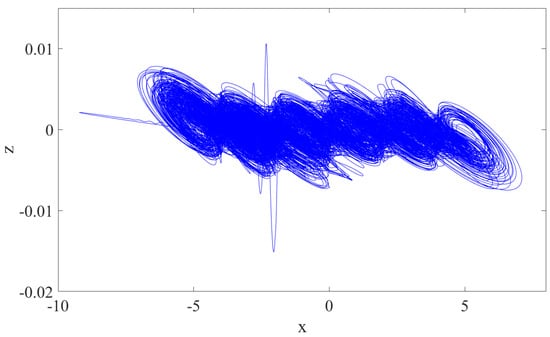
Figure 2.
plane diagram of the system.
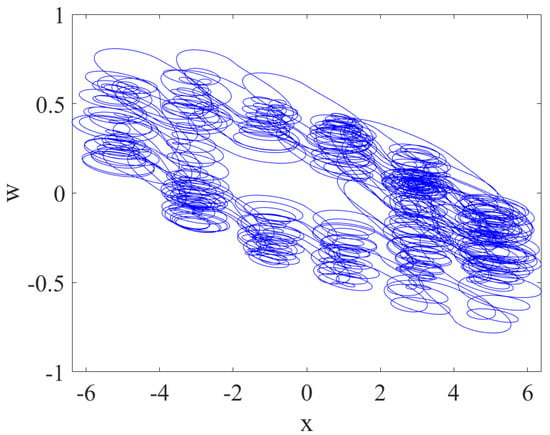
Figure 3.
plane diagram of the system.
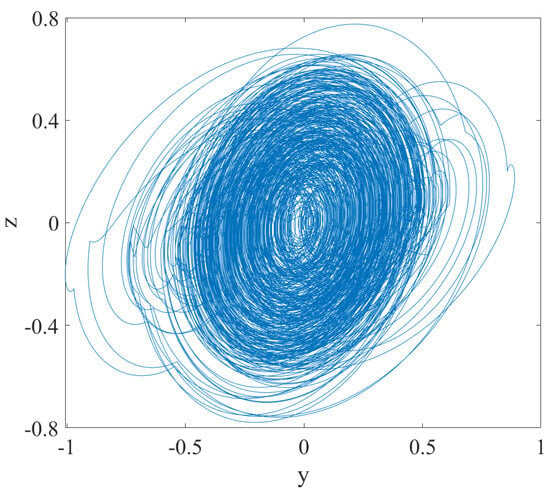
Figure 4.
plane diagram of the system.
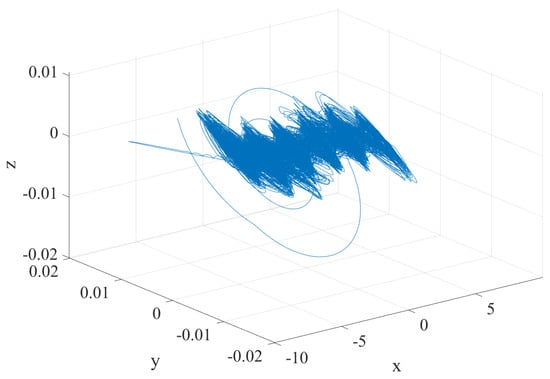
Figure 5.
space diagram of the system.
2.2. Equilibrium Point Analysis
The equilibrium point refers to the state where the interaction between various parts of the system reaches equilibrium, meaning that the system is no longer undergoing changes. The study of equilibrium points plays a significant role in the properties of chaotic systems. Once the equilibrium point is found, we can use it to control the system. The equilibrium point is the point where all state derivatives are 0, so that the left side of Equation (2) is equal to 0, resulting in the following equation
After calculation, Equation (5) has infinite solutions, the equilibrium points , where R can be any number, so the system has a hidden attractor. Hidden attractors have only recently been defined, and chaotic systems with hidden attractors generally have more complex dynamic characteristics compared to other systems, which can help people understand and control the operational behavior of the system. The Jacobian matrix of the system at equilibrium point E can be obtained by linearizing Equation (5).
By solving , the characteristic equation of the system can be obtained as follows
The corresponding eigenroot can be solved as , it can be seen that the stability of the parameters of the system are set to and , with initial conditions set as [0.12, 0.27, 0.92, 0.56, 0.1] and order . In order to examine the stability of the system, we selected five special equilibrium points: and , calculated the Jacobian matrix corresponding to these five equilibrium points, and calculated their eigenvalues. The relevant results are shown in Table 1. From Table 1, it can be seen that the five eigenvalues of system (2) are all real numbers, where is a positive real root and is a negative real root. Therefore, these five equilibrium points are unstable saddle points with index-1.

Table 1.
Eigenvalues corresponding to equilibrium points.
2.3. Adomian Decomposition
The dynamic behavior of fractional-order chaotic systems is usually described by fractional-order differential equations. Fractional-order differential equations include fractional-order ordinary differential equations, fractional-order partial differential equations, etc. The Caputo differential equation is a variant of ordinary differential equations that uses Caputo derivatives, which were introduced by Italian mathematician Michel Caputo in the 1960s. Unlike traditional derivatives, Caputo derivatives can handle nonsmooth initial conditions, making them particularly useful in describing dynamic systems with fractional-order damping or memory effects. The Caputo differential equation is defined as
where is a caputo differential operator of order q. is the gamma function.
Fractional-order chaotic systems can be represented as
Among them, is the linear part, is the nonlinear part, and is the constant part, according to the Adomian decomposition method, nonlinear terms of the system can be represented as Equation (10)
The solution of can be expressed as
The Adomian decomposition method is a method of gradually solving unknown functions by representing them as infinite series and then iteratively solving them. This method first transforms the fractional differential equation into an infinite series form, and then gradually approximates the solution form by solving a recursive relationship. The Adomian decomposition method is simple and intuitive, suitable for different types of fractional differential equations.
3. Dynamics Analysis
3.1. Phase Analysis
Under the influence of initial conditions, for a given parameter, the system may eventually stabilize in one or more states, which is called the phenomenon of attractor coexistence. The proposed 5D multi-scroll FOMHS exhibits the coexistence of attractors. The system parameters are fixed at and ; the system order q is 0.9; and the number of simulations is 100,000. Set the initial conditions to and , respectively. The phase diagram of the plane and the appearance of the space of the system are different states, as shown in Figure 6 and Figure 7. The red line represents the phase diagram of the system under initial conditions of , and the blue line represents the phase diagram of the system under initial conditions of .
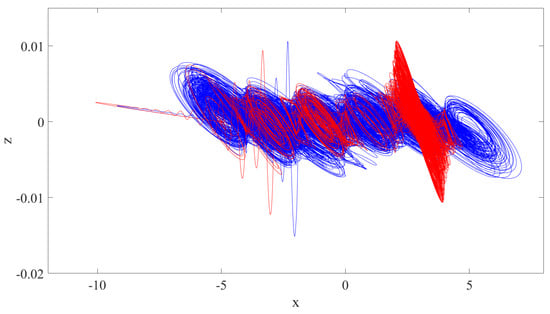
Figure 6.
Coexistence of attractors on the plane of the system. The red line represents the phase diagram of the system under initial conditions of , and the blue line represents the phase diagram of the system under initial conditions of .
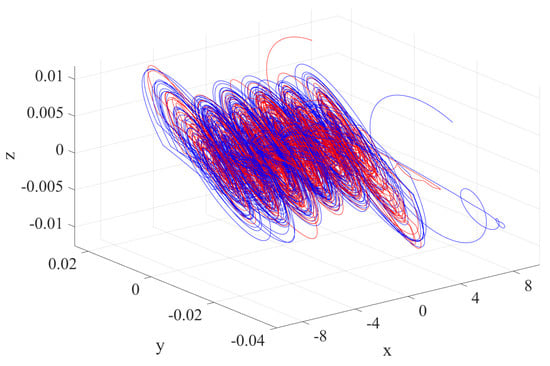
Figure 7.
Coexistence of attractors on the space of the system. The red line represents the phase diagram of the system under initial conditions of , and the blue line represents the phase diagram of the system under initial conditions of .
3.2. Lyapunov Exponents Analysis
Lyapunov exponent is an important quantitative indicator in chaotic systems. By calculating the Lyapunov exponent of a chaotic system, the chaotic characteristics of the system can be determined. Through images, it can be visually seen whether a system is a chaotic system or a hyperchaotic system. Set the control parameters of the system to and , with initial values of , step size of 0.001, and obtain the Lyapunov exponent spectrum of order q using MATLAB simulation tools, as shown in Figure 8. From the graph, it can be seen that when the order q is at , there are always two Lyapunov exponent and greater than 0 in the exponential spectrum, and the system is always in a hyperchaotic state. Furthermore, when the order q is within a certain range, the system has three positive Lyapunov exponents. For this, a Lyapunov exponent spectrum with a smaller range of q values was plotted, as shown in Figure 9. From Figure 9, it can be seen that when the order q is at , the system has three positive Lyapunov exponents. When describing a chaotic system, having three positive Lyapunov exponents can emphasize that the system has strong chaotic characteristics, and its dynamic behavior is highly uncertain and difficult to predict.
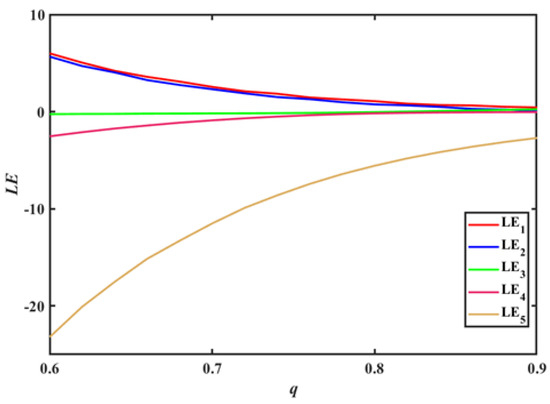
Figure 8.
Lyapunov exponent spectrum of order q.
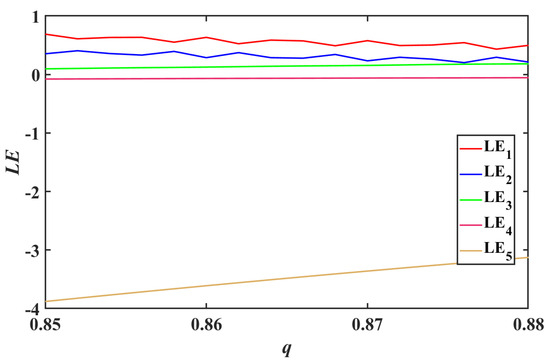
Figure 9.
Lyapunov exponent spectrum with a smaller range of q values.
Furthermore, the Lyapunov exponent spectrum regarding parameter a was plotted, as shown in Figure 10. From the graph, there were two Lyapunov exponents and greater than 0 in the system, and the system remained in a hyperchaotic state. In addition, when , , , , , , and , the third Lyapunov exponent is greater than 0 and greater than the fourth Lyapunov exponent , so the system has three positive Lyapunov exponents. For a 5D chaotic system, having three positive Lyapunov exponents means that the sensitivity of the system to initial conditions in three directions is exponentially increasing, indicating the high complexity and chaotic properties of the system. In this case, the behavior of the system will be more difficult to predict, as small disturbances may cause rapid separation between system trajectories, making long-term behavior difficult to predict.
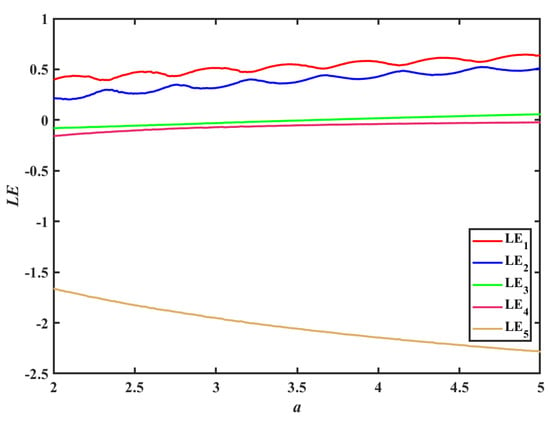
Figure 10.
The Lyapunov exponent spectrum of the system regarding parameter a.
3.3. Bifurcation Analysis
The bifurcation diagram of a chaotic system is a chart that describes the bifurcation phenomenon that occurs when the system parameters change. In a bifurcation diagram, a certain state of the system (usually an equilibrium point or period) exhibits different branching or periodic changes with the variation of parameters. The parameters of the system were set to and . The bifurcation diagram of a fractional-order chaotic system with initial conditions of was plotted with respect to order q, as shown in Figure 11. Based on the Lyapunov exponent spectrum of order q, it can be concluded that when the range of q is , the system remains in a hyperchaotic state and exhibits good chaotic characteristics.
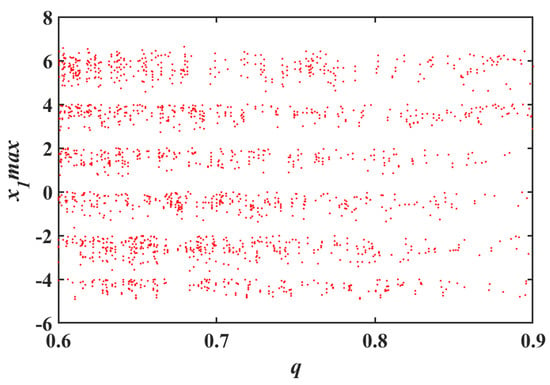
Figure 11.
The bifurcation diagram of the system with respect to order q.
When a chaotic system has bifurcations, it is common to observe the coexistence of bifurcations. This means that there are multiple different bifurcation points or periods coexisting in the parameter space of the system. In this case, the system may exhibit multiple stable states or periodic trajectories near a certain parameter value, and these states may have different bifurcation types between them. Figure 12 shows the bifurcation coexistence diagram of a fractional-order chaotic system with respect to order q. The blue line represents the bifurcation diagram with initial values of , while the red line represents the bifurcation diagram with initial conditions of . Bifurcation coexistence is a very important phenomenon in chaotic systems, which reflects the complex dynamic behavior of the system under different parameter conditions. The understanding of this phenomenon is of great significance for studying the behavior of chaotic systems and predicting their behavior.
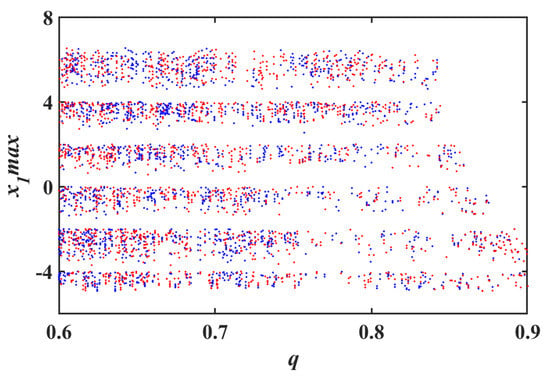
Figure 12.
Bifurcation coexistence of system with respect to order q. The blue line represents the bifurcation diagram with initial values of , while the red line represents the bifurcation diagram with initial conditions of .
In addition, when the system parameters were set to , order , and the initial conditions were set to , step size was set to 0.001, and simulation times were 20,000, we plotted a bifurcation diagram about parameter a, as shown in Figure 13. From the graph, it can be seen that the system has always been in a chaotic state, and combined with the Lyapunov exponent spectrum of the system with respect to parameter a, it can be inferred that when the range of a is , the chaotic system remains in a hyperchaotic state.
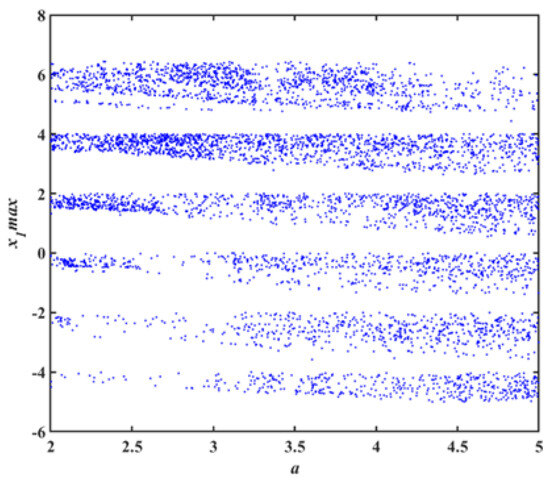
Figure 13.
The bifurcation diagram of the system regarding parameter a.
4. Hardware Implementation
The hardware implementation of fractional-order chaotic systems on FPGA mainly involves the following processes:
(1) System modeling and discretization: Firstly, based on the selected 5D multi-scroll FOMHS model, the fractional differential equation or difference equation of the system is discretized to adapt to the digital computing environment of FPGA. This may involve selecting appropriate numerical solution methods and discretization techniques, and the Adomian decomposition method is used in this paper.
(2) Hardware Description Language Writing: Use the hardware description language Verilog to write model code for fractional-order chaotic systems. When writing code, it is necessary to convert the discretized system equations into digital circuit implementations suitable for FPGA execution.
(3) Numerical Calculation Module Design: Design and implement a module for performing numerical calculations on an FPGA. This paper adopts the high-precision fourth-order Runge–Kutta method (RK4), which involves designing numerical calculation algorithms suitable for hardware execution. This article uses the RK4 method to numerically simulate 5D multi-scroll FOMHS on FPGA. The mathematical equations of the numerical algorithm are as follows
where is the step size of each iteration, , and represent the slope of the iteration at four points of the five initial states. During the iteration process, provides data to the system, and obtains data to provide data for the next iteration [11].
(4) Floating-point operation IP core selection: Select and integrate appropriate floating-point operation IP cores to support floating-point operation on FPGA. These IP cores can be used to perform floating-point addition, subtraction, multiplication, division, and other operations. The standard for floating-point numbers used in this paper is IEEE 754.
(5) System parameter setting: Set the system parameters and initial conditions based on the selected fractional-order chaotic system model. Here, the system parameters are set to and , and the system order q is 0.9.
(6) FPGA development environment configuration: Use FPGA development tools (Vivado 2018.3) to configure the development environment, including selecting target FPGA chips, designing constraint files, setting clocks, etc.
Figure 14 shows the plane phase diagram of the 5D multi-scroll FOMHS on an oscilloscope, and Figure 15 shows the FPGA experimental equipment diagram. Table 2 shows the system resource utilization statistics of the system implemented on the XC7Z0202CLG400I FPGA chip. The FPGA experimental results are consistent with the MATLAB simulation, proving the correctness of using FPGA to implement chaotic systems.

Figure 14.
The plane phase diagram of the system on the oscilloscope.

Figure 15.
FPGA experimental equipment.

Table 2.
System resource utilization rate.
5. Application in Medical Image Encryption
In recent years, digital image processing technology has been widely applied in fields such as intelligent transportation, facial recognition, biomedical, and object recognition [54,55,56,57,58]. When digital images are transmitted through public channels, they are easily obtained through illegal eavesdropping, resulting in the leakage of confidential information. Image encryption hides visual information through certain operations to ensure information security, preventing illegal users from obtaining image content. The receiver can obtain the entire content of the image through the decryption key, which is one of the most commonly used ways to protect image security. Chaotic systems have complex nonlinear dynamic performance, good pseudo-random characteristics, unpredictability of orbits, and extreme sensitivity to initial states and control parameters. Therefore, chaotic systems are widely used in fields such as image encryption and secure communication [10,11,12,13,14,15,16,17].
5.1. Encryption Scheme Design
Medical data is extremely sensitive information. Once data leakage occurs, it will have a serious impact on patient privacy, social stability, and even national security [5,48,52,59,60,61,62]. To avoid data leakage, we provide a simple and efficient solution for medical data encryption.
Assuming that “” is used as the encryption object, the main steps of encryption are as follows:
(1) The initial value of the fractional order hyperchaotic system is set as and , substituted into the chaotic system to iterate out the one-dimensional chaotic sequence, and take a value every 100 points from the initial value of the chaotic sequence. Take a long enough sequence to encrypt the image.
(2) A simple Arnold scrambling algorithm is used to scramble the image. The so-called scrambling is to shuffle the position of each pixel on the image to eliminate the correlation between the adjacent pixels of the original image. Suppose the size of the 2D image is and the original pixel point is , resulting in the pixel . The formula is as follows
where T is the integer transformation matrix, set the scrambling key , matrix , and inverse matrix .
(3) The scrambled image is processed by XOR diffusion. Diffusion processing is to hide the information of plaintext pixels in ciphertext pixels without changing the position of pixels. Xor diffusion also includes two steps: forward diffusion and backward diffusion. The plaintext two-dimensional image is expanded into a one-dimensional vector P, and the cipher vectors are Q and R. The formulas of the forward and inverse algorithms for XOR diffusion are as follows
where . The backward algorithm and the inverse formula are:
Finally, we have the encrypted image, and decryption is the reverse process of image encryption, the overall flow chart is shown in Figure 16.
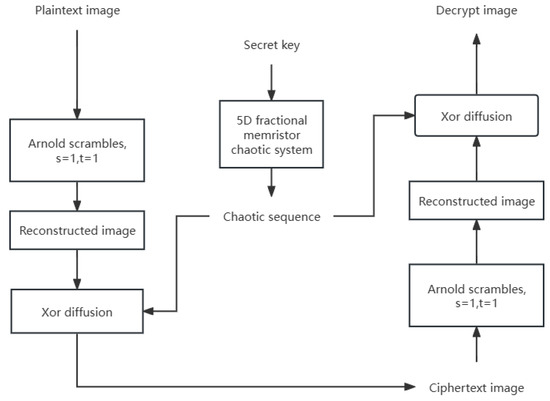
Figure 16.
Design of image encryption scheme.
5.2. Security Analysis
5.2.1. Histogram
After the encryption algorithm in this paper, as shown in Figure 17, the plaintext image, encrypted image, and decrypted image of the medical picture are obtained, respectively. The corresponding histograms are shown in Figure 17d–f. It can be seen that the histogram of the encrypted image is evenly distributed and significantly different from the histogram of the original image. The decrypted image histogram can restore the statistical characteristics of the original image well, which means that the encryption application of fractional order hyperchaotic model has strong anti-attack ability.
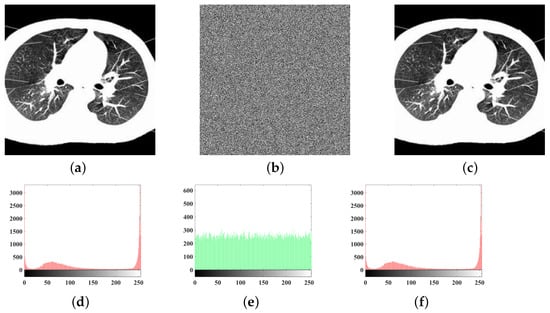
Figure 17.
Image encryption and decryption results and their histograms: (a) Original image. (b) Encrypted image. (c) Decrypted image. (d) Original image histogram. (e) Encrypted Image histogram. (f) Decrypted image histogram.
5.2.2. Correlation
The correlation of image pixels describes the relationship between two pixels in an image and is formulated as:
where and denote the positions of the corresponding pixels in the two images, respectively. The results of calculating the correlation coefficients in horizontal, vertical, and diagonal directions are recorded in Table 3 and shown in Figure 18. Obviously, the correlation coefficients of plaintext images are close to 1 in both horizontal and vertical diagonal directions, which indicates a strong correlation. The correlation coefficients of the ciphertext image in these directions are close to 0, and its adjacent pixels have little correlation. Compared with refs. [63,64,65] as shown in Table 3. The results show that the algorithm has better encryption effect.

Table 3.
Correlation coefficient between encrypted and decrypted images.
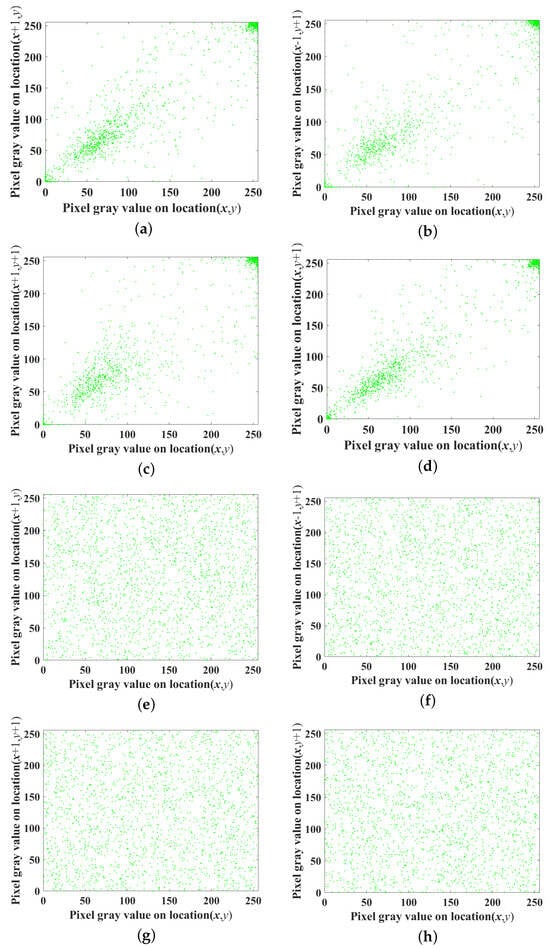
Figure 18.
Correlation analysis between the original image and the encrypted image, (a–d) is the correlation map of the original image, and (e–h) is the correlation coefficient map of the encrypted image: (a) Horizontal. (b) Negative diagonal. (c) Positive diagonal. (d) Vertical. (e) Horizontal. (f) Negative diagonal. (g) Positive diagonal. (h) Vertical.
5.2.3. Running Time
Security is the primary consideration of image encryption, followed by performance and efficiency. A good encryption and decryption algorithm should be both secure and efficient. We test the speed of the encryption and decryption process, and the data is given in Table 4. Through the test of the algorithm, it is found that the encryption and decryption time is about 0.18 s, and the running speed of the encryption and decryption algorithm is fast.

Table 4.
Speed test of encrypted and decrypted images.
5.2.4. Information Entropy
Information entropy can be used to measure the complexity and information content of an image. If the information entropy of the encrypted image is close to the ideal value of 8, it means that the randomness of the sequenced column is better, and the encryption security is higher. The information entropy formula is
where represents the probability of each gray level. As shown in Table 5, the information entropy of our encrypted image is 7.9968, which is closer to the ideal value of 8 than other works.

Table 5.
Information entropy comparison.
6. Conclusions
The purpose of this work is to design a hidden hyperchaotic multi-scroll fractional-order system. According to the dynamic characteristics of the memristor, a novel five-dimensional memristive fractional-order system based on the memristor is constructed in this paper. By analyzing the equilibrium points, phase diagram, Lyapunov exponent, and bifurcation diagram of the fractional-order system, it is proved that the fractional-order system based on a memristor has complex dynamical characteristics, such as hidden dynamics, hyperchaotic behavior, multi-scroll attractors, and coexisting behaviors. Moreover, FPGA implementation is carried out to demonstrate the effectiveness and feasibility of the proposed method. The experimental results further prove the theoretical analysis and numerical simulation results. Finally, a medical image encryption algorithm based on the proposed fractional-order system is designed in this paper. The simulation results show that the medical image scheme based on hidden hyperchaotic multi-scroll attractors has better security performance. This work significantly contributes to the field of chaotic systems, offering new insights and tools for designing advanced chaotic models with enhanced performance and security features.
In the future, we will apply fractional-order chaotic systems to the field of information security, such as developing fractional-order chaotic encryption algorithms or authentication protocols, to improve information security and resist cryptographic attacks. We will also study the synchronization phenomenon between fractional-order chaotic systems and how to use fractional-order chaotic synchronization to design new communication systems for reliable data transmission and information exchange.
Author Contributions
F.Y.: Conceptualization (equal); Investigation (equal); Methodology (equal); Project administration (equal); Software (equal); Validation (equal); Visualization (equal); and Writing—review and editing (equal). S.X.: Conceptualization (lead); Data curation (equal); Formal analysis (lead); Investigation (equal); Methodology (equal); and Writing—original draft (lead). Y.L.: Methodology (equal); Software (equal); Validation (equal); and Visualization (equal). T.H.: Investigation (equal); Validation (equal); and Visualization (equal). C.W.: Supervision (equal); Validation (equal); and Visualization (equal). H.L.: Project administration (equal); Software (equal); Supervision (equal); Validation (equal); and Visualization (equal). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Postgraduate Scientific Research Innovation Project of Changsha University of Science and Technology (CSLGCX23091); the National Natural Science Foundation of China (62201204); the Natural Science Foundation of Hunan Province (2023JJ40168, 2022JJ30624, 2022JJ10052, 2021JJ30741); and the Postgraduate Training Innovation Base Construction Project of Hunan Province (2020-172-48).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
Thank you to the editors for organizing and optimizing the structure and language of the paper. Sincere thanks to the reviewers for their strict requirements on the quality of the paper and suggestions for further improvement.
Conflicts of Interest
The authors have no conflicts to disclose.
References
- Yu, F.; Kong, X.; Mokbel, A.A.M.; Yao, W.; Cai, S. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive Hopfield neural network with a novel local active memeristor. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 326–330. [Google Scholar] [CrossRef]
- Wang, C.; Liang, J.; Deng, Q. Dynamics of heterogeneous Hopfield neural network with adaptive activation function based on memristor. Neural Netw. 2024, 178, 106408. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Kong, X.; Yao, W.; Zhang, J.; Cai, S.; Lin, H.; Jin, J. Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor. Chaos Solitons Fractals 2024, 179, 114440. [Google Scholar] [CrossRef]
- Yao, W.; Liu, J.; Sun, Y.; Zhang, J.; Yu, F.; Cui, L.; Lin, H. Dynamics analysis and image encryption application of Hopfield neural network with a novel multistable and highly tunable memristor. Nonlinear Dyn. 2024, 112, 693–708. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Yu, Q.; Kong, X.; Sharma, P.K.; Cai, S. Privacy protection of medical data based on multi-scroll memristive Hopfield neural network. IEEE Trans. Netw. Sci. Eng. 2023, 10, 845–858. [Google Scholar] [CrossRef]
- Lin, H.; Deng, X.; Yu, F.; Sun, Y. Grid multi-butterfly memristive neural network with three memristive systems: Modeling, dynamic analysis, and application in police IoT. IEEE Internet Things J. 2024. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Liu, P.; Wen, S.; Wang, Y. Memristor-based neural network circuit with multimode generalization and differentiation on pavlov associative memory. IEEE Trans. Cybern. 2022, 53, 3351–3362. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Hong, Q.; Xu, C.; Sun, Y. A triple-memristor Hopfield neural network with space multistructure attractors and space initial-offset behaviors. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2023, 42, 4948–4958. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Zhang, Y. Color-gray multi-image hybrid compression–encryption scheme based on BP neural network and knight tour. IEEE Trans. Cybern. 2023, 53, 3267785. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.; Yu, F.; Yao, W.; Cai, S.; Zhang, J.; Lin, H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: Image encryption and FPGA implementation. Neural Netw. 2024, 171, 85–103. [Google Scholar] [CrossRef]
- Yu, F.; Xu, S.; Xiao, X.; Yao, W.; Huang, Y.; Cai, S.; Li, Y. Dynamics analysis, FPGA realization and image encryption application of a 5D memristive exponential hyperchaotic system. Integration 2023, 90, 58–70. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Lin, H. Chaotic dynamical system of Hopfield neural network influenced by neuron activation threshold and its image encryption. Nonlinear Dyn. 2024, 112, 6629–6646. [Google Scholar] [CrossRef]
- Kong, X.; Yu, F.; Yao, W.; Xu, C.; Zhang, J.; Cai, S.; Wang, C. A class of 2n+1 dimensional simplest hamiltonian conservative chaotic systems and fast image encryption schemes. Appl. Math. Model. 2024, 125, 351–374. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C. Hyper-chaotic image encryption system based on N+2 ring Joseph algorithm and reversible cellular automata. Multimed. Tools Appl. 2023, 82, 38967–38992. [Google Scholar] [CrossRef]
- Wang, M.; Ding, J.; Li, J.; He, S.; Zhang, X.; Iu Herbert, H.-C.; Li, Z. A novel multistable chaotic system with 2 m-scroll attractor and its application. Eur. Phys. J. Plus 2024, 139, 64. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Liu, L.; Shen, H.; Huang, Y.; Shi, C.; Cai, S.; Song, Y.; Du, S.; Xu, Q. Secure communication scheme based on a new 5D multistable four-wing memristive hyperchaotic system with disturbance inputs. Complexity 2020, 2020, 5859273. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Kocamaz, U.E.; Uyaroglu, Y.; Calgan, H. A novel five-term 3D chaotic system with cubic nonlinearity and its microcontroller-based secure communication implementation. AEU-Int. J. Electron. Commun. 2023, 160, 154497. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Ouyang, A.; Yu, F.; Liu, H. A time-varying fuzzy parameter zeroing neural network for the synchronization of chaotic systems. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 364–376. [Google Scholar] [CrossRef]
- Yao, W.; Wang, C.; Sun, Y.; Gong, S.; Lin, H. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef]
- Ma, M.L.; Xie, X.H.; Yang, Y.; Li, Z.J.; Sun, Y.C. Synchronization coexistence in a Rulkov neural network based on locally active discrete memristor. Chin. Phys. B 2023, 32, 058701. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Y.; Iu, H.H.C.; Wang, N.; Bao, H. Locally active memristor-based neuromorphic circuit: Firing pattern and hardware experiment. IEEE Trans. Circuits Syst. Regul. Pap. 2023, 70, 3276983. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Liu, P.; Wen, S.; Wang, Y. Memristor-based circuit design of PAD emotional space and its application in mood congruity. IEEE Internet Things J. 2023, 10, 16332–16342. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K.; Fotsin, H. Coexisting attractors, circuit implementation and synchronization control of a new chaotic system evolved from the simplest memristor chaotic circuit. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105341. [Google Scholar] [CrossRef]
- Yu, F.; Yuan, Y.; Wu, C.; Yao, W.; Xu, C.; Cai, S.; Wang, C. Modeling and hardware implementation of a class of Hamiltonian conservative chaotic systems with transient quasi-period and multistability. Nonlinear Dyn. 2024, 112, 2331–2347. [Google Scholar] [CrossRef]
- Murillo-Escobar, D.; Murillo-Escobar, M.Á.; Cruz-Hernández, C.; Arellano-Delgado, A.; López-Gutiérrez, R.M. Pseudorandom number generator based on novel 2D Hénon-Sine hyperchaotic map with microcontroller implementation. Nonlinear Dyn. 2023, 111, 6773–6789. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Jin, J.; Du, S. Design and FPGA implementation of a pseudo-random number generator based on a Hopfield neural network under electromagnetic radiation. Front. Phys. 2021, 9, 690651. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Ren, F.; Yang, Z. Design of a high throughput pseudorandom number generator based on discrete hyper-chaotic system. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 806–810. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Li, Y. Dynamic analysis and FPGA implementation of a new, simple 5D memristive hyperchaotic Sprott-C system. Mathematics 2023, 11, 701. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Kokate, P.P. Memristor-based chaotic circuits. IETE Tech. Rev. 2009, 26, 417–429. [Google Scholar] [CrossRef]
- Hu, X.; Liu, C.; Liu, L.; Yao, Y.; Zheng, G. Multi-scroll hidden attractors and multi-wing hidden attractors in a 5-dimensional memristive system. Chin. Phys. 2017, 26, 110502. [Google Scholar] [CrossRef]
- Wang, M.; Deng, Y.; Liao, X.; Li, Z.; Ma, M.; Zeng, Y. Dynamics and circuit implementation of a four-wing memristive chaotic system with attractor rotation. Int. J. -Non-Linear Mech. 2019, 111, 149–159. [Google Scholar] [CrossRef]
- Gu, J.; Li, C.; Chen, Y.; Iu, H.H.; Lei, T. A conditional symmetric memristive system with infinitely many chaotic attractors. IEEE Access 2020, 8, 12394–12401. [Google Scholar] [CrossRef]
- Wan, Q.; Zhou, Z.; Ji, W.; Wang, C.; Yu, F. Dynamic analysis and circuit realization of a novel no-equilibrium 5D memristive hyperchaotic system with hidden extreme multistability. Complexity 2020, 2020, 7106861. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Li, W.; He, S.; Li, C. Extremely rich dynamics in a memristor-based chaotic system. Eur. Phys. J. Plus 2020, 135, 579. [Google Scholar] [CrossRef]
- Qiu, J.; Ding, D.; Weng, Y.; Qian, X. A fractional-order memristive system with time-delay and no equilibrium points. In Proceedings of the 2018 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 20–22 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1025–1029. [Google Scholar]
- Qiu, L.; Zhang, J.; Dai, Y.; Ding, Z.; Li, S.; Wang, L. Characteristic analysis of a fractional-order memristive hyperchaotic system. In Proceedings of the 2023 International Conference on Neuromorphic Computing (ICNC), Wuhan, China, 15–17 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 189–194. [Google Scholar]
- Liu, T.; Yu, J.; Yan, H.; Mou, J. A fractional-order chaotic system with infinite attractor coexistence and its DSP implementation. IEEE Access 2020, 8, 199852–199863. [Google Scholar] [CrossRef]
- Higazy, M.; Hamed, Y.S. Dynamics, circuit implementation and control of new caputo fractional order chaotic 5-dimensions hyperjerk model. Alex. Eng. J. 2021, 60, 4177–4190. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Li, Y. Dynamic analysis and field-programmable gate array implementation of a 5D fractional-order memristive hyperchaotic system with multiple coexisting attractors. Fractal Fract. 2024, 8, 271. [Google Scholar] [CrossRef]
- Cui, L.; Lu, M.; Ou, Q.; Duan, H.; Luo, W. Analysis and circuit implementation of fractional order multi-wing hidden attractors. Chaos Solitons Fractals 2020, 138, 109894. [Google Scholar] [CrossRef]
- Sahoo, S.; Roy, B.K. A new multi-wing chaotic attractor with unusual variation in the number of wings. Chaos Solitons Fractals 2022, 164, 112598. [Google Scholar] [CrossRef]
- Sahoo, S.; Roy, B.K. Design of multi-wing chaotic systems with higher largest Lyapunov exponent. Chaos Solitons Fractals 2022, 157, 111926. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, L.; Yu, X.; Kuznetsov, N.V.; Lai, Q. Generating multi-wing hidden hyperchaotic attractors with a single stable equilibrium. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 2374–2378. [Google Scholar] [CrossRef]
- Tang, Z.; Yu, S. Design and realization of digital image encryption and decryption based on multi-wing butterfly chaotic attractors. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1143–1147. [Google Scholar]
- Grassi, G.; Khennaoui, A.A.; Ouannas, A.; Pham, V.T. Three-dimensional chaotic fractional maps without fixed points: Dynamics, coexisting hidden attractors and hardware implementation. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA), Ajman, United Arab Emirates, 14–16 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Yu, H.; Dong, E.; Du, S.; Jia, C. Transient chaos analysis of a modified Sprott-C system with hidden attractor and multistability. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 808–813. [Google Scholar]
- Wen, J.; Feng, Y.; Tao, X.; Cao, Y. Dynamical analysis of a new chaotic system: Hidden attractor, coexisting-attractors, offset boosting, and DSP realization. IEEE Access 2021, 9, 167920–167927. [Google Scholar] [CrossRef]
- Chen, S.; Ding, D.; Yang, Z. Multistability and hidden attractors in a fractional-order memristive Tabu learning neuron model and its medical image encryption. In Proceedings of the 2023 IEEE International Conference on Memristive Computing and Applications (ICMCA), Jinan, China, 8–10 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Lin, H.; Wang, C.; Sun, Y. A universal variable extension method for designing multiscroll/wing chaotic systems. IEEE Trans. Ind. Electron. 2024, 71, 7806–7818. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K. Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 70, 1324–1336. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Bao, H.; Chen, M.; Bao, B. Generating multi-scroll Chua’s attractors via simplified piecewise-linear Chua’s diode. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 4767–4779. [Google Scholar] [CrossRef]
- Yu, F.; Chen, H.; Kong, X.; Yu, Q.; Cai, S.; Huang, Y.; Du, S. Dynamic analysis and application in medical digital image watermarking of a new multi-scroll neural network with quartic nonlinear memristor. Eur. Phys. J. Plus 2022, 137, 434. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Li, L.; Gu, B.; Cui, Y.; Wang, J.; Song, J. Design of hyperchaotic system based on multi-scroll and its encryption algorithm in color image. Integration 2023, 88, 203–221. [Google Scholar] [CrossRef]
- Zhang, J.; Lv, Y.; Tao, J.; Huang, F.; Zhang, J. A robust real-time anchor-free traffic sign detector with one-level feature. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 1437–1451. [Google Scholar] [CrossRef]
- Deng, Z.; Zhou, B.; He, P.; Huang, J.; Alfarraj, O.; Tolba, A. A position-aware transformer for image captioning. Comput. Mater. Contin. 2021, 70, 2005–2021. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; He, S.; Sharma, P.K.; Yu, X.; Alfarraj, O.; Tolba, A. Lightweight single image super-resolution convolution neural network in portable device. KSII Trans. Internet Inf. Syst. 2021, 15, 4065–4083. [Google Scholar]
- Zhang, J.; He, Y.; Chen, W.; Kuang, L.D.; Zheng, B. CorrFormer: Context-aware tracking with cross-correlation and transformer. Comput. Electr. Eng. 2024, 114, 109075. [Google Scholar] [CrossRef]
- Gui, Y.; Zeng, G. Joint learning of visual and spatial features for edit propagation from a single image. Vis. Comput. 2020, 36, 469–482. [Google Scholar] [CrossRef]
- Liu, H.; Teng, L.; Zhang, Y.; Si, R.; Liu, P. Mutil-medical image encryption by a new spatiotemporal chaos model and DNA new computing for information security. Expert Syst. Appl. 2024, 235, 121090. [Google Scholar] [CrossRef]
- El-Shafai, W.; Khallaf, F.; El-Rabaie, E.S.M.; El-Samie, F.E.A. Proposed 3D chaos-based medical image cryptosystem for secure cloud-IoMT eHealth communication services. J. Ambient. Intell. Humaniz. Comput. 2024, 15, 1–28. [Google Scholar] [CrossRef]
- Pankaj, S.; Dua, M. Chaos based medical image encryption techniques: A comprehensive review and analysis. Inf. Secur. J. Glob. Perspect. 2024, 33, 332–358. [Google Scholar] [CrossRef]
- Jamal, S.S.; Hazzazi, M.M.; Khan, M.F.; Bassfar, Z.; Aljaedi, A.; ul Islam, Z. Region of interest-based medical image encryption technique based on chaotic S-boxes. Expert Syst. Appl. 2024, 238, 122030. [Google Scholar] [CrossRef]
- Ye, G.; Wong, K.W. An efficient chaotic image encryption algorithm based on a generalized Arnold map. Nonlinear Dyn. 2012, 69, 2079–2087. [Google Scholar] [CrossRef]
- Mirzaei, O.; Yaghoobi, M.; Irani, H. A new image encryption method: Parallel sub-image encryption with hyper chaos. Nonlinear Dyn. 2012, 67, 557–566. [Google Scholar] [CrossRef]
- Yavuz, E.; Yazıcı, R.; Kasapbaşı, M.C.; Yamaç, E. A chaos-based image encryption algorithm with simple logical functions. Comput. Electr. Eng. 2016, 54, 471–483. [Google Scholar] [CrossRef]
- Natiq, H.; Al-Saidi, N.M.G.; Said, M.R.M.; Kilicman, A. A new hyperchaotic map and its application for image encryption. Eur. Phys. J. Plus 2018, 133, 6. [Google Scholar] [CrossRef]
- Saljoughi, S.; Ahmad; Mirvaziri, H. A new method for image encryption by 3D chaotic map. Pattern Anal. Appl. 2019, 22, 243–257. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, D.; Nkapkop, J.D.D.; Njitacke, Z.T.; Ahmad, M.; Zhu, L.; Tsafack, N. A memristive autapse-synapse neural network: Application to image encryption. Phys. Scr. 2023, 98, 035222. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).