Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations
Abstract
1. Introduction
2. The Existence of the Optimal Control for the Semilinear Problem
3. Optimal Control Problem for the Linear Equation
4. Optimal Control Problem for the Nonlinear Equation
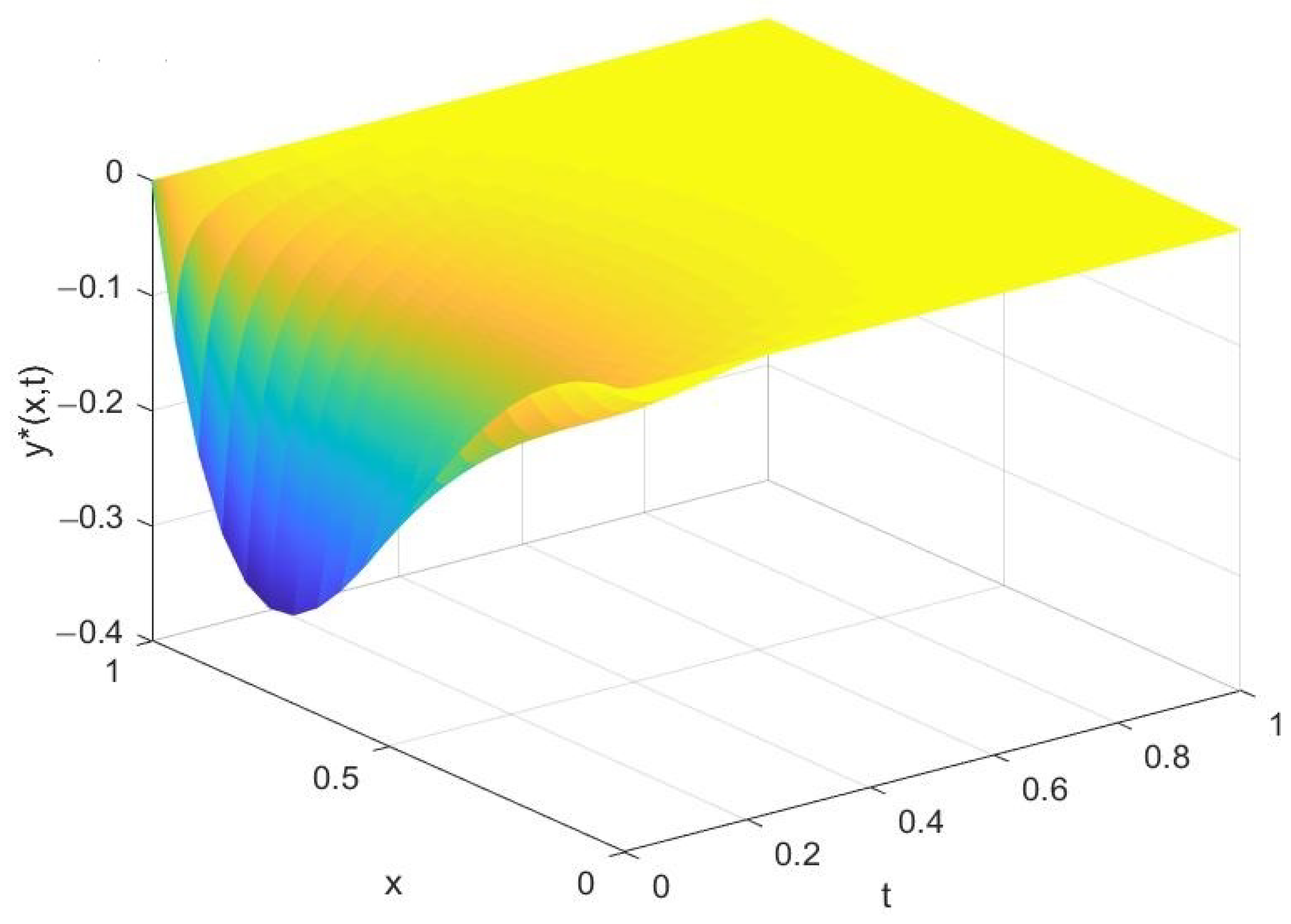
5. A Numerical Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baranovskii, E.S. Feedback optimal control problem for a network model of viscous fluid flows. Math. Notes 2022, 112, 26–39. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Optimal control for steady flows of the Jeffreys fluids with slip boundary condition. J. Appl. Ind. Math. 2014, 8, 168–176. [Google Scholar] [CrossRef]
- Hu, W.; Lai, M.J.; Lee, J. Optimal control for suppression of singularity in chemotaxis via flow advection. Appl. Math. Optim. 2024, 89, 57. [Google Scholar] [CrossRef]
- Casas, E.; Kunisch, K. Infinite horizon optimal control problems for a class of semilinear parabolic equations. SIAM J. Control Optim. 2022, 60, 2070–2094. [Google Scholar] [CrossRef]
- Casas, E.; Yong, J. Optimal control of a parabolic equation with memory. ESAIM COCV 2023, 29, 23. [Google Scholar] [CrossRef]
- Tröltzsch, F. Optimal Control of Partial Differential Equations: Theory, Methods, and Applications; American Mathematical Society: Providence, RI, USA, 2010; Volume 112. [Google Scholar]
- Lions, J.L. Optimal Control of Systems Governed by Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Cannarsa, P.; Martinez, P.; Vancostenoble, J. Null controllability of degenerate heat equations. Adv. Differ. Equ. 2005, 10, 153–190. [Google Scholar] [CrossRef]
- Jiang, L.S.; Tao, Y.S. Identifying the volatility of underlying assets from option prices. Inverse Problems 2001, 17, 137–155. [Google Scholar]
- North, G.R.; Howard, D.; Pollard, D.; Wielicki, B. Variational formulation of Budyko-Sellers climate models. J. Atmos. Sci. 1979, 36, 255–259. [Google Scholar] [CrossRef][Green Version]
- Deng, Z.; Yang, L. An inverse problem of identifying the radiative coefficient in a degenerate parabolic equation. Chin. Ann. Math. Ser. B 2014, 35, 355–382. [Google Scholar] [CrossRef]
- Lenhart, S.M.; Yong, J. Optimal control for degenerate parabolic equations with logistic growth. Nonlinear Anal. 1995, 25, 681–698. [Google Scholar] [CrossRef]
- Marinoschi, G.; Mininni, R.M.; Romanelli, S. An optimal control problem in coefficients for a strongly degenerate parabolic equation with interior degeneracy. J. Optim. Theory Appl. 2017, 173, 56–77. [Google Scholar] [CrossRef]
- Cannarsa, P.; Martinez, P.; Vancostenoble, J. Carleman estimates for a class of degenerate parabolic operators. SIAM J. Control Optim. 2008, 47, 1–19. [Google Scholar] [CrossRef]
- Du, R. Null controllability for a class of degenerate parabolic equations with the gradient terms. J. Evol. Equ. 2019, 19, 585–613. [Google Scholar] [CrossRef]
- Wang, C. Approximate controllability of a class of semilinear systems with boundary degeneracy. J. Evol. Equ. 2010, 10, 163–193. [Google Scholar] [CrossRef]
- Wang, C.; Du, R. Approximate controllability of a class of semilinear degenerate systems with convection term. J. Differ. Equ. 2013, 254, 3665–3689. [Google Scholar] [CrossRef]
- Wang, C.; Du, R. Carleman estimates and null controllability for a class of degenerate parabolic equations with convection terms. SIAM J. Control Optim. 2014, 52, 1457–1480. [Google Scholar] [CrossRef]
- Yin, J.; Wang, C. Evolutionary weighted p-Laplacian with boundary degeneracy. J. Differ. Equ. 2007, 237, 421–445. [Google Scholar] [CrossRef]
- Casas, E.; Fernández, L.A. Distributed Control of Systems Governed by a General Class of Quasinlinear Elliptic Equations. J. Differ. Equ. 1993, 104, 20–47. [Google Scholar] [CrossRef]
- Stojanovic, S. Optimal damping control and nonlinear elliptic systems. SIAM J. Control Optim. 1991, 29, 594–608. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, Y.; Men, T.; Du, R.; Zhu, Y. Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations. Mathematics 2024, 12, 2181. https://doi.org/10.3390/math12142181
Na Y, Men T, Du R, Zhu Y. Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations. Mathematics. 2024; 12(14):2181. https://doi.org/10.3390/math12142181
Chicago/Turabian StyleNa, Yang, Tianjiao Men, Runmei Du, and Yingjie Zhu. 2024. "Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations" Mathematics 12, no. 14: 2181. https://doi.org/10.3390/math12142181
APA StyleNa, Y., Men, T., Du, R., & Zhu, Y. (2024). Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations. Mathematics, 12(14), 2181. https://doi.org/10.3390/math12142181




